H3 and H4 Histone Tails Play a Central Role in the Interactions of Recombinant NCPs

Abstract

Using small-angle x-ray scattering, we probe the effect of histone tails on both internucleosomal interactions and nucleosome conformation. To get insight into the specific role of H3 and H4 histone tails, perfectly monodisperse recombinant nucleosome core particles were reconstituted, either intact or deprived of both H3 and H4 histone tails (gH3gH4). The main result is that H3 and H4 histone tails are necessary to induce attractive interactions between NCPs. A pair potential model was used to describe interactions between NCPs. At all salt concentrations, interactions between gH3gH4 NCPs are best described by repulsive interactions exclusively. For intact NCPs, an additional attractive term, with a 5–10 kT magnitude and 20 Å range, is required to account for interparticle interactions above 50 mM monovalent salt. Regarding conformation, intact NCPs in solution are similar to NCPs in 3D crystals. gH3gH4 NCPs instead give rise to slightly different small-angle x-ray scattering curves that can be understood as a more opened conformation of the particle, where DNA ends are slightly detached from the core.

INTRODUCTION

A left-handed helix of 146 DNA basepairs wraps around a histone octamer to form the nucleosome core particle. The histone octamer assembles four different histones each in two copies, forming an H3-H4 heterotetramer and two H2A-H2B dimers. These core histones contain folded globular domains that are mainly responsible for the structural organization of the nucleosome and unstructured amino-acids portions, the N- and C-terminal tails that represent ∼30% of the histone total mass (1). These tails are highly positively charged, with a ratio of basic to acidic amino acids higher than in the global histone sequence. NCPs are not static objects, fixed in a given conformation. An NCPs breathing mechanism has been proposed recently by several groups (2–4) based on FRET and FCS experiments. A spontaneous wrapping-unwrapping mechanism of nucleosomal DNA would occur and makes it accessible for interactions with proteins. The histone tails are also mobile (5,6) and can extend beyond the particle core (7,8). The N-terminal tails are of particular interest since they can be the target of a variety of posttranslational modifications and to a certain extent, these tails may control the dynamics and accessibility of nucleosomal DNA to proteins (9,10). In nucleosomal arrays, the presence of the tails is also required to keep the DNA wrapped around the histone core at the nucleosome periphery under low salt conditions (11), and to obtain the salt-induced folding and aggregation of the nucleosomal arrays. Moreover, selective trypsinization of only the H3/H4 or the H2A/H2B N-tails from these nucleosomal arrays reveal that the two groups of tails have specific roles in the condensation mechanisms; the H3/H4 N-tails mediate the formation of the moderately folded state while contributions from both H3/H4 and H2A/H2B tails are required to mediate formation of the extensively folded state and oligomers (review in (12)). H3 and H4 N-tails also interact with sites on other nucleosomes during chromatin condensation, leading to the formation of individual 30 nm fibers (intrachain process) (13) and multimolecular aggregates (oligomers of arrays) (14). It was recently demonstrated that the H3 tail domain is relocated from mainly intranucleosomal interaction within the extended nucleosomal array at low salt, to internucleosomal interactions upon the formation of compacted structures (15). Furthermore, it was shown recently that all different histone tails H2A, H2B, H3, and H4 are involved in the salt-dependent oligomerization of nucleosome arrays and that they function independently and additionally (14).

Because of their amino-acid sequence, the histone tails, with their rich content in basic Lys and Arg residues, are likely to interact with DNA phosphates. They also interact with protein sites on neighboring nucleosomes in NCPs crystals and chromatin and with other proteins (16,17). It has been assumed that, although intrinsically disordered, they may adopt a well-defined conformation when they interact with a target molecule (18). An interesting possibility is that their amino-acid composition determines which type of secondary structure is formed when they bind to a target. In this respect, acetylation and methylation that affect the charge density, size, and hydrophobicity of the Lys side chains may alter not only the charge but also the general properties of the tails, and make possible a coupled folding and target binding (18).

Histones are hyperacetylated on lysines at actively transcribed genes. Since acetylation neutralizes the positive charge of the lysine, acetylation was thought to reduce interactions with DNA phosphates, making the DNA more accessible for active processes such as transcription. More recently, the histone code hypothesis, proposing that covalent posttranslational modifications of histone tails are interpreted by the cell to yield a rich combinatorial complexity of the acetylation code, has been very popular. This hypothesis was tested recently on the budding yeast (19), using a series of strains in which one, two, or three lysines on the N-terminal tail of histone H4 have been substituted to arginine, thus preventing acetylation while retaining the positive charge. These experiments reveal that at least two mechanisms exist by which histone modifications can alter transcriptional states: a specific mechanism on Lys-16, and a nonspecific cumulative mechanism on other sites. As pointed out by Henikoff (20), the general interchangeability of sites of histone H4 acetylation provides a new support for the charge neutralization model, and should renew attention to charge-dependent interactions. Another argument in favor of these charge effects is the observation that upon transcriptional activation, nucleosomes are first hyperacetylated and then ejected from the DNA at the yeast PHO5 promoter (21,22). Although the process is not understood yet and may involve histone chaperones (23), it would occur for most, if not all RNA polymerase II promoters in yeast and in mammalian cells.

There is no doubt that modifications of the histone tails have both either intra- and internucleosome effects that have consequences on the activity of the genome. These are coupled and difficult to evaluate separately. Pulling single chromatin fibers and designing force-extension curves, Cui and Bustamante (24) have observed internucleosomal global attractive interactions within fibers at relatively high ionic strength (40–150 mM). A significant fiber elongation was observed for an applied force of ∼5–6 pN. Considering those findings and the fiber length, a binding energy was found to amount to 3.4 kT per nucleosome. Widlund et al. (25) compared interactions inside chromatin fibers for native intact and trypsinized histones, using competitive reconstitution assays with H1-depleted chromatin. They found out a 1.7 kT histone tail's contribution to internucleosome interaction energy. Linker DNA and/or linker histones are present in such experiments and interfere in the internucleosome attractive energy. Moreover, those energy assessments are global and therefore include both attractive and repulsive terms. We propose here to use a simplified model, the nucleosome core particle (where linker DNA and histones are disregarded), to quantitatively evaluate internucleosome interactions only. The contribution from either repulsive or attractive terms will be precisely differentiated here and evaluated separately. We have previously shown with isolated particles that histone tails are necessary for building attractive interactions between nucleosome core particles. Mangenot et al. (8,26) have shown that attractive interactions between chicken erythrocytes NCPs occur simultaneously with histone tails extension above 50 mM monovalent salt. A tail-bridging hypothesis for attractive interaction has been proposed (26). Bertin et al. (7) have tested and confirmed this hypothesis using trypsinized calf thymus nucleosome core particles. Removal of histone tails actually cuts down the attractive interaction term.

The purpose of this study is to get more insight in the specific role of H3 and H4 histone tails in these internucleosomal attractive interactions. Intact NCPs and NCPs deprived of both H3 and H4 histone tails (designed as gH3gH4, globular histones being distinguished by the letter g) were reconstituted from recombinant DNA and histones. Using perfectly monodisperse particles of defined size and charge, particles interactions and conformation could be considered more accurately. Small-angle x-ray scattering (SAXS) was used to evaluate conformation and interactions simultaneously. An interaction pair potential model was also used to assess the second virial coefficient and to describe interactions between NCPs.

MATERIALS AND METHODS

Recombinant reconstituted nucleosome core particle preparation

Nucleosome core particles were prepared as described by Dyer et al. (27).

146 5S-DNA basepairs purification

HB101 Escherichia coli cells were transformed by pTJR2 plasmids (28) and grown in “Terrific Broth”. Amplified plasmids containing repeats of 146 basepairs from a segment of the 5S RNA gene of Lytechinus variegatus (28) were purified by an alkaline lysis process. Plasmids were digested with ECO 32I (Fermentas, Euromedex, Mundolsheim, France) restriction enzyme, an ECO RV analog. Linearized pUC9 plasmid was separated from the fragments of the 146 basepairs by precipitation with 6% PEG 6000. The fragments of the 146 5S-DNA basepairs were eventually purified using an anion exchange chromatography column (DEAE-5PW, Tosoh Bioscience GmbH, Stuttgart, Germany).

Intact and globular histone purification

BL21DE3-pLysS E. coli cells were transformed with pET plasmids corresponding to either intact or globular histones (29). Histones were expressed during 2 h after IPTG induction. After growth and harvest, cells were subjected to a flash freeze/thaw cycle. Cells were homogenized using a blender. Inclusion bodies were then isolated. Histones purification was carried on in two steps in buffers containing 7 M urea, 20 mM NaAC, pH 5.2, 5 mM β-mercaptoethanol, and NaCl. They were first purified by size-exclusion chromatography using a Sephacryl S-200 1.8 L column (GE Healthcare Europe GmbH, Saclay, France) and purified again by ion-exchange chromatography on a TSK SP-5PW TosoHaas gel. Purified histones were finally dialyzed against 5 mM β-mercaptoethanol in water, lyophilized, and aliquoted. After histone production and purification, the histone purity was checked by electrophoresis on 15% SDS-PAGE polyacrylamide gels. Mass spectrometry experiments were also performed on individual histones to confirm their purity. Measured histone masses are in excellent agreement with theoretical masses calculated from the web site http://www.expasy.org/tools/peptide-mass.html, using the protein sequences (see Table 1). Table 2 gives, for each intact or globular histone, the number of positive and negative charges.

TABLE 1.

Xenopus laevis histone molecular mass

Histone	Amino-acid sequence	Measured mass*	Calculated mass†
H2A	1–128	13949.0	13950.2
H2B	1–122	13493.7	13493.7
H3	1–135	15272.3	15270.9
H4	1–102	11236.5	11236.2
gH3	27–135	12656.2	12653.9
gH4	20–102	9522.9	9521.2

^*Measured masses were determined with a MALDI-TOF mass spectrometry apparatus.

^†Calculated masses were obtained from the web site: http://www.expasy.org/tools/peptide-mass.html after entering the histone sequences.

TABLE 2.

Amount of charges carried by recombinant full-length or tailless Xenopus laevis histones

Histone	Basic a.a.	Acid a.a.	Global charge	Positive charges in tails	Negative charges in tails
H2A (128 a.a.)	24	9	+15	N-ter: 4	C-ter: 1
				C-ter: 3
H2B (122 a.a.)	28	9	+19	N-ter: 8	N-ter: 1
H3 (135 a.a.)	30	11	+19	N-ter: 9	0
H4 (102 a.a.)	25	7	+18	N-ter: 7	0
gH3 (a.a. 27–135)	21	11	+10
gH4 (a.a. 20–102)	18	7	+11

Histone octamer assembly and purification

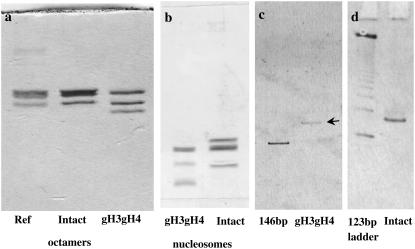
Lyophilized histones were dissolved and incubated in denaturing buffer (7 M guanidinium hydrochloride, 10 mM DTT, 20 mM Tris-HCl, pH 8) for 1 h at room temperature. Chosen combinations of intact and globular histones were mixed in a stoichiometric ratio for a final histone concentration of 1 mg mL⁻¹. The mixture was transferred to a dialysis tubing (MW cutoff: 6000–8000; Spectra/Por, Spectrum Europe BV, Breda, The Netherlands) and dialyzed against a renaturation buffer (2 M NaCl, 5 mM DTT, 1 mM EDTA, 10 mM Tris-HCl, pH 8) at 4°C. Compared to the protocol described by Dyer et al. (27), DTT was chosen instead of β-mercaptoethanol to improve octamer reconstitution. After two changes of renaturation buffer, the histone solution was concentrated to 10 mg mL⁻¹ by ultrafiltration using a Vivascience Vivaspin concentrator (10,000 MW cutoff; Vivascience, Sartorius, Palaiseau, France). Concentrated histone octamers were purified by size exclusion chromatography using a Superdex S-200HR Hiload (GE Healthcare) gel filtration column equilibrated in renaturation buffer. Fractions containing the four histones in equimolar amounts were combined and concentrated up to 10 mg mL⁻¹. After histone octamer reconstitution, protein composition was checked on SDS-PAGE polyacrylamide electrophoresis gels (Fig. 1 a). Two octamer types were reconstituted: intact and gH3gH4 (without H3 and H4 tails).

FIGURE 1.

Nucleosome core particles characterization. (a, b) Histone content in reconstituted octamers (a) and nucleosomes (b) analyzed by electrophoresis on 15% SDS-PAGE polyacrylamide gels and staining by Coomassie blue. The ref corresponds to commercial calf thymus histones. Octamers and nucleosomes were dissociated at high salt (2 M), so proteins could be analyzed on gels. Proteins are present in stoichiometric amounts and no contaminant can be seen. (c, d) Nondenaturing 5% polyacrylamide gels of purified NCPs. The absence of aggregates or free DNA is checked for intact (d) and gH3gH4 (c) NCPs. Comparisons are made with 146 bp (in c) and 123 bp ladder DNA (in d).

Nucleosome core particle reconstitution and purification

Pure histone octamer and 146 DNA basepairs were mixed in a DNA/histone octamer ratio of 1:1.2 in a high salt containing buffer (2 M KCl, 10 mM DTT, 0.5 mM EDTA, 10 mM Tris-Cl pH 8). The solution was dialyzed to a low salt buffer (0.25 M KCl, 5 mM DTT, 0.5 mM EDTA, 10 mM Tris-Cl pH 8) using a gradient at 4°C as described by Dyer et al. (27), further dialyzed another 4 h in this low salt buffer and equilibrated in TCS buffer (20 mM Tris-HCl, 1 mM EDTA, pH 7.6). To achieve homogeneous positioning of DNA around histones octamers (27), NCPs were heated to 37°C. Appropriate shift in DNA positioning was checked by nondenaturing electrophoresis on 5% polyacrylamide gels (not shown). Pure NCPs fractions were purified from free DNA, aggregates, and unshifted NCPs by preparative gel electrophoresis on a 6%, 7.5 cm high nondenaturing polyacrylamide gel casted in a Bio-Rad Prep-cell apparatus run at a constant power of 10 W (Bio-Rad Laboratories, Marnes-La-Coquette, France). Diluted pure NCPs fractions were immediately concentrated by ultrafiltration to prevent any nucleosome dissociation. The absence of any free DNA or aggregates was checked by 5% acrylamide nondenaturing gels (Fig. 1, c and d). Histone purity and stoichiometric was assessed by electrophoresis on 15% SDS-PAGE polyacrylamide gels (Fig. 1 b).

Samples preparation

Intact and gH3gH4 NCPs were dialyzed against 10 mM Tris-HCl, pH 7.6 buffer containing 1 mM EDTA, 0.1 mM PMSF, and 2 mM DTT. NCPs concentration was adjusted to 8 mg mL⁻¹ and assessed by UV-absorbance measurements. Various NaCl buffer solutions were prepared and added to dialyzed NCP solutions to adjust final monovalent salt concentrations Cs to 10, 25, 50, 100, and 150 mM. Both Tris⁺ and Na⁺ ions are included in the total monovalent salt concentration Cs. The concentration of added NaCl solution never exceeded 300 mM to prevent any NCPs dissociation. For each salt concentration, NCPs were diluted to 4, 2, and 1 mg mL⁻¹. Sample volumes were adjusted to 50 μL.

Small-angle x-ray scattering experiments (SAXS)

The small-angle x-ray scattering experiments (SAXS) were carried out on a laboratory equipment. The instrument used is a commercially available small-angle x-ray camera (NanoStar, Bruker-AXS, Karlsruhe, Germany) adapted to a rotating anode x-ray source (CuKα, λ = 1.54 Å). The experimental setup has been optimized by Jan Skov Pedersen (University of Aarhus, Denmark) to obtain higher flux (30). The instrument has an integrated vacuum to reduce background. The scattering vector range was 0.008 Å⁻¹ < q < 0.35 Å⁻¹, where q = 4π sinθ/λ, with 2θ being the scattering angle. The sample-to-detector distance was 662 mm. Samples were enclosed into 1.7–1.8 mm diameter reusable quartz capillaries directly inserted into the vacuum of the camera. Measurements were performed at 5°C. Both buffers and samples were exposed for 7200 s. Data were collected using a position-sensitive gas detector (HiSTAR, Bruker-AXS, Madison, WI). The SAXS data were azimuthally averaged, corrected for variations in detector efficiency and for spatial distortions. Buffer measurements were used as background and subtracted from the recorded integrated curves. Finally, the data were converted to absolute scale using the scattering from pure water as primary standard.

SAXS data analysis

Particles size and conformation

Considering noninteracting particles, the scattering intensity at small q-values can be written according to the Guinier approximation of

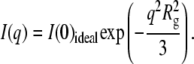(1)

The intensity at null scattering angle (q = 0) is expressed by

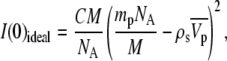(2)

where C is the sample concentration (w/v), M is the molecular weight of NCPs, N_A is the Avogadro number, m_p is the number of electrons in the dry protein, ρ_s is the electronic density of the buffer, and 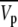is the partial specific volume of the particle.

R_g is the radius of gyration of the particle, which can be expressed as

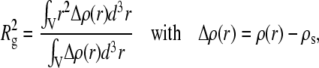(3)

where ρ(r) is the particle electronic density.

For a nearly spherical particle, this approximation can be used when qR_g < 1.3. Experimentally, R_g and I(0) can be obtained by fitting ln(I(q)) as a function of q². Additional information about the particle conformation can be obtained from the distance distribution function of the particle, which is the Fourier transform of the scattering intensity I(q):

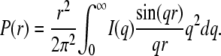(4)

P(r) represents all distances that can be found within the particle. P(r) goes to zero for distances larger than the maximal dimension D_max of the particle. P(r) was evaluated by an indirect procedure using the program GNOM (31). The radius of gyration can also be assessed from the distance distribution function P(r):

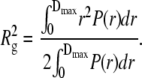(5)

We prefer this method for R_g evaluation since the Eq. 5, making use of the whole scattering curve, is much less sensitive to residual interparticle interactions.

Scattering intensities I(q) can be also calculated from PDB crystallographic structural files using the program CRYSOL (32). Some of the structures considered in this work have been modified with WebLab Viewer Lite (MSI, Accelrys, San Diego, CA) that creates new PDB files. Calculated scattering curves can be fitted and compared with experimental data.

Interactions between particles and second virial coefficient

For interacting monodisperse spherical particles, the scattering intensity can be written as

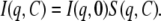(6)

I(q,0) is the scattering intensity for ideal solutions when all interactions between particles are neglected and it is also called the form factor. S(q,C) is the structure factor and characterizes interactions between particles. S(q,C) is the Fourier transform of the autocorrelation function of the pair-distribution function g(r) (Eq. 7). It describes the probability for a given particle to be located at a distance r from another particle located at the origin:

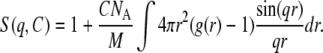(7)

In the case of nonspherical particles, Eq. 6 is best rewritten as (33):

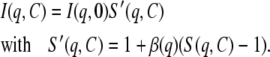Here, β(q) varies as a function of q between zero and one. Kotlarchyk and Chen (33) have evaluated β(q) for prolate and oblate ellipsoids. Disk-shaped particles like NCPs can be considered as oblate particles with an axial ratio a/b of 2. In this case, Kotlarchyk and Chen have shown that β(q) = 1 in the q-range q ≤ 2/a. For NCP, a = 55 Å so q = 2/a = 0.036 Å⁻¹. Therefore S'(q,C) = S(q,C) in the range q ≤ 0.036 Å⁻¹. At larger q-values, we experimentally observe that the effect of interactions disappears for dilute NCP solutions, (i.e., with C ≤ 5 mg.mL⁻¹), thus S'(q,C) = S(q,C) = 1. We can therefore conclude that Eq. 6 is valid for our system at all q-values under the very dilute conditions used in this work.

When interactions are weak and solutions are dilute, the structure factor is related to the second virial coefficient that describes interactions between pair of particles. The structure factor at null scattering angle can, in this case, be expressed as a function of particle concentration,

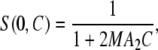(8)

with M the molecular mass of the particle and A₂ the second virial coefficient. A₂ is associated to the pair interaction potential V(r) by the relationship

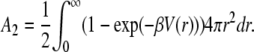(9)

For positive A₂ values, interactions are repulsive while for negative values interactions are globally attractive. Thus, the sign of A₂ discriminates between repulsive and attractive interactions.

Form and structure factors determination

The experimental form factor I_exp(q,0), free from interparticle interactions, was obtained by collecting the scattering pattern at a very low concentration (i.e., 1 mg mL⁻¹). To improve the statistic in the high q-region, this form factor was spliced with the data obtained at higher concentration (i.e., 4 mg mL⁻¹) in the q-range q ≥ 0.03 Å⁻¹. The program GNOM was then used from the experimental spliced curve to obtain a fitted form factor I_f(q,0) deprived of statistical errors. Finally the structure factors S(q,C) were obtained by dividing the scattering total intensities I(q,C) by the form factor I_f(q,0).

Structure factors simulation using a pair potential model

Structure factors were also numerically assessed as explained by Bonneté et al. (34), Tardieu et al. (35), and Niebuhr and Koch (36), using an algorithm written by L. Belloni (37). A simulation model was used to compare experimental structure factors with numerically calculated ones. Experimental data below 0.013 Å⁻¹ were not exploitable and were disregarded. Experimental and numerical structure factors were compared for scattering angles ranging from 0.0142 Å⁻¹ to 0.0498 Å⁻¹. The iterative calculations are based on the Orstein-Zernike equation and the hypernetted chain integral that associate the pair distribution function g(r) to the total h(r) = g(r)⁻¹ and direct c(r) correlation functions:

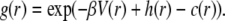(10)

NCPs were considered as spherical particles of 10 nm in diameter. The model used here for the potential is inspired from the DLVO theory. Two repulsive and one attractive term compose the pair potential we used. A repulsive hard core term describes the impossibility for particles of diameter σ to interpenetrate. Repulsive Coulombic long-range interactions and short-range interactions (van der Waals, hydrophobic, and hydrogen bridging forces) are represented by the sum of two Yukawa potentials: an attractive and a repulsive term. The final potential is written as

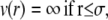(11)

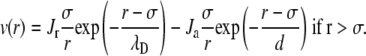(12)

The values J_r and J_a are given in kT energy units and σ was set constant at 100 Å in any conditions. In Eq. 12, the range of the repulsive contribution to the Yukawa potential is equal to the Debye screening length λ_D expressed in Å. The value λ_D depends on the solution ionic strength,

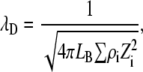(13)

where L_B is the Bjerrum length 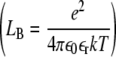, Z_i the charge of ion i, and ρ_i the ions density.

The strength of the repulsive Coulombic potential J_r is directly related to the particles effective charge Z_eff:

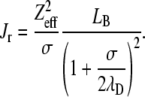(14)

In this expression, the effective charge is the one as calculated by Alexander et al. (38). The particles' effective charge is smaller than the actual structural charge. Alexander et al. (38) have renormalized the charge by solving the Poisson-Boltzmann equation numerically in a spherical Wigner-Seitz cell. For each salt concentration, the particles effective charge Z_eff was assessed from the structural charge using a program that is based on a Poisson-Boltzmann Wigner-Seitz cell calculation (39).

In the attractive part of the Yukawa expression (Eq. 12), both the strength J_a and the range d of the potential are parameters to be optimized by comparing to the measured data.

Second virial coefficient determination

Following Bonneté et al. (40), second virial coefficients can be obtained by two distinct means, depending on the interactions strength:

1. When interactions are attractive or slightly repulsive, scattering intensities at null scattering angles I(0,C) can be evaluated from Guinier approximation (Eq. 1). Guinier plots, displaying ln(I(q)) versus q², are actually linear in a large domain of scattering angles. A₂ is then deduced from the slope of the curve 1/I(0,C) as a function of the particle concentration C. This method is based on the expression .

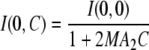2. Upon strong repulsion, Guinier approximation is no longer reliable for assessing interactions. The best agreements between experimental and calculated structure factors were used for determining values for S(0,C). Second virial coefficients are calculated from Eq. 8 and S(0,C) values.

From 10 to 50 mM salt, interactions were strong enough to proceed by Method 2 whereas the Guinier approximation (Method 1) was used for higher salt concentrations.

RESULTS

D_max and R_g evolution with salt concentration

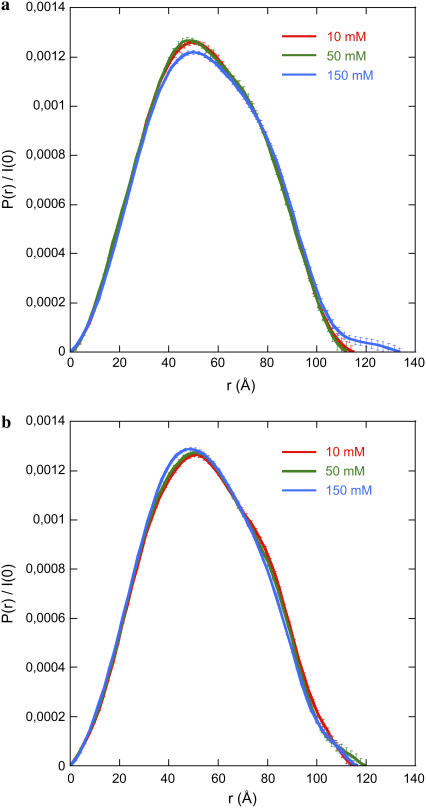
Scattering curves I(q,C)/C recorded at C = 1 mg mL⁻¹ for 0.0128 < q < 0.03Å⁻¹ and at C = 4 mg mL⁻¹ for q > 0.03 Å⁻¹ were merged to obtain a scattering curve free from interparticle interactions. The resulting curve was used to derive the distance distribution function P(r) from the program GNOM using a cutoff value q_min = 0.0128 Å⁻¹. Eliminating a few points in the low-q region did not modify the P(r) curves, indicating the absence of interaction effects. The results are shown in Fig. 2. For gH3gH4 NCPs that are deprived of both H3 and H4 tails, the P(r) functions superimpose for all salt concentrations (Fig. 2 b). On the other hand, for intact particles, P(r) is different at 10, 25, and 50 mM as compared to 100 mM and 150 mM. For the latter, the maximal particles extension D_max values are slightly higher (Fig. 2 a).

FIGURE 2.

Distance distribution functions P(r) calculated using GNOM from scattering curves recorded at 1 mg mL⁻¹ (q ≤ 0.03 Å⁻¹) and merged with data collected at 4 mg mL⁻¹ (q ≥ 0.03 Å⁻¹). P(r) was evaluated for intact (a) and gH3gH4 (b) NCPs. (Data at 25 and 100 mM monovalent salt have been omitted for clarity).

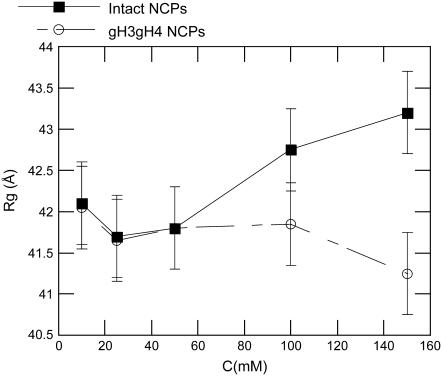
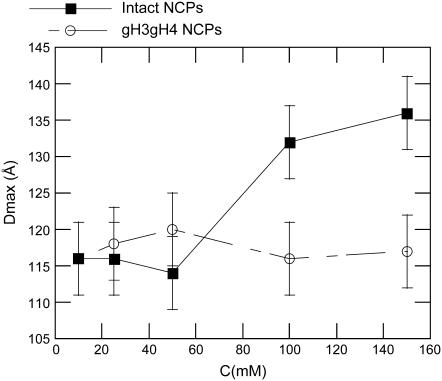
In Fig. 3, D_max is plotted as a function of the monovalent salt concentration. For gH3gH4 NCPs, D_max remains constant within error bars in the whole range of salt concentrations. Its value fluctuates at ∼115–120 Å. However, for intact particles, D_max increases from 116 to 136 ± 5Å with monovalent salt concentration. Its maximum value is reached above 100 mM. The D_max increase with salt is significant and is consistent with the D_max rise observed with native nucleosome core particles (7,8). The radius of gyration displays also global size modifications as a function of the monovalent salt concentration (Fig. 4). The radii of gyration were calculated from the P(r) functions (see Eq. 5). In parallel with the D_max increase, a radius of gyration increase for intact NCPs is visible at 150 mM salt concentration. However, at 150 mM, such an increase is not noticed for gH3gH4 NCPs.

FIGURE 3.

Maximal particle extension D_max as a function of monovalent salt concentration for intact (▪) and gH3gH4 (○) NCPs.

FIGURE 4.

Radius of gyration R_g as a function of monovalent salt concentration for intact (▪) and gH3gH4 (○) NCPs.

Form factors analysis

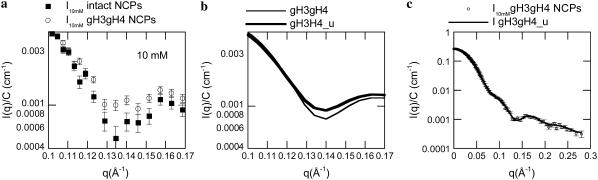
Experimental form factors from intact and gH3gH4 NCPs were compared at all salt concentrations. Discrepancies are present around the second minimum at q = 0.135 Å⁻¹.This is displayed in Fig. 6 a at 10 mM. More specifically, the second minima at 0.135 Å⁻¹ for the gH3gH4 NCPs is not as deep as the one obtained from the intact NCPs. This effect is consistently observed at all salt concentrations. Despite the large error bars it cannot be an artifact. Scattering intensity resulting from a hollow flat cylinder comparable to the NCPs peripheral DNA corona would feature such a marked second minimum. A disruption in the DNA superhelix regularity was therefore suspected to be responsible for the differences observed.

FIGURE 6.

(a) Comparison of experimental scattering intensities of intact (▪) and gH3gH4 (○) NCPs at 10 mM monovalent salt concentration. (b) Comparison of calculated scattering intensities resulting from gH3gH4 (thin line) and gH3gH4_u (thick line) structures. (c) Experimental scattering intensity for gH3gH4 NCPs (○) is fitted to gH3gH4_u (solid line) calculated scattering intensity.

To simulate the experimental form factors, we constructed structural models from the last published PDB crystallographic structure file 1KX5 (41). As already reported in Mangenot et al. (8) and in Bertin et al. (7), in the case of native NCPs, two models were built to describe intact recombinant particles: one with the tails extended away from the particle, in the extended conformation, and the others with the tails close to the DNA surface, in the compact conformation. The I(q) curves were then calculated for ideal solutions of these two modeled conformations, using the program CRYSOL. As for native particles (7,8) a good fit between calculated and experimental curves was obtained at low (10 mM, 25 mM, and 50 mM) and high (100 mM and 150 mM) salt by using compact and extended conformations, respectively.

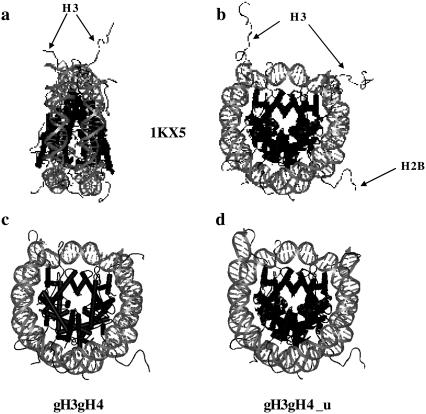
For gH3gH4 NCPs, two different structures were built, namely:

1. gH3gH4: H3 and H4 N-terminal tails were removed from the 1KX5 structure (Fig. 5 c).

2. gH3gH4_u: gH3gH4 with DNA ends opened from the particle core (Fig. 5 d).

FIGURE 5.

NCPs structures visualized using WebLab Viewer Lite. Histone and DNA structural modifications were performed with WebLab Viewer Lite as well. Histone tails are pointed and specified for clarity. (a, b) 1KX5 NCP crystallographic structure (41) from side and top views, respectively. (c, d) 1KX5 structure where H3 and H4 N-terminal tails were removed. (d) DNA ends were partially unwrapped from the nucleosome core, denoted gH3gH4_u.

In both cases, one H2B tail is rather extended while the other one is rather folded on the DNA. We have built other structures with both H2A and H2B tails folded or extended and checked that the three form factors corresponding to both H2B tails folded, both H2B tails extended and a single one folded and the other extended are indistinguishable. Consequently, only gH3gH4 and gH3gH4_u will be considered in the following.

In Fig. 6 b, the form factors calculated from gH3gH4 and gH3gH4_u structures using CRYSOL are compared in the range 0.1 ≤ q ≤ 0.17 Å⁻¹. When DNA entry and exit sides were slightly unwrapped from the nucleosome core, the second minimum is partially filled (Fig. 6 b). Fig. 6 c displays indeed a perfect agreement between the experimental form factor measured for gH3gH4 NCPs at 10 mM salt concentration and the calculated one corresponding to the gH3gH4_u structure. For all salt concentrations, the best fits are obtained with the model displaying slightly opened DNA ends. Consequently the discrepancies between curves from intact and gH3gH4 NCPs could result from a slight unwinding of DNA.

Interactions between nucleosome core particles

Pair potential interaction model

Effective charges, Z_eff, were evaluated as in Alexander et al. (38) as already described above. Results are displayed in Table 3 for both types of particles. Z_eff increases in absolute value with monovalent salt concentration. With increasing ionic forces, electrostatic interactions are screened and less counterions are condensed on particles. Consequently, effective charges increase with salt concentration. These values were inserted in Eqs. 12 and 14 for the description of the Coulombic repulsive interactions.

TABLE 3.

Effective charges of intact and gH3gH4 recombinant NCPs

Total monovalent salt concentration (mM)	Effective charge* for intact recombinant NCPs	Effective charge* for gH3gH4 recombinant NCPs
10	−69.9	−73.3
25	−80.15	−85.15
50	−91.55	−98.3
100	−104.1	−114.5
150	−111.55	−124.3

^*The calculation using a program written and provided by L. Belloni is based on a Poisson-Boltzmann Wigner-Seitz cell calculation (39). The effective charges displayed above are the effective charges as calculated by the method of Alexander et al. (38). NCPs were considered as spherical particles of 50 Å radius. Structural charges are −150 and −182 for recombinant intact and gH3gH4 NCPs, respectively. Structural charge is the net actual particle charge, considering the whole set of charges carried by histones and DNA.

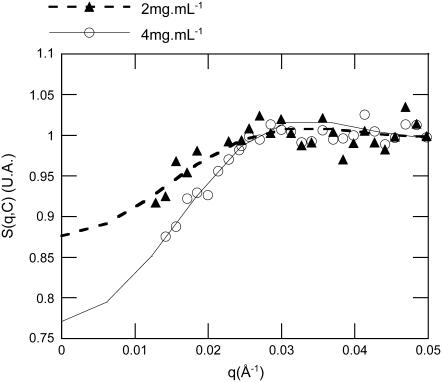
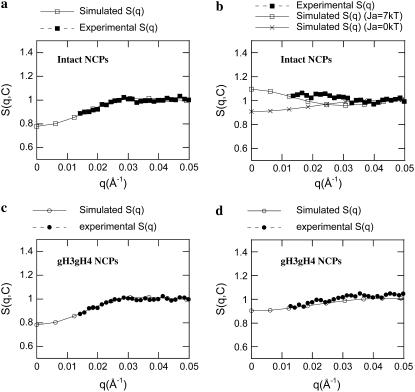
Fig. 7 displays a typical comparison between experimental and numerically calculated structure factors for gH3gH4 NCPs at 25 mM salt. With decreasing particle concentrations, structure factors values at null scattering angle increase, indicating that interactions are here repulsive. Experimental and simulated data are in good agreement at 2 and 4 mg mL⁻¹. For intact recombinant NCPs at low salt concentrations (10 and 25 mM), the best agreements between experimental and numerical data S(q,C) were obtained with no attractive terms involved (Fig. 8 a). Under those conditions, J_a, the potential strength of the attractive term (Eq. 12) was set to zero. At higher salt concentrations (50, 100, and 150 mM), experimental structure factors cannot be properly described any more without adding an attractive term to the pair interaction potential (J_a > 0 in Eq. 12). Obviously, the structure factor calculated using repulsive terms exclusively cannot describe the experimental curve (Fig. 8 b). In Eq. 12, both the potential depth J_a and its range d have been varied. Best agreements were obtained when the interaction range d was set as high as 20 Å and for J_a values at ∼5–10 kT. It is noteworthy that the best d value is in good agreement with the D_max increase due to the tail extension (7,8). Fig. 8 b presents the best agreement we could obtain between experimental and calculated structure factors at 150 mM salt. At this high salt concentration, the interactions for intact NCPs are better described with attractive potentials term included.

FIGURE 7.

Comparison between experimental and simulated structure factors for gH3gH4 recombinant NCPs, at 25 mM monovalent salt. Simulated structure factors are represented by continuous or dashed lines and symbols correspond to experimental data. For experimental curves, data were disregarded for q below 0.013Å⁻¹. NCPs concentrations of 4 mg mL⁻¹ (○) and 2 mg mL⁻¹ (▴) are displayed.

FIGURE 8.

Comparison between simulated and experimental structure factors S(q,C) for intact (a, b) and gH3gH4 (c, d) NCPs at low salt (25 mM, a, c) and high salt (150 mM, b, d) for C = 4 mg mL⁻¹.

For gH3gH4 NCPs, the best agreements between experimental and numerical structure factors were obtained when calculations were performed considering the repulsive potentials only. The attractive term in the Yukawa potential was disregarded for all salt concentrations (J_a = 0 kT). Consequently, no fitting parameter was introduced in the calculation since the repulsive term of the Yukawa potential is only dependent on the effective particle charges imposed by the Poisson-Boltzmann network calculation. The agreement between experimental and numerical structure factor at low salt concentration is very satisfactory (Fig. 8 c). At high salt concentration (150 mM, Fig. 8 d) the fit is not as outstanding but the addition of an attractive term would worsen the agreement between calculated and experimental curves.

Second virial coefficients

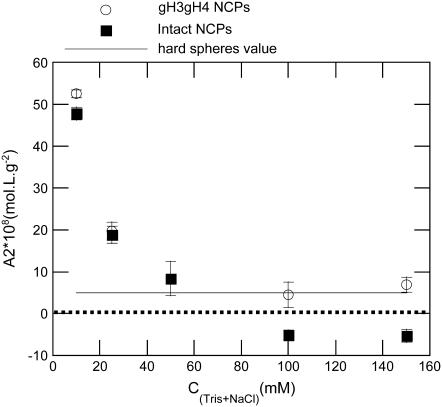
Second virial coefficients for intact and gH3gH4 NCPs are reported in Fig. 9. At low salt concentrations (10 and 25 mM monovalent salt), the A₂ values are quite similar for intact and gH3gH4 NCPs. At high salt concentrations, the second virial coefficient for intact particles turns negative. For intact NCPs at high salt concentration, interactions are therefore globally attractive. However, for gH3gH4 NCPs, A₂ values remain positive for all ionic strengths investigated and remain close to the hard-sphere value. The hard-sphere value for a particle of volume V_NCP can be expressed as 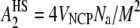and it is equal to 3.8 × 10⁻⁸ mol L g⁻² for a radius of gyration of 42 Å. Consequently, for NCPs deprived of the H3 and H4 N-terminal tails, interactions remain repulsive for all investigated ionic strengths.

FIGURE 9.

Second virial coefficient as a function of monovalent salt concentration. A₂ values are shown for intact (▪) and gH3gH4 (○) NCPs. Second virial coefficient for hard spheres is indicated with a thin line.

DISCUSSION

NCPs conformation

Intact recombinant NCPs

The results for intact recombinant NCPs are fully similar to those previously obtained on native NCPs (7,8). Both D_max and R_g increase significantly with monovalent salt concentration. At low salt concentration, the experimental curves are perfectly fitted with calculated form factors resulting from a histone folded tail configuration. At high salts, best fits are obtained building a structure where the histone tails are extended. It can be concluded that experimental data are compatible with tail extension. This phenomenon has been suspected years ago from NMR experiments that have shown that the tail domains interact with DNA at low salt and are released and mobile at moderate salt (0.3–0.4 M) (5,6,42). More recently Arya et al. (43) have calculated D_max and R_g as a function of salt concentration, using a simulation model incorporating flexible histone tails. Their results are in quite good agreement with our findings. Absolute sizes and size increase were of larger extent using native calf thymus (7). However, these NCPs cannot be as monodisperse as recombinant ones since nucleosomal DNA length and polydispersity are dependent on the enzymatic Micrococcal nuclease digestion conditions of DNA. Native NCPs prepared in Bertin et al. (7) were monodisperse enough to achieve good SAXS data but a small fraction of particles with longer DNA might have increased the particle apparent sizes evaluated from D_max and R_g.

gH3gH4 recombinant NCPs

In gH3gH4 NCPs, the experimental scattering curve is compatible with a more opened conformation at the entry-exit DNA sides than in intact NCPs (Fig. 6). Similar results have recently been obtained (44) by FRET, using chemically acetylated recombinant NCPs. Upon specific H3 and H4 histone tails acetylation, 160-bp nucleosomal DNA end-to-end distances are 10 Å higher than those of nonacetylated histones in nucleosomes. H3 histone tails are located at the entry/exit DNA sites, close to its ends. These specific H3 histone tails pass through the gyres of nucleosomal DNA 13 basepairs from the DNA ends (1) and might therefore be involved in keeping the DNA ends attached to the particle.

In Bertin et al. (7), we already noticed that trypsinized NCPs, depleted of all tails, showed an opened conformation that was even more pronounced at low salt concentration (10 mM). However, according to previous in vitro analysis, the conformation of tailless NCPs was supposed to be similar to that of intact NCPs (29,45–48). SAXS has proven to be sensitive enough to detect small conformational changes as compared with other techniques and our novel data set confirms the observations made using trypsinized NCPs.

For gH3gH4 NCPs, the P(r) and D_max are independent of the salt concentration. The H2A and H2B histone tails are still present and the question remains as to whether they extend beyond the particle core when increasing the salt concentration. No evidence of such extension can be seen in our results. Here, it is important to note that for NCPs with all extended tails, the experimental D_max values are significantly lower than the actual maximal particle extension (26) that would be assessed from the end-to-end distances of the structural models built and displayed in Fig. 5 d. Since the histone tails represent a very low fraction of the scattering mass, compared with the central core of the NCP, the largest distances (separating the extremities of the tails) inside the particle in the extended conformation contribute too few vectors to be fully detected in the calculated scattering pattern. The end-to-end distance is therefore underestimated. The D_max value extracted from the P(r) distribution corresponds to the maximal overall diameter of the particle only in the compact conformation. Consequently, it is probable that the increase of D_max due to the tail extension can be observed if all tails extend but becomes undetectable if only the H2A tails (very short) and H2B tails extend. The conformational state of the H2B histone tails cannot be elucidated. It could either be folded or extended. From its conformation and charge distribution, we would nevertheless assume that it will behave as H3 and H4 tails do, and extend for salt concentrations above 50 mM.

H3 and H4 histone tails are required for attractive interactions between the isolated NCPs

Pair potential interaction model

A pair potential model for the numerical calculation of structure factors gives information about the nature of the interparticle interactions. A procedure involving such a calculation has been successfully used for globular proteins such as lysozyme or γ-crystalline (34–36,40) but had not yet been tested on NCPs. Although NCPs are much more complicated particles than globular proteins in terms of both geometry and charge distribution, our simulations provide fine results.

For gH3gH4 NCPs, interactions are best described by exclusively repulsive potentials at all salt concentration (Fig. 8, c and d). In the numerical structure factor calculation, no adjustable parameter was involved since the particle size was fixed and the effective charge was imposed by the Poisson-Boltzmann network calculation. Interactions for gH3gH4 NCPs are therefore only driven by Coulombic and hard-spheres repulsions.

For intact NCPs, at low salt concentration (10 and 25 mM), interactions are also described without adding any attractive term (Fig. 8 a). Above 50 mM salt, an attractive contribution to the potential had to be included. In the attractive term, two parameters could be varied, the range d and the potential strength J_a. The interaction range was found to be 20 Å. Best agreements were obtained for J_a values varying between 5 and 10 kT (Fig. 8 b). Within the same salt concentration range as investigated in this work, Mangenot et al. (8) evaluated, from osmometry measurements, the potential strengths to vary between 5 and 10 kT for native calf thymus NCPs, which is in good quantitative agreement with our current findings. However, agreements are not as good as the ones obtained at low salt concentrations. The deviations between the experimental and calculated curves might result from geometrical issues. Calculations were performed considering that particles were perfectly spherical and covered with a homogeneous distribution of charges. In fact, NCPs can be described better as flat cylinders with a highly heterogeneous charge distribution, and the situation is even worse when the histone tails extend. Because of that heterogeneous geometry, interactions are not isotropic. The Yukawa expression used to describe attractive interactions is probably not elaborate enough for providing a realistic description of the structure and charge distribution.

Interaction energies assessed using oligonucleosomes (24) include attractive and repulsive interaction terms and derive from multiple components: NCPs, linker DNA, and linker histones. The presence of linker histones and DNA contributes to the global charges and modifies electrostatic interactions. Although in nucleosomal arrays the attractive terms cannot be discriminated from repulsive ones, we have managed here to differentiate and evaluate pure internucleosome attractive interactions. Internucleosomal attractive energies per NCP are found to equal 5–10 kT and are far from being negligible as compared with the global internucleosomal interaction energy (3.4 kT) (24), measured in arrays. Since no attractive terms are required, in our case, to describe interactions for gH3gH4 NCPs, one can conclude that H3 and H4 tails induce attractive interactions with a magnitude of 5–10 kT. Widlund et al. (25) have performed competitive reconstitution assays. They have compared mononucleosome formation on short DNA fragments in the presence of either intact or tailless H1-depleted chromatin chains. The energetic contribution of histone tails to internucleosome stabilization in nucleosomal arrays was found to be 1.7 kT. Using mononucleosomes, the histone tails contribution for attractive interactions is therefore higher than that found by Widlund et al. (25). The presence of linker DNA is probably responsible for this difference. As proposed by Angelov et al. (49), histone tails in oligonucleosomes might be at least partially involved in binding DNA linkers and make attractive interactions significantly lower.

Second virial coefficients

In Bertin et al. (7), second virial coefficients were assessed using I(0,C) resulting from Guinier plots at all salt concentrations. Using this method, the A₂ values might have been underestimated, especially at low salt concentrations where interactions are strongly repulsive and where Guinier plots are actually only linear in a very small range of scattering angles. At 10 mM salt, A₂ values in Bertin et al. (7) did not exceed 25.10⁸ mol L g⁻², while in this study, A₂ values reach 50.10⁸ mol L g⁻². These data (7) were reprocessed using the same pair potential model as used in the present work. The new A₂ values obtained in this way for native NCPs are much higher and similar to values obtained for the recombinant NCPs data set. At higher salt concentrations (above 50 mM), the A₂ values for calf thymus NCPs and recombinant intact NCPs are similar. Consequently, native and recombinant NCPs display comparable behavior in terms of interparticle interactions.

At the lowest salt concentrations (10 and 25 mM), the second virial coefficients for intact or gH3gH4 recombinant NCPs are equal within error. At low ionic strength, both types of particles may interact via similar means. At higher salt concentration, interactions turn attractive for intact NCPs (A₂ < 0 on Fig. 9) but interactions remain repulsive for gH3gH4 NCPs. These results are consistent with previous experiments that compared intact and trypsinized NCPs purified from calf thymus (7). At high salt concentrations (above 50 mM), interactions were repulsive for tailless trypsinized NCPs and attractive for intact NCPs. Moreover, the second virial coefficients for both gH3gH4 and trypsinized NCPs remain close to the hard-spheres value above 50 mM salt.

Attractive interactions: role of H3 and H4 histone tails

Previous experimental studies have reported that histones tails extension was responsible for attractive interactions via a tail-bridging mechanism (7,26). Attractive interactions occur simultaneously with a D_max increase. Our results on recombinant NCPs are therefore in good agreement with the tail-extension hypothesis previously proposed for native NCPs. Moreover, we show here that attractive interactions are suppressed consecutively to the removal of H3 and H4 histone tails. Recently, theoretical and simulation studies have been carried out to describe and demonstrate the NCP tail-bridging hypothesis. The used models are often simplified compared to real NCP solutions but the results confirm our interpretation. Boroudjerdi and Netz (50,51) modeled NCPs as complexes of charged spheres associated with a polyelectrolyte chain of opposite charge. The authors described interactions between two complexes using Debye-Hückel interactions between the polyelectrolytes and spheres, a short-range repulsive term, a curvature polyelectrolyte energy, and an electrostatic Coulombic repulsion between polyelectrolytes and spheres. A negative second virial coefficient was found at intermediate salt concentration, demonstrating attractive interactions. R. Podgornik (52) has built a theoretical model where the polyelectrolyte chains are grafted to pointlike macroions of opposite charge. He considered chain configurational entropy and rigidity, interactions between polyelectrolytes and macroions, and interactions within the polyelectrolytes chains. The equations were solved numerically and bridging attractive interactions were observed. Mülbacher et al. (53) have carried out molecular dynamics simulations on isolated charged spheres carrying eight identical grafted flexible chains. In the simulations, tail extension occurs above an ionic force threshold where the second virial coefficient is at a minimum. Korolev et al. (54) have performed molecular dynamics computer simulations where NCPs are modeled by negatively charged spheres from which flexible polycations are grafted to represent histone tails. Both the location on the sphere and the cations density of each of the histone tails are here considered (54). With salt concentration increase, NCPs form condensed systems via histone tails bridging (54). The theoretical models and computer-simulations approaches, briefly presented above, confirm the presence of histone tails bridging interactions.

In addition to that, we have demonstrated that H3 and H4 histone tails are essential for building those attractive interactions. In future studies it is relevant to elucidate whether H3 or H4 histone tails alone are able to establish these attractive interactions. The H2A and H2B may also build attractive interactions but their contribution would be of a lesser extent than the H3 and H4 histone tails. H2A N and C-terminal extensions are quite short in terms of amino-acid sequence (see Tables 1 and 2) and have probably little contribution to the interactions. In crystals (1), H4 histone tails contact acidic patches from the core octamers of adjacent NCPs and are therefore supposed to significantly contribute to the crystals cohesion. At the chromatin level, H3 and H4 are more involved than other tails in compacting chromatin and therefore in building attractive interactions (13,55,56). Indeed, removal of both H3 and H4 histone tails prevents chromatin from complete folding (55,56). H3 histone tails seem to participate in intranucleosome interactions when nucleosome arrays are decondensed while they engage internucleosomal interactions upon salt-dependent folding (15). Dorigo et al. (13) have shown that histone H4 tails alone appear to be necessary for getting fully compacted chromatin. More recently, Gordon et al. (14) have shown that all four histone tails contribute additively and independently to chromatin chains oligomerization. Sun et al. (57) have performed Monte Carlo simulations on nucleosome fibers where each NCP is represented as a nonhomogeneous charged surface. The authors have evaluated internucleosomal interactions and concluded that the histone tail H3 is essential for building attractive interactions in nucleosome arrays. We have shown here that H3 histone tails may not exclusively interact with linker DNA but might also interact with adjacent NCPs. In vivo, H3 histone tails might as well be able to shift their binding from linker DNA to adjacent NCPs. Not only linker histones but other proteins such as HMGB proteins (58) may prevent H3 histone tails from binding to linker DNA and may induce attractive interactions between NCPs.

As a conclusion, we have demonstrated that H3 and H4 histone tails are necessary to observe attractive interactions between NCPs. In addition to that, removal of H3 and H4 histone tails lead to a more opened conformation, where DNA ends are probably slightly released from the particle core, leading to a rather more opened conformation.