Anisotropy and Temperature Dependence of Myoglobin Translational Diffusion in Myocardium: Implication for Oxygen Transport and Cellular Architecture

Abstract

Pulsed field gradient NMR methods have determined the temperature-dependent diffusion of myoglobin (Mb) in perfused rat myocardium. Mb diffuses with an averaged translational diffusion coefficient (D_Mb) of 4.24–8.37 × 10⁻⁷cm²/s from 22°C to 40°C and shows no orientation preference over a root mean-square displacement of 2.5–3.5 μm. The D_Mb agrees with the value predicted by rotational diffusion measurements. Based on the D_Mb, the equipoise diffusion PO₂, the PO₂ in which Mb-facilitated and free O₂ diffusion contribute equally to the O₂ flux, varies from 2.72 to 0.15 in myocardium and from 7.27 to 4.24 mmHg in skeletal muscle. Given the basal PO₂ of ∼10 mmHg, the Mb contribution to O₂ transport appears insignificant in myocardium. In skeletal muscle, Mb-facilitated diffusion begins to contribute significantly only when the PO₂ approaches the P50. In marine mammals, the high Mb concentration confers a predominant role for Mb in intracellular O₂ transport under all physiological conditions. The Q₁₀ of the D_Mb ranges from 1.3 to 1.6. The Mb diffusion data indicate that the postulated gel network in the cell must have a minimum percolation cutoff size exceeding 17.5 Å and does not impose tortuosity within the diffusion root mean-square displacement. Moreover, the similar Q₁₀ for the D_Mb of solution versus cell Mb suggests that any temperature-dependent alteration of the postulated cell matrix does not significantly affect protein mobility.

INTRODUCTION

A key tenet in respiration physiology rests on the capacity of myoglobin (Mb) to store O₂ or to facilitate O₂ transport. Although in vitro experiments have presented supporting evidence, in vivo experiments on respiring vertebrate muscle have yet to provide convincing data (1). In marine mammals, the high concentration of Mb could certainly supply O₂ during a dive or apnea (2,3). High altitude adaptation increases the expression of Mb and therefore the O₂ store (4,5). These observations agree with the tacit correlation between Mb concentration (O₂ supply) and oxidative capacity in different species (6). Yet, in spontaneously beating rat heart, Mb can prolong normal heart function for only a few seconds (7). Without any Mb, neither myocardial nor skeletal muscle function suffers any apparent impairment (8,9). The viability of an Mb-free mouse elicits two different interpretations: Mb still has a critical O₂ storage and transport function role, as evidenced by the compensating increase in capillary density. Alternatively, Mb does not have the commonly accepted O₂ storage and transport function role, and its function remains unclear.

From the vantage of facilitated O₂ diffusion, the physiology canon states that in contrast to the low solubility of O₂, the high O₂-carrying capacity of Mb confers an advantage in transporting O₂ from the sarcolemma to the mitochondria (1,10). In vitro studies have indeed confirmed that O₂ diffuses faster in Mb solution than in Mb-free solution. Mb exhibits sufficient mobility and O₂-carrying capacity to compete effectively with free O₂ (11). In vivo, however, the contribution of Mb diffusion remains uncertain, since no experiments have determined the averaged translational diffusion coefficient of myogolobin (D_Mb) in respiring tissue. In effect, the theory of Mb-facilitated diffusion has languished over several decades for definitive experimental confirmation.

Over the years, researchers have attempted to estimate the cellular Mb D_Mb by measuring Mb diffusion in concentrated solution or by following the diffusion of injected metMb in tissue homogenate or in myoglobinless frog muscle (12–14). Recent studies have taken a similar approach and have utilized fluorescence recovery after photobleaching (FRAP) technique to track injected Mb in isolated muscle (15). Observing the photooxidation of Mb in superfused rat diaphragm muscle has led to a calculated diffusion coefficient of 1.7 × 10⁻⁷ cm²/s at 37°C (16,17). Measuring the diffusion of microinjected metMb with an attached fluorophore in isolated muscle fiber has yielded an even lower diffusion coefficient ∼1.2 × 10⁻⁷ cm²/s at 22°C (17). These reported diffusion coefficients raise questions about any significant Mb role in facilitating O₂ transport in the cell.

The FRAP results have not engendered sufficient confidence to overturn a rubric of physiology, because they do not actually measure endogenous Mb diffusion, contain an uncertain overlay of Mb oxidation/reduction kinetics in the analysis, and utilize an isolated fiber model that does not adequately mimic the physiological environment of respiring tissue (18). Moreover, the FRAP results disagree with the in vivo NMR observation of endogenous Mb rotational diffusion, which predicts a much faster translational diffusion coefficient (19,20).

Because ¹H-NMR studies have demonstrated the feasibility of detecting the distinct γ-CH₃ Val E11 signal of MbO₂ in myocardium at −2.8 ppm, an opportunity now arises to apply a pulsed field gradient technique to map endogenous Mb translational diffusion in respiring, perfused myocardium (21,22). At 22°C, MbO₂ diffuses with an averaged coefficient of 4.24 × 10⁻⁷ cm²/s. In contrast, solution Mb diffuses with an averaged coefficient of 11.6 × 10⁻⁷ cm²/s. At 35°C, MbO₂ diffuses with an averaged coefficient of 7.85 × 10⁻⁷ cm²/s and shows no orientation preference over a root mean-square (RMS) displacement of 3.4 μm. The translational diffusion coefficient matches precisely the value predicted by the NMR rotational diffusion analysis (20).

Given the reported free O₂ diffusion coefficient in the cell, a myocardium Mb concentration of 0.19 mM, and a P50 of 1.98 mmHg at 35°C, the cell reaches an equipoise diffusion PO₂ at 1.67 mmHg, where Mb and free O₂ contribute equally to the O₂ flux. Since the basal PO₂ in skeletal muscle and myocardium in vivo stands well above 10 mmHg, Mb cannot contribute significantly to the O₂ flux in the basal normoxic state (23–25).

The Q₁₀ of the D_Mb ranges from 1.3 to 1.6 and casts a perspective on cellular architecture. In the postulated gel network model of the cell, small molecule escapes restricted diffusion by staying below a percolation cutoff size. The Mb data indicate a cutoff of at least 17.5 Å, the hydrodynamic diameter of Mb (26–28). The unrestricted Mb diffusion reveals no significant tortuosity within the RMS displacement. Moreover, the similar Q₁₀ for the D_Mb of solution versus cellular Mb suggests that any temperature-dependent alteration or phase transition of a postulated cell matrix does not significantly affect protein mobility.

THEORETICAL BACKGROUND

NMR diffusion experiment

The effect of diffusion modifies the Bloch equation:

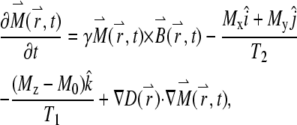(1)

where γ is the magnetogyric ratio. The first three terms on the right correspond to the general Bloch equation; the last term, 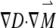, reflects the effect of diffusion in anisotropic medium, first shown by Torrey (29). Its solution, based on the NMR diffusion experiment, requires measurements of the echo amplitude S(G) as a function of the applied field gradient G(t). The analysis utilizes the following equation (30):

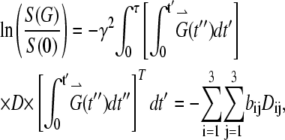(2)

where S(0) is the intensity of echo with no gradient, S(G) is the intensity of echo with the applied field gradient, G is the applied field gradient, τ is the echo time, D is the 3 × 3 rank-two diffusion tensor, D_ij is an element of the tensor D, and b_ij is the element of the 3 × 3 matrix b

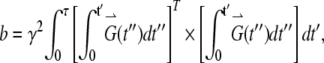(3)

in which G(t) = [G_x(t), G_y(t), G_z(t)], a field gradient vector. According to Eqs. 2 and 3, the diffusion experiments can be designed to observe different linear combinations of the components of D by applying field gradients along various oblique directions. For well-described anisotropic diffusion, no less than seven experiments are required to evaluate all diagonal and off-diagonal elements of the symmetrical 3 × 3 matrix D and S(0) (31).

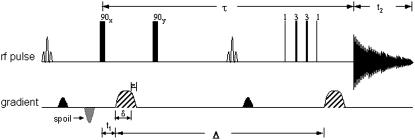
Specifically, pulsed field gradient spin echo (PGSE) or pulsed field gradient stimulated echo (PGSTE) sequences can determine the self-diffusion coefficients (30). However, the utilization of rectangular gradient pulses generates significant eddy current, which is proportional to dI/dt. Decreasing the rate of change in the gradient pulses reduces the eddy current. Trimming the G(t) gradient pulse utilizes ramp functions to create a modified pulse train (Fig. 1). The time intervals are as follows:

FIGURE 1.

The modified PGSTE sequence in the NMR diffusion measurements used two modified CHESS pulse sequences (one inserted in front of the first 90° pulse and the other one located between the second 90° pulse. The binomial pulse suppress the water and fat signals. The 1331 binomial pulse excite selectively the γ-CH₃ Val E11 signal of MbO₂ (or MbCO).

Table 6.

Functional forms of G(t) in the serial time subintervals

Pulse sequence subinterval t	Ramped rise and fall of G(t)
0 < t ≤ t1	0
t1 < t ≤ t1 + ɛ	Gsin(t − t1)π/2t
t1 + ɛ < t ≤ t1 + δ	G
t1 + δ < t ≤ t1 + δ + ɛ	Gsin(t − t1 − δ)π/2ɛ+π/2
t1 + δ + ɛ < t ≤ t1 + Δ	0
t1 + Δ < t ≤ t1 + Δ + ɛ	Gsin(t − t1 − Δ)π/2ɛ
t1 + Δ + ɛ < t ≤ t1 + Δ + δ	G
t1 + Δ + δ < t ≤ t1 + Δ + δ + ɛ	Gsin((t − t1 − Δ − δ)(π/2ɛ+π/2))
t1 + Δ + δ + ɛ < t ≤ τ	0

Adjusting for the nonrectangular gradient pulses yields a modified equation for b_ij.

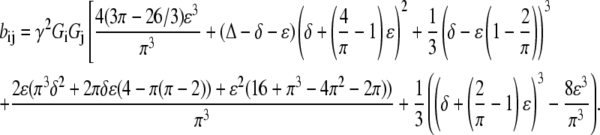(4)

In the case of isotropic diffusion, the observations corresponding to the diagonal elements of D will not differ. All off-diagonal elements, however, will vanish.

O₂ diffusion in muscle cell

Oxygen transport from the sarcolemma to the mitochondria has contributions from free O₂ and Mb-facilitated diffusion, as expressed in the following equation (11,18):

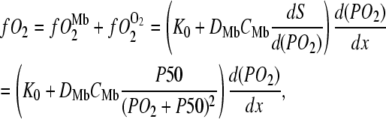(5)

where PO₂ = partial pressure of O₂, 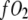= O₂ flux density, 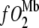= O₂ flux density from Mb, 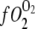= O₂ flux density from free O₂, K₀ = Krogh's diffusion constant for free O₂, D_Mb = Mb diffusion coefficient, C_Mb = Mb concentration, 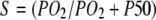= fraction of Mb saturated with O₂. P50 = the PO₂ that half saturates Mb, which reflects the O₂-binding affinity of Mb. The overall Mb-facilitated and free O₂ flux in the cell requires the integration of the MbO₂ and O₂ distribution, which in turn depends upon the PO₂ gradient between the sarcolemma and the surface of mitochondria. Integrating Eq. 5 with the mitochondria PO₂ boundary condition assumed as 0 mmHg and with the sarcolemma to mitochondria distance along X set as unit length yields 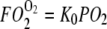for the free O₂ flux and 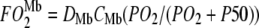for the Mb-facilitated O₂ diffusion. Mb-facilitated diffusion of O₂ depends upon PO₂, C_Mb, and P50. Equation 6 then describes the relative Mb-facilitated versus free O₂ flux

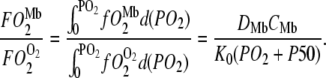(6)

When 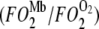= 1, Mb-facilitated O₂ and free O₂ contribute equally to the O₂ flux. The associated PO₂ is defined as the equipoise diffusion PO₂.

MATERIALS AND METHODS

Protein preparation

Mb solution was prepared from lyophilized horse heart protein (Sigma Chemical, St. Louis, MO). The preparation of MbO₂ and MbCO solution followed the procedure described previously (32).

Animal preparation and heart perfusion

The procedure for rat heart perfusion was performed as previously described (33,34). Male Sprague-Dawley rats (350–400 g) were anesthetized by an intraperitoneal injection of sodium pentobarbital (65 mg/kg) and heparinized (1000 units/kg) by injection into the femoral vein. The heart was quickly isolated and placed in ice cold buffer solution until aortic cannulation, followed by perfusion in Langendorff mode with Krebs-Henseleit buffer containing (in mM) 118 NaCl, 4.7 KCl, 1.2 KH₂PO₄, 1.8 CaCl₂, 23 NaHCO₃, 1.2 MgSO₄, 15 glucose. The perfusate was maintained by a peristaltic pump (Rainin, Oakland, CA) at a constant, nonrecirculating perfusion flow of 12–19 ml/min and at the respective temperatures. Perfusion pressure was measured with a pressure transducer (Medex, Hilliard, OH) via a Y-connection in the aortic cannula. A saline-filled latex balloon inserted in the left ventricle monitored the heart rate (HR) and left ventricular pressure (LVP) via a second pressure transducer. Both transducers were connected to a Biopac (Goleta, CA) recording system. The balloon volume was adjusted to give an end-diastolic pressure of 4–6 mmHg. Rate pressure products were calculated from HR × the left ventricular developed pressure (LVDP). The perfusate was gassed with 95% O₂, 5% CO₂ and was passed through a 5-μm and a 0.45-μm Millipore filter. The perfusate temperature was maintained with a heat-regulated circulating water bath and water-jacketed reservoirs and tubings. A microthermocouple inserted into the left ventricle calibrated the buffer temperature, heater output, and thermal sensor to maintain the tissue at a defined temperature of 22°C, 30°C, 35°C, or 40°C. All target temperatures have a deviation of <±1°C.

K⁺ arrest

After a 20-min control period the perfusate was switched to Krebs-Henseleit buffer containing 92.7 mM NaCl and 30 mM KCl. Other buffer components remained the same, as listed above. With 30 mM KCl, the heart stopped beating. Ten minutes after the heart stopped beating, the perfusate flow rate was reduced to 50% of control. Heating power was readjusted because of the reduction of flow rate. High K⁺ perfusion continued for ∼4–6 h, which depended upon the experiment at different temperature. The perfusate was then switched back to 118 mM NaCl, 4.7 mM KCl, and the flow returned to its control level. Perfusion continued then for 20–30 min.

NMR

An Avance 400-MHz Bruker (Billerica, MA) spectrometer measured the ¹H/³¹P signals with a 20-mm microimaging gradient probe. The ¹H 90° pulse, calibrated against the H₂O signal from a 0.15 M NaCl solution or perfusate, was 65 μs. A modified Stejskal-Tanner PGSE or PGSTE sequence followed the Val E11 resonance of MbCO and MbO₂ at −2.4 ppm and −2.8 ppm, respectively (22,35,36). The gradient field strength ranged from 0 to 95 G (G/cm). A typical spectrum required 1024 scans and used the following signal acquisition parameters: 8,192-Hz spectral width, 4,096 data points, and 255-ms acquisition time. Zero-filling the free induction decay and apodizing with an exponential-Gaussian window function improved the spectra. A spline fit then smoothed the baseline. The H₂O line served as the spectral reference, 4.75 ppm at 25°C relative to sodium-3-(trimethylsilyl)propionate-2,2,3,3-d4 at 0 ppm.

Diffusion measurements in perfused heart experiments utilized a modified PGSTE sequence that included chemical shift selective (CHESS) pulses (37). One CHESS pulse suppressed the water signal; the other CHESS pulse, inserted between the second and third 90° pulses, attenuated the fat signal at 1 ppm. The trapezoidal pulsed field gradients with various magnitudes and directions were applied to measure diffusion coefficients in different orientations. In addition, a 1331 pulse replaced the third 90° pulse. For the diffusion measurements, the acquisition parameters included the following: acquisition time, 38.5 ms; spectral width, 10 KHz; data points, 768. A typical spectrum required 16,000 transients or ∼24 min of signal accumulation. The PGSTE, as illustrated in the pulse train diagram, had the following intervals: Δ = 24 ms, δ = 2.4 ms, ɛ = 0.6 ms, and τ = 27.5 ms.

Seven non-co-linear pulsed field gradient directions G = (G_x, G_y, G_z) were selected to measure the diffusion tensor components (31). In each direction, the gradient strength, G_i, was 0 or increased incrementally from 18.2 G/cm to 73.0 G/cm in 18.3 G/cm steps.

For the ³¹P spectra, the signal acquisition utilized a 55° pulse angle, 6494-Hz spectral width, 4096-point data size, and 0.65-s repetition time. The ³¹P 90° pulse was 72 μs, calibrated against a 0.1 M phosphate solution. All ³¹P signals were referenced to PCr peak as 0 ppm. A typical spectrum required 256 scans. The PCr/ATP ratio was corrected by a scaling factor calculated from fully relaxed spectra.

Statistical analysis

Statistical analysis used the Sigma Plot/Sigma Stat program (Systat Software, Point Richmond, CA) and expressed the data as mean ± SE. Linear least squares regression analysis of the individual data points determined the slopes, intercepts, and correlation coefficients. Statistical significance was determined by two-tailed student's t-test, P < 0.05. For evaluating the six independent components of the self-diffusion tensor, the method of multivariate linear regression was utilized to estimate the regression parameters of the system of linear equations. All regression analyses used primary data points and the ANOVA statistics for the regression and the corresponding F test value for each step.

RESULTS

The perfused rat myocardium shows physiological characteristics consistent with previous literature reports (33,34). Introducing 30 mM KCl stops heart contraction and removes any cardiac motional artifact from the diffusion measurements. At 35°C, K⁺ induces a rate pressure product (RPP) drop from 27.5 ± 1.7 × 10³ mmHg min⁻¹ to zero. During the K⁺ arrest period, MVO₂ reduces from 26.8 ± 2.0 to 7.3 ± 1.2 μmol min⁻¹ g⁻¹ dry weight (dw); ATP declines to 93.0% ± 3.7% of control. PCr decreases to 95.5% ± 3.8% of the basal level. During reperfusion with K⁺ free, control state buffer, MVO₂ returns to 30.6 ± 3.5 μmol min⁻¹ g⁻¹ dwt. ATP and PCr recover to 83.6% ± 3.1% and 84.9% ± 3.5% of the control level. RPP returns to 28.1 ± 1.5 × 10³ mmHg min⁻¹. Table 1 summarizes the physiological parameters from 22°C to 40°C.

TABLE 1.

Physiological parameters for perfused heart

	LVDP (mmHg)	HR (min−1)	RPP (mmHg min−1 × 103)	MVO2 (μmol min−1 g−1 dwt)	PCr (%)	ATP (%)	PCr/ATP ratio	pH	n
				22°C
Control	150.9 ± 7.2	72.3 ± 2.6	10.9 ± 0.4	14.1 ± 0.6	100	100	1.75 ± 0.04	7.18 ± 0.03	6
K+ Arrest	n/a	0	0	5.0 ± 0.4*	120.6 ± 4.3*	95.4 ± 1.6	2.28 ± 0.10	7.22 ± 0.02	6
Reperfusion	148.9 ± 8.4	71.0 ± 4.6	10.5 ± 0.7	14.6 ± 1.0	93.2 ± 3.2	93.9 ± 1.3	1.75 ± 0.12	7.19 ± 0.03	6
				30°C
Control	133.4 ± 7.8	173.1 ± 11.3	22.8 ± 1.5	20.1 ± 26	100	100	1.37 ± 0.11	7.19 ± 0.00	5
K+ Arrest	n/a	0	0	4.3 ± 0.6*	106.2 ± 2.6*	101.2 ± 1.8	1.43 ± 0.09	7.20 ± 0.00	5
Reperfusion	134.8 ± 9.4	177.8 ± 12.1	23.5 ± 1.7	21.4 ± 2.5	88.5 ± 3.8*	96.9 ± 3.7	1.24 ± 0.05	7.19 ± 0.01	5
				35°C
Control	118.3 ± 5.0	231.5 ± 7.69	27.5 ± 1.7	26.8 ± 2.0	100	100	1.39 ± 0.07	7.17 ± 0.01	8
K+ Arrest	n/a	0	0	7.3 ± 1.2*	95.5 ± 3.8	93.0 ± 3.7	1.36 ± 0.04	7.19 ± 0.01	8
Reperfusion	125.4 ± 6.4	222.2 ± 7.4	28.1 ± 1.5	30.6 ± 3.5	84.9 ± 3.5*	83.6 ± 3.1	1.34 ± 0.04	7.14 ± 0.01	8
				40°C
Control	127.7 ± 10.9	294.4 ± 16.4	36.8 ± 5.7	33.5 ± 4.6	100	100	1.28 ± 0.07	7.12 ± 0.01	4
K+ Arrest	n/a	0	0	9.7 ± 2.4*	103.7 ± 5.3	94.4 ± 0.5*	1.40 ± 0.10	7.15 ± 0.01	4
Reperfusion	130.9 ± 12.3	294.2 ± 26.3	37.4 ± 5.1	34.1 ± 3.2	76.0 ± 2.4*	87.2 ± 5.1*	1.12 ± 0.06	7.10 ± 0.02	4

LVDP, left ventricular developed pressure; HR, heart rate; RPP, rate pressure product; PCr, phosphocreatine.

^*Indicates statistical significance.

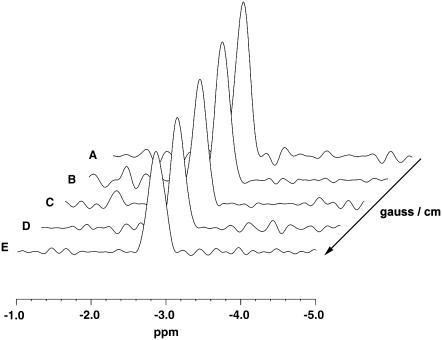
Fig. 1 displays the NMR pulse sequence used to detect the Mb signal. Fig. 2 shows the ¹H-stacked spectra of the Val E11 γ-methyl signal of MbO₂ at −2.8 ppm from perfused myocardium at 30°C. The measurement utilizes a modified PGSTE sequence at different gradient fields applied in the X-direction. At 0.9 G/cm, the Val E11 γ-methyl signal of MbO₂ shows the highest signal intensity (Fig. 2 A). For trace B to E, the signal intensity decreases incrementally as the gradient strength increases stepwise from 18.2 G/cm to 73.0 G/cm.

FIGURE 2.

¹H-NMR diffusion-weighted spectra of MbO₂ from perfused rat heart under K⁺ arrest at 30°C: A modified pulse PGSTE sequence detects the γ CH₃ Val E11 signal at −2.8 ppm. The peak intensity changes as a function of gradient field strength in the X direction: (A) 0.9 G/cm, (B) 18.2 G/cm, (C) 36.5 G/cm, (D) 54.7 G/cm, and (E) 73.0 G/cm.

For the perfused rat myocardium at 22°C, the apparent diffusion tensor, D, estimated by a set of seven non-co-linear pulsed field gradients, is shown with its standard error matrix below:

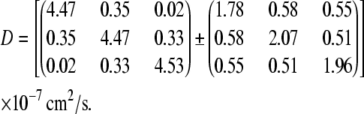(7)

The correlation coefficient R = 0.725.

In addition, to investigate if the diffusion tensor D is an isotropic matrix, a null hypothesis of isotropic diffusion, D = D₀I, is applied. Assuming that the null hypothesis is true, the diffusion tensor is D = (5.22 ± 0.57) × 10⁻⁷ I (cm²/s), estimated from the same data set. R = 0.717.

F distribution examines whether the null hypothesis is acceptable, using the relevant F equation

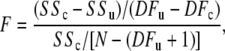(8)

where SS_c and SS_u are the residual sum of squares due to regression in the constrained and unconstrained models, respectively; DF_u represents the regression degrees of freedom in the unconstrained model as well as DF_c does in the constrained model, and N is the total number of data points. Given DF_u = 6, DF_c = 1, and N = 79 in this experiment, the value of F is 0.31 according to Eq. 8, which is smaller than F[DF_u − DF_c, N − (DF_u + 1)] = 3.30 and 2.35 for the 1% and 5% confidence limits, respectively; therefore, the null hypothesis of isotropic diffusion is accepted. Given the isotropic diffusion at 22°C, a restricted time window to maintain a viable perfused myocardium above 30°C, and an extended signal acquisition time required to achieve sufficient signal to noise, the experiments at 30°C and 35°C have only investigated Mb diffusion with applied field gradients in three orthogonal directions.

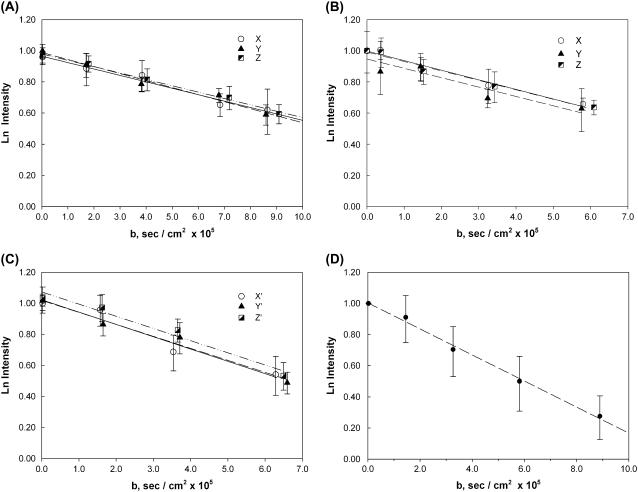
Fig. 3 shows the natural logarithm of the MbO₂ signal intensity from perfused hearts (n = 5) as a function of b (Eqs. 3 and 4) from 22°C to 40°C. The slope of the graph leads to the determination of the translational diffusion coefficient. Applying the gradient field along X, Y, or Z does not produce any significant deviations in the slopes under all temperature conditions, consistent with isotropic diffusion. Table 3 lists the temperature-dependent diffusion coefficients.

FIGURE 3.

Plots of the natural logarithm of the MbO₂ Val E11 peak intensity at different temperatures as a function of b: The MbO₂ signals reveal decreasing the intensity with each stepwise increase in gradient field strength applied along the X, Y, and Z directions. The translational diffusion coefficients are as follows: (A) 22°C: 4.12, 4.51, and 4.08 × 10⁻⁷ cm²/s (n = 5), (B) 30°C: 6.18, 6.07, and 6.07 × 10⁻⁷ cm²/s (n = 5), (C) 35°C: 7.97, 7.76, and 7.85 × 10⁻⁷ cm²/s (n = 5), and (D) 40°C: 8.37 × 10⁻⁷ cm²/s in the XY direction (n = 4). The standard error on each point was calculated from five (or four) different perfused heart measurements. In addition, the regression lines for the respective data points show no significant difference at any measuring temperature from 22°C to 35°C.

TABLE 3.

Diffusion coefficients of Mb in solutions and in muscles

Sample	Method	DMb × 10−7 cm2/s	Q10 [T1, T2], °C	°C	Reference
MbCO solution (1.8 mM)	NMR	11.6		22	This work
		16.5	1.31 [22, 35]	35	This work
MbO2 solution (1.8 mM)	NMR	11.6		22	This work
Mb diluted solution	Diffusion tube	11.3		20	(12)
Mb diluted solution in capillary	Photobleaching	9.9		22	(16,17)
		14.8	1.31 [22, 37]	37	(16,17)
Mb in rat myocardium	Perfused heart, NMR	4.24		22	(74)
		7.85	1.61 [22, 35]	35	This work
Isolated rat soleus muscle fiber	Microinjection of metMb, photobleaching	1.2		22	(16,17)
		2.2	1.50 [22, 37]	37	(16,17)
Isolated rat cardiac muscle fiber	Microinjection of metMb, photobleaching	1.1		22	(16,17)
		1.7	1.49 [22, 37]	37	(16,17)
Mb in undiluted homogenates of rat skeletal muscle	Multilayer diffusion	1.5		20	(14)
Injected Mb in frog skeletal muscle	Microinjection of Mb, fluorescence, and photooxidation	2.7	1.41 [20, 37]	37	(14)
		1.6	1.60 [16, 22]	22	(13)

Q₁₀ is the relative change in the diffusion coefficient corresponding to 10°C change in temperature as defined by Q₁₀ = .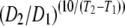

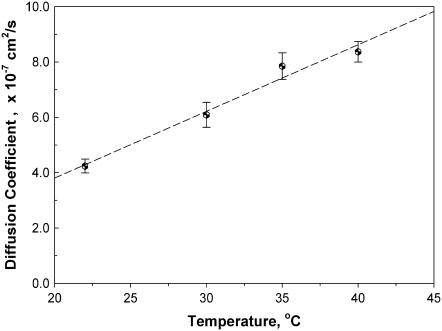
Fig. 4 shows a linear relationship between the averaged value of the diffusion coefficient D and temperature. The slope of the linear regression line, 2.41 × 10⁻⁸ cm²/s °C, depicts a 73.8% increase in D from 22°C to 35°C, corresponding to the temperature coefficient (Q₁₀) of 1.53. In addition, the temperature coefficient calculated from D at any two temperature points ranges between 1.3 and 1.6, which agrees with literature values. The Q₁₀ of cellular MbO₂ diffusion agrees with previous literature reports and the Q₁₀ of 1.31 observed in solution MbO₂ (Tables 3 and 4).

FIGURE 4.

Plot of MbO₂ diffusion coefficient versus temperature (°C): The MbO₂ diffusion coefficient in tissue increases proportionally as temperature rises. Regression analysis of the temperature-dependent D_Mb data gives a linear equation with an R² = 0.986 within the temperature range of 22°C–40°C. The slope is 2.41 × 10⁻⁸ cm²/s °C.

TABLE 4.

Q₁₀ of Mb and free O₂ diffusion in the cell

DMb	[T1, T2], °C	[20, 30]	[25, 35]	[30, 40]	[35, 45]
	Q10	1.51	1.41	1.34	1.29
K0*	[T1, T2], °C	[22.8, 37]
	Q10	1.56

Regression analysis of the temperature-dependent D_Mb data gives a linear equation D_Mb = cT − 1.00 × 10⁻⁷ cm²/s. The slope c is 2.41 × 10⁻⁸ cm²/s °C. Q₁₀ is the relative change in the diffusion coefficient corresponding to 10°C change in temperature as defined by Q₁₀ = .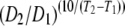

^*Values extrapolated from literature data (38).

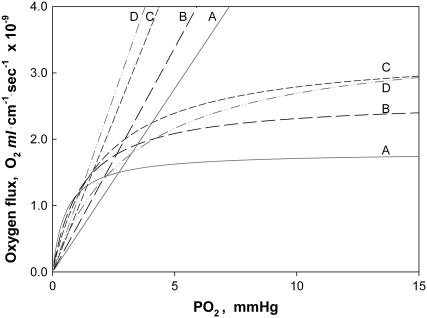
Fig. 5 compares the relative O₂ flux contribution of free O₂ transport with Mb-facilitated diffusion. Free O₂ flux has a linear dependence on K₀, the Krogh's diffusion coefficient, whereas Mb-facilitated O₂ diffusion has a nonlinear dependence on D_Mb and P50. As temperature rises from 22°C to 40°C, K₀ increases from 2.52 to 4.81 × 10⁻⁵ ml O₂ cm⁻¹ × min⁻¹ × atm⁻¹ (38); D_Mb increases from 4.24 to 8.37 × 10⁻⁷ cm²s⁻¹. The equipoise diffusion PO₂ changes with only a modest temperature dependence. Mb-facilitated diffusion begins to dominate the O₂ flux below the equipoise diffusion PO₂. Table 5 summarizes the equipoise diffusion PO₂ values at different D, K₀, and temperatures. Altering the temperature from 22°C to 40°C changes the equipoise diffusion PO₂ from 2.72 to 0.15 mmHg in myocardium and 6.67 to 4.24 mmHg in skeletal muscle.

FIGURE 5.

Plot of Mb-facilitated O₂ diffusion versus free O₂ flux as a function of PO₂ at different temperatures: The equation 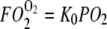describes the linear rise of free O₂ flux with PO₂. Krogh's diffusion coefficient, K₀, is the proportionality constant and the slope. Four straight lines reveal the rate of change at different K₀ values: A) 2.52 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹ at 23°C, B) 3.08 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹ at 30°C, C) 4.18 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹ at 34.2°C, and D) 4.81 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹ at 40.4°C. The equation 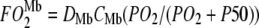describes the Mb-facilitated O₂ diffusion as a function of PO₂, P50, C_Mb, and D_Mb and gives rise to a set of nonlinear curves. The PO₂ corresponding to the condition, 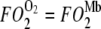, denotes the equipoise diffusion PO₂. Temperature affects both D_Mb and P₅₀ and consequently the O₂ flux contribution from Mb-facilitated diffusion at A) 22°C, B) 30°C, C) 35°C, and D) 40°C.

TABLE 5.

Equipoise diffusion PO₂ in heart and skeletal at different temperatures

	Temperature (°C)
	22*	30	35	40
K0 (ml O2 cm−1 × min−1 . atm−1) × 10−5	2.52	3.08	4.18	4.81
P50 (mmHg)†	0.55	1.21	1.98	3.23
DMb (cm2s−1) ×10−7	4.24	6.09	7.85	8.37
DMbCMb(cm2s−1 mM) × 10−7 myocardium‡	0.81	1.16	1.49	1.59
DMbCMb(cm2s−1 mM) × 10−7 skeletal muscle‡	1.79	2.56	3.29	3.54
Equipoise diffusion PO2 (mmHg) myocardium	2.72	2.63	1.67	0.15
Equipoise diffusion PO2 (mmHg) skeletal muscle	6.67	7.27	6.08	4.24

^*Actual temperature for K₀ measurements: 23°C, 30°C, 34.2°C, 40.4°C (38).

^†P50 calculated from the equation P50 = e^{0.098T–2.748}, where T is in °C (49). Experimentally determined P50 of 1.5 mmHg at ∼25°C and K₀ = 2.52 × 10⁻⁵ ml O₂ cm⁻¹ × min⁻¹ × atm⁻¹ yields equipoise diffusion PO₂ 1.77 mmHg for myocardium and 5.72 for skeletal muscle (10,74).

^‡Mb concentration in rat myocardium assumed as 0.19 mM and 0.42 mM in rat skeletal muscle (10).

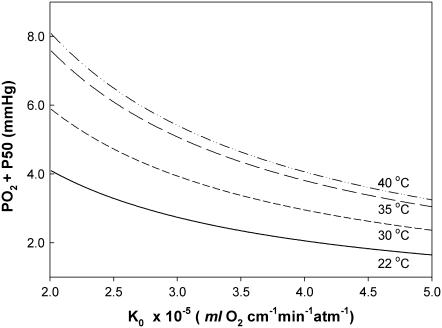
Fig. 6 maps the hyperbolic relationship between K₀ and (PO₂ + P50), given C_Mb of 0.19 mM for Mb and D_Mb at different temperatures (see Table 2) based on the relationship 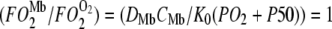. At the equipoise diffusion PO₂, 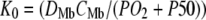. As the P50 value increases, the free O₂ flux required to match Mb-facilitated diffusion decreases. Temperature also alters the D_Mb and the P50 and will introduce a new set of curves.

FIGURE 6.

Plot of K₀ versus (PO₂ + P50) based on the equation 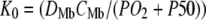under the condition 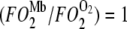. K₀ shows a hyperbolic relationship with (PO₂ + P50), given a C_Mb of 0.19 mM and D_Mb (Table 2). Since K₀, D_Mb, and P50 depend upon temperature, different graphs reflect the hyperbolic relationship at 22°C, 30°C, 35°C, and 40°C. The graph accommodates the broad range of literature reported P50 and K₀ values. At ∼22°C, the Mb P50 value can vary from 0.55 to 2.3 mmHg, whereas the K₀ values can vary from 2.52−4.28 × 10⁻⁵ ml O₂ cm⁻¹ × min⁻¹ × atm⁻¹.

TABLE 2.

Mb translational diffusion in myocardium at different temperatures

Gradient direction	DMb (×10−7 cm2/s) at different temperatures
	22°C	30°C	35°C	40°C
X	4.12 ± 0.32	6.18 ± 0.65	7.97 ± 1.03
Y	4.51 ± 0.38	6.07 ± 1.00	7.76 ± 0.68
Z	4.08 ± 0.19	6.07 ± 0.64	7.85 ± 0.79
Averaged DMb*	4.24 ± 0.25*	6.09 ± 0.45*	7.85 ± 0.49*	8.37 ± 0.37†

^*The translational diffusion coefficients were obtained by analyzing all the data points collected in all gradient directions to run statistics tests (n = 75 at 22°C, 72 at 30°C, and 60 at 35°C).

^†The self-diffusion coefficient of Mb at 40°C was measured in one gradient direction, XY (45° between X and Y directions) only.

DISCUSSION

Physiological model

The K⁺-arrested perfused rat myocardium provides a convenient physiological model to interrogate endogenous Mb diffusion. Under control conditions without K⁺ at physiological temperature of 35°C, RPP (27.5 ± 1.7 mmHg min⁻¹ × 10³), MVO₂ (26.8 ± 2.0 μmol min⁻¹ g⁻¹ dwt), and other metabolism parameters agree with literature reports of saline-perfused rat myocardium (33,34). Introducing 30 mM KCl stops the heart contraction and removes cardiac motion artifact from the diffusion measurements. Even though RPP falls to zero, MVO₂ continues at 27% of its control level (7.3 ± 1.2 μmol min⁻¹ g⁻¹ dwt) and maintains the heart at a high energy charge (39). The noncontractile energy demand of the heart consumes ATP at a rate of 21.9 μmol min⁻¹ g⁻¹ dwt, assuming a P/O ratio of 3:1. During recovery from K⁺ arrest, MVO₂ (30.6 ± 3.5 μmol min⁻¹ g⁻¹ dwt) and RPP (28.1 ± 1.5 mmHg min⁻¹ × 10³) return to their respective control levels. PCr and ATP also approach their respective control levels. The slight deviation from full PCr and ATP recovery requires additional experiments to clarify but does not impair the use of the K⁺-arrested perfused heart in investigating Mb diffusion in the cell (7). At all temperatures 22°C–40°C, the hearts exhibit previously observed physiological and metabolic profiles.

Cellular Mb

The detectable NMR signal of the MbO₂ Val E11 signal in myocardium and skeletal muscle presents an opportunity to investigate the endogenous D_Mb in the cell with pulsed field gradient techniques. Using the NMR data to quantitate the translational diffusion coefficient requires defining two premises: Mb visibility and O₂ heterogeneity.

A significant pool of bound Mb would complicate the diffusion analysis. Comparative in vitro and in vivo experiments, however, indicate an entirely free, mobile, and NMR-detectable pool of Mb. ¹H-NMR spectral analysis of the in situ Mb signal and biochemical assay of the tissue yield matching concentration values for Mb. Moreover, the Val E11 signal line shape in the cell versus in solution shows no significant deviation (32). Mb appears to diffuse freely in cell. No significant compartmentalization exists.

Any O₂ heterogeneity can also pose an analysis hurdle, since the Val E11 signal intensity corresponds directly to the oxygenation level. Under normoxic conditions, the perfused myocardium model in this study reveals no sign of O₂ heterogeneity, which would give rise to a regional distribution of partially saturated MbO₂ (40). Infusing high affinity CO into perfused myocardium produces an equivalent MbCO Val E11 signal intensity. The MbCO signal intensity never exceeds the corresponding one from MbO₂, and the total integrated signal area remains constant (36,41). Any O₂ heterogeneity would yield a higher MbCO signal intensity. Even though some investigators have reported O₂ heterogeneity in the perfused heart, these contrasting observations arise most likely from differences in the experiment model (42).

Given these premises, the diffusion analysis yields diffusion coefficients of solution state of dilute Mb (11.6 × 10⁻⁷ cm²/s) and Hb (7.53 × 10⁻⁷ cm²/s), which agree with literature values (Table 3). In myocardial tissue at 35°C, Mb diffusion decreases from 16.5 to 7.85 × 10⁻⁷ cm²/s.

Averaged translational diffusion coefficients

The literature has reported cellular D_Mb estimates ranging from 1.2–23 × 10⁻⁷ cm²/s, in contrast to the D_Mb of 5–7 × 10⁻⁷ cm²/s at 20°C for 18 g/dl Mb (12,43,44). In rat skeletal muscle homogenate and isolated fiber, metMb exhibits a D_Mb, 1.2–1.5 × 10⁻⁷ cm²/s at ∼20°C (13,14). FRAP experiments have measured a D_Mb of 1.7–2.2 × 10⁻⁷ cm²/s at 37°C following the diffusion of a microinjected horse metMb conjugated with a fluorescence dye in isolated muscle fiber (16,17). According to the FRAP experiments, cellular Mb diffuses 10 times slower than dilute Mb solution.

Even though the fluorescence recovery experiments yield a cellular D_Mb, the uncertain contribution of metMb reaction kinetics with Mb reductase, the nonphysiological nature of an isolated fiber model, and differential bound and free metabolite pool in homogenate versus in the cell raise questions about the validity of the FRAP determined D_Mb in respiring tissue (18,45). According to the NMR analysis, Mb diffusion in respiring tissue slows to ∼48% of the solution state value at 35°C. Mb diffuses 3.6 times faster than the Mb mobility determined by FRAP.

Rotational diffusion plays a very minor role in facilitating O₂ transport, since O₂ remains bound during the correlation time and does not move a significant distance (46,47).

D_Mb and Mb contribution to O₂ flux

The D_Mb and K₀ provide a means to partition the contribution from free O₂ and MbO₂. K₀ depends upon temperature and has reported values ranging from 2.52 to 4.81 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹ (38). With a K₀ of 4.18 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹, a P50 of 1.98 mmHg, and a myocardium Mb concentration of 0.19 mM, the averaged cellular D_Mb of 7.85 × 10⁻⁷ cm²/s yields a equipoise diffusion PO₂ of 1.67 mmHg. Below a PO₂ of 1.67 mmHg, the Mb-dependent contribution to the O₂ flux begins to dominate.

Given that sufficient O₂ exists to saturate Mb > 90% in the basal state, the basal PO₂ must stand poised well above 10 mmHg. Even with increased workload and respiration, in vivo myocardium experiments have not detected partial O₂ saturation of Mb (23,25,48). No transient fluctuation in MbO₂ saturation appears over the cardiac contraction cycle (33). In the basal state myocardium at 35°C, Mb does not play a significant role in regulating respiration under normoxic conditions.

As temperature increases from 22°C to 40°C, myocardial function and Mb diffusion increase. Mb P50 rises from 0.55 to 3.23 mmHg; D_Mb increases from 4.24 to 8.37 × 10⁻⁷ cm²/s. The increased Mb diffusion with temperature enhances its ability to transport O₂.

However, the contribution of free O₂ flux also increases linearly with PO₂ and K₀. K₀ increases from 22°C to 40°C (2.52, 3.08, 4.18, and 4.81 × 10⁻⁵ ml O₂ cm⁻¹min⁻¹atm⁻¹). Moreover, P50 also increases from 0.55 to 3.23, extrapolated from equation of temperature-dependent Mb P50 (49). The competing effects of K₀ and P50 versus D_Mb create a decrease in the equipoise diffusion PO₂ from 2.72 to 0.15 mmHg in myocardium as tissue temperature rises. A similar trend appears in skeletal muscle.

A definitive equipoise diffusion PO₂ analysis requires firm experimental K₀ and P50 values. Unfortunately, the literature contains a range of P50 and K₀ values, especially with respect to temperature. For Mb P50, the values can vary from 0.55 to 1.5 mmHg at 25°C (10,49). For K₀, the values also vary widely (38). At a given P50 value, an increase in the experimentally determined K₀ value will decrease the equipoise diffusion PO₂. Similarly, at any given K₀, a rising P50, as observed with increasing temperature, will decrease the equipoise diffusion PO₂.

D_Mb and myocardial function

Mb-facilitated diffusion appears to have no significant role in regulating myocardial respiration. In the basal state, in situ myocardium exhibits no detectable ¹H-NMR signal of the deoxy Mb proximal histidyl N_δH proton (23,25,48). The basal PO₂ must then saturate over 90% of MbO₂. With Mb p50 of 2.3 at 37°C, the basal PO₂ exceeds 10 mmHg. Even when myocardial respiration increases by a factor of 2 in the in situ myocardium, NMR still cannot detect any deoxy Mb signal. Certainly, in whole animals, myocardial work can increase 5 times above the basal level. However, if Mb does not desaturate as work increases 2 times above the basal level, increasing the work 2.5 times more would probably still not drop the PO₂ from >10 mmHg to the equipoise diffusion PO₂ of 1.67 mmHg, in which Mb can begin to contribute significantly to the O₂ flux.

The O₂ saturation state of the residual 10% of the MbO₂ reflects a measurement uncertainty and not the presence of any partially saturated MbO₂ pool. Given the signal to noise and baseline contribution, rigorous NMR spectral interpretation usually avoids ascribing statistical significance to any peak that has a 1.1:1.0 signal/noise ratio, especially with respect to calculating a PO₂ in the basal state from a hyperbolic relationship describing O₂ binding to Mb. With PO₂ well above the P50, a small change in the deoxy Mb signal intensity can correspond nonlinearly to a large change in the PO₂. Even if the cell contains a 10% partially saturated Mb pool, such a small pool would permit only 10% of the Mb to contribute to the O₂ flux and decrease dramatically the equipoise diffusion PO₂.

The insignificant contribution of Mb to myocardial O₂ flux agrees with Mb inactivation studies (36,41). Under a range of normoxic, hypoxic, and work conditions, acute CO inactivation of up to 80% of Mb in the myocardium produces no respiratory, contractile, or metabolic alteration in the myocardium. Even under conditions that should accentuate the purported Mb-facilitated O₂ diffusion, Mb inactivation still does not trigger any significant physiological response (36,41).

D_Mb and skeletal muscle function

In human skeletal muscle, most NMR studies have also not detected the proximal histidyl N_δH signal of deoxy Mb in the resting state, consistent with a PO₂ above 10 mmHg (24,50,51). Only one recent study has invoked the increased sensitivity of a 4 T (Tesla) magnetic field over 1.5–2 T used in previous experiments to claim the detection of a deoxy Mb signal in resting muscle, ascribed to a PO₂ of 34 mmHg (52). The primary spectral evidence, however, appears quite poor and unconvincing. Moreover, the purported sensitivity enhancement of 4 T over 1.5–2 T overlooks the reported sensitivity loss arising from field-dependent relaxation of the deoxy Mb proximal histidyl N_δH signal, which broadens the line width and decreases the signal to noise with a quadratic dependence on field (20). Nevertheless, in all cases, given the equipoise diffusion PO₂ of 4.24 mmHg at 40°C, Mb has no significant contribution to O₂ flux in the resting state of skeletal muscle.

As muscle starts to contract, however, Mb desaturates rapidly and reaches within ∼30 s a steady-state level (24,50). In one report, the steady-state Mb desaturation level declines from 30% to 48% as work in the gastrocnemius muscle increases from 7.8 to 15.1 W (24). In another report, Mb desaturation in exercising quadriceps reaches a steady-state level of ∼50% and does not change as work increase from 50% to 100% of VO_2max (50). A simple reconciliation of the discordant observations has focused just on the different exercise protocol and intensity (53). The D_Mb, however, casts another perspective.

With muscle contraction, the rising energy demand decreases the intracellular PO₂ and can confer an increasing role for Mb-facilitated diffusion. However, the intracellular PO₂ must fall from 10 mmHg or precipitously from 34 mmHg to reach a level of 4.24 mmHg, just above the P50 of 3.23 mmHg at 40°C, before Mb contributes equally with free O₂ to the overall O₂ flux. Mb desaturation coincides with the notion that Mb-facilitated diffusion predominates and rises when muscle contraction energy demands more O₂ flux to meet the rising VO₂.

A constant Mb desaturation from 50% to 100% VO_2max, however, fixes the intracellular PO₂ at a certain level. That, then, defines correspondingly a constant contribution from Mb-facilitated diffusion. The constant PO₂ implies an unchanging intracellular gradient. According to Eq. 5, the intracellular O₂ flux depends upon a PO₂ gradient 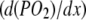. The integration of Eq. 5 across an unchanging dimension from the sarcolemma to the mitochondria will yield a constant PO₂ associated with a constant level of Mb desaturation. But the same intracellular gradient also governs free O₂ diffusion. Regardless of the increase in conductive or convective diffusion, the intracellular O₂ gradient cannot enhance either the Mb or free O₂ flux to match the rising O₂ demand with work. So explaining away the discordant observations of Mb desaturation as a consequence of light versus heavy workload skirts a fundamental question about the impact of the intracellular O₂ gradient in controlling the intracellular O₂ flux. Certainly additional experiments must continue to clarify this.

Transient versus steady state

The role of Mb may vary dramatically in different tissues and in different organisms. Mb concentration appears to confer a different role in myocardium versus skeletal muscle. In marine mammalian muscle, the high Mb concentration leads to a very high equipoise diffusion PO₂ and confirms a prominent role for Mb to serve as an O₂ depot and as a significant transporter of O₂ (3). In seal muscle, the 4 mM Mb concentration raises the equipoise diffusion PO₂ to 67 mmHg. Mb-facilitated diffusion predominates under all physiological conditions.

Mb kinetics experiments cast another perspective on Mb function. At the beginning of muscle contraction, Mb releases rapidly its O₂ store and deoxygenates within ∼30 s to a steady-state level (24,54). Focusing only the steady-state changes in Mb desaturation would miss the rapid kinetics that implicate a role for Mb to catalyze the bioenergetics transition from rest to work (33,55).

Isotropic versus anisotropic diffusion

The assessment of Mb contribution to O₂ transport with an averaged D_Mb assumes isotropic diffusion. Because the muscle fiber has a longer axial than radial dimension, the diffusion paths should differ correspondingly. Given nonuniform distribution of subcellular structures and the attendant anisotropic tortuosity in the sarcoplasm, the expected D_Mb anisotropy can alter the equipoise diffusion PO₂ analysis (13,18). Indeed, researchers have ascribed anisotropic diffusion to PCr and ATP in the sarcoplasm (56).

For Mb, under temperature conditions from 22°C to 35°C, the translational diffusion shows no orientation preference. At 35°C, Mb exhibits an averaged D_Mb of 7.85 ± 0.49 × 10⁻⁷ cm²/s mobility. In the X, Y, and Z directions, the Mb diffuses at 7.97 ± 1.03, 7.76 ± 0.68, and 7.85 ± 0.79 × 10⁻⁷ cm²/s, respectively. FRAP experiments have also not discerned any diffusion anisotropy (17).

The NMR determined cellular D_Mb of 4.24 × l0⁻⁷ cm²/s at 25°C agrees well with the isotropic rotational diffusion analysis (20). In the field-dependent measurements to determine the rotational correlation time (τ_r) of Mb in solution (9.7 ± 0.3 × 10⁻⁹ s) and in perfused myocardium (13.6 ± 1.3 × 10⁻⁹ s), the 1.4 time increase in the τ_r corresponds most likely to a comparable increase in the cellular microviscosity, based on the Stokes-Einstein relationship. If the solution and cellular molecular hydrodynamics behave identically and if unrestricted diffusion exists, then the increased viscosity and the solution D_Mb of 5–7 × 10⁻⁷ cm²/s at 20°C for 18 g/dl Mb lead to an estimated cellular D_Mb of 3.6–5.0 × l0⁻⁷ cm²/s (12,43,44).

In contrast to the D_Mb (1.7 × 10⁻⁷ cm²/s at 37°C) determined in FRAP experiments using microinjected metMb with an attached fluorophore, the D_Mb (7.85 × 10⁻⁷ cm²/s at 35°C), derived from NMR translational diffusion analysis, shows a much higher Mb diffusion mobility in respiring myocardium (16).

At this time, measurements cannot follow Mb diffusion over a long observation time to detect any restricted diffusion boundaries. For NMR, the available spectrometer has an insufficient detection sensitivity limit to overcome the relaxation losses to observe diffusion or a longer RMS displacement. Such observations would clarify the dimensions of the restricted diffusion boundaries and define any diffusion anisotropy.

RMS displacement

To assess the RMS displacement of Mb, previous studies have used the O₂ off rate constant for MbO₂ of 12 s⁻¹ to obtain a t_½ of 58 ms at 20°C (6,57). The displacement reflects the effective Mb diffusion distance before it loses one-half of its O₂. Given D_Mb of 4.24 × 10⁻⁷ cm²/s, the Einstein-Smoluchowski equation, 〈r²〉 = 6 Dt, yields an RMS displacement of 〈r〉 = 3.8 μm (6). The analysis approach would predict a 〈r〉 = 96 μm for MbCO, given a CO off rate constant of 19 × 10⁻³ s⁻¹ (58). Both MbCO and MbO₂, however, exhibit a similar diffusion coefficient, 11.6 × 10⁻⁷ cm²/s at 22°C.

Another approach to estimate the RMS displacement uses the PGSTE pulse train interval, Δ = 24 ms. Such analysis reveals an 〈r〉 = 2.5–3.5 μm from 22°C to 40°C. Within 2.5–3.5 μm, the data do not indicate any diffusion restriction imposed by subcellular organelles or macromolecules. The insufficient signal sensitivity of the available spectrometer precludes measurements in this study at longer PGSE time intervals that can determine the restricted diffusion boundary. However, according to previous studies of PCr and ATP diffusion in muscle cell, the unrestricted displacement extends radially 8–11 μm from the longitudinal fiber axis and circumscribes a cylindrical boundary that demarcates unrestricted from restricted diffusion (56,59).

Since muscle cells have a typical dimension of 10 × 100 μm, the 〈r〉 of 2.5–3.5 μm represents a small portion of the cell and stays well within the unrestricted diffusion region (60). Moreover, electron microscopy analysis has revealed that many mitochondria cluster near the capillary and form a reticulum. Within an RMS displacement of 2.5–3.5 μm, Mb encounters no diffusion barrier to O₂ delivery (61). Any limitation in the contribution of Mb to the overall O₂ flux must arise from the interaction of microviscosity on Mb mobility.

Cytoplasmic property and architecture

Both the translational and rotational diffusion analyses point to a local cellular environment that slows Mb diffusion. Cellular Mb exhibits a rotational diffusion ∼1.4 slower than solution Mb (20). Translational diffusion shows a decrease from 11.6 to 4.24 × 10⁻⁷ cm²/s at 22°C, 2.7 times slower. The observation stands in excellent agreement with the fluorescence diffusion measurements. Relative to the diffusion in saline solution, green fluorescent protein in the cytoplasm exhibits rotational (1.5 times) and translational diffusion (3.2 times) times slower than in saline solution (62). Moreover, parvalbumin diffuses out of frog skinned fibers with an isotropic, averaged diffusion coefficient of 3.74 ± 0.81 × 10⁻⁷ cm²/s at 4°C, also ∼1/3 the solution diffusion rate (63). These observations do not agree with the reported 10 time decrease in the cytoplasmic D_Mb (16). The discrepancy may arise from model-dependent difference that affects the cellular volume (62).

The decreased diffusion in the cytoplasm can originate from increased cellular viscosity, tortuosity, and protein interaction with the cytomatrix or diffusible particles. If only viscosity contributes to the decrease in Mb mobility, then the relative D_Mb in solution and in the cell yields an estimate of the relative viscosity change. Based on H₂O or dilute solution Mb viscosity of 0.95 cP (centipoise) at 22°C, the cellular viscosity must reach 2.6 cP, about a 2.74 increase in viscosity, to account for the observed D_Mb (64). FRAP experiments have also determined a cellular viscosity between 2–3 cP (65).

However, the viscosity values predicted by the rotational diffusion measurements appears 2 times smaller. Part of the discordance may arise from the assumptions underlying the derivation of the Stokes-Einstein equation, which expresses a linear relationship between the rotational correlation time and viscosity. The derivation assumes a Brownian particle moving in an ideal, homogeneous, and isotropic solvent. Given an extremely small solvent particle size, classical hydrodynamics then just regards the solvent as continuum. Unfortunately, the cytosol contains a dispersion of large molecular weight cosolutes, such as proteins and ribosomes. The solvent no longer acts as a continuous medium. These cosolutes can disrupt assumptions leading to a linear relationship between correlation time and viscosity. Indeed, recent studies have demonstrated that the microviscosity experienced by a particle in the cell exhibits a power dependence with respect to the bulk viscosity, 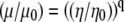, where μ and μ₀ represent the microviscosity in the cell and in the reference state, respectively; η and η₀ represent the bulk viscosity in the cell and in the reference state, respectively. Based on the viscosity 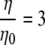predicted by cell models and a reported estimate of q ∼ 0.3, 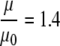. The calculated microviscosity value matches the relative microviscosity of 1.4 derived from the rotational diffusion measurements (66,67). Such a perspective agrees with the premise that viscosity instead of tortuosity or macromolecular interaction contributes predominantly to the decreased Mb diffusion in the cytoplasm. Additional insights on the cellular microviscosity derived from rotational and translational diffusion measurements await further theoretical clarification.

The temperature-dependent change in D_Mb and the attendant alteration of viscosity shed additional insight into the current models of the cytoplasm. These models envision the cytoplasm as a concentrated macromolecular solution, a rigid gel network, or an entangled filament network. Distinguishing these different models requires diffusion measurement and modeling of different size molecular probes. As the molecule size increases, a gel network will permit molecular movement until the molecule reaches a percolation cutoff size. Above the percolation cutoff, the probe becomes trapped in the finite volumes of the network. A concentrated macromolecular solution has no percolation cutoff as molecular radius increases. All cytoplasm models, however, envision proteins diffusing at least three times slower in the cell than in solution (27).

Mb diffuses in the cell slightly faster than the value predicted by the cytoplasm models. Its diffusion property casts a perspective on the postulated gel network model. In such a model, the observed D_Mb would indicate a percolation cutoff that must exceed 17.5 Å, the hydrodynamic molecular diameter of Mb (26). It is much larger than expected. Without such a large cutoff size, the NMR data would reveal compartmentalization and restricted diffusion. Any cellular network does not impede significantly the mobility of a monomeric 17-kD protein.

Given that both Mb and a 0.5-kD molecular probe diffuse 3 times slower in the cell than in solution, cellular crowding also cannot impose a significant diffusion barrier within an ∼2.5–3.5 μm RMS displacement (68). Indeed, the NMR determined Mb rotational diffusion and the Val E11 line width argue for a local fluid phase that approximates water, in agreement with recent time-resolved fluorescence anisotropy measurements of the cell fluid phase viscosity (28,69,70). The mobility of cellular Mb raises a question about the impact of any postulated cellular crowding on chemical reactions, such as the ones maintaining metabolic homeostasis (71–73).

Finally, the Q₁₀ analysis yields another perspective. Because the Q₁₀ of Mb diffusion in the cell from 25°C to 35°C (1.41) approximates the corresponding Q₁₀ of solution Mb (1.31), no temperature-dependent alteration of the postulated gel phase in the cell has any significant impact on the Mb or monomeric protein mobility.

CONCLUSION

The averaged translational Mb diffusion coefficient of 4.24–8.37 × 10⁻⁷ cm²/s, Mb concentration, P50, and K₀ lead to the determination of equipoise diffusion PO₂ values, which indicate that Mb has no significant role in facilitating O₂ transport in myocardium, has a potential role in skeletal muscle, especially during the onset of contraction and only if PO₂ falls significantly and plays a dominant role for Mb-facilitated diffusion in marine mammals with high Mb concentration in their muscle. The diffusion data also indicate that any postulated cellular gel network must have a percolation cutoff larger than 17.5 Å.