Abstract
Studies performed in our laboratory demonstrated the formation of two thermodynamically distinct complexes on binding of netropsin to a number of hairpin-forming DNA sequences containing AATT-binding regions. These two complexes were proposed to differ only by a bridging water molecule between the drug and the DNA in the lower affinity complex. A temperature-dependent isothermal titration calorimetry (ITC)-binding study was performed using one of these constructs (a 20-mer hairpin of sequence 5′-CGAATTCGTCTCCGAATTCG) and netropsin. This study demonstrated a break in the heat capacity change for the formation of the complex containing the bridging water molecule at ∼303 K. In the plot of the binding enthalpy change versus temperature, the slope (ΔCp) was −0.67 kcal mol−1 K−1 steeper after the break at 303 K. Because of the relatively low melting temperature of the 20-mer hairpin (341 K (68°C)), the enthalpy change for complex formation might have included some energy of refolding of the partially denatured hairpin, giving the suggestion of a larger ΔCp. Studies done on the binding of netropsin to similar constructs, a 24-mer and a 28-mer, with added GC basepairs in the hairpin stem to increase thermal stability, exhibit the same nonlinearity in ΔCp over the temperature range of from 275 to 333 K. The slopes (ΔCp) were −0.69 and −0.64 kcal mol−1 K−1 steeper after 303 K for the 24-mer and 28-mer, respectively. This observation strengthens the argument regarding the presence of a bridging water molecule in the lower affinity netropsin/DNA complex. The ΔCp data seem to infer that because the break in the heat capacity change function for the lower affinity binding occurs at the isoequilibrium temperature for water, water may be included or trapped in the complex. The fact that this break does not occur in the heat capacity change function for formation of the higher affinity complex can similarly be taken as evidence that water is not included in the higher affinity complex.
INTRODUCTION
Physiologically relevant solution studies of macromolecular interactions with small molecules are performed in water with dissolved ions at near neutral pH. The role of water in binding small molecules to nucleic acids and other biopolymers therefore is an important consideration in drug design strategy. Water is generally believed to play a significant role in a number of biological interactions including the formation of binding complexes between small molecules and nucleic acids, as well as complexes of small molecules and proteins (1–14). Not only is it essential to study how the size, structure, and charge density of a small molecule dictate its interactions with a macromolecular target structure, it is also important to understand how solvent water participates in this interaction.
The most well known role of water in the formation of small molecule/DNA complexes is its contribution to the thermodynamics of complex formation. For example, disruption of the solvent cage around a nucleic acid can affect binding affinity through the entropically favorable disordering of the solvent cage (3,15–21). Another role that water has been demonstrated to play in forming small molecule/DNA complexes is by allowing molecules which are not the “right” shape to fit into a binding site by bridging between the nucleic acid and the small molecule (6–8,12–14). Complexes formed between minor groove-binding agents and the DNA minor groove have been a topic of biophysical interest for some time (22–36). Previously published work from our laboratory identified the formation of two thermodynamically distinct complexes upon binding netropsin to a number of hairpin and duplex DNA constructs (13,14). This study proposed that the binding of netropsin occurred in two conformations: one was an ideally suited crescent shape (which would fit nicely into the minor groove), and the other was a less favorable conformer that was not bent like a typical minor groove-binding agent. It was proposed that the latter conformer of the drug molecule is aided in binding to the minor groove by a water molecule that forms a bridge between the nucleic acid and the drug compound.
The purpose of this study is to probe the thermodynamics of the binding interaction between netropsin and the minor groove of DNA in more detail than that performed in the previous study. The main focus is on the temperature dependence of the enthalpy change of binding (i.e., ΔCp), which may give more insight into the nature of formation of both complexes. The main construct probed in the previous study was a 20-mer hairpin with an AATT-binding site. The 20-mer original hairpin (OHP) construct has a melting temperature of 341 K (68°C) under the solution conditions studied. Titration data collected for netropsin binding at temperatures above 323 K were expected to contain some energy of refolding the hairpin structure simultaneously with the drug-binding energy. In this study we used 24-mer and 28-mer hairpin constructs containing additional GC pairs in the stem while maintaining the same AATT netropsin-binding site. These constructs were stabilized over the OHP by 13 and 20 K, respectively. This allowed temperature-dependent netropsin-binding experiments to be performed at temperatures in excess of 333 K without any concern about including refolding energy in the measured binding enthalpies. The more in-depth study of the change in heat capacity for the binding of netropsin to these more stable hairpin constructs gives more insight into the complex binding described previously and aids in the further understanding of the role of water in the formation of complexes between minor groove-specific small molecules and DNA.
MATERIALS AND METHODS
Isothermal titration calorimetry
Oligonucleotides were obtained from Oligos Etc. (Wilsonville, OR). The oligonucleotide “code” or reference names, e.g., OHP, n-mer length, e.g., 20-mer, complete sequences, e.g., 5′-d(CGAATTCGTCTCCGAATTCG)-3′, and netropsin-binding site sequence, i.e., AATT/AATT, are given in Table 1. Netropsin was obtained from Sigma Aldrich (St. Louis, MO). Oligonucleotides were prepared in MES (2-(N-morpholino)-ethanesulphonic acid) buffer (0.01 M MES, 0.001 M EDTA, 0.2 M NaCl, pH 6.2) and dialyzed against two changes of buffer (24 h each) at 277 K (4°C). Oligonucleotide concentrations for isothermal titration calorimetry (ITC) were nominally 1.0 × 10−5 M. The concentrations of all of the DNA solutions were verified using ultraviolet/visible (UV/Vis) spectrophotometry with molecular extinction coefficients determined using a nearest-neighbor calculation for single-strand DNA (37) and the absorbance of thermally denatured constructs extrapolated back to 298 K (25°C) and/or a total phosphate analysis technique (38). The extinction coefficients determined for the 20-mer OHP, 24-mer long stem hairpin (LSHP), and 28-mer double long stem hairpin (DLSHP) by these techniques were ɛ260 = 1.76 × 105 M−1 cm−1, 2.07 × 105 M−1 cm−1, and 2.39 × 105 M−1 cm−1, respectively.
TABLE 1.
The OHP along with alternate hairpin sequences including base additions in the stem, loop, and tail regions as well as the duplex structure
| Code name | Complete hairpin sequence | n-mer |
|---|---|---|
| OHP | 5′-d(CGAATTCGTCTCCGAATTCG)-3′ | 20-mer |
| LSHP | 5′-d(CGAATTCGCGTCTCCGCGAATTCG)-3′ | 24-mer |
| DLSHP | 5′-d(CGCGAATTCGCGTCTCCGCGAATTCGCG)-3′ | 28-mer |
The code names stand for OHP, LSHP, and DLSHP. The code names are given to simplify the results and discussion references to individual DNA constructs. The bases located in the netropsin-binding region are shown in bold. The bases added to the OHP to lengthen the stem above or below the binding site are indicated by underlining.
All netropsin solutions were prepared using the final dialysate from the oligonucleotide solutions. Concentrations of netropsin were nominally 1.5 × 10−4 M. Concentrations for netropsin were verified with UV/Vis spectrophotometry using a published molar extinction coefficient of ɛ296 = 2.15 × 104 M−1 cm−1 (39).
ITC experiments were performed using a Microcal (Northhampton, MA) VP-ITC. Titrations were typically done at temperatures from 275 K to 333 K and involved overfilling the ITC cell with ∼1.5 ml of dilute oligonucleotide solution and adding as many as 50–60 injections (5 μl) of the dilute solution ligand. Typically three replicate measurements were made. The raw calorimetric data were corrected for the heat of dilution of the netropsin and oligonucleotide by subtracting the heats from the appropriate blank titrations. These heats were small in comparison to the binding interaction heats, and the data shown in Fig. 1 are the blank corrected data. At high stoichiometries the corrected heats approach zero, although a small effect from nonspecific aggregation of netropsin with the oligonucleotide may be present. The thermograms (integrated heat/injection data) obtained in ITC experiments were fit with our own “two-fractional-sites” model fitting algorithm developed for use with Mathematica 5.0 software (13). (The “two-fractional-sites” fitting model is described in more detail in the Results section and in the accompanying Supplementary Materials.) The ITC-binding data obtained for netropsin could only be fit within expected experimental error using our “two-fractional-sites” binding model and our Mathematica-based nonlinear regression algorithm. Values for ΔG1 (K1), ΔG2 (K2), ΔH1, ΔH2, −TΔS1, −TΔS2, n1, and n2 were extracted directly from the fits obtained for our “two-fractional-sites” model. The ∂Δ parameters were obtained by simple subtraction of the second site parameter from the first site parameter (ΔG, ΔH, or −TΔS). ΔCp1 and ΔCp2 values were obtained by plotting ΔHi versus temperature (K) and fitting the temperature data with a simple linear regression model over the appropriate narrow temperature ranges within the entire temperature-dependent data set (275–333 K).
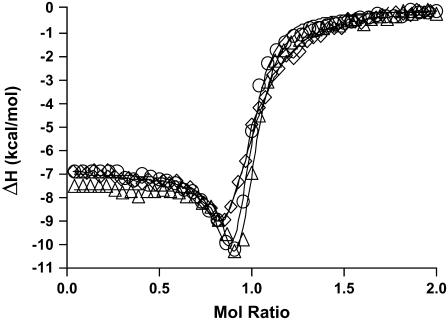
FIGURE 1.
Representative nonlinear regression fits of the ITC-integrated heat data for netropsin binding to the AATT containing OHP (◊), LSHP (Δ), and DLSHP (○) DNA constructs at 298 K (25°C). The fits shown as solid lines are for the “two-fractional-sites” model described by Eqs. 1 and 2. This model is represented by two fractional sites that are constrained to have a combined stoichiometry of 1.0 mol of ligand/mol of DNA. The fit lines shown above were obtained with a user-defined fitting routine coded in Mathematica 5.0 by our laboratory.
Differential scanning calorimetry
For differential scanning calorimetry (DSC) experiments the oligonucleotide concentration was nominally 1 × 10−4 M and netropsin concentrations ranged from 5 × 10−5 M to slightly greater than 1 × 10−4 M. The DSC experiments were performed on a Microcal VP-DSC instrument. The experiments cover the temperature range from 10°C to 110°C. Typically the scan rate was set to 90°C/h, and the typical scanning experiment involved at least three temperature scans for each filling. Replicate experiments were done on separate fillings of the DSC cell. The DSC thermograms (excess heat capacity versus T plots) were analyzed using the Origin 7.1 software and were well fit in all cases with a single “two-state” process. The Origin analysis reported values for the melting temperature, Tm, and the calorimetric and van 't Hoff enthalpies for the transition.
RESULTS
Thermograms obtained for the titration of netropsin with all three of the hairpin constructs are shown in Fig. 1. The symbols represent the corrected heat data, and the lines represent the nonlinear regression fit to our “two-fractional-sites” model. These thermograms could only be fit within experimental error with a two-site model where the total number of sites is one per hairpin, but it is defined as two fractional sites having approximate stoichiometries of 0.66 and 0.33. The equations given below describe a two-site model for the oligonucleotide-drug complex. This model could result, for example, from a situation in which one molecule of drug can bind to the DNA in two different orientations (two fractional sites) having slightly different affinities. In such a model, binding of the drug to the DNA results in two structural conformers for the complex, for example, one conformer that contains the drug molecule and a water molecule bound in the minor groove and one conformer that contains only the drug bound in the minor groove. The following two equations demonstrate the two different pathways for binding the drug to the minor groove, resulting in two different final products: one where all of the groove water has been displaced and one where a single water molecule is trapped (or left behind):
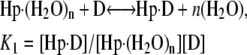 |
(1) |
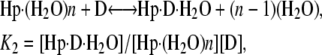 |
(2) |
where K1 and K2 are the equilibrium constants for binding to the higher and lower affinity sites, respectively. The nonlinear regression was constrained to yield values for n1 and n2 that summed to 1 as the stoichiometry for the netropsin-binding interaction is known to be 1:1 for a single A2T2-binding site in the DNA construct. (The “two-fractional-sites” model is described in more detail in the Supplementary Materials.)
The ITC titration data for all three constructs were unusually complex and consistent with the formation of two thermodynamically distinct drug/DNA complexes during the first mol ratio of titrated drug. Representative titration data for all three hairpin constructs are shown in Fig. 1. The enthalpy change for formation of complex 1 between all three hairpin constructs and netropsin is nominally −7 kcal mol−1 (as shown by the y-intercept in Fig. 1, which closely approximates the value for ΔH1). The enthalpy change for formation of complex 2 for the three hairpin constructs varies from a low of −12.0 to a high of −15.9 kcal mol−1 for the OHP and LSHP constructs, respectively. The minima in the three enthalpograms underestimate the fit values for ΔH2. Even as the mol ratio approaches 1, the observed heat (shown in Fig. 1) is a linear combination of both ΔH1 and ΔH2. The difference in binding enthalpy between the formation of complex 1 and complex 2 at 298 K is more exothermic for the second process by 4.9, 8.8, and 6.6 kcal mol−1 for the OHP, LSHP, and DLSHP constructs, respectively. The free energy change for the formation of complex 1 in all three hairpin constructs is nominally −11 kcal mol−1. The difference in the free energy change for complex formation between complex 1 and complex 2 at 298 K is less favorable by 2.9, 2.7, and 2.4 kcal mol−1 for the OHP, LSHP, and DLSHP constructs, respectively.
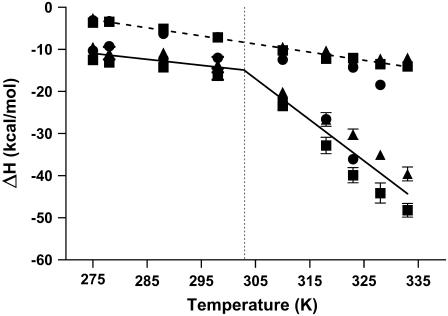
ITC titrations were performed at a range of temperatures from 275 to 328 K for the OHP (Table 2) (due to the low melting temperature of 341 K) and 275 to 333 K for the two longer hairpin constructs (Tables 3 and 4). A plot of the enthalpy change for formation of complexes 1 and 2 is shown in Fig. 2 for all three hairpin constructs. All three systems demonstrate the linearity of the enthalpy change of formation of complex 1 with respect to temperature with ΔCp1 values of −0.26, −0.16, and −0.13 for the OHP, LSHP, and DLSHP hairpin constructs, respectively. The plot also includes the data for the formation of complex 2 for each construct that does not demonstrate the same linearity with respect to temperature as seen with the formation of complex 1.
TABLE 2.
ITC-derived thermodynamic parameters, ΔGi, ΔHi, and −TΔSi for the OHP DNA construct binding netropsin in MES buffer (0.01 M MES, 0.001M EDTA, 0.2 M NaCl, pH 6.2) at a range of temperatures from 275 to 328 K
| Temp (K) | ΔG1* (kcal/mol) | ΔH1* (kcal/mol) | −TΔS1 (kcal/mol) | ΔG2* (kcal/mol) | ΔH2* (kcal/mol) | −TΔS2 (kcal/mol) |
|---|---|---|---|---|---|---|
| 275 | −9.7 | −3.1 | −6.6 | −7.7 | −10.3 | 2.6 |
| 278 | −9.2 | −3.3 | −5.9 | −7.4 | −9.2 | 1.8 |
| 288 | −9.7 | −6.3 | −3.4 | −8.0 | −12.2 | 4.2 |
| 298 | −11.2 | −7.1 | −4.1 | −8.3 | −12.0 | 3.7 |
| 310 | −10.9 | −12.4 | 1.5 | −8.6 | −21.7 | 13.1 |
| 318 | −11.2 | −11.9 | 0.7 | −8.8 | −26.6 | 17.8 |
| 323 | −11.4 | −14.3 | 2.9 | −8.4 | −36.1 | 27.7 |
| 328 | −8.9 | −18.4 | 9.5 | na | na | na |
The parameters are for the “two-independent-sites” binding model.
The uncertainties (not shown here) for fit parameters ΔG1, ΔG2, ΔH1, and ΔH2 were taken directly from the fitting program and were typically <2% of the listed parameter value.
TABLE 3.
ITC-derived thermodynamic parameters, ΔGi, ΔHi, and −TΔSi, for the LSHP DNA construct binding netropsin in MES buffer (0.01 M MES, 0.001 M EDTA, 0.2 M NaCl, pH 6.2) at a range of temperatures from 275 to 333 K
| Temp (K) | ΔG1 (kcal/mol) | ΔH1 (kcal/mol) | −TΔS1(kcal/mol) | ΔG2 (kcal/mol) | ΔH2 (kcal/mol) | −TΔS2 (kcal/mol) |
|---|---|---|---|---|---|---|
| 275 | −9.8 (±0.2) | −3.6 (±0.5) | −6.2 | −8.3 (±1.3) | −14.8 (±2.0) | 6.5 |
| 278 | −9.5 (±0.1) | −3.4 (±0.5) | −6.1 | −8.3 (±0.4) | −13.1 (±0.5) | 4.8 |
| 288 | −10.0 (±0.2) | −5.1 (±0.6) | −4.9 | −8.3 (±0.4) | −14.2 (±0.7) | 5.9 |
| 298 | −10.9 (±0.5) | −7.1 (±0.5) | −3.8 | −8.5 (±0.2) | −15.9 (±2.3) | 7.4 |
| 310 | −10.9 (±0.1) | −9.5 (±0.8) | −1.4 | −8.6 (±0.2) | −23.4 (±1.4) | 14.8 |
| 318 | −11.2 (±0.1) | −12.2 (±0.3) | 1.0 | −8.7 (±0.2) | −32.8 (±3.4) | 24.1 |
| 323 | −11.1 (±0.2) | −−12.0 (±1.3) | 0.9 | −8.5 (±0.2) | −39.8 (±3.1) | 31.3 |
| 328 | −11.2 (±0.2) | −13.5 (±2.0) | 2.3 | −8.3 (±0.2) | −44.1 (±4.2) | 35.8 |
| 333 | −11.4 (±0.4) | −13.2 (±1.9) | 1.8 | −8.3 (±0.2) | −46.8 (±2.8) | 38.5 |
The parameters are for the “two-independent-sites” binding model. The uncertainties listed for ΔGi and ΔHi are ±1 standard deviation from the mean values determined by averaging triplicates for each experiment.
TABLE 4.
ITC-derived thermodynamic parameters, ΔGi, ΔHi, and −TΔSi, for the DLSHP DNA construct binding netropsin in MES buffer (0.01 M MES, 0.001 M EDTA, 0.2 M NaCl, pH 6.2) at a range of temperatures from 275 to 333 K
| Temp (K) | ΔG1 (kcal/mol) | ΔH1 (kcal/mol) | −TΔS1 (kcal/mol) | ΔG2 (kcal/mol) | ΔH2 (kcal/mol) | −TΔS2 (kcal/mol) |
|---|---|---|---|---|---|---|
| 275 | −9.7 (±0.3) | −2.6 (±0.2) | −7.1 | −7.8 (±0.5) | −9.4 (±0.2) | 1.6 |
| 278 | −9.9 (±0.1) | −3.4 (±0.1) | −6.5 | −7.4 (±0.3) | −10.9 (±2.6) | 3.5 |
| 288 | −10.4 (±0.1) | −5.1 (±0.3) | −5.3 | −8.0 (±0.1) | −10.8 (±0.5) | 2.8 |
| 298 | −11.0 (±0.5) | −7.0 (±0.1) | −4.0 | −8.6 (±0.2) | −13.6 (±3.2) | 5.0 |
| 310 | −11.5 (±0.3) | −9.4 (±0.2) | −2.1 | −8.8 (±0.3) | −20.1 (±1.2) | 11.3 |
| 318 | −11.3 (±0.2) | −10.3 (±0.8) | −1.0 | −8.9 (±0.1) | −26.7 (±2.9) | 17.8 |
| 323 | −11.5 (±0.3) | −12.6 (±0.9) | 1.1 | −8.8 (±0.1) | −30.1 (±2.1) | 21.3 |
| 328 | −11.3 (±0.6) | −12.2 (±0.7) | 0.9 | −9.1 (±0.6) | −35.0 (±0.6) | 25.9 |
| 333 | −11.3 (±0.2) | −12.1 (±0.5) | 0.8 | −9.1 (±0.2) | −39.6 (±2.9) | 30.5 |
The parameters are for the “two-independent-sites” binding model. The uncertainties listed for ΔGi and ΔHi are ±1 standard deviation from the mean values determined by averaging triplicates for each experiment.
FIGURE 2.
Temperature dependence of the enthalpy change for netropsin binding to the AATT containing hairpins OHP (•), LSHP (▪), and DLSHP (▴). In all three systems the first binding mode (dashed line) demonstrates a linear dependence of the enthalpy change on the temperature over the measurement range of 275–328 K (for OHP) or 275–333 K (for LSHP and DLSHP). The slope of the simple linear regression line shown corresponds to a global fit line with a slope of ΔCp1 = −0.19 ± 0.01 kcal mol−1 K−1. Fitting each system individually yielded ΔCp1 values of −0.26, −0.16, −0.15 kcal mol−1 K−1 for the OHP, LSHP, and DLSHP, respectively. The second binding mode (solid line) demonstrates two different heat capacity profiles, one at temperatures below 303 K and a significantly steeper heat capacity profile at temperatures above 303 K. The slope of the low temperature simple linear regression line shown corresponds to a global fit line with a slope of ΔCp2 = −0.14 ± 0.04 kcal mol−1 K−1. Individual linear regression analyses on the data below 303 K on all three systems yielded ΔCp2 (1) values of − 0.19, − 0.16, and −0.89 kcal mol−1 K−1 for the OHP, LSHP, and DLSHP, respectively. The slope of the high temperature simple linear regression line shown corresponds to a global fit line with a slope of ΔCp2 = −0.98 ± 0.09 kcal mol−1 K−1. Linear regression analyses on the data above 303 K for all three systems yielded ΔCp2 (2) values of − 1.06, − 0.79, and −0.89 kcal mol−1 K−1 for the OHP, LSHP, and DLSHP, respectively.
These lines instead contain a break at ∼303 K, where there is a significant change in the slope of the line yielding two values for the heat capacity change, one below 303 K and one at temperatures higher than 303 K. The OHP construct demonstrated ΔCp2 values of −0.19 and −1.06 kcal mol−1 K−1, the LSHP demonstrated ΔCp2 values of −0.16 and −0.79 kcal mol−1 K−1, and the DLSHP demonstrated ΔCp2 values of −0.15 and −0.89 kcal mol−1 K−1.
Because of the low melting temperature of the OHP construct, it is assumed that the measured binding enthalpy in experiments performed above 323 K contains some refolding energy. Close inspection of the DSC curve for melting the OHP (Fig. 3) allows the unfolded fraction of the hairpin to be estimated for these temperatures. By subtracting the estimated refolding energy obtained from the DSC experiments, the 323 K experiment point for ΔH2 moved up and onto the line defined by the ΔH2 values at temperatures above 303 K. Because the 328 K experiment with the OHP appeared to be well fit with a single binding process, no attempt was made to correct and include the 328 K titration data point for the OHP in the heat capacity plot for binding process 2.
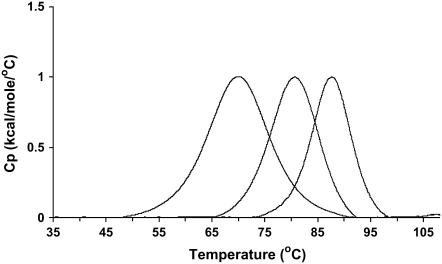
FIGURE 3.
DSC data of all three hairpin constructs showing the shift in melting temperature upon addition of GC interactions in the hairpin stem. The melting temperatures for the OHP, LSHP, and DLSHP are 68°C, 80°C, and 87°C, respectively.
DSC experiments with the three hairpin constructs demonstrated melting temperatures of 341, 354, and 361 K (68°C, 81°C, and 88°C) (Fig. 3). The enthalpy of unfolding all three hairpin structures was nominally 70 kcal mol−1 (62, 68, and 72 kcal mol−1 for the OHP, LSHP, and DLSHP constructs, respectively). Profiles for the naked hairpin and the 1:1 complexes were fit with a simple two-state model, and the addition of one mol ratio of netropsin shifted the melting temperatures from 10°C to 20°C above the melting temperatures for the naked hairpins, demonstrating tight binding of netropsin to all three hairpin constructs (data not shown).
DISCUSSION
ITC titrations with the two modified hairpin constructs demonstrated the same complex binding behavior observed previously for the OHP system (13,14) and other systems (40). The modifications performed on the stem of the hairpin DNA did not eliminate the complex binding. It should be noted here that ITC, because it allows for the simultaneous determination of the free energy, enthalpy, and entropy changes for complex formation, is a technique that is uniquely suited to observe this complex binding behavior. Equilibrium methods, for example SPR, DSC, and various spectroscopic methods, would fail to identify the presence of two distinctly different binding modes (one involving the trapping of a water molecule) for the netropsin hairpin interaction (14).
The temperature-dependent data for binding netropsin to the OHP have been analyzed to yield values of heat capacity change at constant pressure, ΔCp, for both the site 1 and site 2 interactions. The site 1 interaction exhibits a ΔCp1 of −0.19 kcal mol−1 K−1 275–328 K (2°C–55°C). This is a typical average value that has been observed previously for a number of minor groove binders (5,16,18). This large negative value for ΔCp has been interpreted in terms of the expulsion of 8–10 water molecules from the DNA minor groove on ligand binding (5,16,18). There is not much new in these data for site 1 binding. However, the site 2 enthalpy change is not a simple linear function of temperature (see Fig. 2). The site 2 binding interaction exhibits a different value for ΔCp2 at temperatures below 303 K and a second even more negative value for ΔCp2 at temperatures above 303 K. The two values for ΔCp2 are −0.14 kcal mol−1 K−1 at the lower temperatures and −0.97 kcal mol−1 K−1 at temperatures above 303 K. Enthalpy-entropy compensation has been a poorly understood but much discussed topic for more than 35 years (41). It is often discussed in terms of either isokinetic or isoequilibrium relationships (17). Linear-free energy relationships, plots of ΔH versus ΔS, are often analyzed in terms of the slope, β, or isoequilibrium temperature. For nonionic ligand interactions in water, β values have been reported to range from 280 to 320 K. Dunitz reported an isoequilibrium temperature for hydrogen bonding in water of 300 K (17). The isoequilibrium or often-observed enthalpy-entropy compensation phenomenon is almost certainly a ubiquitous property of water. The observation here that the heat capacity breaks at or near the isoequilibrium temperature of water (303 K) is almost certainly not a coincidence.
Binding of netropsin or other ligands to partially unfolded DNA is known to stabilize the DNA and obviously refold the partially denatured structure. When measuring the binding enthalpies of netropsin complexation with the OHP construct at higher temperatures (approaching the melting temperature), the binding enthalpy would necessarily include some refolding heat. This prompted the experiments done in this study, which employed hairpin constructs with additional GC bases in the stem and having melting temperatures increased by 13 and 20 K for the LSHP or the DLSHP, respectively (Fig. 3). These two constructs also demonstrated the same break in the heat capacity slope at 303 K. This verified that the break in slope seen in the OHP construct was not the result of refolding energy alone but the result of the restructuring of water molecules in the groove of the DNA that affected the energy of binding netropsin into the hairpin groove. In addition it also validated the estimation of the enthalpy of refolding the hairpin structure upon drug binding to the OHP construct in the 323 K experiments.
The temperature dependence of the ΔCp of water was reviewed in an attempt to explain the observed break in the heat capacity plot for formation of complex 2 with all three of these hairpin constructs using the work from Dougherty et al. (42). When the change in ΔCp was calculated with respect to temperature, it was determined that the contribution of temperature-dependent change in ΔCp to the observed ΔH was fairly minimal (∼3.7 kcal mol−1) in comparison to the enthalpy changes observed for the entire binding process (from −10 to −35 kcal mol−1 for mode two, depending on the construct and the reaction temperature). The possibility of modeling the structure of water in the minor groove after the structure of water in ice was suggested as another possible explanation for the observed break in the heat capacity for the formation of complex 2. A heat of fusion term for trapping water in an “ice-like” structure could contribute to the enthalpy change for complex 2 formation. Again, the temperature dependence of the heat of fusion of water (42) cannot be used to explain the change in the slope of the heat capacity change data at 303 K. If all of the 8–10 water molecules purported to be expelled from the minor groove were included in the calculation, the corrected enthalpy change values would shift to values that are less exothermic than those observed in the formation of complex 1.
Any difference in the enthalpy change for formation of complexes 1 and 2 must be the result of the combination of the differences in energy between binding the two different conformers of netropsin as well as the energy of trapping a bridging water molecule in the hairpin/netropsin complex. The free energy change for the formation of complex 2 remains fairly constant over the entire temperature range explored with all three hairpin constructs. Thus the large observed temperature-dependent increase in the enthalpy change is another example of enthalpy-entropy compensation. The entropy of complex 2 formation becomes largely unfavorable as the temperature increases and thus the favorable exothermic enthalpy change must increase to maintain a fairly constant favorable free energy change. Because the structure of the water surrounding the hairpin constructs in solution becomes more highly disordered at higher temperatures, the energy price for trapping a water molecule in a highly ordered netropsin/hairpin complex increases accordingly.
It is important to note that the proposed binding model including a trapped water molecule in complex 2 is somewhat speculative. However, it is entirely consistent with and inferred from the calorimetric results obtained in this study. We would like to further point out that this hypothetical structural model has yet to be verified in complementary experiments and would need to be corroborated in future studies.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
This work was supported in part by an NAU Prop-301 (EAL) award and Arizona Biomedical Research Commission (EAL) award numbers 0014 and 0015.
References
- 1.Ladbury, J. E. 1996. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 3:973–980. [DOI] [PubMed] [Google Scholar]
- 2.Swaminathan, C. P., N. Surolia, and A. Surolia. 1998. Role of water in the specific binding of mannose and mannooligosaccharides to concanavalin A. J. Am. Chem. Soc. 120:5153–5159. [Google Scholar]
- 3.Holdgate, G. A., A. Tunnicliffe, W. H. J. Ward, S. A. Weston, G. Rosenbrock, P. T. Barth, I. W. F. Taylor, R. A. Pauptit, and D. Timms. 1997. The entropic penalty of ordered water accounts for weaker binding of the antibiotic novobiocin to a resistant mutant of DNA gyrase: a thermodynamic and crystallographic study. Biochemistry. 36:9663–9673. [DOI] [PubMed] [Google Scholar]
- 4.Courtenay, E. S., M. W. Capp, C. F. Anderson, and M. T. Record Jr. 2000. Vapor pressure osmometry studies of osmolyte-protein interactions: implications for the action of osmoprotectants in vivo and for the interpretation of “osmotic stress” experiments in vitro. Biochemistry. 39:4455–4471. [DOI] [PubMed] [Google Scholar]
- 5.Schwabe, J. W. 1997. The role of water in protein-DNA interactions. Curr. Opin. Struct. Biol. 7:126–134. [DOI] [PubMed] [Google Scholar]
- 6.Pal, S. K., L. Zhao, and A. H. Zewail. 2003. Water at DNA surfaces: ultrafast dynamics in minor groove recognition. Proc. Natl. Acad. Sci. USA. 100:8113–8118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bailly, C., G. Chessari, C. Carrasco, A. Joubert, J. Mann, W. D. Wilson, and S. Neidle. 2003. Sequence-specific minor groove binding by bis-benzimidazoles: water molecules in ligand recognition. Nucleic Acids Res. 31:1514–1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Breusegem, S. Y., S. E. Sadat-Ebrahimi, K. T. Douglas, E. V. Bichenkova, R. M. Clegg, and F. G. Loontiens. 2001. Experimental precedent for the need to involve the primary hydration layer of DNA in lead drug design. J. Med. Chem. 44:2503–2506. [DOI] [PubMed] [Google Scholar]
- 9.Bergqvist, S., M. A. Williams, R. O′Brien, and J. E. Ladbury. 2004. Heat capacity effects of water molecules and ions at a protein-DNA interface. J. Mol. Biol. 336:829–842. [DOI] [PubMed] [Google Scholar]
- 10.Jayaram, B., and T. Jain. 2004. The role of water in protein-DNA recognition. Annu. Rev. Biophys. Biomol. Struct. 33:343–361. [DOI] [PubMed] [Google Scholar]
- 11.Williams, H. E. L., and M. S. Searle. 1999. Structure, dynamics and hydration of the nogalamycin-d(ATGCAT)2 complex determined by NMR and molecular dynamics simulations in solution. J. Mol. Biol. 290:699–716. [DOI] [PubMed] [Google Scholar]
- 12.Kiser, J. R., R. W. Monk, R. L. Smalls, and J. T. Petty. 2005. Hydration changes in the association of Hoechst 33258 with DNA. Biochemistry. 44:16988–16997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Freyer, M. W., R. Buscaglia, D. Cashman, S. Hyslop, W. D. Wilson, J. B. Chaires, and E. A. Lewis. 2007. Binding of netropsin to several DNA constructs: evidence for at least two different 1:1 complexes formed from an −AATT- containing ds-DNA construct and a single minor groove binding ligand. Biophys. Chem. 126:186–196. [DOI] [PubMed] [Google Scholar]
- 14.Freyer, M. W., R. Buscaglia, B. Nguyen, W. D. Wilson, and E. A. Lewis. 2006. Binding of netropsin and DAPI to an A2T2 DNA hairpin: a comparison of biophysical techniques. Anal. Biochem. 355:259–266. [DOI] [PubMed] [Google Scholar]
- 15.Haq, I. 2002. Thermodynamics of drug-DNA interactions. Arch. Biochem. Biophys. 403:1–15. [DOI] [PubMed] [Google Scholar]
- 16.Cooper, A., C. M. Johnson, J. H. Lakey, and M. Nollmann. 2001. Heat does not come in different colours: entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 93:215–230. [DOI] [PubMed] [Google Scholar]
- 17.Dunitz, J. D. 1995. Win some, lose some; enthalpy-entropy compensation in weak intermolecular interactions. Chem. Biol. 2:709–712. [DOI] [PubMed] [Google Scholar]
- 18.Chervenak, M. C., and E. J. Toone. 1994. A direct measure of the contribution of solvent reorganization to the enthalpy of ligand-binding. J. Am. Chem. Soc. 116:10533–10539. [Google Scholar]
- 19.Chaires, J. B. 2006. A thermodynamic signature for drug-DNA binding mode. Arch. Biochem. Biophys. 453:24–29. [DOI] [PubMed] [Google Scholar]
- 20.Hyun, K. M., S. D. Choi, S. Lee, and S. K. Kim. 1997. Can energy transfer be an indicator for DNA intercalation? Biochim. Biophys. Acta. 1334:312–316. [DOI] [PubMed] [Google Scholar]
- 21.Chaires, J. B. 2001. Analysis and interpretation of ligand-DNA binding isotherms. Methods Enzymol. 340:3–22. [DOI] [PubMed] [Google Scholar]
- 22.Wartell, R. M., J. E. Larson, and R. D. Wells. 1974. Netropsin. A specific probe for A-T regions of duplex deoxyribonucleic acid. J. Biol. Chem. 249:6719–6731. [PubMed] [Google Scholar]
- 23.Zimmer, C. 1975. Effects of the antibiotics netropsin and distamycin A on the structure and function of nucleic acids. Prog. Nucleic Acid Res. Mol. Biol. 15:285–318. [DOI] [PubMed] [Google Scholar]
- 24.Luck, G., H. Triebel, M. Waring, and C. Zimmer. 1974. Conformation dependent binding of netropsin and distamycin to DNA and DNA model polymers. Nucleic Acids Res. 1:503–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pilch, D. S., M. A. Kirolos, X. Liu, G. E. Plum, and K. J. Breslauer. 1995. Berenil [1,3-bis(4′-amidinophenyl)triazene] binding to DNA duplexes and to a RNA duplex: evidence for both intercalative and minor groove binding properties. Biochemistry. 34:9962–9976. [DOI] [PubMed] [Google Scholar]
- 26.Sriram, M., G. A. van der Marel, H. L. P. F. Roelen, J. H. van Boom, and A. H. J. Wang. 1992. The molecular origin of DNA-drug specificity in netropsin and distamycin. Biochemistry. 31:11823–11834. [DOI] [PubMed] [Google Scholar]
- 27.Coll, M., J. Aymani, G. A. van der Marel, J. H. van Boom, A. Rich, and D. E. Wemmer. 1992. Molecular structure of the netropsin-d(CGCGATATCGCG) complex: DNA conformation in an alternating AT segment. Biochemistry. 28:310–320. [DOI] [PubMed] [Google Scholar]
- 28.Kopka, M. L., C. Yoon, D. S. Goodsell, P. Pjura, and R. E. Dickerson. 1985. The molecular origin of DNA-drug specificity in netropsin and distamycin. Proc. Natl. Acad. Sci. USA. 82:1376–1380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goodsell, D. S., M. L. Kopka, and R. E. Dickerson. 1992. Refinement of netropsin bound to DNA: bias and feedback in electron density map interpretation. Biochemistry. 34:4983–4993. [DOI] [PubMed] [Google Scholar]
- 30.Wang, L., A. Kumar, D. W. Boykin, C. Bailly, and W. D. Wilson. 2002. Comparative thermodynamics for monomer and dimer sequence-dependent binding of a heterocyclic dication in the DNA minor groove. J. Mol. Biol. 317:361–374. [DOI] [PubMed] [Google Scholar]
- 31.Marky, L.A. 1986. Polym. Prepr. (Am. Chem. Soc., Div. Polym. Chem.) 27:417–418.
- 32.Marky, L. A., and K. J. Breslauer. 1987. Origins of netropsin binding affinity and specificity. Correlations of thermodynamic and structural data. Proc. Natl. Acad. Sci. 84:4359–4363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Patel, D. J. 1982. Antibiotic-DNA interactions: intermolecular nuclear Overhauser in the netropsin-d(CGCGAATTCGCG) complex in solution. Proc. Natl. Acad. Sci. USA. 79:6424–6428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nguyen, B., D. Hamelberg, C. Bailly, P. Colson, J. Stanek, R. Brun, S. Neidle, and W. D. Wilson. 2004. Characterization of a novel DNA minor-groove complex. Biophys. J. 86:1028–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Neidle, S. 2001. DNA minor-groove recognition by small molecules. Nat. Prod. Rep. 18:291–309. [DOI] [PubMed] [Google Scholar]
- 36.Haq, I., J. E. Ladbury, B. Z. Chowdhry, T. C. Jenkins, and J. B. Chaires. 1997. Specific binding of Hoechst 33258 to the d(CGCAAATTTGCG)2 duplex: calorimetric and spectroscopic studies. J. Mol. Biol. 271:244–257. [DOI] [PubMed] [Google Scholar]
- 37.Cantor, C. R., M. M. Warshaw, and H. Shapiro. 1970. Oligonucleotide interactions. 3. Circular dichroism studies of the conformation of deoxyoligonucleotides. Biopolymers. 9:1059–1077. [DOI] [PubMed]
- 38.Plum, G. E. 2000. Determination of oligonucleotide molar extinction coefficients. In Current Protocols in Nucleic Acid Chemistry. S. L. Beaucage, D. E. Bergstrom, G. D. Glick, and R. A. Jones, editors. John Wiley & Sons, New York. 7.3.1–7.3.17.
- 39.Tanious, F. A., W. D. Wilson, D. A. Patrick, R. R. Tidwell, P. Colson, C. Houssier, C. Tardy, and C. Bailly. 2001. Sequence-dependent binding of bis-amidine carbazole dications to DNA. Eur. J. Biochem. 268:3455–3464. [DOI] [PubMed] [Google Scholar]
- 40.Rentzeperis, D., T. J. Dwyer, B. H. Geierstanger, J. G. Pelton, D. E. Wemmer, and L. A. Marky. 1995. Interaction of minor groove ligands to an AAATT/AATTT site: correlation of thermodynamic characterization and solution structure. Biochemistry. 34:2937–2945. [DOI] [PubMed] [Google Scholar]
- 41.Lumry, R., and S. Rajender. 1970. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: a ubiquitous property of water. Biopolymers. 9:1125–1227. [DOI] [PubMed] [Google Scholar]
- 42.Dougherty, R. C., and L. N. Howard. 1998. Equilibrium structural model of liquid water: evidence from heat capacity, spectra, density, and other properties. J. Chem. Phys. 109:7379–7393. [Google Scholar]