Modeling RNA tertiary structure motifs by graph-grammars

Abstract

A new approach, graph-grammars, to encode RNA tertiary structure patterns is introduced and exemplified with the classical sarcin–ricin motif. The sarcin–ricin motif is found in the stem of the crucial ribosomal loop E (also referred to as the sarcin–ricin loop), which is sensitive to the α-sarcin and ricin toxins. Here, we generate a graph-grammar for the sarcin-ricin motif and apply it to derive putative sequences that would fold in this motif. The biological relevance of the derived sequences is confirmed by a comparison with those found in known sarcin–ricin sites in an alignment of over 800 bacterial 23S ribosomal RNAs. The comparison raised alternative alignments in few sarcin–ricin sites, which were assessed using tertiary structure predictions and 3D modeling. The sarcin–ricin motif graph-grammar was built with indivisible nucleotide interaction cycles that were recently observed in structured RNAs. A comparison of the sequences and 3D structures of each cycle that constitute the sarcin–ricin motif gave us additional insights about RNA sequence–structure relationships. In particular, this analysis revealed the sequence space of an RNA motif depends on a structural context that goes beyond the single base pairing and base-stacking interactions.

INTRODUCTION

Recently, RNA X-ray crystal structures revealed, in the context of their biologically active hosts, several RNA motifs that were previously studied experimentally as individual fragments. Many of these motifs have been predicted from comparative sequence analysis (1), indicating the existence of a relationship between their sequence and structure. The recent structures confirmed that these RNA motifs fold in stable conformations, and are involved in important intra- and inter-molecular stabilization interactions, as well as in catalytic domains (2,3). Consequently, it is now largely recognized that RNA motifs are crucial elements of RNA tertiary structure (The tertiary structure of an RNA is defined by all its nucleotide interactions: base pairs (canonical and non-canonical) and stacking.) and function (4–7).

During the last decade, RNA motifs have been computationally represented by stochastic context-free grammars (SCFGs) (8), covariance models (9–11), secondary structure profiles (12,13) and constraint networks (14,15). Most of these computational models are inferred from sequence alignments. They allow us to parse, or fit, RNA sequences into their plausible secondary structure (The secondary structure of an RNA is defined by the canonical base pairs of its double-helical regions: Watson-Crick A • U, C • G and G • U.) and seek for new instances in genomic data. In addition to parsing RNA sequences, some computational models, such as SCFGs, directly generate a set of sequences that are compatible with the motif they represent, a necessary step towards in silico selection and engineering of RNA sequences with predetermined structure and function (16).

Current computational RNA motif representations are, to some degree, sensitive to their input sequence alignments, which are, unfortunately, not always reliable. They are also limited by the complexity of RNA tertiary structure, which goes beyond secondary structure, co-variations and sequence similarities. Aligning RNA sequences involves an iterative process of pattern matching and modeling (2). Putative RNA patterns inferred from sequence must be validated in terms of their tertiary structure. For instance, one needs to establish the base-pairing substitution rules that are constrained by the structural context, which may include subtle factors such as base stacking outside the canonical stems (2,17). Isostericity matrices are useful in such situations (2).

However, now that RNA crystallographic data accumulate rapidly (18), we can now conceive a direct inference of RNA tertiary structure information. Here, we show that a graph-grammar (19,20) has the required complexity to encode RNA motifs in the context of their tertiary structures. The graph-grammar of an RNA motif can parse and derive RNA sequences that are compatible to it (i.e. sequences that are predicted to fold in it). The graph-grammar of an RNA motif is built of the fundamental structural elements (21) of an instance of its 3D structure (The 3D structure of an RNA is defined by its atomic coordinates in 3D space.) or alternatively tertiary structure.

In this work, the building and use of a graph-grammar are exemplified with the classical sarcin–ricin motif. This motif is found in the sarcin–ricin loop (22,23) (ribosomal loop E), conserved among 23–28S ribosomal RNAs (rRNAs). We chose the sarcin–ricin motif for the diversity of its nucleotide interactions. It includes all base-stacking types and many non-canonical base pairs. Using the sarcin–ricin graph-grammar, we derived four putative sarcin–ricin sequences, of which three are found in published X-ray crystallographic structures. We then compared the derived sequences against an alignment of over 800 bacterial 23S rRNAs. The comparison highlighted few possible alternative alignments that we could not refute by tertiary structure predictions or 3D modeling. Further analyses and laboratory experiments will be needed to confirm the right alignment and to bring light about the structural events that occurred during the evolution.

MATERIALS AND METHODS

RNA graph, tertiary structure and motifs

The tertiary structure of an RNA can be represented computationally by a graph, G = {V, E}, where V is the set of nucleotides (vertices or nodes) and E is the set of interactions (edges or arcs). In comparison to secondary structure, which describes the sequence (backbone interaction) and the canonical Watson–Crick base pairs of the RNA, the tertiary structure includes all nucleotide interactions: the backbone, the canonical and non-canonical base pairs (base–base H-bonds), the base–backbone and base–sugar H-bonds, and the base stacking. In an RNA graph, the interaction arcs are labeled according to the observed interactions between nucleotides. Note that more than one interaction per arc can exist simultaneously between two nucleotides. The arc types therefore need to be able to reflect these possible combinations (i.e. backbone–stack, backbone–pair, etc.).

Arc-type nomenclature

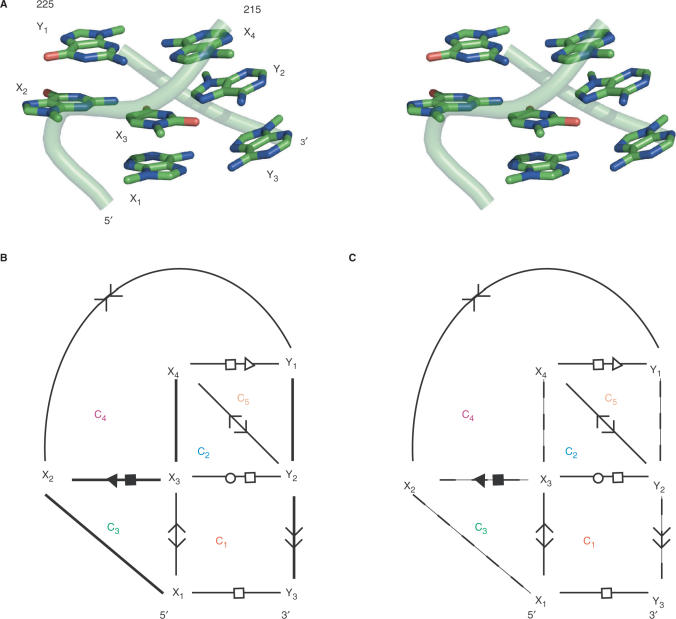
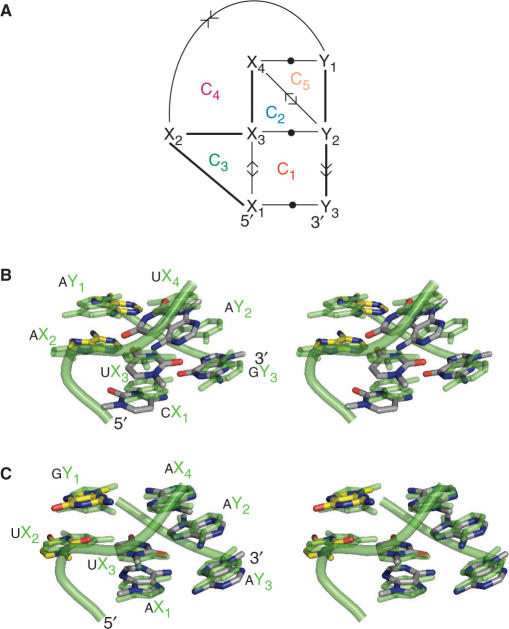
Consider the 3D structure of the sarcin–ricin motif shown in Figure 1A. In order to represent this structure in an RNA graph, we need to specify the nucleotide nodes and the type of their interacting arcs. Figure 1B shows the tertiary structure and the resulting graph returned by MC-Annotate (24,25) from the atomic coordinates of the sarcin–ricin motif.

Figure 1.

The sarcin–ricin motif. (A) Stereoview of the 3D structure. The nucleotides are labeled by the X_i (5′-strand) and Y_i (3′-strand). The backbone is shown using a light green cylinder. Nitrogen atoms are in blue; oxygen in red; and carbon in green. The hydrogen atoms are not shown. (B) Tertiary structure and cycles. A minimal cycle basis of the sarcin–ricin motif is made of five minimum cycles: C₁ to C₅. The symbols used to indicate base stacking and base pairing are described in the Materials and methods section (see arc-type nomenclature). The backbone interactions are shown with bold lines. (C) The same minimum cycle basis as in (B), but without the backbone interactions (indicated by dotted lines).

Base stacking

Arrowheads are used to indicate the orientation of a base, independently of the backbone direction. The tips of the arrows indicate the normal of the base pyrimidine plane, as defined in a classical A-RNA-type double helix, where the normal vectors are oriented towards the 3′-strand endpoint (26). In pyrimidines, this normal vector is the rotational vector obtained by a right-handed axis system defined by N1 to N6 around the pyrimidine ring. The pyrimidine ring in purines is reversed with respect to that of pyrimidines, and therefore the pyrimidine ring normal vector for purines must be reversed to reflect stacking as in the A-RNA double-helix (26).

Two possible orientations of two stacked bases result in four base-stacking types: upward (>>), downward (<<), outward (<>) and inward (><). Two arrows pointing in the same direction (upward and downward) corresponds to the stacking type in the canonical A-RNA double-helix. Upward or downward is chosen depending on which base is referred first (i.e. A >> B means B is stacked upward of A, or A is stacked downward of B). The two other types are less frequent in RNAs, respectively inward (A >< B; A or B is stacked inward of, respectively B or A) and outward (A <> B; A or B is stacked outward of, respectively B or A). Note that all base-stacking types are present in the sarcin–ricin motif shown in Figure 1.

Base pairing

We employ the Leontis and Westhof nomenclature to describe the base-pairing types (27), and to indicate the base edges involved in H-bonding. The following names and symbols have been defined to represent each of the three edges of a base: the Watson–Crick edge, • (cis); ○ (trans), the Hoogsteen edge, ▪ (cis); □ (trans) and the sugar edge, ◂ (cis); ◃ (trans) (27). The cis/trans notation reflects the relative orientation of the backbone according to the median of the plane formed by the two bases. When two bases interact by the same edge, only one symbol is used. For instance, X□□Y is written X□Y. We also indicate the relative orientation of two bases in a pair by using the arrows described above for base stacking. Similarly, a base pair can be parallel, if their normal vectors point in the same direction, or antiparallel, if not.

Seed motif

A classical instance of the sarcin–ricin motif is located in domain VI of the 23S rRNA of Haloarcula marismortui, at the end of helix 95 and is made of nucleotides: U2690–A2694/G2701–C2704 (17,28). The high-resolution 3D structure of this sarcin–ricin motif is available in the Protein Data Bank (18) file 1JJ2. The stem loop including this sarcin–ricin motif (also referred to as the loop E) is sensitive to two cytotoxins, α-sarcin and ricin, which block the translation activity of the ribosome.

Six other instances of the sarcin–ricin motif are found in the 23S rRNA of H. marismortui. One of these instances is shown in Figure 1. It is located at position A‘0’212-G‘0’213-U‘0’214-A‘0’215/G‘0’225-A’0’226-A‘0’227, in the chain ‘0’ of PDB file 1JJ2. We chose this instance arbitrarily among all instances and used it as a seed to build the graph-grammar of the sarcin–ricin motif. Note that choosing any instance of the sarcin–ricin motif results in the same graph-grammar, as all instances are composed of the same nucleotide interactions.

Note that the classical definition of the sarcin–ricin differs from that of Figure 1 by the addition of a Hoogsteen/sugar C□▹U base pair flanking the Hoogsteen, X₁□Y₃. However, a study of the seven instances of the sarcin–ricin motif in the 23S rRNA of H. marismortui indicates that the additional C□▹U base pair is absent (no base pair) in two instances or varies in sequence and geometry. Consequently this extra base pair is not coherent with the definition of motif and we did not include it in our formal definition of the sarcin–ricin motif.

The graph of the sarcin–ricin motif is composed of seven nucleotides, 212–215 and 225–227, which form two strands, five backbone interactions, four base pairs and four base stacking; 7 nodes and 11 arcs. In Figure 1, we generalize the graph by renaming its nodes using the variables X₁ to X₄ and Y₁ to Y₃. The graph reads as follows: X₁ and X₃ stack outward, X₁ <> X₃; X₁ and Y₃ form a parallel trans Hoogsteen/Hoogsteen base pair, X₁□Y₃; X₂ and X₃ form a parallel cis sugar/Hoogsteen base pair, X₂◂ ▪X₃; X₂ and Y₁ stack inward, X₂ >< Y₁; X₃ and Y₂ form an antiparallel trans Watson–Crick/Hoogsteen base pair, X₃○□Y₂; X₄ and Y₁ form an antiparallel trans Hoogsteen/sugar base pair, X₄□◃Y₁; X₄ and Y₂ stack outward, X₄ <> Y₂; and, finally, Y₂ and Y₃ stack upward, Y₂ >> Y₃.

Shortest cycle basis

In Figure 1B, the indivisible cycles (in the following abbreviated as ‘cycles’), of the sarcin–ricin motif are identified by C₁ to C₅. RNA cycles are small RNA fragments defined by cycles of nucleotide interactions (arcs) in the RNA graph (21). The cycles of the sarcin–ricin graph shown in Figure 1B form a ‘shortest cycle basis’, a term used in graph theory to define a minimal set of cycles that include all arcs of a graph (29).

In the first step of building an RNA motif graph-grammar, we determine a shortest cycle basis of the motif. For some motifs, more than one shortest cycle bases are possible. The MC-Cycle computer program, developed in our laboratory, computes one or the union of all shortest cycle bases of an RNA graph. To develop MC-Cycle, we implemented, respectively, the Horton (21) and Vismara (unpublished results) algorithms, which were developed for general graphs (29,30). Here, one arbitrary shortest cycle basis returned by Horton's algorithm has been used to define the graph-grammar of the sarcin–ricin motif. In the case of the sarcin–ricin motif, the sequences derived from the shortest cycle basis shown in Figure 1B are the same as those derived from the union of the shortest cycle bases. Note, however, that for the implementation available via the Internet, MC-Seq (Contact the corresponding author to get the current web address), the union of the sequences produced by all possible shortest cycle bases, returned by Vismara's algorithm, is used.

Graph-grammars

Formally, a graph-grammar, H = {N, Σ, P}, is constituted of a set of non-terminal symbols (N), a set of terminal symbols (Σ) and a set of production rules (P). In the context of the sarcin–ricin motif, N = {C₁, C₂, … , C₅} is the set of cycles (see Figure 1B), Σ = {S₁, S₂, … , S₅} is the set of cycle sequences for each cycle, where S_i is the set of sequences for cycle C_i and P is a consistent assignment of the sequences in Σ to the cycles in N (see derivation below).

Terminal symbols

In order to obtain the cycle sequences, we search the instances of each individual cycle in a database, RNA-3A, of high-resolution (3 Å or better) X-ray crystallographic structures found in the Protein Data Bank (18). The cycle instances are found by using a tool available in our laboratory, MC-Search, which takes as input an RNA graph and a database of 3D structures (here RNA-3A), and returns the structural fragments in the database that match the interactions of the input RNA graph. A classical graph isomorphism algorithm (31) is employed in MC-Search to implement the RNA graph matching (our unpublished data). For each cycle, we consider all sequences of the instances matched in RNA-3A.

Derivation

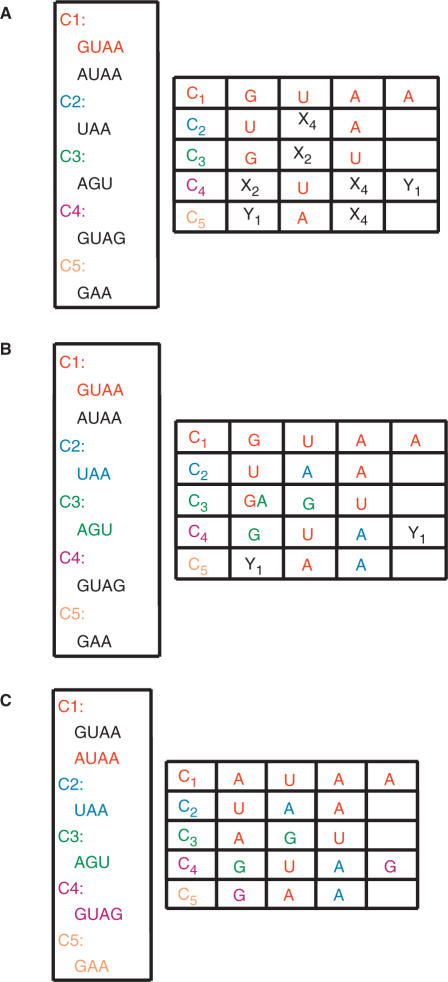
We derive a set of consistent sequences for the entire motif by assigning the cycle sequences (terminals) to the cycles (non-terminals). This process is called ‘derivation’ in formal grammar. Consider, once again, the five cycles of the sarcin–ricin motif in Figure 1. C₁ and C₂ share X₃ and Y₂, and C₁ and C₄ share X₃. We define a 2D table: cycle nucleotides (columns) × cycles (rows) (see Figure 2), where a unique identifier labels each nucleotide. For each cycle and for each cycle sequence, the identifiers are systematically replaced by their corresponding nucleotides. If the introduction of a cycle sequence does not introduce two different nucleotides in the same position, then it is accepted and we proceed to the next cycle. If, on the contrary, the cycle sequence creates a conflict with at least one of the previously assigned positions, then it is rejected and we try the next sequence for this cycle. If all the cycle sequences have been tried without success, then we ‘backtrack’ to the next sequence of the previous cycle (see Figure 3). A sequence is compatible to a motif if a cycle sequence can be found compatible for each cycle of the motif.

Figure 2.

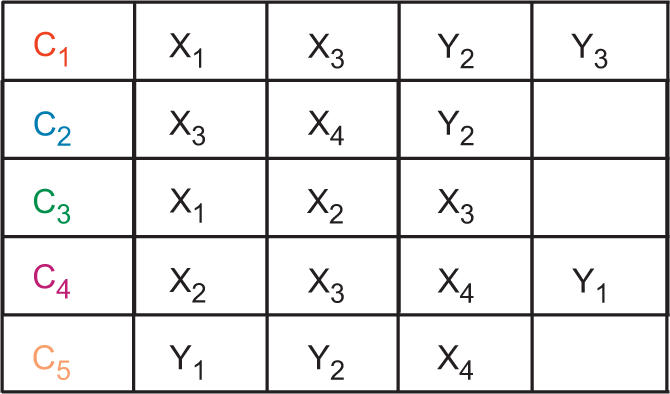
Derivation table. The table is made of one cycle per row and their corresponding nucleotides in the columns. The colors match the colors in Figure 1.

Figure 3.

Graph-grammar derivation (on a reduced set of sequences). The box on the left indicates the set of sequences found for each cycle. The derivation table is on the right. (A) Insertion of the first C₁ sequence: GUAA (in red). (B) Insertion of the first C₃ sequence, AGU (in green). This insertion is not possible because the first nucleotide of C₃, A, does not match with the first nucleotide of C₁, G, which was previously inserted in the table. Since no other sequence is available for C₃, the algorithm backtracks to the previous cycle, C₁, and selects its next sequence, AUAA. (C) Last step. The insertion of the C₅ sequence, GAA, completes the sequence of the entire motif and represents a valid derivation of the graph-grammar: AGUA/GAA. The order of the nucleotides corresponds to the order given by the labels in Figure 2.

Insertions

RNA cycles are subject to nucleotide insertions (21). Two different instances of a motif can differ by the insertion of one nucleotide. If the inserted nucleotide bulges out of the motif, then the original base pairing and stacking interactions are preserved without affecting the original cycles. To measure the impact of the backbone arcs in the formation of the cycles, as well as in the derivation results of the graph-grammar, we considered two versions of the cycle instances. The first includes the backbone interactions, whereas the second does not (see Figure 1C). Note that removing the backbone interactions does not break the cycles when the arcs are combined with at least another interaction, and in particular base stacking. However, when the backbone is the sole interaction, the cycles are broken. The consideration of broken cycles may increase the number of sequences and may introduce geometrical variability.

Alignment

We used an alignment of the bacterial sequences of the 23S rRNA, which was established for developing and assessing the validity of the concept of isostericity matrices (2). The sequence of the Escherichia coli X-ray crystal structure was used as a reference and to properly align structural sites, such as its five sarcin–ricin motif sites.

For each motif site in the reference sequence and each sequence in the alignment, we search for the closest derived sequence (see Figure 4). We define the closest derived sequence by the Manhattan distance, a simple sum of the absolute differences of the coordinates (instead of the classical Euclidean distance that extracts the square root of the sum of the squares of the coordinate differences):

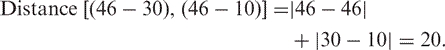Figure 4.

Simplified example of the closest derived sarcin–ricin sequences in an alignment. (A) Two derived sarcin–ricin motif sequences. (B) All possible matches (bold underlined) of the two sequences in the alignment. (C) One structural site in the reference (E. coli) sequence. The first strand matches in the reference sequence at position 20, and the second strand matches at position 40. For each sequence of the alignment, we choose the positions (bold underlined), among all possible matches, that minimizes the Manhattan distance. (D) Resulting alignment. The closest matches, in each sequence, are shown in bold-underlined characters.

Tertiary structure prediction

The sequences in the alignment that were not consistent with the derived sequences were submitted to MC-Fold, a tertiary structure prediction program currently under development in our laboratory. MC-Fold is dual to MC-Seq, since it is used to systematically assign and score possible cycles in an RNA sequence. The best cycle assignments represent plausible tertiary structures of the sequence (cycle bases). Among the optimal and suboptimal solutions proposed by MC-Fold, we considered the prediction that minimizes the edit distance with the alignment.

Root-mean-square deviations

We used a specific RNA 3D fragment distance metric (25) to compute the root-mean-square deviations (RMSDs) between pairs of 3D structures.

RESULTS AND DISCUSSION

Sarcin–ricin cycle sequences

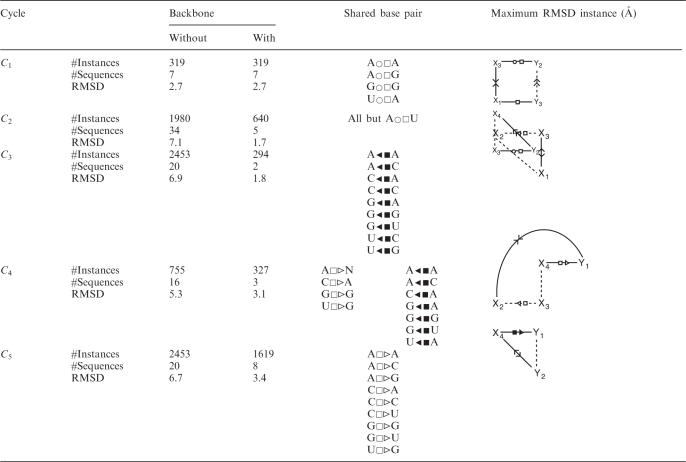
The 3D structure and shortest cycle basis of the sarcin–ricin motif are shown in Figure 1. 3D instances of the five individual cycles of the motif were searched in RNA-3A using MC-Search. In Table 1, we report for each cycle of the motif the number of 3D instances (with and without the backbone interactions), the number of sequences and the highest RMSD between any 3D instance and that of the seed motif. Table 1 also shows the sequences of the base pairs shared by two adjacent cycles and the RNA graphs of the most distant 3D instances.

Table 1.

Sarcin–ricin cycle sequences

For each cycle, we have the number of instances found in RNA-3A, the number of different sequences, the RMSD between the most distant instance and the seed motif, the base pairs shared with its adjacent cycle, and the cycle topology of the most distant instance. The dotted lines represent the arcs where the backbone interactions were removed.

We note no variation in the number of C₁ 3D instances, 319, and sequences, 7, with or without the backbone interactions. This suggests that the structural context of the non-Watson–Crick tandem, defined by the ○□/□ pairs, limits the sequence variability. Among the 256 (16 × 16) possible theoretical sequences for this tandem, 120 = 10 (○□) × 12 (□) would be supported by isostericity matrices (2), whereas only 7 are observed in the 3D structures of RNA-3A. Outside the context of the X₁□Y₃ base pair, such as in C₂, the X₃○□Y₂ base pair accommodates more sequences, up to 15 observed in the 3D structures in RNA-3A without the backbone interactions. Only 10 sequences for ○□ base pairs are supported by isostericity matrices, and therefore observed in sequence alignments (2). For C₂, there are 64 (16 × 4) theoretical sequences, of which 34 were observed in RNA-3A without the backbone, and only 5 with the backbone interaction. In this case, the backbone constrains the sequence space of the cycle. This observation has been made in all cycles but C₁, where the backbone interaction is combined with base stacking. This suggests that the effect of base stacking on the sequence space is weaker than that of the backbone, assuming there are enough examples in the RNA structure database.

The high RMSD of the most distant C₂ 3D instance is introduced by a flipping of the base at position X₃. We have observed that base flipping occurs in all opened cycles but C₁, whereas, when the backbone interaction is considered, base flipping occurs only in C₃ and C₄. Consequently, the backbone interaction restricts, but does not avoid, base flipping.

The sequence space of C₃ is highly constrained by the backbone and includes a rare base pair between two adjacent nucleotides in the sequence, here the X₂◂ ▪X₃ base pair. This base-pairing type can accommodate up to 14 sequences according to the isostericity matrices (2), but the specific context of C₃ in the sarcin–ricin motif allows for only one. The two possibilities for X₁ (A and G) bring to two the number of sequences for C₃.

Sarcin–ricin sequences

An assignment of derived sequences that is compatible to each cycle results from the application of the production rules of the sarcin–ricin graph-grammar (see Table 2). Four sarcin–ricin sequences are found when the backbone interactions are imposed: AGUA-AAA, AGUA-GAA, GGUA-AAA and GGUA-GAA (in bold in Table 2), and 22 sequences are found when the backbone interactions are removed. Which set or sequences would actually fold in the sarcin–ricin motif is an open question that will need to be resolved experimentally. Interestingly, if we restrict the set of 3D instances of the individual cycles, where the backbone interactions were removed, to a maximum of 3 Å of RMSD with the 3D cycles of the seed motif, then the set of 22 sequences is reduced to the four sequences obtained when the backbone interactions are imposed (data not shown). This suggests that the backbone interactions should probably not be removed when they are not combined with other interaction types, such as base stacking. However, in a 3D-motif-searching context, removing the backbone allows us to find 3D instances of the sarcin–ricin motifs that are made of three strands. For instance, sarcin–ricin motifs with inserted nucleotides between X₁ and X₂ are found in RNA-3A: G‘0’1071-G’0’1292-U’0’1293-A’0’1294/G’0’911-A’0’912-A’0’913 in chain ‘0’ of PDB entry 1JJ2 and other related 23S, and A‘A’2302-G’A’953-U’A’954-A’A’955/A’A’1012-A’A’1013-A’A’1014 in chain ‘A’ of PDB entry 1K8A and other related 50S.

Table 2.

Sarcin–ricin sequences

Backbone	#Sequences	Sequences
		AAAA-AGA	AAAA-GGA	AAAU-GGA	AGAA-AGA	AGAA-GGA	AGAU-GGA
Without	22	AGGA-GGA	AGGA-GGC	AGGC-AGA	AGGC-AGC	AGUA-AAA	AGUA-GAA
		CAAA-AGG	CAAA-GGG	CAAU-GGG	GAAA-AAA	GAAA-GAA	GGAA-AAA
		GGAA-GAA	GGAG-GAA	GGUA-AAA	GGUA-GAA
With	4	AGUA-AAA	AGUA-GAA	GGUA-AAA	GGUA-GAA	AGUA-AAA	AGUA-GAA

With (bold) or without (regular) backbone interactions, the numbers and the sequences derived by the graph-grammar are listed.

If the instances of the sarcin–ricin motifs are removed from RNA-3A, the same four sequences are derived, showing that the cycles making the sarcin–ricin motif appear elsewhere in RNA-3A and outside the context of the sarcin–ricin motif. Indeed, the sequences derived by the graph-grammar are subject to the quality and quantity of the X-ray crystal structures, and precision of the annotation methods (here MC-Annotate). Consequently, the graph-grammar circumscribes the sequence space of the sarcin–ricin motif in the context of currently available 3D structures and RNA 3D structure annotation procedures.

Sarcin–ricin alignment

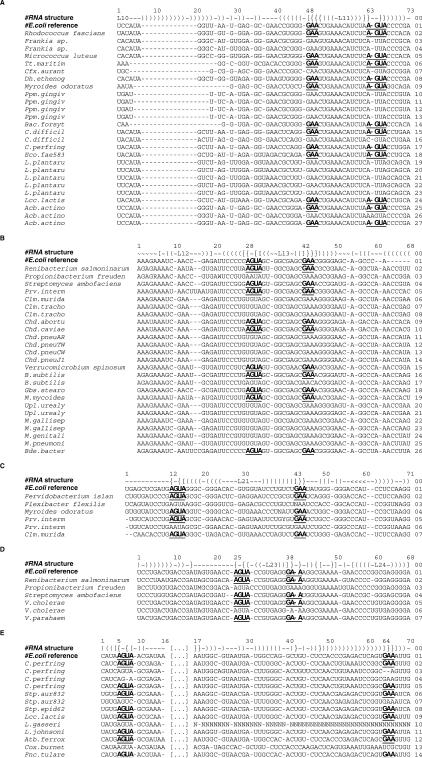
Figure 5 shows the sarcin–ricin sites in the alignment of the bacterial 23S rRNAs, as confirmed by the graph-grammar-derived sequences (shown in bold and underlined in Figure 5). In Figure 5A, only 14 underived sequences have been found. For visibility purposes, only a small number of sequences surrounding the underived sequences are displayed. Figure 5A shows the alignment of 27 sarcin–ricin sites near loop L11 (see the ‘#RNA structure’ line), which includes the 14 underived sequences (among the 806 sequences in the original alignment). The derived sequences are located at position 63-48, where the first nucleotide of the 4-nt strand is at position 63 and the first nucleotide of the 3-nt strand is at position 48.

Figure 5.

Alignment of the bacterial 23S rRNA sequences. The alignment contains 806 sequences. The alignment was broken in five alignments: (A–E). Each smaller alignment was made of the sequences that were not derived by the graph-grammar and their above and below sequences. The parentheses represent canonical base pairs. The braces and brackets represent non-canonical base pairs. The tilde characters, ‘∼’, are used for the unpaired nucleotides. Each sarcin–ricin site is assigned a loop number (i.e. L11, L13, etc.). The last site is span by too many nucleotides to be assigned a loop. Each sequence is given a unique number (on the right side). The source species of the sequences are indicated on the left. The sequence of E. coli is the structural reference, indicated by ‘#’ character. The nucleotides shown in bold and underlined correspond to the sarcin–ricin sites that are derived by the graph-grammar. (A) Site ‘B’204-‘B’205-‘B’206-‘B’207/‘B’189-‘B’190-‘B’191 in chain ‘B’ of PDB entry 2AWB, corresponding to position (63-48) in the alignment. (B) ‘B’241-‘B’242-‘B’243-‘B’244/‘B’254-‘B’255-‘B’256; (28–42). (C) ‘B’371-‘B’372-‘B’373-‘B’374/‘B’400-‘B’401-‘B’402; (12–43). (D) ‘B’457-‘B’458-‘B’459-‘B’460/‘B’469-‘B’470-‘B’471; (25–38). (E) ‘B’1265-‘B’1266-‘B’1267-‘B’1268/‘B’2012-‘B’2013-‘B’2014; (5–64).

For each sarcin–ricin site, we make three possible hypotheses for each underived sequence: (i) a tertiary structure different from that of the sarcin–ricin motif (see Materials and methods section); (ii) a sequencing error; and (iii) an alternative alignment. All sarcin–ricin sites in the alignment are supported by isostericity matrices, but for one exception in the last sarcin–ricin site of Cox burnet (discussed below).

In Figure 5A, the hypothesis of a different tertiary structure is supported for 13 of the 14 underived sequences (see below for the 14th sequence). The 13 sequences of the sarcin–ricin site and surrounding stems were extracted from the alignment and submitted to tertiary structure prediction (see Materials and methods section). A tertiary structure common to all 13 sequences suggests an alignment of the sarcin–ricin site at position 62-49. This hypothetical tertiary structure and its cycles are shown in Figure 6A. An interesting feature of this structure is the presence of canonical Watson–Crick base pairs. To measure the distance of such structure with the seed motif, we built a 3D model using the computer program MC-Sym (32). A superimposition (2.1 Å RMSD) of the model with the seed motif is shown in Figure 6B. The characteristic inward X₂ >< Y₁ stacking of the seed sarcin–ricin motif is reproduced in the putative structure. However, the nucleotides A and U do not allow for the formation of the characteristic X₂◂ ▪X₃ base pair, even though X₂ and X₃ are positioned face-to-face and close to form H-bonds (Figure 6B).

Figure 6.

Hypothetical sarcin–ricin structure. (A) Tertiary structure and cycles. The shortest cycle basis of the hypothetical sarcin–ricin structure shows five cycles, C₁ to C₅, characterized by canonical Watson–Crick base pairs. The backbone interactions are shown with bold lines. (B) Stereoview of the MC-Fold/MC-Sym model (2.1 Å RMSD). The model (colored) is superimposed on the seed motif (green). The nucleotides are labeled by the X_i (5′-strand) and Y_i (3′-strand). The backbone of the seed motif is shown using a light green cylinder. The backbone of the model is not shown. The nitrogen atoms in the model are in blue; oxygen in red; and carbon in gray. The carbon atoms shown in yellow emphasize the unconventional inward stacking between X₂ and Y₁, a characteristic feature of the sarcin–ricin motif. X₂ and X₃ do not pair. The hydrogen atoms are not shown. (C) Stereoview of the alignment model (0.9 Å RMSD). The model (colored) is superimposed on the seed motif (green). The color and numbering nomenclature is the same as in (B). X₂ and X₃, U and U, base pair as in the seed motif.

We also built a 3D model of a different structure suggested by the original alignment (AUUA-GAA), which is shown in Figure 6C. This 3D model fits better the seed motif (0.9 Å RMSD), since the sequence is closer to that of the seed motif. In this case, the typical sarcin–ricin X₂◂ ▪X₃ base pair is played by an isosteric U◂ ▪U.

We hypothesized possible sequencing errors. In the sequence of Chloroflexus aurantiacus, at position 48, a G would make more sense than a C because even though the C is supported by isostericity matrices, a G is found in all other 805 sequences. In the Clostridium difficil #16 sequence, the C at position 63 could have been the result of an insertion, or of a sequencing error, rather than playing the role of X₁, which can be played by the preceding A if we assume an insertion. Here again, an A is found in all other 805 sequences. Finally, the graph-grammar showed the inserted A at position 64 in the sequence of Actinobacillus actinomycetemcomitans #26. Interestingly, the hypothesis of the insertion is equally sound as that shifting the gap in all other sequences.

Figure 5B shows the alignment of the sarcin–ricin site near loop L13 at position 28–42. Among the 806 sequences, only 15 sequences are not derived by the graph-grammar. All but one sequence are also supported by tertiary structure prediction (MC-Fold data not shown). In the sequence of Bacillus subtilis #17, MC-Fold predicts a sarcin–ricin motif at position 28–41, also compatible with isostericity matrices. In order to accommodate this prediction, we need to create a new gap, at position 40 for instance. Another possibility is a sequencing error at position 44, where the C is more likely to be an A. If this was the case, then all approaches would support the current alignment without any modification. Another possible sequencing error would be at position 29 in the sequence of Propionibacterium freudenreichii, where a G would fit better with all other 805 sequences. Finally, in the 13 unsupported sites with a U at position 29, a gap could be inserted leading to the use of the G at position 27. The U in this case would be seen as an insertion.

Figure 5C shows the sarcin–ricin site near loop L21 at position 12–43, where only two sequences are not derived by the graph-grammar. However, if the N in position 43 of the Flexibacter flexilis sequence is a G, then the graph-grammar can parse it and MC-Fold supports it as well. MC-Fold also supports the alignment of the Prevotella intermedia #06 sequence. To be supported by the graph-grammar, the A at position 13 in this sequence must be a G, such as in all other 805 sequences.

Figure 5D shows the sarcin–ricin site near loop L23 at position 25–38, where only two sequences are not derived by the graph-grammar. MC-Fold supports a sarcin–ricin at the same position in the sequence of P. freudenreichii, but keeps the gap at position 40. In the sequence of Vibrio cholerae #06, MC-Fold positions the sarcin–ricin at 25–37, but shifts the gap to position 37. The two above hypotheses are valid for the graph-grammar.

Figure 5E shows the last sarcin–ricin site at position 5–64, where five sequences are not derived by the graph-grammar. The first four underived sequences would be valid for the graph-grammar if sequencing errors are hypothesized: ‘–’ to GA in position 64 in Clostridium perfring #03; ‘−’ to U in position 7 in C. perfring #04; C to A in position 8 in ‘Stp.aur832’ #07; and NNN by GAA in position 64 in Lactobacillus gasseri. For the fifth sequence, Cox burnet, we noted that shifting to the right the sequence by 10 positions, starting at position 36, moves the GAA from position 54 to 64, and then makes it valid for all approaches. Recall here that the original alignment shows a AGUA/UCG sarcin–ricin, which is not supported by isostericity matrices either.

CONCLUSIONS

We encoded essential tertiary structural elements of the sarcin–ricin motif in a graph-grammar and used it to derive four sarcin–ricin sequences, which were compared to those in an alignment of over 800 bacterial sequences of 23S rRNAs. Although producing and using graph-grammars require algorithms that are exponential in time, in the case of the sarcin–ricin motif they were executed in seconds.

We used RNA interaction cycles as first-order objects of the graph-grammar. We showed that these cycles are separate RNA-building blocks, since they are found in different contexts of natural sequences and structures. We removed the occurrences of the sarcin–ricin motifs from the RNA structure database, and were still able to derive the same set of sarcin–ricin sequences.

Deriving the sequences of an RNA motif can be thought of as a generalization of the isostericity base-pairing concept to larger tertiary structure fragments that include all types of nucleotide interactions. For instance, the observed sequences for the X₃○□Y₂ base pair are not the same in two different contexts (C₁ and C₂). Other factors play a role in the sequence space of an RNA motif, since removing the backbone, for instance, increased the number of derived sequences that preserve all other interactions and, therefore, possibly its function.

Tertiary structure prediction and 3D modeling, when combined with graph-grammars, are even more powerful tools to assess and formulate sequence alignment hypotheses. Tertiary structure predictions can be transformed in precise 3D models, which, fed to a graph-grammar, can be used to derive additional valid sequences. For instance, building a graph-grammar from the new hypothetical sarcin–ricin 3D structure that includes canonical Watson–Crick base pairs would derive more sequences than the original set of four.

In the current status of available structural and genomic data, the alignment protocol we propose can generate many valid hypotheses. However, it is unclear at this time if a graph-grammar search engine to identify RNA motifs in genomic data is necessary. Perhaps the use of currently available models for searching motifs in genomic data combined with better sequence alignments may improve greatly the current rates of false positives and negatives. Perhaps the interplay of the nucleotide interactions that compose specific motifs reduces the sequence–structure signal to a point where identifying RNA families in genomic data is and will remain a challenge.

The definition of RNA motifs is in general vague and subjective. Even though we use a precise definition of the sarcin–ricin motif, we might have addressed only a sub-family of the actual motif. In particular, choosing to include or not a specific base pair in the seed motif is arbitrary. In addition, many RNA families have stems that vary in length, and base pairing and stacking types that change from species to species. An effective, but different, graph-grammar for each such motif can be produced automatically. We could combine several graph-grammars to accommodate many motif versions. However, it would be more practical to consolidate many motif versions in a single graph-grammar.