Skip to main content
NCBI home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2007 Apr 24;3:110. doi: 10.1038/msb4100149

Revealing static and dynamic modular architecture of the eukaryotic protein interaction network

Kakajan Komurov 1,a, Michael White 1
PMCID: PMC1865589  PMID: 17453049

Abstract

In an effort to understand the dynamic organization of the protein interaction network and its role in the regulation of cell behavior, positioning of proteins into specific network localities was studied with respect to their expression dynamics. First, we find that constitutively expressed and dynamically co-regulated proteins cluster in distinct functionally specialized network neighborhoods to form static and dynamic functional modules, respectively. Then, we show that whereas dynamic modules are mainly responsible for condition-dependent regulation of cell behavior, static modules provide robustness to the cell against genetic perturbations or protein expression noise, and therefore may act as buffers of evolutionary as well as population variations in cell behavior. Observations in this study refine the previously proposed model of dynamic modularity in the protein interaction network, and propose a link between the evolution of gene expression regulation and biological robustness.

Keywords: dynamic modularity, network robustness, protein interaction networks

Introduction

Revealing complex patterns and organizational principles of biological systems is an important goal of systems biology. Recent studies have considerably expanded our understanding of organizational principles underlying biological networks. Much of the past effort in this field has focused on the topological properties of protein interaction and gene regulation networks and many of their design principles have been uncovered, such as the scale-free topology (Albert et al, 2000; Jeong et al, 2000), modularity (Ihmels et al, 2002; Ravasz et al, 2002; Spirin and Mirny, 2003; Han et al, 2004; Gavin et al, 2006), disassortativeness (Maslov and Sneppen, 2002) and enrichment for certain network motifs (Milo et al, 2002; Harbison et al, 2004; Luscombe et al, 2004). At the level of cell behavior, these properties are thought to promote robustness (Albert et al, 2000; Jeong et al, 2001; Maslov and Sneppen, 2002) and reliability of information processing (Klemm and Bornholdt, 2005). The studies described above mainly analyzed static protein interaction networks without accounting for dynamic properties that arise as a result of gene expression programs that modulate the expression of proteins in the network. Integration of protein interaction data with the gene expression data in recent years, however, has given some important insights into the dynamic organization of the eukaryotic protein interaction network (Ge et al, 2001; Han et al, 2004; Ihmels et al, 2004; Kharchenko et al, 2005; de Lichtenberg et al, 2005). For example, it has been found that co-regulated proteins frequently interact with each other (Ge et al, 2001), and metabolic enzymes topologically close to each other in the metabolic network (Kharchenko et al, 2005) or those that participate in the same metabolic pathway (Ihmels et al, 2004) are also frequently co-regulated. Another study has reported differential positioning of proteins in the protein interaction network based on their coexpression properties with their interacting neighbors in the network (Han et al, 2004). These studies have suggested that a strong correlation exists between topological positioning of proteins in the network and their expression properties.

Recent large-scale experimental and computational studies have delineated the action of gene expression programs under various conditions (Gasch et al, 2000; Segal et al, 2003a; Harbison et al, 2004; Luscombe et al, 2004). Importantly, these studies defined both condition-dependent and condition-independent (constitutive) expression patterns (Luscombe et al, 2004; de Lichtenberg et al, 2005). Given that proteins are subject to variable modes of regulation, we considered the topological positioning of proteins with different levels of transcriptional regulation in protein interaction networks. Previous studies have examined the correlation of co-regulation of proteins with their topological positioning in the network. Instead, we examined how the protein products of regulated versus nonregulated genes (dynamic and static proteins, respectively) are positioned in the protein interaction network relative to each other. We identified organizational principles in the protein interaction network that appear to dictate the specific relative topological positioning of dynamic and static proteins. This information expands our understanding of protein network dynamics, gives systems-level insights into how gene expression programs may modulate the protein network architecture and cell behavior, and suggests a link between the evolution of cellular robustness and the evolution of gene expression regulation.

Results

Expression variance of genes across multiple conditions

To identify genes with condition-dependent or constitutive expression, we leveraged legacy genomic expression profiles derived from cells exposed to multiple conditions. A compendium of 272 microarray experiments from six different data sets from the Saccharomyces Genome Database (SGD, ftp://ftp.yeastgenome.org/yeast/) was compiled and used to calculate the statistical variance of expression profiles for each gene across these 272 experiments. The statistical variance of the expression profile of a gene was assumed to reflect the frequency and magnitude of modulation of its gene product under diverse conditions, such that a low variance would indicate that the protein is relatively static and a high variance would indicate that the protein is relatively dynamic.

For each gene in the genome, an expression variance (EV) was assigned, as defined by the quantile value of the variance of its expression profile in the genomic distribution of variances, such that the EV closest to 0 indicates the gene with the lowest variance in the genome (least dynamic), and the EV value of 1 indicates the gene with the most dynamic expression pattern in the genome. The expression dynamics of the bottom 10 and top 10 genes in the genome-wide EV distribution are shown in Supplementary Figure 1.

We considered that this metric may capture random noise in the expression of genes with low mRNA levels as high EV, and/or may capture the low overall variations in the levels of highly abundant mRNAs as low EV. However, we found that there is a significantly high positive correlation between the calculated EV values of genes and their mRNA abundance values in the cell (Spearman's ρ=0.21, P<1 × 10−16), indicating that low-EV genes are expressed at lower levels than the high-EV genes. This positive correlation indicates that the high-EV gene set is not enriched for low-abundance genes and reflects the extent of gene regulation rather than measuring artifacts owing to low mRNA abundance.

A high-confidence yeast protein interaction network of 2315 proteins connected with 5356 interactions was derived using the confidence scores assigned to each interaction by the study of Bader et al (2004). Importantly, all findings presented below were reproducible using a scoring scheme different from the same study to obtain a slightly different network, or by using an independent high-quality network from a recent large-scale study (Krogan et al, 2006) (data not shown).

Interaction preferences of static and dynamic proteins

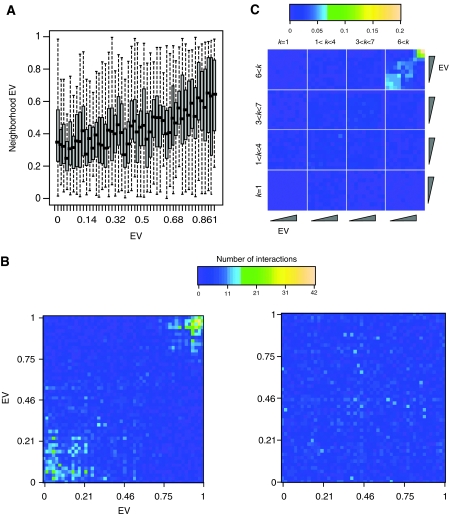
In order to understand how proteins with different expression dynamics assemble within the network, proteins were analyzed in the context of their network neighborhoods; here, defined as the set of binding partners of a protein. A comparison of EVs of proteins with the EVs of their neighbors was used to examine the relative distribution of static and dynamic proteins within the network. For this purpose, we defined neighborhood EV of a protein to be the average of EV values of its interacting partners (neighbors) in the network. There is a strikingly high positive correlation between EVs of proteins and their neighborhood EVs (Spearman's ρ=0.32, n=2245; P=1 × 10−54) (Figure 1A), which suggests that proteins have similar expression dynamics as their immediate neighbors in the protein interaction network. To examine this correlation at a higher resolution, proteins were grouped into 50 bins according to similarity of EV scores and a 50 × 50 interaction preference matrix was constructed. The density of interactions between every bin pair was displayed as the total number of ‘interbin' protein interactions. Consistent with the statistical correlation above (Figure 1A), there is a high density of interactions among the low-EV bins or among the high-EV bins (Figure 1B). Moreover, the interaction densities between low-EV and high-EV bins appear to be extremely low. This interaction pattern was not observed in a randomized network (Figure 1B). These results suggest that the protein interaction network is enriched for sub-networks that are primarily composed of either static proteins or dynamic proteins, but not both.

Figure 1.

Figure 1

Open in a new tab

Interaction pattern of proteins according to their EV. (A) Boxplot of proteins in each of 50 bins with the given EV versus their neighborhood EV. (B) Interaction preference matrix of the yeast network. Each square represents the number of interactions between corresponding bins. Left panel: Interaction preference matrix of the actual network, right panel: Interaction preference matrix of randomized network achieved by randomly shuffling the positions of proteins in the network (right panel). (C) Interaction preference matrix of proteins with different node degrees corresponding to the four quartiles of the node degree distribution. Proteins were binned according to their EVs and node degrees. Each square represents the normalized number of interactions between proteins with given node degree (k) and EV. Normalization of a square (i, j) in the matrix was carried out by calculating the number of interactions between proteins in the bins i and j, and dividing that number with the total number of interactions that proteins in bins i and j have. Color key shows the normalized number of interactions between bins.

The interaction preference matrix shows the number of interactions between bins, which may bias the matrix for the interaction profiles of highly connected proteins. In order to check this, we tested the interaction profiles of proteins with different numbers of interactions (node degrees) and different EVs. We found that the strong correlation in Figure 1B is most apparent for proteins with high node degrees (hubs) (Figure 1C), although the statistical correlation between EV and neighborhood EV in less-connected proteins is also significantly high (data not shown). These observations suggest that proteins having more interaction partners in the network are segregated into distinct network neighborhoods that are characterized by low and high EVs, respectively.

Functional specialization of static and dynamic neighborhoods

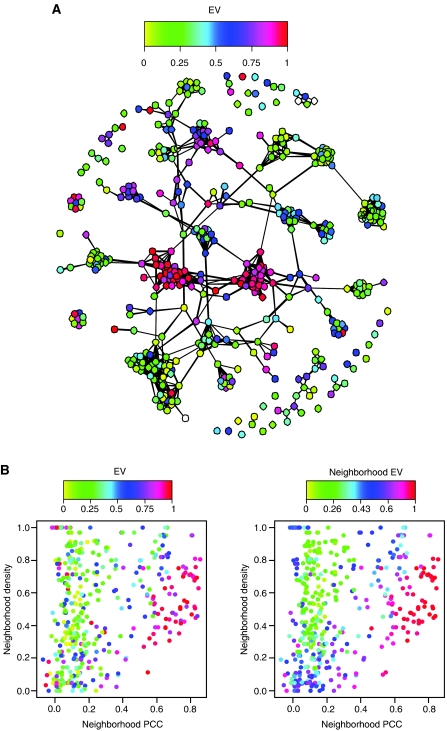
In order to understand what these distinct protein neighborhoods represent, the sub-network formed by hubs, defined as proteins with greater than six interactions, was visualized. A plot of interactions between hubs reveals that the static and dynamic neighborhoods represented distinct densely connected large clusters of static and dynamic proteins (Figure 2A). A densely connected cluster of proteins in the network is likely to represent a functional module (Pereira-Leal et al, 2004), that is, a set of interacting proteins dedicated to a specific cellular process such as the mRNA splicing machinery or the proteasome. Dynamically expressed proteins within a functional module are expected to be coexpressed with each other (Ge et al, 2001; Segal et al, 2003b). In order to check this, we defined neighborhood Pearson correlation coefficient (PCC) as a measure of how well proteins in a neighborhood are coexpressed with each other (see Materials and methods). In agreement with previous studies (Ge et al, 2001; Segal et al, 2003b), we found that neighborhoods of dynamic proteins in clusters are highly coexpressed with each other (Figure 2B). Consistent with their static nonvariant expression pattern, static proteins within clusters had lower neighborhood PCC (nPCC) (Figure 2B). These observations suggest the existence of two distinct types of large modules in the cell: those composed of static proteins (static modules), which are presumably always present in the cell as the expression of their members does not seem to be regulated, and those composed of co-regulated dynamic proteins (dynamic modules), which are expressed in a condition-dependent manner.

Figure 2.

Figure 2

Open in a new tab

Static and dynamic neighborhoods resemble functional modules. (A) Plot of the sub-network formed by hubs. Proteins are colored according to their EV. (B) Plot of hubs' nPCC values against their neighborhood density. Neighborhood density (see Materials and methods) is a measure of how densely the neighbors of a protein are connected to each other, and ranges from 0, for the least dense neighborhood, to 1, for a maximally densely connected neighborhood. Proteins within dense clusters are expected to have high neighborhood densities. Dots (hubs) are colored according to the hub EVs (left panel) and neighborhood EVs (right panel).

The current notion of functional modules predicts that a set of interacting proteins that are highly coexpressed is likely to be specialized to a specific process (Ihmels et al, 2002; Segal et al, 2003b; Kharchenko et al, 2005), and some studies suggest that the protein interaction network is enriched for interactions between co-regulated proteins (Ge et al, 2001; Ihmels et al, 2004). We show that sets of interacting static proteins, which are supposedly constitutively present in the cell but do not have high statistical correlation in their expressions, also may represent specialized functional modules, and that they are at least as abundant in the cell as the sets of interacting dynamic proteins that are highly coexpressed. In order to test this hypothesis, a simple function that compares a protein's Gene Ontology (GO) (Ashburner et al, 2000) annotations with that of its neighbors was derived to quantitate the functional specialization of a protein's neighborhood. This function, ‘neighborhood function homology' (see Materials and methods), generates values in the range from 0 (no shared GO terms between a protein and its neighbors) to 1 (all of GO terms assigned to a protein are shared with its neighbors).

Neighborhood function homology of static proteins (EV<0.25, i.e. lower quartile of genomic distribution) in the network negatively correlates with their neighborhood EV with a high significance (Spearman's ρ=−0.41, P=1.8 × 10−18), suggesting that static proteins interacting with other static proteins are found in functionally specialized neighborhoods. On the other hand, neighborhood function homology of dynamic proteins (EV>0.75, higher quartile of EV distribution) positively correlates with their neighborhood EV (Spearman's ρ=0.40, P=1.5 × 10−12). This indicates that dynamic proteins, in contrast to static proteins, are more functionally homologous to their neighbors when they are in dynamic neighborhoods. Neighborhood function homology of dynamic proteins correlates even more significantly with their average interactor PCC (avPCC) (Spearman's ρ=0.57, P=8 × 10−27), a measure of how well a protein is coexpressed with its neighbors (Han et al, 2004; see Materials and methods). Together, these observations suggest that network neighborhoods composed of constitutively expressed proteins (static neighborhoods) are highly specialized modules, much like the neighborhoods of highly coexpressed proteins (dynamic neighborhoods).

Identification of static and dynamic modules and their functions

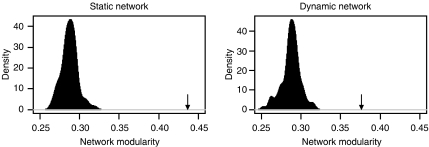
Past studies have measured statistical correlation of gene expression in order to assign proteins to specific modules and also to assign new functions to previously uncharacterized proteins (Ihmels et al, 2002; Segal et al, 2003b, 2003c). As static neighborhoods also seem to be functionally coherent, it should be possible to assign proteins to specific modules by the virtue of their associations with static neighborhoods. To this end, all static neighborhoods in our network were identified by compiling all the interactions between static proteins in the network (static network, 491 proteins connected by 897 interactions). The static network consists of 82 distinct disconnected sub-networks ranging in size from 2 to 86 proteins (Supplementary Table 1). The functional annotations associated with these static sub-networks appear to be functionally coherent, representing various functions including mRNA transcription and splicing, vesicle transport and cell-cycle regulation (see Supplementary Table 1). This apparent functional coherence suggests that the static network is enriched for functional modules. In order to test the significance of modular composition of the static network and to see if it is possible to achieve a similar level of functional coherence in a network generated by random draws of interactions, a network modularity metric was defined to measure functional specialization of the interactions in a network (see Materials and methods). The static network shows significantly higher network modularity than what would be expected by random draws of interactions from the large network (Figure 3), suggesting that the association of functionally coherent sets of proteins with each other within static neighborhoods reflects a biological phenomenon. We compared the static network modularity with that of the network formed by highly coexpressed proteins, which is expected to be enriched for functional modules, in agreement with the previous studies showing modularity of coexpressed proteins (Segal et al, 2003b; Han et al, 2004). We identified the dynamic network by taking all interacting pairs of proteins that also have pairwise PCCs of at least 0.65 (383 proteins connected by 777 interactions). This dynamic network, therefore, contains interactions between those proteins that are also highly transcriptionally co-regulated. The dynamic network consists of 77 sub-networks mainly composed of dynamic proteins (data not shown) and, as expected from previous publications, the dynamic sub-networks are highly functionally coherent (see Supplementary Table 2). The dynamic network also shows a significantly high network modularity that is comparable to that of the static network (Figure 3). This indicates that both networks are enriched for functional modules. The fact that only 15 proteins and six interactions are common to both networks indicates that the modules in the two networks are distinct, and that the high modularity of the static network is not a consequence of a significant overlap with the dynamic network. These observations argue that the static protein neighborhoods represent functional modules, and it should be possible to assign proteins to functional modules by virtue of their association with static proteins.

Figure 3.

Figure 3

Open in a new tab

Functional specialization in the static and dynamic networks. Comparison of network modularity in the static and dynamic networks with that of 100 networks formed by random draws of interactions from the original network. The plot shows the distributions of network modularity values for random draws of 897 (left panel, for comparison with the static network) and 777 (right panel, for comparison with the dynamic network) protein–protein interactions out of the original network. Arrows show the actual network modularity values of the static and dynamic networks (P<0.01 in both cases).

In order to see if either network is specifically enriched for certain cellular functions, we performed enrichment analyses of the two networks for overrepresentations of MIPS functional categories (Mewes et al, 2004). Interestingly, the most significant relative enrichment is seen in the functional categories related to mRNA transcription and processing (static network) and rRNA transcription and processing as well as translation (dynamic network) (see Supplementary Table 3). The static network is enriched for general mRNA transcription (RNA polymerase II holoenzyme complexes), splicing (the pre-mRNA splicing complex) and processing (CPF and CCR4-NOT) as well as co-regulator complexes like the chromatin remodeling complexes (SWI/SNF and INO80), histone acetyl-transferase complexes (SAGA and NuA4), histone methylase (COMPASS) as well as mRNA nuclear export (TREX) (see Supplementary Table 1). The dynamic network, in addition to RNA polymerase I and III components, contains modules like the SSU processome, involved in rRNA processing, and translation initiation factor complexes (see Supplementary Table 2), which is consistent with studies reporting extensive regulation of these modules under various stress conditions (Warner, 1999; Gasch et al, 2000). In addition, the dynamic network contains most of the proteasomal proteins, whereas the static network also contains many of the mitochondrial ribosomal proteins.

There are many modules in the two networks that also seem to perform similar functions. For example, components of the mitotic cohesin complex, which holds sister chromatids together, and the septin ring complex, which is required for cytokinesis, are in the dynamic network (sub-networks 63 and 55; Supplementary Table 2), whereas the DASH complex, which plays a role in chromosome segregation, and the COMA complex, which is involved in the kinetochore assembly, are in the static network (sub-networks 51 and 58; Supplementary Table 1). Components of the anaphase-promoting complex (APC) are also static (sub-network 4), as reported previously (de Lichtenberg et al, 2005). These complexes are all involved in the final stages of cell division, yet their regulation is markedly different. Another potentially interesting correlation relates to vesicle trafficking, where proteins associated with clathrin-coated vesicles (AP-1 and AP-3 complex proteins) seem to be static (sub-networks 9 and 69), whereas those associated with coatomer protein-coated vesicles that are involved in vesicle transport between Golgi and ER (COPI and COPII complex proteins) are dynamic (sub-networks 10, 45 and 76). The dynamic expression pattern of the latter may stem from the involvement of the early secretory pathway in various stress responses like unfolded protein response or osmotic stress (Lee and Linstedt, 1999; Higashio and Kohno, 2002; Sato et al, 2002), whereas clathrin-coated vesicles may play role in constitutive transport. These examples suggest that although some functions in the cell can be classified as static or dynamic (like mRNA and rRNA synthesis, respectively), many others are carried out through dynamic interplay between distinct static and dynamic modules. A closer analysis of expression dynamics of functional modules under various conditions may provide an in-depth insight into the regulation of cellular behavior by transcriptional programs.

Expression properties of centrally positioned proteins

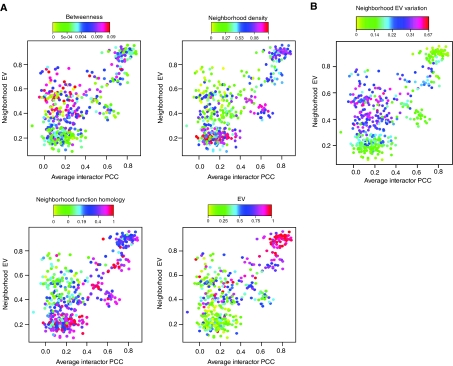
A recent study classified hub proteins into two based on their coexpression with their neighbors. They reported that hubs that do not statistically correlate with their neighbors in expression are positioned centrally in the network, meaning that they function between modules as organizers of cellular processes rather than having a specialized function inside a module (Han et al, 2004). However, as shown above, hubs that are found within static neighborhoods also do not statistically correlate with their neighbors in expression even though they are within modules, and therefore are not central. The bona fide central hubs, therefore, could be proteins that have low avPCC (i.e. those that do not belong to dynamic modules) and relatively high neighborhood EV (i.e. those that do not belong to static modules). In order to test this hypothesis, we tested the ‘betweenness' centralities of hub proteins with different avPCC as well as neighborhood EV values. Betweenness centrality is a graph theoretic measure of network centrality that measures how frequently a node is found ‘on the path' between other nodes in the network, and therefore scores how ‘important' a node is for communication between other nodes in the network (Wasserman and Faust, 1994) (see Materials and methods). As expected, proteins with low avPCC and relatively high neighborhood EV have high betweenness centralities and low neighborhood densities, strongly suggesting that these hubs are positioned centrally in the network (Figure 4A). Their low neighborhood function homologies, in turn, suggest that they are involved in multi-functional interactions, indicating that they may have roles as integrators of multiple processes in the cell (Figure 4A). Unlike hubs in modules, central hubs and their neighbors have a broad distribution of EV values (Figure 4B), suggesting that true central hubs interact with proteins of diverse expression patterns.

Figure 4.

Figure 4

Open in a new tab

Distinct neighborhood EV and avPCC characteristics of central and modular hubs. (A) Plots of hubs' avPCC versus neighborhood EV; each dot (hub) is colored according to the value of the corresponding measure. (B) Hubs are colored according to the neighborhood EV variation, which is the standard deviation of the neighbors' EV values of a protein and shows how diverse the EVs of proteins in the neighborhood of a protein are.

In their study, Han et al (2004) defined hubs that are highly coexpressed with their neighbors as ‘party' hubs, which are modular, and those that are not coexpressed with their neighbors as ‘date' hubs, which they reported as central. However, the set of date hubs also contains hubs that are found within static modules (where there is also no statistical correlation of expression among neighbors). Therefore, based on our findings, we propose that static hubs interacting with static proteins within static modules be excluded from date hubs and, in analogy to the party–date hub terminology, be named ‘family' hubs, as they are always present in the network and interact with their neighbors constitutively. Therefore, family and party hubs form static and dynamic modules, respectively, whereas date hubs (family hubs excluded) organize the network. In concordance with their central functions, our date hubs are enriched for signal transducing and signal regulating proteins like protein kinases, phosphatases, small G-proteins and molecular chaperones (Table I). Date hubs contain 20 out of 22 hub protein kinases (the two hub kinases excluded from date hubs being YAK1, a kinase in the glucose sensing pathway, and SSN3, a C-terminal kinase in the RNA polymerase holoenzyme complex), five out of six hub phosphatases and all of hub small GTPases in the network, indicating that these proteins constitute the true central coordinators of the cellular network.

Table 1.

Enrichment of date hubs for signaling proteins

MIPS protein classes Number in date hubs Total number in hubs P-value
Small GTP-binding proteins (RAS superfamily) 4 4 0
Molecular chaperones 3 4 0.02
Protein kinases 20 22 <1.41E-07
 CaMK group 2 2 0
 CMGC group 7 9 0.003
 OPG group 7 8 0.0005
Unique Saccharomyces cerevisiae kinases 3 3 0
Protein phosphatases 5 6 0.003
Ubiquitin system proteins 3 3 0
Open in a new tab

Date hubs were defined as hubs that have neighborhood EVs greater than 0.3 and avPCC less than 0.45. For protein classes, we used the MIPS (Mewes et al, 2004) protein classification catalogue. Only the classes with most significant P-values are shown. P-values of enrichment were calculated using the cumulative hypergeometric distribution function.

Protein-expression noise and evolutionary rate in the static and dynamic networks

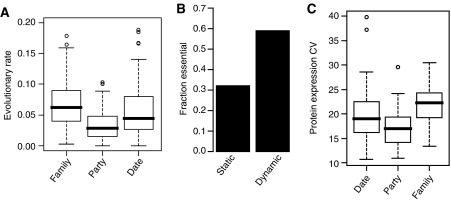
Based on the classification of hubs by Han et al (2004), it was suggested that centrally positioned hubs in the network evolve faster than hubs in modules, and that modularity imposes a constraint on the evolvability of proteins, suggesting an evolutionary scenario where protein networks evolve mainly by modifying their central coordinators (Fraser, 2005). We examined this hypothesis in the context of our modified hub classification, and also found that party hubs evolve at a significantly slower rate than other hubs (Figure 5A). However, surprisingly, family hubs do not evolve slower than date hubs (Figure 5A). By extrapolation, this suggests that hubs present in dynamic modules are evolutionarily constrained, whereas those present in static modules are not. Accordingly, proteins in the dynamic network have significantly lower evolutionary rates than proteins in the static network (P<1 × 10−16, Wilcoxon's test), and there is a significant negative correlation between EV values of proteins and their rates of evolution (Spearman's ρ=−0.21, P=4.5 × 10−15). These results suggest that proteins in static modules have more freedom of variation than proteins within dynamic modules.

Figure 5.

Figure 5

Open in a new tab

Evolutionary rate and expression noise of the static and dynamic modules. Evolutionary rates of yeast proteins derived by Hirsh et al (2005) were used. (A) Boxplot of evolutionary rates of family, party and date hubs. Family hubs are static hubs with neighborhood EVs of <0.3, party hubs are hubs with avPCC>0.45 and date hubs are those with neighborhood EV>0.3 and avPCC<0.45. (B) Fractions of proteins in the static and dynamic networks whose gene deletion is lethal to yeast. (C) Boxplot of protein expression noise in the different hub classes.

Less evolutionary constraint of static modules may indicate that proteins in these modules are largely dispensable for the module function due to compensation in the network. A prediction of this hypothesis is that proteins in static modules are less likely to be essential for cell survival, perhaps owing to their functional redundancy. Indeed, proteins in dynamic modules are almost twice as likely to be essential as proteins in static modules (Figure 5B), which is also true for party hubs when compared to family hubs (data not shown), indicating that the cell is highly tolerant of the loss of proteins in static modules, a property that may allow them to evolve at a faster rate than proteins in dynamic modules.

The significant correlation of protein EVs with their evolutionary rates suggests that the static network may be a buffer of evolutionary variations in the protein interaction network, granting static proteins a role as evolutionary modifiers of cell behavior. We reasoned that if the cell is more tolerant of genetic variations in the components of static modules, then the cell may also be more tolerant of variations in the expression of these proteins within a cell population. Expression variation of proteins between cells within a population, or protein expression noise, is a major factor contributing to the variations of cell behavior among cells within a cell population (Blake et al, 2003; Raser and O'Shea, 2005). Therefore, we compared the expression noise of proteins in static modules with that of proteins in dynamic modules. Using the coefficients of variation of protein expression levels (CV values) within a clonal cell population derived by a recent study (Newman et al, 2006), we found that proteins in dynamic modules are significantly less noisy in their expression when compared to proteins in static modules (P=3 × 10−15, Wilcoxon's test), indicating that the expression levels of static proteins are the ones that show most cell-to-cell variations within a population. Accordingly, family hubs have significantly higher CV values than other hubs (Figure 5C). It is surprising to find that proteins with least variable mRNA expression patterns are most variable between cells and during evolution. These observations argue that static components of the eukaryotic protein interaction network are a source of robustness in cell regulatory networks that allows for evolutionary as well as populational variations in cell behavior (see Discussion).

Expression levels of static and dynamic modules

EV of genes positively correlates with their mRNA abundance (Spearman's ρ=0.21, P<1 × 10−16), and accordingly, proteins in static modules are expressed at a significantly lower level than those in dynamic modules (Wilcoxon's test, P<1 × 10−16). This may suggest that the correlation of EV with the organizational layout in the protein interaction network may be a reflection of the effect of expression levels of proteins rather than their EV. The expression levels of proteins does seem to contribute to the protein network layout, as there is a high positive correlation between mRNA abundance values of hub proteins and that of their neighbors in the network (i.e. average neighborhood mRNA abundance, Spearman's ρ=0.43), although the correlation is significantly less than that between EV and neighborhood EV (Spearman's ρ=0.61). This correlation is not surprising given that the expression levels of proteins participating in the same protein complex are generally similar (Papp et al, 2003). The relatively low correlation between EV and mRNA abundance and the fact that the correlation of mRNA abundance between neighboring proteins is less than that of EV suggests that our observations with EV above are not an artifact of the underlying mRNA abundance values. In order to rule out the possibility that our observations with EV values of proteins presented above are an artifact of their expression levels, we performed partial correlation analyses (see Materials and methods) between EV, neighborhood EV, neighborhood function homology and mRNA abundance values of proteins. Partial correlation between EV and neighborhood EV while controlling for mRNA abundance is almost as high (rEV∼neigh.EV, mRNA=0.66) as their normal correlation (rEV∼neigh,EV=0.67). Similarly, partial correlation between neighborhood function homologies of static proteins with their neighborhood EV while controlling for mRNA abundance or average neighborhood mRNA abundance is almost as high as their normal correlations (data not shown). These observations argue that the observed effects of EV on the organizational layout of the protein interaction network are not an artifact of expression levels of proteins, and that proteins segregate into different modules according to their EVs.

Discussion

A proper stoichiometry in the expression levels of components of a module is essential as an imbalance in the levels of the module constituents can be deleterious (balance hypothesis) (Papp et al, 2003). A priori, there are two simple ways to control stoichiometry of module components at the level of transcription: by maintaining constant expression and by co-regulated expression of all components. Both mechanisms are apparently employed for the design of cellular modules, leading to an organizational model of the network resembling a circuit board with integrated ‘built-in' as well as removable ‘plug-and-play' components. For example, the functionally ubiquitous process of mRNA synthesis and splicing is carried out by proteins organized in modules with apparent invariant expression. The highly dynamic nature of ribosome biogenesis modules, on the other hand, has been suggested to be a mechanism of energy preservation for the cell under stress, as transcription of ribosomal genes accounts for around 80% of all RNA synthesis in the cell (Warner, 1999).

Although the expression variations of modular proteins are constrained by those of their neighbors, central proteins, which are versatile in their functions, are also more versatile in their expression patterns. The existence of both static and dynamic central hubs, which are presumably the coordinators of cellular processes, suggests that some connections between processes in the cell are ‘hard-wired', whereas some are adjustable depending on the cellular requirements. For example, the sub-network 2 in our static network (Supplementary Table 1) indicates that the TFIID/SAGA complex is hard wired to the nuclear proteasomal complex (Supplementary Figure 2), suggesting an integral function of the proteasome in sequence-specific transcription, consistent with previous reports (Lee et al, 2005; Auld et al, 2006). This sub-network also indicates an integral connection of vesicle trafficking with general mRNA synthesis, a relationship that to our knowledge has not yet been explored. Therefore, in addition to revealing some novel architectural characteristics of the protein network, the analysis employed in this study also helps reveal how local dynamics of the network architecture may shape cell behavior.

The faster evolutionary rate and higher expression noise in static modules suggests that robustness to variations in these modules may be a selected trait during evolution. As expression noise may contribute to population fitness of unicellular organisms (Kaern et al, 2005; Raser and O'Shea, 2005), localization of noise to static modules may reflect a specific fitness advantage to the population. An interesting observation consistent with this hypothesis is that proteins functioning in the regulation of mRNA synthesis, which are mostly static in yeast, have been found to be phenotypic enhancers of genetic mutations in worm as well as of oncogenic mutations in human cancers (Lehner et al, 2006). This suggests that fluctuations in the levels of these modules may largely enhance cell-to-cell variations within a population and consequently increase robustness of the population to environmental fluctuations. Similarly, genetic variations in static modules during evolution may result in the phenotypic enhancement of other mutations in the cell, which may facilitate adaptation. As mRNA abundance is a major factor contributing to protein expression noise (Newman et al, 2006) and evolutionary rate (Pal et al, 2001), it is conceivable that relatively lower expression levels of static modules is an evolutionarily selected trait to maximize variations in these modules.

A future comparison of the expression dynamics of the protein network of yeast with that of higher eukaryotes should give an insight into the evolution of expression dynamics in concordance with the evolution of protein network connectivity and robustness.

Materials and methods

Microarray data sets

The microarray gene expression data sets from various conditions (cell cycle, sporulation, stress response, unfolded protein response and diauxic shift) were obtained from the Saccharomyces Genome Database (ftp://ftp.yeastgenome.org/yeast/). In order for the data to account for true fold differences in the expression of genes relative to the control (i.e. 0′ time point), 0′ time points were removed from the data sets, and the corresponding later time points were zero-transformed by subtracting the expression values at these time points from those at the 0 time point.

Protein interaction network

The protein interaction network was obtained using the confidence scores assigned to potential interactions in the study of Bader et al (2004). Following the original study (Bader et al, 2004), a high cutoff of 0.65 was used to obtain a high confidence network. The giant connected component of the network was used in the analyses.

NeighborhoodPCC

nPCC of a protein is defined as the average of all pairwise PCCs between all the proteins in its neighborhood including itself;

graphic file with name msb4100149-i1.jpg

where nPCCa is the nPCC of a protein a, n is the node degree of protein a plus 1 (for itself) and PCCij is the PCC between proteins i and j.

Neighborhood function homology

Let Gi be the set of GO terms assigned to protein i that has a node degree of k. Neighborhood function homology Fi of the protein i is defined as

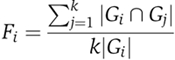graphic file with name msb4100149-i2.jpg

where Gj is the set of GO terms assigned to the jth neighbor of protein i. Fi ranges from 0, where there are no shared GO terms between protein i and its neighbors, to 1, where all GO terms assigned to the protein i are also present in all of its neighbors.

Average interactor PCC

Following Han et al (2004), we defined avPCC as the average of pairwise PCC values between a protein and its neighbors. Differently from nPCC, which is a measure of how the proteins in the neighborhood are coexpressed, avPCC measures how a protein is coexpressed with its neighbors.

Neighborhood density

Neighborhood density of a protein is its clustering coefficient. Clustering coefficient CCi of a protein i is defined as

graphic file with name msb4100149-i3.jpg

where N is the number of interactions between the neighbors of protein i, and k is its node degree.

Network modularity

First, a function similarity matrix was constructed by measuring all pairwise function similarities between proteins in the network. The pairwise function similarity between proteins i and j was defined as

graphic file with name msb4100149-i4.jpg

where Gi and Gj are the sets of GO terms assigned to proteins i and j, respectively. For a network of n proteins, the function similarity matrix S would be a matrix of dimensions n × n. The network modularity M is calculated by summing the pairwise function similarities between every interacting pair of proteins in this network and dividing by the total number of interactions in the same network:

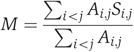graphic file with name msb4100149-i5.jpg

where A is the adjacency matrix of the network and has the same dimensions as S. A is boolean, Ai,j being 1 only if proteins i and j interact, and 0 otherwise.

Betweenness centrality

Betweenness centrality of a node i in the network, shown as CB(i), is given by

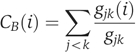graphic file with name msb4100149-i6.jpg

where gjk(i) is the number of shortest paths between nodes j and k that pass through node i and gjk is the total number of shortest paths connecting nodes j and k (Wasserman and Faust, 1994).

Protein-expression noise values

For protein-expression noise values, we used the values derived by a large-scale single-cell proteomic analysis of Newman et al (2006). They defined protein-expression noise as CV (s.d. divided by mean expression) of protein expression between cells in a population.

Partial correlation analysis

Linear correlation between two variables a and b is given by

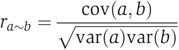graphic file with name msb4100149-i7.jpg

where cov(a,b) is covariance between a and b, and var(a) is variance of a. Partial correlation between a and b while controlling for a variable c is given by

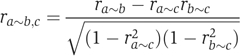graphic file with name msb4100149-i8.jpg

Equations were taken from (de la Fuente et al, 2004).

Supplementary Material

Supplementary Figure 1

msb4100149-s1.jpg (114.7KB, jpg)

Supplementary Figure 2

msb4100149-s2.jpg (139.8KB, jpg)

Legends to Supplementary Figures

msb4100149-s3.doc (19KB, doc)

Supplementary Table 1

msb4100149-s4.xls (144KB, xls)

Supplementary Table 2

msb4100149-s5.xls (114.5KB, xls)

Supplementary Table 3

msb4100149-s6.xls (28.5KB, xls)

Acknowledgments

We thank Dr Chin-Rang Yang for helpful comments and discussions on the manuscript. This work was supported by the Robert E Welch Foundation I-1414.

References

  1. Albert R, Jeong H, Barabasi AL (2000) Error and attack tolerance of complex networks. Nature 406: 378–382 [DOI] [PubMed] [Google Scholar]
  2. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G (2000) Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat Genet 25: 25–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Auld KL, Brown CR, Casolari JM, Komili S, Silver PA (2006) Genomic association of the proteasome demonstrates overlapping gene regulatory activity with transcription factor substrates. Mol Cell 21: 861–871 [DOI] [PubMed] [Google Scholar]
  4. Bader JS, Chaudhuri A, Rothberg JM, Chant J (2004) Gaining confidence in high-throughput protein interaction networks. Nat Biotechnol 22: 78–85 [DOI] [PubMed] [Google Scholar]
  5. Blake WJ, M KA, Cantor CR, Collins JJ (2003) Noise in eukaryotic gene expression. Nature 422: 633–637 [DOI] [PubMed] [Google Scholar]
  6. de la Fuente A, Bing N, Hoeschele I, Mendes P (2004) Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 20: 3565–3574 [DOI] [PubMed] [Google Scholar]
  7. de Lichtenberg U, Jensen LJ, Brunak S, Bork P (2005) Dynamic complex formation during the yeast cell cycle. Science 307: 724–727 [DOI] [PubMed] [Google Scholar]
  8. Fraser HB (2005) Modularity and evolutionary constraint on proteins. Nat Genet 37: 351–352 [DOI] [PubMed] [Google Scholar]
  9. Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO (2000) Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell 11: 4241–4257 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gavin AC, Aloy P, Grandi P, Krause R, Boesche M, Marzioch M, Rau C, Jensen LJ, Bastuck S, Dumpelfeld B, Edelmann A, Heurtier MA, Hoffman V, Hoefert C, Klein K, Hudak M, Michon AM, Schelder M, Schirle M, Remor M, Rudi T, Hooper S, Bauer A, Bouwmeester T, Casari G, Drewes G, Neubauer G, Rick JM, Kuster B, Bork P, Russell RB, Superti-Furga G (2006) Proteome survey reveals modularity of the yeast cell machinery. Nature 440: 631–636 [DOI] [PubMed] [Google Scholar]
  11. Ge H, Liu Z, Church GM, Vidal M (2001) Correlation between transcriptome and interactome mapping data from Saccharomyces cerevisiae. Nat Genet 29: 482–486 [DOI] [PubMed] [Google Scholar]
  12. Han JD, Bertin N, Hao T, Goldberg DS, Berriz GF, Zhang LV, Dupuy D, Walhout AJ, Cusick ME, Roth FP, Vidal M (2004) Evidence for dynamically organized modularity in the yeast protein–protein interaction network. Nature 430: 88–93 [DOI] [PubMed] [Google Scholar]
  13. Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, Jennings EG, Zeitlinger J, Pokholok DK, Kellis M, Rolfe PA, Takusagawa KT, Lander ES, Gifford DK, Fraenkel E, Young RA (2004) Transcriptional regulatory code of a eukaryotic genome. Nature 431: 99–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Higashio H, Kohno K (2002) A genetic link between the unfolded protein response and vesicle formation from the endoplasmic reticulum. Biochem Biophys Res Commun 296: 568–574 [DOI] [PubMed] [Google Scholar]
  15. Hirsh AE, Fraser HB, Wall DP (2005) Adjusting for selection on synonymous sites in estimates of evolutionary distance. Mol Biol Evol 22: 174–177 [DOI] [PubMed] [Google Scholar]
  16. Ihmels J, Friedlander G, Bergmann S, Sarig O, Ziv Y, Barkai N (2002) Revealing modular organization in the yeast transcriptional network. Nat Genet 31: 370–377 [DOI] [PubMed] [Google Scholar]
  17. Ihmels J, Levy R, Barkai N (2004) Principles of transcriptional control in the metabolic network of Saccharomyces cerevisiae. Nat Biotechnol 22: 86–92 [DOI] [PubMed] [Google Scholar]
  18. Jeong H, Mason SP, Barabasi AL, Oltvai ZN (2001) Lethality and centrality in protein networks. Nature 411: 41–42 [DOI] [PubMed] [Google Scholar]
  19. Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL (2000) The large-scale organization of metabolic networks. Nature 407: 651–654 [DOI] [PubMed] [Google Scholar]
  20. Kaern M, Elston TC, Blake WJ, Collins JJ (2005) Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet 6: 451–464 [DOI] [PubMed] [Google Scholar]
  21. Kharchenko P, Church GM, Vitkup D (2005) Expression dynamics of a cellular metabolic network. Mol Syst Biol 1: 2005.0016 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Klemm K, Bornholdt S (2005) Topology of biological networks and reliability of information processing. Proc Natl Acad Sci USA 102: 18414–18419 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Krogan NJ, Cagney G, Yu H, Zhong G, Guo X, Ignatchenko A, Li J, Pu S, Datta N, Tikuisis AP, Punna T, Peregrin-Alvarez JM, Shales M, Zhang X, Davey M, Robinson MD, Paccanaro A, Bray JE, Sheung A, Beattie B, Richards DP, Canadien V, Lalev A, Mena F, Wong P, Starostine A, Canete MM, Vlasblom J, Wu S, Orsi C, Collins SR, Chandran S, Haw R, Rilstone JJ, Gandi K, Thompson NJ, Musso G, St Onge P, Ghanny S, Lam MH, Butland G, Altaf-Ul AM, Kanaya S, Shilatifard A, O'Shea E, Weissman JS, Ingles CJ, Hughes TR, Parkinson J, Gerstein M, Wodak SJ, Emili A, Greenblatt JF (2006) Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature 440: 637–643 [DOI] [PubMed] [Google Scholar]
  24. Lee D, Ezhkova E, Li B, Pattenden SG, Tansey WP, Workman JL (2005) The proteasome regulatory particle alters the SAGA coactivator to enhance its interactions with transcriptional activators. Cell 123: 423–436 [DOI] [PubMed] [Google Scholar]
  25. Lee TH, Linstedt AD (1999) Osmotically induced cell volume changes alter anterograde and retrograde transport, Golgi structure, and COPI dissociation. Mol Biol Cell 10: 1445–1462 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lehner B, Crombie C, Tischler J, Fortunato A, Fraser AG (2006) Systematic mapping of genetic interactions in Caenorhabditis elegans identifies common modifiers of diverse signaling pathways. Nat Genet 38: 896–903 [DOI] [PubMed] [Google Scholar]
  27. Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, Gerstein M (2004) Genomic analysis of regulatory network dynamics reveals large topological changes. Nature 431: 308–312 [DOI] [PubMed] [Google Scholar]
  28. Maslov S, Sneppen K (2002) Specificity and stability in topology of protein networks. Science 296: 910–913 [DOI] [PubMed] [Google Scholar]
  29. Mewes HW, Amid C, Arnold R, Frishman D, Guldener U, Mannhaupt G, Munsterkotter M, Pagel P, Strack N, Stumpflen V, Warfsmann J, Ruepp A (2004) MIPS: analysis and annotation of proteins from whole genomes. Nucleic Acids Res 32: D41–D44 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002) Network motifs: simple building blocks of complex networks. Science 298: 824–827 [DOI] [PubMed] [Google Scholar]
  31. Newman JR, Ghaemmaghami S, Ihmels J, Breslow DK, Noble M, DeRisi JL, Weissman JS (2006) Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature 441: 840–846 [DOI] [PubMed] [Google Scholar]
  32. Pal C, Papp B, Hurst LD (2001) Highly expressed genes in yeast evolve slowly. Genetics 158: 927–931 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Papp B, Pal C, Hurst LD (2003) Dosage sensitivity and the evolution of gene families in yeast. Nature 424: 194–197 [DOI] [PubMed] [Google Scholar]
  34. Pereira-Leal JB, Enright AJ, Ouzounis CA (2004) Detection of functional modules from protein interaction networks. Proteins 54: 49–57 [DOI] [PubMed] [Google Scholar]
  35. Raser JM, O'Shea EK (2005) Noise in gene expression: origins, consequences, and control. Science 309: 2010–2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabasi AL (2002) Hierarchical organization of modularity in metabolic networks. Science 297: 1551–1555 [DOI] [PubMed] [Google Scholar]
  37. Sato M, Sato K, Nakano A (2002) Evidence for the intimate relationship between vesicle budding from the ER and the unfolded protein response. Biochem Biophys Res Commun 296: 560–567 [DOI] [PubMed] [Google Scholar]
  38. Segal E, Shapira M, Regev A, Pe'er D, Botstein D, Koller D, Friedman N (2003a) Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet 34: 166–176 [DOI] [PubMed] [Google Scholar]
  39. Segal E, Wang H, Koller D (2003b) Discovering molecular pathways from protein interaction and gene expression data. Bioinformatics 19 (Suppl 1): i264–i271 [DOI] [PubMed] [Google Scholar]
  40. Segal E, Yelensky R, Koller D (2003c) Genome-wide discovery of transcriptional modules from DNA sequence and gene expression. Bioinformatics 19 (Suppl 1): i273–i282 [DOI] [PubMed] [Google Scholar]
  41. Spirin V, Mirny LA (2003) Protein complexes and functional modules in molecular networks. Proc Natl Acad Sci USA 100: 12123–12128 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Warner JR (1999) The economics of ribosome biosynthesis in yeast. Trends Biochem Sci 24: 437–440 [DOI] [PubMed] [Google Scholar]
  43. Wasserman S, Faust K (1994) Social Network Analysis. Cambridge: Cambridge University Press [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1

msb4100149-s1.jpg (114.7KB, jpg)

Supplementary Figure 2

msb4100149-s2.jpg (139.8KB, jpg)

Legends to Supplementary Figures

msb4100149-s3.doc (19KB, doc)

Supplementary Table 1

msb4100149-s4.xls (144KB, xls)

Supplementary Table 2

msb4100149-s5.xls (114.5KB, xls)

Supplementary Table 3

msb4100149-s6.xls (28.5KB, xls)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES