Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2002 May;12(5):824–831. doi: 10.1101/gr.165102

RePS: A Sequence Assembler That Masks Exact Repeats Identified from the Shotgun Data

Jun Wang 1,2,3,5, Gane Ka-Shu Wong 1,2,4,5, Peixiang Ni 2, Yujun Han 2, Xiangang Huang 2, Jianguo Zhang 2, Chen Ye 2, Yong Zhang 2,3, Jianfei Hu 2,3, Kunlin Zhang 2,3, Xin Xu 1, Lijuan Cong 1, Hong Lu 1, Xide Ren 1, Xiaoyu Ren 1, Jun He 1, Lin Tao 1,2, Douglas A Passey 4, Jian Wang 1,2, Huanming Yang 1,2, Jun Yu 1,2,4, Songgang Li 2,3
PMCID: PMC186573  PMID: 11997349

Abstract

We describe a sequence assembler, RePS (repeat-masked Phrap with scaffolding), that explicitly identifies exact 20mer repeats from the shotgun data and removes them prior to the assembly. The established software Phrap is used to compute meaningful error probabilities for each base. Clone-end-pairing information is used to construct scaffolds that order and orient the contigs. We show with real data for human and rice that reasonable assemblies are possible even at coverages of only 4× to 6×, despite having up to 42.2% in exact repeats.

[The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: P. Green and A.F. Smit.]

All large-scale genome-sequencing projects to date have used a shotgun strategy in which some target region is oversampled by a random collection of sequence reads of typical 500 bp length. There is a wide variation in the size of the target region. The International Human Genome Sequencing Consortium (IHGSC; 2001) targeted bacterial artificial chromosome (BAC) clones of size ∼150-kb. Celera, however, targeted the entire 3-Gb human genome (Venter et al. 2001). Regardless of the size of the target region, the primary difficulty for assembling a shotgun data set is the frequent appearance of repeated motifs. The difficulty is affected by how many repeats there are, how large they are, how similar they are, and how they cluster. All these characteristics are organism specific. The objective is to put the reads together in the correct order and orientation, despite the repeat-induced ambiguities.

Software used by the IHGSC included Staden (Staden et al. 2000), Phrap (P. Green, unpubl.), and GigAssembler (Kent and Haussler 2001). Phrap pioneered the concept of using base-level error probabilities (Ewing and Green 1998; Ewing et al. 1998) to help distinguish nearly identical but distinct repeats from identical repeats that differ because of a sequencing error. This was effective because many of the troublesome repeats were derived from transposon insertions that diverged over evolutionary time (Smit 1996) and therefore were nearly identical but distinct. Distinction of transposon repeats was not scalable to larger data sets because the explosion in the number of putative overlaps consumed an intolerable amount of computer time. Even so, Phrap's ability to compute a meaningful error probability for each base has been instrumental in the IHGSC's efforts to establish a data quality standard of 1 error per 10,000 bases.

The Celera assembler (Myers et al. 2000; Huson et al. 2001) tamed the overlap explosion problem by masking all known repeat classes. To further reduce the number of false joins, it estimated the likelihood that an overlap was unique before joining any two sequences together (Myers 1995). This procedure resulted in a fragmentary assembly, but because Celera sequenced both ends of the shotgun-library clones, masked repeats could be inserted back into the assembly, guided by the clone-end-pairing information, as long as both ends were not masked. The clone-end-pairing information allowed them to bridge across many of the remaining gaps, due either to repeat masking or to missing sequence (Edwards and Caskey 1991; Fleischmann et al. 1995; Roach et al. 1995). Because their clone-insert sizes were so tightly controlled (e.g., 2 kb with ±10% variance), they could also estimate the sizes of the bridged gaps.

METHODS

We have combined all the hard-earned lessons of the past into a single software package, RePS (repeat-masked Phrap with scaffolding). Rather than reinvent the wheel, we used Phrap to handle the detailed sequence assembly, preserving its ability to compute a meaningful base-level error probability. As the critical pre-Phrap process, we explicitly identify exactly repeated 20mers and mask them out (i.e., remove them from consideration by Phrap). This eliminates the overlap explosion problem. At the same time, it also minimizes the likelihood of making a false join. As a post-Phrap process, we analyze the clone-end-pairing information to fill gaps due to repeat masking and construct scaffolds across any other gaps. In essence, we borrowed concepts used by the Celera assembler to create a scalable version of Phrap for whole-genome shotgun assembly. RePS is available by contacting the authors at reps@genomics.org.cn.

There are advantages to explicitly identifying exact 20mer repeats without regard to their underlying biological context. Mathematically defined repeats (MDRs) are more useful than biologically defined repeats. From an algorithmic perspective, it does not matter if the sequence is a transposon, a microsatellite, or a gene duplication. If it is repeated, it will hinder the assembly process. To the extent that the repeat databases are incomplete, it should be more reliable to identify MDRs from the shotgun data set itself. This will be an increasingly important issue as the large sequencing centers move to less well-characterized genomes. Our software was tested on a data set of genuine sequence reads, taken from an 11.9-Mb region of human chromosome 3, which was finished to the standards set by the IHGSC with a BAC-by-BAC approach. Because the key analysis steps were effectively decoupled, we could explore tradeoffs between different aspects of data quality and how they might be affected by different experimental parameters. The results were used to guide our assembly of the 430-Mb rice shotgun sequence (Yu et al. 2002), for which RePS was originally created.

[Note: As we were preparing this paper, a similar algorithm was submitted for publication and has been published [Batzoglou et al. 2002]. A comparison would have been interesting, but it was not practical because the two programs were optimized for different multiprocessor supercomputers and not readily ported.]

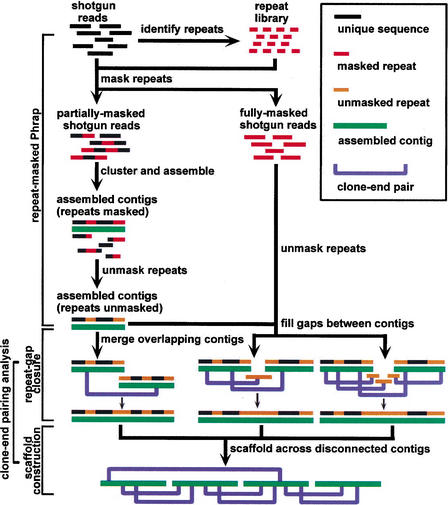
We adopt a purely mathematical definition of repeats. Any 20mer that is exactly duplicated in the target region is a repeat. The Nmer unit cannot be too small because, at some point, every Nmer is repeated. The number of different 20mers is 420 ≈ 1012, which is larger than any genome that we might reasonably try to assemble. However, it does not help to make the Nmer unit much larger than the minimum detectable overlap, which is 14 to 26 bp, based on our Phrap minmatch and minscore settings. Figure 1 depicts the two primary components, repeat-masked Phrap and clone-end-pairing analysis. The latter is divided into repeat-gap closure and scaffold construction. All of the sequence joins are made with Phrap. Repeat masking is used only to prevent Phrap from making a false join. Clone-end pairs are used only to tell Phrap when an otherwise ambiguous join can safely be made. By letting Phrap handle all the details at the base level, we preserve its ability to compute a meaningful base-level error probability.

Figure 1.

Figure 1

Open in a new tab

The RePS algorithm. Any 20mer that appears in the shotgun data set more often than a threshold depth is likely to be an exact repeat and is therefore masked out. Some sequence reads end up fully masked, but most have enough unique sequence in them to be used by Phrap. Repeat gaps are those for which the gap sequence is in the reads, but masked out by our procedure. LW gaps are those for which the gap sequence is not in the reads for statistical reasons (i.e., Lander-Waterman). Clone-end-pairing information is employed to help close the smaller repeat gaps. Large repeat gaps cannot be closed in this manner. Neither can LW gaps. But as long as the clone-insert sizes are larger than the remaining gaps, there is a reasonable probability that we can build scaffolds to bridge over the gaps and order and orient the contigs.

Repeat-Masked Phrap

Let C be the coverage, or the number of times, that a genome is represented in the shotgun data set. The number of times that any 20mer appears in the shotgun data set is its depth D. Consider a 20mer with copy number N across the genome. It should have an average depth of N × C. For masking purposes, we define repeats as 20mers with a depth that is greater than some preset threshold. There are tradeoffs between false-positives (unique 20mers incorrectly called repeated) and false-negatives (repeated 20mers incorrectly called unique). False-positives result in excessive masking and smaller contigs. False-negatives are difficult to avoid for low-copy repeats, but the potential for misassemblies is not as serious as it might appear. Expected overlaps are 500 bp divided by coverage, or 125 bp at 4× coverage. To result in a misassembly, the low-copy repeat must be exactly duplicated across the entire 125 bp, which is unlikely but not impossible. In the end, one must test the algorithm on genomes with substantial repeat fractions, like the human and rice genomes, to assess the severity of this problem.

Masking the 20mer repeats serves two purposes simultaneously. The first is that it liberates Phrap from having to decide among an exponential number of possible joins, and so the algorithm runs much faster. The second is that it prevents Phrap from making ambiguous joins with a high probability of being incorrect. On the other hand, Phrap does not assemble the sequence in a masked region, let alone compute an error probability. To recover this information, we use a local reassembly. After the initial Phrap assembly, all repeats are unmasked and every contig is Phrap-ed again. Using a 100-bp sliding window, we search for discrepancies. Wherever we find them, we extract all sequence reads that fall within the window, Phrap them again, and replace the 100 bp of contig sequence with this local reassembly. In essence, the initial assembly puts the reads into more or less the right place, while the local reassembly recovers any masked sequences and establishes a Phrap quality for each base.

From an implementation perspective, the existing version of Phrap is constructed for a single-processor environment. To make it work in our multiprocessor environment, we first do a pairwise comparison of all the reads using BLAST (Altschul et al. 1990) to cluster any reads that have even a remote chance of being joined. The clusters can then be distributed among as many processors as desired and assembled independently using the single-processor version of Phrap.

Clone-End-Pairing Analysis

The clone-end-pairing analysis examines the names of the sequence reads that are already assembled into a Phrap contig, considers the sizes of the clone inserts, and on that combined basis, existing contigs are validated and gaps between contigs are closed. There are two different types of gaps, repeat gaps and LW gaps, which are depicted in Figure 1. In a repeat gap, the sequence is in the shotgun data, but it has been masked out. If the gap is small, the existing contigs may already overlap, and all we need is clone-end evidence that they can be joined. Even if the gap is bridged by fully masked sequence reads, it can be filled in if the opposite clone ends are not fully masked. In contrast, for an LW gap, the required sequence is not even in the shotgun data, due to sampling statistics (Lander and Waterman 1988). In practice, LW gaps are usually smaller than a read. Regardless of the nature of the remaining gaps, as long as they are smaller than our clone-insert sizes, there is a good chance that they can be scaffolded across to order and orient the contigs, even if the gap sequences remain undefined.

Although the widespread use of capillary sequencers has reduced the frequency of mislabeled clone-end pairs to well under 1%, it is more prudent to always make decisions based on at least two sets of clone-end pairs. We adhered to this rule for scaffold construction; but we relaxed this rule for repeat-gap closure because we used Phrap to validate the sequence overlap before the join is made. Specifically, we extracted 500 bp of sequence from the two flanking contigs and fed the constituent reads to Phrap, along with the unmasked reads from the gap, as identified by the clone-end pairs.

Glossary

Shotgun Assembly

Shotgun library. A collection of clones that over-sample the target genome.

Clone-end pair. Sequence reads derived from both ends of a shotgun-library clone.

Clone-insert size. The size of the clone-insert from which a clone-end pair is taken.

Contig. The result of joining an overlapping collection of sequence reads.

Scaffold. The result of connecting non-overlapping contigs by using clone-end pairs.

LW-gap. A gap in the assembly resulting from Lander-Waterman statistics.

Repeat Analysis

Coverage. The number of times a genome is represented by the shotgun data.

Copy number. The number of times a sequence occurs in the genome.

Depth. The number of times a sequence appears in the shotgun data set. For example, if a transposon has copy number N, and the shotgun data set has coverage C, the transposon will appear at an average depth of N×C.

20-mer repeat. Any 20-mer with a depth D beyond a preset threshold.

Repeat-masked Phrap. A shotgun-assembler based on Phrap, for which all the 20-mer repeats are first eliminated from consideration, before determining the extent of overlap between different sequence reads.

Repeat-gap. A gap in the assembly that is attributed to the repeat masking.

Quality Measures

N50 size. As applied to contigs or scaffolds, that size above which 50% of the assembled sequence can be found.

Single-base error rate. The number of small-scale discrepancies per unit length, from a comparison with the reference sequence. Small-scale means smaller than a typical 500-bp sequence read, and usually just a few bases.

Contig mis-assembly. An error in how the sequence reads are assembled. By definition, it involves segments larger than a 500-bp sequence read. Comparisons with the reference sequence might reveal missing segments, segments in the wrong orientation, or segments in the wrong order.

Scaffold mis-assembly. An error in how the non-overlapping contigs are linked together. Comparisons with the reference sequence might reveal interleaving scaffolds, or contigs in the wrong orientation or order.

Mis-assembly rate. The number of erroneous contigs (or scaffolds) divided by the total number of contigs (or scaffolds).

RESULTS

We selected an 11.9-Mb region of human chromosome 3, from 3p24.3 to 3p26.1, which was sequenced at the Beijing/Hangzhou Genome Center as part of our contribution to the Human Genome Project. The region was covered by an 87 BAC-clone tiling path, finished to an error rate of <10−4. Each BAC was shotgun sequenced by subcloning into plasmids. Two simulated data sets, at 4× and 4× + 2× coverage, were created by uniformly thinning the plasmid subclone sequences to the desired coverage, thereby preserving any cloning biases. Clone ends were simulated by pairing subclones separated by the desired clone-insert distance in the finished sequence. Because the BACs were covered by 11× of plasmid subclones, and we allowed for a ±10% variance in clone-insert sizes, there were relatively few practical constraints. Clone-end pairs were also deliberately mislabeled, to a worst-case frequency of 1%. A proportionate number of contaminant reads (chimeras, clone deletions, and rearrangements) were included in these simulated data sets to be as realistic as possible.

The 4.2× data set for the 430-Mb rice genome is discussed in another paper (Yu et al. 2002). To validate this sequence assembly, we used finished BAC sequences from a related cultivar of Oryza sativa ssp. indica. The whole-genome shotgun data came from the 93–11 cultivar, whereas the BAC sequences came from the Guang-Lu-Ai cultivar, with the GenBank accession nos. AL442007, AL442112, AL442114, AL442115, AL512542, AL512545, AL512546, and AL512547. The cumulative length of all these finished BAC sequences was 0.89 Mb.

Contig-Assembly Accuracy

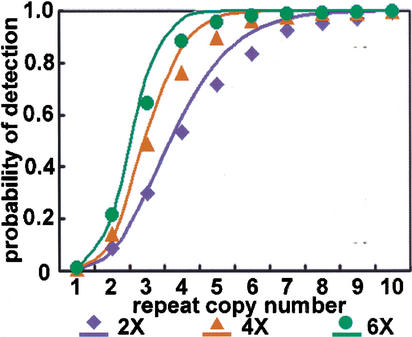
As an initial test of our algorithm for identifying 20mer repeats, we compared the predicted to the actual probability-of-detection. The key parameter is the threshold depth, which we chose to make the false-positive rate nearly 0.1%. For shotgun coverages of 2×, 4×, and 6×, the threshold depths were 7, 11, and 14, respectively. Our concern was whether or not there are cloning biases that are repeat sensitive. As we show in Figure 2, actual performance was in agreement with expectations based on Poisson statistics, which means that the cloning biases are not a major problem. However, perfect repeat detection is only possible in the limit of infinite coverage.

Figure 2.

Figure 2

Open in a new tab

Probability of detection for repeats of given copy number at a shotgun coverage of 2×, 4×, and 6×. The threshold depths are 7, 11, and 14, respectively. The solid lines are theoretical predictions, which assume Poisson statistics, and symbols of the same color refer to actual performance on the human data sets. Ideally, the probability is 0 at copy number 1, and 1 at copy numbers larger than 1. We cannot detect every low-copy repeat, but the number of Alu and Line1 transposons in this target region is 4749 and 1797, respectively, so we should be able to detect virtually every transposon.

In the human 4× data set, 15.9% of the finished BAC sequences and 17.2% of the shotgun sequences are masked by 20mer repeats identified from the shotgun data. These numbers are comparable to the 19.4% and 15.4% of the finished BAC sequences that are attributable to repeats of copy numbers at least 2 and 3. RepeatMasker (A.F. Smit and P. Green, unpubl.), however, identifies 43.7% of the finished BAC sequences as being of transposon origin. The difference is that we mask 20mers that are exactly duplicated in the target region; RepeatMasker identifies anything exhibiting similarity to a known transposon sequence. In contrast, for the rice 4.2× data set, 32.1% of the finished BAC sequences and 42.2% of the shotgun sequences are masked. This larger fraction of masked sequences reflects the fact that rice transposons are of more recent origin (Mao et al. 2000; Turcotte et al. 2001), less diverged from their ancestral sequences, and more likely to lead to exactly duplicated 20mers. To a lesser extent, it also reflects the fact that our rice data set comes from a larger target region.

Table 1 assesses the performance of RePS to unmasked Phrap. The metrics include the number of contigs, the size of the contigs, the single-base error rate, and the contig or scaffold misassembly rates. The number of contigs is compared to the Lander-Waterman expectation. However, it is often the case that, even when there are a large number of small contigs, the bulk of the assembled sequence may be contained in a small number of large contigs. A simple mean or median would obscure this possibility. We therefore characterize the assembly using N50 sizes, defined to be that number above which 50% of the contig or scaffold sequences can be found. Repeat-masked Phrap does produce more (and smaller) contigs than unmasked Phrap, but this is all right, as it is only the first of many steps, and it is more important to avoid making mistakes early on than it is to build large contigs from the outset.

Table 1.

Software Performance

Human 4× Human 4× + 2× Rice 4.2×
Target region (Mb) 11.9  11.9  430
Masked sequence 17.2%  17.2%  42.2% 
Number of contigs by LW 2018 462 59512
Unmasked Phrap
 Max. memory use (Gb) 3.085  x x
 Computer time (h) 48 x x
 Number of contigs 2703 x x
 N50 contig size (kb) 7.05  x x
 Phrap error estimate 0.099% (0.086%) x x
 BAC discrepancies 0.066% (0.063%) x x
 Contig misassembly 5.77%  x x
Repeat-masked Phrap
 Max. memory use (Gb) 0.614  1.040  50
 Computer time (h) 1.8  3.4  79
 Number of contigs 3536 2219 167,975
 N50 contig size (kb) 5.35  11.12  3.41 
 Phrap error estimate 0.091% (0.13%) 0.043% (0.096%) 0.129% (0.145%)
 BAC discrepancies 0.077% (0.076%) 0.044% (0.059%) 0.52% (0.78%)
 Contig misassembly 0.51%  0.68%  0.71% 
Repeat-gap closure
 Max. memory use (Gb) 0.007  0.007  2
 Computer time (h) 2.0  3.0  50
 Number of contigs 3181 1810 127,550
 N50 contig size (kb) 6.13  14.51  6.69 
 Phrap error estimate 0.09% (0.108%) 0.041% (0.076%) 0.111% (0.103%)
 BAC discrepancies 0.075% (0.065%) 0.042% (0.05%) 0.54% (0.73%)
 Contig misassembly 1.1%  1.33%  1.85% 
Scaffold construction
 Max. memory use (Gb) 0.035  0.08  1.3 
 Computer time (h) 0.05  0.07  2
 Number of scaffolds 2284 750 103,044
 N50 scaffold size (kb) 10.61  196.80  11.76 
 Phrap error estimate 0.09% (0.108%) 0.041% (0.076%) 0.111% (0.103%)
 BAC discrepancies 0.075% (0.065%) 0.042% (0.05%) 0.54% (0.73%)
 Scaffold misassembly 0%  0.13%  0% 
Open in a new tab

There are two human data sets, at coverage 4× and 4×+2×. The clone-insert size is 2-Kb for the first 4×. In the 4×+2× data set, the clone-insert size is 15-Kb for the last 2×. The rice data set is discussed in another paper (Yu, et al. 2002). We list the total size of the target region, and the fraction of the shotgun sequence masked by exact 20-mer repeats determined from the shotgun data. Statistics are listed after each RePS stage: repeat-masked Phrap, repeat-gap closure, and scaffold construction. Computations were done on a Sun E10K, employing only 1 of the 64 CPUs for the human data, but 40 of 64 CPUs for the rice data. Lander-Waterman numbers assume 26-bp minimum detectable overlap, based on Phrap's minscore setting. N50 contig or scaffold sizes are the sizes above which 50% of the assembled sequence can be found. Single-base error rates are computed separately for both unique and repeated (parenthesis) sequence. Phrap-derived error estimates are compared to measurements based on alignments with finished BACs. Misassembly rate are defined as the number of bad contigs (or scaffolds) divided by the total number of contigs (or scaffolds). Notice that interleaving scaffold problems are counted as bad in our definition of scaffold mis-assembly. 

Comparisons against the reference sequence reveal two kinds of problems: single-base errors and misassemblies. The single-base error rate is the quantity that is estimated by Phrap. It is measured by counting the number of base discrepancies per unit length in a BLAST-alignment segment (Altschul et al. 1990). Separate error rates are quoted for unique and repeated sequence. In the human 4× data set, the measured rates are 0.066% (0.063%) for unmasked Phrap and 0.077% (0.076%) for repeat-masked Phrap. These differences are negligible. The estimated error rates from Phrap are somewhat higher, but not by much, and our experience with Phrap is that it tends to overestimate the error rate at low coverages. We add that most of the sequencing errors are at the ends of the contigs. If we restrict the BAC comparisons to contigs >3 kb and trim 500 bp off both ends, the error rates become 0.042% (0.025%) for repeat-masked Phrap. In rice, most of these BAC discrepancies were actually polymorphisms, not sequencing errors, as different rice cultivars were used. This is also reflected by the large differences between the Phrap estimates and the BAC discrepancies.

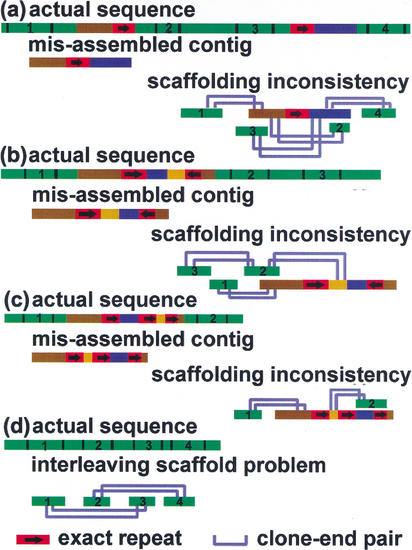
By our definition, contig misassemblies involve segments larger than the typical 500-bp sequence read. They are revealed by a BLAST-alignment with missing segments, segments in the wrong orientation, or segments in the wrong order. These reflect each of the specific problems in Figure 3. We define the contig misassembly rate as the ratio of bad contigs to total contigs. There is a tradeoff between the contig size and misassembly rate, as shown in Figure 4, but for low-copy repeats, the tradeoff is minor. Only in the limit of no repeat masking would the misassembly rates increase dramatically, say by a factor of 11, in the human 4× data set. This reflects the fact that transposon copy numbers run into the thousands, whereas, gene duplications rarely go past 10 in copy number (Yu et al. 2002). Although some of the misassemblies made by unmasked Phrap are in those repeat-masked regions that are never assembled into a contig by repeat-masked Phrap, a huge majority, 79.5%, are not.

Figure 3.

Figure 3

Open in a new tab

Common contig misassemblies, and how they may be detected during scaffold construction. There are three common problems: missing segment as a result of two repeats in the same direction (a), segment orientation error due to inverted repeats in opposite direction (b), and segment ordering mixed up as a result of three repeats all in the same direction (c). A consistent scaffold is a unidirectional path that puts the contigs in a definite order. It will not turn around and suggest that different contigs should be put in the same place. However, this is precisely what happens if the scaffold is forced to use a misassembled contig. A different scaffolding problem is depicted in d. When the clone-insert sizes are too large, the scaffolds start skipping contigs, leading to an interleaving morass of scaffolds with no obvious relation between overlapping scaffolds.

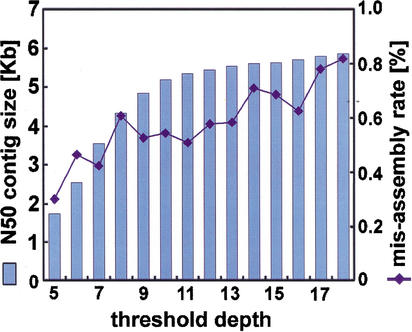
Figure 4.

Figure 4

Open in a new tab

Tradeoff between contig size and accuracy of assembly. This analysis is based on the human 4× data set, using only repeat-masked Phrap without the clone-end-pairing analysis. Increasing the threshold depth results in less of the sequence being masked, so the N50 contig sizes increase. For low-copy repeats, the resultant increase in misassembly rates is minor. The asymptotic contig size and misassembly rate, in the limit of no repeat masking, is somewhat larger than implied by this figure because transposon copy numbers run into the thousands, and this is well off the scale of the figure.

One could argue that by not counting the number of misassemblies in the contig, we are underestimating the severity of the problem in the largest contigs, which are likely to have more than one misassembly. In principle, this is certainly true, but in practice, it is a problem only if the distance between misassemblies is small compared to the contig size, which it is not. As supporting evidence, we did the BAC comparisons using a 1-kb window and searched for breakpoints at which the window could only be matched to disjoint loci. In the human 4×, human 4× + 2×, and rice 4.2× data sets, such breakpoints were found on average once for every 649 kb, 825 kb, and 425 kb, respectively, after repeat-masked Phrap. In no case did we find more than two breakpoints per contig. Therefore, as long as the contigs are relatively small, there is little practical difference between these two definitions of contig misassembly rates.

After repeat-masked Phrap, we are left with many gaps that are due to the repeat masking. If these gaps are small enough, the clone-end-pairing information can be used to tell Phrap how to close them. How aggressively repeat gaps must be closed is debatable, especially in the grass genomes, like rice, where most of these repeats are attributable to nested retrotransposons in the intergenic regions between genes (SanMiguel et al. 1996, 1998). The resultant improvements in N50 contig size after repeat-gap closure are larger in rice than in human because rice has a higher repeat-masked fraction. In every instance, the contig misassembly rates increase significantly, from 0.51% to 1.1%, in the human 4× data set. Comparisons against the BAC sequences reveal that the contig order and orientation are correct and that it is the sequences inside the repeat-gaps that are being misassembled.

One outstanding issue is that we do not know how well our software will work on outbred organisms in which there are large polymorphic differences between homologous chromosomes. Perhaps if we fix the sequencing errors in advance (Pevzner et al. 2001), it might be easier to resolve the homologs. However, this is not a problem for data from human BACs or inbred rice strains.

Scaffold-Assembly Accuracy

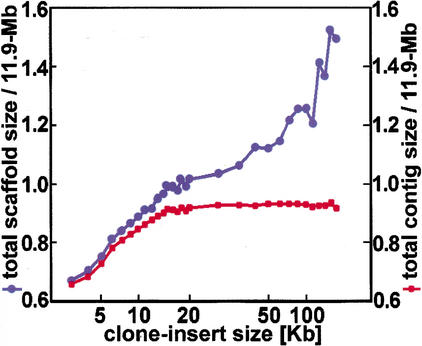
After repeat-gap closure, the contigs are as big as they will ever be, and all we can do is build scaffolds to order and orient the contigs. The remaining gaps are either repeat gaps that are too large to be closed or LW gaps, which are typically smaller than a 500-bp sequence read. Scaffold construction is therefore mostly dependent on how the 20mer repeats cluster in the target genome. In practice, one has to generate a certain amount of whole-genome shotgun data just to compute the 20mer repeats. It is this scenario that we are simulating in our 4× + 2× human data set, in which the clone-insert size is 2 kb in the first 4× and 15 kb in the last 2×. The repeat-cluster size distributions of Figure 5 give us an idea of what we have to do to close the gaps. Notably, when the clone-insert sizes are too large, the scaffolds skip over adjacent contigs, resulting in the interleaving problem of Figure 3d. This problem can be minimized if the scaffolding starts with the smaller clone inserts and slowly works up to the larger clone inserts. Nevertheless, there are limits, and they become apparent for clone-insert sizes that exceed the contig sizes prior to scaffold construction. In the human 4× + 2× data set, clone-insert sizes >15 kb result in total scaffold sizes that exceed the target genome, as shown in Figure 6, and indicative of serious interleaving scaffold problems.

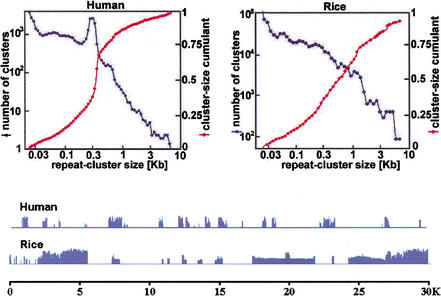
Figure 5.

Figure 5

Open in a new tab

Repeat-cluster size characteristics. Clusters are defined by placing the 20mer repeats, determined from the shotgun data, onto 11.9 Mb and 0.89 Mb of finished human and rice bacterial artificial chromosome sequence, respectively. Any 20mers separated by <26 bp of unique sequence are merged together, and it is the sizes of these merged clusters that are plotted. In the distribution function for human, the peak near 300 bp is due to Alu transposons. In rice, the distribution is scaled up to reflect the entire rice genome. The cumulants show that a significant fraction of rice repeats lie in kilobase-sized clusters. Another way to demonstrate this fact is to highlight 20mer repeats by blue histogram bars proportional to copy number in typical human and rice segments.

Figure 6.

Figure 6

Open in a new tab

Optimization of clone-insert size. This analysis is based on the human 4× + 2× data set. The first 4× of data has a 2-kb clone-insert size, and the final 2× has the clone-insert sizes indicated here. Scaffold size is the sum of the contigs, plus the estimated gaps between these contigs. For this figure, we plot only the scaffolds with two or more contigs, sum over all the scaffolds, and then divide by 11.9 Mb. Similarly, we plot only contigs that are part of such a scaffold, sum over all the scaffolds, and again divide by 11.9 Mb. As the clone-insert sizes increase, more of the target region is subsumed. After 15 kb, however, the total contig size stops growing, but the total scaffold size does not. This can be explained by the interleaving scaffold problem of Fig. 3d.

In the process of building the scaffolds, we can detect some fraction of the contig misassemblies. A consistent scaffold describes a unidirectional path that puts the contigs in the correct order and orientation. However, as shown in Figure 3, when the scaffold encounters a misassembled contig, the clone-end analysis tells the path to turn around and put different contigs in the same place. Clearly, this cannot be the correct answer, but the fact that the path misbehaves at a specific contig can identify misassembled contigs and these can be left out of the scaffolds. The scaffold misassembly rate is defined as the ratio of bad scaffolds to total scaffolds. In addition to contigs with the wrong orientation or order, interleaving problems are counted as bad. In fact, we had only one bad scaffold in the entire human 4× + 2× data set, and it was an interleaving problem. The benefits of scaffolding are worthwhile, nevertheless, because the resultant N50 scaffold size is 14 times larger than the initial N50 contig size. Even larger scaffolds would be possible if we linked contigs joined by only a single clone-end pair.

DISCUSSION

One could ask if there is an advantage to explicitly identifying the 20mer repeats. Notwithstanding the possibility of fine-tuning the Nmer length, the concept is similar to Celera's estimation of the probability that any overlap is unique (Myers 1995). Both are reliant on Poisson sampling statistics and hence we would expect their abilities to detect misassemblies to be similar, given equivalent data sets. On the other hand, some of the arguments for (Weber and Myers 1997) or against (Green 1997) whole-genome shotgun were based on the precise nature of the repeats. By being more explicit about the repeats that matter, not the biological repeats, but the mathematical repeats, one can begin to put the arguments on a concrete foundation. For example, how large are the repeat clusters? What is the typical copy number for a transposon and a gene duplication? Where are the high copy number repeats with respect to the genes? All the answers are highly organism specific, and only by being explicit about the repeats can we design the experiment to suit the organism being sequenced.

As sequencing moves on to nonhuman genomes, with more limited funding, the continuing high costs of sequencing will place a premium on strategies that can generate useful information at the earliest stages of the project. Even at rough-draft coverages of 4× to 6×, in which sequence assemblies are necessarily more fragmentary, the resultant data can be useful (Bouck et al. 1998). Frankly, single-base error rates are largely dependent on coverage, and the only real challenge is to build ever larger contigs and scaffolds with as few mistakes as possible. Our scaffolding strategy does leave the larger repeat clusters unassembled, but whether or not this matters depends on the organism being sequenced. In rice, we achieved an estimated 92.% functional coverage (i.e., genes and immediate regulatory sequences), despite leaving a large fraction of the repeats unassembled (Yu et al. 2002). Therefore, the approach embodied by RePS is appropriate when sequencing through every last repeat is not a high priority.

WEB SITE REFERENCES:

http://ftp.genome.washington.edu/RM/RepeatMasker.html. RepeatMasker screen for intersperesed repeats and low complexity DNA.

http://www.phrap.org.Phred/Prap/Consed; Shotgun sequence assembly.

Acknowledgments

We thank Drs. Will Gillett, Maynard Olson, Lee Rowen, and Jared Roach for their comments and suggestions. We also thank Amersham Pharmacia Biotech, SUN Microsystems, Digital China, and Dawning Computer for their continuous support and excellent service. This work was jointly sponsored by Chinese Academy of Sciences, Commission for Economy Planning, Ministry of Science and Technology, National Natural Science Foundation of China, Beijing Municipal Government, Zhejiang Provincial Government, and Hangzhou Municipal Government. Some of the analysis was also supported by a grant from the National Institute of Environmental Health Sciences (1 RO1 ES09909).

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Footnotes

E-MAIL wangj@genomics.org.cn; FAX 0086-10-80498676.

E-MAIL gksw@u.washington.edu; FAX (206) 685-7344.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.165102.

REFERENCES

  1. Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. J Mol Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
  2. Batzoglou S, Jaffe DB, Stanley K, Butler J, Gnerre S, Mauceli E, Berger B, Mesirov JP, Lander ES. ARACHNE: A whole-genome shotgun assembler. Genome Res. 2002;12:177–189. doi: 10.1101/gr.208902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bouck J, Miller W, Gorrell JH, Muzny D, Gibbs RA. Analysis of the quality and utility of random shotgun sequencing at low redundancies. Genome Res. 1998;8:1074–1084. doi: 10.1101/gr.8.10.1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Edwards A, Caskey T. Closure strategies for random DNA sequencing. Methods Companion Methods Enzymol. 1991;3:41–47. [Google Scholar]
  5. Ewing B, Green P. Base-calling of automated sequencer traces using phred. II. Error probabilities. Genome Res. 1998;8:186–194. [PubMed] [Google Scholar]
  6. Ewing B, Hillier L, Wendl MC, Green P. Base-calling of automated sequencer traces using phred. I. Accuracy assessment. Genome Res. 1998;8:175–185. doi: 10.1101/gr.8.3.175. [DOI] [PubMed] [Google Scholar]
  7. Fleischmann RD, Adams MD, White O, Clayton RA, Kirkness EF, Kerlavage AR, Bult CJ, Tomb JF, Dougherty BA, Merrick JM, et al. Whole-genome random sequencing and assembly of Haemophilus influenzae Rd. Science. 1995;269:496–512. doi: 10.1126/science.7542800. [DOI] [PubMed] [Google Scholar]
  8. Green P. Against a whole-genome shotgun. Genome Res. 1997;7:410–417. doi: 10.1101/gr.7.5.410. [DOI] [PubMed] [Google Scholar]
  9. Huson DH, Reinert R, Kravitz SA, Remington KA, Delcher AL, Dew IM, Flanigan M, Halpern AL, Lai Z, Mobarry CM, et al. Design of a compartmentalized shotgun assembler for the human genome. Bioinformatics (Suppl 1) 2001;17:S132–S139. doi: 10.1093/bioinformatics/17.suppl_1.s132. [DOI] [PubMed] [Google Scholar]
  10. International Human Genome Sequencing Consortium. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
  11. Kent WJ, Haussler D. Assembly of the working draft of the human genome with GigAssembler. Genome Res. 2001;11:1541–1548. doi: 10.1101/gr.183201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lander ES, Waterman MS. Genomic mapping by fingerprinting random clones: A mathematical analysis. Genomics. 1988;2:231–239. doi: 10.1016/0888-7543(88)90007-9. [DOI] [PubMed] [Google Scholar]
  13. Mao L, Wood TC, Yu Y, Budiman MA, Tomkins J, Woo S, Sasinowski M, Presting G, Frisch D, Goff S, et al. Rice transposable elements: a survey of 73,000 sequence-tagged-connectors. Genome Res. 2000;10:982–990. doi: 10.1101/gr.10.7.982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Myers EW. Toward simplifying and accurately formulating fragment assembly. J Comput Biol. 1995;2:275–290. doi: 10.1089/cmb.1995.2.275. [DOI] [PubMed] [Google Scholar]
  15. Myers EW, Sutton GG, Delcher AL, Dew IM, Fasulo DP, Flanigan MJ, Kravitz SA, Mobarry CM, Reinert KH, Remington KA, et al. A whole-genome assembly of Drosophila. Science. 2000;287:2196–2204. doi: 10.1126/science.287.5461.2196. [DOI] [PubMed] [Google Scholar]
  16. Pevzner PA, Tang H, Waterman MS. An Eulerian path approach to DNA fragment assembly. Proc Natl Acad Sci. 2001;98:9748–9753. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Roach JC, Boysen C, Wang K, Hood L. Pairwise end sequencing: A unified approach to genomic mapping and sequencing. Genomics. 1995;26:345–353. doi: 10.1016/0888-7543(95)80219-c. [DOI] [PubMed] [Google Scholar]
  18. SanMiguel P, Tikhonov A, Jin YK, Motchoulskaia N, Zakharov D, Melake-Berhan A, Springer PS, Edwards KJ, Lee M, Avramova Z, et al. Nested retrotransposons in the intergenic regions of the maize genome. Science. 1996;274:765–768. doi: 10.1126/science.274.5288.765. [DOI] [PubMed] [Google Scholar]
  19. SanMiguel P, Gaut BS, Tikhonov A, Nakajima Y, Bennetzen JL. The paleontology of intergene retrotransposons of maize. Nat Genet. 1998;20:43–45. doi: 10.1038/1695. [DOI] [PubMed] [Google Scholar]
  20. Smit AF. The origin of interspersed repeats in the human genome. Curr Opin Genet Dev. 1996;6:743–748. doi: 10.1016/s0959-437x(96)80030-x. [DOI] [PubMed] [Google Scholar]
  21. Staden R, Beal KF, Bonfield JK. The Staden package, 1998. Comput Methods Mol Biol. 2000;132:115–130. doi: 10.1385/1-59259-192-2:115. [DOI] [PubMed] [Google Scholar]
  22. Turcotte K, Srinivasan S, Bureau T. Survey of transposable elements from rice genomic sequences. Plant J. 2001;25:169–179. doi: 10.1046/j.1365-313x.2001.00945.x. [DOI] [PubMed] [Google Scholar]
  23. Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, Sutton GG, Smith HO, Yandell M, Evans CA, Holt RA, et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
  24. Weber JL, Myers EW. Human whole-genome shotgun sequencing. Genome Res. 1997;7:401–409. doi: 10.1101/gr.7.5.401. [DOI] [PubMed] [Google Scholar]
  25. Yu J, Hu S, Wang J, Wong GKS, Li S, Liu B, Deng Y, Dai L, Zhou Y, Zhang X, et al. A draft sequence assembly of the rice genome (Oryza sativa L. ssp. indica) Science. 2002;296:79–92. doi: 10.1126/science.1068037. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES