Long-term impacts of the Exxon Valdez oil spill on sea otters, assessed through age-dependent mortality patterns

Abstract

We use age distributions of sea otters (Enhydra lutris) found dead on beaches of western Prince William Sound, Alaska, between 1976 and 1998 in conjunction with time-varying demographic models to test for lingering effects from the 1989 Exxon Valdez oil spill. Our results show that sea otters in this area had decreased survival rates in the years following the spill and that the effects of the spill on annual survival increased rather than dissipated for older animals. Otters born after the 1989 spill were affected less than those alive in March 1989, but do show continuing negative effects through 1998. Population-wide effects of the spill appear to have slowly dissipated through time, due largely to the loss of cohorts alive during the spill. Our results demonstrate that the difficult-to-detect long-term impacts of environmental disasters may still be highly significant and can be rigorously analyzed by using a combination of population data, modeling techniques, and statistical analyses.

On 24 March, 1989, the tanker vessel Exxon Valdez ran aground on Bligh Reef in Prince William Sound, Alaska, spilling an estimated 42 million liters of Prudhoe Bay crude oil. Sea otters, a species highly susceptible to oil-related mortality (1–5), occupied the coastal waters affected by the spill. By September 1989, nearly 1,000 dead otters had been recovered in the spill area (6), and total mortality because of the spill was undoubtedly higher (7–9). While acute, short-term effects of the Exxon Valdez oil spill (EVOS) on sea otters are indisputable, longer-term effects on this or other species are much more difficult to document. In this paper, we use a combination of field data, demographic modeling, and maximum likelihood analysis to show that sea otters of western Prince William Sound (WPWS) have incurred continuing, highly significant effects from the EVOS. Our goal is both to evaluate impacts on this particular population and to illustrate a method that can be adapted to improve assessment of environmental impacts on populations of long-lived species.

Several lines of evidence suggest that sea otters might have faced oil-related effects long after the spill. Acute oil exposure in sea otters resulted in lung, liver, and kidney damage (10, 11). Sea otters placed in aquaria after the spill had relatively poor survival rates, and at necropsy showed pathologies similar to those documented at the time of the spill (T. Williams, personal communication). Acute pathologies also resulted in abnormal hematological and serum chemistry values before death (12). Analogous changes in serum enzymes associated with liver damage were documented in wild sea otters from 1989 to 1992, and again, although to a much lesser extent, in 1996–1998 (13). Thus, individuals surviving initial exposure to oil but remaining in the wild are likely to have experienced sublethal pathologies similar to those seen in animals dying shortly after the spill.

Continued exposure to oil remaining in the environment may have contributed to persistent spill effects. After the spill, an estimated 40% of the oil (16 million liters) beached in WPWS (14); by 1992 an estimated 2% of the original oil remained on beaches (14), and oil was still present in sediments on some beaches in 1997 (15). Although most remaining oil residues were deemed nontoxic by the summer of 1991 (16, 17), toxic components persist where oil is protected from weathering and may be mobilized after high-energy storms (15, 18). Thus, oiled shorelines provided a reservoir for continued contamination of adjacent intertidal areas and nearshore waters. From 1996 to 1998 wild otters in an oiled area had significantly higher induction of cytochrome P4501A (CYP1A), a bioindicator of exposure to aromatic hydrocarbons, than did otters from an unoiled area (13), indicating some level of continued exposure.

While these facts suggest the possibility of lingering spill effects, evaluating this possibility has proven difficult and costly. At the individual level, “clinically ill” individuals are not likely to survive to be sampled, fresh carcasses for postmortem examination are rarely found, and small sample sizes and high variability in data from live captures result in low statistical power. At the population level, comparisons of pre- and postspill survey data were not ideally suited to a straightforward analysis of spill effects, and have proven inconclusive (7–9, 19, 20). However, in some oiled areas otter numbers remain at about half their prespill densities (21). Prespill carcass collections were available, which may provide an index of over-winter sea otter mortality. However, weather patterns, searcher experience, effort, and timing of collections can all influence deposition and/or recovery rates independent of actual mortality rates, making a simple comparison of the number of dead otters uninformative.

In contrast, the age distribution of otters found dead each year can be used to infer mortality patterns (22). In this paper we use time-varying population models in combination with maximum likelihood methods to evaluate alternative hypotheses about changing demographic rates for otters after the EVOS. Our analyses are based on age-at-death data and estimated demographic rates (23, 24). We use a simple demographic model with time-varying, age-specific survival rates to predict the observed age distributions of dead otters recovered each year after the spill. By modifying survival rates in the model away from prespill values and evaluating the fit of different modifications, we can identify the most likely ways in which the spill has influenced the demography of the population (25).

Methods

Study Area and Data Collection.

Our primary data are the ages of sea otters found dead in WPWS both before and after the 1989 EVOS. From 1976 to 1985, the U.S. Fish and Wildlife Service systematically collected sea otter carcasses each spring from Green Island, with an additional collection in 1979 from Northwest Montague Island. From April through September 1989 and again in the summers of 1990 and 1991, spill response crews collected carcasses throughout oiled portions of WPWS. In addition, an unknown number of carcasses were recovered offshore within the oil slick during early spill response efforts (9). Systematic beach surveys at Green Island were resumed in 1990 and continued through 1998. In 1996 and 1997 opportunistic collections in the oiled northern Knight Island area increased with implementation of a new research project in this area. We systematically surveyed beaches in the larger area of oiled WPWS in 1998.

We conducted systematic beach surveys in April or May soon after snow melt, and before the regrowth of beach grasses, which can conceal carcass remains. Beaches were walked by one or two observers, searching below and up to the strand line (the area of debris deposition from the previous winter's storms). Observers recorded location, condition of carcasses, and sex if identifiable. However, sex often could not be determined, so all carcasses were combined for analysis. The skull was collected when present, and a tooth (preferentially a premolar) was removed for age analysis. Pups were identified by open skull sutures and deciduous teeth. Longitudinal sections of the tooth were decalcified for cementum annuli readings, generally providing age estimates ± 1 yr (26). Matson's Laboratory (Milltown, MT) sectioned and aged all teeth.

Sea otters collected in 1989 were judged to be either pre- or postspill deaths, based on the carcass condition at the time of recovery relative to time since the spill (27). Beginning in 1990 we used only carcasses showing signs of recent deposition (i.e., remains included cartilaginous material and located above previous year's vegetation or in the intertidal) to avoid including prespill and spill-year mortalities. Because carcass persistence is not known, this practice was continued through 1991, after which all recovered carcasses were included.

Data Analysis and Modeling.

We first compared the age distributions of otters collected over different time intervals and in different areas by using Kolmogorov–Smirnov (K-S) two-sample tests (28). We used two prespill time periods (1976–1985 and 1989 prespill) and three postspill periods (1989 postspill, 1990–1991, and 1992–1998), and two areas: Green Island (the site of systematic pre- and postspill collections) and the rest of WPWS. We excluded 0-yr-olds from all analyses because carcasses of the youngest animals are relatively unlikely to persist on beaches (29).

Next we constructed demographic models with survival rates varying from prespill estimates (“baseline rates”) across both ages and years. We did not alter fecundities, as independent evidence indicates no change in otter reproductive values after the spill (30, 31), and age-specific birth rates normally do not vary across populations (32–34). Each model was run for 9 yr, corresponding to the 1990–1998 postspill years. For each simulation, we compared the predicted age distributions of otters dying in each year with those actually seen in the field, and used maximum likelihood methods to determine the most likely patterns of change. This technique provides a clear way to infer changes in demography from age-at-death data by obviating the need to make assumptions such as constant vital rates or stable age distributions (22, 23).

We used a deterministic, two-sex, age-structured matrix model to simulate populations and ran the model with a large number of baseline demographic estimates and model forms to test the robustness of our results. We initialized models by using one of three sets of baseline age- and sex-specific survival estimates from smoothed maximum likelihood analyses of ages-at-death based on carcasses collected before and/or immediately after the spill (following methods in refs. 23 and 24; Fig. 1 A and B) and one set of fecundity estimates from 1989 carcass data (24, 35). Although we did not formally account for uncertainty in these estimates, using three separate sets of demographic estimates does allow us to test for effects of estimation error on our results. We began different simulated populations either at the stable age and sex distribution corresponding to the baseline demographic rates used or the distribution indicated by the presumably age and sex independent mortality patterns generated by the acute effects of the spill (refs. 23 and 24; Fig. 1B).

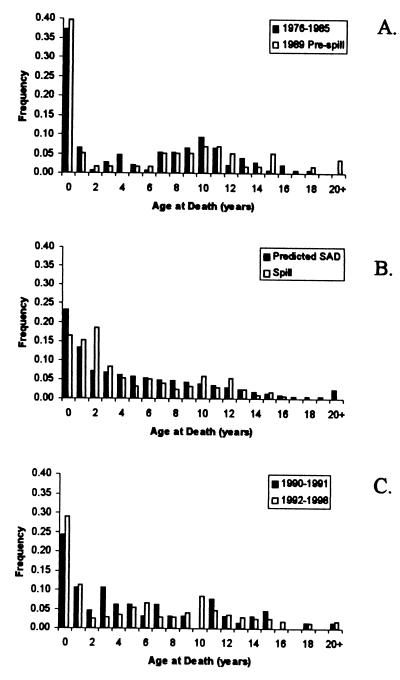
Figure 1.

Age distributions of sea otters found dead in WPWS. (A) From 1976 to 1985 and in 1989 but judged to be prespill moralities. (B) 1989 spill-related sea otter moralities and the predicted stable age distribution (SAD). (C) 1990–1991 and 1992–1998.

We created three families of models with differing functions to modify survival rates across ages and years. These functions span a range of possible forms for spill effects across years and ages. First, the survival rate for each age i and sex (male or female) in each year j was estimated as the baseline rate for that sex and age multiplied by a Logit function: Modeled survival_i,j = (baseline survival)(Logit_i,j), where Logit_i,j = exp(fn_i,j)/(1 + exp(fn_i,j)) and fn_i,j = a + b⋅(i years since spill) + d⋅(age j) + e⋅(i years since spill)⋅(age j). While baseline survival rates differed for males and females, we did not include sex as a factor in fn_i,j, assuming that the proportional deviations in survival away from sex-specific baseline values were the same for all animals of a given age.

While the Logit function allows quite complicated age and time-specific alterations in survival rates, it does not allow for survival rates higher than those estimated from before the oil spill, as might be predicted due to a release from density-dependent constraints (21). Therefore, we also used two other functions. The first is a Modified Logit function, with each age, sex, and year-specific demographic rate equal to

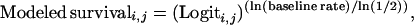1

where Logit_i,j is defined as above. This function allows modeled survival rates to vary between {0, 1}, both higher and lower than the baseline rate, with the modeled rate equaling the baseline when Logit_i,j = 0.5. Finally, we also used a linear model, with the fn_i,j function described above:

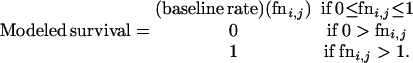2

For each combination of baseline survival rates, functions, and initial age distributions (= 18 models) we found the best-fit values and the confidence limits for the four parameters in fn_i,j, using each of six age-at-death data sets: otters collected before the spill or otters dying after 1989 and from Green Island, the rest of WPWS, or all areas (= 54 post- and 54 prespill model fits). Although the model tracks male and female animals separately, most carcasses were not sexed, so we use the model to predict the relative number of animals dying in each age class each year by sex, but then lump across sexes. For each year, we calculated the likelihood of the observed age distribution of 1-yr-old and older carcasses, given this predicted frequency distribution, using multinomial probabilities (23, 25). The negative log-likelihoods (−LLs) from each year were then summed to yield a final estimate for each model (36). Relative −LL (−LL minus constant terms) values provide the means to compare models with different functional forms (using Akaike's information criterion, AIC; ref. 36) and to identify the best-fit parameter values and confidence limits on these parameters (using likelihood profiles; ref. 36). Because our models did not differ in number of free parameters, differences between twice the −LL values are equivalent to differences in AICs (with smaller AIC values reflecting greater support for a model). To find best-fit values and confidence limits, we used downhill simplex and parabolic interpolation methods (37).

After identifying the best model forms and most likely parameter values, it is important to ask whether these models generate accurate predictions of the observed carcass age distributions. To determine the goodness of fit between the predicted and observed age distributions, we conducted one-sample K-S tests for each year of age-at-death data from 1990 to 1998 for both the linear and logistic models.

Results

Observed Age Distributions of Otter Carcasses.

Green Island is the only site with consistent carcass collections both before and after the spill. Green Island was also on the periphery of the spill area (potentially more influence from carcasses coming from unoiled areas) with shores ranging from unoiled to heavily oiled. Therefore, we first asked whether there is evidence of demographic differences between Green Island and the rest of WPWS. For none of the time periods did age distributions differ between the two areas (K-S, P > 0.05 for all time periods; D_0.05, the minimum significant difference in cumulative distributions, varied from 0.24 to 0.48). While we still perform some analyses for the Green and WPWS areas separately, these results give no reason to suspect differences in the two areas in otter demography before or after the EVOS.

Next, we asked whether age-at-death distributions differed across the five time periods, combining data from Green Island and WPWS collections (D_0.05 varied from 0.16 to 0.30 for these tests). While the 1976–1985 and 1989 prespill distributions did not differ from one another (K-S, P > 0.05), both were significantly different from the age distributions of direct spill mortalities (postspill 1989 carcasses) and also from the 1990–1991 distributions (Fig. 1). The 1992–1998 age distribution did not differ significantly from the prespill or 1990–1991 distributions, but it was different from the distribution of direct spill deaths. In general, these changes in age distributions suggest a shift in mortality patterns after the spill, with a gradual return toward the prespill pattern.

Modeling of Survival Changes.

We first checked the reasonableness of our approach by fitting the 54 models to prespill carcass data. For the best-fit models of all three functional forms, the confidence values for the two parameters controlling time effects on survival (b and e) bracketed zero, indicating a lack of temporal changes in survival rates in the prespill years (Table 1). Since no shifts in prespill demography are likely, this result confirms that our approach is unlikely to give spurious predictions of change. The 95% confidence limits of the other two parameters (a and d) encompass zero, include only very small values, or are very broad, also supporting the lack of strong differences between the basic age-specific demographic rates and assumptions used in our analyses and those operating before the 1989 spill.

Table 1.

Best-fit parameter values for different models of changing otter demography fit to age distributions of sea otters found dead before or after EVOS

Model family	Relative log-likelihood	Maximum likelihood (95% confidence limits)
		Parameter a (constant)	Parameter b (year effect)	Parameter d (age effect)	Parameter e (interaction)
Fit to prespill carcasses:
Logistic	374.55	−47.7348   (−86.4115, 4.1017)	−0.1501   (−2.7285, 0.3162)	0.02285  (0.00545, 17.5616)	0.00097  (−0.00090, 5.7620)
Modified logistic	371.52	2.38747  (0.82337, 3.58883)	0.10258  (−0.01390, 0.24090)	−0.31686  (−0.44277, −0.17741)	0.00874  (−0.00367, 0.01995)
Linear	369.88	0.00509  (0.00509, 0.38982)	−0.00034  (−0.00034, 0.0000)	0.00018  (0.00018, 0.01785)	−0.00001  (−0.00001, 0)
Fit to postspill carcasses:
Logistic	503.72	−0.8379   (−2.1982, 0.7026)	0.5133   (0.2035, 0.8375)	0.1798   (0.0812, 0.3179)	−0.0576  (−0.0922, −0.0269)
Modified logistic	507.55	−1.1747   (−2.2327, 0.2638)	0.5225   (0.3141, 0.7037)	0.06915  (−0.0570, 0.1842)	−0.0706  (−0.0980, −0.0436)
Linear	503.12	0.2536   (−0.0033, 0.3332)	0.1062   (0.0612, 0.1150)	0.03455  (0.0179, 0.0495)	−0.0107  (−0.0135, −0.0064)

Relative negative log-likelihood values, maximum likelihood parameter estimates, and one-dimensional 95% confidence limits are given for the best-fit model for each model family. All six best-fit models assumed an initial stable age distribution. See text for definitions of parameter effects. 

Next, we fit the 54 models to the postspill carcass data. In general, the lowest −LL (and hence AIC) values resulted from models using an initial stable age distribution, our first set of baseline demographic rates (24), and the logistic or linear functional form. However, the striking result of all these analyses is the consistency of the effects across data-sets and model assumptions. The best-fit models of each form predict a complex but consistent pattern of demographic change after the EVOS (Table 1), regardless of carcass data (Green Island vs. the rest of WPWS), initial age distribution, baseline demographic estimates, or functional form. Thus, we report detailed results only from the best-fit model in each family, fit to all postspill carcass data. While the best-fit linear and logistic models are both well supported by the data, the modified logistic is substantially less likely (Table 1); Akaike weights (38) estimate the relative likelihood of the logistic, modified logistic, and linear model forms as 0.35, 0.01, and 0.64, respectively.

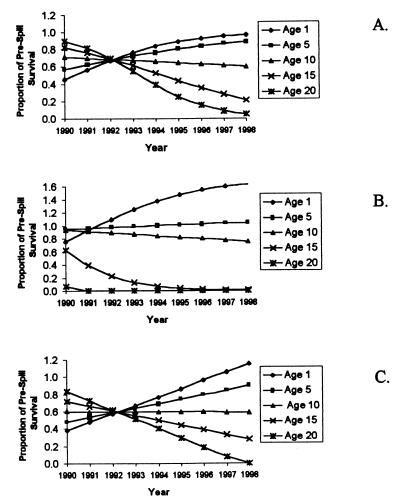
The easiest way to convey the influence of the oil spill on predicted otter survivorships is as a proportion of the prespill survival rates for a given age in each year after the spill: values greater than 1 indicate higher survival after the spill, and values lower than 1 the converse (Fig. 2). Immediately after the spill, young animals are predicted to have suffered the greatest decrease in survivorship, but these effects dissipated rapidly with time (Fig. 2). In contrast, survival of older adults (≥10 yr old) was initially only slightly reduced, but this effect increased with time, with poorer and poorer performance each year after the spill for a given age group. The best-fit models predict that survival of prime reproductive age otters (e.g., age 5) was reduced by as much as 50% initially and then slowly increased to values near or above prespill levels by 1998 (Fig. 2). The predicted effects on the oldest animals (≥15 yr old) are likely to be somewhat inaccurate because of the small number of older carcasses found to fit this part of the distribution.

Figure 2.

Estimated postspill effects on age-specific survival rates. Estimated effects on survival rates are shown as proportions of prespill (baseline) rates for five representative ages. Shown are best-fit results for the logistic model (A), the modified logistic model (B), and the linear model (C).

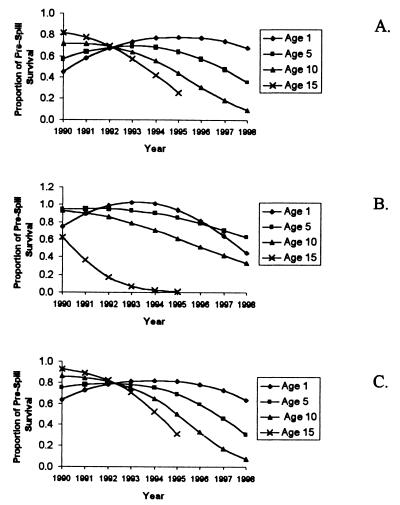
It is also instructive to consider how otters of a given age at the time of the spill were influenced as they aged (Fig. 3). These results suggest that young cohorts at the time of the spill (e.g., age 1) experienced substantially higher mortality rates in the first several years after the spill, but that annual survival improved (relative to prespill rates) as they aged. In contrast, animals in their prime reproductive years and older (i.e., ≥5 yr old) in 1989 have suffered strongly increasing mortality effects as time has passed. Only as these cohorts are lost from the population have demographic rates returned to normal.

Figure 3.

Changing postspill effects for cohorts of otters. Each line represents annual survivals experienced each year for an aging group of otters that were 1, 5, 10, or 15 yr old at the time of the 1989 spill, expressed as a proportion of prespill survival rates. Shown are best-fit results for the logistic model (A), the modified logistic model (B), and the linear model (C).

While these predicted patterns of change are robust to the range of analyses explored so far, we also ran four additional analyses to gauge their strength and accuracy. First, we added environmental variability in first-year survivorship, the demographic rate most likely to show substantial random variability (ref. 37; estimated from tagged otters in WPWS in 1990–1991: refs. 33, 34, and 39), and fit these stochastic simulations to postspill carcass data (25). The best-fit parameter values of these stochastic models are essentially identical to the deterministic results and showed similar confidence limits. Second, to ask whether spill effects on otters born after 1989 were likely, we ran models that only modified survivorships of animals that lived through the spill. These altered models resulted in substantially worse fits for all three model functions (increases in AIC = 19.62, 30.64, and 21.34 for the best-fit logistic, modified logistic, and linear models, respectively), directly supporting the conclusion that otters born after 1989 also have experienced spill effects. Third, we modified the linear model to include quadratic terms and interactions and fit a suite of these more complicated nested models. Likelihood ratio tests suggested no justification for these more complicated models, and none yielded predictions qualitatively different from those of our simpler models. Finally, although we have reliable estimates of the initial postspill age distribution (23), we also tested whether modifications of the initial population structure (e.g., from nonrandom acute spill mortality) could explain observed carcass distributions. Starting with the linear model, we added a second-order polynomial function with two fitted parameters to modify the initial age distribution. This addition, which changes the initial age distribution to help explain the observed carcass data, barely altered model fit (change in −LL = 0.52). Conversely, a model allowing modification of initial age distribution but no changes in demographic rates through time fit carcass data substantially worse than did the original model (change in −LL = 32.37). We also reran linear and logistic models, using fitted estimates of initial age distributions (controlled by a six-parameter logistic function with third-order age effects and main and interaction effects of sex) that made no use of observed age distributions. Neither model compared favorably with the originals (increases in AIC = 2.70 and 2.32). Moreover, these models predict the same significant patterns of change in demography after the spill and fit much more poorly if changing demography was not allowed (increases in AIC = 8.34 and 9.98), further showing that changes in the initial population distribution cannot explain the carcass data after the EVOS. In sum, all these tests confirm the robustness of our basic results.

Finally, we asked whether the predictions of our models accurately reflect our observed age distributions. For the linear model (the single best model) we find no significant departure in observed carcass age distributions from those predicted until the last 2 yr (K-S one-sample tests): in these years, a surplus of older otters results in a significant deviation from the age distributions predicted by either model. For the logistic model, 3 yr, including the last yr, show significantly different distributions; again, a surplus of older otters explained this mismatch in 1998. Overall, these results suggest that the best-fit models do a good job of accurately predicting otter age-at-death distributions, but that the model predications are worst at the end of the data collection period; as we discuss below, census data of live otters suggest an explanation for this pattern.

Discussion

Our results lend strong support to the hypothesis that the EVOS has had continuing impacts on the sea otter population of WPWS. In particular, we found no evidence of improved performance for any age-class immediately after the 1989 spill due to a release from density-driven competition (a reasonable scenario if no lingering effects persisted). Rather, otters of all ages have shown elevated mortality rates in the 9 yr after the spill. These long-term effects are strongest on otters that were 4–5 yr or older during 1989, but the modeling results also suggest that at least through 1996, animals born after the spill were also affected by the events of 1989. Thus, while lingering effects of acute oil exposure may account for much of the longer-term spill effects, less direct impacts are also likely to have occurred, due either to maternal influences or to continued exposure to oil residues.

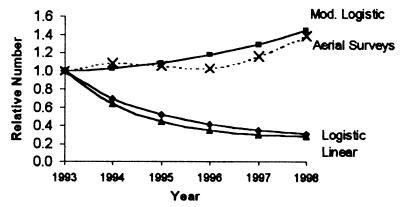
While the immediate loss of otters in the aftermath of the spill resulted in a decline in the local population (40), our results suggest that important long-term demographic changes limited recovery after 1989. In our analyses, we use one population-level effect (age distributions of dead otters) as a tool to infer individual demography. However, the resulting demographic inferences can then be used to predict changes in another population attribute, total numbers. The two best-fit models suggest continuing decline of otters through 1998, whereas the modified logistic predicts no growth until the mid-nineties, when populations are predicted to have slowly risen (Fig. 4).

Figure 4.

Proportional changes in population size predicted from the three best-fit demographic models (Table 1) and actual trends from aerial surveys of WPWS (31).

Direct postspill boat surveys indicated continued declines in sea otter numbers the first year after the spill, and no subsequent increase in population size in the spill area through at least 1991 (40). In addition, low weanling survival rates were observed in WPWS after the spill (6). Although these findings are consistent with predictions of our models, early boat surveys were not sensitive to small changes in abundance, and weanling survival rates can normally be quite variable (34). We began more accurate aerial surveys in 1993, and found significant growth in the WPWS sea otter population, particularly since 1995 (31). At first glance, recent censuses of the live population appear inconsistent with the predictions of our two best models (although they match predictions of the modified logistic extremely well; Fig. 4). However, the models rely on carcass data collected only in oil-affected portions of WPWS, including some of the most heavily oiled, lowest-density sea otter habitat in WPWS. In contrast, aerial surveys include large areas of unoiled, relatively high-density otter habitat. In fact, much of the observed population growth occurred in unoiled or less affected areas, where sea otter densities can be as much as 10 times greater than in the most heavily oiled areas (21, 31). These differences, combined with the demographic results reported here, suggest that oil-affected areas may continue to represent a population “sink” that benefits from immigration from healthy segments of the greater WPWS sea otter population. Although sea otters generally occupy relatively small home ranges, longer-range movements, particularly by males and/or young animals, are common (41, 42).

Several other lines of evidence are consistent with the conclusion that sea otters have experienced significant long-term effects of the spill and that otter movements may account for much of the apparent recovery in oiled areas. Sea otter numbers in the most heavily oiled areas of northern Knight Island have shown no sign of recovery through 1999 (21, 31). Lower tagged otter retention rates in this area, compared with those in an unoiled area of Montague Island, suggest sea otters at Knight Island experienced higher mortality and/or emigration rates even though food resources and body condition of animals there suggest the area should support some population growth (31, 43). Sea otters living in oiled areas have consistently expressed higher levels of cytochrome P4501A than those captured in unoiled areas, indicating continued exposure to petroleum hydrocarbons at least through 1998 (13). Similar biomarker and demographic patterns for harlequin ducks (44, 45), another nearshore predator of benthic invertebrates, also support continuing spill-related effects in oiled areas of WPWS. These similarities suggest that additional species may have suffered consequences analogous to those we find for sea otters. However, while our findings document continuing demographic effects of the EVOS, we also show that these effects have gradually dissipated with time—largely because of the death of cohorts most affected by the spill. This finding suggests that cautious optimism is warranted concerning the gradual return of the ecological communities of WPWS to prespill conditions.

Major anthropogenic “disasters” are usually labeled such because of their immediate and obvious impacts. However, there is increasing recognition that long-term, large-scale effects of events such as oil spills also pose a significant threat to affected populations and ecosystems (46). Unfortunately, accurate assessment of these impacts is not always attainable using the simplistic statistical methods usually advocated for environmental impact monitoring (e.g., ref. 47). Here, we have used a more complex mixture of modeling, statistics, and population data to quantify and understand the effects of the EVOS, one of the best-studied but also most controversial of recent environmental oil disasters (48). Recognition that such events can have strong, long-term impacts on populations of sea otters and other near-shore species demands greater caution in short-term assessment of environmental impacts and suggests that greater efforts are needed to understand the community-wide effects of spill events.

Abbreviations

WPWS

western Prince William Sound

K-S

Kolmogorov–Smirnov test

AIC

Akaike information criterion

EVOS

Exxon Valdez oil spill

−LL

negative log-likelihood