Abstract
Spontaneous liposome formation is predicted in binary mixtures of fluid phase phospholipids and poly(n)ethylene oxide (PEO)-bearing lipids by using single chain mean field theory. The range of stability of the spontaneous liposomes is determined as a function of percentage of PEO-conjugated lipids and polymer molecular weight. These predictions were tested by using cast films of 1,2-diacyl-sn-glycerophosphocholines (e.g., egg l-α-lecithin, 1,2-dimyristoyl-sn-glycero-3-phosphocholine, 1,2-dipalmitoyl-sn-glycero-3-phosphocholine, and 1,2-distearoyl-sn-glycero-3-phosphocholine) and 1,2-dipalmitoyl-sn-glycerophosphatidylethanolamine-PEO conjugates (i.e., 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene glycol)2000]carboxamide and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene oxide)5000]carboxamide) that were hydrated above their gel-liquid crystal phase transition temperatures. Particle sizes of the resulting dispersions, analyzed by quasielastic light scattering, solute retention, 31P NMR, and freeze-fracture electron microscopy measurements, confirmed the single chain mean field predictions. These data indicate that thermodynamically stable, unilamellar liposomes are formed spontaneously by simple hydration of fluid phase phospholipid bilayer films containing low molar ratios of PEO-based amphiphiles. They further suggest that the equilibrium size and colloidal properties of fluid phase, PEO-modified liposomes can be predicted by using this theoretical approach. The implication of these results on the design and processing of sterically stabilized liposomes used in drug delivery applications also is described.
Since their discovery by Bangham in 1965, many processing methods for liposome production have been developed. The majority of these methods require the input of high energy (e.g., ultrasonic treatment, high pressure, and/or elevated temperatures) to disperse low critical micelle concentration phospholipids as a metastable liposome phase. A limited number of alternative procedures that do not use external energy sources, however, have been described. Particles formed from a spontaneous vesiculation process have been reported that use temperature jumps near the phospholipid phase transition (1–3), pH jumps (4–7), and admixtures of high surface tension surfactants (8–17), which produce vesicles that are stable within a narrow regime of solution conditions. These methods are not used, however, to produce poly(n)ethylene oxide (PEO)-modified sterically stabilized liposomes with long circulation times in vivo (18) and other commercialized liposome formulations. Given the diverse nature of their applications in biotechnology and pharmacology, we sought a simple methodology for producing thermodynamically stable spontaneous liposomes, derived from commercially available phospholipids, that could survive in more challenging chemical environments. Our strategy for discovering these conditions focused on using a quantitative theoretical approach to analyze how phospholipids bearing hydrophilic polymer head groups, such as PEO-modified 1,2-dipalmitoyl-sn-glycerophosphoethanolamine [e.g., 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene glycol)2000]carboxamide (DPPE-PEG2000) and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene oxide)5000]carboxamide (DPPE-PEG5000)], could be used to induce spontaneous curvature in the planar lamellar phases preferred by pure 1,2-diacyl-sn-glycerophosphocholines. We present quantitative predictions and supporting experimental evidence for spontaneous liposome formation in phosphocholine (PC)/phosphoethanolamine (PE)-PEO mixtures.
Safran, Pincus, and Andelman (19) have shown that spontaneous vesicle formation may take place in mixed aggregates caused by curvature-induced asymmetry in composition of the monolayers. Wang (20) has shown that even in one component bilayer formed by diblock copolymers, spontaneous vesicle formation is possible if the “head-group” block is much longer than the core forming block. Later, Dan and Safran (21) showed that spherical aggregates are stable in mixtures of diblock copolymers with “head blocks” of different chain length. Porte and Liguore (22) have generalized the Safran, Pincus, and Andelman ideas to show that if the elastic constants of mixed films are calculated at constant chemical potential, the bending constant undergoes softening that may lead to spontaneous vesicle formation. They applied the analytical self-consistent-field approach for polymer brushes and showed that polymer-decorated bilayers may form spontaneous vesicles above some critical polymer densities. Porte and Liguore (22) considered systems in the brush regime that is well above the regime of surface densities that we consider in this work. The common denominator in all of these studies is that the driving force for spherical aggregate formation is caused by the asymmetric partition of the molecules between the monolayers for finite curvatures (19–22). These approaches, however, are not applicable in a quantitative way to the system of interest here because none of them combines quantitative predictions for polymers and short chain lipid molecules in the relevant regimes of surface densities (see below). A molecular theory, therefore, is needed for quantitative predictions of PC bilayers at low surface coverages of PEO.
Single chain mean field (SCMF) theory was chosen as the starting point for our investigations (23–30). This theory has been shown to provide quantitative predictions for (i) the pressure-area isotherms of PEO tethered layers (25, 26), (ii) the adsorption isotherms of proteins on surfaces with grafted PEO (27–29), and (iii) the elastic constants of monolayers and bilayers formed by amphiphilic molecules and polymeric molecules (23, 24, 30). Further, SCMF theory provides detailed information on the molecular organization of the aggregates and provides insights on how different molecular factors determine the macroscopic phase behavior of these systems.
By using the SCMF approach, we compare the thermodynamic stability of PEO-grafted bilayers as planar lamellae with that of spherical phospholipid aggregates. The free energy of curvature, f(c), per unit bilayer area expanded around a planar symmetric film can be described by the quadratic expression
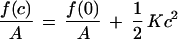 |
1 |
where c = 1/R, R is the radius of curvature of the bilayer surface of inextension (neutral surface), A is the area at the surface of inextension, and K is the elastic constant describing the free energy cost of forming a spherical aggregate of radius R = 1/c. This expression states that a planar film will be the thermodynamically stable configuration when K > 0, however, spontaneous liposomes are predicted when K becomes negative. A more detailed consideration of the contributions to K, therefore, should reveal the conditions required to form spontaneous liposomes.
In a bilayer composed of two different amphiphilic species such as egg l-α-lecithin (EPC) and PEO-conjugated PE, we need to consider the possibility of compositional variations of both species within the monolayers as a function of curvature (i.e., redistribution of both types of lipid molecules between the inner and outer monolayers relative to the planar bilayer state where their composition is identical). It is important to consider this effect because the bending constant in a system that maintains a constant number of molecules in each monolayer (i.e., blocked exchange) is more than an order of magnitude greater than that of a freely exchanging system (i.e., minimum free energy at each c) (30). Furthermore, because we are interested in the equilibrium structure and not bilayer fluctuations, the only relevant case is that of free exchange in which the chemical potentials of each component is the same on both monolayers. Thus, we are concerned with the optimal stability of the structure, not the kinetics of vesiculation or exchange processes.
By using Helfrich’s description of bilayer elastic constants (31), we can write K = kb + k̄/2, where kb is the bending elastic constant and k̄ is the saddle-splay constant. It has been shown (30) that k̄ is independent of composition, however, kb depends on the asymmetry in the number of molecules in the two monolayers (i.e., kb is composition-dependent). We then need to determine the minimum kb as a function of inner and outer monolayer composition for both lipid components. The constants kb and k̄ can be shown to be given by the moments of the lateral pressures and their derivatives (30). Expressions for the elastic constants must include contributions from the repulsive interactions of the bilayer core arising from chain confinement, the attractive interaction associated with the water-hydrophobic core interface, the repulsion of the phospholipid headgroups, and the repulsions of the polymer chains attached to the bilayer surface. We will refer to repulsions and attractions as positive and negative pressures, respectively.
Elastic constants have been calculated for phospholipid bilayers and for polymers tethered at surfaces by using SCMF theory (23, 24, 30). These results have shown that (i) the sign of kb is positive for both the phospholipid and polymer contributions and (ii) the magnitude of kb depends on both the area per molecule and the chain lengths of the lipid and the PEO. In our case, there also will be a strong dependence on composition because an increase in the molar ratio of PEO-modified PE is equivalent to an increase in the number of polymer molecules per unit bilayer area. The area per molecule can be determined by minimizing the total free energy with respect to area while including the phospholipid, polymer, and surface tension contributions (it should be noted that we are assuming that the lipids are water-insoluble and that all molecules in the system exist within aggregates). For each EPC/PEO-modified PE composition, the equilibrium area per molecule needs to be determined before K can be calculated.
Because kb is positive, the only way to achieve a negative K is if k̄ is negative and its value is larger than 2 kb. Successful design of a molecular system with these properties requires that we look in more detail at k̄. In terms of the lateral pressures acting on the molecules, the saddle-splay constant, k̄, is given by
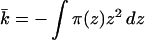 |
2 |
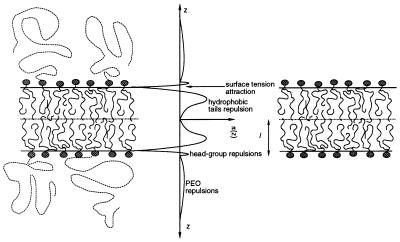
where the z axis is normal to the lamellar plane, its origin is at the bilayer midplane and π(z) includes all contributions to the lateral pressure. We divide the lateral pressure into four main contributions: (i) repulsions arising from the lipid alkyl chains, πl(z); (ii) repulsions arising from the polymer molecules, πp(z); (iii) γb, the attractive surface tension term and (iv) the head-group repulsions†, πhg (which, for the cases of interest here, are a small contribution). The requirement of minimal free energy with respect to area per molecule implies that ∫π(z)dz = 0, such that γb = ∫[πl(z)+πp(z)]dz + πhg and its value is that of the oil/water surface tension (Fig. 1).
Figure 1.
Schematic representation of planar bilayers formed by mixtures of lipids and lipid-PEO (Left) and pure lipid molecules (Right). Also shown is the qualitative shape of the lateral stresses acting on the film (Center). The polymers, lipid chains, and head group have repulsive interactions (i.e., positive pressures π(z) > 0); the water-oil surface tension is the only attractive contribution (i.e., π(z) < 0) that tends to minimize the area per molecule. The relative contributions to the lateral pressures are plotted to scale. The large repulsive interactions arise from packing of the lipid hydrophobic tails; the head-group repulsions are much smaller in magnitude. The contributions of the polymers, at the concentrations treated here, are also small in magnitude. Note, however, that they will provide a finite contribution at large z. The bilayer without the polymers will have an average area per molecule that is smaller than that of the mixed lipid-PEG system because the total repulsions must exactly match the attractive contribution arising from the water-oil surface tension (which is the same for both bilayers). l denotes the thickness of the pure lipid bilayer.
For a pure lipid bilayer of thickness l, k̄ is positive because the attractions act at a larger distance from the bilayer midplane than the repulsions (see Eq. 2 and Fig. 1). The sign of k̄ will change, however, for a system that possesses relatively small repulsive interactions at a very large distance from the bilayer midplane. This effect can be achieved by attaching hydrophilic polymers of sufficient chain length at the surface of the bilayer at low concentrations. Because kb is related to the first moment of the derivative of the lateral pressure the increase in kb with polymer chain length will, in general, be smaller than the decrease produced in k̄, thereby leading to a K < 0.
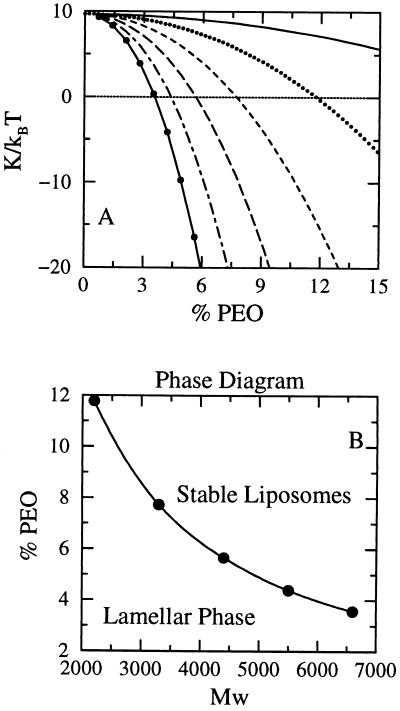
Fig. 2A shows the elastic constant K calculated from SCMF theory as a function of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC)/PEO-modified PE bilayer compositions for a variety of PEO molecular weights. Note that for a fixed molecular weight of polymer, K decreases as the concentration of surface-grafted PEO increases, leading to a change in sign at relatively low molar ratios of PEO. There are limits to the molar ratio of PEO-modified PE that can be incorporated into DMPC bilayers, because (i) the total repulsive interactions must equal the water-oil surface tension, and (ii) the lateral pressures of tethered polymers are a very sharply increasing function of the surface coverage and may lead to unstable films, i.e., induced micelle formation (32). The polymer concentrations at which K changes signs for the molecular weights of PEO treated here are well within the range of compositions typically used in sterically stabilized liposome formulations (18). The decrease of K is caused by the sharp decrease of k̄ with composition. The contribution of the polymer to kb is around 20% of its total value for the highest studied concentration in DPPE-PEG2000 and around 50% for DPPE-PEG5000, in agreement with recent experimental observations (40, 41).
Figure 2.
(A) Elastic constant, K = kb + k̄/2 as a function of the lipid-PEO composition. The different curves represent different molecular weights of the PEO chains: full line, 1,375 D; dotted line, 2,750 D; dashed line, 3125 D, long dashed line, 5,500 D; dot dashed line, 6,875 D; and full line with circles, 8,250 D. The horizontal dashed line is a guide to the eye for the zero of K. (B) Stability range for spherical liposomes and lamellar phases in the plane of percentage of PEO as a function of polymer molecular weight. The line represents the percentage of PEO as a function of molecular weight at which the elastic constant K is zero. Note how the percentage decreases as the molecular weight increases because of the larger distances that contribute to k̄ (see Fig. 1 and Eq. 2).
The results of Fig. 2A have been used to construct the range of stability of the aggregates (Fig. 2B) where the K = 0 points denote the boundary between the stability regimes for planar bilayers and spherical liposomes. The region below the line indicates the molecular weights and compositions of PEO where planar symmetric bilayers are the most stable structures, whereas the phase space above the curve is the region where thermodynamically stable liposomes will form. The change in compositions at the inner and outer monolayers as a function of bilayer curvature also is predicted within the regime of thermodynamically stable liposomes.
The phase diagram of Fig. 2 was obtained by considering the energetics of liposome formation. Entropic effects may change the phase diagram and thus, they need to be discussed. There are two main entropic contributions to consider. First, there is the translational entropy of the aggregates. This contribution will favor liposome formation and also favors small aggregates. The larger the number of the aggregates the larger the translational (or mixing) entropy of the aggregates. The second contribution is related to shape fluctuations of the liposomes. This contribution was studied by Morse and Milner (33). They found that fluctuations tend to destabilize large aggregates. In the cases studied here, however, the bending constant is very large (mostly because of the lipid contribution) and, therefore, we expect these fluctuations to be largely suppressed (33).
At very low concentrations of PEO, aggregates may form in which the polymer is present only on the outer monolayer of the bilayer. Formation of these aggregates will be favored because of (i) the asymmetry of the monolayers, and (ii) the gain in translational entropy compared with large planar films, however, they will be disfavored by the larger lateral repulsions in the outer monolayer compared with a planar bilayer in which half of the polymer will be present at each monolayer. Preliminary calculations (not included in the phase diagram of Fig. 2) indicate that large liposomes with PEO present only in the outer monolayer may coexist with planar bilayers at very low PEO surface coverages. Experimentally, therefore, we can expect the existence of planar bilayers to compete with the formation of large liposomes with PEO existing predominantly in the outer monolayer at very low PEO surface concentrations (up to ≈1.5%).
The complete phase diagram of a lipid/lipid-PEO mixture requires the consideration of many different topologies of aggregates, different molecular organizations (e.g., the highly asymmetric aggregates described above), their polydispersities, shape fluctuations, etc. We believe, however, that the main contribution to the understanding of the formation of spontaneous liposomes is the stability of the planar film as presented in Fig. 2. Furthermore, it also provides a very simple physical picture of the behavior of these systems and the guidelines of how to “molecularly design” systems with desired aggregation properties. The confirmation that the stability of the planar film is the main factor contributing to the spontaneous formation of liposomes will be shown in the experimental observations described below.
What size aggregates are formed in the stable liposome regime? Precise determination of liposome diameters from the free energy expression (Eq. 1) requires the addition of fourth order terms. Another method for obtaining the sizes is by calculating the asymmetry in composition as a function of curvature. We predict that EPC/PEO-modified PE liposomes will have an asymmetry in the number of PEO molecules on the inner and outer surfaces on the order of 0.5–1% (this number is obtained from the theory by determining the minimal kb as a function of composition). This degree of asymmetry will produce thermodynamically stable liposomes with diameters ranging between 100 and 200 nm for DPPE-PEG5000-containing PC dispersions.
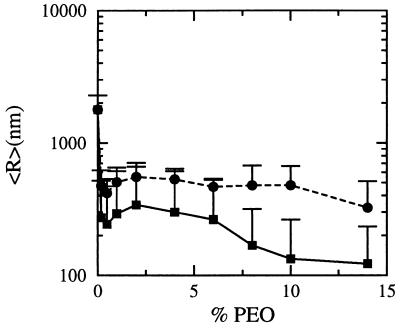
Quasielastic light scattering experiments of EPC/PEO-modified PE dispersions, hydrated in pure water and vortexed for 5–10 sec, were in good agreement with these predictions (Fig. 3). EPC/DPPE-PEG5000 liposomes containing less than 2% PEO-modified PE were in the 450–600 nm size range. As the mol fraction of PEO-conjugate was increased, the observed average diameters gradually decreased to the 225 nm ± 41 nm at 10 mol% DPPE-PEG5000. Liposome diameters were less sensitive to the PEO-modified PE mol fraction for hydrated EPC/DPPE-PEG2000 lipid films of similar compositions; mean diameters ranged between 420 and 550 nm between 0.2–10 mol% DPPE-PEG2000. The observed differences between the DPPE-PEG2000 and DPPE-PEG5000 spontaneous liposome diameters are in very good agreement with the theoretical predictions that longer polymers stabilize smaller aggregates at lower loadings (see Fig. 2).
Figure 3.
EPC liposome size as a function of mol% DPPE-PEG5000 (▪) and mol% DPPE-PEG2000 (•). Spontaneous liposome dispersions (0.3–10 mM total lipid) were prepared by vortexing lipid films with water in a glass tube for 5–10 sec at either 23°C or 37°C (the results were the same regardless of the hydration temperature for EPC). The number of vortexing cycles varied between 1 and 3, depending on the lipid concentration. Dry lipid films were formed by mixing EPC and PEO-modified DPPE in chloroform, followed by solvent evaporation for ≥4 hr at 23°C under a 50-μm vacuum. Liposome size was determined by diluting a 50- to 200-μl aliquot of lipid dispersion into a 2-ml cuvette for quasielastic light scattering analysis at 25°C using a Coulter N4 Plus instrument. Particle sizes reported are based on a unimodal size distribution analysis of 90° scattering data. The observed sizes were not dependent on lipid concentration over the 0.5–10 μmol lipid/ml range or on the presence of either 0.9% NaCl or 20% glycerol in the aqueous phase.
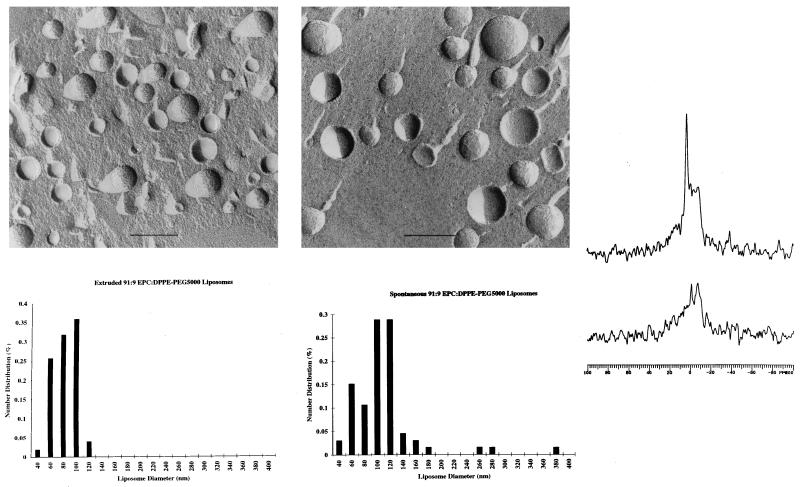
Freeze-fracture electron microscopy experiments indicated the presence of spherical liposomes (Fig. 4) whose size and polydispersity were in reasonable agreement with the quasielastic light scattering data. Simple hydration and vortexing of 91:9 EPC/DPPE-PEG5000 films produced 109-nm average diameter liposomes (Fig. 4B), whereas 90-nm liposomes were observed with samples that were dispersed by standard extrusion techniques using 100-nm track-etch membranes (34) (Fig. 4A). Freeze-fracture behavior characteristic of multilamellar lipid structures was observed for hydrated PEO-free EPC controls. 31P NMR of spontaneous EPC/DPPE-PEG5000 dispersions produced lineshapes comprised of isotropic and powder-like components (Fig. 4C). Addition of 5 mM Mn2+ to these samples resulted in powder pattern 31P NMR spectra that were 57% of the original signal intensity. Assuming spherical geometry and little or no transmembrane permeation of Mn2+ on the timescale of the experiments, these values suggest that the spontaneous liposome diameters measured by NMR are consistent with the sizes reported by the freeze-fracture electron microscopy experiments. The excess inner phosphorus atom sites observed (i.e., 57% instead of the 45% expected for liposomes in the 100-nm size regime) suggests that ≈5% of the lipid remains dispersed as multilamellar material.
Figure 4.
Freeze-fracture electron micrographs of 9:1 EPC/DPPE-PEG5000 dispersions. All liposome samples were cryoprotected with 20% (vol/vol) glycerol before freezing in liquid nitrogen. Samples were fractured at −196°C, shadowed at 45° with platinum, and at 90° with carbon before digesting in bleach solution. Replicas were rinsed in distilled water and dried before visualization with a Phillips CM-12 microscope operating at 60 kV. Magnification calibrations were performed by using a carbon waffle grid. (A) (Upper) Extruded (34) at 30°C. (Lower) Distribution of observed liposome diameters as determined by analysis of electron micrographs. (B) (Upper) Vortexed at 23°C. (Lower) Distribution of observed liposome diameters as determined by analysis of electron micrographs. (C) 31P NMR of spontaneous 9:1 EPC/DPPE-PEG5000 liposome dispersions without (Upper) and with (Lower) extraliposomal Mn2+. NMR spectra were acquired at 81 MHz by using a 90° pulse width, with decoupling gated on during acquisition (off during the 3.16-s delay), on 5-mm samples. The appearance of the powder pattern component in the composite 31P lineshape is in part because of sample viscosity effects (39).
Hydration of EPC/DPPE-PEG5000 in the presence of 50 mM calcein and 0.9% NaCl, followed by chromatography on Sepahdex-G50M using 0.9% NaCl as eluent, produced a calcein-containing fraction that eluted at the column void volume. The entrapped volume of these samples was consistent with 100–200-nm diameter liposomes. Calcein leakage rates from 95:5 and 91:9 EPC/DPPE-PEG5000 liposomes prepared in this manner were slow at room temperature and at 37°C (<7% over 20 hr). Spontaneous 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) liposomes containing the same molar ratios of DPPE-PEG5000 also retained >90% of their encapsulated calcein for 20 hr at 37°C. These suspensions, however, were less stable in 50% fetal calf serum at 37°C. DPPC/DPPE-PEG5000 (95:5) liposomes leaked 10% and 81% of their calcein at 2 hr and 20 hr, respectively, whereas calcein leakage from 95:5 EPC/DPPE-PEG5000 liposomes was 18% and 41% over the same time intervals.
Similar results were obtained for DMPC (Tm = 23°C), DPPC (Tm = 41°C), and distearoyl-sn-phosphatidylcholine (DSPC, Tm = 55°C) lipid films containing DPPE-PEG5000 when they were hydrated and vortexed 15°C above their respective phase transition temperatures. The size of spontaneous liposomes formed by hydrating these materials was sensitive to both the molar ratio of DPPE-PEG5000 present and the alkyl chain length of the PC forming the host bilayer. Dispersions containing 5 mol% DPPE-PEG5000 increased in diameter over the series of DMPC (150 nm), DPPC (370 nm), and DSPC (500 nm), however, the observed diameters decreased as the molar ratio of DPPE-PEG5000 was increased to 9 mol% in these host bilayers (140 nm, 200 nm, and 290 nm, for DMPC, DPPC, and DSPC, respectively). These observations are consistent with the predictions of SCMF theory, because increases in alkyl chain length correspond to increases in K for the membrane bilayer. Because liposome size is determined by a balance of forces between the intrinsic curvature of surface-grafted PEO bilayers and the bending rigidity of the bilayer (at K ≤ 0), the larger bending constants for the longer chain lipids leads directly to larger spontaneous liposome sizes as the chain length increases.
We have shown that spontaneous liposome formation is the result of a large and negative saddle-splay constant and a low bending constant. The low contribution of the PEO chains to the bending constant is obtained by breaking the symmetry in composition between the two monolayers of the bilayer, whereas a large (negative) saddle-splay constant is obtained when low pressures act at very large distances from the bilayer midplane. The picture that emerges is that spherical aggregates are more stable than planar bilayers because the transfer of polymer from the inner monolayer to the outer one at finite curvatures releases some of the stresses associated with the packing of the polymer chains in the symmetric planar bilayer. There is a minimal amount of polymer redistribution necessary to relieve molecular packing stresses to allow the formation of a stabilized spherical bilayer film. It also should be recognized that low molecular weight polymers do not have large enough lateral pressures at the compositions treated here to achieve a free energy minimum by relaxing into an asymmetric distribution of PE-PEO molecules in a spherical bilayer configuration. The interplay of these factors determines the boundary curve shown in Fig. 2 and is supported by our experimental observations.
The driving force for spherical aggregate formation has the same origin as predicted by Porte and Liguore (22), namely the free energy gain by molecular redistribution among the monolayers. They associate the effect, however, with a reduction of the bending constant because of the composition redistribution. We find that the polymer layer does not appreciably change the value of kb (in agreement with experimental observations; refs. 40 and 41); rather, it is the sharp decrease of the saddle-splay constant, k̄, with polymer loading that makes the planar film unstable. In addition, our results are obtained for polymer loadings in the mushroom and brush-mushroom transition regimes. The higher polymer surface coverages relevant to Porte and Liguore’s predictions (22) will result in very high lateral pressures making the phospholipid bilayer unstable (41).
It is interesting to note that the compositions used for sterically stabilized liposomes in drug delivery (18) is within the ranges of thermodynamically stable aggregates predicted by SCMF theory. This finding may suggest that the longevity of these liposomes in blood may arise not only from the steric barrier presented by the PEG layer, but also because of the thermodynamic stability of the aggregates.
Are spontaneous liposomes true equilibrium structures? Kinetically trapped liposome structures may be formed when either extrusion or spontaneous vesiculation methods are used. Because investigations with other phospholipid/PEO-modified lipid mixtures (35, 36) have shown that surface-grafted PEO molecules prevent close apposition and fusion of highly curved extruded liposomes, relief of curvature strain in nonequilibrium structures may be inhibited because of the prevention of interlamellar contact by the PEO layer. We believe, however, that the spontaneous liposomes formed in these experiments are at true thermodynamic equilibrium because (i) the liposomes are formed in the same region of phase space predicted by the theory for equilibrium liposome structures, (ii) the measured diameters are in the same size regime as that predicted by theory, (iii) the measured liposome diameters are very reproducible on hydration of multiple samples of the same bilayer composition, and (iv) the observed sizes and polydispersities of spontaneous liposome samples stored at room temperature remained constant over the course of several weeks. Important questions concerning the detailed kinetics, mechanism, and cooperativity of spontaneous vesiculation, however, remain unresolved. Additional efforts will be required to clarify these issues.
The simplicity of this combined theoretical and experimental approach may have profound implications on the practical development of PEO-modified stable liposomes for drug delivery applications (37). Application of a quantitative theory to PEO-grafted liposome systems can greatly reduce the experimental effort required to develop stable formulations with favorable biological and pharmacological properties (18) as well as improve our understanding of how the molecular structure of the polymer and lipid components determine the microstructural and physical behavior of the layers. The understanding of this relationship will lead to the ability to design polymers that will form aggregates with tailored physical properties (23–30) (e.g., phase behavior, steric repulsion, size distribution, and targeted delivery). Our results also indicate that this spontaneous vesiculation technique can be used to rapidly prepare samples with a narrow size distribution without exposing labile encapsulant molecules, such as peptides and oligonucleotides, to potentially damaging shearing effects. These opportunities are currently under investigation.
Acknowledgments
We would like to acknowledge the financial support of the National Science Foundation (to D.H.T., MCB-9319099 and to I.S., CTS-9624268). D.H.T. also acknowledges the partial financial support of the Purdue Research Foundation. I.S. is a Camille Dreyfus Teacher-Scholar. I.S. acknowledges the Petroleum Research Fund administered by the American Chemical Society for partial support of this work.
ABBREVIATIONS
- DMPC
1,2-dimyristoyl-sn-glycero-3-phosphocholine
- DPPC
1,2-dipalmitoyl-sn-glycero-3-phosphocholine
- DPPE-PEG2000
1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene glycol)2000]carboxamide
- DPPE-PEG5000
1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-[methoxypoly(ethylene oxide)5000]carboxamide
- EPC
egg l-α-lecithin
- FFEM
freeze-fracture electron microscopy
- PC
phosphocholine
- PE
phosphoethanolamine
- PEO
poly(n)ethylene oxide (a.k.a. polyethylene glycol, PEG)
- SCMF
single chain mean field
Footnotes
The repulsions of the headgroups for the double chain phospholipids are small. The head-group interactions (surface tension term and head-group repulsions) are modeled by using the opposing forces model (38), i.e., the free energy of the heads (including the surface tension attraction) is fhg = γb (a − ah2/a). In the calculations presented here we used γb = 60 dyn/cm and ah = 22.3 Å2. The resulting (optimal) average area per lipid molecule in the one component bilayer is a0 = 63.2 Å2.
References
- 1.Madden T D, Tilcock C P, Wong K, Cullis P R. Biochemistry. 1988;27:8724–8730. doi: 10.1021/bi00424a006. [DOI] [PubMed] [Google Scholar]
- 2.Nezil F A, Bayerl S, Bloom M. Biophys J. 1992;61:1413–1426. doi: 10.1016/S0006-3495(92)81947-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dobereiner H G, Kas J, Noppl D, Sprenger I, Sackmann E. Biophys J. 1993;65:1396–1403. doi: 10.1016/S0006-3495(93)81203-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hauser H, Gains N. Proc Natl Acad Sci USA. 1982;79:1683–1687. doi: 10.1073/pnas.79.6.1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hauser H. Proc Natl Acad Sci USA. 1989;86:5351–5355. doi: 10.1073/pnas.86.14.5351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hauser H, Mantsch H H, Casal H L. Biochemistry. 1990;29:2321–2329. doi: 10.1021/bi00461a016. [DOI] [PubMed] [Google Scholar]
- 7.Lin B Z, Yin C C, Hauser H. Biochim Biophys Acta. 1993;1147:237–244. doi: 10.1016/0005-2736(93)90008-n. [DOI] [PubMed] [Google Scholar]
- 8.Hauser H, Gains N, Eibl H J, Muller M, Wehrli E. Biochemistry. 1986;25:2126–2134. doi: 10.1021/bi00356a042. [DOI] [PubMed] [Google Scholar]
- 9.Hauser H. Chem Phys Lipids. 1987;43:283–299. doi: 10.1016/0009-3084(87)90024-7. [DOI] [PubMed] [Google Scholar]
- 10.Yin C C, Schurtenberger P, Wehrli E, Paltauf F, Hauser H. Biochim Biophys Acta. 1991;1070:33–42. doi: 10.1016/0005-2736(91)90143-v. [DOI] [PubMed] [Google Scholar]
- 11.Kaler E W, Murthy A K, Rodriguez B E, Zasadzinski J A. Science. 1989;245:1371–1374. doi: 10.1126/science.2781283. [DOI] [PubMed] [Google Scholar]
- 12.Kaler E W, Herrington K L, Miller D D, Zasadzinski J A. In: Structure and Dynamics of Strongly Interacting Colloids and Supramolecular Aggregates in Solution. Chen S H, Huang J S, Tartaglia P, editors. Dordecht, The Netherlands: Kluwer; 1992. pp. 571–577. [Google Scholar]
- 13.Kaler E W, Herrington K L, Murthy A K, Zasadzinski J A. J Phys Chem. 1992;96:6698–6707. [Google Scholar]
- 14.Herrington K L, Kaler E W, Miller D D, Zasadzinski J A, Chiruvolu S. J Phys Chem. 1993;97:13792–13802. [Google Scholar]
- 15.Gabriel N E, Roberts M F. Biochemistry. 1984;23:4011–4015. doi: 10.1021/bi00313a001. [DOI] [PubMed] [Google Scholar]
- 16.Gabriel N E, Roberts M F. Biochemistry. 1986;25:2812–2821. doi: 10.1021/bi00358a012. [DOI] [PubMed] [Google Scholar]
- 17.Cevc G. In: Handbook of Biological Physics. Lipowsky R, Sackmann E, editors. Vol. 1. Amsterdam: Elsevier; 1995. pp. 466–490. [Google Scholar]
- 18.Lasic D, Martin F, editors. Stealth Liposomes. Boca Raton, FL: CRC; 1995. [Google Scholar]
- 19.Safran S A, Pincus P, Andelman D. Science. 1990;248:354–356. doi: 10.1126/science.248.4953.354. [DOI] [PubMed] [Google Scholar]
- 20.Wang Z-G. Macromolecules. 1992;25:3702–3705. [Google Scholar]
- 21.Dan N, Safran S. Europhys Lett. 1993;21:975–980. [Google Scholar]
- 22.Porte G, Liguore C. J Chem Phys. 1995;102:4290–4298. [Google Scholar]
- 23.Szleifer I, Carignano M A. Adv Chem Phys. 1996;94:165–260. [Google Scholar]
- 24.Ben-Shaul A. In: Structure and Dynamics of Membranes. Lipowsky R, Sackmann E, editors. 1A. Amsterdam: Elsevier; 1995. pp. 359–402. [Google Scholar]
- 25.Szleifer I. Curr Opin Colloid Interface Sci. 1996;1:416–423. [Google Scholar]
- 26.Szleifer I. Curr Opin Solid State Mat Sci. 1997;2:337–344. [Google Scholar]
- 27.Szleifer I. Biophys J. 1997;72:595–612. doi: 10.1016/s0006-3495(97)78698-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Szleifer I. Physica A. 1997;244:370–387. [Google Scholar]
- 29.McPherson, T., Kidane, A., Szleifer, I. & Park, K. (1998) Langrmuir, in press.
- 30.Szleifer I, Kramer D, Ben-Shaul A, Gelbart W M, Safran S A. J Chem Phys. 1990;92:6800–6817. [Google Scholar]
- 31.Helfrich W. Z Naturforsch. 1973;28C:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 32.Hristova K, Kenworthy A, McIntosh T J. Macromolecules. 1995;28:7693–7699. [Google Scholar]
- 33.Morse D C, Milner S T. Europhys Lett. 1994;26:565–570. [Google Scholar]
- 34.Hope M J, Bally M B, Webb G, Cullis P R. Biochim Biophys Acta. 1985;812:55–65. doi: 10.1016/0005-2736(85)90521-8. [DOI] [PubMed] [Google Scholar]
- 35.Holland J W, Cullis P R, Madden T D. Biochemistry. 1996;35:2610–2617. doi: 10.1021/bi951999j. [DOI] [PubMed] [Google Scholar]
- 36.Nikolova A N, Jones M N. Biochim Biophys Acta. 1996;1304:120–128. doi: 10.1016/s0005-2760(96)00112-9. [DOI] [PubMed] [Google Scholar]
- 37.Gerasimov O V, Rui Y, Thompson D H. In: Vesicles. Rosoff M, editor. New York: Dekker; 1996. pp. 679–746. , and references therein. [Google Scholar]
- 38.Israelachvili J. Intermolecular and Surface Forces. London: Academic; 1991. [Google Scholar]
- 39.Fenske D B, Cullis P R. Biophys J. 1993;64:1482–1491. doi: 10.1016/S0006-3495(93)81515-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Joannic R, Auvray L, Lasic D D. Phys Rev Lett. 1997;78:3402–3405. [Google Scholar]
- 41.Evans E, Rawicz W. Phys Rev Lett. 1997;79:2379–2382. [Google Scholar]