The use of flexible arm muscle synergies to perform an isometric stabilization task

Abstract

Objective

To evaluate if functional synergies are comprised of flexible combinations of a small number of ensembles of upper limb muscles to stabilize a particular performance variable during a force production task.

Methods

Electromyographic (EMG) signals of wrist, elbow and shoulder muscles were recorded. Linear combinations of indices of the integrated EMG of nine muscles (muscle modes or M-modes) and their relationship to changes in the moment of force produced by the right arm of subjects about the horizontal axis of a handle were first determined. Uncontrolled manifold (UCM) analysis was performed to determine the extent to which variance of the M-modes acted to produce a consistent change in the moment of force.

Results

Subjects exhibited three M-modes, two of which were ‘reciprocal’ while the third mode was considered a co-contraction mode. The three M-modes were found to be combined to form synergies that produced a consistent change in the moment of force across repetitive trials. Variance in the M-mode space that led to consistent changes in the moment of force across repetitions was significantly higher than variance that tended to produce inconsistent changes in the moment of force.

Conclusions

Flexible combinations of activations of ensembles of muscles are organized to stabilize the value of or produce consistent changes in the value of important performance variables.

Significance

The study of flexible muscle synergies in healthy individuals paves the way to understanding abnormal postural and movement patterns in individuals with neurological disorders.

Introduction

A frequently debated issue in motor control is how the central nervous system (CNS) coordinates motor elements (i.e., degrees of freedom or DOFs), particularly when more DOFs (e.g. joint motions or muscle activations) are available to accomplish a task than are required (e.g. to position the hand in space; Bernstein, 1967)? This issue is particularly relevant in the space of muscles, where muscle activations typically are not independent of each other (Hughlings Jackson, 1889; Lee, 1984; Soechting and Lacquaniti, 1989). In the current article, we examine the formation of muscle synergies related to performance of an upper limb task.

The application of one or more optimization criteria has been suggested to solve the DOFs ‘problem’, resulting in relatively unique solutions for coordinating redundant DOFs (for reviews, see Seif-Naraghi, 1990; Rosenbaum et al., 1995; Latash, 1996). In contrast, the uncontrolled manifold (UCM) hypothesis proposes that a specific control law primarily constrains combinations of DOFs only if they lead to unwanted changes in the value of important performance variables (Martin et al., 2004; Scholz and Schöner, 1999; see also Todorov, 2004). Multiple combinations of the same DOFs that lead to equivalent values of the performance variable are less constrained, providing for performance flexibility (Martin et al., 2005). From the UCM perspective, therefore, all DOFs play a role in task performance; only certain combinations of these DOFs are constrained. Evidence for such a control law has been provided in a variety of tasks involving analyses of kinematics (Scholz and Schöner, 1999; Scholz et al., 2000; Scholz et al., 2001; Tseng et al., 2002; Tseng et al., 2003) and forces (Latash et al., 2002; Latash et al., 2003; Shinohara et al., 2004).

The same UCM control law is hypothesized to underlie the formation of muscle synergies as well; i.e. muscle synergies are comprised of flexible combinations of different muscles acting to stabilize important performance variables, for example, a shift of the center of pressure in postural tasks (Krishnamoorthy et al 2003b). Because muscles typically are not activated independently of other muscles (Hughlings Jackson, 1889; Lee, 1984; Soechting and Lacquaniti, 1989), we suggest that search for multi-muscle synergies should happen not in the space of individual muscle activations. Rather, they should occur in the space of muscle groups (muscle modes, see later) that can, at least hypothetically, be independently manipulated by the controller. Although the UCM approach provides a potential framework to study muscle synergies, its application to muscle synergies has been difficult because the approach requires a formal model relating motor element space to variables more directly related to task performance, such as the hand’s position in a reaching task (Scholz and Schöner, 1999; Scholz et al., 2000; Scholz et al., 2001; Tseng et al., 2002; Tseng et al., 2003). Recently, a method was developed in the context of postural control studies that overcame this problem (Krishnamoorthy et al., 2003b; Krishnamoorthy et al., 2004). Principal component analysis (PCA) first was used to transform the electromyographic (EMG) activity of individual muscles into a space of ‘muscle-modes’ (M-modes), capturing the natural co-variation among muscles. It was hypothesized that the CNS forms functional synergies by combining these independent modes, and appropriate adjustment of the gain of each mode.

M-modes are similar to the notion of fixed synergies or primitives in earlier work (e.g. Nashner, 1977; Bizzi et al., 1991; Giszter et al., 1993; Mussa-Ivaldi et al., 1994). However we view M-modes as elemental variables, not synergies themselves, which are flexibly combined to form functional synergies, as described above.

The current experiments tested the hypothesis that skilled arm function in humans also involves the formation of muscle synergies by flexibly combining muscle modes. Two dissimilar tasks were used to test the general nature of the M-mode concept, i.e. that the same set of elementary control variables (M-modes) are used to form functional synergies across a range of tasks. The first task required the explicit production of different isometric moments of force. The second task involved the implicit production of a moment of force in order to stabilize a tilt board on which a subject sat on a chair.

Methods

Subjects

Ten healthy subjects, five male and five female, of mean age 26 yr. (± 3.2 SD) without reported neurological or motor disorders, participated in the experiment. All subjects except one were right-handed based on their preferential hand use during activities of daily living, such as writing. Comparison of the results of this one subject with those of the other 9 subjects revealed no qualitative differences. The subjects gave written informed consent according to the procedures approved by the Human Subjects Review Committee of the University of Delaware.

Apparatus

Surface electromyographic activity was collected using disposable self adhesive Ag/AgCl snap dual electrodes (Noraxon, Scottsdale, AZ) applied on the muscle bellies of the following upper extremity muscles: flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), extensor carpi radialis (ECR), extensor carpi ulnaris (ECU), brachioradialis (BR), biceps brachii (BIC), the medial head of triceps brachii (TRI), anterior deltoid (AD) and posterior deltoid (PD). Care was taken to minimize cross talk between muscles. Results of pilot studies indicated that electromyographic activity of the erector spinae and abdominal muscles was not above noise level during the experimental tasks. Therefore, EMG of the trunk muscles was not collected during the actual experiments. The inter-electrode distance was two centimeters. A Motion Labs MA-300 system (Motion Labs Systems, Baton Rouge, LA) was used to collect EMG signals. Every EMG channel was amplified (× 20) by a pre-amplifier connected to the electrodes. Further, the gain for individual channels was adjusted (× 200 - 10,000) after viewing the individual signals on a computer monitor. Data were recorded at a sampling frequency of 1000 Hz with a 16-bit resolution after band pass filtering at 20–500 Hz. A laptop computer with a Pentium III processor with customized software based on the LabView-6 (National instruments, Austin, TX) package was used to control the experiment and collect the data.

A six component force/torque transducer (Model PY6-250, Bertec Corporation, OH) recorded the hand forces and moments (transducer-1; Fig. 1). A rigid horizontal metal handle was attached to the transducer through a small vertical post, such that, any forward or backward directed force on the handle created a moment about the horizontal axis of the transducer parallel to the frontal plane of the body (x-axis of the transducer). Subjects grasped this handle with their right hand. A second one-dimensional force transducer (Omega, Stamford, CT) was used to record forces applied by the left hand (transducer-2; Fig. 1) in the anterior-posterior (AP) direction. A horizontal wooden handle was attached to this transducer, such that any forces directed forward or backward on the handle, were along the axis of measurement of the force transducer. Both transducers were rigidly attached to a table in front of the subject.

Figure 1a. Experimental set-up for the Step task.

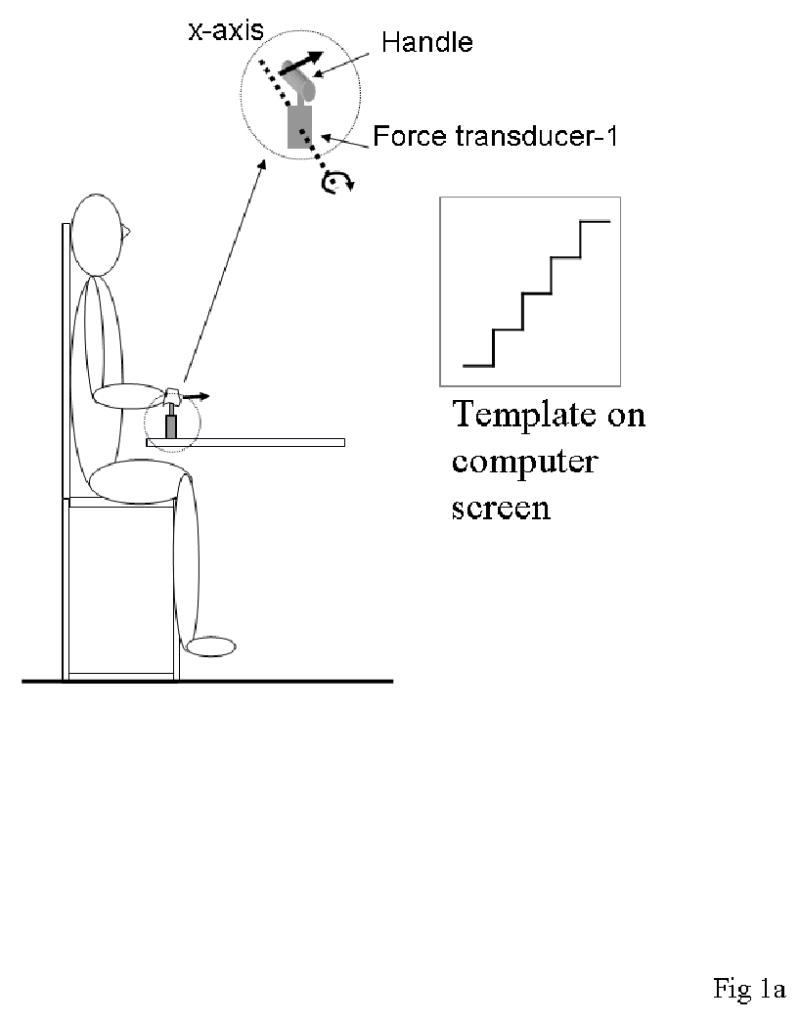
Monitor showing the template was placed in front of the subject. Electromyograms (EMGs) from nine muscles of the shoulder, elbow and wrist of the right side were collected (not shown in figure). The subject pushed forward (pulled backward) on the handle, resulting in a positive (negative) moment of force about the x-axis of force transducer-1. The x-axis of the transducer is indicated by the dashed line.

Procedure

Control trials

At the beginning of the data collection, two maximal voluntary isometric contractions (MVCs) of the wrist, elbow and shoulder flexors and extensors were collected. The wrist muscles were tested with the arm positioned by the side of the body, elbow at 90 degrees of flexion, the wrist in neutral position and the forearm supinated (FCR and FCU), or pronated (ECR and ECU). The BIC and BR muscles were tested in the same position as the wrist flexors. To test the TRI muscle, the shoulder was abducted to 90 degrees and elbow flexed to 90 degrees. AD and PD were tested by asking the subject to attempt shoulder horizontal adduction and abduction with the arm in a neutral position. The peak value of rectified and filtered EMG was determined for each trial and the trial with higher peak was subsequently used for normalization of EMG data.

In addition, the maximum moment of force was estimated for each subject by collecting two trials in which they pushed forward or pulled backward as hard as possible on the right handle. Twenty-five percent of the maximum moment of force generated about the x-axis of transducer-1 in either direction was used as the maximum moment required in the Step Task as described below.

Task 1 - Step changes in moment of force

This task was used to define muscle-modes (M-modes) in the right arm and to relate changes in the magnitudes of M-modes to step-like changes in moment of force produced by the right hand about the x-axis of transducer-1 (T_X: moment of force; Fig. 1).

Subjects sat on a chair placed on a stable chair while grasping the handle attached to transducer-1 with his/her right hand. The height of the chair was adjusted such that the upper arm was held vertically against the body, the elbow was at 90º of flexion and the forearm was pronated and parallel to the floor. The chair had a high seat, so that the subject’s feet could not touch the floor. The subjects were instructed to rest their back against a high back rest throughout the data collection and not involve their trunk in the task. The trunk was not restrained by straps but the experimenter monitored the subject and reminded him/her periodically to use only the upper extremity in the task.

A computer monitor in front of the subject displayed the template of required step changes in the moment of force produced about the x-axis of transducer-1 (see Fig. 1a). Subjects were asked to move a trace corresponding to their applied moment to match the displayed template by either pushing forward on the handle (Step-push; positive moment of force; illustrated in Fig. 1a) or pulling backwards (Step-pull; negative moment).

Data was collected over a 43 s period for every trial. The subject was instructed to initially rest the hands on the legs. After the first second of data collection the subject heard a beep, which indicated that he/she should place the right hand over the handle and grasp it lightly. The average data from the transducer over the first second were subtracted from subsequent data to zero the readings. For the next 10 seconds, the subject held the transducer lightly without producing any moments of force, keeping the cursor on the zero line of the template. The remaining 32 seconds were evenly divided into 4 steps of 8 s each. The last and highest step corresponded to 25% of the subject’s maximum moment of force (see ‘control trials’ above). The lower three steps corresponded to 6.25%, 12.5% and 18.75% respectively of the maximum moment of force. The subject was instructed to match the template as closely as possible, especially at the steady state portions of the step. Every subject was given 3 trials of practice for both the Step-push and Step-pull conditions prior to data collection. Fifteen trials at each condition were collected. Sufficient rest periods were given in between trials such that fatigue was not an issue. The order of the Step-push and Step-pull conditions was randomized across subjects.

Task 2 - Balance Task

This task was used to determine how magnitudes of the M-modes, identified in the right arm during the first task, were organized to maintain a stable horizontal position of an inherently unstable chair on which subjects sat when they produced a sudden release of a force applied to transducer-2 by the left hand.

Subjects sat on a chair attached to a platform with a fixed 5 cm diameter cylindrical pipe at the center of its base running medial to lateral (Fig. 1b). This introduced instability in the AP direction. The subject grasped the handle attached to transducer-1 with the right hand and the wooden handle attached to transducer-2 with the left hand. A digital monitor displayed to the subject the numerical value corresponding to forces applied by the left hand. No other feedback was provided.

Figure 1b. Experimental set-up for the Balance task.

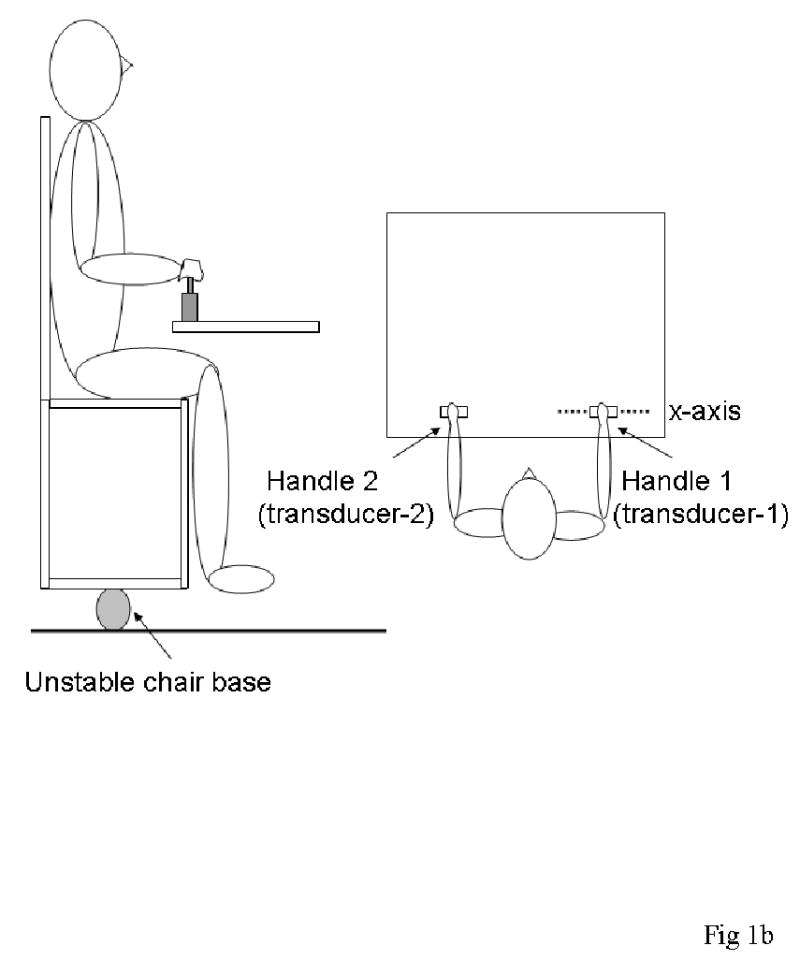
The subject sat on a chair with an unstable base. Both hands grasped handles on the table in front of them. Push (pull) forces on the right side countered pull (push) forces on the left, producing positive (negative) moments of force about the x-axis (dashed line) of transducer-1, thereby stabilizing the subject on the chair.

There were two conditions in the Balance task: Push (Balance-push) and Pull (Balance-pull). For the Balance-push (Balance-pull) condition, the subject was instructed to push forward (pull backward) as hard as possible into the (left) handle attached to transducer-2, while keeping the chair horizontal (not allowing it to tip forward or backward), which required exertion of a counter force with the right hand on transducer-1. After 5 seconds, subjects were told to release rapidly the force being applied to transducer-2 (left hand) at a time of their choice (i.e. this was not a reaction time task) while maintaining the horizontal position of the chair. They were instructed not to move their trunk or to use their feet to help maintain balance. Thus, the subject was required to implicitly use the right arm to counter the effect of force changes in the left arm for platform stability.

The order of the Balance-push and Balance-pull conditions was randomized across subjects. Fifteen trials at each direction were collected. Each trial lasted 10 seconds and there was an interval of 30 seconds to 1 minute between trials. Subjects did not report feeling fatigued during the experiment. They were able to maintain a consistent force level from trial to trial. In addition, spectral analysis on EMGs indicated that the mean power frequencies were similar between the initial and later trials confirming that fatigue was not an issue in these experiments.

Data analysis

All signals were processed off-line, rectified and filtered with a 50 Hz low-pass, fourth order, zero-lag Butterworth filter using Matlab 7 (The Mathworks Inc., Natick, MA).

Step task

The average baseline EMG values were computed over a 100 ms interval at the beginning of the trial while subjects lightly held the transducer without producing any forces (baseline EMG activity). This value was subtracted from EMG activities for the entire trial. An algorithm was written in Matlab to pick the time (t_peak) at which the largest value of T_X occurred during the steady state phase after each step increase or decrease in the moment of force. Trials that had large moment of force fluctuations, or large deviations from the required steady state moment specified by the template were excluded from further analysis. On average, one trial per subject was rejected. All EMG signals were then integrated over a 150 ms window prior to t_peak. A matrix of these EMG integrals then was created. For example, for a subject producing the step task involving pushing on the handle for which all 15 trials were retained, a 60 (EMGs across 4 steps of force moments for 15 trials) × 9 (muscles) matrix was created and used in the analysis.

Balance task

Individual trials were viewed on a computer screen and aligned according to the change in the signal of the left transducer (transducer-2; point of force release). This time will be referred to as “time zero” (t₀). Anticipatory postural adjustments (reviewed in Massion, 1992) of the muscles of the right arm were analyzed as follows: EMG signals were integrated over a 150 ms window, including 100 ms before t₀ and 50 ms after t₀. The IEMG produced between 1000 ms and 850 ms before t₀, when subjects maintained a steady-state push (pull) force (EMG_bl), was subtracted from this value.

$${\text{IEMG}}_{\text{Balance}-\text{pull}/\text{push}}=\underset{{\text{t}}_0-100}{\overset{{\text{t}}_0+50}{\int }}\text{EMGdt}-\underset{{\text{t}}_0-1000}{\overset{{\text{t}}_0-850}{\int }}{\text{EMG}}_{\text{bl}}\text{dt}$$ (1)

IEMG indices were further normalized them by dividing with the integrals of EMGs over a 150 ms period centered at the peak EMG collected in the control trials described above.

$${\text{IEMG}}_{\text{norm}}={\text{IEMG}}_{\text{Step}-\text{pull}/\text{push},\hspace{0.17em}\text{Balance}-\text{pull}/\text{push}}{/\text{IEMG}}_{\text{control}}$$ (2)

Note that IEMG_norm is a dimensionless measure of integrated EMG activity.

The change in moment of force produced on transducer-1 (ΔT_X) that corresponded to the EMG activity calculated above in the Step task, was computed by subtracting the average T_X value over a 1 s period when no forces are exerted on the transducer at the beginning of the trial (baseline T_X value) from the T_X value at time t₀ (t_peak) + 50 ms to account for electromechanical delay (Krishnamoorthy et al., 2003b).

Statistics

The steps in data analysis are similar to the procedures used previously (see Krishnamoorthy et al., 2003b for details) and are summarized here.

Analysis 1: Defining M-modes using Principal Component Analysis (PCA)

For each of the Step-push and Step-pull conditions, a 4- step (moments of force) across N-trials by 9 muscle (i.e., 4N by 9) IEMG_norm data matrix was defined for each subject’s data. PCA was performed on the covariance matrix of the IEMG_norm matrices to identify the M-modes (i.e. PCs accounting for at least 90% of the variance), following varimax rotation (SPSS 12.0, SPSS Inc., Chicago, IL).

Analysis 2: Defining the Jacobian using multiple regression

Changes in the magnitudes of M-modes (ΔM-mode) over each step of changes in the moment of force were computed by multiplying the IEMG_norm data (4N × 9) by the PCs (9 × 3) obtained in Analysis 1, separately for the Step-push and Step-pull tasks. Multiple linear regression analysis was used to relate ΔM-mode to observed change in T_X (ΔT_X) over a set of trials by a subject. The analysis resulted in sets of coefficients, k, representing the Jacobian matrix (a vector in this case because of the one degree of freedom of the task variable) relating small M-mode changes to ΔT_X:

$$\mathrm{\Delta }{\text{T}}_{\text{X}}={\text{k}}_{\text{1}}\mathrm{\Delta }\text{M}-{\text{mode}}_1+{\text{k}}_{\text{2}}\mathrm{\Delta }\text{M}-{\text{mode}}_2+{\text{k}}_{\text{3}}\mathrm{\Delta }\text{M}-{\text{mode}}_3$$ (3)

$$\mathbf{J}\mathbf{a}\mathbf{c}\mathbf{o}\mathbf{b}\mathbf{i}\mathbf{a}\mathbf{n}=[{\text{k}}_{\text{1}}\hspace{0.17em}{\text{k}}_{\text{2}}\hspace{0.17em}{\text{k}}_{\text{3}}]$$ (4)

Separate ‘push’ and ‘pull’ Jacobians were obtained from the results of Step-push and Step-pull tasks, respectively, to check whether they were specific to the direction of the moment of force production.

Analysis 3: UCM Analysis

The hypothesis that flexible synergies in the M-mode space act to stabilize ΔT_X (i.e. moment of force about dimension x of the transducer) accounts for one DOF. The space of ΔM-modes is three dimensional. Thus, the system is redundant with respect to the task of stabilizing ΔT_X (i.e. there are two redundant DOFs). The UCM in this analysis represents combinations of M-modes that are consistent with a stable value of ΔT_X. The UCM was computed as the null space of the Jacobian using procedures in Matlab. Estimates of variance of ΔM-mode within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) were computed (for details see Krishnamoorthy et al. 2003b). The variance estimates per DOF were obtained by dividing the components of M-mode variance that lie (1) orthogonal to the UCM by 1 (the task variable, moment about the x-axis is a 1 DOF control hypothesis) to obtain V_ORT and (2) within the UCM by 2 (3 M-modes minus 1 DOF in task space) to obtain V_UCM. These measures then were used in the data analyses. Repeated measures ANOVAs were used to determine if there was a significant difference between V_UCM and V_ORT for the two Balance conditions.

Results

General EMG Patterns

Step tasks

When the subjects produced step-like changes in the moment of force measured by the transducer-1, most muscles showed an increase in EMG with increasing moments of force in both directions of step changes of ΔT_X. The only exception was AD, which showed a drop in EMG with increasing moment of force in the Step-pull condition. These muscle patterns varied across subjects. Fig. 2 shows a representative trial of the Step-push condition. Note that all muscles show an increase in activation with increasing moment of force.

Figure 2. EMGs from a representative trial (subject s8) in the Step-push condition.

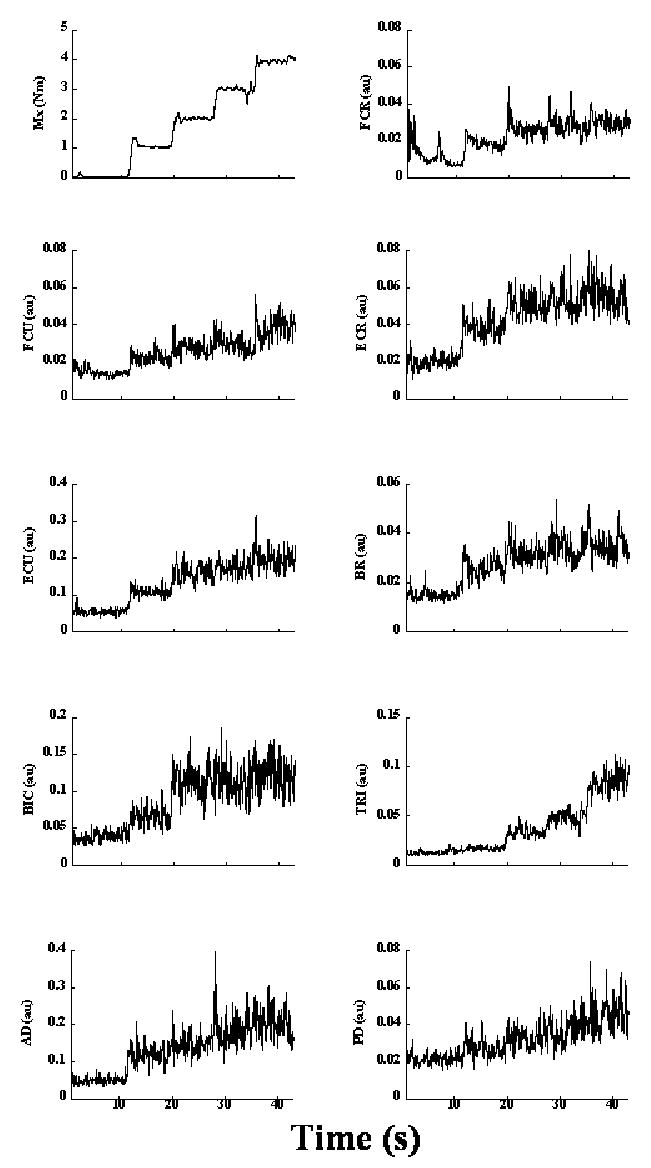
The top left panel shows the moment of force produced about the x-axis of transducer-1. All the remaining panels show corresponding EMG changes in the following muscles: flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), extensor carpi radialis (ECR), extensor carpi ulnaris (ECU), brachioradialis (BR), biceps brachii (BIC), the medial head of triceps brachii (TRI), anterior deltoid (AD) and posterior deltoid (PD). The bursts in EMGs in some muscles (e.g. FCR) at the beginning of the trial correspond to the period when the arm was lifted to place the hand on the handle.

Balance tasks

When the subjects sat on the (AP) unstable chair and produced pushing or pulling forces with the two arms on the two transducers, all muscles showed an increase in activity. When the subject released the force applied by the left arm at a self-selected time, there was an anticipatory change in the counter-force on the right side about 100 ms prior to the left arm force release, typically representing a drop in the muscle activity. These muscle patterns also varied across subjects. Fig. 3 shows the forces and EMGs associated with a representative Balance-pull trial. Prior to the release of the backward pull force on transducer-2 (top left panel, time of force release indicated by dotted line) typically there was an anticipatory release in the right arm force (a drop in the right forward force and moment of force, T_X produced about the x-axis of transducer-1 in the top middle and right panels respectively) and a corresponding drop in EMG of all muscles. Note that the initial forces on the two transducers were in opposite directions and similar in magnitude (top left and middle panels). The force on transducer-2 and the corresponding moment of force produced (top right panel) drop sharply just prior to the left force release.

Figure 3. Anticipatory postural activity in the right arm in a Balance-pull trial from a representative subject (s8).

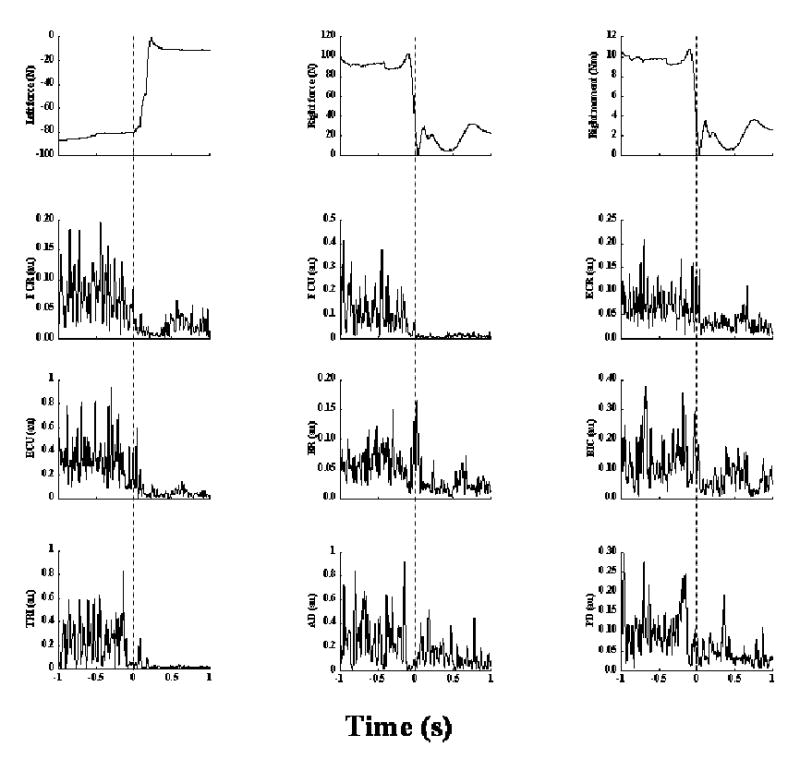
The top left panel shows the force change resulting from a release of pull on transducer-2 (left side). The top middle and right panels show the change in push force and the corresponding moment of force about the x-axis of transducer-1 (right side) respectively. The remaining panels show EMG changes corresponding to the force release in transducer-2. Muscles are abbreviated as in Fig. 2. The time zero corresponds to time of force release. Note the early changes in EMG, force and the resulting moment of force change in transducer-1, compared to the time of force release in transducer-2.

Identification of M-modes: Results of PCA

PCA analysis of each subject’s indices of integrated muscle activity (IEMG_norm indices, see the Methods), obtained separately for push and pull step-trials, revealed that the fourth through the ninth PCs explained only a small percentage of variance in the IEMG_norm space, only rarely had muscles with a significant loading (above ± 0.5; see Hair et al., 1995), and were poorly reproduced across subjects. There were three consistent PCs accounting on average for about 95.2% (± 1.3%) and 92.3% (± 0.7%) of the total variance in the Step-push and Step-pull conditions respectively. The average amount of variance explained by PC1 was 52.7% (±4.3%), by PC2 was 28.5% (± 3.1%) and by PC3 was 12.5% (±2.0%) across all subjects for both conditions.

Tables 1a and 1b show the loadings of all the muscles on the three PCs for representative subjects in the Step-push and Step-pull conditions respectively. The significant loadings are in bold. We refer to a mode as ‘reciprocal’ if the muscles that loaded on it were either flexor muscles or extensor (antagonist) muscles at a joint, while a mode was called ‘co-contraction’ if both flexors and extensors at a joint loaded on it. In the Step-push condition, two of the PCs were apparently ‘reciprocal’ modes while the third was usually a ‘co-contraction’ mode. One of the reciprocal modes usually included one or both wrist extensors (ECR, ECU) and one or both elbow flexors (BR, BIC) (significant loadings on PC1 in Table 1a). The other reciprocal mode included one or both wrist flexors (FCR, FCU) and the elbow extensor (TRI) loaded significantly (PC2 in Table 1a). The third mode was usually a co-contraction mode including significant loadings of both shoulder muscles (AD and PD; PC3 in Table 1a).

Table 1.

PC loadings from a representative subjects in the Step-push (s1) and Step-pull (s4) conditions.

Muscle	M-mode1 (PC1)	M-mode2 (PC2)	M-mode3 (PC3)	M-mode1 (PC1)	M-mode2 (PC2)	M-mode3 (PC3)
	Step-push condition (s1)			Step-pull condition (s4)
FCR	0.32	0.91	−0.11	−0.15	0.48	0.55
FCU	0.31	0.91	0.23	0.04	0.56	0.36
ECR	0.98	0.16	0.00	0.25	0.36	0.87
ECU	0.98	0.12	0.15	0.21	0.52	0.67
BR	0.96	0.27	0.01	0.42	0.22	0.54
BIC	0.14	0.00	0.86	0.66	0.01	0.38
TRI	0.00	0.69	−0.14	0.11	0.62	0.21
AD	−0.10	−0.08	0.98	0.99	0.16	−0.04
PD	0.08	−0.02	0.83	0.18	0.95	0.21

Numbers in bold indicate significant loadings. Muscle abbreviations: flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), extensor carpi radialis (ECR), extensor carpi ulnaris (ECU), brachioradialis (BR), biceps brachii (BIC), the medial head of triceps brachii (TRI), anterior deltoid (AD) and posterior deltoid (PD).

In the Step-pull condition, the shoulder muscles frequently did not show co-contractions as in Step-push, but AD and PD loaded significantly on different PCs (PC1 and PC2 in Table 1b). Also, either the elbow or the wrist muscles also showed co-contraction (e.g. FCU with ECU in PC2 and FCR with ECR and ECU in PC3 in Table 1b). Both the Step-push and Step-pull PCs had reciprocal and co-contraction modes.

We evaluated the similarity of PCs between subjects by taking the dot-product between different subjects’ PCs. To ensure that similar PCs were compared irrespective of the amount of variance explained by those PCs, we first computed the dot product of a given PC in a subject with all the three PCs in other subjects. The largest dot product was then considered (see Tresch et al., 1999; Hart and Giszter, 2004). We found that on average the correlation between PCs was 0.77 (± 0.02 SE) and 0.66 (± 0.01 SE) for the Step-push and Step-pull conditions respectively, confirming their similarity across subjects.

Identifying the Jacobians: Results of multiple regression procedure

Table 2 presents a summary of the regression coefficients to estimate the two Jacobians by regressing changes in the magnitudes of the three M-modes (ΔM-modes) on changes in T_X, separately for the Step-push and Step-pull conditions. Note that the two Jacobians (pull and push) vary in the magnitudes of the coefficients. The three M-modes accounted for 76.9% (± 3.5%) of the total variance in ΔT_X in the Step-push condition and 77.1% (± 3.7%) of the total variance in ΔT_X in the Step-pull condition.

Table 2.

Regression coefficients from the two Step tasks for all subjects.

Task	Subject	k1 (PC1)	k2 (PC2)	k3 (PC3)
Step-push	s1	7.70	−7.77	−11.50
	s2	−0.83	7.18	−18.12
	s3	−3.14	4.94	−8.76
	s4	2.32	−17.40	8.64
	s5	−2.36	−9.49	0.22
	s6	14.96	−18.59	−1.89
	s7	0.03	−5.03	−5.08
	s8	1.88	1.05	−10.71
	s9	12.39	−14.45	−0.64
	s10	6.05	−9.63	−7.59
Step-pull	s1	7.27	−2.06	8.34
	s2	13.65	7.20	−3.73
	s3	−12.67	3.53	24.00
	s4	−10.21	17.07	1.21
	s5	−7.93	24.66	−7.02
	s6	−0.62	−1.44	14.40
	s7	−4.12	8.51	1.10
	s8	0.04	16.20	−8.45
	s9	0.10	4.11	−3.33
	s10	−16.22	21.42	12.67

UCM analysis

Data from the Balance task were used to test the hypothesis that flexible patterns of M-mode combinations, or M-mode synergies, were used to produce stable changes in T_X applied to transducer-1 that stabilized the platform position when force on transducer-2 was suddenly released. Early shifts of T_X applied to transducer-1 reflected postural adjustments in the right arm in anticipation of the drop in force on transducer-2.

The total variance in the M-mode space across repetitions of the balance task was partitioned into V_UCM and V_ORT separately, with respect to each of the Jacobians defined at the previous step, and for each subject. Fig. 4 shows the distribution of the three ΔM-modes (* in figure) for the Balance-pull condition using M-modes from Step-push in a representative subject. The plane composed of grey dots represents a portion of the UCM in the 3 dimensional M-mode space, representing combinations of ΔM-modes that lead to the same ΔT_X. Note that the variance of ΔM-modes parallel to the UCM is larger than the variance perpendicular to it. The values of ΔM-modes are negative since anticipatory postural adjustments were computed as a change in EMG just prior to release of force by the left hand compared to EMG when forces were produced in opposite directions by the two arms and this change was usually negative (see Fig. 3).

Figure 4. Distribution of ΔM-modes in the Balance-pull conditions in a representative subject (s3) when M-modes and Jacobian from Step-push were considered.

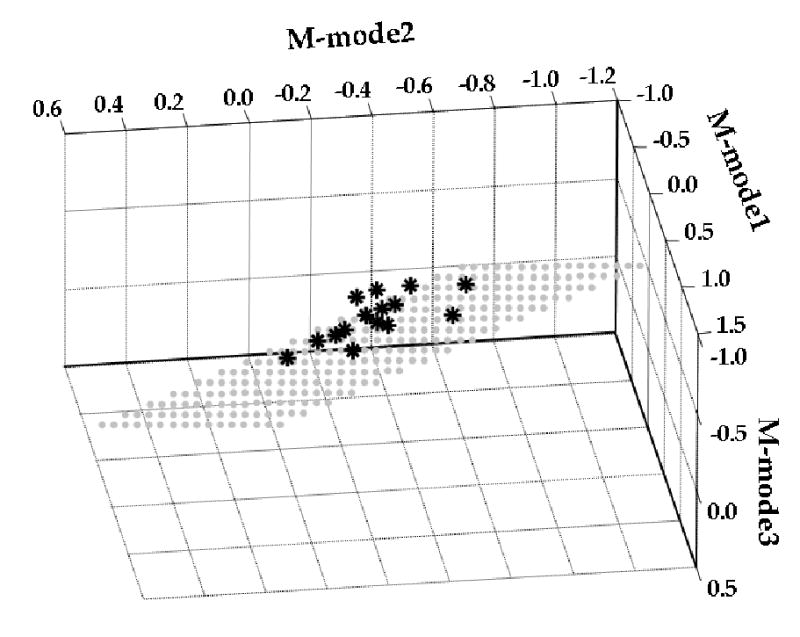
The stars indicate the location of the three M-modes in each trial of the Balance-pull condition. The UCM is the plane in the M-mode space which represents all combinations of M-modes leading to a stable ΔT_X.

A three-way ANOVA with factors: TASK (two levels: Balance-pull. Balance-push), JACOBIAN (two levels: pull and push) and VARIANCE (two levels: V_UCM, V_ORT) revealed no significant main effects for the factor Jacobian (p>0.4). Therefore, we collapsed data across the two Jacobians and ran a two-way TASK × VARIANCE ANOVA.

Fig. 5 shows V_UCM and V_ORT averaged across subjects with standard error bars, for the Balance-pull and Balance-push conditions. High values of V_UCM relative to V_ORT were found for both the Balance-pull and Balance-push conditions. Repeated-measures ANOVA confirmed these observations. There was a main effect of the factor VARIANCE showing that V_UCM was significantly higher than V_ORT (F_(1,9) = 11.064, p < 0.01) across both Balance tasks. Post-hoc comparisons for each of the Balance tasks revealed V_UCM was higher than V_ORT (F_(1,9) > 5.3, p < 0.05) for both Balance tasks.

Figure 5. UCM results across subjects.

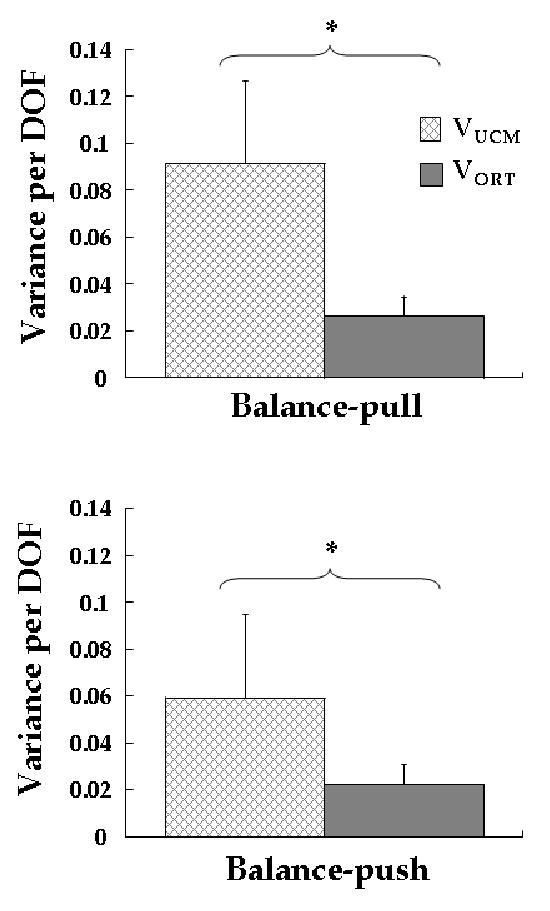
Variance within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) per degree of freedom averaged across subjects. The top and bottom panels show results for the Balance-pull and Balance-push conditions respectively. Results are collapsed across analysis on M-modes and Jacobians from Step-push and Step-pull. Significant differences between V_UCM and V_ORT are indicated by * (p < 0.05).

Figure 6 provides an illustration of individual differences in the reported effects, comparing subjects 1 and 2. Table 3 shows results of PCA for subject s2 for the Step-push condition. Note the differences in the groupings of muscles for the same task in the two subjects (Table 1a: subject s1 and Table 3: subject s2). Even though the mode structure had similarities between the two subjects (e.g. PCs 1 and 3), there are individual differences as well. Nonetheless, both subjects exhibited differences in the amounts of variance within and orthogonal to the UCM (see Fig. 6, V_UCM > V_ORT) in the Balance-pull task when M-modes and Jacobian from Step-push were used. The higher value of V_ORT relative to V_UCM for subject 1 indicates that this subject’s M-mode combinations were less effective in stabilizing T_X in this task than was the case for subject 2.

Figure 6. UCM results in individual representative subjects.

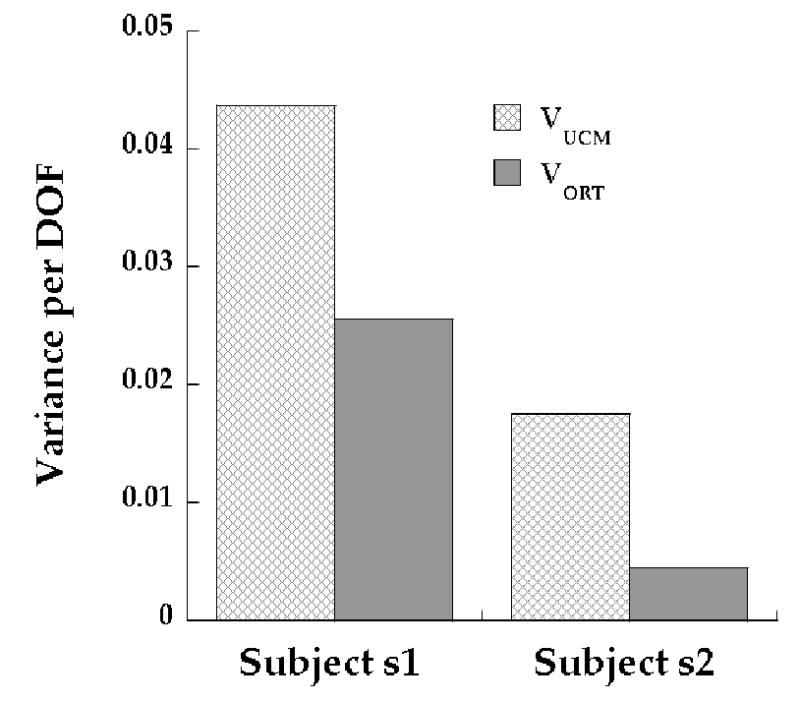
Variance within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) per degree of freedom are shown in subjects s1 (left bars) and s2 (right bars) respectively. Results for the Balance-pull task using M-modes and Jacobians from Step-push are shown. Note the high values of V_UCM compared to V_ORT in both subjects. Corresponding M-modes for the two subjects are shown in Table 1a (s1) and Table 3 (s2).

Table 3.

PC loadings from subject s2 in the Step-push condition

Muscle	M-mode1 (PC1)	M-mode2 (PC2)	M-mode3 (PC3)
FCR	0.11	0.72	−0.03
FCU	0.17	0.32	0.56
ECR	0.86	0.20	0.36
ECU	0.77	0.54	0.34
BR	0.92	0.00	−0.05
BIC	0.51	−0.06	0.06
TRI	0.44	0.05	−0.03
AD	0.13	−0.20	0.94
PD	−0.32	0.56	0.58

Numbers in bold indicate significant loadings. Muscles are abbreviated as in Table 1a.

To examine if there was any systematic relationship between the amount of variance explained by the M-modes, the R-square values of regression analysis and the orthogonal variance (V_ORT) we performed multiple regression analysis across subjects with V_ORT as the dependent variable. The predicting variables were 1) amount of variance accounted for by M-modes and 2) the R-square value of the regression analysis used to estimate the Jacobian. We found that neither M-mode variance nor R-square values were significant predictors of V_ORT suggesting that the quality of these fits did not have a significant effect on the analysis of muscle synergies in this study.

Discussion

This study extends recent work on upright postural control (Krishnamoorthy et al., 2003b; Krishnamoorthy et al., 2004; Wang et al., 2005; Wang et al., 2006), providing a further test of the hypothesis that the CNS forms muscle synergies by flexibly combining a small number of muscle ensembles, or muscle modes (M-modes), which act to stabilize important performance variables. Results of the current study support this hypothesis, revealing that three ensembles of arm muscles (M-modes) were flexibly combined with varying gains to produce a consistent change in the moment of force about the horizontal axis of a force transducer, which stabilized subjects’ position on an unstable chair in response to release of the left hand’s force. We assumed that the same three M-modes were used in both the Step and Balance tasks, despite the fact that production of a moment of force was not an explicit requirement of the second task. The results generally support this assumption.

We designed a task that produced instability primarily in the AP direction and found that most forces/moments of force applied by the subject acted to balance the platform in this direction. Forces in the other two directions were less than a third of the AP-directed force. The lack of a complete mechanical analysis is a limitation of the study, but with our current methods it would be unrealistic to accomplish it together with appropriate EMG analysis. Therefore, we limited our analyses in this study to consider only the primary constraint; that of balancing the value of the desired T_X in order to keep the platform horizontal. This analysis could be expected to produce a conservative estimation of UCM effects in comparison to a situation where all the forces and moments are accounted for.

In this study, we examined the organization of muscle synergies during a somewhat artificial task in which the arm contributed to sitting balance, although the use of the arm to stabilize objects is not uncommon. Previous studies have shown that the upper limbs are sometimes involved in reactions to postural perturbations (McIlroy and Maki, 1995) and locomotion (Elger et al., 1999; Misiaszek, 2003). Sensory information from even a light finger touch reduces postural sway (Holden et al., 1994; Jeka and Lackner, 1994) and anticipatory postural adjustments in leg and trunk muscles prior to self-initiated perturbations during quiet stance (Slijper and Latash, 2000).

Muscle modes and Muscle synergies

Several investigators have referred to the eigenvectors obtained from PCA or other types of matrix factorization procedures as muscle synergies (Tresch et al., 1999; Sabatini, 2002; d’Avella and Bizzi, 2005; Ting and Macpherson, 2005). We do not view fixed groups of muscles obtained from such procedures, whose activity scales together (e.g. Saltiel et al., 2001) as muscle synergies, but rather as elemental variables or M-modes, which can hypothetically be manipulated independently by the controller or combined with different gains to produce task-specific functional synergies. The concept of muscle synergies used in most studies suggests a reproducible pattern of activity among muscles. While this helps to reduce the dimensionality of a large number of muscles to a smaller dimensional set of variables, it ignores the possible interaction among these new variables with respect to important task-related variables such as the change in the moment of force in this study. By using the UCM approach we were able to show that the three experimentally identified M-modes were combined in a flexible manner to produce a consistent change in the moment of force. This flexibility feature among elemental variables is not commonly addressed in studies of muscle synergies or synergies in general, but we believe that it is an important feature of a synergy. Therefore, we prefer the term M-modes for muscle groupings and synergies for the co-variations among M-modes to preserve a given value of a performance variable.

Some studies have also explored the relationship between the activity of muscle combinations and the values of other variables that are more directly related to task performance (e.g. Ting and Macpherson, 2005; Valero-Cuevas, 2000). It has been suggested that new behaviors are built by recombining already existing neuromuscular primitives (Kargo and Giszter, 2000; Kargo and Nitz, 2003; Ivanenko et al., 2005). These studies emphasize how task-relevant variables (i.e. end-point force) are produced by combining a set of neuromuscular primitives or synergies. If the m-modes of the current analysis are considered neuromuscular primitives, then the important contribution of the current results is in showing that such primitives are flexibly combined to produce stable values of the task-relevant variables. That is, fixed combinations of the m-modes, or muscle primitives, were not used to produce fixed values of the task-relevant variable. This was true of all subjects studied, despite the presence of individual differences in the nature of the identified M-modes across subjects. Thus, although muscles may be organized into different combinations (M-modes) for different subjects, all subjects flexibly combined their available M-modes to stabilize the moment of force about the frontal axis of the transducer.

Recently, Tresch et al. (Tresch et al., 2006) suggested that PCA was not very good at identifying underlying synergies when compared with some other matrix factorization methods. Our method requires an important step beyond finding a lower dimensional space, however; that is, the identification of functional synergies. We computed M-modes and related their changes to those of important performance variables. This would be impossible with many of the other techniques. Moreover, PCA has been shown to be a very useful method to determine the subspace spanned by the underlying ‘synergies’ (Tresch et al., 2006). Finally, the fact that our method resulted in relatively consistent UCM results across subjects, and supported the experimental hypotheses despite individual variations in the mode structure supports the validity of our approach.

Reciprocal and Co-contraction Muscle modes

In this study, we found three M-modes that explained more than 92% of the variance in the EMG data of nine muscles. This compared favorably with previous studies of M-modes in the leg and trunk muscles that typically explained about 60–70% of the total variance in the space of integrated EMG indices (Krishnamoorthy et al., 2003a; Krishnamoorthy et al., 2003b; Wang et al., 2005; Wang et al., 2006) and we believe that they are well representative of the variance in the overall muscle space.

Among the three M-modes found for each of the Step tasks, two appeared to be ‘reciprocal’ modes; each of these modes consisted of only flexors or extensor muscles at individual joints, but not both. The Step-push and Step-pull conditions have the same two reciprocal modes, although the net force produced is in opposite directions. This is done by combining the M-modes in different ways in the two conditions. The reciprocal modes in this study are reminiscent of the ‘push-forward’ and ‘push-back’ modes in recent studies of upright postural tasks (Krishnamoorthy et al., 2003b).

In the Step-push condition, the third mode was a shoulder co-contraction mode. Similarly, in the Step-pull condition, co-contraction was frequently seen in the wrist flexor-extensor muscles or in the elbow muscles. Although this means that the two antagonistic muscles (AD and PD in Step-push or wrist/elbow flexors and extensors in Step-pull) changed in parallel, it is possible for this mode to result in either a positive or negative force moment, depending on which muscle’s activity was greater. The co-contraction modes may have helped improve performance by stiffening the joints, which is known to help resist perturbations (Gribble et al., 2003) or may be used as a strategy to reach sections of ‘feasible’ joint torque space which cannot be done by action of a single muscle alone (Valero-Cuevas, 2005). Co-contraction patterns have been seen in individuals with Down’s syndrome (Aruin and Almeida, 1997), elderly subjects, and persons with neurological disorders (Woollacott et al., 1988; Woollacott and Burtner, 1996). A co-contraction strategy may be adaptive, compensating for the lack of the ability to fine-tune postural responses (Woollacott et al., 1988) or used to increase safety while possibly compromising movement efficacy (Aruin et al., 1996). Higher co-contraction has also been observed during faster single-joint movements interpreted as a means of achieving high stiffness in a spring-like system (Gribble and Ostry, 1998; Suzuki et al., 2001).

Relation to equilibrium-point control

Previous studies on postural control under conditions of instability have shown co-contraction and reciprocal patterns similar to those in this study (Slijper and Latash, 2000; Krishnamoorthy et al., 2004). The idea of reciprocal and co-contraction M-modes can be related to the R and C commands within the λ-model or equilibrium point (EP) hypothesis (Feldman 1986; Feldman and Levin 1995) if the notions of these commands are generalized from the joint level of analysis to any multi-link effector including the whole human body (Latash, 1998). One can view the task of maintaining sitting posture on an unstable chair as that of stabilizing the location of the center of mass (CM) over the area of support. Postural control can either produce shifts of the CM (analogous to effects of the R command on a joint position) or change the apparent stiffness of the system producing restoring forces in response to shifts from the equilibrium position (analogous to effects of the C command). This idea corresponds in general to the reciprocal and co-contraction M-modes and the idea that the central nervous system controls angular joint ranges where muscles acting at a joint can be active individually or simultaneously (Levin and Dimov, 1997). However, the present analysis deals with elemental variables (i.e. EMGs and their linear combinations), rather than central control variables presumed to account for the ‘R’ and ‘C’ commands of the λ-model.

Effect of direction of force application on coordination among muscles

In our previous study of postural muscles, we found that the same set of modes could describe EMGs across a variety of postural tasks (Krishnamoorthy et al., 2003a), but different combinations of M-modes, or synergies, caused COP shifts in opposite directions (Krishnamoorthy et al., 2003b). This suggested that even though the same M-modes were the elemental variables for COP shifts in opposite directions, the coordination among the modes differed in the two conditions. In the current study, we found that the M-modes for the forward and backward Step conditions were different (e.g. co-contraction of shoulder muscles in Step-push condition but not in Step-pull condition). Thus, unlike previous studies, here we found different sets of elemental variables or M-modes that were organized to stabilize the performance variable in a similar way. That either Jacobian worked in the current study may stem from the fact there was a drop in the EMG of all muscles for both directions of moment of force. Future studies requiring an increase in the moment of force may help to disambiguate these results.

Clinical Implications

People with neurological dysfunction have known difficulties coordinating their muscles to produce appropriate functional synergies (e.g. following a stroke; Brunnstrom, 1970 ). Gaining insight about the nature of coordination deficits is critical for the purpose of differential diagnoses and individual treatment planning. The method outlined in this article, although complicated, provides a means for understanding the nature of altered muscle synergies in populations of neurological patients. One can not only identify atypical muscle groups or M-modes in these populations, but also relate combinations of these atypical M-modes to the values of important performance variables. Such modeling might be useful for clinical planning, for example, to determine the effect of selectively eliminating particular muscles from an identified atypical M-mode, e.g. through the use of Botulism toxin injection, on functional performance.

In summary, this study indicates that individuals used flexible patterns of M-mode organization of the arm muscles to produce consistent moments of force to stabilize their sitting position on an unstable base. The study extended previous work that identified muscle (M-mode) synergies acting to produce consistent shifts of the center of pressure across repetitions related to anticipatory postural adjustments in upright postural tasks (Krishnamoorthy et al., 2003b; Krishnamoorthy et al., 2004). This approach, thus offers promise for identifying and studying the nature of muscle synergies in relation to the stabilization of performance-related variables for a variety of functional tasks, including their evolution with learning through practice, development, aging, and rehabilitation.