A novel scratching approach for measuring age-related changes in the in situ toughness of bone

Abstract

A scratch test using a nanoindentation system was proposed in this study to assess the age-related changes in the in situ toughness of bone matrix at ultrastructural levels. A tissue removal energy density (u_r) was defined and estimated as the work done by the scratch (U_T) divided by the total volume of the scratch groove (u_s). The value of u_s was used as a relative measure of the in situ toughness of the tissue. Human cortical bone specimens obtained from middle-aged (between 49 and 59 years old) and elderly groups (over 69 years old) were tested using this technique. A significant difference in the estimated removal energy density (u_s) in the secondary osteons was found between the middle-aged and elderly groups (5.49±0.696 vs. 4.09±1.30 N/mm², respectively).

1. Introduction

Bone has a highly hierarchical structure and the bone quality may be affected by factors at different length scales: (1) microstructural changes (Nyssen-Behets et al., 1997), (2) microdamage formation (Burr et al., 1997; Fazzalari et al., 1998; O'Brien et al., 2000; Turner, 2002), (3) integrity of bone constituents (Nyman et al., 2005a; Turner, 2002; Wang et al., 2000, 2001; Wang and Puram, 2004), and (4) interactions between bone constituents (Boskey, 1992; Walsh and Guzelsu, 1994).

At the ultrastructural level (i.e., submicron scale), the mechanical behavior of bone is poorly understood (Nyman et al., 2005a) although the bulk mechanical behavior of bone has been extensively studied in the past (Ascenzi and Bonucci, 1971; Beck et al., 1990; Bouxsein and Radloff, 1997; Caler and Carter, 1989; Choi and Goldstein, 1992; Currey, 1988; Norman et al., 1995; Pidaparti and Vogt, 2002). Recently, measurements of the elastic and yield behavior of the tissue at the ultrastructural level have been attempted using nanoindentation methods (Rho et al., 2000, 2001; Swadener et al., 2001). In addition, a microindentation test on an existing microcrack has been reported recently to assess the fracture toughness of bone (Fan et al., 2006). However, application of this microindentation technique is significantly limited by the fact that the test is at the micrometer level and can be performed only at the locations where microcracks are present. In this study, we propose a simple scratch technique using a nanoindentation system to determine the in situ toughness of bone at submicron and even nano length scales. This scratch technique would be suitable for assessing the in situ toughness of bone not only for osteonal bone tissues but also for small animal models.

2. Scratch test

Scratch tests have been widely used to investigate the material behavior of thin films or coatings (Bellido-Gonzalez et al., 1995; Sekler et al., 1988), and they can be characterized as a combination of two simultaneous processes: indentation and cutting (Tabor, 1956). In this study, we proposed a scratch test with a cube corner indentation tip to estimate the in situ toughness of bone (Fig. 1). Since the scratch groove is generated by both tissue removal and plastic deformation (Fig. 2), the toughness of bone could be estimated by the energy consumed during the scratch test.

Fig. 1.

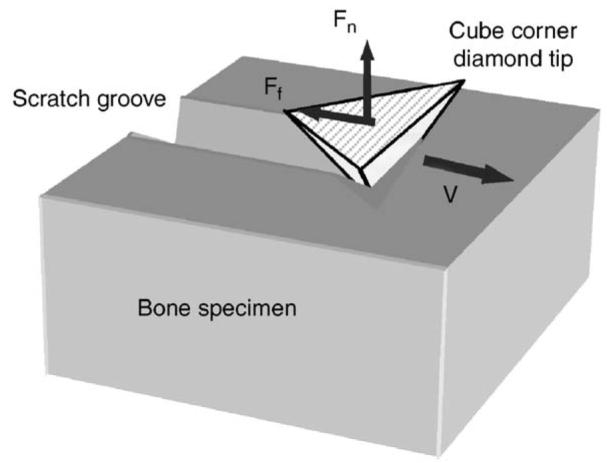
Schematic diagram of the scratch test using a cube corner diamond tip.

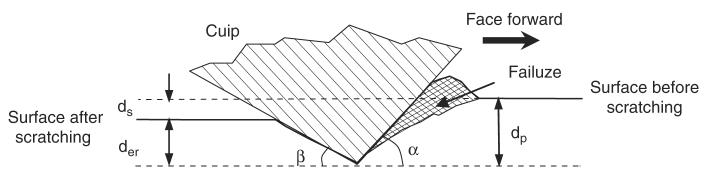
Fig. 2.

Schematic representation of the scratch test and the definitions: the initial penetration depth (d_p), the actual scratch depth (d_s), and the elastic recovery depth (d_er).

As a quasi-brittle material, the post-yield to failure behavior of bone is dominated by microdamage accumulation and permanent deformation. Considering possible energy dissipation pathways, the total energy required for the scratch (U_T) may be defined in terms of several energy terms as shown in the following equation:

$$U_T=U_f+U_e+U_d+U_p+U_r,$$ (1)

where U_f is the energy dissipated by friction, U_e the energy stored in elastic deformation, U_d and U_p the energy dissipated by damage accumulation and permanent deformation in the post-yield region of the deformed tissue, and U_r the energy required for removal of the tissue in the failure region in front of the tip. Since the energy term U_r represents the total energy dissipation to failure of removed tissue, it should be representative of the toughness of tissue.

It has been reported that the nanoindentation modulus was not significantly dependent on age (Hoffler et al., 2000; Rho et al., 2002). In addition, little age-related differences were found in the elastic modulus loss during the post-yielding of bone (Courtney et al., 1996). Thus, no significantly differences in the elastic strain energy (U_e) and damage accumulation energy (U_d) would be expected among different age groups. Moreover, U_f is largely dependent on the normal force exerted and surface features of specimens. If the normal force and surface roughness of bone specimens are constant, U_f would unlikely be affected. In a recent study, it was also observed that the post-yield permanent deformation of bone is not significantly related to age (Nyman et al., 2005b). Thus, changes in the energy required for removal U_r is most likely reflected by that of U_T.U_T can be expressed by integrating the lateral scratch force (F_f) along the scratching path as follows:

$$U_T=W=\int F_f\mathrm{d}x,$$ (2)

where the lateral scratching force (F_f) is measured during the scratch test. Then, the energy required to create a unit volume of the groove (U_s) could be estimated as

$$u_s=\frac{U_T}{V_s},$$ (3)

where, V_s can be obtained from the cross-sectional area (A_s) of the scratch groove obtained from the cross profile and the length (L_s) of the scratch (Fig. 3). By substituting Eq. (1) into Eq. (3),

$$u_s=\frac{U_f+U_e+U_d+U_p+U_r}{V_s}.$$ (4)

As discussed earlier, since the energy terms U_f, U_e, U_p and U_d are unlikely significantly different among age groups, the age-related changes in the energy density for removing a unit volume tissue (Δu_r = ΔU_r/V_s) would be proportional to Δu_s:

$$\Delta u_r\propto \Delta u_s.$$ (5)

Therefore, by comparing the total scratch energy density u_s, the difference in the in situ tissue toughness could be relatively estimated for different age groups.

Fig. 3.

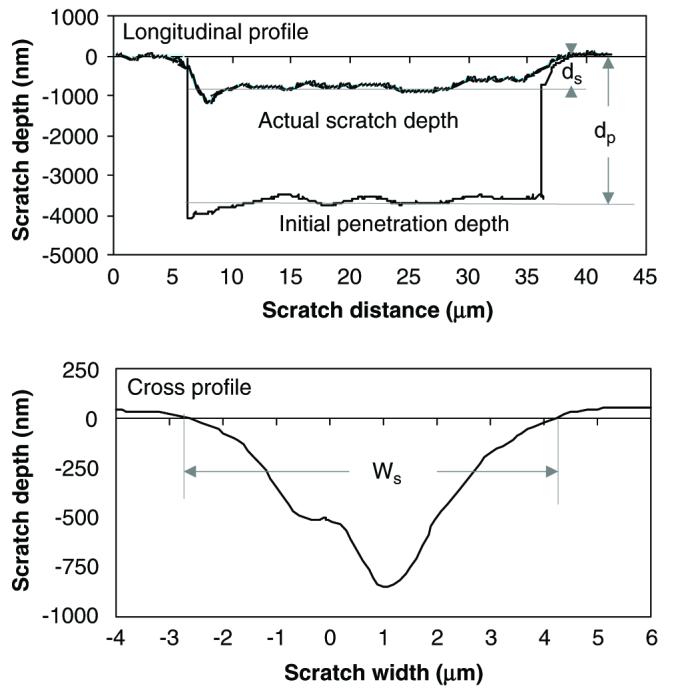
The longitudinal and cross-sectional profile of a scratch groove.

3. Materials and methods

Human cadaveric femurs were obtained from two age groups: middle-aged (between 49 and 59 years old) and elderly (over 69 years old), with each consisting of six male donors. Cross-sectional slices of 2 mm thickness were dissected from the medial aspect of each diaphyseal femur, and polished to a surface roughness between 50 and 100 nm using sequential grit sandpapers and abrasive particles. The polished specimens were glued to a holder and mounted on a MTS Nanoindenter XP system with scratching capability. A cube corner diamond tip was used for the scratch test (Fig. 2), with α being 55° and β 35°. The area of interest in secondary osteons was identified under a microscope attached to the system. The pretest surface profile (surface roughness) was obtained by running the scratch tip along the scratch path with a 50 μN contact force, and then the 30 μm long scratch was made in a face-forward mode (i.e., the flat surface of the tip faces the scratch direction). The penetration load was kept constant (5 mN) and the scratch velocity was set at 0.5 μm/s. The longitudinal profiles of the penetration depth (d_p) and the residual scratch depth (d_s) after the scratch test were recorded (Fig. 3a). In addition, the cross-sectional profile was also recorded to determine the width (W_s) of scratch grooves (Fig. 3b). It is noteworthy that very little pile up was observed on the both sides of the groove in these tests, suggesting that the plastic deformation is limited. All tests were conducted under a wet condition by submerging the specimen in a physiological saline in the holder chamber.

The experimental data were analyzed using Student's t-tests (unpaired), and the statistical significance was considered only if p-value was less than 0.05 (p < 0.05).

4. Results and discussion

The experimental results exhibit that the energy density required for creating a unit groove volume (u_s) of middle-aged bone is significantly greater compared with that of the elderly bone (Table 1). It is noteworthy that there were no significant differences in the lateral scratching force (F_f) and the scratch width (W_s) between the middle and elderly groups. Since the scratch tip geometry is fixed, F_f is most likely determined by the ultimate stress (or strength) of bone through cutting. It has been reported that the ultimate stress of bone is much less age-dependent compared with its toughness (McCalden et al., 1993; Zioupos and Currey, 1998). This may be the reason why F_f exhibited less age-related changes in the scratch test.

Table 1.

Age-dependent differences in nanoscratch resistance of osteons (n =6)

Age groups	Ff (mN)	Ws (μm)	ds (nm)	us (N/mm2)
Middle-aged	8.83±0.40	5.84±0.29	557±53.0	5.49±0.70
Elderly	8.46±0.22	6.24±0.55	703±149	4.09±1.30
Student's t-test	p>0.05	p>0.05	p<0.05	p<0.05

F_f: scratch force; W_s: width of scratch; d_s: depth of scratch; u_s: deformation energy density.

However, the actual scratch depth (d_s) was significantly different between the two age groups, with 557±53 nm for the middle-age group and 703±149 nm for the elderly group, respectively. This suggests that a larger volume of bone tissue was removed during the scratch test for the elderly bone than its younger counterpart. This is understandable because elderly bone is much easier to be removed by cutting during the scratch process (Fig. 2) compared with the younger bone.

There exist some limitations for the present form of this scratch technique to assess the toughness of bone. First, the scratch tests were performed in relatively large dimensions (30 μm long, 4–5 μm wide and 1.5 μm deep) in this study. At this length scale, vascular channels, Haversian and Volkmann's canals, and lacunae would not have little effects on the measurements, but canalicular network may still have an effect on the measurement. However, scratch tests can be performed at much smaller length scales (e.g., submicron levels), which would fall in the region between canalicular channels. Thus, it is possible to measure bone mechanical properties without confounding effects induced by the anatomic features. Second, the scratch energy density (u_s) estimated in this study can only allow for relative comparison of the toughness of bone tissues. Thus, further investigation is needed to fully develop the technique as a quantitative tool. Finally, the potential of this technique is not fully explored for even smaller scales (i.e., nanometers).