Stochastic payoff evaluation increases the temperature of selection

Abstract

We study stochastic evolutionary game dynamics in populations of finite size. Moreover, each individual has a randomly distributed number of interactions with other individuals. Therefore, the payoff of two individuals using the same strategy can be different. The resulting “payoff stochasticity” reduces the intensity of selection and therefore increases the temperature of selection. A simple mean-field approximation is derived that captures the average effect of the payoff stochasticity. Correction terms to the mean-field theory are computed and discussed.

1 Introduction

Traditional evolutionary game theory has been formulated for infinitely large populations, where stochastic effects can be neglected. The relative abundances of different strategies in a population change according to deterministic differential equations (Taylor and Jonker, 1978; Hofbauer et al., 1979; Maynard Smith, 1982; Weibull, 1995; Samuelson, 1997; Hofbauer and Sigmund, 1998; Fudenberg and Tirole, 1998; Gintis, 2000; Cressman, 2003; Hofbauer and Sigmund, 2003; Nowak and Sigmund, 2004). Due to their nonlinearity, such equations can show very complex dynamics.

Game dynamics in finite populations require a stochastic approach (Schaffer, 1988; Ficci and Pollack, 2000; Fogel et al., 1998; Nowak et al., 2004; Taylor et al., 2004; Antal and Scheuring, 2005; Imhof et al., 2005; Traulsen et al., 2005; Nowak, 2006; Fudenberg et al., 2006). In finite populations, the traditional concept of an evolutionarily stable strategy (ESS) is no longer decisive and instead one has to calculate fixation probabilities in order to determine if a given resident strategy is protected by natural selection (Nowak et al., 2004; Traulsen et al., 2006b).

In most approaches, there is still the simplifying assumption that each individual interacts with each other individual in the population and therefore the payoff is determined by a deterministic process. Here, we relax this assumption and introduce a new system in which different individuals have a different numbers of interactions. Hence, two individuals of the same type can obtain different payoffs, leading to a heterogeneity in the system. Instead of sharp payoff values, there is a distribution of payoffs for the same type of individuals. While the analytical solution of this system is no longer possible, we can derive approximations that agree well with (numerically exact) individual based simulations of the process.

This approach is related to formulations of the evolutionary dynamics on networks, in which every individual interacts only with a small subset of the population (Nowak and May, 1992; Ellison, 1993; Blume, 1993; Herz, 1994; Brauchli et al., 1999; Abramson and Kuperman, 2001; Szabó and Hauert, 2002; Ebel and Bornholdt, 2002; Hauert and Doebeli, 2004; Santos and Pacheco, 2005; Lieberman et al., 2005; Santos et al., 2006; Ohtsuki et al., 2006; Ohtsuki and Nowak, 2006). However, in these studies the interaction network is usually fixed during the evolutionary game. Our approach corresponds to a random interaction network that changes after each update step (Bala and Goyal, 2001; Skyrms and Pemantle, 2000; Pacheco et al., 2006).

2 Evolutionary dynamics in finite populations

In evolutionary game dynamics, individuals obtain a fitness associated with the payoff from a game. Let us consider the following evolutionary process: two individuals 1 and 2 with payoffs π₁ and π₂, respectively, are chosen at random. Their payoff difference π₁₂ = π₁ − π₂ is computed. The first individual changes to the strategy of the second individual with probability

$$p=\frac{1}{1+exp[-\beta {\pi }_{12}]}.$$ (1)

We chose the Fermi function from statistical physics for p as proposed by Blume (1993), Szabó and Tõke (1998) and Traulsen et al. (2006a). With probability 1 − p, individual 2 changes to the strategy of individual 1. The parameter β measures the intensity of selection. For β ≪ 1, selection is weak and the payoffs are only a small perturbation of random drift. For β ≫ 1, selection is strong and the individual with the lower payoff will change its strategy. In statistical physics, β is the inverse temperature: for β → 0, the dynamics of the system is dominated by stochasticity (the temperature of selection is high), whereas in the limit β → ∞ stochastic effects can be neglected (the temperature of selection is zero).

In a finite population of size N with two types A and B, A individuals can interact either with other A individuals and obtain a payoff a or with B individuals, which leads to a payoff b. Similarly, the interaction of B individuals with A individuals leads to a payoff c, whereas they get d from interacting with B individuals. This is captured by the payoff matrix

$$\begin{array}{c}\begin{array}{ccc}\hspace{0.17em}& A& B\end{array}\\ \begin{array}{l}A\hfill \\ B\hfill \end{array}\left(\begin{array}{ll}a\hfill & b\hfill \\ c\hfill & d\hfill \end{array}\right)\end{array}.$$ (2)

If every individual interacts with every other individual, each A individual obtains the same average payoff

$${\pi }_A=\frac{a(i-1)+b(N-i)}{N-1}.$$ (3)

Here i is the number of A individuals and N − i is the number of B individuals. Self interactions have been excluded. Similarly, the payoff of each B individual is

$${\pi }_B=\frac{ci+d(N-i-1)}{N-1}.$$ (4)

From these payoffs, the transition probabilities to change the number of i individuals to i ± 1 can be calculated as

$$T^{\pm }(i)=\frac{i}{N}\frac{N-i}{N}\frac{1}{1+e^{\mp \beta ({\pi }_A-{\pi }_B)}}.$$ (5)

Based on these probabilities, a closed equation for the probability that a group of i mutants of type A reaches fixation in a population of N individuals can be derived (Traulsen et al., 2006a,c).

However, the idea that every individual of a certain type has the same fitness is a simplification. Individuals may have different numbers of interactions. The simplest means to model such effects is to introduce a probability q that an interaction occurs between any two individuals. For q = 1, we recover the standard theory outlined above. For q < 1, heterogeneity is introduced in the system as individuals of the same type can now have different payoffs. When q = 0 every individual has payoff zero and the system becomes homogeneous again. This, in turn, is equivalent to the limit β = 0 (neutral selection). Consequently, we expect q < 1 to lead to an average weakening of the intensity of selection in the population, and, therefore, to an increase in the temperature of selection.

3 Analytical results for stochastic payoff evaluation

3.1 Stochastic Transition probabilities

The exact fixation probabilities of the system with 0 < q < 1 cannot be calculated in a simple way, as the transition probabilities of Eq. (5) are now random numbers. However, we can calculate the average probability that the number of A individuals increases or decreases by one. The number of interactions that an A individual has with other A individuals is a binomial distributed random number. We use j_AA for the number of interactions of an A individual with other A individuals and j_AB for its interactions with B individuals. Similarly, a B individual has j_BA interactions with A individuals and j_BB interactions with others of type B. If the population consists of i A individuals, the probability that a focal A individual interacts with exactly j_AA of them is

$$P(j_{AA})=\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}.$$ (6)

The minimum number of these interactions is 0 and the maximum number is i − 1. Similarly, the number of A interactions with B individuals is a number between 0 and N − i. For B individuals, similar equations hold. The average payoff of an A individual is now

$$\begin{array}{l}\langle {\pi }_A\rangle =\sum _{j_{AA}=0}^{i-1}\sum _{j_{AB}=0}^{N-i}\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}\left(\begin{array}{c}N-i\\ j_{AB}\end{array}\right)q^{j_{AB}}{(1-q)}^{N-i-j_{AB}}\\ \times \left(a\frac{j_{AA}}{N-1}+b\frac{j_{AB}}{N-1}\right)\\ =q\left(a\frac{i-1}{N-1}+b\frac{N-i}{N-1}\right).\end{array}$$ (7)

Similarly, for B individuals we obtain

$$\langle {\pi }_B\rangle =q\left(c\frac{i}{N-1}+d\frac{N-i-1}{N-1}\right).$$ (8)

The payoffs values enter in the transition probabilities in a nonlinear way and the reasoning for the transition probabilities is more intricate. The average transition probabilities can be calculated as

$$\langle T^{\pm }(i)\rangle =\frac{i}{N}\frac{N-i}{N}\sum _{j_{AA}}\sum _{j_{AB}}\sum _{j_{BA}}\sum _{j_{BB}}P(j_{AA})P(j_{AB})P(j_{BA})P(j_{BB})\frac{1}{1+e^{\mp \beta ({\pi }_A-{\pi }_B)}}$$

Since j_AA, j_AB, j_BA, and j_BB are random numbers with a Binomial distribution, we obtain

$$\begin{array}{l}\langle T^{\pm }(i)\rangle =\frac{i}{N}\frac{N-i}{N}\sum _{j_{AA}=0}^{i-1}\sum _{j_{AB}=0}^{N-i}\sum _{j_{BA}=0}^i\sum _{j_{BB}=0}^{N-i-1}\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}\\ \times \left(\begin{array}{c}N-i\\ j_{AB}\end{array}\right)q^{j_{AB}}{(1-q)}^{N-i-j_{AB}}\left(\begin{array}{c}i\\ j_{BA}\end{array}\right)q^{j_{BA}}{(1-q)}^{i-j_{BA}}\\ \times \left(\begin{array}{c}N-i-1\\ j_{BB}\end{array}\right)q^{j_{BB}}{(1-q)}^{N-i-1-j_{BB}}\frac{1}{1+e^{\mp \beta (a{j}_{AA}+b{j}_{AB}-c{j}_{BA}-d{j}_{BB})/(N-1)}}.\end{array}$$ (9)

Note that for q = 0 and q = 1, these expressions vastly simplify. For q = 0 we have $T^{\pm }(i)=\frac{1}{2}\frac{i}{N}\frac{N-i}{N}$ and for q = 1 we recover the conventional Eq. (5).

Eq. (9) makes the simplifying assumption that the interactions of player A and B are independent. However, if A and B interact with each other, then j_AB and j_BA are no longer independent. This particular interaction occurs for each player with probability q. Therefore, the probability that one of them interacts with the other one, but not vice versa, is 2q(1 − q), having a maximum at q = 0.5. The contribution of every interaction to the overall payoff of an individual is of the order of 1/N. Hence, asymmetric interactions lead to an error of the order of 2q(1 − q)/N, vanishing rapidly with N. Exact computer simulations for the process, with and without such asymmetric interactions lead to fixation probabilities which are indistinguishable, for population sizes as small as N = 20, and therefore still agree perfectly with our analytical approximation. A formulation of Eq. (9) which accurately describes the symmetry in the interactions is discussed in Appendix A.

From the average transition probabilities, the probability that k individuals reach fixation can be approximated as

$${\phi }_k=\frac{{\sum }_{i=0}^{k-1}{\prod }_{j=1}^i\langle T^{-}(j)\rangle /\langle T^{+}(j)\rangle }{{\sum }_{i=0}^{N-1}{\prod }_{j=1}^i\langle T^{-}(j)\rangle /\langle T^{+}(j)\rangle }.$$ (10)

The fixation probabilities calculated in this way are in excellent agreement with simulations, as shown in Figs. 1, 2 and 3.

Figure 1.

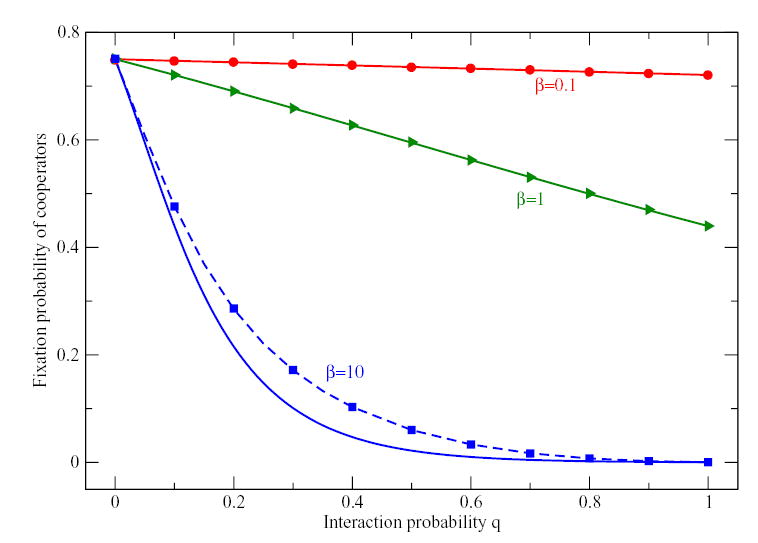
Fixation probability of k = 15 cooperators in a Prisoner’s Dilemma for different interaction probability q and different intensities of selection β. Symbols are computer simulations of the process. Full lines represent the mean-field approximation Eq. (13), whereas dashed lines are the fixation probabilities computed with the approximated transition probabilities given by Eq. (9). For small β, the mean-field approximation agrees well with simulation results. Only for very high β, the fixation probabilities of the mean-field approximation do not longer agree with simulations and the more sophisticated theory based on Eq. (9) has to be applied (Parameters: N = 20, payoff matrix a = 0.9, b = − 0.1, c = 1.0, d = 0.0, averages over 10⁶ realizations of the process).

Figure 2.

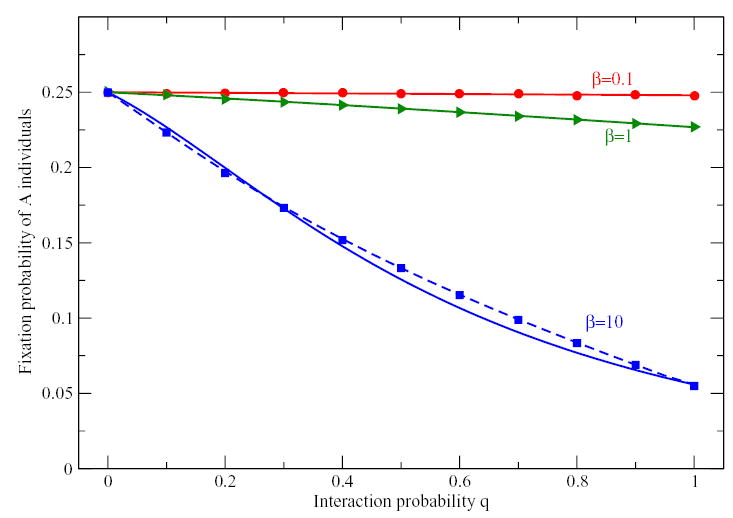
Fixation probability of k = 5 A individuals in a Coordination game for different interaction probability q and different intensities of selection β. Computer simulations (symbols) agree perfectly with the fixation probabilities computed from the transition probabilities of Eq. (9) shown as dashed lines. Full lines show the mean-field approximation of Eq. (12) that is in perfect agreement with simulations for β = 0.1 and β = 1.0. (Parameters: N = 20, payoff matrix a = 1, b = 0.2, c = 0.8, d = 0.3, averages over 10⁶ realizations of the process).

Figure 3.

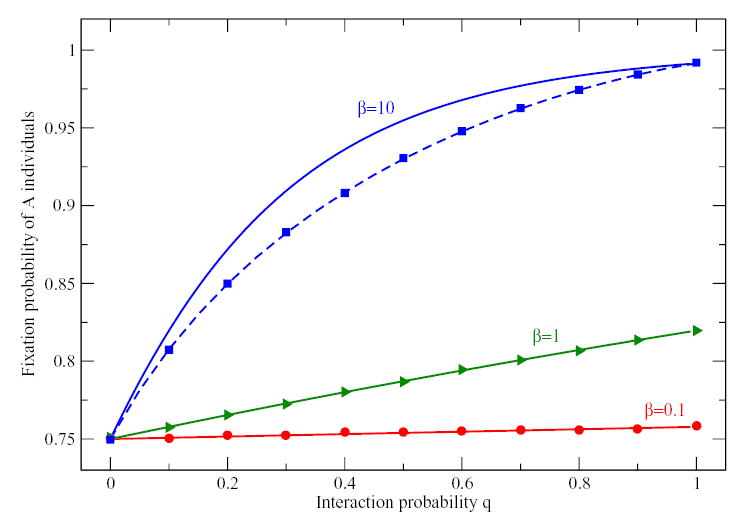
Fixation probability of k = 15 A individuals in a Coordination game for different interaction probability q and different intensities of selection β. Computer simulations (symbols) agree perfectly with the fixation probabilities computed from the transition probabilities Eq. (9) shown as dashed lines. Full lines show the mean-field approximation Eq. (12) that is in perfect agreement with simulations for β = 0.1 and β = 1.0. (Parameters: N = 20, payoff matrix as in Fig. 2, a = 1, b = 0.2, c = 0.8, d = 0.3, averages over 10⁶ realizations of the process).

Unfortunately, the four sums in the transition probability make it inconvenient to work with Eq. (10): The computation of a single transition probability for a population of size N = 20 requires the summation of more than 10⁵ terms. Therefore, it is useful to derive an approximation for these probabilities.

3.2 Mean-field approximation

Following a long tradition in physics, we calculate the payoffs in the mean-field approximation. This means that, instead of averaging the transition probabilities, as in Eq. (9), we average the payoff for individuals of a given type. In other words, we neglect fluctuations in the payoffs. Their average values read π̃_A = q π_A and π̃_B = q π_B. Eq. (5) changes to

$${\tilde{T}}^{\pm }(i)=\frac{i}{N}\frac{N-i}{N}\frac{1}{1+e^{-\beta q({\pi }_A-{\pi }_B)}}.$$ (11)

The only thing that changes from the original system with transition probabilities given by Eq. (5) is the intensity of selection, which is reduced to β_eff = q β. In statistical physics, this corresponds to an increase of the temperature, T_eff = 1/β_eff = T/q > T. Hence, the heterogeneity introduced in the system simply increases the temperature of selection. In Traulsen et al. (2006a,c) we have shown that the fixation probability of such systems, i.e. the probability that a group of k individuals of type A reaches fixation can be well approximated by

$${\phi }_k=\frac{\text{erf}[{\xi }_k]-\text{erf}[{\xi }_0]}{\text{erf}[{\xi }_N]-\text{erf}[{\xi }_0]}.$$ (12)

Here ${\xi }_k=\sqrt{\frac{{\beta }_{\text{eff}}(N-1)}{u}}(ku+v),$ 2u = a − b − c + d ≠ 0, 2v = − a + bN − dN + d and erf(x) is the error function. For u = 0, the fixation probabilities reduce to

$${\phi }_k=\frac{e^{-2{\beta }_{\text{eff}}(N-1)vk}-1}{e^{-2{\beta }_{\text{eff}}(N-1)vN}-1}.$$ (13)

These expressions allow the calculation of the fixation probabilities using the mean-field approximation. For weak selection, β ≪ 1, the mean-field approximation agrees well with simulations, see Fig. 1. However, for very high values of β, fluctuations in the payoff values can no longer be neglected and the fixation probabilities have to be calculated in a more sophisticated way via Eqs. (9) and (10) where the averaging is considered at the level of transition probabilities instead of being done already at the level of payoffs. Note that in the whole parameter range of the frequency dependent Moran process (Nowak et al., 2004), the mean-field approximation agrees well with computer simulations. As a further approximation, corrections to the mean-field theory can be calculated by developing the transition probabilities around the mean-field theory, as shown in Appendix B.

4 Individual based simulations

To confirm our analytical results and to explore the range in which the mean-field approximation works well, we performed individual based simulations of the process in a population of two different types A and B. We select two individuals 1 and 2 at random. Both interact with each of the remaining N − 1 individuals in an evolutionary game, where the probability for each interaction is q, leading to payoffs π₁ and π₂. Since only these two individuals are involved in the strategy update, the remaining payoffs do not have to be computed. For the particular interaction between 1 and 2, the symmetry of interactions has to be taken into account. This interaction takes place if either one of them wants to interact. Hence, the payoff values of the two individuals are not independent of each other. After computing the payoffs, individual 1 switches its strategy to the strategy of individual 2 with probability p given by Eq. (1). Similarly, 2 switches to 1 with probability 1 − p. Hence, the number of A individuals can change by at most one in each time step. In this process, we compute the probability that A individuals reach fixation and wipe out B individuals.

In Fig. 1, we show simulations of a Prisoner’s Dilemma starting with k = 15 cooperators. Since cooperation is dominated by defection, stronger selection decreases the fixation probability of cooperators. For β = 0.1 and β = 1, the mean-field approximation agrees very well with individual based simulations. When selection is very strong, fluctuations in the payoffs that increase the odds for cooperators can no longer be neglected and the mean-field approximation is no longer valid. Using instead the fixation probabilities of Eq. (10) derived from the averaged transition probabilities of Eq. (9) leads to perfect agreement again.

As a second example, we show the fixation probabilities in a coordination game starting from k = 5 individuals of type A in Fig 2 and k = 15 in Fig. 3. Again, the simulations agree perfectly with the fixation probabilities from the mean-field approximation given Eq. (12) for β = 0.1 and β = 1. For higher intensity of selection, the mean-field approximation deviates from the fixation probabilities derived from the averaged transition probabilities Eq. (9), which are in good agreement with individual based simulations. Here, we have restricted ourselves to a coordination game in which all payoffs are positive, i.e. interacting is always better than not interacting. The situation can become more complex if not playing can be advantageous as in (Hauert et al., 2002b,a; Szabó and Hauert, 2002).

5 Fixation times

So far, we have only considered the fixation probabilities that the system will reach a given absorbing state. Often, the duration of this process is also of interest, i.e. the average time it takes until fixation. As for the fixation probabilities, we can make an approximation for the fixation times by replacing the payoffs by the average payoffs in the case of q < 1. This approximation corresponds to a rescaling of the temperature by a factor q in the equation for the fixation times. Antal and Scheuring (2005) and Traulsen et al. (2006c) have shown that the conditional average time ${\tau }_i^N$ to reach state N with A individuals only is for q = 1 given by

$${\tau }_i^N=\frac{1}{{\phi }_i}(R_0-R_i)-R_0,$$ (14)

The quantity R_i is defined as

$$R_i=N^2\sum _{n=i+1}^{N-1}{\chi }_n^{1-n}\sum _{k=n}^{N-1}{\phi }_k\frac{1+{\chi }_{2k}^{-1}}{k(N-k)}{\chi }_{k+1}^k$$ (15)

where X_j = exp [qβ(ju + 2v)/(N − 1)]. Fig. 4 shows a comparison of the fixation times obtained from Eq. (14) and numerical simulations, which agree very well for small β. The remarkable agreement with the mean-field approximation shows again that the stochastic payoff evaluation can be mapped to a higher temperature of selection. In other words, the heterogeneity introduced by q < 1 simply weakens selection.

Figure 4.

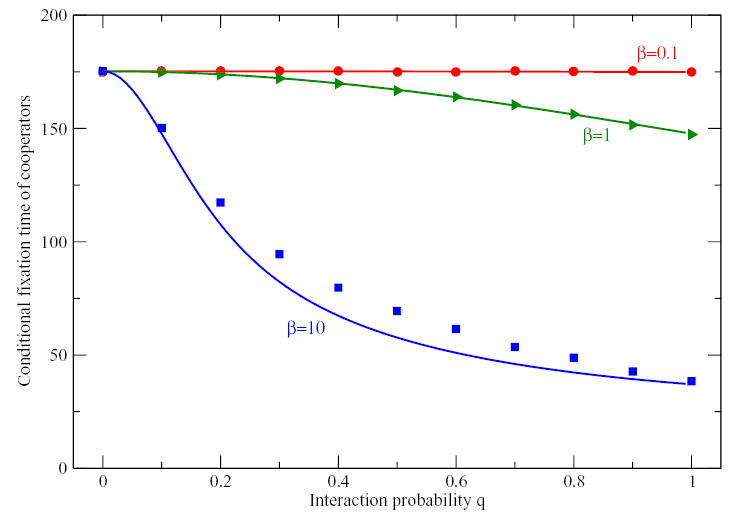
Conditional average time to end up in the state with 100% cooperators in a Prisoners Dilemma, starting from k = 15 cooperators, for different interaction probability q. For q = 0, we recover the result from neutral selection for any value of β.. For small β, numerical simulations (symbols) agree perfectly with the mean-field theory for all values of q, Eq. (14) depicted by full lines. Deviations become larger when selection is stronger (Payoff matrix as in Fig 1, a = 0.9, b = − 0.1, c = 1.0, d = 0).

Here, we restricted ourselves to the conditional average time it takes to reach the absorbing state where only A individuals are present. Similar results based on the theory for 1 = 1 can be derived for the unconditional fixation times or fixation in i = 0 (Traulsen et al., 2006c).

6 Comparison with previous models

Sánchez and Cuesta (2005) have recently introduced a model in which altruism may arise solely from individual selection, see also (Sánchez et al., 2005; Roca et al., 2006). In their model, agents reproduce after interactions among randomly chosen individuals. A parameter s is introduced which specifies the number of interactions taking place in a population of size N between two successive strategy updates, which in the limit s/N ≫ 1 leads to the usual assumption that all individuals interact with all others. Similar to our interaction probability q, a small number of interactions leads to strong fluctuations in the system that may dominate the dynamics.

However, Sánchez and Cuesta (2005) choose a different update mechanism for the evolutionary dynamics: they choose deterministically the worst player and replace it by a copy of the best player, keeping the payoff of the best player. Hence, new agents are immediately equipped with the same survival opportunities as their ancestors, which makes it difficult to compare their results with our model. Employing a fixed number of interactions s between successive updates leads to results comparable to our model if a background fitness is introduced (Roca et al., 2006): For s ≪ N, stochastic effects dominate and selection is weak. For s ≫ N, selection is strong and more successful strategies will spread.

7 Discussion

We have added an additional source of stochasticity to evolutionary game dynamics of finite populations. The payoff of each individual is no longer deterministically given, but evaluated in a stochastic process. For each pair of individuals there is a probability p that an interaction will occur. Hence, individuals using the same strategy can differ in their payoff values when selection operates. We have used a pairwise comparison update rule where the parameter β acts like an inverse selection temperature (Traulsen et al., 2006a).

The resulting system is complicated and can be studied with individual based computer simulations. We have presented a simple mean-field approximation that gives a good description of fixation probabilities and times for a wide range of parameter values (as long as the intensity of selection is not too strong). We have shown that the heterogeneity arising from the stochastic payoff evaluation increases the temperature of selection.

Appendix A: Average transition probabilities for symmetric interactions

In Eq. (9), we have assumed that j_AB and j_BA are independent random numbers. For the particular interaction between individuals A and B, this is not the case, as A interacting with B leads to B interacting with A. We have to distinguish two cases: With probability q² + 2q(1 − q) = q(2 − q), the link between A and B is active. With probability (1 − q)², it is not active. Hence, Eq. (9) modifies to

$$\begin{array}{l}\langle T^{\pm }(i)\rangle =q(2-q)\frac{i}{N}\frac{N-i}{N}\sum _{j_{AA}=0}^{i-1}\sum _{j_{AB}=0}^{N-i-1}\sum _{j_{BA}=0}^{i-1}\sum _{j_{BB}=0}^{N-i-1}\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}\\ \times \left(\begin{array}{c}N-i-1\\ j_{AB}\end{array}\right)q^{j_{AB}}{(1-q)}^{N-i-1-j_{AB}}\left(\begin{array}{c}i-1\\ j_{BA}\end{array}\right)q^{j_{BA}}{(1-q)}^{i-1-j_{BA}}\\ \times \left(\begin{array}{c}N-i-1\\ j_{BB}\end{array}\right)q^{j_{BB}}{(1-q)}^{N-i-1-j_{BB}}\frac{1}{1+e^{\mp \beta (a{j}_{AA}+b(j_{AB}+1)-c(j_{BA}+1)-d{j}_{BB})/(N-1)}}\\ +\hspace{0.17em}{(1-q)}^2\frac{i}{N}\frac{N-i}{N}\sum _{j_{AA}=0}^{i-1}\sum _{j_{AB}=0}^{N-i-1}\sum _{j_{BA}=0}^{i-1}\sum _{j_{BB}=0}^{N-i-1}\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}\\ \times \left(\begin{array}{c}N-i-1\\ j_{AB}\end{array}\right)q^{j_{AB}}{(1-q)}^{N-i-1-j_{AB}}\left(\begin{array}{c}i-1\\ j_{BA}\end{array}\right)q^{j_{BA}}{(1-q)}^{i-1-j_{BA}}\\ \times \left(\begin{array}{c}N-i-1\\ j_{BB}\end{array}\right)q^{j_{BB}}{(1-q)}^{N-i-1-j_{BB}}\frac{1}{1+e^{\mp \beta (a{j}_{AA}+b{j}_{AB}-c{j}_{BA}-d{j}_{BB})/(N-1)}}.\end{array}$$ (16)

The first summand describes the situation in which interaction between the focal individuals A and B takes place and the remaining A − B interactions are chosen at random. There are N − i − 1 remaining B interactions for A and i − 1 remaining A interactions for B. The A − B interaction that is present is taken into account in the argument of the exponential function. The second summand describes the situation in which the focal individuals do not interact. Again, the remaining links are chosen at random.

Appendix B: Corrections to the mean-field theory

Here, we derive a closed formula as an approximation for the transition probabilities Eq. (9). We consider corrections to the mean-field approximation. Defining

$$f=exp[-\beta q(a(i-1)+b(N-i)-ci-d(N-i-1))],$$ (17)

we can write the mean-field transition probability as

$${\tilde{T}}^{\pm }(i)=\frac{i}{N}\frac{N-i}{N}\frac{1}{1+f^{\pm 1}}$$ (18)

We can now rewrite

$$F(z)=\frac{1}{1+exp[-\beta (a{j}_{AA}+b{j}_{AB}-c{j}_{BA}-d{j}_{BB}]}=\frac{1}{1+f{e}^{-z}},$$ (19)

where

$$z=-\beta \left(a\frac{j_{AA}-q(i-1)}{N-1}+b\frac{j_{AB}-q(N-i)}{N-1}-c\frac{j_{BA}-qi}{N-1}-d\frac{j_{BB}-q(N-i-1)}{N-1}\right)$$ (20)

measures deviations from the mean-field theory. For q = 0 and q = 1, we have z = 0. Also for β ≪ 1, the term z becomes small. The development of F (z) for z ≪ 1 yields

$$\begin{array}{l}F(z)=\tilde{F}+\tilde{F}{\tilde{G}}_z+(\tilde{F}{\tilde{G}}^2-\frac{1}{2}\tilde{F}\tilde{G})z^2+\left(\tilde{F}{\tilde{G}}^3-\tilde{F}{\tilde{G}}^2+\frac{1}{6}\tilde{F}\tilde{G}\right)z^3\\ =\tilde{F}+\tilde{F}(1-\tilde{F})z+\tilde{F}(1-\tilde{F})(\frac{1}{2}-\tilde{F})z^2+\tilde{F}\left(\frac{1}{6}-\frac{7}{6}\tilde{F}+2{\tilde{F}}^2-{\tilde{F}}^3\right)z^3,\end{array}$$ (21)

where F̃ = 1/(1 + f) and G̃ = f/(1 − f) = 1 − F̃.

Let us now consider the effect of the sums in Eq. (9) on the terms in Eq. (21). We use the abbreviation C_k for the term of order z^k in Eq. (21).The term independent of z gives the mean-field result described above, C₀ = F̃.

The linear order term vanishes C₁ when the sums are performed, due to the symmetry of the Binomial distribution.

In the quadratic term C₂, all cross terms are linear and consequently vanish. Only the terms in a²(j_AA − q(i − 1))² are nonzero (similarly for b, c, and d) and give basically the variance of the distributions. Hence, the quadratic term is given by

$$\begin{array}{l}{C}_2=\tilde{F}\sum _{j_{AA}=0}^{i-1}\sum _{j_{AB}=0}^{n-i}\sum _{j_{BA}=0}^i\sum _{j_{BB}=0}^{n-i-1}\left(\begin{array}{c}i-1\\ j_{AA}\end{array}\right)q^{j_{AA}}{(1-q)}^{i-1-j_{AA}}\left(\begin{array}{c}N-i\\ j_{AB}\end{array}\right)q^{j_{AB}}{(1-q)}^{N-i-j_{AB}}\\ \times \left(\begin{array}{c}i\\ j_{BA}\end{array}\right)q^{j_{BA}}{(1-q)}^{i-j_{BA}}\left(\begin{array}{c}N-i-1\\ j_{BB}\end{array}\right)q^{j_{BB}}{(1-q)}^{N-i-1-j_{BB}}{z}^2\\ =\tilde{F}{\beta }^2[a^2(i-1)+b^2(n-i)+c^{2}i+d^2(n-i-1)]\hspace{0.17em}q(1-q)\end{array}$$ (22)

This first correction term vanishes for q = 0 and q = 1, as it should.

The cubic term in z simplifies in a similar way to

$$C_3=\tilde{F}{\beta }^3[a^3(i-1)+b^3(n-i)+c^{3}i+d^3(n-i-1)]q(1-3q+2q^2)$$ (23)

For terms of higher order in z, the skewness of the Binomial distribution enters and leads to a more complicated structure.

The transition probabilities finally yield

$$T^{+}(i)\approx {\tilde{T}}^{+}(i)\left[1+(1-\tilde{F})(\frac{1}{2}-\tilde{F})\frac{C_2}{\tilde{F}}+\left(\frac{1}{6}-\frac{7}{6}\tilde{F}+2{\tilde{F}}^2-{\tilde{F}}^3\right)\frac{C_3}{\tilde{F}}\right]$$ (24)

The second transition probability T⁻(i) can be obtained by changing the sign of β in Eq. (24). Inserting these terms in Eq. (10) yields the fixation probabilities, which do not longer reduce to a simple equation if higher order corrections are taken into account. However, for high temperature, β ≪ 1, the mean-field term is sufficient, as C₂ is quadratic in β. For q = 0 and q = 1, all correction terms vanish, as the mean-field theory becomes exact in these limits.