Abstract
Repetitive sequences make up a major part of eukaryotic genomes. We have developed an approach for the de novo identification and classification of repeat sequence families that is based on extensions to the usual approach of single linkage clustering of local pairwise alignments between genomic sequences. Our extensions use multiple alignment information to define the boundaries of individual copies of the repeats and to distinguish homologous but distinct repeat element families. When tested on the human genome, our approach was able to properly identify and group known transposable elements. The program, RECON, should be useful for first-pass automatic classification of repeats in newly sequenced genomes.
[The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: R. Klein.]
A significant fraction of almost any genome is repetitive. Repetitive sequences fall primarily into three classes: local repeats (tandem repeats and simple sequence repeats), families of dispersed repeats (mostly transposable elements and retrotransposed cellular genes), and segmental duplications (duplicated genomic fragments). The role of repeated, transposed, and duplicated sequence in evolution is an interesting and controversial topic (Doolittle and Sapienza 1980; Orgel and Crick 1980, McClintock 1984), but repetitive sequences are so numerous that simply annotating them well is an important problem in itself. This is particularly the case for repeat sequence families, which often carry their own genes (e.g., transposases and reverse transcriptases), and can confuse large-scale gene annotation.
Computational tools have been developed for systematic genome annotation of repeat families. Perhaps the best known is the program RepeatMasker (A.F.A. Smit and P. Green, unpubl.), which uses precompiled representative sequence libraries to find homologous copies of known repeat families. RepeatMasker is indispensable in genomes in which repeat families have already been analyzed. However, it does not pass the “platypus test” (Marshall 2001): Repeat families are largely species-specific, so if one were to analyze a new genome (like the platypus), a new repeat library would first need to be manually compiled. With sequencing efforts moving toward large-scale comparative genome sequencing of a wide variety of organisms, it is desirable to also have a de novo method that automates the process of compiling RepeatMasker libraries.
Several de novo approaches have been attempted with limited success. They generally start with a self-comparison with a sequence similarity detection method to identify repeated sequence and then use a clustering method to group related sequences into families (Agarwal and States 1994; Parsons 1995; Kurtz et al. 2000). Detecting repetition by sequence alignment methods is relatively easy. Automatically defining biologically reasonable families is more difficult. Local sequence alignments do not usually correspond to the biological boundaries of the repeats because of degraded or partially deleted copies, related but distinct repeats, and segmental duplications covering more than one repeat. Difficulty in defining element boundaries then causes a variety of subsequent problems in clustering related elements into families.
Similar problems arise in automated detection of conserved protein domains. Curated databases such as Pfam (Bateman et al. 2000) play a role equivalent to RepeatMasker by providing precompiled libraries of known domains. Automated clustering approaches are used to help detect new domains (Sonnhammer and Kahn 1994; Gracy and Argos 1998). These automated algorithms combine pairwise alignments with a variety of extra information to try to define biologically meaningful domain boundaries; most importantly, they look at multiple sequence alignments, not just pairwise alignments, to find significantly conserved boundaries.
Here, we describe an automated approach for de novo repeat identification. Our approach uses multiple alignment information to infer element boundaries and biologically reasonable clustering of sequence families.
RESULTS
Given a set of genomic sequences, {Sn}, our goal is to identify the repeat families therein (denoted by {Fα}), so that each family corresponds to a particular type of repeat containing all and only copies of that repeat in {Sn}. Each individual repeat is a subsequence Sn(sk, ek), where sk and ek are start and end positions in sequence Sn. Therefore, the output is (Fα ={Sn(sk, ek)}.
We define the following terms: element, image of an element, and syntopy. An individual copy of a repeat, Sn(sk, ek), is called an element. A subsequence involved in an alignment is called an image (Fig. 1). An element is the biological entity we are trying to infer. Images are observations from a pairwise comparison of the genome sequences {Sn}. One element forms many images because of its repetitive nature. We call two images of the same element syntopic images (syntopy is a neologism from syn—“same,” tope—“site”). Because observed alignments may extend well beyond the bounds of an element and may even include unrelated elements (e.g., because of segmental duplication or coincidental juxtaposition of abundant repeats), syntopy cannot be inferred just by image overlap, and this is the problem we must address.
Figure 1.
Flowchart of the de novo strategy. Input genomic sequences (black lines on top) contain a family of repeats with three copies (i.e., elements); two full length (blue and red boxes) and one partially deleted (green box). These elements, unknown at this point, will yield three alignments in an all versus all pairwise comparison of the genomic sequences. The aligned fragments (i.e., images), colored as their corresponding elements for clarity, are sorted to their corresponding genomic region, and those coming from the same element (i.e., syntopic images) can be grouped together according to their overlaps. On the basis of the syntopic sets, elements can be defined. These defined elements are then clustered into one family because they are all similar to each other.
The Existing Single Linkage Clustering Algorithms
The existing de novo repeat identification algorithms can be summarized in our terms as single linkage clustering algorithms as follows:
- 1.
Obtain pairwise local alignments between sequences in {Sn}.
- 2.
Define elements {Sn(sk, ek)} from the obtained alignments or images:
- a.
Construct graph G(V,E), where V represents all the images and E represents the syntopy between images. Two images are considered syntopic if they overlap, regardless of strand, beyond some threshold.
- b.
Find all connected components in G (Skiena 1997).
- c.
For each connected component, define an element Sn(sk, ek) as the shortest fragment that covers all images in the component.
- 3.
Group defined elements into families on the basis of their sequence similarity:
- a.
Construct graph H(V‘, E‘), where V‘ represents all the elements, and E‘ represents similarity (two elements are connected by an edge if they form alignments in Step 1).
- b.
Find all connected components of H.
- c.
For each connected component, define a family as the set of all elements in the component.
Problem 1: Inference of Syntopy
The main problems with this approach arise from the use of overlap to infer syntopy. If all repeat elements were full length, well conserved, and well separated by unique sequence in the genome, all syntopic images would be equivalent to their corresponding element, and single linkage clustering would work fine. However, two major phenomena distort this ideal picture. One is drift (both deletion and substitution mutation), which causes partial images (Fig. 2B), and the other is segmental duplication and juxtaposition of common repeats, which produce images containing more than one element (Fig. 2C).
Figure 2.
Different biological scenarios require different methods of syntopy inference. (A) For three images (thin black lines) in a genomic region (top bold black line), the single and double coverage methods lead to different definitions of elements. (B) A full-length element and its images (black and grey lines below). The top long image is formed with another full-length member in its family, whereas the shorter images are formed with the fragmented members. (C) A segmental duplication covering two kinds of elements. The top long image is formed with the other copy of this segmental duplication, whereas the shorter images are formed with other members in the two families, respectively.
Various strategies have been suggested for inferring syntopy from image overlap. Two typical measurements, termed single coverage method and double coverage method, require the overlap to be longer than a certain fraction of either or both of the images, respectively. When overlapping images are of different length, the two methods make different inference of syntopy, which leads to different definitions of elements (Fig. 2A). The single coverage method is suitable for the scenario in Figure 2B, whereas the double coverage is suitable for that in Figure 2C.
However, either strategy leads to errors. When the double coverage method is applied to partial images (Fig. 2B), it yields many spurious, overlapping elements for one true biological copy. When the single coverage method is applied to multielement images (Fig. 2C), it yields a composite element corresponding to the whole segmental duplication, which will lump families together later in family definition. Simply tuning the thresholds of these methods will not solve the problem: The two biological scenarios require opposite measurements of overlap to correctly infer syntopy (Agarwal and States 1994; I. Holmes pers. comm.). Furthermore, because these algorithms use only pairwise relationships between images, they are not able to distinguish the two biological scenarios and choose the proper criterion. The example in Figure 2 therefore indicates that no algorithm of this type can work.
However, one also sees in Figure 2 that there is useful information in the pattern of the multiple alignment of the images. In both cases, most image endpoints agree on the boundaries of an independent repeat. The key distinction lies in the endpoints of the shorter images. In Figure 2B, these endpoints are quasi-randomly dispersed throughout the multiple alignment, whereas in Figure 2C the endpoints pile up. Biologically, this distinction will hold true as long as the independent replication of repeats is more frequent than the generation of composite elements (e.g., by segmental duplications) and deletion is a random process, which are usually (but not always) the case.
Our approach to the problem is based on the above observation (Fig. 3). After an initial definition using the single coverage method, elements are split according to significant aggregations of image endpoints. As shown in Figure 3, a composite element will be split into several pieces (right panel, five pieces in this case), whereas a full-length element will be preserved (left panel). Details are specified in the element reevaluation and update procedure (see Methods).
Figure 3.
The RECON algorithm uses the aggregation of endpoints in the multiple alignment of images to distinguish between different biological scenarios.
Certain images complicate the above splitting process, such as those formed between related but distinct elements (Fig. 4A,B), which may lead to an incorrect splitting of an element. Unlike those in Figure 2, these misleading image endpoints do not occur at the termini of either of the two elements involved (Fig. 4C, open circles). We use this difference to filter the misleading endpoints before the element reevaluation and update procedure (see image end selection rule in Methods).
Figure 4.
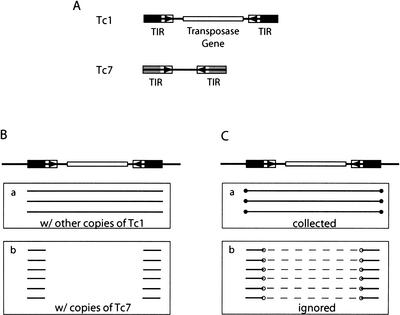
Complications because of sequence similarity between related families. (A) The schematic structure of Tc1 and Tc7, two related DNA transposons that are similar at the end of their terminal inverted repeats (black and grey blocks) but not in the rest of the sequences (Plasterk and von Luenen 1997). (B) A Tc1 element and its images. (C) Images in B are filtered, and only those ends labeled with closed circles will be collected to determine whether the element should be split. Open circles in Box b mark the misleading ends. Dashed lines link the pairs of images formed with the same copy of Tc7 and represent the unalignable sequences between a Tc1 and a Tc7. Although not shown in the figure, the two TIRs of Tc1 also form alignments in the opposite strands, and images from these alignments are also filtered.
Problem 2: Interfamily Similarity
Many repeat families are evolutionarily related (e.g., the autonomous Tc1 DNA transposons and the smaller nonautonomous Tc7 elements in Caenorhabditis elegans, Fig. 4). Although the reality is that repeats, like Pfam’s protein domain families or biological species, are a hierarchical evolutionary continuum that defies classification, it is still desirable to impose a simplistic classification that pretends that repeat families are distinct, for the purpose of practical genome annotation. Inasmuch as related families may form significant sequence alignments, we will have to impose arbitrary criteria to avoid lumping related but “distinct” families together.
We consider two elements to be distinct if the length of the nonconserved regions adds up to more than certain ratio of both of the two sequences (Fig. 4C, dashed lines). The family relationship determination procedure (see Methods) implements this definition. When constructing the graph for clustering (Step 3 in the above algorithm), elements belonging to the same family are linked with primary edges, and those belonging to different families but still forming significant alignments are linked with secondary edges. Families (connected components) are defined by primary edges.
Incorrect primary edges can arise in the presence of certain partially deleted elements (Fig. 5A). As shown in Figure 5B, primary and secondary edges are properly constructed between full-length copies of Tc1 and Tc7 by the family relationship determination procedure. However, edges between the partial copy of Tc7 and the Tc1s are rendered primary, as there are no nonconserved regions in this Tc7 compared with Tc1s. These false primary edges will lump the two families. Such a situation can be recognized by finding triangles involving two primary edges and a secondary edge (e.g., Tc1-2 → Tc7-1 → Tc7-partial). Once an element yielding incorrect primary edges is recognized, all its primary edges are removed except for the one linking to its most closely related element (Fig. 5C). More rules are specified in the family graph construction procedure with edge reevaluation (see Methods).
Figure 5.
False primary edges because of partial elements. (A) The schematic structure of full-length Tc1 and Tc7 (see also Fig. 4) and a partially deleted Tc7, which preserves only the region similar to Tc1. (B) Graph constructed for Tc1s and Tc7s. Closed nodes represent full-length elements. Solid and dashed lines represent primary and secondary edges, respectively. (C) Certain primary edges are removed from the partial Tc7 to eliminate the false ones.
The RECON Algorithm
Our algorithm is summarized as follows:
- 1.
Obtain pairwise local alignments between the input sequences.
- 2.
Define elements from the obtained alignments:
- a.
Elements are first defined using the single coverage method, as described in Step 2 of the existing algorithm.
- b.
Each element defined is reevaluated after the image end selection rule (Fig. 4) and the element reevaluate and update procedure (Fig. 3).
- c.
If an element defined is considered composite and is split, elements forming alignments with the composite element will be reevaluated. The process continues until all definitions of elements stabilize.
- 3.
Group elements defined into families on the basis of their sequence similarity:
- a.
Elements and their family relationship are determined and converted to a graph H(V‘, E‘) according to the family relationship determination procedure and the graph construction procedure with edge reevaluation (Fig. 5).
- b.
Find all connected components of H according to the primary edges constructed. For each connected component, define a family as a set of all elements in the component.
The algorithm has been implemented as RECON, a set of C programs, and Perl scripts. The RECON package, including a demo and more materials, is available at http://www.genetics.wustl.edu/eddy/recon.
Assessment
To assess the performance of RECON, we used it to analyze a random sample of 3 Mb, or ∼0.1%, of the human genome (Lander et al. 2001) and compared the results with RepeatMasker annotation as a “gold standard.” For purpose of comparison, we also implemented and tested the basic single linkage clustering algorithm using both the single or double coverage element definition methods. All three de novo methods use the same set of 453,896 pairwise alignments generated by WU-BLASTN (W. Gish unpubl.) (see Methods).
It took RECON 4 central processing unit (CPU) hr and a maximum of 300 MB random-access memory (RAM) to analyze this set of alignments on a single Intel Xeon 1.7GHz processor. A RECON analysis of a set of alignments from a three-fold larger sample (9 Mb) took 39 CPU hr and 750 MB RAM. We cannot give a useful asymptotic analysis of memory/CPU usage in terms of genome or sample size, because RECON’s computational complexity is strongly dependent on repeat density and composition. For example, an analysis of the alignments from the same 3-Mb sample with known repeats masked out by RepeatMasker took <1 min and 900 KB of RAM. This indicates that for a large, repeat-rich genome, it will be possible (and necessary) to carry out an iterative RECON analysis; for example, first find the most abundant families in a small sample of the genome, and then analyze progressively larger samples after masking families that have already been confidently identified.
In regard to the quality of the results, we first looked specifically at the definition of Alu, which is the most numerous repeat element and therefore the most prone to many sorts of clustering artifacts (Table 1). We identified each de novo constructed family that contained one or more sequences that overlapped Alu elements defined by RepeatMasker. For the largest family defined by each method, we also counted how many of the defined elements contained non-Alu repeat sequences as defined by RepeatMasker. A “correct” result would be that a de novo method would identify a single family of 1260 Alu elements covering 318,927 bases of the genome sample, exactly matching the RepeatMasker annotation.
Table 1.
Definition of the Alu Family
| Method | No. of elements | Total length, bp | Genomic coverage, bp | No. of families | Largest Family | |
|---|---|---|---|---|---|---|
| Non-Alus | Alus | |||||
| RepeatMasker | 1260 | 318,938 | 318,927 | 1 | 0 | 1260 |
| Single | 1389 | 357,830 | 331,593 | 1 | 576 | 1378 |
| Double | 56,925 | 7,908,428 | 330,830 | 19 | 6 | 54,615 |
| RECON | 1468 | 285,747 | 285,000 | 2 | 2 | 1423 |
The single coverage method defined 1389 elements that overlapped the Alus defined by RepeatMasker. The number is >1260 because some Alu copies are broken into several fragments by the method. The 1389 elements covered too much of the genome (331,593 bp), because some of the “elements” are actually segmental duplications that happen to contain Alus. This method overclusters. In the largest family defined, it mixed 576 of non-Alu sequences (most of which are L1 elements, the second most abundant human repeat family) with the 1378 Alu elements. The double coverage method underclusters images, defining many “elements” that completely overlap each other, leading to a huge number of “elements” (56,925) clustered into too many families (19). RECON minimizes both problems, leading to two Alu-containing families (one of which dominates) with 1468 elements covering 285,000 bp, with minimal contamination from other repeat families. Some Alu elements are still inappropriately broken into two or more fragments (leading to significantly >1260 elements). The somewhat lower genomic coverage of RECON compared with RepeatMasker results from the higher sensitivity of RepeatMasker's similarity search algorithm and threshold (CROSSMATCH with an aggressive threshold, as opposed to RECON's use of WU-BLAST with a conservative threshold).
To evaluate how reliable RECON annotation is overall, we systematically compared every RECON family containing 10 elements to RepeatMasker annotation (Table 2). Each RECON family was labeled according to which RepeatMasker annotation made up the majority of its elements. Any element that was annotated as a different family or not annotated at all was considered a false positive element (cluster fp1 and cluster fp2 columns in the Table, respectively). These results indicate that RECON's families are almost completely “pure” with very little contamination from unrelated repeat families. The families are usually a subset of their corresponding biological families; for example, one large family with the majority of the L1 elements is found (f7), along with several smaller families of partial L1 elements (f8, f13, f22, f57, and f146), which are not clustered with f7. f179, a “new” family, is a family of retroposed protein-coding genes, which are a class of repeats not annotated by RepeatMasker.
Table 2.
The Larger Human Repeat Families Defined by RECON
| RECON family | RepeatMasker family | Copy numbera | Clusterb | Consensusc | ||
|---|---|---|---|---|---|---|
| fp1 | fp2 | fp | fn | |||
| f1 | Alu | 1425 | 1 | 1 | 1/424 | 16/311 |
| f230 | Alu | 10 | 0 | 0 | 3/77 | 111/185 |
| f7 | L1 | 292 | 2 | 1 | 0/6139 | 15/6152 |
| f8 | L1 | 28 | 0 | 0 | 0/906 | 5391/6305 |
| f13 | L1 | 22 | 0 | 0 | 1/518 | 5668/6184 |
| f22 | L1 | 17 | 0 | 0 | 3/1481 | 4655/6146 |
| f57 | L1 | 14 | 0 | 0 | 1/690 | 5429/6146 |
| f146 | L1 | 13 | 0 | 0 | 2/273 | 6031/6305 |
| f10 | MaLR(LTR) | 63 | 0 | 0 | 0/365 | 1/364 |
| f46 | MaLR(LTR+internal) | 44 | 0 | 0 | 3/2116 | 0/1935 |
| f12 | MaLR(LTR) | 17 | 0 | 0 | 3/211 | 218/426 |
| f28 | MER41 | 18 | 0 | 0 | 2/559 | 1/554 |
| f17 | Tigger1 | 14 | 0 | 0 | 2/1021 | 1405/2418 |
| f179 | New | 13 | 0 | 13 | n/a | n/a |
| f156 | MER1 | 10 | 0 | 0 | 3/199 | 99/297 |
Number of defined elements in RECON family.
fp1: Number of elements in RECON family corresponding to a different RepeatMasker family. fp2: Number of elements in RECON family not annotated by RepeatMasker.
fp: False positive positions vs length of the consensus. fn: False negative positions vs length of the RepeatMasker sequence. The consensus of the L1-corresponding families match different L1 sequences in RepeatMasker, as do the MaLR-corresponding families.
An important usage of a de novo method is to generate repeat libraries for the incremental analysis of a genome. To evaluate how useful RECON families would be for genome annotation of elements in a subsequent sample of human sequence, we compared the consensus sequence of each RECON family to their most similar sequences used in RepeatMasker (Table 2; see Methods). Bases in RECON's consensus that are not in RepeatMasker's sequence are counted as false positives (consensus fp column), measuring to what extent RECON defines too large of a consensus element. Bases in RepeatMasker's sequence that are not in RECON's consensus are counted as false negatives (consensus fn column), measuring to what extent RECON only recovers part of the consensus element. For four of the six known transposable elements found, the canonical sequence is reconstructed essentially intact (f1/Alu, f7/L1, f46/MaLR, and f28/MER41). For Tigger1 and MER1, however, only part of the canonical sequence is recovered in families f17 and f156. Manual inspection indicates that this is due to the truly fragmented nature of the copies in our sample, rather than erroneous splittings by RECON.
The canonical Alu sequence is dimeric, containing a left (L) and a right (R) monomer (Jurka and Zuckerkandl 1991). It is interesting that the consensus sequence identified by RECON family f1 contains exactly one and a half Alu elements in the configuration LLR. The longest six elements in f1 are all in this configuration. Such trimeric Alus have been noted before (Perl et al. 2000), and RECON's annotation indicates that they have been actively transposed in the human genome.
DISCUSSION
The problem of automated repeat sequence family classification is inherently messy and ill-defined and does not appear to be amenable to a clean algorithmic attack. The heuristic approach we have taken in RECON appears to be satisfactory for many practical purposes. Our use of multiple sequence alignment information, specifically the clustering of observed alignment endpoints, is a significant improvement over single linkage clustering on the basis of pairwise sequence relationships alone. Several aspects of the RECON algorithm are probabilistic in nature. For example, the split ratio n/m in the element reevaluation and update procedure is correlated with the probability of two repeats being adjacent by chance. We could take a more formal approach evaluating the significance of n/m. However, a simple cutoff value appears to be sufficient.
The evaluation of RECON's performance indicates several issues that could use improvement. It slightly underclusters elements, failing to appropriately link some small fragmentary families to a large full-length family. This might be addressed by a postprocessing step that merges RECON families when the consensus of one family covers the consensus of the other.
RECON is sometimes unable to recover a highly fragmented family in one piece. To overcome this, we could use a statistical test to identify RECON families whose copies tend to be physically adjacent to each other. The more diverged families, such as the ancient human L2 family, was not recovered in our test because of the chosen sensitivity settings of WU-BLAST.
RECON can also fail when its simple assumptions about alignment end clustering are violated. For example, when a particular form of partial copy is generated preferentially (e.g., solo long terminal repeats [LTRs] for retrovirus-like elements [Kim et al. 1998] formed by high-frequency deletion between the directly repeated LTRs), it can lead to an erroneous splitting of the full-length copies. Also, if a particular combination of repeat elements can itself be duplicated at high frequency (e.g., the composite bacterial Tn5 element [Berg 1989]), it may not be recognized as composite.
Different repeat composition may require tuning of parameters. For example, if elements are largely fragmented, one may lower the requirements of overlap between images at the risk of producing more composite elements. When solo LTRs are predominant, one may raise the ratio cutoff for element splitting at the risk of failing to break truly composite elements. One can only hope to optimize among conflicting situations in a genome-scale analysis.
We envision using RECON as a tool for initial analysis of a genome sequence. Much like automatically identified ProDom protein domain families aid the construction of curated Pfam multiple alignments, the families identified by RECON can be the basis of a higher quality level of analysis, such as using RECON families to build a RepeatMasker library or using RECON multiple alignments to build a library of profile hidden Markov models.
METHODS
Components of RECON
Image End Selection Rule
This rule filters misleading images (Fig. 4) by considering the length and arrangement of the aligned and unaligned sequences between two elements as follows:
- 1.
For each pair of defined elements that form alignments, find all maximal groups of alignments in which all alignments are part of one (but not necessarily the optimal) global alignment of the two given elements. This is performed by finding maximal cliques (Skiena 1997) in a graph in which the vertices represent the alignments and two vertices are linked if the two corresponding alignments can be seen as part of one global alignment of the two given elements.
- 2.
For each group found above, order the alignments according to their coordinates; eliminate the group if the sequences outside the outermost alignment or between any two adjacent alignments in the group are longer than a given length cutoff in both elements; and if not eliminated, assign a score to the group as the sum of scores of all alignments in the group. The length cutoff is chosen so that sequences shorter than the cutoff can be considered as generated by the random extension of true alignments by the pairwise alignment tool.
- 3.
If more than one group remains, take the one with the highest score and discard the others. Ends of the images in the remaining group (if any) are collected for further analysis.
Element Reevaluation and Update Procedure
This procedure updates the definition of a given element (Fig. 3) by evaluating the aggregation of image endpoints collected according to the rule above.
- 1.
Choose a length cutoff so that sequences shorter than the cutoff are considered generated by the random extension of true alignments by the pairwise alignment tool.
- 2.
Slide a window of the chosen length cutoff along the given element. Within each window, cluster the collected image ends as follows: Seed a cluster with the leftmost end not yet clustered; if an end is within a certain distance to any member in the cluster, it is assigned to the cluster; and when no more ends can be assigned to the cluster, start a new cluster if necessary until all ends in the window are clustered.
- 3.
For each cluster found above, let n denote the number of ends in the cluster, c denote the mean position of these n ends, and m denote the number of images of the given element spanning position c. If n/m is greater than a given threshold, c is considered a significant aggregation point.
- 4.
If no significant aggregation point is accepted, the original definition of the given element is maintained.
- 5.
Otherwise, update the given element as follows: Split the element and its alignments at the aggregation points, discard the original definition of the given element, discard the split products (new elements and alignments) that are shorter than the chosen length cutoff at the beginning, and assign alignments to proper new elements.
- 6.
If more than one new element remains, the original element is considered composite.
Family Relationship Determination Procedure
This procedure determines for a given pair of defined elements that form alignments whether the two belong to the same family or to two related but distinct families (Fig. 4). The procedure, which considers the relative length of the aligned sequences compared with the length of the elements, is as follows:
- 1.
For a given pair of defined elements that form alignments, find all maximal groups of alignments in which all alignments are part of one (but not necessarily the optimal) global alignment of the two given elements. See Step 1 in the image end selection rule for detail.
- 2.
The total length of each group found above is calculated as the sum of the length of all alignments in the group. The longest total length among the groups is treated as the alignable length between the two elements.
- 3.
If the alignable length is longer than a certain fraction of the length of either element, the two elements are considered to belong to the same family. Otherwise, they are not.
Family Graph Construction Procedure with Edge Reevaluation
- 1.
Each element defined is represented by a vertex.
- 2.
Edges are constructed as follows: If two elements are considered to belong to the same family by the family relationship determination procedure, a primary edge is constructed between the two corresponding vertices; if two elements form significant alignments but do not belong to the same family, a secondary edge is constructed between the two; if two elements do not form significant alignments, no edge is constructed between the two.
- 3.
For each vertex v, its primary edges are reevaluated as follows (Fig. 5): Let N(v) denote the set of vertices directly connected to v via primary edges. If any pair in N(v) is connected by a secondary edge, then ∀ v‘ε N(v), the primary edge between v and v‘ is removed unless v‘ is the most closely related element to v in N(v) (on the basis of alignment score and/or percent identity) or v is the most closely related element to v‘ in N(v‘). In the latter case, the primary edges of v‘ will be updated as just described.
- 4.
Remove all secondary edges.
Implementation Details
RECON starts from a datafile containing pairwise alignments, which allows a user to choose a tool other than WU-BLAST to do the initial all-versus-all comparison of the genome to itself.
A major issue is memory usage. To avoid holding all alignments from a genome-scale analysis in RAM at once, RECON manipulates files on disk (including a separate file for each currently defined element). It is therefore extremely input/output intensive.
RECON is not useful for processing short-period tandem repeats; these are split down to shorter forms or even monomers, a process that can take many iterations to converge. To improve time efficiency, we filter these by ignoring the initially defined elements that have >1000 images and in which the number of partner elements is less than one fifth of the number of images. Furthermore, because we discard short elements generated during splitting (element reevaluation and update procedure), the whole family can suddenly disappear when it decreases below the minimum element length cutoff.
In addition to the threshold and parameter choices in the initial pairwise comparison, RECON has four tunable parameters:
- 1.
The cutoff for fractional overlap between images, which is used in the initial inference of syntopy by the single coverage method. (Default = 0.5.)
- 2.
The minimum length of an element, for example, the maximal length that we expect the pairwise alignment tool to spuriously extend by chance from a true element boundary, used in the image end selection rule and the element reevaluation and update procedure. (Default = 30 nt.)
- 3.
The ratio cutoff for splitting an element at a given position used in the element reevaluation and update procedure. (Default = 2.)
- 4.
The minimal fraction of alignable sequences between two elements before they are considered to belong the same family. (Default = 0.9.)
To guide parameter optimization, we have developed an objective function that measures errors in the recovery of known families in a genome (Z. Bao and S. Eddy, unpubl.). A detailed description of the function is available at http://www.genetics.wustl.edu/eddy/recon.
The default parameters were hand optimized on the basis of the recovery of four experimentally verified DNA transposons (Tc1, Tc2, Tc3, and Tc5 [Plasterk and von Luenen 1997]) from the C. elegans genome sequence (The C. elegans Sequencing Consortium 1998). The human genome is dominated by retro-transposons (Alu, L1, and MaLR) and old, fragmented DNA transposons (Lander et al. 2001), and these families yield different patterns in multiple alignments than the young DNA transposons in the C. elegans training set, so the test on human data was reasonably independent of our training of these few parameters.
Human Genome Analysis
A total of 3 Mb of sequence was randomly sampled as 20-kb chunks from the 796 contigs in the December 12, 2000, release of the human genome (Lander et al. 2001) (http://genome-test.cse.ucsc.edu/goldenPath/12dec2000/bigZips). All-versus-all comparison of the sampled sequences was performed using WU-BLASTN 2.0 (W. Gish unpubl.) (http://blast.wustl.edu) with options M = 5 N = −11 Q = 22 R = 11 −kap E = 0.00001 wordmask = dust wordmask = seg maskextra = 20 −hspmax 5000.
Known repeats were identified using the July 7, 2001, version of RepeatMasker (http://ftp.genome.washington.edu/RM/RepeatMasker.html) with default options.
Consensus sequences of RECON families were made by aligning the 10 longest members of the family with DIALIGN2 (Morgenstern 1999), with default options, then selecting a simple majority rule consensus residue for each column.
WEB SITE REFERENCES
http://blast.wustl.edu; WU-BLAST.
http://ftp.genome.washington.edu/RM/RepeatMasker.html; Repeat Masker.
http://genome-test.cse.ucsc.edu/goldenPath/12dec2000/bigZips; University of California, Santa Cruz, Human Genome Project Working Draft.
Acknowledgments
We thank Dr. Elena Rivas for discussions and advice. The sequence sampling tool was provided by Mr. Robert Klein. We gratefully acknowledge financial support from the National Science Foundation (Grant No. DBI-0077709) and the Howard Hughes Medical Institute.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL eddy@genetics.wustl.edu; FAX (314) 362 7855.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.88502. Article published online before print in July 2002.
REFERENCES
- Agarwal P, States DJ. The Repeat Pattern Toolkit (RPT): Analyzing the structure and evolution of the C. elegans genome. In: Altman R, et al., editors. Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. Menlo Park, CA: AAAI Press; 1994. pp. 1–9. [PubMed] [Google Scholar]
- Bateman A, Birney E, Durbin R, Eddy SR, Howe KL, Sonnhammer ELL. The Pfam protein families database. Nucleic Acids Res. 2000;28:263–266. doi: 10.1093/nar/28.1.263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg DE. Transposon Tn5. In: Berg DE, et al., editors. Mobile DNA. Washington, DC.: American Society for Microbiology; 1989. pp. 185–210. [Google Scholar]
- Doolittle WF, Sapienza C. Selfish genes, the phenotype paradigm and genome evolution. Nature. 1980;284:601–603. doi: 10.1038/284601a0. [DOI] [PubMed] [Google Scholar]
- Gracy J, Argos P. Automated protein sequence database classification. II. Delineation of domain boundaries from sequence similarities. Bioinformatics. 1998;14:174–187. doi: 10.1093/bioinformatics/14.2.174. [DOI] [PubMed] [Google Scholar]
- Jurka J, Zuckerkandl E. Free left arms as precursor molecules in the evolution of Alu sequences. J Mol Evol. 1991;33:49–56. doi: 10.1007/BF02100195. [DOI] [PubMed] [Google Scholar]
- Kim JM, Vanguri S, Boeke JD, Gabriel A, Voytas DF. Transposable elements and genome organization: A comprehensive survey of retrotransposons revealed by the complete Saccharomyces cerevisiae genome sequence. Genome Res. 1998;8:464–478. doi: 10.1101/gr.8.5.464. [DOI] [PubMed] [Google Scholar]
- Kurtz S, Ohlebusch E, Schleiermacher C, Stoye J, Giegerich R. Computation and visualization of degenerate repeats in complete genomes. In: Altman R, et al., editors. Proceedings of the Eighth International Conference on Intelligent Systems for Molecular Biology. Menlo Park, CA: AAAI Press; 2000. pp. 228–238. [PubMed] [Google Scholar]
- Lander ES, Linton LM, Birren B, Nusbaum C, Zody MC, Baldwin J, Devon K, Dewar K, Doyle M, FitzHugh W, et al. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Marshall E. Genome teams adjust to shotgun marriage. Science. 2001;292:1982–1983. doi: 10.1126/science.292.5524.1982. [DOI] [PubMed] [Google Scholar]
- McClintock B. The significance of responses of the genome to challenge. Science. 1984;226:792–801. doi: 10.1126/science.15739260. [DOI] [PubMed] [Google Scholar]
- Morgenstern B. DIALIGN 2: Improvement of the segment-to-segment approach to multiple sequence alignment. Bioinformatics. 1999;15:211–218. doi: 10.1093/bioinformatics/15.3.211. [DOI] [PubMed] [Google Scholar]
- Orgel LE, Crick FH. Selfish DNA: The ultimate parasite. Nature. 1980;284:604–607. doi: 10.1038/284604a0. [DOI] [PubMed] [Google Scholar]
- Parsons JD. Miropeats: Graphical DNA sequence comparisons. Comput Appl Biosci. 1995;11:615–619. doi: 10.1093/bioinformatics/11.6.615. [DOI] [PubMed] [Google Scholar]
- Perl A, Colombo E, Samoilova E, Butler MC, Banki K. Human transaldolase-associated repetitive elements are transcribed by RNA polymerase III. J Biol Chem. 2000;275:7261–7272. doi: 10.1074/jbc.275.10.7261. [DOI] [PubMed] [Google Scholar]
- Plasterk RHA, von Luenen HGAM. Transposons. In: Riddle D, et al., editors. C. elegans II. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1997. pp. 97–116. [PubMed] [Google Scholar]
- Skiena SS. The algorithm design manual. New York: Telos/Springer-Verlag; 1997. [Google Scholar]
- Sonnhammer EL, Kahn D. Modular arrangement of proteins as inferred from analysis of homology. Protein Sci. 1994;3:482–492. doi: 10.1002/pro.5560030314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The C. elegans Sequencing Consortium. Genome sequence of the nematode C. elegans: A platform for investigating biology. Science. 1998;282:2012–2018. doi: 10.1126/science.282.5396.2012. [DOI] [PubMed] [Google Scholar]