How Many Mutations in a Cancer?

The role of genomic instability in causing and promoting tumor growth remains controversial. 1,2 Some argue that instability is necessary for tumorigenesis, 3 while others take the view that Darwinian selection is the driving force. 2 It is becoming clear that many cancers harbor multiple mutations, the great majority of which probably have no significant effect on tumor growth. Gross karyotypic abnormalities, 4 widespread microsatellite instability, 5 very frequent allelic loss, 6 and multiple small-scale insertions and deletions 7 have all been found in common types of cancer. Recent estimates have put the total number of mutations in a cancer at more than 10,000. 7 There is, moreover, evidence that some benign 8 or supposedly non-neoplastic 9 lesions harbor many or several mutations, although such findings are by no means universal. The finding of so many mutations has generally been unexpected by most commentators. 10 These data have been taken as evidence to support the central, and perhaps even necessary, role of genomic instability in tumorigenesis. 11

We wonder, however, whether the expectations and the data interpretation might be wrong. The number of mutations in a tumor seems very high, but is it? Interestingly, there are few, if any, estimates of the predicted number of mutations in a cancer given plausible tumor growth rates, mutation rates, and final size of the lesion. Mutations occurring during tumorigenesis are, moreover, just one component of the total number of mutations in the cancer. Mutations could also occur in the cell from which the tumor arises, starting from the moment of fertilization, accumulating during fetal and immature growth, as clonal expansion proceeded from the single cell to the adult, and then continuing to accumulate during steady-state maintenance of cell numbers in mature tissues. Considerable numbers of cell divisions (and considerable cell death) probably occur during each of these stages.

The balance between division and death is just one critical parameter about which little is known: two tissues may comprise exactly the same number of cells, but if one tissue has a higher rate of cell turnover, it will evidently acquire more mutations, because it replicates its DNA more often. For normal development and steady-state tissue maintenance, the kinetics of stem cell proliferation, differentiation, and programmed death are therefore important determinants of mutation accumulation. Other, largely unknown, factors which influence the number of mutations in a tumor operate during tumor growth. For example, during tumorigenesis, successive expansion of new, advantageous clones may reduce the number of mutations in the tumor, but the extent of this will depend on the degree to which the new clone obliterates the existing tumor. Alternatively, the new clone may have a higher rate of cell turnover, thus increasing the number of mutations.

Complex models are required to provide a full analysis of the expected rates of cell division, and hence the number of mutations, which occur at each of the three stages. For the purposes of this discussion, however, we shall consider highly simplified models of the three components of tumor-specific mutations: our discussion will focus on bowel cancer, but is applicable to any common, adult cancer.

First, for growth from the single cell to the adult, assume that the body is composed of 5 × 10 13 cells and, very conservatively and quite implausibly, that no cell death occurs during developmental growth. Solving the simple equation for exponential cell growth through doubling gives an estimate of 45 cell divisions for this process to occur. If a mutation rate of 5 ×10⁻⁹ per nucleotide per generation is assumed and the genome consists of 5 × 10 9 base pairs (bp), then an average of about 25 mutations occurs per generation. Thus, about 1000 mutations will be present in the stem cell of, for example, the colonic crypt of a 15-year-old human. All of these mutations will subsequently be detectable throughout the tumor. Most of them will occur in non-coding DNA. Of course, it is entirely improbable that no cell death (programmed or otherwise) occurs during human development and thus the estimate of 10,000 mutations is likely to be a gross underestimate, perhaps by several orders of magnitude.

Second, for mutations occurring in the cell of origin before tumorigenesis, we shall use a model 12 which is based on widely accepted theories of cell differentiation and turnover in the colonic crypt (Figure 1) ▶ . Stem cells (F₀) divide and self-renew, but a proportion of their daughters partially differentiate. Similar processes occur in F₁ to produce fully differentiated cells in F_2, of which a proportion undergo apoptosis each generation. Equations relating steady-state levels of cell numbers to turnover time and the proportion of cells renewing, differentiating, and dying each generation have been given by Tomlinson and Bodmer. 12 No selection is incorporated into the model.

Figure 1.

Model of cell division, differentiation and death in the colonic cript. F₀ represents the stem cell compartment, F₁, partly differentiated cells, and F₂, fully differentiated cells. Numbers of cells in each compartment are given by N₀, N₁, N₂ and N₃. Proportions of cells dying, differentiating, and renewing are given by α₁, α₂, α₃, etc. t₀, t₁ and t₂ represent the times taken for these processes to occur.

The population of fully differentiated cells has been estimated to renew about 100 times per year in the colonic crypt, implying from our previous work 12 that t₂/γ (Figure 1) ▶ is about 3 to 4 days (details not shown). The value of t₀ corresponding to this value varies according to the parameters of the model (N₀, N₁, N₂, α, β, and γ), but a conservative estimate of t₀ 12 corresponds to the stem cells or partly differentiated cells in F₀ or F₁ undergoing a minimum of 100 generations per year.

Let us assume that a cell in F₀ or F₁ is the tumor progenitor and that the patient’s tumor starts to grow at age 65 years. Then, ignoring any steady-state turnover during childhood, the stem cell will already have undergone 5000 normal divisions between the ages of 15 and 65 years. Once more, assuming a mutation rate of 5 × 10⁻⁹ per nucleotide per generation, a genome of 5 × 10 9 bp, an average of about 25 mutations occurs in the stem cell per generation, and a total of about 125,000 mutations will have occurred in the mature colon stem cell before the tumor starts to grow. Again, all of these mutations will be detectable throughout the tumor.

For the third type of mutation, those occurring during tumorigenesis, let us use a separate simplified model. Assume that a large adenoma comprises 10 9 cells and that a malignant tumor comprises 10 11 cells. Conservatively, we assume that all tumors take 10 years to grow from a single cell and that tumor cells replicate at approximately the same rate as normal colonocytes (100 generations per year). For simplicity, multistage carcinogenesis, with successive rounds of clonal expansion, is not incorporated into this model. Instead, a uniform rate of clonal expansion is assumed to occur. Cells in the tumor are associated with a selective advantage w, and the tumor clone therefore expands at a rate (1 + w) per generation (t). Death of a number of tumor cells is assumed to occur at random, so that w < 1.

Solving the simple equation

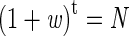where t = 1000 (100 generations/year × 10 years) shows that the selective advantage w is estimated to be about 0.021 for the colorectal adenoma and 0.026 for the carcinoma. Thus, the tumor clone is predicted to expand slowly and a considerable proportion of daughter cells dies in each generation. (Alternatively, we could have assumed a common w for both adenomas and carcinoma and that the latter require more generations).

Mutations in surviving cells are assumed to occur at random at rate μ (corresponding to number of mutations per genome per generation) in the expanding tumor clone (N(t) cells) in every generation. Mutations are assumed to be cumulative and to have no effect on w.

Starting with a tumor progenitor cell which has acquired two mutations at the APC locus, we know that

The number of new mutations (newM) in the tumor as a whole at (t + 1) is given by

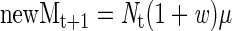and the total accumulated mutations (totalM) by

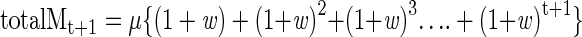and solving the classical geometric series

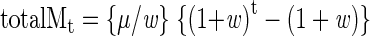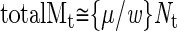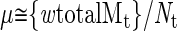If we assume that normally μ = 25 (for a 5 × 10 9 bp-sized genome) and w ≅ 0.02, then the total number of mutations expected (totalM_t) in a colorectal adenoma is

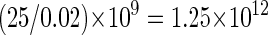and the equivalent for a carcinoma is about 10¹⁴.

However, many mutations will occur in such a low proportion of the tumor cells that they will be undetectable. We shall assume that mutations must comprise at least 10% of the sampled tumor to be detectable using standard molecular techniques; in other words, the mutations must have occurred before the tumor reached 10% of its final size. Thus, the effective size of an adenoma of 10 9 cells is 10 8 and the expected number of detectable mutations is approximately 1.25 × 10¹¹; the equivalent number of mutations for the carcinoma considered above is 10¹³. In fact, because small portions of tumors are generally analyzed and clonal expansion may maintain spatial architecture, many mutations occurring below the 10% threshold may be detected.

Our model does not incorporate replacement of old clones by new clones with increased selective advantages which may replace or obliterate the old clones, particularly in carcinomas. In reality, evidence suggests that there is likely to be partial replacement of old clones by new expanding clones, particularly in carcinomas. But even if there is total replacement, the final clone must have expanded from one cell to comprise the whole tumor. There is also a paradox in that we would predict a slow-growing, benign tumor—all things being equal—to have accumulated more mutations than a fast-growing malignancy, because the former has undergone more cell divisions. In practice, however, all things are not equal, and cancers are generally found to have more mutations than adenomas. There are several reasons for this. Cancers usually develop from slower-growing adenomas, cancers comprise more cells than adenomas, and many cancers do have intrinsic genomic instability. Moreover, cancers may have higher rates of both cell birth and death, compared with adenomas, a feature which would greatly increase the number of generations, and hence the number of mutations, in the latter. For simplicity, the above model only takes into account the balance between birth and death, not the values of each, but it should be noted that incorporating higher birth and death rates would actually increase our estimates of mutation numbers.

We thus predict a total of 1000 + 125,000 + 10 13 detectable mutations in a cancer. Our simple models predict that, even with normal mutation rates, a tumor may harbor many, many millions of mutations: some arise before tumorigenesis and others arise during tumor growth. Cancers with mutator phenotypes will have even more mutations. The number of mutations appears to be surprisingly large, but this result derives from three factors in the model: the accumulation of somatic mutations by normal stem cells over time; the large number of generations for most tumors to grow; and the large number of cells comprising the tumor itself and the high rate of cell death which must occur during tumorigenesis. These factors can be illustrated by a simple consideration of one generation of cell division in a tumor of 10 10 cells. It is conservative to assume that the great majority of these cells acquires at least one mutation of some sort in this one division. Thus, the tumor can theoretically acquire many millions of mutations by that single round of replication (although none will be detectable if present in such a small proportion of the tumor’s cells).

Recent estimates by Stoler et al, 7 based on assessment using intersimple sequence repeat polymerase chain reaction (PCR), suggested that benign and malignant colorectal tumors may contain about 10,000 mutations of an insertion/deletion type detectable by their methods. Our data show that, even allowing for this type of mutation being relatively uncommon compared with point mutations and for inefficient mutation detection methods, the true number of mutations in benign and malignant colorectal tumors is certainly several magnitudes greater. Genomic instability is not necessary to explain Stoler et al’s 10 estimate of 10,000 mutations and we do not agree with the view that 10,000 mutations is an unexpectedly high figure.

Stoler et al 7 did not observe the effects of mutation at normal rates because they used normal tissue as controls. Unlike the tumors studied, this control tissue would have been composed of a very large number of different clones, each of which would have acquired independent mutations; but each mutation would have been too rare to be detected. More appropriate controls would have been single stem cell clones, ideally cultured over many generations. Clearly, the use of such clones is unrealistic. Nevertheless, even the use of single genome-equivalent PCR 13 using DNA from blood or normal tissue would have revealed many more mutations in normal tissue than were actually found by Stoler et al 7 in the controls which they used.

If stem cells and cancers acquire so many mutations, why is there not an intolerable mutational load in normal tissues? It is arguable that the organization of tissues into stem cell compartments with a limited number of divisions and partly, or fully, differentiated cells with inevitable programmed death prevents a massive accumulation of deleterious mutations. However, it is probable that a more important reason for the lack of mutational load is that most mutations are not deleterious. It follows that when biallelic mutation is observed in tumors, for example at tumor suppressor loci, this is excellent evidence that these mutations have a functional effect and confer a selective advantage.

In our view, almost all tumors accumulate a very large number of mutations over time, typically 10 12 or more, both as a result of pre-existing changes in the stem cell of origin and of subsequent mutations during tumorigenesis. Evidently, tumors with inherent genomic instability will, things being equal, accumulate more mutations in a shorter time. It is clear, however, that genomic instability is not necessary to explain the existing data on the number of mutations detected in tumors and that studies of the numbers of mutations in tumors currently provide little evidence concerning the role of genomic instability in tumorigenesis.