Bayesian Analysis and Risk Assessment in Genetic Counseling and Testing

Abstract

Risk assessment is an essential component of genetic counseling and testing, and Bayesian analysis plays a central role in genetic risk assessment. Bayesian analysis allows calculation of the probability of a particular hypothesis, either disease or carrier status, based on family information and/or genetic test results. Genetic risk should be assessed as accurately as possible for family decision making. Additional information, from the pedigree and/or from genetic testing, can often dramatically improve the accuracy of genetic risk assessment. We illustrate herein the application of Bayes’ theorem and describe important basic principles in genetic risk assessment.

The purpose of this article is to introduce basic and general principles of Bayesian analysis and genetic risk assessment for molecular pathologists who are involved in genetic testing. For further reading and for specific examples of risk calculations for autosomal recessive, autosomal dominant, and X-linked disorders, we would refer to “Introduction to Risk Calculation in Genetic Counseling” by Young1 and “The Calculation of Genetic Risks” by Bridge,2 both of which illustrate a variety of worked examples with in-depth discussions. We have illustrated detailed methods for systematic genetic risk calculations for spinal muscular atrophy (SMA) in a variety of clinical settings.3 More advanced examples can also be found in “Bayesian risk assessment for autosomal recessive diseases: fetal echogenic bowel and one or no detectable CFTR mutation”4 in which we delineate how to incorporate into risk calculations information such as the presence of an independent risk factor from genetic test results, genetic test results on either or both of the parents, the ethnic background of each parent, the overall mutation detection rate for each parent’s ethnicity, and the frequency of a mutation, if detected, among all disease alleles for a particular ethnicity.

Section 1: Introduction to Bayesian Analysis

Reverend Thomas Bayes first described the theorem named after him in an essay on “the doctrine of chances,” published posthumously in 1763, and republished in 1958.5 Analyses based on Bayes’ theorem are routinely applied to calculate probabilities in a wide variety of circumstances, not limited to medicine or genetics. In genetic testing, Bayesian analysis is commonly used to calculate genetic risks in complex pedigrees, and to calculate the probability of having or lacking a disease-causing mutation after a negative test result is obtained. Here, we introduce Bayesian analysis with two simple, concrete examples. In subsequent sections, we will discuss the general principles illustrated by these examples and apply these principles to more complex scenarios.

Bayesian Analysis Using Pedigree Information

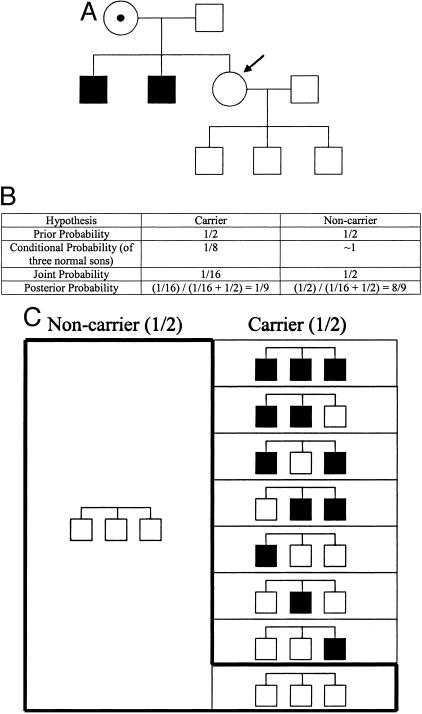
Consider the pedigree shown in Figure 1A, in which the two brothers of the consultand (the consultand is indicated by the arrow) have Kennedy disease [X-linked spinal and bulbar muscular atrophy, On-line Mendelian Inheritance in Man (OMIM) No. 300377], which is caused by a CAG trinucleotide expansion in the androgen receptor (AR) gene (OMIM No. 310200). Because both of the consultand’s brothers are affected, we assume that the consultand’s mother is an obligate carrier of a disease allele. Before learning that the three consultand’s sons are unaffected, we would say that the probability or risk of her being a carrier like her mother is 1/2. This is because there is a 1/2 chance that she will inherit the normal X chromosome from her mother and a 1/2 chance that she will inherit the X chromosome with the disease allele. If we now take into account the fact that she has three unaffected sons, how does the consultand’s carrier risk change?

Figure 1.

A: A pedigree of a family with individuals affected with Kennedy disease (see text). B: The Bayesian analysis for A. C: A schematic representation of the Bayesian analysis of B. Pedigrees shown in the boxes represent the third generation of the pedigree in A. Each small box to the right represents 1/16 of the total area.

Bayesian analysis starts with mutually exclusive hypotheses, usually two (but sometimes three or more). In this example, the first hypothesis is that the consultand is a carrier and the second hypothesis is that she is a non-carrier. We generally set up our Bayesian analyses in the form of a table, as shown in Figure 1B, with a separate column for each hypothesis. The first row of a Bayesian analysis table contains what is referred to as the “prior” probability for each hypothesis. In this example, the prior probabilities are the probability that she is a carrier (1/2), and the probability that she is a non-carrier (also 1/2), prior to taking into account the subsequent information that she has three unaffected sons.

The second row of a Bayesian analysis table contains what is referred to as the “conditional” probability for each hypothesis. To determine the conditional probability for each hypothesis, we ask the following question: what is the probability that the subsequent information would occur if we assume that that hypothesis is true? In this example, the subsequent information is that the consultand has three unaffected sons. Thus, the conditional probabilities are the probability that the consultand would have three unaffected sons under the assumption (or “condition”) that she is a carrier, and the probability that she would have three unaffected sons under the assumption (or “condition”) that she is a non-carrier. If we assume that she is a carrier, the probability that she would have three unaffected sons is 1/2 × 1/2 × 1/2 = 1/8. This is because she would have to have passed the normal X chromosome three times in succession, each time with a probability of 1/2. If we assume that she is a non-carrier, the probability that she would have three unaffected sons is ∼1, since only in the event of a rare de novo mutation would a non-carrier have anything but unaffected sons. Thus, the conditional probabilities in this example are 1/8 and 1 (Figure 1B).

The next row of a Bayesian analysis table contains what is referred to as the “joint” probability for each hypothesis. The joint probability for each hypothesis is simply the product of the prior and conditional probabilities for that hypothesis, ie, the probability of a particular hypothesis and the subsequent information. For the first hypothesis in this example, ie, that the consultand is a carrier, the joint probability is the prior probability that she is a carrier, times the conditional probability that a carrier would have three normal sons, or 1/2 × 1/8 = 1/16 (Figure 1B). For the second hypothesis in this example, ie, that the consultand is a non-carrier, the joint probability is the prior probability that she is a non-carrier, times the conditional probability that a non-carrier would have three normal sons, or 1/2 × 1 = 1/2 (Figure 1B).

The last row of a Bayesian analysis table contains what is referred to as the “posterior” probability for each hypothesis. The posterior probability for each hypothesis is the probability that each hypothesis is true after (or “posterior” to) taking into account both prior and subsequent information. To calculate the posterior probability for each hypothesis, one simply divides the joint probability for that hypothesis by the sum of all of the joint probabilities. In this example, the posterior probability that the consultand is a carrier is the joint probability for the first hypothesis (1/16), divided by the sum of the joint probabilities for both hypotheses (1/16 + 1/2 = 9/16), or 1/16 ÷ 9/16 = 1/9. The posterior probability that the consultand is a non-carrier is the joint probability for the second hypothesis (1/2 = 8/16), divided by the sum of the joint probabilities for both hypotheses (1/16 + 1/2 = 9/16), or 8/16 ÷ 9/16 = 8/9. Thus, taking into account the prior family history, and the subsequent information that she has three unaffected sons, the probability that the consultand is a carrier is 1/9 (Figure 1B).

We illustrate the preceding example graphically in Figure 1C. The total area of the figure represents the total prior probabilities, ie, 1. The right half of the figure represents the prior probability that the consultand is a carrier (ie, 1/2), and the left half represents the prior probability that the consultand is a non-carrier (also 1/2). Under the hypothesis that the consultand is a carrier, there are eight possibilities for three sons: all three sons affected, only the first and second sons affected, only the first and third sons affected, only the second and third sons affected, only the first son affected, only the second son affected, only the third son affected, and all three sons unaffected. The area of the small rectangle that contains three unshaded squares (for three unaffected sons) comprises 1/8 of the right (carrier) half of the figure and represents the conditional probability of three normal sons under the hypothesis that the consultand is a carrier. The area of this small rectangle is 1/16 of the total area and therefore also represents the joint probability that the consultand is a carrier (1/2), and that as a carrier she would have three normal sons (1/8), or 1/2 × 1/8 = 1/16.

Under the hypothesis that the consultand is a non-carrier, there is essentially only one possibility for three sons: all three sons unaffected. The area of the larger rectangle that contains three unshaded squares (for three unaffected sons) comprises all of the non-carrier half of the figure and represents the conditional probability of three normal sons under the hypothesis that the consultand is a non-carrier. The area of this larger rectangle is 1/2 of the total area and therefore also represents the joint probability that the consultand is a non-carrier (1/2), and that as a non-carrier she would have three normal sons (∼1), or 1/2 × 1 = 1/2. The area of the “L-shaped” box, which is demarcated by a bold line, comprises the areas of the small rectangle with three unshaded squares (for three unaffected sons) and the larger rectangle with three unshaded squares (for three unaffected sons). The L-shaped box represents the sum of the joint probabilities, or 9/16 of the total figure.

Because the consultand has three unaffected sons, the area of the L-shaped box represents the only component of the prior probabilities that we must consider to determine the posterior probability that the consultand is a carrier. For example, taking into account that all three of the consultand’s sons are unaffected, Bayesian analysis allows us to exclude 7/16 of the prior probabilities, those that include one or more affected sons, from consideration. (Note that this explains why the joint probabilities sum to less than one.) The posterior probability that the consultand is a carrier is therefore the area of the small rectangle with three unshaded squares (for three unaffected sons) divided by the area of the entire L-shaped box, which represents the only probabilities relevant to the consultand’s risk, or 1/16 ÷ 9/16 = 1/9. Likewise, the posterior probability that the consultand is a non-carrier is the area of the larger rectangle with three unshaded squares (for three unaffected sons) divided by the area of the entire L-shaped box, or 8/16 ÷ 9/16 = 8/9.

Bayesian Analysis Using Genetic Test Results

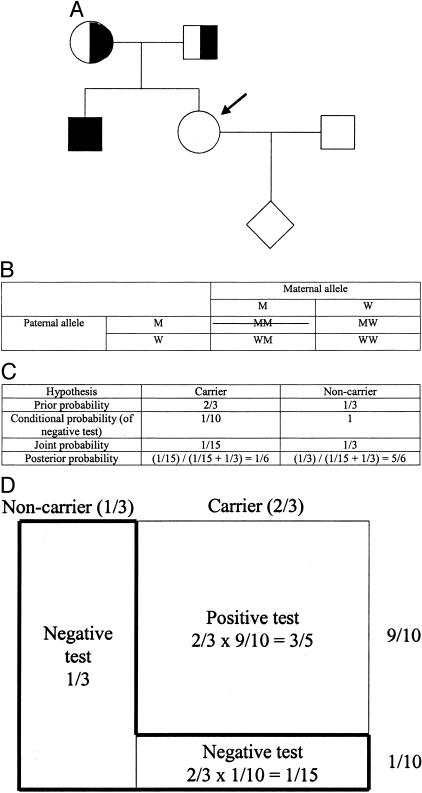
In the first example above, we used information from the pedigree to modify the carrier risk. In the second example, we use information from a test result to modify the prior risk. Consider the pedigree shown in Figure 2A, in which the consultand is pregnant with her first child and has a family history of cystic fibrosis (CF). CF is caused by mutations in the cystic fibrosis transmembrane conductance regulator (CFTR) gene [OMIM Nos. 602421; 219700 (CF)]. The consultand is an unaffected European Caucasian and her brother died years earlier of complications of CF. She undergoes carrier testing for the 25 mutations recommended by the American College of Medical Genetics (ACMG) CF screening guidelines,6,7 which detects 90% of disease alleles in European Caucasians. She tests negative for all 25 mutations. What is her carrier risk?

Figure 2.

A: A pedigree of a family with an individual affected with CF (see text). B: Possible genotypes of the sibling of the affected before genetic testing. The crossed box is excluded based on the fact that the sibling is unaffected. Abbreviations: M, mutant; W, wild-type. C: The Bayesian analysis for A. D: A schematic representation of the Bayesian analysis of C (see text). Note that the areas of the boxes are not proportional to the actual probabilities.

As in the first example, the two hypotheses in the Bayesian analysis are that the consultand is a carrier and that she is a non-carrier. The prior probability that she is a carrier is 2/3, and the prior probability that she is a non-carrier is 1/3 (Figure 2B). (Because the consultand is unaffected, she could not have inherited disease alleles from both parents. Three equal possibilities remain: she could have inherited a disease allele from her father and a normal allele from her mother, she could have inherited a disease allele from her mother and a normal allele from her father, or she could have inherited a normal allele from each parent. In 2/3 of these scenarios, she would be a carrier; see Figure 2B).

As in the first example, to determine the conditional probability for each hypothesis, we ask the following question: what is the probability that the subsequent information would occur if we assume that that hypothesis is true? In this example, the subsequent information is that the consultand tests negative for all 25 mutations in the testing panel. Thus, the conditional probabilities are the probability that the consultand would test negative under the assumption (or “condition”) that she is a carrier, and the probability that she would test negative under the assumption (or “condition”) that she is a non-carrier. If we assume that she is a carrier, the probability that she would test negative is 1/10. This is because the test detects 90% of European Caucasian carriers. If we assume that she is a non-carrier, the probability that she would test negative is ∼1. Thus, the conditional probabilities in this example are 1/10 and 1 (Figure 2C).

Again, the joint probability for each hypothesis is simply the product of the prior and conditional probabilities for that hypothesis. For the first hypothesis in this example, ie, that the consultand is a carrier, the joint probability is the prior probability that she is a carrier (2/3), times the conditional probability that a carrier of European Caucasian ancestry would test negative (1/10), or 2/3 × 1/10 = 1/15 (Figure 2C). For the second hypothesis in this example, ie, that the consultand is a non-carrier, the joint probability is the prior probability that she is a non-carrier (1/3), times the conditional probability that a non-carrier would test negative, (1) or 1/3 × 1 = 1/3 (Figure 2C). Again, to calculate the posterior probability for each hypothesis, one simply divides the joint probability for that hypothesis by the sum of all of the joint probabilities. In this example, the posterior probability that the consultand is a carrier is the joint probability for the first hypothesis (1/15), divided by the sum of the joint probabilities for both hypotheses (1/15 + 1/3 = 2/5), or 1/15 ÷ 2/5 = 1/6. The posterior probability that the consultand is a non-carrier is the joint probability for the second hypothesis (1/3), divided by the sum of the joint probabilities for both hypotheses (2/5), or 5/6.

We illustrate the preceding example graphically in Figure 2D. The total area of the figure represents the total prior probabilities. The right 2/3 of the figure represents the prior probability that the consultand is a carrier, and the left 1/3 represents the prior probability that the consultand is a non-carrier. Under the hypothesis that the consultand is a carrier, there are two possibilities for the test result: positive or negative. The area of the small rectangle on the lower right comprises 1/10 of the carrier 2/3 of the figure and represents the conditional probability of a normal test result under the hypothesis that the consultand is a carrier. The area of this small rectangle is 1/10 × 2/3 = 1/15 of the total area and therefore also represents the joint probability that the consultand is a carrier (2/3), and that as a European-Caucasian carrier she would test negative for all 25 mutations (1/10), or 2/3 × 1/10 = 1/15.

Under the hypothesis that the consultand is a non-carrier, there is essentially only one possibility for the test result, which is negative. The area of the rectangle that comprises all of the non-carrier 1/3 of the figure represents the conditional probability of a negative test result under the hypothesis that the consultand is a non-carrier. The area of this rectangle is 1/3 of the total area and therefore also represents the joint probability that the consultand is a non-carrier (1/3), and that as a non-carrier she would test negative (∼1), or 1/3 × 1 = 1/3. The area of the “L-shaped” box, which is demarcated by a bold line, represents the sum of the joint probabilities, or 2/5 (= 1/3 + 1/15) of the total area of the boxes.

Because the consultand tested negative, the area of the L-shaped box represents the only component of the prior probabilities that we must consider to determine the posterior probability that the consultand is a carrier. For example, taking into account that she tested negative, Bayesian analysis allows us to exclude 3/5 of the prior probability, that portion comprising a positive test result, from consideration. (Note again that this explains why the joint probabilities sum to less than one.) The posterior probability that the consultand is a carrier is therefore the area of the small rectangle at the lower right divided by the area of the L-shaped box, which represents the only probabilities relevant to the consultand’s risk, or 1/15 ÷ 2/5 = 1/6. Likewise, the posterior probability that the consultand is a non-carrier is the area of the larger rectangle on the left divided by the area of the L-shaped box, or 1/3 ÷ 2/5 = 5/6.

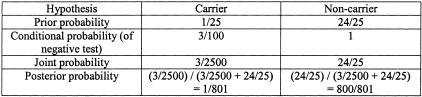
Note that in Bayesian analysis, if one can determine the correct prior and conditional probabilities, all of the rest is simple calculation. We recommend setting up a spreadsheet with four rows (labeled “prior probability,” “conditional probability,” “joint probability,” and “posterior probability”) and two columns (labeled “carrier” and “non-carrier”) to simplify calculations of the type described in the two examples above. Note also that the prior and conditional probabilities often depend on ethnicity. For example, suppose in the second example that the consultand’s husband is Ashkenazi Jewish, that he has no family history of CF, and that he tests negative for all 25 mutations in the panel. What is his carrier risk?

The carrier risk in Ashkenazi Jewish populations, and therefore the husband’s prior carrier risk in the absence of a family history, is approximately 1/25. Thus his prior probability of being a non-carrier is 24/25. The ACMG screening guidelines panel of 25 mutations detects 97% of CF mutations in Ashkenazi Jewish populations, so the conditional probability of a negative test, under the hypothesis that he is a carrier, is 3/100. Under the hypothesis that he is a non-carrier, the conditional probability of a negative test is ∼1. (This is generally the case in genetic testing, since non-carriers by definition lack mutations in the disease gene in question and hence, unless there are technical problems, should essentially always test negative.) The Bayesian analysis table for this example is shown in Figure 3. The joint probabilities are simply the products of the prior and conditional probabilities, and the posterior probabilities derive from each joint probability divided by the sum of the joint probabilities. The husband’s posterior carrier risk is 1/801.

Figure 3.

Bayesian analysis for an Ashkenazi Jewish individual without a family history of CF who tests negative for mutations in CFTR.

What is the risk that the fetus is affected with CF? Before testing, the risk was the prior probability that the mother was a carrier (2/3), times the prior probability that the father was a carrier (1/25), times the probability that two carriers would both pass a disease allele (1/4), or 2/3 × 1/25 × 1/4 = 1/150. After testing, the risk is the posterior probability that the mother is a carrier (1/6), times that posterior probability that the father is a carrier (1/801), times the probability that two carriers would both pass a disease allele (1/4), or 1/6 × 1/801 × 1/4 = ∼1/19,000.

Bayesian Analysis Using Test Results Other than Genetic Test Results

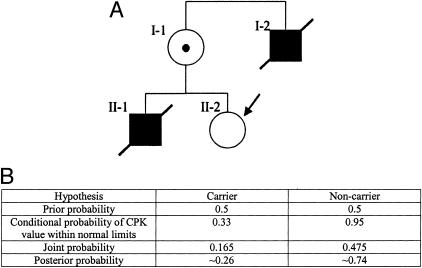
In the third example, we use information from a test result other than a genetic test result to modify the prior risk. The principle is the same as in cases where genetic test results are available. The conditional probabilities depend on the sensitivity and specificity of the test, whether genetic or non-genetic (eg, biochemical). Consider the pedigree shown in Figure 4A, in which the maternal uncle (I-2) and brother (II-1) of the consultand (II-2) were affected with Duchenne muscular dystrophy (DMD), a severe X-linked recessive disease caused by mutations in the DMD gene (OMIM Nos. 300377; 310200). With an affected brother and son, the consultand’s mother (I-1) is essentially an obligate carrier. In addition, I-1 has an elevated level of creatine phosphokinase (CPK) in her serum, which occurs in 67% of DMD carrier women.2 Hence, the sensitivity of the serum CPK test for carrier status in women is 67%. Since 5% of non-carrier women have an abnormal serum CPK,2 the specificity of the serum CPK test for carrier status in women is 95%.

Figure 4.

A: A pedigree of a family with two individuals affected with DMD (see text). B: The Bayesian analysis for A.

Before testing, the carrier risk for II-2 is 50%. If her serum CPK is within normal limits, what is the posterior probability that she is a carrier? The Bayesian analysis for this case is shown in Figure 4B. Because the sensitivity of the serum CPK test for carrier status is 67%, the conditional probability that the consultand would test negative under the assumption that she is a carrier is 33%. Because the specificity of the serum CPK test for carrier status is 95%, the conditional probability that the consultand would test negative under the assumption that she is a non-carrier is 95%. (This contrasts with an essentially 100% specificity in genetic testing; ie, individuals without mutations in a disease gene generally do not test positive. The relationship between conditional probabilities, and the sensitivity and specificity of laboratory tests, is discussed further in “Bayesian Analysis, Contingency Tables, and Odds Ratios” below.)

Again, the joint probability for each hypothesis is the product of the prior and conditional probabilities for that hypothesis, and the posterior probability for each hypothesis is the joint probability for that hypothesis divided by the sum of all of the joint probabilities. In this example, the posterior probability that the consultand is a carrier is the joint probability for the first hypothesis (0.165), divided by the sum of the joint probabilities for both hypotheses (0.165 + 0.475 = 0.640), or 0.165 ÷ 0.640 = ∼0.26. Hence if the consultand had a son, his chance of being affected with DMD would be ∼0.13.

Bayesian Analysis Generalized

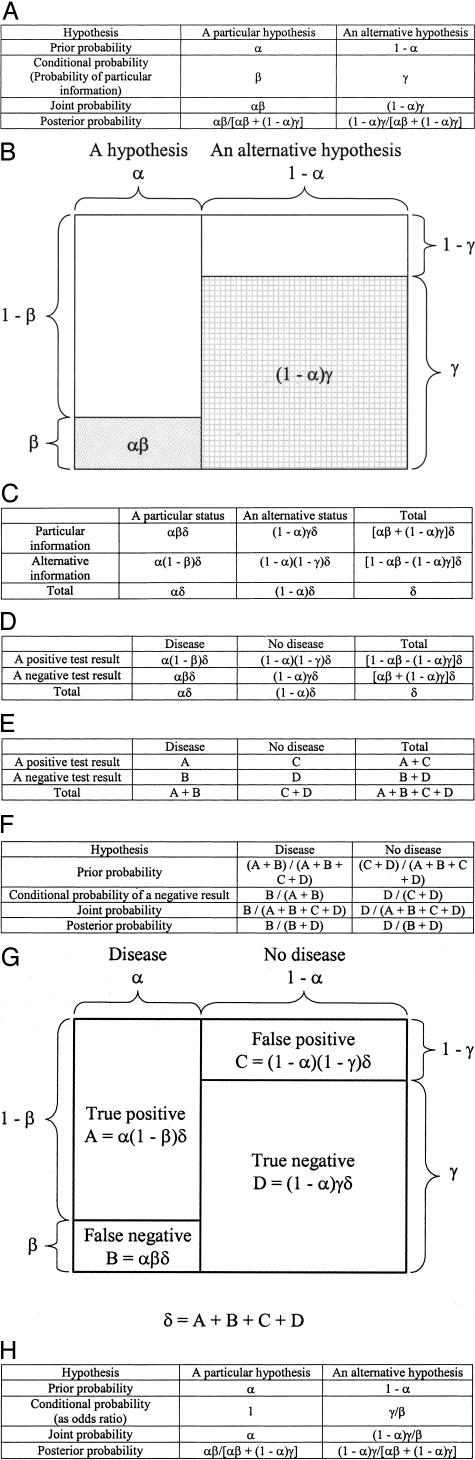
A generalized Bayesian analysis is shown in Figure 5A. The prior probability of a particular hypothesis is designated as α, and the prior probability of an alternative hypothesis is designated as (1 - α). The probability that specific subsequent information would occur if we assume that the particular hypothesis is true (ie, the conditional probability for the particular hypothesis), is designated as β. The probability that specific subsequent information would occur if we assume that the alternative hypothesis is true (ie, the conditional probability for the alternative hypothesis), is designated as γ. The calculations of the joint and posterior probabilities for each hypothesis are shown in Figure 5A.

Figure 5.

A: Generalized Bayesian analysis. B: A schematic representation of generalized Bayesian analysis. C: Generalized contingency table. D and E: Contingency table for “Disease” and “Test results.” F: Bayesian analysis on negative test result. G: A schematic representation of Bayesian analysis (F). H: Bayesian analysis using odds ratios as conditional probabilities. Note that results are exactly the same as with the conventional conditional probabilities (A).

The generalized Bayesian analysis of Figure 5A is illustrated graphically in Figure 5B. The total area of the figure represents the total prior probabilities, ie, 1. The left side of the figure represents the particular hypothesis, and the right side of the figure represents the alternative hypothesis. The stippled box in the lower left represents the probability that specific subsequent information would occur if we assume that the particular hypothesis is true (ie, the conditional probability for the particular hypothesis), or β. The cross-hatched box in the lower right represents the probability that specific subsequent information would occur if we assume that the alternative hypothesis is true (ie, the conditional probability for the alternative hypothesis), or γ. The unfilled boxes in the upper left and upper right represent the probabilities that specific subsequent information would not occur if we assume that the particular and alternative hypotheses are true, respectively.

Bayesian Analysis, Contingency Tables, and Odds Ratios

The generalized Bayesian analysis in Figure 5A corresponds to a contingency table of population data (Figure 5C), where δ indicates the total population in question. In contrast to the Bayesian analysis table, which deals with probabilities for a particular individual, the contingency table is based on population data. Hence “status” replaces “hypothesis.” “Particular information” may be a positive or negative test result. When test results replace “information,” and “Disease” and “No disease” replace the two “statuses,” Figure 5C becomes Figure 5D, which is a contingency table used frequently in laboratory medicine for the evaluation of test performance. In these four figures, α equals the prevalence of a particular disease in the testing population, which is the prior probability in the generalized Bayesian analysis. (1 - β) and γ equal the sensitivity and specificity of the test, respectively. Genetic risk is most often assessed to determine the probability of being affected by a disease, or of being a carrier, after a negative test result. Note that, given a negative test result, the posterior probability of “Disease” as the particular hypothesis in the generalized Bayesian analysis of Figure 5A equals (1 − negative predictive value) in Figure 5D. In other words, Bayesian analysis determines the positive or negative predictive value of a particular test in a particular population.

The close connection between Bayesian analysis and contingency tables is illustrated further in Figure 5E5F5G, in which we have simplified the nomenclature as follows: α(1 - β)δ = A, αβδ = B, (1 - α)(1 - γ)δ = C, and (1 - α)γδ = D. Odds ratios, or relative conditional probabilities, can replace conditional probabilities in Bayesian analyses. An odds ratio implies that a particular condition favors one or the other hypothesis. A generalized example of odds ratios in Bayesian analysis is shown in Figure 5H, using the odds ratios 1 and γ/β for the two hypotheses. Note that the posterior probabilities are exactly the same as with conventional conditional probabilities (Figure 5A).

Unified Approach to Bayesian Analysis

Hodge presented a unified approach to Bayesian analysis.8 The approach is visual, and easy to understand. Essentially, it allows each joint probability to be evaluated separately by depicting each possible combination of probabilities (ie, each column at the bottom of Bayesian analysis tables) as a figure, typically a pedigree. Therefore, one needs to construct as many figures as the number of probability permutations. In combination with the methods illustrated herein, Hodge’s approach may be useful as an introduction to Bayesian analysis for those unfamiliar with the subject.

Section 2: Basic Principles in Genetic Risk Assessment

Genetic risk refers to the probability of carrying a specific disease-associated mutation, or of being affected with a specific genetic disorder. Genetic risk can be calculated using Bayesian analysis without genetic testing, as illustrated in the first example of Section 1, in which only pedigree information was used. Genetic risks from population data are commonly used as prior probabilities in Bayesian analyses. Genetic test results are usually factored in to calculate posterior probabilities. Clinical presentation can also affect genetic risk. In the sections that follow, we discuss principles of genetic risk assessment relevant to various genetic-testing scenarios.

Important Points to Consider in Genetic Risk Assessment

The prior probability of carrying a particular mutation or mutations often differs considerably among populations, among families, and even among individuals within the same family. The disease-allele distribution of the CFTR gene, for example, varies greatly among different ethnic groups.9 Because posterior probabilities rest in part on prior probabilities, genetic risk assessments must integrate all relevant and available information, including ethnicity, family history, clinical presentations, genetic testing results for other family members, and previous genetic testing results for the consultand. The sensitivity of a genetic test for a particular individual, which determines the conditional probability of a negative result under the hypothesis of carrier or disease status, is frequently altered by additional information. For example, if a non-Hispanic Caucasian consultand, whose sibling is affected with cystic fibrosis, is tested only for the ΔF508 mutation in CFTR the sensitivity of the test is approximately 70%.5,6 Hence the conditional probability of a negative result under the hypothesis of carrier status is approximately 30%. However, suppose that the affected sibling is found to be homozygous for the ΔF508 mutation. Assuming the parents are unaffected, the sensitivity of the test for the consultand increases to essentially 100%. This is because the prior probability of carrying a CFTR mutation comprises the ΔF508 mutation only.

A particular genetic risk assessment is a population-based estimate of probability at a particular point in time, and is subject to modification. This is because population-based data, which determine prior probabilities, and testing methods, which affect sensitivity and/or specificity and thereby determine conditional probabilities, are constantly being updated. In addition, families expand, adding new offspring, and adding new clinical and genetic-testing information relevant to genetic risk assessment. Genetic testing of additional family members, in particular, can dramatically affect genetic risk assessments.3

Analytical or interpretive laboratory errors, which are hopefully rare but may still be unavoidable, obviously affect risk assessments directly. Laboratory errors also affect risk assessments indirectly, by altering estimates of allele distributions, carrier frequencies, etc. Using intuition to estimate genetic risk, even after obtaining specific information from pedigrees and/or genetic testing, has been shown to be misleading.10 Hence, genetic risk should be quantified systematically. Other pitfalls in genetic testing have been discussed in depth elsewhere.11

Single-Gene (Mendelian) Disorders versus Polygenic or Multifactorial Disorders

When several genes (and/or environmental factors) are involved in the pathogenesis of a given disorder (ie, the disorder is polygenic or multifactorial), risk assessment is far from straightforward. Examples include multifactorial disorders such as hypertension, adult-onset diabetes, and various cancers. Population-based data and information on multiple genes are required. Risk assessments for multifactorial disorders have been described elsewhere.1,12,13,14,15

The Hardy-Weinberg Principle in Genetic Risk Assessment

The Hardy-Weinberg principle is often used in genetic risk assessment. The most common scenario is that of an individual who marries into a family with a history of an autosomal recessive disorder. The Hardy-Weinberg principle can be used to estimate the probability that this individual, who lacks a family history of the disorder and is therefore representative of the general population, is a carrier. Assuming Hardy-Weinberg equilibrium, and a disease-allele frequency of q, the carrier frequency of 2(1 − q)q, or approximately 2q if q is sufficiently small, can be derived from the disease frequency, which is equal to q². Thus, if a disease frequency can be determined from population-based data, a disease-allele frequency and a carrier frequency in that particular population can be calculated.

Mendelian Genetics in Genetic Risk Assessment

The basic principle of Mendelian genetics is often used in genetic risk assessment, particularly where pedigrees are involved. Simply put, the carrier of a mutation has a 50% probability of passing the mutation to an offspring, and a 50% probability of having received the mutation from a particular parent. Based on this principle, one can estimate the probability of being a carrier by the relatedness of a consultand to an affected family member or obligate carrier. For autosomal recessive diseases, carrier risk decreases by half at each step across a pedigree from the affected family member to the consultand, provided that the carrier frequency in the general population is sufficiently small. For X-linked recessive diseases, carrier risk decreases by half at each step from one female member to another female member in the preceding or successive generation of the pedigree.

If the carrier frequency for an autosomal recessive disorder is not negligible, however, one must also consider the additional carrier risk conferred by mutant alleles different from the mutant alleles present in the index case.

Recessive disorders quite often require genetic risk assessment. Recessive disorders are usually associated with loss-of-function mutations. In addition to being far more common than gain-of-function mutations, loss-of-function mutations tend to be far more diverse, making it nearly impossible to achieve 100% test sensitivity. In the case of CF, where a single mutation (ΔF508) accounts for approximately 70% of all non-Hispanic Caucasian disease alleles, testing for the next most common two-to-three dozen mutations still falls far short of achieving 100% sensitivity. The lack of 100% sensitivity underlies the need for Bayesian analyses of negative carrier-test results. For example, in recessive diseases, there is almost always the inherent possibility of missing a disease-associated mutation. In contrast, dominant or semi-dominant disorders are usually caused by more-specific, gain-of-function mutations, such as the factor V Leiden mutation.

Non-Mendelian Genetics in Genetic Risk Assessment

Non-Mendelian genetics contribute to genetic risk through a number of mechanisms, including de novo (new) mutations and mosaicism. A de novo mutation is a mutation that is absent from the somatic cells of the parents, but present in the somatic cells of the offspring. A de novo mutation may cause a subset of germ cells to have the mutation, ie, isolated germline mosaicism. Germline mosaicism may or may not manifest as a de novo mutation in offspring. The impact of germline mosaicism on genetic risk assessment is described elsewhere.1,16

Non-Mendelian genetics also impact genetic risk assessment through a number of other mechanisms, including genomic instability (anticipation), non-paternity, imprinting (epigenetics), positional effects of two or more genes (which can also be viewed as a multifactorial mechanism), and mitochondrial inheritance. For further reading, we recommend the books by Peter Bridge2 and Ian Young.1

Consanguinity

Consanguinity is particularly important to consider in autosomal recessive disorders. Alleles that are identical because they derive from a single allele present in a common ancestor are defined as being identical by descent (IBD). Alleles that are the same but that derive from two different and apparently unrelated sources are defined as being identical by state (IBS). Consanguineous matings increase the frequency of autozygosity for two mutant alleles that are IBD.

The coefficient of inbreeding (F) is the probability that both alleles at a specific locus are IBD in the child of a consanguineous couple. The coefficient of relationship (R) is the probability that an individual’s allele at a specific locus is IBD to an allele at the same locus in his or her partner due to a consanguineous relationship. Hence, R = 2F. In general, F = Σ1/2^{(n − 1)}, in which “n” is the number of steps (generations) from an ancestor down to the child through one parent and then back up to the same ancestor via the other parent.17 Σ indicates the sum of 1/2^{(n − 1)} for all common ancestors. For example, in a first-cousin couple, where there are two common ancestors, F = 1/2^{(6 − 1)} + 1/2^{(6 − 1)} = 1/16. When the common ancestor is inbred, the equation F = Σ1/2^{(n − 1)} (1 + FA) is used, where FA is the coefficient of inbreeding for the ancestor.

One of the basic prerequisites for the Hardy-Weinberg equilibrium is random mating. Consanguinity can be thought of as a deviation from the assumption of random mating, leading to over-representation of homozygous genotypes. For a two-allele system, A and a, with allele frequencies of p and q, respectively, the distribution of genotypes in a randomly mating population is p², 2pq, and q² for AA, Aa, and aa, respectively. With consanguinity, genotype frequencies change to p² + Fpq, 2pq (1 − F), and q² + Fpq for AA, Aa, and aa, respectively.2 Thus, the risk of homozygosity for mutant alleles in a child of a consanguineous couple, relative to that in a child of a non-consanguineous couple, is (q² + Fpq)/q² = 1 + Fp/q. For example, in a first-cousin union, the relative risk of a child being affected with spinal muscular atrophy (q = 0.01), relative to that of a child in the randomly mating general population, is approximately 7.2, including an approximately 6.2-fold increased risk of being IBD for disease alleles.

Concluding Remarks

Genetic risk assessment is an integral part of genetic counseling and testing. Bayesian analysis plays a central role in genetic risk assessment. Genetic risk should be assessed as accurately as possible, using all available information at a particular point in time, from the pedigree and/or from genetic testing. Although the technologies for genetic testing will continue to change, genetic risk assessment will remain a fundamental aspect of genetic testing.