Abstract
In recent years there have been a number of microarray expression studies in which different types of tumors were classified by identifying a panel of differentially expressed genes. Immunohistochemistry is a practical and robust method for extending gene expression data to common pathological specimens with the advantage of being applicable to paraffin-embedded tissues. However, the number of assays required for successful immunohistochemical classification remains unclear. We propose a simulation-based method for assessing sample size for an immunohistochemistry investigation after a promising gene expression study of human tumors. The goals of such an immunohistochemistry study would be to develop and validate a marker panel that yields improved prognostic classification of cancer patients. We demonstrate how the preliminary gene expression data, coupled with certain realistic assumptions, can be used to estimate the number of immunohistochemical assays required for development. These assumptions are more tenable than alternative assumptions that would be required for crude analytic sample size calculations and that may yield underpowered and inefficient studies. We applied our methods to the design of an immunohistochemistry study for glioma classification and estimated the number of assays required to ensure satisfactory technical and prognostic validation. Simulation approaches for computing power and sample size that are based on existing gene expression data provide a powerful tool for efficient design of follow-up genomic studies.
Although gene expression profiling has proven to be useful as a discovery tool in cancer, and has been used to classify tumor types by identifying a panel of differentially expressed genes, immunohistochemistry will be useful as a validation and implementation tool. Immunohistochemistry, particularly on tissue microarrays, has been cited as “an excellent means” for evaluating large numbers of tissue samples after gene expression profiling, and has been used as the primary means of validating microarray data in more than 50 publications as of late 2002.1 In the long run, immunohistochemistry is also a highly practical approach because it is used in pathology laboratories worldwide and it does not typically require frozen tissue. An essential component of study design for immunohistochemistry panel development is that of sample size; how many assays should be developed to accurately differentiate among classes initially defined by the gene expression data?
Appropriate and well-planned study designs are essential to ensure optimal use of scarce resources, to avoid obvious biases, and to answer the scientific questions of interest. Once a design is selected, the details of the design must be determined. Perhaps most important among these details is the required sample size. Sample size typically refers to the number of participants in a study, but could also refer to the number of variables to be measured in the study, such as genes or immunohistochemical assays. Analytic sample size calculations for study designs in which there are only a few outcomes for each patient and in which the distribution of the outcomes is known appear frequently in the statistics literature. Many of these calculations have been incorporated into statistical software packages for easy implementation (eg, STATA, PASS, EaST). They are typically based on assumptions regarding the general form of the distribution of the data, coupled with specific parameter estimates that define the relevant version of the distribution for application to the data at hand. Under these kinds of assumptions, in addition to a determination of the magnitude of the effect size (eg, treatment difference) of interest, sample size, and power calculations have been derived even for complicated study designs and analysis plans.
In some experimental settings, however, such as that of genetic analyses involving thousands of genes, simple methods for study design are not available. Discussions on study design for gene expression experiments2,3,4 have focused on the considerations involved in the selection of design features that most efficiently satisfy the scientific objectives. Sample size calculations for gene expression experiments have been addressed by only a few authors.2,3 These calculations are difficult for a number of reasons:2 the levels of variability in expression are unknown and differ for each gene, the magnitudes of effects of interest (eg, important differences in gene expression levels) are unknown and differ for each gene, and there is dependence among expression levels across genes.
Importantly, sample size concerns persist after the initial gene expression studies, because validation by follow-up studies, such as immunohistochemistry, are required. As for gene expression data, simple distributional assumptions and corresponding sample size calculations are not available. However, the gene expression data from the initial study serve as an extremely useful resource for this purpose. These data allow for the use of more realistic assumptions in the evaluation of sample size than would otherwise be possible.
To assess the number of immunohistochemistry assays that must be developed, we propose simulation studies for each component of the planned study design that are based on the expression data from the originally profiled tumors. These simulations relate the number of assays required to measures of technical and prognostic validation. Thus, the smallest number of assays necessary to meet the goals for validation can be determined. To conduct these studies, a few key assumptions are required to link the existing gene expression data to the, as yet, unobserved immunohistochemistry data and to link the patients for whom there is gene expression data to the future patients to whom the immunohistochemistry assays will be applied. The inputs to these assumptions (eg, specific probabilities used in probability models) should be based on external sources of data and the experience of the laboratory. The simulation studies should be used to further evaluate the sensitivity of the calculations to the inputs about which there is uncertainty. For illustration, we apply our methods to the design of a future study for immunohistochemistry panel development for the classification of gliomas.
Materials and Methods
Existing Data
Two data sets were available to us for the sample size calculation for the planned immunohistochemistry study. The first was from our gene expression study,5 in which we used the Affymetrix system to assay ∼12,000 genes in 50 adult gliomas (28 glioblastomas and 22 anaplastic oligodendrogliomas). Among these, 21 had classic textbook histology (14 glioblastomas and 7 anaplastic oligodendrogliomas) and 29 had nonclassic histology (14 glioblastomas and 15 anaplastic oligodendrogliomas). We refer to these cases as the Nutt et al cases. The second data set was from a detailed clinical database of all glioma patients seen at the Brain Tumor Center at Massachusetts General Hospital (MGH). The relevant data that are currently available from this source are times to death or last follow-up for 308 glioblastomas and 51 oligodendrogliomas. We refer to these cases as the MGH cases. For future analyses, we expect to have available from MGH 135 classic glioblastomas, 23 classic oligodendrogliomas, and similar numbers of nonclassic cases, all with sufficient amounts of tissue and follow-up.
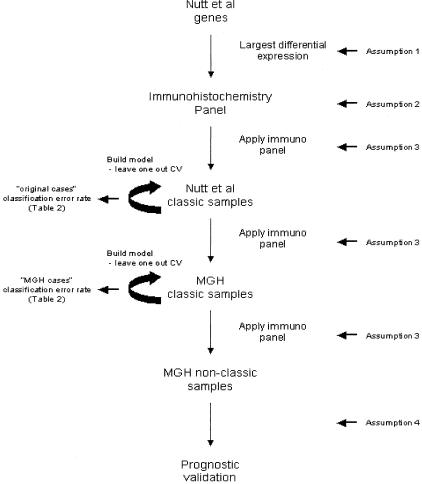
Design of Future Immunohistochemistry Study (Figure 1)
Figure 1.
Schematic of study design using original Nutt et al data and new MGH data. Locations in the design where the assumptions are invoked are indicated.
The design of the future immunohistochemistry study is based on the availability of glioma samples and the need to logically link the immunohistochemistry study to the completed gene expression study. In the immunohistochemistry study, immunohistochemical markers will be developed for the smallest number of expressed proteins capable of distinguishing the classic oligodendrogliomas from the classic glioblastomas. Although the current best model5 is based on 20 features/19 genes from our gene expression study, it is likely that more features/genes will initially require consideration to obtain enough immunohistochemical markers for accurate classification. This will be done by initially considering a larger number of genes that displayed the largest differential expression between the classic oligodendrogliomas and glioblastomas. The first step will be to apply this candidate immunohistochemical marker panel to the classic cases in the Nutt et al data set in the same way that the differentially expressed genes were applied to those cases to build a classification model in our original gene expression analysis.5 The supervised learning technique of k-nearest neighbors (k-NN),6 coupled with leave-one-out cross-validation techniques,7 will be used to build a glioma classification scheme based on the marker panel. This will serve to validate that the immunohistochemical panel is recognizing the classic molecular signature. Such validation is necessary because there may not be a simple relationship between overexpression at the RNA and protein levels and because there may be differences in sensitivity between the detection approaches. The measure of technical validation that will be derived from this analysis is the cross-validation error rate.
Next, the future study will use the candidate panel to build a classification rule through the same techniques of supervised learning for the classic MGH cases. This will serve to validate that the immunohistochemical panel that was selected on the basis of the gene expression data from the Nutt et al classic cases is able to recognize the classic molecular signature among the MGH cases for which we do not have gene expression data. The MGH cases will serve as an independent test set on which to assess the prediction error rate of the panel (the originally profiled cases do not comprise an independent set as they directed the choice of genes for which the panel was developed). Again, the measure of technical validation that will be derived from this analysis is the cross-validation error rate.
After testing the ability of the immunohistochemical panel to identify classic glioblastomas and classic oligodendrogliomas in these two sets, we will apply the derived classification scheme to the nonclassic MGH cases. The measures of prognostic validation that will be derived from this analysis are the estimated hazard ratio for the marker panel-based oligodendrogliomas versus the marker panel-based glioblastomas, after adjusting for pathological classification and the power to detect a hazard ratio that is significantly different from one (indicating added predictive power of the marker panel). A schematic of this design is displayed in Figure 1.
Simulation Studies for Sample Size Calculation
To assess the number of immunohistochemistry assays that we will need to develop in the planned study, we conducted simulation studies of each component of the planned study. We conducted our simulations in the freely available statistical programming language, R (http://www.r-project.org), and used 5000 repetitions. The simulation program is available for downloading at http://www.biostat.harvard.edu/∼betensky/papers.html.
Assumptions
To conduct the simulation studies, we were required to make a few key assumptions to link our existing gene expression data to the, immunohistochemistry data (to be generated) and to link the patients for whom we have gene expression data to the patients to whom we will be applying the immunohistochemistry assays. These assumptions (explained below and summarized in Table 1) are based on external sources and the past experience of our group. In our view, they are good approximations to the truth, and are far preferable to the alternative assumptions of normally distributed gene expression values, independence of gene expression values across genes, and homogeneous parameter values for the underlying distributions, for example, which are required by other proposed methods. The actual numerical inputs to these assumptions can and should be varied in multiple runs of the simulation study, especially where there is uncertainty as to their values. We have indicated these inputs in bold typeface.
Table 1.
Assumptions
| 1. Selection of genes: |
| A gene whose mRNA was differentially expressed will exhibit differential protein expression with 50% probability. |
| 2. Optimization of antibodies: |
| We will have 75% success rate optimizing commercially available antibodies for immunohistochemical assays on formalin-fixed paraffin-embedded tissues. |
| 3. Individual assay outcomes: |
| For a given gene and subject and mRNA expression level, probabilities of immunohistochemistry outcomes relative to the median expression level for that gene are: |
| IHC outcome | mRNA ≥125% of median | mRNA ≤75% of median | MRNA within 25% of median |
|---|---|---|---|
| 0 | 0% | 75% | 0% |
| 1+ | 5% | 15% | 25% |
| 2+ | 5% | 5% | 50% |
| 3+ | 15% | 5% | 25% |
| 4+ | 75% | 0% | 0% |
| 4. Comparability of subjects: |
| The subjects for whom there is mRNA expression data are comparable to the subjects for whom there will be immunohistochemistry data. |
Boldfaced numbers are also assumptions and can be varied.
Assumption 1 (Selection of Genes)
There is most likely not a simple one-to-one relationship between mRNA expression as detected by the Affymetrix system and immunohistochemistry to detect individual proteins. For one, there may be complex relationships between mRNA and protein levels due to posttranscription cellular regulation and turnover of proteins. Two, biological levels may not always be represented equivalently by the assays because there may be sensitivity differences between the Affymetrix system and immunohistochemistry. In this regard, recent informal estimates have suggested gross concordance of changes in mRNA and protein expression only ∼50% of the time.4 We assume that a gene that was differentially expressed among the classic oligodendrogliomas versus the classic glioblastomas will likewise exhibit differential protein expression with 50% probability.
Assumption 2 (Optimization of Antibodies)
For selected highly differentially expressed transcripts, we would optimize appropriate antibodies for immunohistochemistry. Given our experience throughout the past decade,8,9,10,11,12,13 and given the wide variety of tissue digestion (eg, different soaps and proteases) and antigen retrieval (eg, microwaving in different buffers and for different times) approaches currently available, we anticipate a high rate of success. We assume that we will have an ∼75% success rate optimizing commercially available antibodies for immunohistochemical assays on formalin-fixed, paraffin-embedded tissues. Issues of quality control are critical for any planned immunohistochemistry study, and our premise is that these have been well established by the laboratory. These include the use of proper controls and the interpretation of immunohistochemical intensities.
Assumption 3 (Individual Assay Outcomes)
We need to simulate immunohistochemistry data, for example a set of immunopositivity scores on a 0 to 4+ scale, for each patient for whom we have gene expression data. To do this, we need to posit a probability model that links the two kinds of data. We roughly estimate the inputs of this model using unpublished supplementary data from Shipp and colleagues14 and from a small subset of our samples (six cases). We assume that: 1) if a patient’s gene expression value is at least 25% greater than the median level for that gene, their corresponding immunohistochemical assay outcome will be scored as 4+ with 75% probability, 3+ with 15% probability, 2+ with 5% probability, 1+ with 2.5% probability, and 0 with 0% probability; 2) if a patient’s gene expression value is at least 25% less than the median level for that gene, their corresponding immunohistochemical assay outcome will be scored as 4+ with 0% probability, 3+ with 2.5% probability, 2+ with 5% probability, 1+ with 15% probability, and 0 with 75% probability; and 3) if a patient’s gene expression value is within 25% of the median level for that gene, their corresponding immunohistochemical assay outcome will be scored as 4+ with 0% probability, 3+ with 25% probability, 2+ with 50% probability, 1+ with 25% probability, and 0 with 0% probability. Alternatively, if the actual intensity of expression were of interest for analysis, the probability model could be revised to handle a continuous outcome. For example, immunohistochemical expression and gene expression, or some transformation of them, could be assumed to be correlated normal variables.
Assumption 4 (Comparability of Patients)
Assumption 3 provides us with a link between the existing gene expression data of Nutt et al and the planned immunohistochemistry data for those same patients. It does not, however, provide us with a way of generating immunohistochemistry data for the MGH patients (for whom we do not have gene expression data). If the MGH cases are sufficiently similar to the Nutt et al cases, we will be able to use the gene expression data from the Nutt et al cases to infer gene expression data for the MGH cases. We are able to partially test this hypothesis with respect to the survival distributions because we currently do have available the pathological diagnoses and survival data for the current MGH cases, as well as for the Nutt et al cases. In fact, the survival distribution of the Nutt et al oligodendroglioma cases was not significantly different from that of the MGH oligodendroglioma cases (log rank, P value = 0.43) and similarly the survival distribution of the Nutt et al glioblastoma cases was not significantly different from that of the MGH glioblastoma cases (P = 0.70). We assume that the original Nutt et al set of 21 classic cases are comparable to the classic MGH cases and that the original Nutt et al set of 29 nonclassic cases are comparable to the nonclassic MGH cases.
Results and Discussion
The current histopathological classification and grading systems for malignant gliomas fall short of their ultimate goals of estimating prognosis and guiding therapy. Through gene expression profiling, our group recently identified highly significant genetic markers that could be used to distinguish glioblastomas and anaplastic oligodendrogliomas with classic textbook histology.5 Further, we found that genetic classification of the nonclassic cases provided stronger outcome prediction than did classification based on standard pathology. In future work, we will use the initial mRNA profiles to develop practical protein-based, immunohistochemistry marker panels for the subgroups. To find the optimal number of assays that we will need to develop (N), we designed and conducted a simulation study that implemented our future study. Through the simulations, we evaluated the planned technical and prognostic validations for several candidate immunohistochemistry panels, in conjunction with our assumptions.
Simulation Study Design
Initial Selection of Genes Based on Differential Expression and Assumptions 1 and 2
We initially aimed to select those genes for possible immunohistochemistry assay development that had the highest likelihood of displaying differential protein expression. For a given number of initially considered genes (N), we selected the half (N/2) that were most differentially expressed in the classic glioblastomas and the half (N/2) that were most differentially expressed in the classic oligodendrogliomas. For further consideration, based on assumption 1 (Table 1), we randomly selected 50% of these N genes as having correspondingly differential protein expression. For further consideration, based on assumption 2 (Table 1), we also randomly selected 75% or 50% or 25% of these N/2 genes as those for which we expect to be successful at optimizing antibodies.
Technical Validation Using the Original Classic Cases, Incorporating Assumption 3
Given that we had selected the genes for consideration, we next needed to validate that the immunohistochemical panel is able to recognize the classic molecular signature, as we know the gene expression panel is able to do. For each of the immunohistochemistry assays ultimately developed (ie, 75% × N/2 or 50% × N/2 or 25% × N/2 assays) and for each of the original 21 classic cases, we randomly assigned the immunohistochemistry outcome (ie, 0, 1+, 2+, 3+, 4+) according to the probability model given in assumption 3. Although this is a univariate model, for each gene separately, correlation among the assay outcomes across genes is naturally induced by the correlation among the expression values across genes. Using this simulated set of immunohistochemistry assay outcomes for the Nutt et al 21 classic cases, we built k-nearest neighbor classification models, with k = 3, and calculated the classification error rate (ie, the proportion of classic cases that were misclassified through use of the k-NN derived classification rule).
Technical Validation Using the Simulated MGH Classic Cases, Incorporating Assumption 4
The next step is to validate that the immunohistochemical panel that was selected on the basis of the gene expression data from original Nutt et al cases is able to recognize the classic molecular signature among the MGH cases. To generate the MGH classic gene expression data, we randomly sampled 135 classic glioblastoma cases, and their corresponding collection of gene expression values, with replacement (see below), from among the 14 Nutt et al classic glioblastoma cases and 23 classic oligodendroglioma cases, and their corresponding collection of gene expression values, with replacement (see below), from among the 7 Nutt et al classic oligodendroglioma cases. Under sampling with replacement, each case always has the same probability of being sampled, regardless of whether it has already been sampled. This resampling approach amounts to generating gene expression data for the MGH cases from the unknown and complicated distribution that generated the gene expression data for the original cases. It is justified by assumption 4 and exemplifies the use of bootstrap methods for power and sample size calculations.15 We further simulated immunohistochemistry assay data for the simulated MGH cases according to the probability model posited in assumption 3. This induces variability among even the replicated cases (present due to the sampling with replacement). Using this simulated set of immunohistochemistry assay outcomes for the MGH classic cases, we built k-nearest neighbor classification models, with k = 3, and calculated the classification error rate.
Prognostic Validation Using the Simulated MGH Nonclassic Cases
Lastly, we will evaluate the prognostic power of the immunohistochemical panel, beyond what is afforded by pathological classification, with regard to patient survival. To generate the MGH nonclassic gene expression data, we randomly sampled 158 cases, and their accompanying gene expression values, from the 29 Nutt et al nonclassic cases. We simulated the immunohistochemistry assay data according to the probability model posited in assumption 3. We applied the k-NN model derived for the classic cases to these nonclassic cases to achieve an immunohistochemistry panel based classification. We fit a Cox proportional hazards model, with the model-based classification and the pathological diagnosis as the two covariates. We recorded whether or not the P value for the log hazard ratio for the marker panel classification was less than 0.05.
We repeated the above steps 5000 times. We then averaged the classification error rates and summed the number of significant P values recorded to estimate the power for detecting a significant association between the marker classification and survival, after adjusting for pathological diagnosis. We repeated all of these steps for a range of values of N to observe the impact of the number of assays initially considered on the validation measures of interest. In addition, we varied the assumed success rate of antibody optimization (assumption 2). We ran the simulation under three scenarios: 75% success rate, 50% success rate, and 25% success rate. We could have varied other inputs that appear in our assumptions, as well. These include the probability that a gene whose DNA was differentially expressed will likewise exhibit differential protein expression (assumption 1) and the probabilities associated with the model that links the gene expression values with the immunohistochemistry assay outcomes (assumption 3). Varying these inputs would allow for sensitivity analyses of the results with respect to these underlying assumptions and would be appropriate if there were uncertainty about the particular values used in these assumptions.
Simulation Study Results
Table 2 lists the estimated classification error rates, power, and hazard rates based on simulations with 5000 repetitions each, for a range of values of N, the number of assays considered for development (depending on assumption 2, the antibody optimization success rate). We included the minimum N’s possible for each optimization rate; smaller values did not produce stable simulation results. Our results indicate that if our model linking gene expression data to immunohistochemistry outcomes is approximately correct and if we are successful optimizing antibodies 75% of the time, initial consideration of 30 immunohistochemistry assays for development, and thus successful development of ∼11 assays, is sufficient to ensure satisfactory technical and prognostic validation of the panel. If we achieve only a 25% success rate, and if we initially consider 90 immunohistochemistry assays for development, also with successful development of ∼11 assays, we will achieve slightly less satisfactory levels of validation (eg, lower prognostic power of 75% versus 90% in the above example). The reason for this discrepancy in power based on the same number of assays ultimately developed is that the second scenario of 25% optimization success requires consideration of many more genes for assay development than the first scenario of 75% optimization success. Because the genes are ordered with respect to their differential expression, the first 30 genes considered will display higher differential expression than the first 90, and thus the 11 assays ultimately selected in each scenario are not equivalent. That is, those assays selected through initial consideration of the first 30 genes will likewise display higher differential protein expression than will those selected through initial consideration of the first 90 genes. More generally, this explains why the power is not increasing with N; there is a plateau due to the ordering of the genes.
Conclusions
We have demonstrated, through an example of designing an immunohistochemistry study for gliomas, a simulation-based method for assessing the required number of assays for development to ensure adequate technical and prognostic validation. Our simulation study suggests that we need to consider between 30 and 90 of the most differentially expressed genes from our earlier gene expression study for immunohistochemistry assay development. This wide range reflects the influence of the assumption of the success rate of antibody optimization. Based on our laboratory’s experience, we feel comfortable with the assumption of a 75% success rate and thus will consider development of 30 immunohistochemistry assays. Furthermore, given this assumption, our simulation results indicate that consideration of more genes will not add any prognostic power to our ultimate goal of developing a robust method for diagnosis of gliomas that improves on current pathological classification. Completion of the planned immunohistochemistry study will further help us evaluate the plausibility of these assumptions for future designs.
Table 2.
Simulation Results (5000 Repetitions)
| Number of assays (n) | ||||
|---|---|---|---|---|
| 30 | 40 | 50 | 60 | |
| Assay optimization success rate, 75% | ||||
| Classification error rate* | ||||
| Original cases | 0.10 | 0.09 | 0.10 | 0.09 |
| MGH cases | 0.02 | 0.01 | 0.01 | 0.01 |
| Prognostic power† (MGH cases) | 0.90 | 0.91 | 0.91 | 0.87 |
| Hazard rate‡ (MGH cases) | 0.18 | 0.17 | 0.16 | 0.20 |
| Assay optimization success rate, 50% | ||||
| 40 | 50 | 60 | 70 | |
| Classification error rate* | ||||
| Original cases | 0.11 | 0.11 | 0.10 | 0.10 |
| MGH cases | 0.03 | 0.02 | 0.01 | 0.01 |
| Prognostic power† (MGH cases) | 0.86 | 0.87 | 0.82 | 0.84 |
| Hazard rate‡ (MGH cases) | 0.23 | 0.22 | 0.23 | 0.23 |
| Assay optimization success rate, 25% | ||||
| 90 | 100 | 110 | 120 | |
| Classification error rate* | ||||
| Original cases | 0.12 | 0.12 | 0.12 | 0.12 |
| MGH cases | 0.03 | 0.02 | 0.02 | 0.02 |
| Prognostic power† (MGH cases) | 0.75 | 0.70 | 0.75 | 0.77 |
| Hazard rate‡ (MGH cases) | 0.33 | 0.36 | 0.35 | 0.32 |
Estimated classification error rates based on k-NN (k = 3) models fit to immunohistochemistry data for classic cases.
Estimated power for detecting a significantly nonunity hazard rate for comparing nonclassic immunohistochemistry panel-based oligodendrogliomas to glioblastomas after adjusting for standard pathologic classification.
Estimated hazard rates for death for nonclassic panel-based oligodendrogliomas versus panel-based glioblastomas, after adjusting for standard pathologic classification.
Acknowledgments
We thank Dr. Anat Stemmer-Rachamimov for her careful reading of the manuscript and Loc-Duyen D. Pham for preparing the MGH data for analysis.
Footnotes
Supported by the National Institutes of Health (grants CA75971 and CA57683), the Oligo Brain Tumor Fund, and the National Brain Tumor Foundation.
References
- Chuaqi RF, Bonner RF, Best CJM, Gillespie JW, Flaig MJ, Hewitt SM, Phillips JL, Krizman DB, Tangrea MA, Ahram M, Linehan WM, Knezevic V, Emmert-Buck MR. Post-analysis follow-up and validation of microarray experiments. Nat Genet Suppl. 2002;32:509–514. doi: 10.1038/ng1034. [DOI] [PubMed] [Google Scholar]
- Yang YH, Speed T. Design issues for cDNA microarray experiments. Nat Rev Genet. 2002;3:579–588. doi: 10.1038/nrg863. [DOI] [PubMed] [Google Scholar]
- Simon R, Radmacher MD, Dobbin K. Design of studies using DNA microarrays. Genet Epidemiol. 2002;23:21–36. doi: 10.1002/gepi.202. [DOI] [PubMed] [Google Scholar]
- Churchill GA. Fundamentals of experimental design for cDNA microarrays. Nat Genet Suppl. 2002;32:490–495. doi: 10.1038/ng1031. [DOI] [PubMed] [Google Scholar]
- Nutt CR, Mani DR, Betensky RA, Tamayo P, Cairncross JG, Ladd C, Pohl U, Hartmann C, McLaughlin ME, Batchelor TT, Black PM, von Deimling A, Pomeroy SL, Golub TR, Louis DN. Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer Res. 2003;63:1602–1607. [PubMed] [Google Scholar]
- Dejiver PA, Kittler JV. Pattern Recognition: A Statistical Approach. Englewood Cliffs: Prentice Hall,; 1982 [Google Scholar]
- Stone M. Cross-validation and assessment of statistical predictions. J Royal Stat Soc. 1974;B36:111–147. [Google Scholar]
- Burns KL, Ueki K, Jhung SL, Koh J, Louis DN. Molecular genetic correlates of p16, cdk4 and pRb immunohistochemistry in glioblastomas. J Neuropathol Exp Neurol. 1998;57:122–130. doi: 10.1097/00005072-199802000-00003. [DOI] [PubMed] [Google Scholar]
- Murthy V, Stemmer-Rachamimov AO, Beauchamp RL, Pinney D, Candia C, Shaw J, Gonzalez-Agosti C, Louis DN, Ramesh V. Developmental expression of the tuberous sclerosis proteins, tuberin and hamartin. Acta Neuropathol. 2001;101:202–210. doi: 10.1007/s004010000269. [DOI] [PubMed] [Google Scholar]
- Nielsen GP, Stemmer-Rachamimov AO, Shaw J, Koh J, Louis DN. Immunohistochemical survey of p16INK4A expression in human tissues. Lab Invest. 1999;79:1137–1143. [PubMed] [Google Scholar]
- Stemmer-Rachamimov AO, Gonzalez-Agosti C, Xu L, Burwick JA, Beauchamp R, Pinney D, Louis DN, Ramesh V. Expression of NF2-encoded merlin and related ERM family proteins in the human central nervous system. J Neuropathol Exp Neurol. 1997;56:735–742. [PubMed] [Google Scholar]
- Stemmer-Rachamimov AO, Wiederhold T, Nielsen GP, Pinney-Michalowski D, Roy JE, Cohen WA, Ramesh V, Louis DN. NHE-RF, a merlin-interacting protein, is primarily expressed in luminal epithelia, proliferative endometrium and estrogen receptor-positive breast carcinomas. Am J Pathol. 2001;158:57–62. doi: 10.1016/S0002-9440(10)63944-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stemmer-Rachamimov AO, Xu L, Gonzalez-Agosti C, Burwick J, Pinney D, Beauchamp R, Jacoby LB, Gusella JF, Ramesh V, Louis DN. Universal absence of merlin, but not other ERM family members, in schwannomas. Am J Pathol. 1997;152:1649–1654. [PMC free article] [PubMed] [Google Scholar]
- Shipp MA, Ross KN, Tamayo P, Weng AP, Kutok JL, Aguiar RC, Gaasenbeek M, Angelo M, Reich M, Pinkus GS, Ray TS, Koval MA, Last KW, Norton A, Lister TA, Mesirov J, Neuberg DS, Lander ES, Aster JC, Golub TR. Diffuse large B-cell lymphoma outcome prediction by gene-expression profiling and supervised machine learning. Nat Med. 2002;8:68–74. doi: 10.1038/nm0102-68. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. New York: Chapman and Hall; 1993 [Google Scholar]