Quantitative Vibrational Dynamics of Iron in Carbonyl Porphyrins

Abstract

We use nuclear resonance vibrational spectroscopy and computational predictions based on density functional theory (DFT) to explore the vibrational dynamics of ⁵⁷Fe in porphyrins that mimic the active sites of histidine-ligated heme proteins complexed with carbon monoxide. Nuclear resonance vibrational spectroscopy yields the complete vibrational spectrum of a Mössbauer isotope, and provides a valuable probe that is not only selective for protein active sites but quantifies the mean-squared amplitude and direction of the motion of the probe nucleus, in addition to vibrational frequencies. Quantitative comparison of the experimental results with DFT calculations provides a detailed, rigorous test of the vibrational predictions, which in turn provide a reliable description of the observed vibrational features. In addition to the well-studied stretching vibration of the Fe-CO bond, vibrations involving the Fe-imidazole bond, and the Fe-N_pyr bonds to the pyrrole nitrogens of the porphyrin contribute prominently to the observed experimental signal. All of these frequencies show structural sensitivity to the corresponding bond lengths, but previous studies have failed to identify the latter vibrations, presumably because the coupling to the electronic excitation is too small in resonance Raman measurements. We also observe the FeCO bending vibrations, which are not Raman active for these unhindered model compounds. The observed Fe amplitude is strongly inconsistent with three-body oscillator descriptions of the FeCO fragment, but agrees quantitatively with DFT predictions. Over the past decade, quantum chemical calculations have suggested revised estimates of the importance of steric distortion of the bound CO in preventing poisoning of heme proteins by carbon monoxide. Quantitative agreement with the predicted frequency, amplitude, and direction of Fe motion for the FeCO bending vibrations provides direct experimental support for the quantum chemical description of the energetics of the FeCO unit.

INTRODUCTION

Diatomic molecules make essential contributions to the processes of life. Best known is the role of molecular oxygen, which has transformed Earth's biosphere (1) and is central to complex biomolecular networks (2) . There is also growing recognition of the role of diatomic molecules in cellular signaling (3–6). Heme proteins figure prominently in interactions with these diatomic molecules (7–9).

The interactions between CO and heme proteins have drawn particularly intense scrutiny. In part, this stems from a favorable combination of stability and spectroscopic and photochemical properties that enable CO to function as a “stunt double” for O₂ in physical investigations. CO binding confers stability against autooxidation of the heme Fe, and spectroscopic observables, including vibrations of the FeCO group (10), provide sensitive probes of the local environment. In addition, the quantum yield for photodissociation of CO from heme proteins is higher than for other diatomic ligands (11), favoring its use for investigating the conformational response to ligand dissociation (12–14) and migration of CO through the protein interior (15–17) over a wide range of timescales.

There is increasing recognition that CO may participate directly in physiological signaling (6). CO binding to the heme-containing sensor protein NPAS2 is believed to facilitate regulation of circadian rhythms (18). CO also activates soluble guanylate cyclase by binding to its heme site, although it is less effective than NO (19,20). As a result, there is ongoing investigation of the possibility that CO can participate in physiological processes such as neurotransmission (21,22) and smooth muscle relaxation (23), where soluble guanylate cyclase is known to mediate NO signaling. CO, along with biliverdin and iron, are products of heme catabolism by the enzyme heme oxygenase (24–26). A bacterial heme protein CooA regulates DNA expression based on the local concentration of CO (27,28).

The affinity of CO for free heme, 2 × 10⁴ times that of O₂ (7), favors heme proteins as CO sensors. On the other hand, many heme proteins have evolved mechanisms to selectively bind O₂ in the presence of the background of endogenously produced CO. Although hydrogen bonding to the bound dioxygen is now believed to be the primary mechanism for selective O₂ binding in hemoglobins (7,29,30), discrimination against CO binding can also play an important role.

While O₂ binds end on to iron with the O-O axis ∼60° from the normal to the plane of a free porphyrin, CO binds nearly perpendicular to the plane (31). It has long been recognized that proteins can exploit this difference in geometry to sterically destabilize CO binding in favor of O₂ (32). Two discoveries have deemphasized the significance of steric factors in hemoglobins. For one thing, structural investigations of myoglobin with bound CO (MbCO) find much less distortion of FeCO from its energetically favorable linear geometry than was once believed (33–37). Moreover, quantum chemical calculations of the energetic cost of the residual distortion are significantly reduced from earlier estimates (29,38,39). The best available estimates indicate that steric distortion plays a secondary role in discriminating between CO and O₂ binding to hemoglobins (9,29,30), although questions remain about how to evaluate the energy involved in distorting the surrounding protein (35,40,41).

Although the understanding of how respiratory heme proteins avoid being poisoned by CO has advanced significantly, the means by which CO sensing proteins discriminate against false signals due to other diatomic molecules such as NO and O₂ is less well understood. Steric interactions with heme-bound diatomic ligands may also underlie their recognition by sensor proteins, for example by triggering conformational changes that regulate enzymatic activity or protein/DNA interactions (42–45). However, structural changes of the heme upon diatomic ligand binding can also drive allosteric conformational changes through the covalent link with the protein (46,47). Both factors contribute to the oxygen-binding behavior of the paradigmatic allosteric protein, hemoglobin (48–50).

Vibrational spectroscopy can be a sensitive probe of molecular structure and energetics, and traditional methods partially characterize heme Fe-ligand vibrations. Strong absorption in the 1900–2000 cm⁻¹ frequency region, where there is minimal interference from protein or solvent vibrations, makes the bound C-O stretching vibration an effective infrared probe (51–54). Raman measurements in resonance with heme electronic transitions are primarily selective for porphyrin vibrations, but Fe-C stretching and, in some cases, FeCO bending vibrations are detectable in the resonance Raman signal from six-coordinate CO-ligated hemes (55–60).

These vibrations have been heavily exploited to monitor FeCO structure, environment, and energetics in heme proteins. Both Fe-C and C-O frequencies are well-calibrated electrostatic probes (10,61,62), and polarized IR measurements can infer distortion of the FeCO unit by determining the orientation of the C-O infrared transition dipole (33–35). Investigations of the FeCO bending vibration (55–57,63,64) have motivated quantum chemical calculations of the energetics of FeCO distortion (29,38,39), although the relevant lowest frequency distortion mode, predicted to lie below 100 cm⁻¹, has not yet been observed experimentally.

Unfortunately, attempts to identify other Fe-ligand vibrations for CO-ligated heme proteins have been inconclusive. In particular, the vibration of the covalent Fe-histidine link with the protein only contributes strongly to the Raman signal after dissociation of CO (13,14,65), and Fe coordination to the porphyrin is usually probed only indirectly through its influence on high frequency porphyrin vibrations (66). A more comprehensive vibrational picture would identify additional vibrational probes for the Fe nearest-neighbor bonds and address unresolved questions surrounding previously observed vibrations. In particular, a fuller characterization of the FeCO bending vibrations would quantify the asymmetry of the quasi-degenerate bending vibrations, confirm that the observed features are vibrational fundamentals (63,64,67–69), and provide an experimental test of quantum chemical predictions for the FeCO energetics (29,38,39).

Nuclear resonance vibrational spectroscopy (NRVS) provides direct experimental access to all Fe vibrations. NRVS exploits characteristic properties of synchrotron radiation sources to reveal the complete vibrational spectrum of a probe nucleus (70–74) and provides a comprehensive picture of the vibrational dynamics of ⁵⁷Fe in many materials (75–77), including proteins (78–84) and model compounds that mimic protein active sites (85–93). NRVS yields quantitative values for vibrational amplitudes and directions, as well as frequencies, and thus provides a rigorous test of vibrational predictions. This information is proving particularly valuable for evaluating quantum chemical calculations based on density functional theory (DFT), which provide detailed predictions of many molecular ground state properties, including the optimized structure and a comprehensive description of vibrational dynamics (38,39,60,90,93–98).

Here, we use NRVS measurements and DFT calculations to characterize the vibrational dynamics of ferrous carbonyl porphyrins, including [Fe(TPP)(1-MeIm)(CO)] (Fig. 1), that mimic the active site of six-coordinate CO-ligated heme proteins. Fe-ligand vibrations dominate the observed NRVS signal, in contrast to other vibrational techniques. We compare the resulting quantitative information on the amplitude and direction of the Fe motion, as well as mode frequencies, directly with vibrational predictions from DFT calculations. This comparison provides a rigorous and successful test of the predictions, which describe vibrational modes observed in the experimental spectra. Vibrations involving all six covalent bonds to the iron contribute prominently to the NRVS signal, including the imidazole and pyrrole nitrogens as well as FeCO vibrations previously observed using resonance Raman spectroscopy. Lower frequency modes involving heme doming or reorientation of the diatomic CO ligand are likely to control the reactivity of heme proteins. Vibrational frequencies identified here can be used both to probe the Fe coordination structure and to provide quantitative insight into molecular energetics. In particular, experimental confirmation of predicted behavior for FeCO bending vibrations supports quantum chemical estimates of the cost of FeCO distortion.

FIGURE 1.

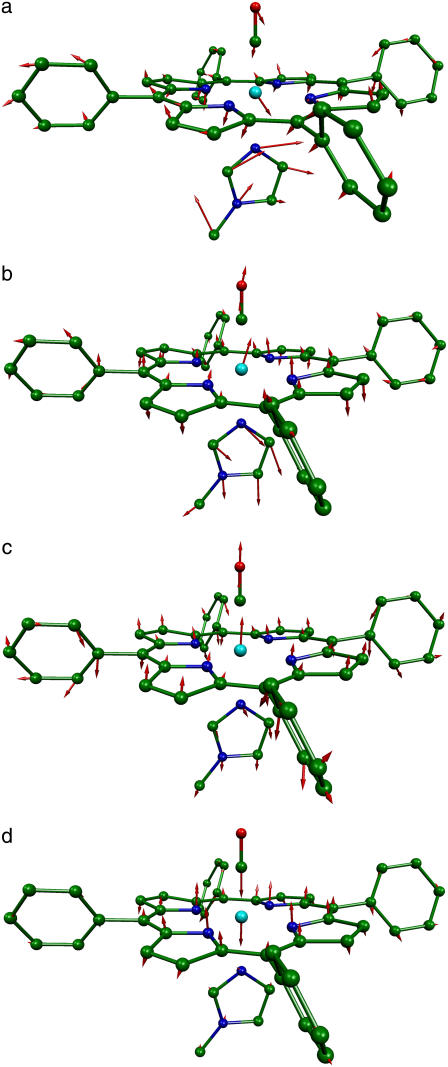
Structure resulting from geometric optimization [Fe(TPP)(1-MeIm)(CO)], showing the 1-MeIm and CO ligands below and above the plane of the porphyrin. Hydrogen atoms are omitted for clarity. (Cyan, iron; green, carbon; blue, nitrogen; and red, oxygen.) Subsequent figures use the same color scheme. Molecular structures and vibrational mode depictions (Figs. 8–11) were generated with the program MOLEKEL (152).

METHODS

Porphyrin synthesis

⁵⁷Fe-enriched porphyrinates were prepared using a small-scale metallation procedure described by Landergren and Baltzer (99). The synthesis of [Fe(TPP)(1-MeIm)(CO)] (88), [Fe(TPP)(1,2-Me₂Im)(CO)] (100), [Fe(OEP)] (90), [Fe(TPP)(2-MeHIm)] (101), and [Fe(OEP)(2-MeHIm)] (102), was described previously. [Fe(OEP)(1-MeIm)(CO)] and [Fe(TPP)(1-PhIm)(CO)] were prepared by a method similar to the preparation of [Fe(TPP)(1-MeIm)(CO)](88). Ambient temperature infrared spectra of these compounds were recorded as Nujol mulls between NaCl windows.

Myoglobin from horse heart (Sigma, St. Louis, MO) was reconstituted following the method of Teale (103) with ⁵⁷Fe-enriched protoporphyrin IX (Frontier Scientific, Logan, UT). Following concentration to 13 mM in pH 8-phosphate buffer, the protein solution was agitated under 1 atm of CO gas and reduced with sodium dithionite to produce the CO derivative (MbCO) (79).

NRVS measurements and analysis

NRVS measurements were performed at sector 3-ID-D of the Advanced Photon Source at Argonne National Laboratory (Lemont, IL). The sample was placed in a monochromatic x-ray beam, whose energy was scanned through the 14.4 keV ⁵⁷Fe resonance using a high resolution monochromator (104) with an energy bandwidth (full width at half-maximum) of 7 cm⁻¹ (0.85 meV) or 8 cm⁻¹ (1.0 meV). X rays were distributed across a 4 × 1 mm² beam cross section and arrived as a train of pulses 70 ps wide at 154-ns intervals, with an average flux of 2 × 10⁹ photons/s = 4 μW incident on the sample. An avalanche photodiode detected photons emitted by the excited ⁵⁷Fe atoms, which arrive with a delay on the order of the 140 ns ⁵⁷Fe excited-state lifetime. The counter was disabled during a time interval containing the arrival time of the x-ray pulse, to suppress the large background of electronically scattered 14.4 keV photons, which arrive in coincidence with the x-ray pulse.

Polycrystalline powders or frozen solutions were loaded into polyethylene sample cups and mounted on a cryostat cooled by a flow of liquid He, with x-ray access through a beryllium dome. Single crystals were mounted on a goniometer and data was recorded in two orthogonal orientations related by rotation about an axis orthogonal to the x-ray beam. Crystal orientation was verified by x-ray diffraction before and after NRVS measurements. A stream of cold N₂ gas from a commercial cryocooler controlled crystal temperature during NRVS measurements.

Both [Fe(TPP)(1-MeIm)(CO)]·C₆H₆ and [Fe(OEP)(2-MeHIm)]·C₇H₈ crystallized in space group 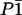with a single porphyrin in the asymmetric unit. In each case, a single ⁵⁷Fe-enriched crystal [1.05 × 1.00 × 0.22 mm³ for Fe(TPP)(1-MeIm)(CO) and 2.00 × 0.50 × 0.40 mm³ for [Fe(OEP)(2-MeHIm)] was oriented with a selected crystallographic plane parallel both to the x-ray beam and to the goniometer rotation axis. For [Fe(TPP)(1-MeIm)(CO)]·C₆H₆, the chosen {24, −2, 1} plane lies 0.6° from the mean plane of the four pyrrole nitrogens, while the {6, 6, 17} plane selected for [Fe(OEP)(2-MeHIm)]·C₇H₈ lies 1.3° from the porphyrin plane. This procedure ensures that only Fe motion parallel to the porphyrin plane contributes to the NRVS signal recorded in the original orientation. In each case, a second data set, recorded after a 90° rotation about the goniometer axis, sampled Fe motion perpendicular to the porphyrin plane.

[Fe(TPP)(1,2-Me₂Im)(CO)]·C₇H₈ crystallized in space group P2₁/n with a single porphyrin in the asymmetric unit. A single crystal with dimensions 1.50 × 0.50 × 0.54 mm³ was oriented with the {12, 1, −8} plane parallel to the plane defined by the x-ray beam and the goniometer rotation axis, with the x-ray beam parallel to the planes of all porphyrins. Because the two symmetry-related porphyrin planes lie ∼77° apart, it was not possible to simultaneously orient both porphyrins orthogonal to the x-ray beam, and data was recorded only for the original in-plane orientation.

A spectrum recorded as a function of x-ray energy consists of a central resonance, due to recoilless excitation of the ⁵⁷Fe nuclear excited state at E₀ = 14.4 keV, together with a series of sidebands corresponding to creation or annihilation of vibrational quanta of frequency which have an area proportional to the mean squared displacement of the Fe and are displaced from the recoilless absorption by an energy 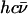(85,105).

Normalization of this spectrum according to Lipkin's sum rule (106) yields the excitation probability 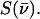Subtraction of the central resonance results in a vibrational excitation probability 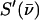(107). Each mode contributes an area

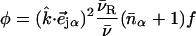(1)

proportional to the mean-square displacement of the Fe atom to 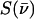or 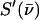(85). Here, 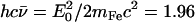meV is the recoil energy of a free ⁵⁷Fe nucleus upon absorption of a photon of energy E₀ = 14.4 keV, 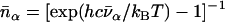is the thermal occupation factor for a mode of frequency 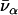at temperature T, the unit vector 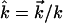is parallel to the wave vector 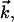and 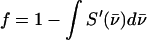is the recoilless fraction. The set of vectors 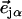describe the linear transformation 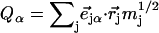from the mass-weighted Cartesian displacements 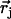of the individual atoms to the normal coordinates Q_α of the system.

The program PHOENIX (108) removes temperature factors, multiphonon contributions, and an overall factor proportional to inverse frequency from 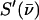to yield an Fe-weighted vibrational density of states (VDOS), which defines the vibrational properties at all temperatures for a harmonic system. For a randomly oriented sample, such as a solution or polycrystalline powder, the total VDOS

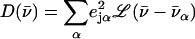(2)

takes the form of a series of bands with areas 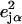(85,105). 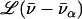is a normalized line shape function with a width greater than or equal to the experimental resolution. Each mode α contributes to 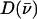an area 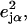with j = Fe, equal to the fraction of the kinetic energy associated with motion of the iron atom (85,90). As a result, the VDOS 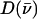determined from ⁵⁷Fe NRVS measurements directly samples the iron contribution to the kinetic energy distribution (KED) of each vibrational mode. Reported frequency shifts in mode α resulting from small changes in the mass of atom j yield an estimate for the mode composition factor (85)

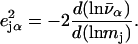(3)

Measurements on a perfectly oriented sample yield a projected VDOS

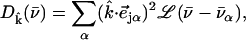(4)

with band areas 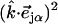equal to the squared projection of 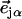along the beam direction 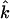(85,105). Thus, 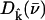gives the contribution of Fe motion along direction 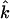to the vibrational KED. Note that the normalization of the projected VDOS, 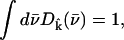differs from that of the total VDOS 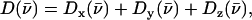which is summed over the Cartesian directions and thus has a total area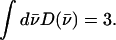

The sample temperatures are determined directly from NRVS, by requiring that the ratio 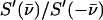equal the Boltzmann factor 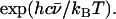For randomly oriented powder and solution samples, we obtained 20 K for [Fe(TPP)(1-MeIm)(CO)], 19 K for [Fe(TPP)(1,2-Me₂Im)(CO)], 33 K for [Fe(TPP)(1-PhIm)(CO)], 25 K for [Fe(OEP)(1-MeIm)(CO)], 25 K for MbCO, 20 K for [Fe(TPP)(2-MeHIm)], and 34 K for [Fe(OEP)]. We found 230 K (123 K) for the in-plane (out-of-plane) orientation of the [Fe(TPP)(1-MeIm)(CO)] crystal, 89 K (140 K) for the in-plane (out-of-plane) orientation of the [Fe(OEP)(2-MeHIm)] crystal, and 86 K for the [Fe(TPP)(1,2-Me₂Im)(CO)] crystal (in-plane orientation only).

DFT computations

DFT calculations provided the optimized structures and detailed vibrational predictions for the six-coordinate porphyrins [Fe(TPP)(1-MeIm)(CO)] (Fig. 1) and [Fe(TPP)(2-MeHIm)(CO)]. Calculations were performed with Gaussian 98 (109), using the 6-31G* basis set for N, O, C, and H atoms, Ahlrichs' VTZ basis set for the Fe atom (110), and the Becke-Lee-Yang-Parr composite exchange correlation functional (B3LYP) (111,112). The kinetic energy distribution (KED) is determined for each vibrational mode from the relative Cartesian displacements of individual atoms, as described previously (90). The calculation describes the atomic vibrations using a set of relative atomic displacements from which the mode composition factors

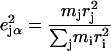(5)

are determined for each atom j and mode α.

For comparison with measurements on oriented samples, the kinetic energy fraction due to motion of atom j along a direction 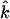is calculated from

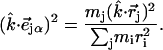(6)

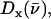
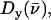
The mode composition factors for iron (j = Fe in Eq. 6) are then used to determine the contributions to from the iron motion in the x, y, and z directions (Eq. 4). These contributions are labeled 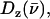with x and y being orthogonal directions in the plane of the porphyrin, and z perpendicular to the mean porphyrin plane. The total VDOS, 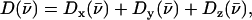is given by Eq. 2 with j = Fe.

EXPERIMENTAL RESULTS

Vibrational frequencies, amplitudes, and directions

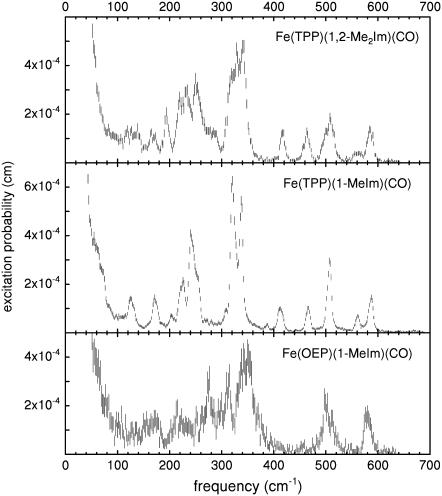
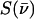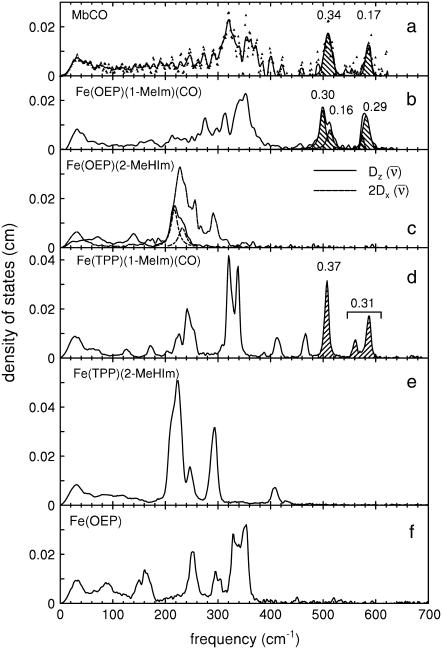
Fig. 2 presents NRVS excitation probabilities recorded on three porphyrins that mimic the active site of CO-ligated heme proteins. These data and the VDOS 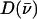derived from them (Fig. 3, b and d) share some similarities with each other and with MbCO (Fig. 3 a), a typical heme protein with the same ligation, and contrast with the vibrational spectra of four- and five-coordinate Fe porphyrins (Fig. 3, c, e, and f). In particular, four- and five-coordinate molecules lack features above 450 cm⁻¹ associated with the FeCO group (see following section).

FIGURE 2.

NRVS data for six-coordinate iron-carbonyl porphyrins. Peaks above 500 cm⁻¹ involve the FeCO fragment. Error bars reflect counting statistics.

FIGURE 3.

Comparison of VDOS for MbCO (a), and for four-, five-, and six-coordinate porphyrins that mimic heme protein active sites (b–f). Features that appear above 500 cm⁻¹ in the CO complexes (crosshatched) are due to FeCO vibrations, which are absent in the VDOS of four- and five-coordinate Fe porphyrins. Values for 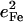are equal to crosshatched areas. Panel c shows in-plane and out-of-plane contributions to the total VDOS of [Fe(OEP)(2-MeHIm)], determined from single crystal data recorded with the incident x-ray beam parallel (dashed line) and perpendicular (solid line) to the mean porphyrin plane, respectively. All other data were recorded on randomly oriented samples (frozen solution or polycrystalline powder). For the porphyrins, the frequencies of the in-plane modes decrease as the Fe-N_pyr bond lengths increase. The line in panel a corresponds to a five-point smoothing of the data.

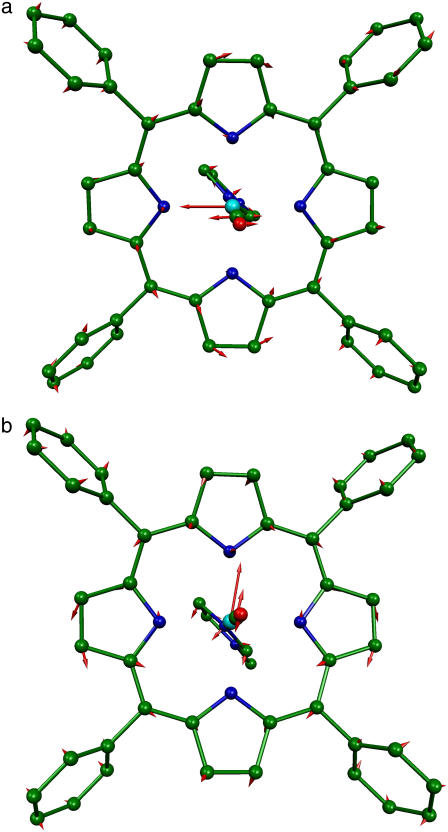
Since the NRVS signal is weighted by the Fe mean-squared displacement, vibrations involving all Fe ligands contribute prominently to the experimental VDOS. These include not only vibrations of the FeCO group in the 500–600 cm⁻¹ region identified in previous investigations of heme-CO complexes (55,113), but also vibrations involving the imidazole and porphyrin ligands and low frequency molecular distortions. Quantitative information on vibrational amplitudes and directions, as well as frequencies, facilitates identification of these modes. Table 1 lists the frequencies and the corresponding areas 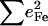of features observed in the VDOS of [Fe(TPP)(1-MeIm)(CO)] (Fig. 4) and two related model compounds, [Fe(TPP)(1,2-Me₂Im)(CO)] and [Fe(TPP)(1-PhIm)(CO)] (Fig. 5).

TABLE 1.

Correspondence between the observed vibrational frequencies and amplitudes for Fe in polycrystalline powders of Fe(TPP)(L)(CO) with L = 1-MeIm, 1,2-Me₂Im, and 1-PhIm

1-MeIm		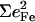1,2-Me2Im		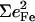1-PhIm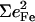
39	0.07	39	0.09
64	0.13	87	0.09
127	0.06	121	0.03	117	0.07
		139	0.04
172	0.08	168	0.07	172	0.08
204	0.04	194	0.08	197	0.06
225	0.15	221	0.17	223	0.29
241	0.15	233	0.08	233	0.05
251	0.21	251	0.26	247	0.22
		280	0.19	293	0.17
320	0.45	314	0.16	313	0.24
326	0.14	327	0.29
338	0.40	341	0.40	330	0.62
388	0.02			385	0.08
413	0.12	417	0.11	416	0.10
466	0.11	463	0.13	468	0.14
		495	0.07	489	0.16
507	0.37	509	0.24	502	0.16
561	0.09	561	0.07	565	0.11
587	0.21	585	0.19	589	0.17

FIGURE 4.

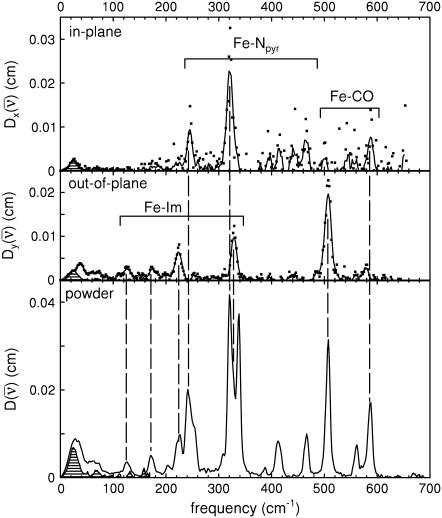
Single crystal, in-plane (upper panel), and out-of-plane (middle panel) orientations, and powder (lower panel) NRVS spectra for [Fe(TPP)(1-MeIm)(CO)]. Lines in the crystal data result from a five-point smoothing of the experimental data. Crosshatching indicates spectral area attributed to acoustic modes.

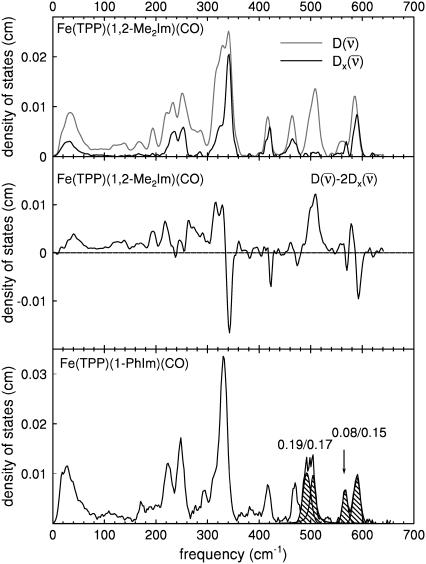
FIGURE 5.

(Upper panel) Comparison between the experimental VDOS for [Fe(TPP)(1,2-Me₂Im)(CO)], powder (black line) and crystal, in-plane orientation (gray line). (Center panel) Positive features corresponding to out-of-plane vibrations of the Fe atom remain after subtraction of in-plane contributions, estimated by doubling the measured in-plane VDOS. Paired positive and negative features reflect in-plane asymmetries neglected in this estimate. (Lower panel) Experimental VDOS for [Fe(TPP)(1-PhIm)(CO)] powder. Cross-hatching and numerical values indicate areas attributed to FeCO vibrations.

Comparison of powder and single crystal NRVS spectra provides information about the directions of the iron vibrations. Fig. 4 compares experimentally determined VDOS for the [Fe(TPP)(1-MeIm)(CO)] crystal with that determined for the polycrystalline powder. Inspection of these data identify out-of-plane modes in the powder spectrum at 39, 64, 127, 172, 225, 331, and 507 cm⁻¹ and in-plane modes at 241, 320, 413, 466, and 587 cm⁻¹. The prominent appearance of the 331 cm⁻¹ out-of-plane mode (Fig. 4, middle panel) indicates unresolved contributions from both in-plane and out-of-plane modes to the 321 cm⁻¹ band in the powder spectrum. Inspection of this feature reveals a high-frequency shoulder, and two peaks are required to fit this asymmetric feature (Table 1).

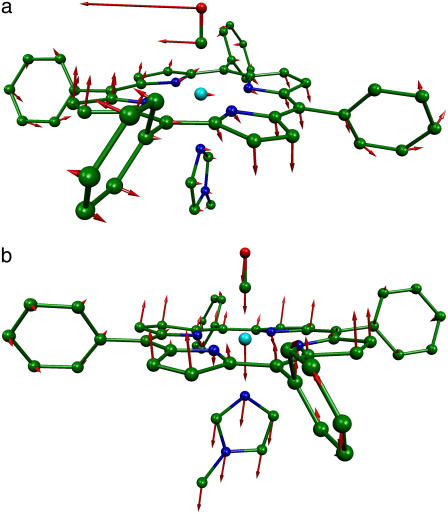
For [Fe(TPP)(1,2-Me₂Im)(CO)], Fig. 5 (top panel) compares the in-plane component of the density of states, as determined from measurements on the oriented crystal, with the total density of states determined for the powder sample. We attribute features appearing at 121, 139, 168, 194, 221, and 509 cm⁻¹ in the powder VDOS to out-of-plane vibrations, based on the absence of significant in-plane contributions at these frequencies. These features are unaffected by subtraction of the estimated in plane contribution 2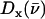 from the powder data (Fig. 5, center panel). In contrast, we attribute features at 233 and 251 cm⁻¹ to in-plane vibrations, because they are eliminated by this subtraction.

The imidazole removes the nominal fourfold symmetry of the Fe environment, and vibrational data show clear evidence for x–y inequivalence in the 320–350 cm⁻¹ region for both compounds. Fe motion along the two directions chosen for the single crystal measurements cannot account for the 338 cm⁻¹ feature in the total density of states of [Fe(TPP)(1-MeIm)(CO)] (Fig. 4), clearly indicating measurable x–y frequency splitting for the in-plane modes in this region. For [Fe(TPP)(1,2-Me₂Im)(CO)], the calculated difference 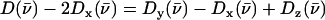(Fig. 5, center panel) reveals paired positive and negative features that suggest frequency differences between the two in-plane directions. Such difference features correspond not only to a broad feature that a fit to the powder data resolves into components at 314, 327, and 341 cm⁻¹, but also to features at 585 cm⁻¹ and possibly at 463 cm⁻¹, for which the powder data do not resolve significant structure.

Addition of a second methyl group to the imidazole increases the Fe-Im bond length by 9 pm (Table 3) and perturbs the vibrational dynamics of the Fe. Nevertheless, the combination of powder and oriented crystal data allows the identification of vibrational features in the two molecules that correspond in frequency, amplitude, and direction. We also propose corresponding vibrational features in the powder data on [Fe(TPP)(1-PhIm)(CO)] (Fig. 5, lower panel, Table 1).

TABLE 3.

Selected structural parameters for Fe(TPP)(1-MeIm)(CO) and Fe(TPP)(2-MeHIm)(CO)

	Bond length (pm)				Angle
	Fe-Npyr	Fe-NIm	C-O	Fe-C	Fe-C-O
Fe(TPP) (1-MeIm)(CO)*	202	208	115	179	180
Fe(TPP) (2-MeHIm)(CO)*	202	216	115	179	180
Fe(TPP) (1-MeIm)(CO)†	200	207	106	179	179
Fe(TPP) (1-MeIm)(CO)‡	201	205	114	176	177
Fe(TPP) (1,2-e2Im)(CO)‡	199	208/214§	114	175	176

^*DFT structural optimization.

^†Experimental crystal structure (138).

^‡Experimental crystal structure (100).

^§Two conformations with relative occupancies 62% and 38% (100).

In addition to intramolecular vibrations, molecular translation contributes to the VDOS (85). For the polycrystalline powders studied here, we expect low frequency acoustic lattice vibrations to be the principal translational contribution. To estimate acoustic mode contributions for [Fe(TPP)(1-MeIm)(CO)], we crosshatch the 0–173 cm⁻¹ region of the in-plane VDOS (Fig. 4, upper panel), which has the area 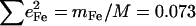expected (85) for translation of the entire molecule along an in-plane direction. Although it is unlikely that the actual acoustic mode spectrum has a sharp cutoff frequency, the frequency separation of the crosshatched area from other spectral features nevertheless suggests that acoustic motions dominate the in-plane VDOS below 200 cm⁻¹. By comparison, excess area due to additional vibrational contributions is evident in the out-of-plane VDOS, and overlay of the spectrum of acoustic modes estimated from the in-plane VDOS onto the out-of-plane and powder VDOS (Fig. 4, middle and lower panel) highlights vibrational features at 39, 64, 127, and 172 cm⁻¹ (Table 1), which we attribute to out-of-plane intramolecular vibrations.

FeCO modes

All of the CO complexes presented in Figs. 2 and 3 display vibrational features above 500 cm⁻¹. Previous Raman measurements on proteins and model compounds (63,114–117) have associated frequencies in this range with vibrations of the FeCO fragment. These modes (crosshatched in Fig. 3) are absent in the four- and five-coordinate complexes (Fig. 3, c, e, and f).

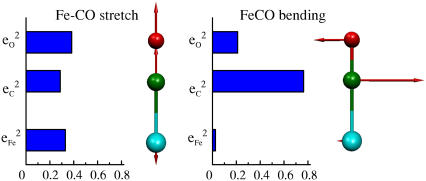
The lower frequency FeCO mode ranges between 499 and 507 cm⁻¹ for the compounds studied here (Table 2). Crystal data (Figs. 4 and 5) reveal the out-of-plane character of these modes, and confirm assignment to Fe-CO stretching. Their mode composition factors range between 0.30 and 0.37, values close to the value 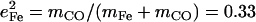expected for a two body Fe-CO oscillator (see Appendix).

TABLE 2.

FeCO vibrations for iron porphyrins. Values for 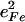are determined directly from NRVS experiments

Compound	ν(Fe − CO)		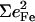δ(FeCO)		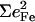ν(C − O)
Fe(TPP) (1-MeIm)(CO)	507	0.37	561/586	0.09/0.21	1969
Fe(TPP) (1,2-Me2Im)(CO)	506	0.31	561/583	0.07/0.19	1948/1953
Fe(TPP) (1-PhIm)(CO)	502	0.32	565/589	0.13/0.17	1975
Fe(OEP) (1-MeIm)(CO)	499/513	0.30/0.16	582/575	0.25/0.04	1951

We attribute higher frequency modes, ranging from 561 to 589 cm⁻¹, to FeCO bending. Single crystal measurements on [Fe(TPP)(1-MeIm)(CO)] and [Fe(TPP)(1,2-Me₂Im)(CO)] confirm that Fe motion is primarily parallel to the porphyrin plane for modes in this region.

Three bands appear in the FeCO region of the VDOS for iron carbonyl tetraphenylporphyrins (Figs. 3 d and 5). We attribute the out-of-plane feature (507 cm⁻¹ for [Fe(TPP)(1-MeIm)(CO)]) to Fe-CO stretching vibration, and the two in-plane features (561 cm⁻¹ and 587 cm⁻¹ for [Fe(TPP)(1-MeIm)(CO)]) to FeCO bending. For MbCO and for [Fe(OEP)(1-MeIm)(CO)] (Fig. 3, a and b), the experimentally determined VDOS resolves only a single peak in the FeCO bending region. However, the [Fe(OEP)(1-MeIm)(CO)] data (Figs. 2 and 3 b) includes an additional band at 513 cm⁻¹, on the high frequency edge of the Fe-CO stretching band at 499 cm⁻¹.

Other out-of-plane modes

NRVS measurements on single crystals reveal additional out-of-plane modes. The feature near 222 cm⁻¹ in the out-of-plane contribution to the [Fe(OEP)(2-MeHIm)] VDOS (Fig. 3 c) can be fit with two peaks, with frequencies 217 cm⁻¹ and 233 cm⁻¹, and areas 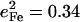and 0.20, respectively. The total 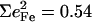approaches the value 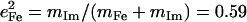expected for a two-body Fe-Im oscillator. Previously, single crystal measurements on [Fe(TPP)(2-MeHIm)] identified out-of-plane modes at 216, 228, and 246 cm⁻¹, with 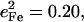0.06, and 0.19, respectively (87,93). The total 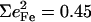is somewhat smaller than for [Fe(OEP)(2-MeHIm)], but an empirical normal mode calculation (87) identified Fe-Im contributions to each of these three modes.

Oriented single crystal measurements on [Fe(TPP)(1-MeIm)(CO)] (Fig. 4) and [Fe(TPP)(1,2-Me₂Im)(CO)] (Fig. 5 a) reveal substantial out-of-plane character for several experimental peaks with frequencies ranging from 39 cm⁻¹ to 331 cm⁻¹. The area of each individual feature is substantially less than expected for an Fe-Im oscillator, as can be seen by comparison with the area associated with Fe-Im stretching in [Fe(OEP)(2-MeHIm)] (Fig. 3).

The highest frequency out-of-plane feature at 331 cm⁻¹ in [Fe(TPP)(1-MeIm)(CO)] is resolved from neighboring in-plane vibrations only in the single crystal data. Competing in-plane vibrations impeded the identification of analogous modes in the other CO complexes. However, modes appearing at 168, 209, and 222 cm⁻¹ in the [Fe(OEP)(1-MeIm)(CO)] powder data appear to correspond to the out-of-plane modes identified at 172, 204, and 225 cm⁻¹ in [Fe(TPP)(1-MeIm)(CO)] (Fig. 3, b and d), suggesting that these modes are weakly perturbed by peripheral substituents. Single crystal measurements help to identify additional out-of-plane modes at 39, 64, and 127 cm⁻¹ for [Fe(TPP)(1-MeIm)(CO)].

In-plane modes

Each of the VDOS in Fig. 3 has a maximum in the 200–400 cm⁻¹ region. We previously associated prominent modes in this region with vibrations of the in-plane Fe-N_pyr bonds in deoxyMb (79), [Fe(TPP)(NO)] (85,86,90), [Fe(TPP)(2-MeHIm)] (87,93), and [Fe(TPP)(1-MeIm)(CO)] (93,88). NRVS measurements on oriented single crystals of CO-ligated porphyrins (Figs. 4 and 5 a) confirm the in-plane character of these modes.

In particular, the absence of the 320 and 338 cm⁻¹ features, which dominate the powder spectrum, in the out-of-plane VDOS of [Fe(TPP)(1-MeIm)(CO)] (Fig. 4) demonstrates the predominant contribution of in-plane Fe motion to the associated vibrational modes. Of these, only the 320 cm⁻¹ peak contributes to the experimental in-plane spectrum. The latter spectrum represents only one of two orthogonal in-plane directions, and these data suggest that the 338 cm⁻¹ mode primarily involves Fe motion along the other in-plane direction. For additional pairs of in-plane modes at 241, 413, 466, and 587 cm⁻¹, the frequency difference appears to be too small to resolve experimentally.

COMPUTATIONAL RESULTS

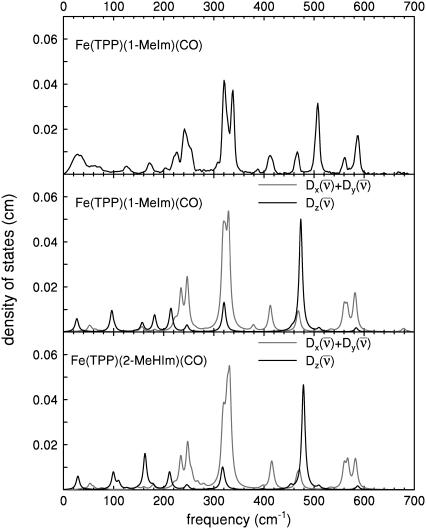
Further insight into the vibrational dynamics results from comparing the experimental results on [Fe(TPP)(1-MeIm)(CO)] with DFT predictions on [Fe(TPP)(1-MeIm)(CO)] and [Fe(TPP)(2-MeHIm)(CO)] (Fig. 6). A number of DFT calculations have been reported for six-coordinate imidazole-CO complexes of porphine (30,38,39,95,98,118–121) rather than tetraphenylporphyrin. However, experimental data in Fig. 3 indicates that the porphyrin peripheral groups significantly influence the Fe vibrational dynamics, as we previously found for five-coordinate iron nitrosyl porphyrins (90). The influence of the peripheral groups is also apparent upon comparison of NRVS spectra recorded on a model compound and on MbCO, which contains protoporphyrin IX (Fig. 3, a, b, and d). Therefore, it is crucial to perform DFT calculations on the complete molecule rather than on a truncated model system. Comparison with NRVS data provides a detailed, rigorous, test of DFT vibrational predictions, as previously shown for [Fe(TPP)(NO)] (90).

FIGURE 6.

Comparison between the measured powder VDOS for [Fe(TPP)(1-MeIm)(CO)] (upper panel), and predicted VDOS for [Fe(TPP)(1-MeIm)(CO)] (center panel) and [Fe(TPP)(2-MeIm)(CO)] (lower panel). In-plane contribution is shown in shaded representation, and out-of-plane contribution in solid representation. Predicted VDOS are convolved with an 8 cm⁻¹ Lorentzian.

The optimized structure correctly reproduces several structural parameters (Table 3), including the linear FeCO geometry (29,30,33,35,38,122). All 3N − 6 = 267 predicted vibrational normal modes have real frequencies, ranging between 10 and 3317 cm⁻¹. Just 24 modes contribute 93% of the area of the total predicted Fe VDOS. 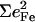for the modes above 800 cm⁻¹ is smaller than 0.02, suggesting that the experimental range 0–800 cm⁻¹ is large enough to offer a comprehensive picture of the Fe vibrational dynamics.

There is overall agreement between the experimental and the predicted vibrational spectra on the same absolute vertical scale without frequency scaling (Fig. 6). We previously suggested a correspondence between the predicted modes and the major experimental features (93) for [Fe(TPP)(1-MeIm)(CO)].

In general, DFT predictions for [Fe(TPP)(1-MeIm)(CO)] and [Fe(TPP)(2-MeHIm)(CO)] (Fig. 6) confirm the character of the vibrational modes determined experimentally from NRVS spectra. In addition to vibrational frequencies and amplitudes, the vibrational predictions are consistent with information on the direction of Fe motion derived from single crystal measurements. Modes above 500 cm⁻¹ are associated with the FeCO group, in-plane Fe-N_pyr vibrations dominate the 300–400 cm⁻¹ region, and Fe motion is predominantly out-of-plane for modes with frequencies below 220 cm⁻¹. The most apparent difference is the 474 cm⁻¹ frequency predicted for the Fe-CO stretching mode of [Fe(TPP)(1-MeIm)(CO)], 33 cm⁻¹ lower than the observed value. Similarly, the Fe-NO vibration was the most significant error in the previously published [Fe(TPP)(NO)] calculation (90). Somewhat unexpectedly, an out-of-plane mode is predicted at 320 cm⁻¹, in a region otherwise dominated by in-plane modes. Observation of an out-of-plane 331 cm⁻¹ peak in the single crystal data (Fig. 4, middle panel) is consistent with this prediction.

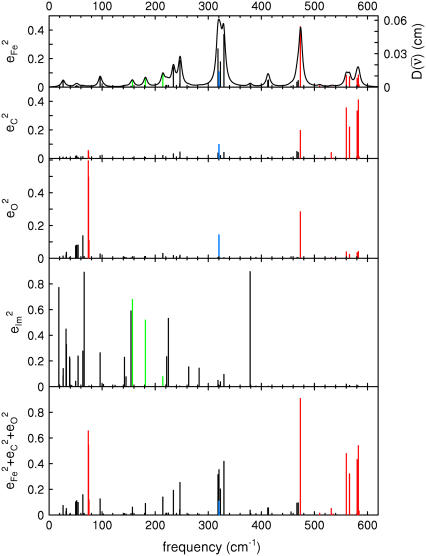
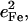
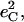
Fig. 7 describes the predicted KED over the Fe and axial ligands of in [Fe(TPP)(1-MeIm)(CO)] in terms of the values 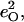and the sum 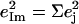over all 12 atoms of the 1-MeIm group. Colors highlight modes with significant involvement of the axial ligands. Green bars represent the 157, 182, and 214 cm⁻¹ modes, which involve significant imidazole motion (i.e., 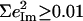) as well as significant Fe motion perpendicular to the porphyrin plane (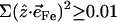). Red bars identify the predicted FeCO stretching mode at 474 cm⁻¹ and modes at 560, 566, 580, and 583 cm⁻¹ with FeCO bending character (Fig. 8). Also shown in red are the in-phase bend-tilt FeCO modes (38,98) at 74, 74.5, and 75.3 cm⁻¹. The 320 cm⁻¹ mode involves Fe-CO translation against the rest of the molecule (Fig. 9).

FIGURE 7.

Predicted KED over Fe, carbonyl C and O, and imidazole atoms (which includes all the 12 atoms on the 1-MeIm group) for [Fe(TPP)(1-MeIm)(CO)]. The heights of the individual bars equal the fraction of the kinetic energy associated with each atom or group. The lower panel shows the sum of the mode composition factors for Fe, C, and O, and gives the fraction of mode energy localized on the FeCO fragment. Green bars indicate Fe-Im modes, and red bars FeCO modes.

FIGURE 8.

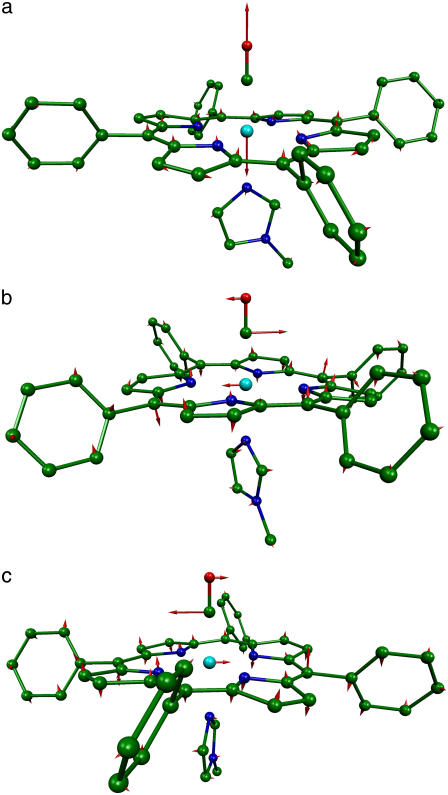
Predicted high frequency vibrational modes of the FeCO fragment of [Fe(TPP)(1-MeIm)(CO)] with frequencies (a) 474 cm⁻¹, (b) 560 cm⁻¹, and (c) 580 cm⁻¹. The relative phase of the FeCO bending and porphyrin motions reverses between the 560 cm⁻¹ and 580 cm⁻¹ modes. In this and subsequent figures, each arrow is 100(m_j/m_Fe)^1/2 times longer than the zero-point vibrational amplitude of atom j, and the bonds to the Fe are omitted to enhance the visibility of the Fe motion.

FIGURE 9.

Predicted vibrational modes of [Fe(TPP)(1-MeIm)(CO)] with frequencies (a) 157 cm⁻¹, (b) 182 cm⁻¹, (c) 214 cm⁻¹, and (d) 320 cm⁻¹ involve Fe-Im motion.

Two low-frequency [Fe(TPP)(1-MeIm)(CO)] modes resemble vibrations also predicted for [Fe(TPP)(NO)] (90). A “doming” mode predicted at 96 cm⁻¹ involves translation of the [Fe(TPP)(1-MeIm)(CO)] fragment coupled with swiveling of the four pyrrole groups to allow the nitrogens to follow the motion of the Fe. A predicted mode with a 26 cm⁻¹ frequency involves translation of the entire porphyrin core, accompanied by motion of the four phenyl groups in the opposite direction.

The predictions for [Fe(TPP)(1-MeIm)(CO)] and [Fe(TPP)(2-MeHIm)(CO)] are similar overall (Fig. 6, Table 3), but closer examination reveals both structural and vibrational differences. In particular, the Fe-Im bond length increases by 9 pm in the optimized [Fe(TPP)(2-MeHIm)(CO)] structure, presumably to minimize nonbonded interactions between the porphyrin and the methyl group on the imidazole. Vibrational modes involving the axial ligands have altered frequencies and Fe amplitudes. The predicted 5 cm⁻¹ increase of the Fe-CO frequency to 479 cm⁻¹ in [Fe(TPP)(2-MeHIm)(CO)] reflects a 1 pm decrease in the Fe-CO bond length (Table 3).

On the other hand, the 9 pm increase of the Fe-Im bond length is correlated with modest decreases of the 182, 214, and 320 cm⁻¹ frequencies predicted for [Fe(TPP)(1-MeIm)(CO)]. The frequencies predicted for the first two vibrations are 179 and 212 cm⁻¹ for [Fe(TPP)(2-MeHIm)(CO)], while an unresolved pair of modes (317 and 319 cm⁻¹) replace the 320 cm⁻¹ mode predicted for [Fe(TPP)(1-MeIm)(CO)]. The splitting of the latter mode reflects vibrational interaction with a porphyrin vibration.

The DFT calculations predict frequency changes for several modes involving rotation of the Im ligand, from 157, 263, 283, and 379 cm⁻¹ in [Fe(TPP)(1-MeIm)(CO)] to 163, 268, 280, and 398 cm⁻¹ in [Fe(TPP)(2-MeHIm)(CO)], perhaps reflecting the increased steric interaction of the methyl group with the porphyrin. The Fe amplitudes predicted for some of these modes also change. For [Fe(TPP)(1-MeIm)(CO)], the predicted Fe amplitude is slightly smaller for the 157 cm⁻¹ than for the 181 cm⁻¹ mode (Table 4), while for [Fe(TPP)(2-MeHIm)(CO)] the mean-squared amplitude predicted for the 163 cm⁻¹ mode (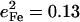) is greater than four times larger than for the 179 cm⁻¹ mode (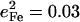). Substitution with 2-MeHIm also increases the Fe amplitude predicted for the 268 and 280 cm⁻¹ modes with respect to the corresponding modes (263 cm⁻¹ and 283 cm⁻¹) in [Fe(TPP)(1-MeIm)(CO)].

TABLE 4.

Predicted ImFeCO kinetic energy distribution for Fe(TPP)(1-MeIm)(CO)

Frequency (cm−1)		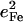		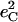		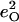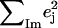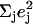Frequency (cm−1)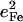
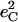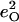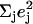	0.05	0.01	0.01	0.09	0.16	321	0.02	0.00	0.00	0.01	0.03
50	0.01	0.02	0.08	0.04	0.15	323	0.18	0.02	0.00	0.04	0.24
52	0.01	0.02	0.08	0.00	0.11	329	0.37	0.04	0.01	0.10	0.52
55	0.01	0.01	0.08	0.24	0.34	379	0.02	0.02	0.00	0.90	0.94
64	0.01	0.01	0.14	0.28	0.44	412	0.05	0.01	0.00	0.00	0.06
96	0.08	0.02	0.03	0.27	0.39	413	0.05	0.01	0.00	0.01	0.06
157	0.05	0.01	0.01	0.68	0.74	467	0.04	0.05	0.01	0.00	0.09
182	0.07	0.01	0.01	0.52	0.61	469	0.05	0.04	0.01	0.00	0.10
214	0.09	0.02	0.03	0.08	0.22	474	0.43	0.20	0.29	0.00	0.91
234	0.14	0.03	0.02	0.00	0.20	560	0.08	0.36	0.04	0.02	0.50
247	0.19	0.05	0.02	0.00	0.26	566	0.08	0.22	0.03	0.01	0.33
318	0.27	0.04	0.01	0.05	0.37	580	0.06	0.33	0.04	0.01	0.44
320	0.11	0.10	0.15	0.00	0.36	583	0.09	0.41	0.04	0.01	0.55

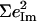is equal to the sum of the mode composition factors for all the 12 atoms in the imidazole group. All modes with 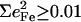are included.

DISCUSSION

Identification of Fe-ligand vibrations

Comparison of experimental and theoretical approaches yields a detailed description of the vibrational dynamics of the ⁵⁷Fe probe nucleus. Quantitative experimental information on the amplitude and direction, as well as the frequency, of Fe motion provides a rigorous test of vibrational predictions. In turn, the quantum chemical vibrational predictions presented here reproduce most features of this data set and thus serve as a reliable guide to identifying the observed Fe vibrations. We identify and describe all vibrational modes with significant involvement of Fe and its nearest neighbors, most of which have not been reported previously.

Because ⁵⁷Fe NRVS reveals the complete Fe vibrational spectrum, all Fe-ligand vibrations contribute to the observed signal, and in fact dominate the experimental spectra. In contrast, porphyrin modes dominate the Raman signal recorded in resonance with porphyrin π → π* electronic transitions, and the Fe-CO stretching vibration is the only Fe-ligand vibration previously identified using Raman spectroscopy for the compounds investigated here. Even for the Fe-CO stretch, careful measurements of isotope sensitivity reveal additional unresolved porphyrin vibrations in the same frequency region of the Raman spectrum (123).

Both experimental and computational results support the identification of modes we observe in the 560–590 cm⁻¹ range with FeCO bending, although the KED differs significantly from the expectations of a simple three-body model (see below). The prominent contribution of these modes to the NRVS signal clearly identifies them as vibrational fundamentals. This disagrees with the proposed assignment of modes in this region to a vibrational overtone (69) or combination (67,68) involving a lower frequency FeCO bending fundamental. In fact, the observed modes at 561 and 587 cm⁻¹ are 20 times larger than weak two-quantum vibrational excitations that we recently reported for [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(1-MeIm)(CO)] (93).

Antisymmetric stretching vibrations of the Fe-N_pyr bonds, analogous to the ν₅₃ modes predicted for Fe(P) (94), dominate the NRVS signal in the 300–350 cm⁻¹ frequency range. Our previous empirical calculation on [Fe(TPP)(1-MeIm)(CO)] (88) modeled this frequency region with two in-plane modes. The present calculation predicts a more complex situation. In addition to four in-plane modes, at 318, 323, 321, and 329 cm⁻¹ (Fig. 10), an out-of-plane mode is predicted in this region at 320 cm⁻¹ (Fig. 9). The total predicted contribution to for these five modes is 0.95 (Table 4), comparable to the sum 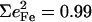of the areas of the observed features at 320/326 and 338 cm⁻¹ (Table 1).

FIGURE 10.

Predicted in-plane vibrational modes of [Fe(TPP)(1-MeIm)(CO)] with frequencies (a) 318 cm⁻¹ and (b) 329 cm⁻¹, as viewed looking from the CO to the imidazole.

The situation shares some similarities with our previous investigation (90) of the five-coordinate complex [Fe(TPP)(NO)], where we found four predicted in-plane modes corresponding to two observed features in this region of the VDOS. However, the present [Fe(TPP)(1-MeIm)(CO)] calculation predicts little CO motion associated with the in-plane modes (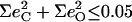 for each of the predicted 318, 321, 323, and 329 cm⁻¹ modes), in contrast with [Fe(TPP)(NO)] (90), in which two of the in-plane modes in this region had some FeNO bending character. In addition, the 331 cm⁻¹ mode observed in single crystal data on [Fe(TPP)(1-MeIm)(CO)] (middle panel in Fig. 4) confirms the predicted additional out-of-plane mode.

As we noted previously for ferrous nitrosyl porphyrins (90), changes at the periphery of the porphyrin influence the in-plane vibrations. Comparison of the VDOS for [Fe(TPP)(1-MeIm)(CO)], [Fe(OEP)(1-MeIm)(CO)], and MbCO (Fig. 3) reveals both frequency and intensity changes for the dominant vibrational features, although the maximum signal remains in the 320–350 cm⁻¹ region. Changes in relative intensity upon substitution of the imidazole ligand are smaller, but noticeable (Figs. 5 and 6).

We are particularly interested in characterizing the Fe-Im modes, which have not been clearly identified for low spin heme complexes with diatomic ligands bound trans to the imidazole (although symmetric Im-Fe-Im stretching modes were reported between 182 and 226 cm⁻¹ in the Raman spectra of several 6-coordinate bis-imidazole Fe(II) porphyrins(124–126) and bis-histidine ligated heme proteins (127,128)). Raman frequencies sensitive to Fe isotope are occasionally reported for diatomic ligand complexes with heme proteins, including Chironomus HbCO (317 cm⁻¹) (129) and MbO₂ (263 cm⁻¹) (130), as well as ferric cyanide complexes with Chironomus Hb (309 cm⁻¹) (131) and Chlamydomonas Hb (315 cm⁻¹) (132), but the Fe isotope shift does not distinguish Fe-Im modes from in-plane Fe vibrations that we observe in the same frequency region. No modes sensitive to isotope labeling of the imidazole were identified in the Raman spectra of metMb or MbCO (133).

A previous analysis of the [Fe(TPP)(1-MeIm)(CO)] powder data, based on an empirical calculation (88), located the Fe-Im stretching mode at 226 cm⁻¹ and the Fe-Im bending mode at 172 cm⁻¹. Again, the present measurements and calculations portray a more complex picture. NRVS data on an oriented single crystal [Fe(TPP)(1-MeIm)(CO)] reveal several modes with out-of-plane character at 331 cm⁻¹ and below (middle panel in Fig. 4, Table 1), in addition to the FeCO modes discussed above.

DFT calculations for [Fe(TPP)(1-MeIm)(CO)] predict six out-of-plane Fe modes below 400 cm⁻¹ (Fig. 6, middle panel), with the 157, 182, and 214 cm⁻¹ modes (Fig. 9) involving both iron and imidazole motion (green bars in Figs. 7 and 9). However, none of them is a pure Fe-Im stretching mode, and each has an 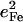value (Table 4) significantly lower than predicted for a two-body Fe-Im oscillator (0.59).

A similar distribution of Fe-Im mode character among multiple vibrational modes appeared in previous calculations on truncated model porphyrins (121). Calculations on five-coordinate porphine also predict significant mixing between Fe-Im stretching and pyrrole tilting modes (96), consistent with an analysis of all available isotope data for deoxyMb, which suggested that the Fe-His vibration could not be described as a simple two-body oscillator (133).

The 331 cm⁻¹ mode is obscured by in-plane modes in the powder spectrum, but is clearly revealed in the single crystal data (Fig. 4). The corresponding shoulder at 326 cm⁻¹ in the fit to the powder data has an area 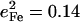(Table 1), comparable to the 0.11 value for the predicted out-of-plane mode at 320 cm⁻¹ (Fig. 6, Table 4). This mode, not identified in the empirical calculation (88), involves the translation of the FeCO group relative to the rest of the molecule, with consequent stretching of the Fe-Im bond but insignificant imidazole motion (Fig. 9).

Deviations from axial symmetry

For the iron carbonyl porphyrins investigated here, the imidazole ligand perturbs the approximate fourfold symmetry of the iron environment imposed by the symmetric porphyrin and the linear FeCO geometry. On the other hand, asymmetrically placed peripheral substituents on naturally occurring hemes and steric or electrostatic interactions with the local environment may further lower the symmetry in heme proteins. The vibrational properties of the more nearly symmetric compounds investigated here thus provide an important baseline for further studies of heme interactions with protein environments.

Frequency splittings between in-plane vibrational modes are sensitive to departures from strict fourfold symmetry, where in-plane vibrations would occur as degenerate pairs with equal Fe amplitudes. As discussed above, both single crystal measurements and DFT predictions provide evidence for significant deviations from fourfold symmetry for the dominant experimental features in the 300–340 cm⁻¹ region. The frequency splitting of a pair of modes approximately related by a 90° rotation in the porphyrin plane, predicted at 234 cm⁻¹ (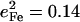) and 247 cm⁻¹ (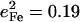), is in reasonable agreement with the separation between the corresponding observed peaks at 241 cm⁻¹ (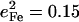) and 251 cm⁻¹ (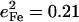) (Table 1). At higher frequencies, predicted frequency splittings at 412/413, 467/469, 560/566, and 580/583 cm⁻¹ are too small to directly resolve in the powder data, given the 7–8 cm⁻¹ experimental frequency resolution, although the frequencies and areas correspond well with observed features at 413, 466, 561, and 587 cm⁻¹. For [Fe(TPP)(1,2-Me₂Im)(CO)], however, spectral differences between powder and single crystal data suggest unresolved frequency splitting for the FeCO bending modes at 587 cm⁻¹ (Fig. 5).

The prominent NRVS signal due to FeCO bending vibrations for these symmetric model compounds contrasts with the absence of these modes in Raman spectra of the same compounds (115–117). The FeCO bending mode is IR active and has been reported at 574 cm⁻¹ in the IR spectrum of [Fe(OEP)(Py)(CO)] (63). However, Raman selection rules forbid resonance enhancement of these nontotally symmetric vibrations for fourfold symmetric model compounds (113,115–117), and the symmetry lowering due to the imidazole ligand in molecules such as [Fe(TPP)(1-MeIm)(CO)] is apparently insufficient to remove this restriction. The observation of FeCO bending vibrations in the Raman spectra of numerous proteins (114,115), and of porphyrins with superstructures that interact with the bound CO (115–117), has been attributed to interactions with the CO ligand that lower the molecular symmetry (56,57). For example, investigation of a series of porphyrins with a hydrocarbon chain strapped across the face of the heme showed that shorter straps led both to greater distortion of FeCO from linearity and to increased Raman enhancement for the FeCO bending vibration, resulting in a suggestion that the intensity ratio of the FeCO bending and Fe-CO stretching bands is a spectral indicator for FeCO distortion (57,117,134).

In the absence of direct evidence that both FeCO bending modes contribute to the observed Raman signal, it has been unclear whether the asymmetric protein environment separates the frequencies of the two FeCO bending vibrations, which would be degenerate for a fourfold symmetric molecule. For the compounds considered here, the imidazole ligand removes the symmetry, but calculations have differed as to the predicted magnitude of the resulting frequency splitting between the FeCO bending modes. Previous DFT calculations on Fe(P)(Im)(CO) identified two FeCO bending modes at 559 and 573 cm⁻¹ (121), and at 572 and 578 cm⁻¹ (98), respectively. An empirical calculation modeled the NRVS bands at 561 and 586 for [Fe(TPP)(1-MeIm)(CO)] as two bending modes, with motions orthogonal to each other, and no mixing with porphyrin distortions was reported (88). We observe similar frequency splittings for [Fe(TPP)(1,2-Me₂Im)(CO)] and [Fe(TPP)(1-PhIm)(CO)] (Table 1).

On the other hand, the observation of single bands near 580 cm⁻¹ for [Fe(OEP)(1-MeIm)(CO)] and for MbCO suggests that the frequency splitting between the two FeCO bending modes is too small to resolve. For MbCO, this disagrees with the ∼30 cm⁻¹ splitting predicted by a recent QM/MM calculation (41). The present DFT calculations for [Fe(TPP)(1-MeIm)(CO)] predict that the directions of Fe, C, and O vibrations for the predicted 580 cm⁻¹ mode are nearly orthogonal to those in the 583 cm⁻¹ mode, but the 3 cm⁻¹ frequency splitting is too small to resolve experimentally. A similar description holds for the predicted 560 cm⁻¹/566 cm⁻¹ mode pair. Instead, the large frequency separation between the 560 cm⁻¹/566 cm⁻¹ and 580 cm⁻¹/583 cm⁻¹ mode pairs results from mixing of the two FeCO bending modes with a degenerate pair of porphyrin distortion modes (Fig. 8), rather than from x–y splitting. Comparison with the experimental data suggests that each of the experimental features observed at 561 cm⁻¹ and 586 cm⁻¹ corresponds to an unresolved pair of modes involving FeCO bending.

Mode localization and limitations of simplified empirical models

Simplified empirical potentials have often been used to model the limited vibrational information available from traditional techniques, and the vibrational KED provides a method to evaluate such approaches. In particular, experimental results directly characterize the KED over the FeCO fragment. Mode composition factors 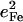are determined directly from NRVS data, while reported isotope shift measurements yield estimates for 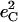and 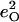according to Eq. 3.

Isotope shifts reported (116) for the picket-fence porphyrin [Fe(TP_pivP)(1-MeIm)(CO)] yield estimates 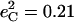and 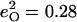for the CO fragment, while NRVS results reported here on the closely related [Fe(TPP)(1-MeIm)(CO)] find 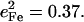The resulting KED suggests that the Fe-CO stretching oscillation is almost entirely localized on the FeCO group, with 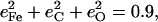in good agreement with the predicted sum 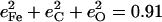in [Fe(TPP)(1-MeIm)(CO)] (Table 4). The values 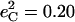and 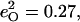calculated with Eq. 3 from ¹³C and ¹⁸O frequency shifts predicted for the truncated molecule [Fe(P)(Im)(CO)] (98), also agree well with the predicted values for the 474 cm⁻¹ mode in [Fe(TPP)(1-MeIm)(CO)] (Table 4).

The observed mode composition factors 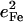range between 0.30 and 0.37 (Table 2), comparable to the value 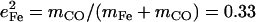expected for a simple two-body Fe-CO oscillator, but somewhat smaller than the value 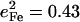predicted for [Fe(TPP)(1-MeIm)(CO)] (Table 4). A similar value 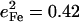results (Eq. 3) from the 3.8 cm⁻¹ frequency shift predicted for ⁵⁶Fe → ⁵⁴Fe substitution in an empirical calculation carried on a four-body ImFeCO oscillator (56). Together, these results suggest that the Fe-CO mode is sufficiently localized that simplified models may provide an adequate description.

However, simplified models fail to describe other vibrational modes. The area of the 581 cm⁻¹ feature attributed to FeCO bending is 0.29 for [Fe(OEP)(1-MeIm)(CO)], a value comparable to the total areas 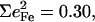0.26, and 0.30 of the two features attributed to FeCO bending in [Fe(TPP)(1-MeIm)(CO)], [Fe(TPP)(1,2-Me₂Im)(CO)], and [Fe(TPP)(1-PhIm)(CO)], respectively (Table 2). The predicted sum 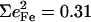for the four corresponding modes of [Fe(TPP)(1-MeIm)(CO)] (Table 4), is almost identical to the total area 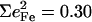of the two experimental features (Table 2). Similar results are predicted for [Fe(TPP)(2-MeHIm)(CO)].

In all cases, the total areas 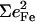observed for the bending modes (Table 2) are much higher than the value 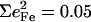expected for a simple three-body FeCO oscillator (Appendix). A four-body calculation with an additional mass representing the imidazole (56) yielded two FeCO bending frequencies at 583.7 cm⁻¹ that shift 0.6 cm⁻¹ upon ⁵⁶Fe → ⁵⁴Fe substitution, corresponding to 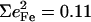(Eq. 3), still significantly lower than the values determined from NRVS measurements (Table 2).

We conclude that such simple models do not adequately describe the FeCO bending modes. Our measurements qualitatively support previous DFT calculations carried on [Fe(P)(Im)(CO)] (38,98), which described the FeCO bending mode as an out-of-phase combination of FeCO bending and tilting of the Fe–C bond with respect to the porphyrin, attributed to a large bend-tilt interaction constant. The corresponding in-phase bend-tilt combination, predicted at 84 cm⁻¹ (38) or 73 cm⁻¹ (98), is discussed below.

Our results indicate that simplified models will also fail to describe other Fe-ligand modes. Although the prominent in-plane vibrations can be qualitatively described as due to stretching of the Fe-N_pyr bonds, these vibrations also involve substantial porphyrin distortion and cannot be described by a simplified model. Similarly, none of the modes with predicted Fe-Im contributions (Fig. 9) represents a two-body Fe-Im oscillation. The observed areas of all out-of-plane modes (Table 1) are substantially smaller than either the 0.59 expectation for a two-body Fe-Im oscillator or the 0.20 value calculated (Eq. 3) from the 0.9 cm⁻¹ shift of the Fe-Im stretching frequency reported upon ⁵⁶Fe → ⁵⁴Fe substitution in a slightly more complex four-body ImFeCO oscillator (56).

Vibrational probes of Fe coordination

In general, stretching frequencies are expected to be sensitive probes for the strength of the corresponding bonds. For example, high precision structural data on a series of iron carbonyl porphyrins revealed an inverse correlation between the C-O bond length and the C-O stretching frequency (100). The results presented here further support the expected sensitivity of Fe-ligand vibrational frequencies to the coordination geometry of the Fe.

The high sensitivity of both C-O and Fe-CO frequencies to the local environment, and to the local electrostatic field in particular, is well established (10,57,61,62,135,136). It is likely that intermolecular interactions in the crystal contribute to the high Fe-CO frequencies observed here in the solid state (Table 2) with respect to the 486, 494, and 496 cm⁻¹ frequencies reported for [Fe(TPP)(1-MeIm)(CO)], [Fe(TPP)(1,2-Me₂Im)(CO)], and [Fe(OEP)(1-MeIm)(CO)], respectively, in solution (116). Intermolecular interactions also lead to variations in the length and frequency of the C-O bond (100). For example, the methyl group on the imidazole of a neighboring molecule interacts with the carbonyl oxygen in the [Fe(TPP)(1,2-Me₂Im)(CO)] crystal. The presence of two imidazole orientations plausibly accounts for the presence of two C-O stretching (100) and two Fe-C stretching (Table 1) frequencies in this crystal. Apparent discrepancies between predicted and observed frequencies may also reflect solid state interactions. Indeed, the 474 cm⁻¹ Fe-CO stretching frequency predicted for [Fe(TPP)(1-MeIm)(CO)] in vacuum (Fig. 8) is much closer to the reported (116) 486 cm⁻¹ solution frequency than to the 507 cm⁻¹ frequency observed in the crystalline state (Table 2).

Prominent contributions to the 200–300 cm⁻¹ region of NRVS data on heme proteins and porphyrins involve antisymmetric stretching of the bonds to the pyrrole nitrogens, and the frequencies are highly sensitive to the Fe-N_pyr bond length. For the six-coordinate, low-spin CO complexes [Fe(OEP)(1-MeIm)(CO)] (200 pm) (137) and [Fe(TPP)(1-MeIm)(CO)] (200 pm) (100,138), the Fe-N_pyr bonds are significantly shorter than in the five-coordinate, high-spin compounds [Fe(OEP)(2-MeHIm)] (208 pm) (102) and [Fe(TPP)(2-MeHIm)] (208 pm) (139). NRVS observations confirm the large shift to higher frequencies expected for the much shorter in-plane bonds (Fig. 3, b–e). On the other hand, the 200 pm Fe-N_pyr bond length reported for [Fe(OEP)] (140) is identical to that of the CO complexes, and the dominant vibrations appear in the same frequency region of the VDOS (Fig. 3).

Axial ligand modes in heme proteins are particularly valuable probes of the only covalent link to the protein. Strong Raman enhancement of the Fe-Im stretching frequency in the 200–250 cm⁻¹ region has proved to be a very useful probe of this bond for five-coordinate histidine-ligated heme proteins (65,113,133,141–145), but efforts to identify the corresponding frequency in six-coordinate systems have been inconclusive. For hemoglobin, the Fe-Im bond is believed to mediate structural changes in the protein structure upon ligand binding (46,47). The Fe-Im frequency is sensitive to H-bonding of the His imidazole in peroxidases (146).

The present results identify several out-of-plane Fe vibrations involving the imidazole ligand, although none can be described as a simple two-body vibration. Nevertheless, measurements and calculations suggest that the frequencies of the features observed at 172, 225, and 331 cm⁻¹ in [Fe(TPP)(1-MeIm)(CO)] have modest sensitivity to the Fe-Im bond length. Experimentally, features corresponding to the first two appear 4 cm⁻¹ lower, at 168 cm⁻¹ and 221 cm⁻¹, in the VDOS of [Fe(TPP)(1,2-Me₂Im)(CO)], for which the Fe-Im bond is 9 pm longer than for [Fe(TPP)(1-MeIm)(CO)] (Table 3). Computationally, replacement of 1-MeIm with 2-MeHIm also increases the predicted Fe-Im bond length by 9 pm and leads to a 2 cm⁻¹ downshift in all three corresponding predicted modes at 182, 214, and 320 cm⁻¹ (Fig. 9).

Quantum chemical description of reaction energetics

Most chemical reactions are driven by thermally induced atomic fluctuations that carry the reacting molecules along the ground state energy surface toward a transition state. Because vibrational spectroscopy yields quantitative information about motion on this surface, it can provide insight into reactive dynamics and the influence of the molecular environment. Vibrations with frequencies below 200 cm⁻¹, which can be thermally excited at physiological temperatures, can contribute to the reactive dynamics of the molecule.

The “doming” motion of the heme upon diatomic ligand binding to heme proteins holds particular interest. This motion was a central element of Perutz's early model for hemoglobin cooperativity (46), and continues to play an important role in models for protein control of reactions at the active sites of heme proteins (47,147–149). Atomic motions in the vibrational mode predicted at 96 cm⁻¹ for [Fe(TPP)(1-MeIm)(CO)] closely resemble structural changes that take place upon diatomic ligand binding to heme proteins (Fig. 11). Specifically, the Fe atom moves perpendicular to the mean plane of the heme, and the four pyrrole groups swivel to follow the Fe. Experimental identification of this frequency would be a crucial step toward quantifying the energetics of this molecular distortion and evaluating its contribution to controlling reactions at heme protein active sites.

FIGURE 11.

Predicted [Fe(TPP)(1-MeIm)(CO)] modes with frequencies (a) 74 cm⁻¹ and (b) 96 cm⁻¹ involve thermally accessible FeCO distortion and heme doming motions relevant to biological reactivity.

NRVS is ideally suited to probe the dynamics of the Fe in this frequency range, which is dominated by motion perpendicular to the porphyrin plane for [Fe(TPP)(1-MeIm)(CO)] (Fig. 4). The out-of-plane density of states determined for an oriented single crystal clearly distinguishes features at 39, 64, and 127 cm⁻¹ from a quasicontinuous background that depends weakly on crystal orientation and has an area consistent with expectations for lattice vibrations. (It is possible that more than one vibration contributes to the broad feature at 64 cm⁻¹.) These features can be compared with vibrational properties predicted from DFT calculations performed on an isolated molecule, for which translational (and rotational) motions appear at zero frequency and do not interfere.

Below 150 cm⁻¹, it becomes difficult to draw a one-to-one correspondence between observed and predicted vibrations. Nevertheless, the predictions (Fig. 6) reproduce the qualitative observation (Fig. 4) that out-of-plane Fe motion dominates the low frequency region. We propose that heme doming contributes strongly to the observed features at 64 and 127 cm⁻¹, which bracket the predicted 96 cm⁻¹ frequency of the heme doming mode. We suggest that the 37 cm⁻¹ mode resembles a mode with a predicted 27 cm⁻¹ frequency that involves translation of the porphyrin core perpendicular to its mean plane, counterbalanced by motion of the four phenyl groups in the opposite direction. The latter mode is presumably not relevant to the reactive dynamics of naturally occurring hemes, which lack the phenyl groups.

An analogous situation occurred during our previous investigations of [Fe(TPP)(NO)], where we identified experimental features at 74 and 128 cm⁻¹ as likely candidates for heme doming (85). Later measurements on oriented [Fe(TPP)(NO)] crystals (86) and DFT calculations (90) confirmed the out-of-plane character of these modes. Comparison with the calculations led us to associate the observed 74 and 128 cm⁻¹ features with modes due to hindered NO rotation and porphyrin doming predicted at 77 cm⁻¹ and 109 cm⁻¹, with the latter vibration responsible for the primary contribution to the Fe motion (90).

The present observation of modes with similar properties (frequency, amplitude, and direction) for [Fe(TPP)(1-MeIm)(CO)] indicates that these vibrations are relatively insensitive to the altered axial ligation, consistent with the primary involvement of porphyrin distortion. These modes will dominate the energetics of thermally driven Fe displacement perpendicular to the porphyrin plane, independent of the detailed normal mode description.

Another motion that has been considered to influence the energetics of ligand binding to heme proteins is the distortion of the FeCO unit due to steric crowding in the protein environment. Although once proposed as a primary factor in preventing inactivation of oxygen-binding sites by CO, this factor is being reevaluated in the light of experimental and theoretical investigation over the past decade. Infrared crystallographic measurements (33,35), confirmed by careful analysis of infrared photoselection measurements (34), by other spectroscopic measurements (137), and ultimately by high-resolution x-ray structures (36,37), indicate that the distortion of the FeCO unit in MbCO is much smaller than in early structural models based on lower resolution x-ray diffraction data (150).

In parallel with revised structural information, quantum chemical calculations suggested that early calculations based on the FeCO bending frequency observed in resonance Raman measurements significantly overestimate the energy required to distort the FeCO unit (38,39). Together, the revised structural and energetic information suggests that electrostatic stabilization of bound O₂ has a stronger influence than steric destabilization of bound CO on the discrimination between these two ligands by heme proteins (29). Nevertheless, the energetic cost of FeCO distortion may be large enough to have physiological consequences (9). Experimental evidence for these quantum chemical predictions would complete the picture and permit a reliable quantitative assessment of the contribution of FeCO distortion to CO affinity in heme proteins.

In addition to the FeCO bending modes discussed above, which are the highest frequency contributions to the observed NRVS signal, the calculations predict a pair of modes with 74 and 75 cm⁻¹ frequencies that involve distortion of the FeCO unit from linearity (Fig. 11). These modes are strongly localized on the FeCO fragment, with >50% of the mode energy associated with motion of the carbonyl oxygen atom (Fig. 7), perpendicular and parallel to the plane of the imidazole, respectively.

Calculations on smaller models for imidazole-ligated heme-CO complexes described low frequency modes near 80 cm⁻¹ and high frequency modes near 580 cm⁻¹ as in-phase and out-of-phase combinations of bending and tilting of the FeCO fragment (38,39), somewhat analogous to the frustrated rotation and translation modes believed to control diffusion of CO on metal surfaces (151). The strong interaction between bending and tilting motions provided an explanation for the unusually high frequency of the observed vibrations near 580 cm⁻¹, and predicted as a corollary a low frequency mode that could accommodate distortion of the FeCO unit with a modest energetic cost (38,39). The NRVS results presented here provide direct experimental support for the quantum chemical description of the high frequency modes. This contrasts with simple empirical models that fail to describe the observed results accurately.

Our experimental observations thus qualitatively confirm the quantum chemical picture of FeCO distortion. However, comparison with low frequency experimental data also raises questions about the quantitative accuracy of the low frequency predictions. Unfortunately, the Fe amplitude predicted for the low frequency modes is too small to allow their direct observation in the NRVS data. This also implies that simple in-phase and out-of-phase combinations of the three-body bending and rotation modes (Table A1) do not provide an accurate description of the quantum chemical descriptions, since both high and low frequency modes would have significant Fe amplitudes. Other methods will be needed to determine the frequency of the low frequency FeCO distortion mode and establish an experimentally based estimate of the energetics of FeCO distortion.

APPENDIX: KINETIC ENERGY DISTRIBUTION FOR A LINEAR THREE-BODY OSCILLATOR

The coefficients 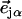governing the transformation 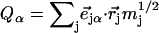to 3N normal coordinates Q_α from mass-weighted Cartesian coordinates 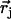of N atoms have a straightforward physical interpretation. In particular, the direction of the vector 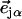is identical to the direction of motion of atom j when mode α is excited. Moreover, the squared magnitudes describe the kinetic energy distribution (KED) over the molecule, with 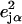equal to the fraction of kinetic energy associated with motion of atom j in mode α. This interpretation is consistent with the orthonormal character 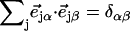of the transformation.

A simple linear three-body oscillator serves to illustrate the KED interpretation. In this case, the character of seven of the 3N = 9 normal modes can be deduced analytically from basic properties of the transformation matrix 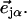This model has also been widely used to model the vibrational properties of diatomic ligands bound to heme proteins. The linear character allows independent consideration of motion along each Cartesian direction. There are three translational modes, each having a KED,

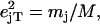(8)

simply weighted by the atomic masses, since all atoms have the same displacement. The presence of the total molecular mass 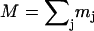in the denominator ensures normalization,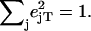

Similarly, the KED

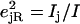(9)

of a rotational mode is weighted by the contributions 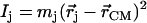of individual atoms to the total rotational inertia 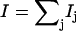of the molecule about a principal axis through the center of mass at 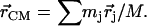A linear molecule has only two rotational modes, with principal axes (x, y) orthogonal to each other and to the molecular axis (z). Without loss of generality, we can number the atoms so that m₂ lies between m₁ and m₃ and define d₁ as the distance between m₁ and m₂ and d₃ as the distance between m₂ and m₃. Furthermore, we take the center of mass to lie between m₁ and m₂, a distance 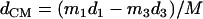from m₂. The resulting contributions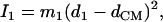 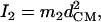and 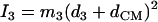to the rotational inertia define the rotational KED according to Eq. 9.

The remaining 3N − 5 = 4 normal modes are vibrations. Since neither rotational mode involves motion along z, there are N − 1 = 2 vibrational modes with atomic motion along z, in addition to the translational mode. Along x or y, there is one vibrational mode in addition to the rotational and translational mode. The orthonormality condition establishes the KED of the latter vibrational modes, which must be orthogonal to both rotational and translational motion; that is, 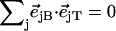and 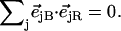The resulting restrictions, 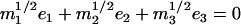and 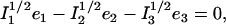completely determine the KED for the two degenerate vibrational modes as

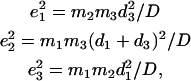(10)

with the denominator 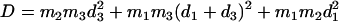ensuring normalization. (For simplicity, we suppress the mode index α.)

As a concrete example, consider the linear ⁵⁷FeCO oscillator that has often been used to model vibrational data on heme proteins (Fig. A1, Table A1). The masses m_Fe = 56.94, m_C = 12.00, and m_O = 15.99, determine the KED of the three translational modes, according to Eq. 8. Taking values for the interatomic distances d₁ = 176 pm between Fe and C and d₃ = 114 pm between C and O, which are typical for the CO-heme complexes considered in this article, determines the displacement d_CM = 96.5 pm of the center of mass toward the Fe from the central C atom. The resulting contributions I_Fe = 0.359 nm², I_C = 0.112 nm², and I_O = 0.709 nm² to the rotational inertia determine the KED of the two rotational modes according to Eq. 9. For the degenerate vibrational modes, the central C atom dominates the KED determined by the expressions in Eq. 10.

FIGURE A1.

Predicted KED for Fe-CO stretching and FeCO bending modes of a three-body FeCO oscillator.

TABLE A1.

Kinetic energy distribution for modes of a linear FeCO oscillator

Mode type	Degeneracy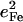
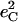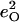Translation	3	0.670	0.141	0.188
Rotation	2	0.305	0.095	0.601
FeCO bending	2	0.025	0.764	0.211
C-O stretch	1	0.000	0.571	0.429
Fe-CO stretch	1	0.330	0.287	0.383

In general, determination of the two vibrational modes involving atomic motion parallel to the molecular axis requires additional information. However, because of the high C-O bond order and the large Fe mass, the motion of the Fe can be neglected (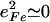) for the high frequency mode. In this approximation, the required orthogonality with translational motion requires that 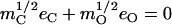and determines the KED of the high frequency C-O stretching mode as

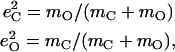(11)

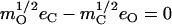with Continuing with this approximation, orthogonality with the high frequency mode as well as with translation then establishes restrictions, and 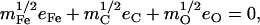that determine the KED of the remaining vibrational mode as

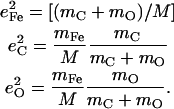(12)

In this approximation, both modes have the character of two-body oscillators. For the lower frequency Fe-CO vibration, the energy distribution between the C and O atoms is weighted proportionally to their masses, as expected for translation of the CO fragment. In contrast, the energy distribution between the Fe and CO is weighted inversely with their masses, mimicking the energy distribution between C and O masses in the higher frequency C-O oscillation.