Dwell Time Symmetry in Random Walks and Molecular Motors

Abstract

The statistics of steps and dwell times in reversible molecular motors differ from those of cycle completion in enzyme kinetics. The reason is that a step is only one of several transitions in the mechanochemical cycle. As a result, theoretical results for cycle completion in enzyme kinetics do not apply to stepping data. To allow correct parameter estimation, and to guide data analysis and experiment design, a theoretical treatment is needed that takes this observation into account. In this article, we model the distribution of dwell times and number of forward and backward steps using first passage processes, based on the assumption that forward and backward steps correspond to different directions of the same transition. We extend recent results for systems with a single cycle and consider the full dwell time distributions as well as models with multiple pathways, detectable substeps, and detachments. Our main results are a symmetry relation for the dwell time distributions in reversible motors, and a relation between certain relative step frequencies and the free energy per cycle. We demonstrate our results by analyzing recent stepping data for a bacterial flagellar motor, and discuss the implications for the efficiency and reversibility of the force-generating subunits.

INTRODUCTION

Progress in single molecule techniques has enabled observations of single steps in many motor proteins, and accurate measurement of the distribution of dwell times, i.e., the periods of little or no motion between steps. Examples are the forward and backward steps of processive molecular motors like kinesin (1–4), myosin V (5–8), cytoplasmic dynein (9), or RNA polymerase (10), and stepwise rotations in ATP synthase (11–17) and the flagellar motor (18). Observations of steps and dwell time distributions offer a route to gain insight into the microscopic mechanism and detailed motion of such systems, beyond what is available through knowledge of average turnover rates alone.

Dwell times are examples of first passage times, which have been extensively studied in the theory of random walks (19). An important modeling step is therefore to formulate a first passage problem describing the experimental situation. Close examination of step trajectories with high time resolution from several motor proteins (1–9,11–18) reveals that the steps are very rapid events compared to typical dwell times. In a discrete-state description, it is therefore reasonable to identify a step with a single transition, and the direction of the step with the direction of that transition (20,21). The identification of steps with single transitions follows naturally from the assumption that each state has a well-defined average position, and is a basic assumption in this article.

Motor proteins are cyclic enzymes, but contrary to earlier assumptions (22,23), the steps and waiting times obtained in many single-molecule experiments are not well described in terms of the cycle completions in enzyme kinetics. This was recently demonstrated for models where a single cycle accounts for both forward and backward steps (20). In this case, the average number of forward and backward steps differs from the average number of completed forward and backward cycles, and the average dwell times between steps differ from the average cycle completion times. The differences can be significant even in conditions where almost no backward steps occur. The basic reason for this difference is that a motor with one or more intermediate states per cycle is in a different state immediately after forward and backward steps. Therefore, an experimental trajectory of forward and backward steps does not give explicit information about completed forward and backward cycles.

The different states obtained just after forward and backward steps also implies that consecutive step directions are correlated (20). This prediction will be confirmed in a later section, where we analyze stepping data from Sowa et al. (18) for a flagellar motor, and find the clear step-step correlations shown in Fig. 8 b. In contrast, consecutive cycle completions are statistically independent (24,25).

FIGURE 8.

Analysis of stepping data from trajectory A. (a) Stepping data and result of step detection (staircase line). Grid lines indicate the theoretical step length d = 13.8°. Stepping is consistent with the theoretical step length in intervals interrupted by drift events (arrows), and adjacent intervals are out of phase with each other. (b) Step-step autocorrelation function as defined in Eq. 15. The measured correlation function (squares) is consistent with the theoretical prediction (circles) using conditional splitting probabilities from Table 1. Symbols are the same size as the estimated error bars. (c) Distribution functions P_±±(t) for the four different dwell times. All error bars show standard deviations from bootstrap estimates.

The observation that steps are correlated has important implications for the interpretation of stepping experiments, and also motivates further theoretical study of stepping statistics that goes beyond the assumption (26–28) of independent steps and dwell times. In this article, we extend the theory of Tsygankov et al. (20) in two ways. First, we consider the distributions of conditional dwell times instead of mean values. Second, we consider a larger class of models, including motor detachments, substeps, and multiple pathways.

Our main results are a distribution symmetry for conditional dwell times, and a simple relation between the dissipated free energy per cycle, ΔG, and certain conditional stepping probabilities. For a large number of models relevant to describe reversible motor proteins, we get

(1a)

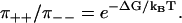(1b)

Here ρ₊₊(t) and ρ₋₋(t) are the probability density functions for the conditional dwell times between two consecutive forward and backward steps respectively, are the corresponding integrated probability functions, π₊₊ is the probability that a forward step is followed by another forward step, and π₋₋ that a backward step is followed by another backward step. The different types of dwell times are illustrated in Fig. 1, and Eq. 1 simply means that the conditional dwell times τ₊₊ and τ₋₋ are random variables with equal distributions. However, Eq. 1 does not say anything about the distributions of dwell times between steps of different directions, which in general have different distributions.

FIGURE 1.

Example of the four different conditional dwell times in a model with one step per enzymatic cycle (synthetic data). The coordinate x(t) could be position of a linear motor, net rotation of a rotary motor, or the net number of a substrate or product in an enzymatic reaction, and changes stepwise in steps of size d. The staircase line is an idealized running average.

Equation 1 holds also at finite average velocity. For example, a forward-moving motor will take mostly forward steps, but might eventually produce two consecutive backward steps. The dwell times between such ++ and −− step pairs have equal distributions, although the probability of observing two consecutive backward steps might be very small for a motor with strong forward bias.

In practice, the need to observe a significant number of ++ and −− events to test or apply Eq. 1 can be an experimental challenge. For example, ATP-driven motors like kinesin or myosin V typically have ΔG_ATP ≈ −25 k_BT in vivo (29). This means that −− events are very rare (see Eq. 18), unless an external load is applied (1–8).

To extract qualitative information out of an experimental test of dwell time symmetry, one needs a characterization of the class of models that satisfy Eq. 1. We try to formulate a general characterization of this class. This means that some of the models within this characterization will not be realistic descriptions of biological systems. On the other hand, a large number of candidate models can be excluded if dwell time symmetry is not observed in some system. We find two sufficient assumptions for Eq. 1 to hold, which we call strong coupling and the bottleneck property. Within the discrete state modeling framework that we use, these assumptions are easy to formulate, but can also be disposed of (30).

The bottleneck property is an assumption about the model topology. It means that both forward and backward steps correspond to transitions to or from a single state in the mechanochemical cycle, which we call the bottleneck state. This ensures that the state of the system is uniquely determined after each observed step, independent of previous step directions. The bottleneck property alone results in a particularly simple form for the step-step correlations, given in Eq. 15, which can be tested experimentally.

The assumption of strong coupling, defined mathematically in Eq. 20, is related to microscopic reversibility. Physically, it means that there is no futile free energy dissipation in the mechanochemical cycle. In addition to tight coupling in the usual sense (30), i.e., a one-to-one correspondence between fuel consumption and forward steps, it includes the assumption that backward steps are tightly coupled to synthesis of fuel. As a result, motors with strong coupling are effectively one-dimensional systems, in the sense that only one reaction coordinate, e.g., position, is needed to describe their operation.

Strong coupling might not necessarily hold for all motors. For example, the forward steps of Myosin V are tightly coupled to ATP hydrolysis, while backward steps independent of ATP binding was recently reported (8). Another example is kinesin, for which ATP binding during steps in both directions has been reported (1,2). On the other hand, strong coupling might be possible in some rotary motors, at least under certain conditions (16,30–32).

Several recent works (33–36) use hidden Markov models to estimate kinetic parameters directly from experimental trajectories, and thus in principle utilize all information in the data and bypass the difficulties associated with step detection. However, this approach does not replace the need for a theoretical understanding of the capabilities and limitations of the underlying stochastic models. Our results should provide useful guidance when applying these techniques.

Equation 1 corresponds to a similar result in cycle kinetics (23–25,37). Using the symbol “∼” to denote cycle time properties, one has

(2)

where are the probability density functions for waiting times before forward (+) or backward (−) cycle completions, are the relative frequencies of completed forward and backward cycles respectively, and 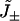are one-way cycle fluxes (37). Equation 2 is based on similar assumptions as Eq. 1 (24,25). However, the waiting times in Eq. 2 do not describe the experimental dwell times observed in stepping experiments on motor proteins (20). Distinguishing between cycle completion times and dwell times results in significant differences when modeling and interpreting stepping data.

One example of such a difference is the possibility to calculate ΔG from observations of forward and backward steps. In this case, using the cycle completion result in Eq. 2 on stepping data can give large systematic errors in the estimated ΔG, which can be avoided if Eq. 1 is used instead.

A related example concerns how to interpret the ratio of observed forward and backward steps, which has been measured for kinesin over a range of forces and ATP concentrations (1–3). The force dependence of this ratio can be described as roughly proportional exp(−cF_xd/k_BT), where d = 8.2 nm is the step length, F_x is the applied load, and c is a numerical factor significantly smaller than unity. The dissipated free energy per cycle depends on applied load as

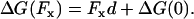(3)

This means that Eq. 2 predicts c = 1 if steps are assumed to correspond to completed cycles. In contrast, Eq. 1 gives no general reason to even expect an exponential behavior of the ratio of forward and backward steps (20), and suggests that π₊₊/π₋₋ is a more relevant quantity to study. As mentioned above, kinesin might not satisfy strong coupling, in which case one must look at more complicated models. In any case, making the distinction between steps and completed cycles is clearly important to interpret the experiments correctly.

The rest of the article is organized as follows. In the next section, we sketch a derivation of our results for the models studied in Tsygankov and colleagues (20) and Qian (21). We also discuss step-step correlations. After that, we generalize our results to a broader class of models, and discuss detachments and multiple pathways in the mechanochemical cycle. We also generalize Eq. 1 to the case of several detectable substeps. To illustrate our results, we then analyze stepping data for the flagellar motor, before the concluding discussion. Detailed derivations are given in the Appendices.

SEQUENTIAL MODELS

In this section, we derive Eq. 1 and some related results in the simplest case, i.e., a sequential model.

Consider a model with a single cycle consisting of a sequence of N states (see Fig. 2), where we defined [k]_l to denote state k in cycle l, associated with position ld. This is a basic model in enzyme kinetics (24,37) and has been used to describe motor proteins like kinesin (23,38,39), myosin V (22), and F₁-ATPase (40). By construction, it satisfies both strong coupling and the bottleneck property.

FIGURE 2.

A simple sequential model of an enzyme or motor protein with N states per cycle, [0]_l, [2]_l, …, [N − 1]_l. The model can be viewed as a biased random walk on the periodic lattice of states. Numbers in brackets represent different states, and indices different cycles. State [k]_l denotes the same structural state as [k + N]_l ≡ [k]_l+1, but with position or angular orientation x (for linear and rotary motors respectively) shifted by the step length d. Arrows indicate the allowed transitions between neighbor states with transition rates u_j, w_j. Fat solid arrows denote the major conformational changes that produce observable steps like those in Fig. 1. The other transitions are indicated by dashed arrows. In a motor protein, these transitions could for example be binding or release of ligands, or small conformational changes that are hidden in the experimental noise.

We denote the forward (backward) transition rates from state j to adjacent states by u_j (w_j) as indicated in Fig. 2. The transition rates are positive and periodic, i.e., u_j+N = u_j, w_j+N = w_j, and possibly functions of external loads and concentrations of various species in the surrounding solution. For the purpose of this discussion, the rates are assumed to be arbitrary positive constants, some of which can be tuned experimentally.

We assume that transitions between different cycles, 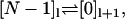produce observable forward (+) or backward (−) steps. If the model describes an enzyme, the observable step could be the release or uptake of a product or substrate molecule.

Counting steps is different from counting cycle completions, which can be illustrated with the following thought experiment. Consider the sequential model in Fig. 2 with N = 2 states per cycle, and a trajectory where the motor goes through the states 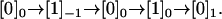This completes one forward cycle from [0]₀ to [0]₁, but produces three steps: one backward ([0] → [1]₋₁), followed by two forward ([0]₋₁ → [0]₀, and [1]₀ → [0]₁). Due to such events, neither the number of steps nor the dwell times between steps are accurately described in terms of cycle completions. A different treatment is needed.

The time evolution of the system is a random walk on the periodic one-dimensional lattice of states, where the average velocity may be nonzero. To simplify the notation, we now use j to denote a state in any cycle, with the convention that j and j + N are equivalent states in different positions.

The probability q_j(t) to be in state j at time t evolves according to a Master equation (19), in this case

(4)

State j has free energy G_j, and according to detailed balance, the free energy difference between two adjacent states is related to the transition rates through From the periodicity of the rates, we find

(5)

The direction of the average drift is positive (to the right in Fig. 2) if the dissipated free energy per cycle, ΔG, is negative, and zero if ΔG = 0 (37,41).

Tracking the position produces a series of forward (+) and backward (−) steps separated by random dwell times, as sketched in Fig. 1. Our aim is to describe the statistics of such a trajectory, i.e., the fluctuations of the dwell times and the number of forward and backward steps, which can then be compared with experimental data.

Following Tsygankov et al. (20), we introduce the pairwise splitting probabilities π₊₊, π₊₋, π₋₊, and π₋₋, where π₊₊ and π₊₋ is the probability that a forward step is followed by a forward step or a backward step, respectively, and similar for π₊₊, π₋₋. The splitting probabilities satisfy

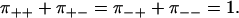(6)

Similarly, we introduce random variables τ₊₊, τ₊₋, τ₋₊, and τ₋₋ for the conditional dwell times, where τ₊₊ is the dwell time between two consecutive forward steps, and so on, as illustrated in Fig. 1. Once the proper first passage problem to describe the dwell times has been formulated, explicit expressions for the splitting probabilities and mean conditional dwell times can be computed for arbitrary N (20), using standard methods (19).

THE FIRST PASSAGE PROBLEM

We now describe the first passage problem for dwell times in sequential models, which we then use to derive Eq. 1. The dwell time symmetry is due to a one-to-one mapping between each −− event, i.e., two consecutive backward steps and the dwell time between them, and a corresponding ++ event. This is the key observation for the generalization of Eq. 1 to more complex models in later sections.

We model the splitting probabilities and probability distribution functions for the dwell times as a first escape problem from the interval of states 0, 1, …, N − 1. One way to approach this problem is the approach with absorbing boundaries (19), which means solving a reduced Master equation for the states 0, 1, …, N − 1, with absorbing boundaries at both ends (20,21). From the assumption that steps are produced by the transition it follows that immediately after a + step, the system is in the state 0 (±lN), and just after a − step, it is in the state N − 1 (±lN).

We write the reduced Master equation in matrix form, where the matrix M has elements

(7)

and 0 ≤ i, j ≤ N − 1. The element M_ij is the transition rate from state j to state i. The probability functions are given by the outgoing probability current,

(8)

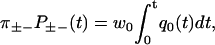(9)

where ± indicates an initial condition q_j(0), given by the direction the of the previous step (see Eq. 39). Normalization of the distributions requires that

(10)

DWELL TIME SYMMETRY

To derive Eq. 1, we show that the Taylor series of π₊₊P₊₊(t) and π₋₋P₋₋(t) are identical up to a factor 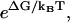from which Eq. 1 follows. The actual calculation is given in Appendix A, and we now discuss some of its consequences.

First, it is interesting to note that the periodicity of the model is not necessary for the dwell time symmetry, only to get the simple relation between π₊₊, π₋₋ and ΔG in Eq. 1b.

Second, the ++/−− probability distribution has a simple closed form for (periodic) sequential models. As we show in Appendix B,

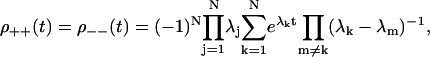(11)

where the λ_j are the eigenvalues of the matrix M. This is the distribution of a sum N of independent exponential random variables with mean values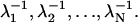

Explicit expressions for all four conditional dwell time distributions for the case N = 3 are given by Qian (21). As expected from the calculations in Appendix B, there is no simple relation between ρ₊₋(t) and ρ₋₊(t).

Equation 12 is only valid if the eigenvalues λ_j are distinct. This is the generic situation, since there are no symmetries or other reasons to expect degeneracies. However, Eq. 1 is valid also in the degenerate case.

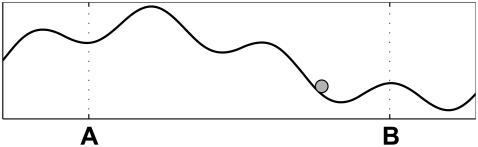
Finally, it is worth noting that the sequential models in this section can also be obtained as a discretization of overdamped one-dimensional diffusion (42) in an arbitrary potential U(x) between two points A and B (see Fig. 3). In this case, our results mean that the waiting time between last touch at A and first touch at B, and the reverse waiting time between last touch at B and first touch at A, have equal distributions. This pair of first passage problems was previously studied by Bier et al. (43).

FIGURE 3.

The equations of motion for a particle (shaded circle) diffusing in an arbitrary potential (solid curve) can be discretized to a sequential model (42). In the continuum limit, the dwell time symmetry for the discretization translates to equal distributions for the two last-touch first-touch waiting times between the (arbitrary) positions A and B.

Step directions as a Markov chain

The fact that the motor is in a different state immediately after steps in different directions means that the step directions might be correlated. In this section, we formulate this observation mathematically, and point out some experimentally relevant consequences.

Let π₊(k) and π₋(k) = 1 − π₊(k) be the probabilities that step k in a trajectory is a forward or backward step, respectively. In the simplest case of no substeps or detachments, the definitions of the pairwise splitting probabilities give

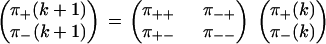(12)

Equation 12 describes the sequence of forward and backward steps as a Markov chain (19,20), and the normalization constraints in Eq. 6 leave two independent parameters in the 2 × 2 transition matrix.

The average frequencies π_±* of forward and backward steps have been measured for several motor proteins (1,2,5,9). In our model, those frequencies are given by the stationary distribution of Eq. 12 (20),

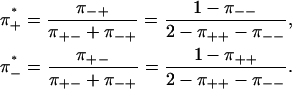(13)

In contrast to the ratio of the number of forward and backward cycles in Eq. 2, the ratio π₊*/π₋* of forward and backward steps is in general not equal to exp(− ΔG/k_BT). Looking back at Eq. 3, we see no general reason to expect the ratio of forward and backward steps to depend exponentially on the applied load.

Several experiments have divided the dwell times according to the direction of the following step (1–3). Our model gives the forward and backward dwell time probability density functions as

(14)

Since ρ₊₋(t) and ρ₋₊(t) are in general not related in a simple way, one should not expect equal dwell times before forward and backward steps, in contrast to the case of forward and backward cycle completion times (23–25).

Equation 12 implies that step directions are correlated, and gives the step-step correlation function

(15)

where s_m = ±1 indicates the direction of step m, and

(16)

is an eigenvalue of the transition matrix in Eq. 12 (20). The other eigenvalue is 1.

Note that |γ| < 1 since π_±± < 1. In addition, it is reasonable to expect π₊₊ ≤ π₋₊, since a forward step following a backward step can be accomplished by a single transition, while the whole cycle must be passed before a forward step is followed by another forward step. Inserting π₊₊ ≤ π₋₊ in Eq. 16, and using the normalization in Eq. 7, we get

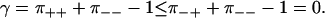(17)

Apparently, we should expect negatively correlated steps, −1 < γ ≤ 0. Uncorrelated steps (γ = 0) occur in systems with N = 1, i.e., simple random walks, as well as some special cases of the extended models in the next section.

An upper bound for the number n₋₋ of −− events is useful to estimate the regime where our results can be applied in practice. A rough estimate is given by

(18)

Hence, the number of steps n_tot required to get adequate statistics grows at least exponentially with decreasing ΔG.

EXTENDED MODELS

Beyond the simplest descriptions in terms of a sequential model for the dominating pathway (if there is one), more complicated situations with multiple pathways are possible (5,44–48). A general (coarse-grained) description of a motor protein would keep track of both the position and the consumption of fuel molecules, which requires the model to include an effective chemical coordinate in addition to the position of the motor (30). Are the dwell time symmetry properties of sequential models valid for more general cases as well? As we will see next, the answer is “yes” for a large class of models, in which the motion is still effectively one-dimensional.

With the extended models, we look for general properties that imply dwell time symmetry, even if not all models with these properties are biologically relevant. We find that the strong coupling and bottleneck assumptions mentioned in the Introduction are sufficient. This means that if dwell time symmetry is observed not to hold for a particular system, then one can conclude that the strong coupling or bottleneck properties are absent. To model such a system, one must go beyond the extended models presented below, for example along the lines discussed by Bustamante and colleagues, Reimann, and Jülicher and colleagues (30,49,50). The special situation without strong coupling but with the bottleneck property is illustrated below for an example model (Fig. 7).

FIGURE 7.

A model with one spatial and one chemical reaction coordinate, denoted by indices l and m, respectively. Shaded boxes are bottleneck states. Projecting out the chemical coordinate as explained in the text, this model can be brought to the same form as in Fig. 6. In general, the resulting effective one-dimensional model does not satisfy the strong coupling assumption of Eq. 28.

The extension of our results to detachments and observable substeps in later subsections is directly motivated by experimental observations of such events (2,3,5).

THE CLASS OF EXTENDED MODELS

In this section, we describe a large class of extended models that display dwell time symmetry in a little more detail, and indicate how the dwell time symmetry is derived. We use chemical kinetics, but write a Master equation with arbitrary transition rates w_ij from state j to i,

(19)

Non-zero “diagonal” rates w_ii are allowed, for example, to describe irreversible detachments of motors from their tracks (23,51), or other events that can be filtered out experimentally.

We also need to specify the condition of strong coupling. One way is to demand that the transition rates around any closed loop i₀, i₁, i₂, …, i_m = i₀ of transitions satisfy

(20)

This property is automatically fulfilled for sequential models, and makes it possible to define a free energy G_j for each state j, up to an additive constant. From detailed balance, we have 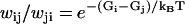for the free energy difference along the transition 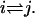Hence, Eq. 20 says that the sum of free energy differences along any closed loop is zero, which means that free energy consumption that produces no net motion, e.g., futile ATP hydrolysis, is ruled out. (Note that the mechanochemical cycle, say, from a state (k) to (k + N), is not a closed loop in our description.) We also assume that no transition is irreversible, i.e., w_ij ≠ 0 ⇔ w_ji ≠ 0, although the transition rates may be arbitrarily small.

To reflect the cyclic operation of motor proteins, the transition rates are periodic with period N, and there is a well-defined free energy per period,

(21)

An important step in the derivation of Eq. 1 is to conclude that the state of the motor immediately after a step is independent of earlier steps. In a sequential model, this occurs because there is only one step-producing transition per cycle. This condition can be relaxed somewhat. It is sufficient to assume the bottleneck property mentioned in the Introduction, i.e., that all transitions corresponding to a step are either to or from a single state, the bottleneck state, as illustrated in Fig. 4. As the term indicates, the system must visit the bottleneck state each time it goes through the cycle.

FIGURE 4.

Example of a model with the bottleneck property and N = 6 states per cycle. All states inside the shaded area belong to the same cycle. The bottleneck states are 0, ±N, ±2N…. Solid arrows denote transitions coupled to a mechanical step of length d, and dashed arrows indicate transitions within a cycle, which are undetectable. It is not possible to go from one cycle to the next without either leaving or arriving at a bottleneck state. In general, transitions between any states within a cycle are allowed, and bottleneck states might have a transition to any state in the neighbor cycle.

Whether the bottleneck assumption holds must be determined for each system separately. For example, deviations from the step-step correlations predicted in Eq. 15 means that the assumption is not valid.

Although the models considered in this section are more general than the sequential ones, several properties of the sequential models are retained. These include strong coupling, periodicity, and that steps (roughly) correspond to one transition in the enzymatic cycle. They therefore describe an effectively one-dimensional motion, where the motions along the spatial and chemical reaction coordinates (30) are tightly coupled to each other for motion in both directions. Hence, backward and forward motion proceeds in opposite directions along the same reaction paths, just as for the sequential models.

Dwell time symmetry and detachments

Dwell time symmetry for the extended models with detachments can be derived using the same methods as for sequential models, and further details on that derivation are given in Appendix C. Just as in the sequential case, periodicity is only necessary to establish Eq. 2, while the dwell time symmetry, Eq. 1, follows also without assuming periodicity.

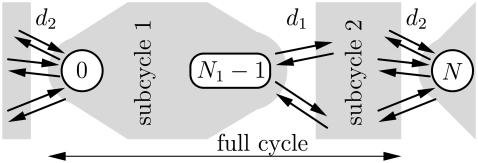
Examples of the nonperiodic case are the subcycles in Fig. 5, which shows a model with two observable substeps per cycle. Each step in the example satisfies the bottleneck property, but both bottleneck states are in the same subcycle. Deriving dwell time symmetry for the different subcycles proceeds as in Appendix C, with slightly different initial conditions.

FIGURE 5.

Simple periodic model with two substeps per cycle, with step lengths d₁ and d₂. Subcycle 1 has N₁ states, and subcycle 2 has N − N₁ states. Both steps have the bottleneck property, although the bottleneck states 0 and N₁ − 1 are both in subcycle 1. If strong coupling is satisfied, both subcycles display dwell time symmetry.

As mentioned above, detachments of a motor from its track are observed in several systems (2,3,5). We model detachments by introducing death rates (23,51) as extra terms in the diagonal elements of the Master equation and M matrix of Eqs. 7 and 49.

The presence of detachments affects the long time behavior of the model (51), as well as dwell time distributions and pairwise splitting probabilities. Conditional detachment probabilities also have to be added to Eqs. 6 and 12.

However, in the derivations of dwell time symmetry in Appendix C, the transition rates always enter as ratios of forward and reverse rates, e.g., 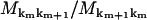in Eq. 42, so that diagonal elements (k_m = k_m+1) always cancel. Hence, Eq. 1 remains valid even in the presence of detachments.

Observable substeps

For some motors, the full forward and backward steps are divided into observable substeps (5,17). In this section, we show how the relation between splitting probabilities in Eq. 1 can be generalized, if strong coupling holds and all substeps satisfy the bottleneck property.

To start with, consider the system in Fig. 5, which produces substeps d₁ and d₂ = d − d₁ during each cycle, and assume that each subcycle displays dwell time symmetry. From now on, we denote a forward step of length d₁ with ₊₁, and similarly for the other substeps. Keeping track of only the d₂-steps, we can analyze the system as in previous sections, using four splitting probabilities 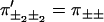and dwell times which satisfy Eq. 1.

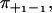
On the other hand, if we keep track of and discriminate between all substeps, we could instead measure eight splitting probabilities: 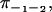and so on.

Summing over all paths between two consecutive ₊₂-steps, we get

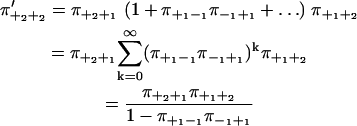(22)

and similarly

(23)

This means that the relation between free energy and splitting probabilities for a system with only one step per cycle generalizes to

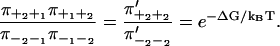(24)

Note that we summed over all paths between two ₊₂ steps without explicit reference to all paths that start with a ₊₂ step and end with something else. This means that Eq. 24 is valid also for a system with detachments, or with several parallel pathways.

For systems that go through substeps d₁, d₂ …d_K in each cycle, we can use the same argument to relate the splitting probabilities of the full analysis (all substeps included) to one where the first substep (d₁) is ignored:

(25)

(26)

Iterating this transformation to ignore substeps 2, 3, …, K − 1 as well, we find the following relation for a cycle with K visible substeps:

(27)

In a complicated system with parallel pathways where a cycle can be completed using different sequences of substeps, Eq. 27 holds for every such sequence separately.

An example model

In this section, we consider a small but nontrivial model with two states per cycle, to present an explicit example that illustrates the results of the previous sections.

The model has two parallel pathways as sketched in Fig. 6, and the steady-state velocity and effective dispersion are known exactly (44). The bottleneck property is satisfied, and strong coupling is equivalent to

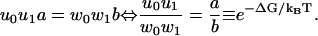(28)

Computing the dwell time distributions and splitting probabilities (see Appendix D for details), we get

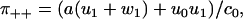(29)

(30)

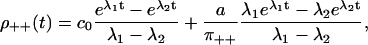(31)

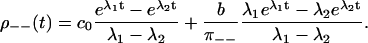(32)

FIGURE 6.

Example of a nonsequential model with N = 2 states per cycle, with two parallel pathways that produce a step in the x direction. Solid arrows are step-producing transitions, while dashed arrows indicate hidden transitions that do not produce an observable step. Shaded boxes are bottleneck states.

The eigenvalues λ_{1, 2} are given in Appendix D, and c₀ = λ₁λ₂ > 0. For this model, Eq. 28 is obviously equivalent to the dwell time symmetry of Eq. 1. For the other two pairs of steps, we get

(33)

(34)

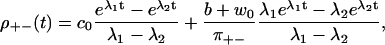(35)

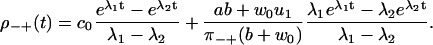(36)

We see that ρ₊₋(t) and ρ₋₊(t) differ both from each other and from the ++ and −− distributions, independent of whether Eq. 28 holds or not. The step directions are anticorrelated, since

(37)

The example illustrates the logic of our results. Strong coupling and the bottleneck property together are sufficient conditions for the dwell time symmetry. The bottleneck property alone is sufficient for the Markov-chain description of step directions in Eq. 12, which remains valid even if Eq. 28 is not satisfied.

A possible reason for why the model in Fig. 6 might not satisfy Eq. 28 is illustrated in Fig. 7. This is again an N = 2 state model, but with an independent “chemical” reaction coordinate (the superscript m on the states), e.g., the number of hydrolyzed ATP molecules (30). For example, the path could be a step-driven ATP hydrolysis, while the reaction 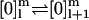could describe an ATP independent step.

This model can be transformed to the one-dimensional model in Fig. 6 through the projection which leaves the rates unaffected. However, the open-ended reaction path is transformed into the closed loop 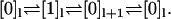Since strong coupling places no constraints on the rates in the original model in Fig. 7, there is no reason to assume that Eq. 28 holds for the projected model. In the effective one-dimensional description, this loop then becomes a slip loop, which dissipates free energy without producing net motion. Hence, the simple step-step correlations of Eq. 15 are retained, but not the dwell time symmetry.

In systems where it is not possible to measure the “chemical position” with single molecule precision, the resulting violation of dwell time symmetry is a useful test for such projected slip loops, if the bottleneck property is satisfied. This property can in turn be ruled out, for example, if the step-step correlations are more complicated than predicted in Eq. 15.

The most interesting candidates for such tests seem to be the rotary motors driven by ion fluxes, e.g., the F_O part of ATP synthase, or the bacterial flagellar motor, since it is difficult to measure the ion flow with single molecule precision. We are not aware of any experiments on ATP synthase under conditions that produce both forward and backward steps. Data from a flagellar motor will be analyzed in the next section.

Application to the flagellar motor

In this section, we apply our theoretical results to analyze stepping data from a recent experiment with a chimeric flagellar motor (18). As we will see, the data is consistent with the predicted dwell time symmetry and step-step correlations within the experimental uncertainty. We also estimate the free energy per cycle, and show that the estimate based on cycle completions can have a significant systematic error, compared to Eq. 1b.

The flagellar motor propels many swimming bacteria, by driving the rotation of flagellar filaments. Each filament is driven at its base by a transmembrane rotary motor, powered by ion flux (Na⁺ in this case (18)) down an electrochemical gradient across the cell membrane. The motor is ∼45 nm in diameter, and is believed to contain 13 torque-generating units (18,52). In this experiment, only one unit was active, and the flagellum is expected to switch between 26 distinct orientations per turn, corresponding to a step length of 360°/26 ≈ 14° (18). We analyzed one trajectory with close to zero net velocity, and one with finite velocity.

Aided by Chung-Kennedy filtering (53) to enhance the steps, and the step-finding algorithm described in Sowa et al. (18), the raw data was converted to staircase stepping data, as shown in Fig. 8 a. Upon close inspection, the trajectory seems to be divided into intervals where the step lengths are consistent with each other, but out of phase with steps outside. This apparent drift might be due to dynamical exchange of the stator units (54) that anchor the motor to the cell.

We identified intervals of consistent stepping by inspection (see Fig. 8 a), and excluded the drift from our analysis by treating inconsistent steps as detachments, i.e., each interval of consistent stepping was treated as an independent run. The result is summarized in Table 1, and we now proceed to compare step-step correlations and dwell time distributions from trajectory A with the theoretical predictions. Trajectory B contained too few steps to make such comparisons meaningful.

TABLE 1.

Steps (±) and drift (δ) events for the two analyzed stepping trajectories

ij	+	−	δ	++	+−	+δ	−+	−	−δ
Trajectory A
nij	108	103	13	30	68	10	69	30	3
πij	0.48	0.46	0.06	0.28	0.63	0.09	0.68	0.29	0.03
Trajectory B
nij	43	27	11	20	16	6	17	5	5
πij	0.53	0.33	0.14	0.48	0.38	0.14	0.63	0.19	0.19

A forward step followed by a drift step is denoted +δ. The rows display the number of events (n_ij) and the corresponding conditional probabilities (π_ij). The average velocities and average dwell times are zero and 0.04 s for trajectory A, and 1.1 Hz and 0.007 s for trajectory B.

The step-step autocorrelation function for trajectory A is shown in Fig. 8 b. The prediction C(n)/C(0) = γⁿ of Eq. 13 is valid for trajectories without detachments. To compare theory and experiments, the splitting probabilities in Table 1 must therefore be renormalized by a factor (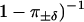 to account for the fact that intervals of consistent stepping (by definition) contain no drift events. This gives the theoretical prediction

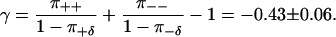(38)

A least-squares fit to the experimental correlations gives γ = −0.40, in agreement with Eq. 38, but inconsistent with uncorrelated step directions.

Having confirmed that the step-step correlations are consistent with Eq. 16, we go on to test the dwell time symmetry. The empirical distribution functions P_±±(t) are plotted in Fig. 8 c, for trajectory A. Error bars are standard deviations from bootstrap estimates (55). Using the Kolmogorov-Smirnov test (56), we conclude, with 95% confidence, that τ₋₊ have different distribution than τ₊₊ and τ₋₋, and that τ₊₋ have different distribution than τ₋₋. However, the test could not detect significant differences between the other three pairs (++/−−, +− /−−, and +− /−+). This is again consistent with the theoretical predictions, and also shows that the statistics is good enough to detect differences between distributions that are not equal. It is also interesting to note from Fig. 8 c that τ₊₊ and τ₋₋ are longer than τ₊₋ and τ₋₊ on average. This is reasonable, since +−/−+ events in principle only requires a single transition, while the system must go through a complete cycle to complete a ++ or −− event.

The ionic motive force was not measured independently (18), so it is not possible to compare the free-energy estimate of Eq. 1 with an experimental value. However, we can compare our result with that based on Eq. 2, which was used in Sowa et al. (18). The results are summarized in Table 2. As expected, the free energy per cycle is close to zero in trajectory A, which has almost no net velocity, while trajectory B clearly has a finite free energy per cycle to drive the rotation. Also note the differences in the estimates based on Eq. 1 and Eq. 2, which show that the cycle-completion estimate can give rise to significant systematic errors in estimated free energies if applied to stepping data.

TABLE 2.

Free energy estimates for trajectories A and B, in units of k_BT

	ΔGsteps	ΔGcycles
Trajectory A	0.06 ± 0.23	−0.05 ± 0.10
Trajectory B	−0.94 ± 0.28	−0.47 ± 0.13

The estimate ΔG_steps is based on our main result, Eq. 1, while ΔG_cycles comes from Eq. 2, i.e., treating steps as cycle completions.

CONCLUSION AND OUTLOOK

The statistical properties of steps in reversible molecular motors are not the same as that of cycle completions in enzyme kinetics. To interpret stepping trajectories correctly, this difference must be taken into account.

In this article, we have extended the theory for dwell times in sequential models (20,21), and derived a symmetry relation for the conditional dwell time distributions for a large class of experimentally relevant models, including parallel pathways, visible substeps, and detachments. In contrast to the statistics of cycle completions (23–25), the dwell time distributions and splitting probabilities of steps depend on the step directions of both steps before and after the dwell period.

The dwell time symmetry is a consequence of strong coupling, i.e., tight coupling for both forward and backward steps, and a bottleneck property of the underlying kinetic scheme. This means that the motion of the system is essentially a one-dimensional random walk in the (two-dimensional) space of spatial and chemical reaction coordinates. This makes it possible to use our results to infer information about the coupling and efficiency of a system from kinetic data, without detailed assumptions about the underlying kinetic scheme. In this respect, it is similar to the relation r ≥ 1/N between the randomness parameter r and the number of steps N in the mechanochemical cycle of molecular motors (28,57,58).

An alternative to the discrete formalism used here is to include continuous spatial degrees of freedom, as is common, for example, when modeling ratchet-type motor mechanisms (30,49,50). Since such models can be discretized (42), it is in principle possible to inquire about strong coupling and the bottleneck property in continuous models as well. An example of this is diffusion in one dimension (see Fig. 3), which strictly satisfies strong coupling and the bottleneck property. An interesting problem for further research is to quantify how well the dwell time symmetry is preserved in system with small deviations from these assumptions.

We analyzed stepping data from single motor subunits in a flagellar motor (18). The data seems to be consistent with the predicted dwell time symmetry and step-step correlations, although only one trajectory with almost zero velocity had enough steps to make such a comparison meaningful.

The form of the step-step correlations is consistent with an underlying kinetic scheme that satisfies the bottleneck property. So, does the dwell time symmetry in Fig. 8 indicate that the flagellar motor subunits are strongly coupled to the driving ion flow? Another possibility is that the steps are equilibrium fluctuations, as indicated by the low ΔG estimated from the stepping probabilities. In equilibrium, there is no free energy change associated with ion transport, which means that dwell time symmetry could be obtained also for a system with loose coupling. To say anything about the coupling in the flagellar motor, the dwell time symmetry must be tested in a regime with finite (and constant) velocity and ionic driving force. This is in principle a question of observing more steps in such conditions, but a systematic way to identify and separate steps from drift events would also be useful.

The step-step correlations predicted in Eq. 15 might be present also in systems that violate the dwell time symmetry. Deviations from this form would say something about the topology of the kinetic pathways in such systems, and it would probably be useful to apply our analysis also to kinesin and myosin V.

An accurate theoretical model is often crucial for correct interpretation of experiments on systems as complex as those of motor proteins. Many previous theoretical works on steps and dwell times in molecular motors (22,23,26,27) derive or assume descriptions where consecutive steps or cycles are statistically independent of each other. As we have demonstrated, this does not apply to the flagellar motor of Sowa et al. (18). We have also presented a large class of simple models where easily accessible quantities like the dwell times and step directions are correlated.

We expect our results to be of practical use in both data analysis and design of experiments. In particular, further experimental efforts are motivated in order to detect correlations and collect significant statistics for both forward and backward steps.

APPENDIX A

We now give a detailed derivation of Eq. 1 for a sequential model. The initial condition is the state immediately after a step, and can be written

(39)

To derive Eq. 1, we compute and 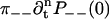using Eq. 8 and the initial conditions in Eq. 39. This gives

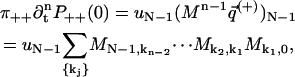(40)

where the summation over k₁, k₂, … goes from 0 to N − 1. The same calculation for P₋₋(t) yields

(41)

The products of matrix elements in Eqs. 40 and 41 correspond to n-step paths between states 0 and N − 1, plus the extra escape step. For sequential models, the shortest such path is N steps, so the first N − 1 derivatives are zero. For n ≥ N, we note that there is a one-to-one correspondence between the nonzero terms in Eq. 40 and Eq. 41. For each term including a path from 0 to N − 1 in Eq. 40, there is a corresponding term for the reverse path from N − 1 to 0 in Eq. 41. The ratio of two corresponding non-zero terms is

(42)

Going back to Eq. 7 for the elements of M, and using w₀ = w_N by periodicity, we see that 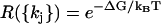for all pairs of corresponding terms. Moreover, P₊₊(0) = P₋₋(0) = 0, as there is no transition which produces two steps at once. Therefore,

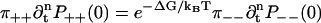(43)

for all n ≥ 0. The underlying reason is that the sum of free energy changes is the same along all possible paths going forward one cycle from 0.

Since P₊₊(t) and P₋₋(t) are integrals of the solutions of the reduced Master equation, which is a finite system of ordinary differential equations with constant coefficients, they are smooth functions which have Taylor series. Hence, Eq. 43 together with the normalization in Eq. 10 implies Eq. 1. A similar correspondence between paths was used in Wang and Qian (25) to derive Eq. 2. The periodicity is necessary to get the simple relationship between π₊₊, π₋₋ and ΔG in Eq. 1b, but not to establish the dwell time symmetry in Eq. 1a. Without the periodicity, Eq. 2 is replaced by

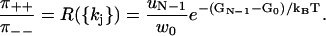(44)

APPENDIX B

To derive explicit expressions for ρ₊₊(t) and ρ₋₋(t) for sequential models, we first note that the occupation probabilities q_j(t) in Eq. 8 are the solution of a system of linear ordinary differential equations with constant coefficients, namely the elements of M in Eq. 7. If the eigenvalues {λ_j} of M are nondegenerate, the solutions have the form Note that the eigenvalues have negative real parts, to guarantee that the system eventually leaves the interval. We make the Ansatz

(45)

where the term 1 ensures proper normalization. We need N equations to determine the coefficients α_j. These are

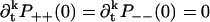(46)

for 0 ≤ k ≤ N − 1. The case k = 0 was argued just before Eq. 43, and 1 ≤ k ≤ N − 1 follows from the argument between Eqs. 41 and 42. The resulting system of equations for α_j is of the Vandermonde type,

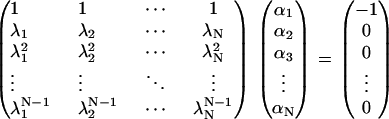(47)

Solving with Cramer's rule and setting

(48)

we arrive at Eq. 11. The distributions of τ₊₋ and τ₊₋ can be computed with the same Ansatz, but the derivatives and 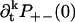are non-zero for k ≥ 1, so the results are more complicated and there is in general no simple relation between ρ₊₋(t) and ρ₋₊(t).

APPENDIX C

In this Appendix, we derive Eq. 1 for a periodic extended model like the one in Fig. 4, generalizing the first passage problem as we go along. The derivation proceeds much as for the sequential model, by solving a reduced Master equation for the states 0, 1, …, N − 1,

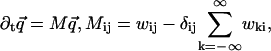(49)

with absorbing boundaries at −1 and N, and allowing w_ii ≥ 0 to model detachments. Note that the sum in Eq. 49 has at most 2N − 1 terms, due to the bottleneck property. After a forward step, the system is in state 0, while it could in principle be anywhere in the cycle after a backward step. The initial conditions, describing the distribution of states just after a ± step, are therefore

(50)

Since there are several escape transitions for each step, Eq. 8 for the dwell time probability functions is generalized to

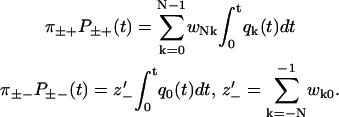(51)

We now proceed to compute derivatives of P₊₊(0) and P₋₋(0), and note that by Eqs. 20 and 21, the free energy difference G_N − G₀ = ΔG is independent of path:

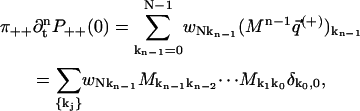(52)

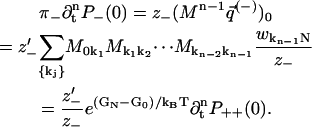(53)

From the periodicity of w_ij expressed in Eq. 22, we get z₋′ = z₋, which proves Eq. 43 and thereby Eq. 1. The derivation for the case when backward steps (instead of forward steps) end in the bottleneck state is analogous.

Note that our definition of the bottleneck property means that there are no transitions that produce two steps at the same time. This rules out discontinuities at t = 0 in the distribution functions P_±±(t), and justifies our use of Taylor expansions.

APPENDIX D

In this Appendix, we solve the example model in Fig. 6 in some detail. In addition to deriving Eqs. 29–37, this also illustrates a method that can easily be generalized to larger systems and implemented on computer algebra systems. For N ≥ 5 states per cycle, the eigenvalues λ_j must be calculated numerically. With this exception, the method gives explicit expressions for the dwell time distributions in the real time domain, which can be directly compared to experimental dwell time histograms.

The first escape problem for the model in Fig. 6 is governed by a reduced Master equation as described in Eq. 49, with the matrix

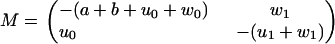(54)

The eigenvalues of M are

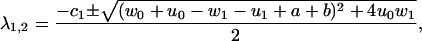(55)

and satisfy the relations

(56)

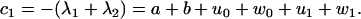(57)

The initial conditions after forward and backward steps are given by Eq. 50, and the conditional dwell time distributions are given by Eq. 51:

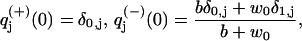(58)

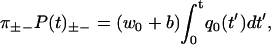(59)

(60)

Using the Ansatz in Eq. 45 together with Eqs. 58–60 to compute ∂_tπ_±−P_±−(t) and ∂_tπ_±+P_±+(t), we get the following systems of linear equations:

(61)

Solving this and using ρ_±±(t) = ∂_tP_±±(t), we eventually arrive at the probability density functions given in Eqs. 29–36.

Finally, we need expressions for the splitting probabilities, which we derive using the adjoint equations (19). Let π_j±, with j = 0, 1, be the probability that a system starting in state j will next produce a ± step. Starting with π₀₋, we note that from state 0, a backward step can be accomplished either by the next transition being a backward step, which has probability (b + w₀)/(a + b + u₀ + w₀), or by jumping to state 1 and from there eventually get a backward step. The last possibility has total probability π₁₋u₀/(a + b + u₀ + w₀), so that

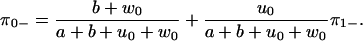(62)

Next, we multiply with and rearrange the terms. Applying the same procedure for the other π_{j ±}, we finally get

(63)

To get the pairwise splitting probabilities in Eqs. 29–37, we first solve for the π_j±, and then weight them according to the initial conditions of Eq. 58:

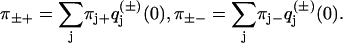(64)