Membrane-Binding/Modification Model of Signaling Protein Activation and Analysis of Its Control by Cell Morphology

Abstract

A mechanism for cell shape control of intracellular signal transduction, whereby the average concentration of activated proteins in the cytosol increases as the height of the cell decreases, has been described recently. An important modification of this analysis is offered, recognizing that signaling proteins are not only activated at the plasma membrane but must first form complexes with signaling molecules that reside there, such as receptors and lipids. With these more realistic boundary conditions, it is shown that the region of parameter space where cell shape amplifies the average cytosolic activity is greatly expanded. Moreover, this model allows for amplification of the activated protein bound at the membrane, which is considered more relevant for certain, spatially driven signaling processes in cell migration.

The spatial distribution of activated enzymes in cells and the role of cytosol-membrane translocation in enzyme activation are appreciated as critical determinants of intracellular signal transduction (1–4). In the arena of biophysical modeling, the role of membrane translocation in enhancing and compartmentalizing the activation of signaling pathways has been evaluated (5). A related consideration is the tendency to form gradients of activated proteins in the cytosol (6), which has been analyzed recently to take into account the effect of cell morphology. By the cell's thinning down toward its leading edge, and in thin structures such as filopodia, the concentrations of active signaling proteins could be amplified, providing a potentially important mechanism for cell migration (7). In this letter, the problem is revisited to include membrane binding as a prerequisite for protein activation.

The formulation of the problem builds upon previous work (5), and, where practical, the same notation is used. In that framework, activation is by phosphorylation, mediated by a kinase, and deactivation is by dephosphorylation, mediated by phosphatases. The cytosolic protein of interest binds to free binding sites on the membrane (association rate constant k_on, dissociation rate constant k_off); it may be activated only while membrane-bound (activation rate constant k_k). The active protein may be deactivated in either the cytosol (rate constant 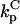) or at the membrane (rate constant 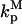). For now, it is assumed that the activation status of the protein does not affect the kinetics of membrane binding, nor does it affect the mobility coefficient of the protein in cytoplasm (D). The lateral mobility of membrane-bound protein is neglected.

Given these assumptions, steady-state conservation equations and boundary conditions are derived for the concentrations of cytosolic protein in the active () and inactive () states and the densities of membrane-bound protein in the active (S_m*) and inactive (S_m) states. An input to the model is the density of free membrane-binding sites, n_m. The problem is solved for an ideal geometry, that of a flat cell of gradually varying height, measured in the z-direction. There is a symmetry condition at the centerline of the cytosol (z = 0), located a distance h(x,y) away from the membrane. For a signaling protein excluded from the nucleus, z = 0 corresponds to the nuclear surface, and h(x,y) in that region is the distance between the plasma membrane and nucleus. As shown by Aris in the context of porous catalysts (8), the flat slab is a reasonable approximation for other geometries, taking the characteristic size to be the volume/surface area ratio.

The derivation is presented in full in the Supplemental Material. The fraction of cytosolic protein in the active state, as a function of z, is given by

(1)

As explained previously (5), the lumped parameter φ characterizes the active fraction of the protein if all of it were membrane-bound, whereas Q is the exchange quotient characterizing the number of protein modifications during a membrane encounter. Two important length scales, other than h, are identified. The first is the penetration depth d_p (L_gradient in (7)), which characterizes the persistence of active signaling protein as it diffuses in the cytosol. Neglecting diffusion in the (x,y) plane is justified when its characteristic dimension, R, is ≫ d_p; corrections for finite R/d_p, and accounting for nonuniform n_m(x,y), are readily obtained (Supplementary Material and (9)). The second length scale, d_c, is defined as the capture distance, the value of h where, in the limit of fast diffusion, membrane binding of active protein and its deactivation in the cytosol are equally probable. When h < d_c, binding is favored based on the higher membrane area per unit volume. The grouping Qd_c recognizes that membrane binding does not necessarily result in a change in activation state. The fraction of membrane-bound protein in the active state is given by

(2)

Eqs. 1 and 2 reveal that both the membrane-proximal cytosolic concentration and membrane-bound density of active protein depend on h, and this dependence does not necessarily go away by assuming a high rate of activation (φ ≈ 1). The accuracy of this model was tested and confirmed by comparison with numerical calculations performed on a nonideal geometry reminiscent of a spreading cell (Fig. S1 in the Supplementary Material).

The following ranges are taken for the parameters: ; k_onn_m ≈ (10⁵−10⁷ M⁻¹s⁻¹)(1–10³ sites/μm²) = 2×10⁻⁴–20 μm/s; D ≈ 1–100 μm²/s. With these conservative estimates, the pertinent length scales d_p and d_c span wide ranges that include cellular dimensions (h ≈ 0.1–10 μm): d_p ≈ 0.1–30 μm, d_c ≈ 2 × 10⁻⁶–200 μm. The ratio of these length scales is given by 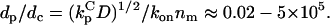From the model equations and parameter estimates, four plausible length-scale regimes are identified (Table 1).

TABLE 1.

Length-scale regimes of the model

Regime	*	†	‡
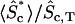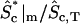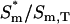I: h ≫ dp ≫ Qdc	φQdc / h	φQdc / dp	φQ
II: dp ≫ h ≫ Qdc	φQdc / h	φQdc / h	φQ
III: h ≫ dp, Qdc ≫ dp	φdp / h	φ	φ
IV: dp ≫ h, Qdc ≫ h	φ	φ	φ

^*Fraction of active protein in the cytosol, averaged over z.

^†Fraction of active protein at the periphery of the cytosol.

^‡Fraction of active protein bound at the membrane.

From this analysis, the following conclusions apply to a cell in which h_max ≥ h ≥ h_min. First, the average cytosolic activity tends to be amplified as h shrinks. This effect will be significant as long as h_max is significantly greater than either d_p or Qd_c (Regime I, II, or III). It is not necessary that h_max > d_p. Second, the cytosolic activity adjacent to the membrane tends to be amplified as h shrinks. This effect is negligible, however, if either d_p < Qd_c or h_min > d_p; h must pass through Regime II. Third, the density of membrane-bound activity tends to be amplified as h shrinks. This effect is negligible, however, if either d_p < Qd_c, h_min ≫ Qd_c, or Q ≈ 1. There must be a transition from Regime II to Regime IV, with Q significantly <1. In the Supplementary Material, it is shown that these two criteria are difficult to reconcile when most of the protein is membrane-bound (k_onn_m ≫ k_offh).

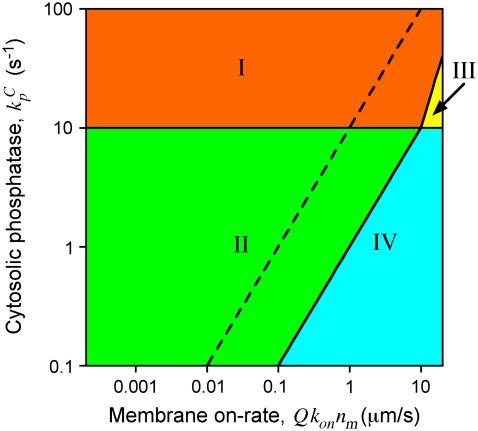
Consider a location where h = 1 μm, characteristic of the average height, and a protein with D = 10 μm²/s. Fig. 1 shows the regions in the plausible 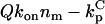parameter space where h is in Regime I, II, III, or IV. If we consider a location where h = 0.1 μm, taken as characteristic of h_min, this location can only lie in Regime II or IV (separated by the dashed line in Fig. 1). From this analysis, it is apparent that significant amplification of the average cytosolic activity will be achieved if either the cytosolic deactivation rate is high or the membrane-binding rate is modest.

FIGURE 1.

Regions in parameter space demarcating the four length-scale regimes for h = 1 μm (D = 10 μm²/s). The dashed line separates Regimes II and IV when h = 0.1 μm.

Amplification of the average cytosolic activity will often be accompanied by amplification at the cytosol periphery (characteristic of Regime II). If h_max is in Regime I, h will transition to Regime II and then possibly to Regime IV as it shrinks. If h_max is in Regime II, h will either remain there or transition to Regime IV. This transition is also marked by amplification of membrane-bound activity, provided that Q ≪ 1, and might be expected for parameter values lying somewhere to the right of the dashed line in Fig. 1.

The alternative possibility is that the activity at the periphery of the cytoplasm remains maximal throughout, while the average cytosolic activity is amplified (Regime III). This regime is found to occupy only a small slice of the plausible parameter space; the effective membrane-binding rate, Qk_onn_m, must be at the extreme end of the plausible range. This is significant because Regime III is, in essence, the situation assumed previously (7), using a different boundary condition.

An important model variation, allowing different binding kinetics for active (k_on* and k_off*) and inactive (k_on and k_off) protein, was also derived (Supplementary Material). The outcome is that the density of membrane-bound protein, S_m,T, depends on the activity in the cytosol. Regimes I-IV are the same as before, except with the effective on-rate in Fig. 1 replaced by AQ*k_on*n_m, where

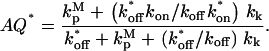(3)

More interesting is the conclusion that the value of AQ* is inversely related to the maximum amplification of the membrane-bound activity, S_m*, as h shrinks from Regime II to Regime IV; AQ* must be significantly <1 for appreciable amplification. This mechanism is possible even when exchange between cytosolic and membrane-bound pools is slow, and it can operate even when most of the protein is membrane-bound, provided that activation enhances membrane binding. Conversely, when AQ* > 1, it is possible to see a significant decrease in S_m* as h vanishes.

Finally, the possibilities for cell shape control of two proteins principally involved in cell migration signaling, phosphoinositide 3-kinase (PI3K) and the Rho-family GTPase Rac, are evaluated. Both execute their functions while associated with the plasma membrane. We have characterized PI3K activation mediated by platelet-derived growth factor (PDGF) receptors (10,11) and have observed that PI3K signaling is enriched in protrusive structures (12). Is this enrichment caused by cell shape amplification of PI3K phosphorylation? Based on findings that nearly all of the intracellular PI3K is membrane-bound in response to PDGF (10,13), and that phosphorylation either does not affect or reduces PI3K binding to receptors (14,15), the analysis argues that such amplification is not significant. By comparison, membrane-bound Rac is a good candidate for cell shape amplification because activation of Rac by guanine nucleotide exchange factors (GEFs) is coupled with its membrane association (16). Indeed, a recent kinetic analysis of Rac translocation dynamics shows that active Rac tends to remain membrane-bound until it is deactivated by GTPase accelerating proteins (GAPs), whereas inactive Rac tends to be sequestered in the cytosol by Rho-GDI (17), consistent with k_off* ≪ k_off and k_on* ≫ k_on. Thus, it is plausible that AQ* ≪ 1 (Eq. 3). Whereas the overall frequency of Rac dissociation is sensitive to modulation of GEF and GAP activities, which determine the value of φ, protrusive and nonprotruding regions in the same cell line exhibit the same membrane dissociation frequency (but different densities of membrane-bound Rac) (17). If these regions are not distinguished by a variation in φ, perhaps they are differentiated by local morphology, which affects the frequency of productive Rac-membrane association.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ online at http://www.biophysj.org.