C-Phycocyanin Hydration Water Dynamics in the Presence of Trehalose: An Incoherent Elastic Neutron Scattering Study at Different Energy Resolutions

Abstract

We present a study of C-phycocyanin hydration water dynamics in the presence of trehalose by incoherent elastic neutron scattering. By combining data from two backscattering spectrometers with a 10-fold difference in energy resolution we extract a scattering law S(Q,ω) from the Q-dependence of the elastic intensities without sampling the quasielastic range. The hydration water is described by two dynamically different populations—one diffusing inside a sphere and the other diffusing quasifreely—with a population ratio that depends on temperature. The scattering law derived describes the experimental data from both instruments excellently over a large temperature range (235–320 K). The effective diffusion coefficient extracted is reduced by a factor of 10–15 with respect to bulk water at corresponding temperatures. Our approach demonstrates the benefits and the efficiency of using different energy resolutions in incoherent elastic neutron scattering over a large angular range for the study of biological macromolecules and hydration water.

INTRODUCTION

Thermal and cold neutrons (with wavelengths of some angstroms (Å) and energies of several millielectron volts (meVs)) are well suited to probe biomolecular structure and dynamics on an atomic lengthscale and pico- to nanosecond timescale (1). Neutron spectroscopy measures the energy and momentum neutrons exchange with nuclei in the sample. The scattered intensity is described by the double differential cross section 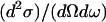where ω stands for the neutron energy and Q for its momentum transfer. It describes the probability that a neutron is scattered into the solid angle dΩ with an energy exchange It can be generally divided into a coherent part (containing structural information on atom-atom pair correlations) and an incoherent part (containing structural and dynamic information on single atoms):

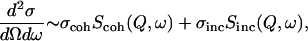(1)

where σ_coh and σ_inc are the coherent and incoherent cross sections and depend on the atomic composition of the sample.

In biological samples, the incoherent signal often dominates and has been widely and successfully used to study the molecular dynamics of proteins and membranes (1,2), hydration water (3–5), and, more recently, even entire cells in vivo (6).

The exact length- and timescale of molecular motions accessible by neutron spectroscopy depend on the energy resolution and momentum range covered by the instrument used (Fig. 1). Observable processes include molecular vibrations, diffusion, relaxation, and others (7). Although there are numerous studies using individual instruments to study molecular dynamics in specific, restricted energy and momentum ranges (for a review, see, e.g., Gabel et al. (2)), the benefit of combining data from different instruments over a large energy and momentum range has hardly been exploited up to date. Given the variety of instruments available and data treatments in use, such an approach is desperately needed to improve the comparability of results obtained under different experimental conditions.

FIGURE 1.

Accessible energy and Q-ranges of the backscattering instruments IN13 and IN16 used in this study.

In this article we propose a method to analyze elastic neutron scattering data from instruments that differ in energy resolution and momentum range covered. It is particularly suited for biological systems (proteins, membranes, hydration water) that contain large amounts of (strongly incoherently scattering) protons and poses no principal restraints on the instrumental energy resolution and momentum range. We demonstrate its efficiency by deriving a scattering law S(Q,ω) for C-phycocyanin (CPC) hydration water in the presence of trehalose by analyzing the Q-dependence of the elastically scattered signal at two different energy resolutions.

CPC is a phycobiliprotein contained in the cyanobacterium Synechococcus lividus (blue-green algae or cyanobacteria) where it plays a central role in the photosynthetic cycle (8). It has been investigated in a number of previous neutron scattering studies (9–15). CPC is excellently suited for our study since it is one of the few proteins that can be obtained in large milligram amounts in perdeuterated form, thus limiting its scattering signal with respect to the protonated solvent.

Similar to other sugar cryoprotectants, trehalose has been shown to influence both the stability and dynamics of biomacromolecules (16–20). Furthermore, in analogy to other saccharides, it is a kosmotropic agent, affecting both structure and dynamics of water molecules in its vicinity (21,22).

MATERIAL AND METHODS

Preparation of a hydrated C-phycocyanin powder for neutron scattering experiments

Perdeuterated C-phycocyanin (130 mg) were obtained from perdeuterated cultures as described (23). A CPC sample for neutron scattering was lyophilized from a 40 ml H₂O CPC solution at 4 mM trehalose (molecular weight is 342). We used perdeuterated trehalose as described (24) to minimize its contribution to the incoherent scattering signal. The freeze-dried batch was dried during 2 days at vacuum over silica gel in a desiccator. The dry weight of the sample, determined by weighing on a high precision balance, was 185 mg (CPC plus trehalose). The lyophilized, dried powder was then rehydrated over a pure H₂O atmosphere during one day until a hydration degree of 0.41 grams of water per gram of dry material (denoted as 0.41 g/g) was obtained. Although this hydration degree is in the usual range of values found in literature (2), the total solvation degree (water + trehalose) of CPC was chosen rather elevated to have a dominant incoherent signal from the H₂O. The sample was enclosed in a standard flat aluminum sample container with a volume of 0.2 × 30 × 40 mm³ sealed by an indium joint. The sample weight was checked before and after the neutron scattering experiments on a high precision balance and no material losses were detected. The same sample was measured on the backscattering spectrometers IN13 and IN16 without any modifications.

Neutron scattering experiments and raw data treatment

Neutron scattering experiments were conducted in the elastic scan mode, i.e., at zero energy transfer, on the Institut Laue-Langevin (ILL) instruments IN13 and IN16 at fixed energy resolutions of 8 μeV (IN13) and 0.9 μeV (IN16) (fullwidths at half-maximum) and in the Q-ranges 0.082 < Q² [Å⁻²] < 16.64 (IN13) and 0.037 < Q² [Å⁻²] < 3.435 (IN16). 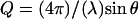is the modulus of the scattering vector Q, with the neutron wavelength λ and the scattering angle 2θ. The sample was oriented at 135° with respect to the incident beam on both instruments. On IN16, intensities were recorded in the temperature range from 20 to 320 K at steps of 2 K. The option of recording data in diffraction mode (25) was activated. No diffraction peaks corresponding to ice formation were observed at any temperature. On IN13, single data points were recorded at 20, 120, and 220 K and a series of data points between 235 and 320 K at intervals of 5 K. On both instruments, the sample was cooled gently from ambient temperature (∼295 K) to 20 K with a temperature gradient of ∼100 K/h. The heating cycle and measurements took place at temperature gradients of 80–100 K/day. The raw data were corrected for the sample container scattering and normalized to 20 K using an updated version of the ILL program SQW (26) based on a correction by Paalman-Pings coefficients. The measured transmission on both instruments was T = 0.89. At this transmission, multiple scattering is low (27) and the data were not corrected for it. The corrected elastic intensities at a given temperature T, S_T(Q,ω = 0), were normalized to the elastic intensities at 20 K:

(2)

The IN13 and IN16 energy resolution functions R(ω) were both assumed to be Lorentzians with halfwidths at half-maximum (HWHM) Γ_Lor = 4 and 0.45 μeV, respectively:

(3)

(The IN16 resolution is in reality better described by a Gaussian resolution function. We used Lorentzian functions here to simplify the mathematics in Eqs. 9a and 9b. The errors committed are negligible in our case (28)). We further assumed that the energy resolutions of both instruments are Q-independent in a first approximation.

Contributions of the different components to the scattered signal

The contributions of the different components (CPC, trehalose, water) to the scattered signal were calculated from their chemical composition and the corresponding atomic scattering cross sections (29). From the trehalose concentration (4 mM) in the solution and the total amount of CPC (130 mg), a ratio of 220 trehalose molecules per 180 kDa CPC αβ-hexamer was calculated. This ratio was checked and confirmed by a ¹H-NMR spectrum by integrating the CPC and trehalose peaks that are at different chemical shifts in the spectrum (not shown). At this CPC/trehalose ratio and the hydration degree determined by weighing, 5714 water molecules are present per CPC αβ-hexamer. The number of labile protons per CPC αβ-hexamer was assumed to be 3564 (11). Furthermore, it was assumed that all eight labile deuterons per trehalose molecule had been replaced by protons during the hydration process. From the molecular ratios, the respective contributions of the components to the total scattered signal can be calculated. The individual contributions are: I_CPC,coh = 8%, I_CPC,inc = 19%, I_{trehalose,coh} = 3%, I_{trehalose,inc} = 9%, I_water,coh = 3%, and I_water,inc = 57%. The indices “coh” and “inc” stand for coherent and incoherent contributions, respectively, and indicate that the total scattering of the system is dominated by the incoherent contributions from its components, the hydration water being the major one.

Analysis of the elastic intensity

The elastic part of the scattered intensity at a given temperature T and instrumental resolution R(ω) can be written as a convolution:

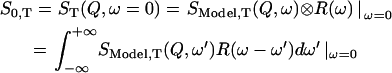(4)

The scattering law describing the motions of the atoms, is composed of an incoherent and a coherent part:

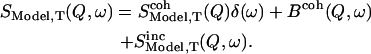(5)

The coherent contribution can be divided into an elastic part and into an inelastic background. Assuming that the coherent inelastic background lies outside the instrumental energy resolution (generally <1 meV), Eq. 4 can then be written as:

(6)

The normalized elastic intensity (Eq. 2) is then:

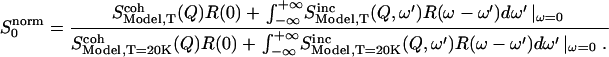(7)

The coherent contributions will generally vary as a function of Q and temperature. However, we do not take them into account in this study for several reasons: 1), They contribute only 14% to the total scattering signal in our case. 2), The normalization (Eq. 7) will tend to cancel coherent peaks partially if they do not shift (in Q) too strongly with T. 3), S_coh(Q) of CPC has been shown to fluctuate only by ∼10% at given Q-values in the temperature range from 180 to 295 K (12).

In a first approach, we analyzed the normalized elastic intensity by the Gaussian approximation (30) (note that we adopted the definition of 〈u²〉 given by Smith (1), which refers to the full amplitude of the motions):

(8)

Apparent mean square displacements (MSDs), 〈u²〉_apparent, were extracted from the slopes in linear regions of lnS₀ vs. Q² (Fig. 2). We termed these plots “Guinier plots” due to their formal analogy with the real Guinier plots in small angle scattering (31). The subscript “apparent” denotes that the MSDs are a quantity obtained formally by the slopes in Fig. 2. (This point is discussed later). The Q-range chosen for the extraction of the MSDs was 1 < Q² [Å⁻²] < 3.3, covered by both instruments (more precisely, the Q-ranges were as follows: IN13, 0.928 < Q² [Å⁻²] < 3.267; IN16, 1.007 < Q² [Å⁻²] < 3.278. The slight discrepancy is due to the different detector and analyzer setup on both instruments that cannot be modified easily). The criterion for the validity of the Gaussian approximation, was checked for each temperature (the factor 2 stems from the definition in Eq. 8). The maximum value of 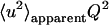found was ∼5.5 at 320 K on both instruments (see comment in the section “Limits of the Gaussian approximation”).

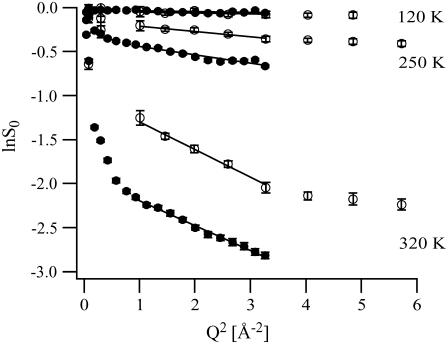
FIGURE 2.

Guinier plots (lnS₀ vs. Q²) at 120, 250, and 320 K (from top to bottom) for C-phycocyanin hydration water in the presence of trehalose on IN13 (open circles) and IN16 (solid circles). The lines show the linear fits used to extract MSDs in the Q-range 1 < Q² [Å⁻²] < 3.3, covered by both instruments.

In a more general approach we fitted the incoherent part of Eq. 7 by a convolution of a model scattering law, S_Model(Q,ω), with the respective instrumental energy resolution functions (Eq. 4). The phenomenological scattering law S_Model(Q,ω) was determined respecting the following constraints:

1. A realistic order of magnitude of the parameters describing the temporal and spatial aspects of the hydration water motions.

2. A limited number of parameters.

3. A good fit of the experimental data over the whole instrumental Q-ranges and at all temperatures measured on both instruments by the same S_Model(Q,ω).

We found that the following law, composed of a dynamical population p that undergoes translational diffusion, and a population 1 − p that diffuses inside a sphere with radius a, fulfilled conditions 1, 2, and 3 best for both instrumental resolutions and at all temperatures:

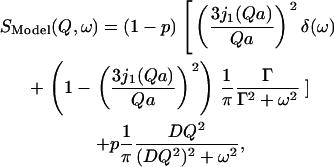(9a)

where j₁(Qa) is the spherical Bessel function of the first order, D is the effective diffusion coefficient of the translational diffusive population, and Γ is the relaxation parameter describing the diffusion of the population inside the sphere (simplified from (32)). Convoluting Eq. 9a with the respective Lorentzian instrumental energy resolution function (Eq. 4) yielded the following elastic intensities:

(9b)

Note that the factor 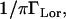caused by the convolution operation, does not appear in Eq. 9b due to the fact that we use a normalization and therefore the condition S₀(Q = 0,ω = 0) = 1 applies (33). A vibrational Debye-Waller factor was not taken into account for two reasons: 1), it has been shown to be close to 1 for supercooled water (34), which is dynamically close to hydration water at higher temperatures (11); and 2), to reduce the number of fitting parameters. The phenomenological scattering law does not take into account the dynamics due to an exchanging dynamical equilibrium between the two populations. Equation 9b was fitted to the experimental scattering curves on IN13 and IN16 by least χ² fits using the respective instrumental energy resolution HWHM Γ_Lor (expressed in s⁻¹, with 1 μeV = 1.52 × 10⁹ s⁻¹). The following algorithm was applied for the fit procedures:

1. A manual, approximate optimization of the four parameters p, a, Γ, and D to match the experimental data from both instruments simultaneously in the Guinier plots (lnS₀ vs. Q²).

2. A least χ² fit with variable parameters Γ and D and with fixed parameters p and a (chosen identical on both instruments). This procedure assured a proper convergence of the fitting procedure by allowing only two variable parameters at a time instead of four. This proceeding can be justified by the fact that the parameters p and a (Eq. 9b) give only rise to elastic intensities independent of the instrumental energy resolutions. The parameters Γ and D, however, contribute differently on both instruments to the elastic intensity since their ratios Γ/Γ_Lor and D/Γ_Lor depend on the respective instrumental energy resolution.

RESULTS

Apparent mean square displacements within the Gaussian approximation

The Guinier plots of the normalized elastic intensities are depicted in Fig. 2 for three temperature points, 120, 250, and 320 K. At 120 K, lnS₀ depended strictly linearly on Q² on both instruments over the whole Q-range measured, indicating a pure harmonic behavior of the hydration water motions. The absolute intensities measured on both instruments in the Q-range 1 < Q² [Å⁻²] < 3.3 were identical within experimental error bars. The loss in elastic intensity at 120 K was very small, even at the highest Q-values, indicating that the neutrons were scattered only from small, vibrational motions, similar to the ones at the normalization temperature (20 K). The same qualitative behavior was observed in the whole temperature range up to ∼230 K, albeit with elastic intensities that decreased more notably with increasing temperature. Above 230 K, however, two qualitatively new phenomena began to set in: On the one hand, lnS₀ was no longer a linear function of Q², indicating that nonharmonic motions were setting in. This tendency was more pronounced for intensities measured on IN16. On the other hand, the lnS₀ measured on both instruments no longer superposed: the elastic intensities measured on IN16 were smaller than those measured on IN13. The IN16 intensities dropped below the IN13 intensities at very low Q-values (Q² < 1 Å⁻²). Above Q² > 1 Å⁻², the elastic intensities from both instruments displayed the same slopes lnS₀ vs. Q². At 320 K, finally, these tendencies were fully developed: nonlinear dependence of lnS₀ on Q² at small Q-values (Q² < 1 Å⁻²) and a Q-independent shift between the IN16 and the IN13 intensities at higher Q-values (Q² > 1 Å⁻²). However, even at this highest measured temperature, a linear fit of lnS₀ vs. Q² could be technically justified in the Q-range 1 < Q² [Å⁻²] < 3.3.

The apparent MSDs extracted from both instruments in the Q-range 1 < Q² [Å⁻²] < 3.3 are depicted in Fig. 3. The normalization to 20 K (Eq. 2) implies the definition 〈u²〉_{apparent,T=20K} = 0. (The error committed hereby is <0.1 Ų, as can be estimated by a linear extrapolation of the data points in Fig. 3 to T = 0 K). In the temperature range from 20 to ∼230 K, the measured MSDs were identical on both instruments and increased steadily with temperature in an almost linear way. In an intermediate temperature range (240–290 K), the MSDs from both instruments underwent a so-called dynamical transition, i.e., their rate of increase with temperature increased dramatically. However, the dynamical transition observed on IN13 was shifted to a slightly higher temperature than the one observed on IN16. Furthermore, throughout the temperature range 240–290 K, the MSDs measured on IN13 were below those measured on IN16. Above 290 K, the MSDs from both instruments merged again and were identical within experimental error bars. Beginning at ∼270 K, the rate of increase of the MSDs with temperature decreased distinctly and at the highest measured temperatures (300–320 K), the MSDs leveled off and did no longer increase with temperature.

FIGURE 3.

Apparent mean square displacements measured on IN13 (open circles) and IN16 (solid circles) with error bars. The IN13 error bars are bigger than the IN16 error bars, mainly due to the smaller number of detectors available on IN13 in the Q-range 1 < Q² [Å⁻²] < 3.3 (Fig. 2).

Convolution of a model scattering law with the instrumental energy resolutions

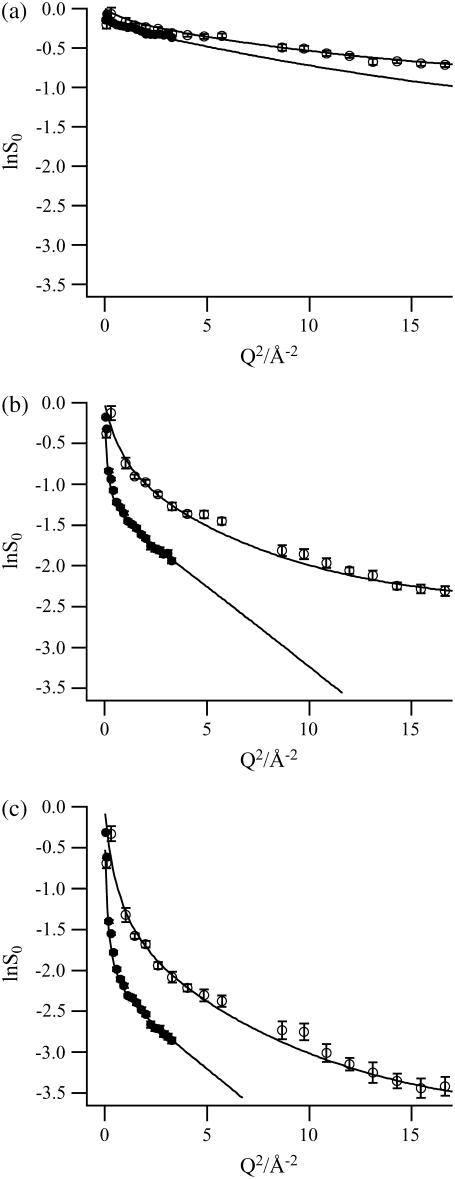
Fig. 4, a–c, show lnS₀ on IN13 and IN16 as well as the corresponding least χ² fits with the model scattering law (Eq. 9b) at three temperatures: 240, 280, and 320 K. The fit parameters extracted are depicted graphically in Fig. 5, a–d, as a function of temperature. The regressions with the model scattering law were in excellent agreement with the experimental data from both instruments in the temperature range 235–320 K. The χ²-values were <0.4 for all temperatures on both instruments. In contrast to the Gaussian approximation (Fig. 2), the convoluted model scattering law represented the experimental data faithfully over a more extended Q-range.

FIGURE 4.

Logarithm of the normalized elastic intensities on IN13 (open circles) and IN16 (solid circles) with error bars at the temperatures (a) 240, (b) 280, and (c) 320 K, as a function of Q². The fits with the model function (Eq. 9b) are depicted by continuous lines. Two IN13 data points (at 2.58 and 2.76 Å⁻¹) were not taken into account since their intensities were not stable during the experiment.

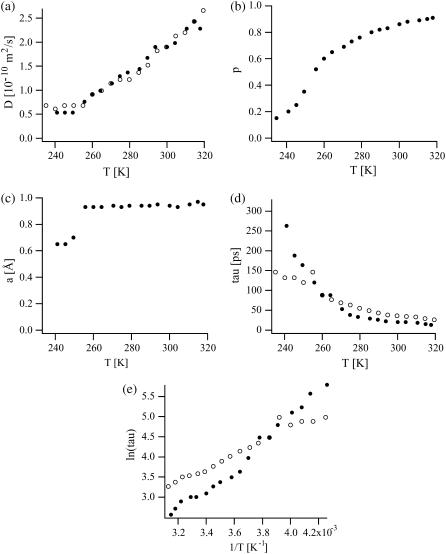
FIGURE 5.

(a) Effective diffusion coefficient D (in 10⁻¹⁰ m²/s), (b) population p, (c) sphere radius a (in Å), and (d) relaxation parameter τ = 1/Γ (in ps) as a function of temperature. (e) Arrhenius plot of lnτ vs. 1/T. IN16 fit parameters are depicted with solid circles, IN13 fit parameters with open circles. The errors of the fit parameters were as follows: ΔD/D < 5%, Δp/p < 5%, Δa/a < 7%, and Δτ/τ < 200%.

The excellent agreement of our fits with the experimental data shows that the ensemble of hydration water, trehalose, and C-phycocyanin labile protons can be described by two dynamically distinct populations over a large temperature range. At the highest temperatures, the major part (∼90%) of these protons is well described by translational diffusion, albeit with an effective diffusion coefficient D that is 10–15 times smaller than the diffusion coefficient of bulk water, D_bulk, at the corresponding temperatures (D_bulk = 1.1 × 10⁻⁹ m²/s (273 K), 2.3 × 10⁻⁹ m²/s (298 K), 3.2 × 10⁻⁹ m²/s (313 K); taken from Bellissent-Funel et al. (11). This implies that part of the trehalose molecules and of the CPC labile protons undergo diffusive motions similar to those of the water molecules at 320 K. From 320 to 250 K, D decreased continuously from 2.4 × 10⁻¹⁰ m²/s to 6.1 × 10⁻¹¹ m²/s (Fig. 5 a). Concomitantly, the proton fraction p dropped, at an increasing rate, in the same temperature range from 90 to 35% (Fig. 5 b). At temperatures below 250 K, the effective diffusion coefficient itself no longer decreased but the proton fraction p, diffusing freely, continued to decrease to 15% at 235 K. At all temperatures, the D extracted independently from IN13 and IN16 intensities were in very good agreement (Fig. 5 a).

The complementary fraction 1 − p of the protons, described dynamically by diffusion inside a sphere with radius a = 1 Å, made up ∼10% at 320 K and increased to 65% at 250 K and ultimately to 85% at 235 K (Fig. 5 b). The relaxation time parameter τ = 1/Γ, associated with this fraction, increased from 26/13 ps (IN13/IN16) at 320 K to 120/164 ps (IN13/IN16) at 250 K (Fig. 5 d). Below 250 K, the radius of the sphere shrank to 0.65 Å whereas the relaxation time increased further to 150/320 ps (IN13/IN16) at 235 K (Fig. 5 c). The discrepancy between the τ-values from both instruments is discussed later (Discussion section). As illustrated in Fig. 5 e, the relaxation time τ displayed an Arrhenius behavior between 320 and 235 K, with an activation energy E_a = 103/58 kcal/mol (IN16/IN13), and a prefactor τ₀ = 0.0011/0.142 ps (IN16/IN13). (As a general rule, the extraction of D was more sensitive at low Q-values, in particular to the slope at the origin. Γ was more sensitive at higher Q-values).

Below 235 K, it was difficult to fit our model scattering law to the experimental data. Instead, a simple linear fit (i.e., the Gaussian approximation) was sufficient to represent the data. It is possible to divide the MSDs below 230 K into two ranges (20–120 K and 120–230 K), that increase linearly with temperature at different rates. This effect has been interpreted as solvent-independent activation of methyl groups (35) but is not discussed here further.

DISCUSSION

Comparison of apparent MSDs with other systems

The observations on MSDs from two different instruments (divergence between 240 and 290 K, leveling off at the same level above 290 K; Fig. 2) have been rarely observed on proteins at temperatures below 320 K with some exceptions, either at large (50 μeV) energy resolutions (36) or with H₂O-hydrated proteins (37). They are directly related to the finite instrumental energy resolution and limits of the Gaussian approximation (37,38).

Whereas a large number of incoherent quasielastic neutron scattering (IQENS) studies on protein hydration water have been published (3,4,9), only a few studies using IENS are available. Our MSDs are ∼20% larger in the temperature range 150–250 K than MSDs reported for 25% hydrated Vycor (a porous hydrophilic silica glass) by incoherent elastic neutron scattering (IENS) on IN16 in a comparable Q-range (39). The slight discrepancy may be due to the higher degree of hydration applied in our case. The temperatures of the dynamical transition of Vycor (220–240 K) and of CPC hydration water (240–250 K) are in good agreement.

Compared to a trehalose/19 H₂O mixture measured on IN13 (22), the presence of CPC seems to reduce the dynamic flexibility of the water and of the trehalose above and below the dynamical transition: the MSDs in our study are more than a factor of two smaller in both temperature ranges than those reported for trehalose alone. This effect would reflect the capacity of the CPC protein surface (in addition to trehalose) to slow down hydration water dynamics (11). However, a direct comparison of both studies is not straightforward since in Magazù et al. (22) a double-well model is used rather than the Gaussian approximation. Interestingly, the temperature where the dynamical transition takes place in both systems (∼230–250 K), is identical (with and without CPC). This observation is analogous to the observed similarity between protein dynamics and the water-sugar environment demonstrated in another study: MSDs of glycerol-coated lysozyme and hydrated glycerol showed no differences (40). These results were interpreted by the authors with the strong coupling of protein dynamics to the sugar-water coating that seems to apply also in our case. Whereas myoglobin coated in pure trehalose (without water) shows no dynamical transition at all (17), the hydration degree in our case is apparently sufficient for CPC to undergo a dynamical transition.

Compared to typical MSDs of proteins determined by IENS (41,42) the CPC hydration water MSDs are by a factor ∼1.5 larger (at comparable Q-ranges) above the dynamical transition, indicating that the ensemble of hydration water, trehalose, and CPC labile protons is more mobile than the ensemble of protein protons at corresponding temperatures. A partial explanation of this feature is certainly the confinement of the conformational space available to protein atoms at higher temperatures that is in contrast to the (principally) unconfined motions of the hydration water molecules. However, below the dynamical transition, our MSDs are slightly smaller than those of proteins, indicating an increased rigidity (43) of the hydration water and trehalose with respect to protein atoms at low temperatures. Moreover, the dynamical transition in our system sets in at temperatures that are ∼30–50 K higher than typical values reported for proteins (41,42). Both phenomena are similar to those observed by IENS in lysozyme embedded in glycerol, another cryoprotectant (44).

Limits of the Gaussian approximation

The proton MSDs did not change significantly by lowering the upper bound of the fit range from Q² = 3.3 to Q² =1.5 Å⁻² (apart from increasing the error bars). In this sense, the formal criterion for the validity of the Gaussian approximation, was respected and a comparison to values reported on other systems by IENS is justified. However, we used the expression “apparent MSDs” since an interpretation of the slopes lnS₀ vs. Q² in terms of the Gaussian approximation is problematic in our case: according to Eq. 8, lnS₀ and the MSDs should not depend on the instrumental energy resolution R(ω) used. This, however, was clearly not the case in the temperature range 240–290 K (Figs. 2 and 3).

These findings can be understood in the following terms: at temperatures below the dynamical transition, neutrons are scattered completely elastically and the MSDs represent a true vibrational Debye-Waller factor (45). In this temperature range, both the intensities S₀ and the MSDs were independent of the instrumental energy resolution (Fig. 2; 120 K). The neutron scattering law is proportional to a Dirac δ-function and does not influence the measured elastic intensity as long as the energy resolution does not extend into the inelastic region of the spectrum. At higher temperatures (T > 235 K), quasielastic, non-Gaussian motions of the hydration water set in and the measured elastic intensities depended on the instrumental energy resolutions. The narrower the instrumental energy resolution, the bigger the decrease in elastically scattered intensity (33,46). It is therefore evident that the intensities measured on IN16 (with a 10-fold narrower energy resolution than IN13) were smaller than those on IN13 (Fig. 4). Likewise, the discrepancy of the IN13 and IN16 MSDs in the intermediate temperature range (240–290 K) is related to the finiteness of the energy resolutions and the onset of the non-Gaussian motions that give rise to resolution-dependent MSDs (37,38).

In conclusion, all points discussed indicate that our data are not adequately described by the Gaussian approximation, motivating the approach of convoluting a scattering law with the respective instrumental energy resolutions.

The phenomenological scattering law

In contrast to linear fits, the more sophisticated regressions (Fig. 4) based on Eq. 9b gave more satisfying results: they described the experimental scattering intensities excellently over a large temperature and Q-range on both instruments. Limitations of the Q-range were not required. Moreover, a convoluted scattering law is certainly a more realistic and comprehensive description for the hydration water dynamics than the Gaussian approximation. The extraordinary property of a single scattering law that accounted excellently for the experimental data on two instruments that differ by a factor of ∼10 in energy resolution is a strong indication that the extracted parameters are realistic.

Although promoted in several studies using either IQENS (47) or IENS (33,48), approaches varying the energy resolution in IENS experiments to extract dynamic information are scarce. In a pioneering work on CPC hydration water (9), the quasielastic broadening from IN10 intensities was investigated at ambient temperature. The results were interpreted in terms of a jump diffusion model with a jump distance of 7–9 Å and residence times of 15–30 ns. One of the few studies available using elastic data from two different instruments (ILL spectrometers IN6 and IN16) investigates the dynamical transition of glutamate dehydrogenase in solution (36). Another study applies the Gaussian approximation in different Q-ranges to separate rotational and translational motions at two instrumental resolutions differing by a factor 100 (39). Several approaches have been used to interpret protein or hydration water dynamics at a single, fixed energy resolution in IENS experiments: jumps between two sites (41), liquid-like diffusion (49), several Gaussian populations (30), diffusion in confined geometry (32), translational and rotational motions (39,50), and others (reviewed by Gabel et al. (2)). We tried to fit several of these scattering laws, convoluted by the IN13 and IN16 instrumental energy resolutions to our experimental data but none of them was able to account for the elastic intensities simultaneously on both instruments. The fits yielded either unrealistic values of the parameters or were not able to account for the data equally well on both instruments. Furthermore, we checked jump diffusion (51) and a combination of diffusive, rotational, and vibrational motions (34,39). A single proton population described by any of these scattering laws failed to represent our data.

As a consequence of these unfruitful attempts, and motivated by a previous work on CPC hydration water showing its dynamic heterogeneity (11), we chose a combination of a dynamically confined population 1 − p, described by a simplified “diffusion inside a sphere” scattering law (32) and a population p, undergoing translational diffusion (Eq. 9a). This phenomenological combination of scattering laws was the only one we investigated that yielded realistic parameters from both instruments over a large temperature range. In particular, the resolution-independent parameters (sphere radius a, and populations p and 1 − p) could be chosen identical on both instruments and at all temperatures and accounted well for the data. The parameters accounting for the quasielastic part of the intensity, D and τ = 1/Γ, were in excellent (Fig. 5 a) or good (Fig. 5 d) agreement on both instruments. The difference between the extracted relaxation parameters τ = 1/Γ amounted up to a factor of 2 between IN16 and IN13 (Fig. 5 d). This discrepancy and the large errors associated with them (Δτ/τ < 200%) were partly explicable by the fact that the extracted Γ and τ (Fig. 5, d and e) correspond to HWHMs that differ by over an order of magnitude from both instrumental HWHMs. At these ratios, an exact determination of Γ and τ via a fit with experimental data is not very precise (33). The lack of data at higher Q from IN16 is an additional error source for τ; fixing the IN16 τ to the one of IN13 at temperatures T > 270 K does not significantly decrease the quality of the fit. It rather approaches the IN16 elastic intensities (predicted for Q² [Å⁻²] > 3.3) to those measured on IN13. Under these conditions, the approximate match of Γ from IN16 and IN13 was satisfactory.

Interpretation of the scattering law parameters and comparison to published data

Our numerical results are situated in an intermediate range of diffusion coefficients D and relaxation times τ of protein hydration water reported in literature. They are ∼3–4× smaller (D, a) or larger (τ) than those reported for pure hydration water (without trehalose) at a comparable hydration level in the temperature range 273–313 K (11). Because the authors used a different model and the instrumental energy resolution (14 μeV, HWHM) and the Q-range (0.04 < Q² [Å⁻²] < 1.64) differed from the ones of this study, a direct comparison of both results is not straightforward. In this context, our results confirm the capacity of trehalose to reduce both protein and water mobility in its vicinity more strongly than other bioprotectants (16,17,21,22,24). Interestingly, they suggest that a proton population exists that undergoes diffusive-like motions setting in at temperatures above the dynamical transition. This proton population rises from ∼15% to 90% from 235 to 320 K. Considering the contributions of the different molecules to the total scattering signal (Material and Methods), this implies that at the highest temperatures not only water molecules but also trehalose and labile CPC protons are involved in these motions. This dynamic population “unfreezes” with increasing temperature both in terms of mobility (increasing D) but also in terms of protons that are associated with these motions. The gradual increase of this population may be spatially ordered: one might hypothesize that it correlates with the distance of the water molecules from the protein surface (in analogy to dynamical populations in CPC itself (14)) with the ones farthest away from the protein surface being the most mobile ones. A spatial order of this population and its temperature dependence might also correlate with the distribution of charged, polar, or apolar CPC surface residues. Even though these hypotheses are compatible with our data they cannot be proven due to the averaging of the incoherent signal over all proton populations that excludes spatially resolved information. In particular, our approach cannot distinguish between a “preferential exclusion” (52) of trehalose molecules from the CPC surface or from a “water replacement mechanism” (53).

The radius a of the sphere associated with the complementary population 1 − p can be interpreted as an H-X bond vector (where X stands for N or O) undergoing relaxational motions confined by the interbond distance. This complementary dynamic population includes CPC labile protons, trehalose molecules as well as water molecules at lower temperatures (<260 K). At higher temperatures, it can be attributed completely to the labile protons and/or some of the trehalose molecules that move in a confined space with respect to the water molecules. However, it cannot be excluded that some of the structural water molecules contribute even at lower temperatures to this population. According to our model, at the highest measured temperatures some of the CPC labile protons must be dynamically very close to the hydration water since a population p = 90% cannot be accounted for by the hydration water and the trehalose alone (see Material and Methods). The activation energy of the relaxation component showing an Arrhenius behavior (Fig. 5 e) is ∼30–50 times higher than that of free water (34). It reflects the strong influence that the presence of the CPC surface and the trehalose molecules exert on the water molecules.

Apart from describing the dynamics of hydration water well and in fair agreement with reported data, our approach bears a significant advantage for future IENS applications: the free choice of instrumental energy resolution and Q-range. These advantages permit to circumvent the unsatisfactory situation where results from two different instruments cannot be compared directly but only via instrument resolution and Q-range dependent scattering laws. Using our approach instead, data sets from two (or more) instruments become readily comparable. It is furthermore well suited to be combined with information from IQENS, such as relaxation times extracted from HWHMs or structural data from elastic incoherent structure factors (54,55). Once such information is available on a system, it can be used as a guideline for the order of magnitude of parameters in IENS analysis (e.g., Γ and D in Eq. 9a).

Our model scattering law may be too simple and other, more sophisticated, scattering laws such as, e.g., a more general distribution of dynamical populations may be better suited to describe the ensemble of hydration water, trehalose, and CPC labile protons. However, our model is very satisfying regarding the number of the fit parameters and is completely sufficient to account for the experimental data. Furthermore, the magnitudes of the spatial and dynamic parameters extracted are in good agreement with results obtained by other studies using different models. We thus have demonstrated that elastic scans at different energy resolutions are well suited to extract spatial and dynamic properties from water in biological samples. It seems very promising to apply our approach to a wide range of such systems, e.g., membranes, proteins in hydrated powders or in solution, hydration water, or for the “screening” of dynamic populations in entire biological cells (6).

CONCLUSIONS

We have presented an efficient approach to describe C-phycocyanin hydration water dynamics in the presence of trehalose by incoherent elastic neutron scattering using two backscattering spectrometers with different energy resolutions. Applying the same phenomenological model scattering law, convoluted with the respective instrumental energy resolutions, we were able to extract effective diffusion coefficients, relaxation times, and linear dimensions describing the dynamic behavior of CPC hydration water over a very large temperature range (235–320 K). Our results are in good agreement with data reported in literature and show that the CPC hydration water mobility is reduced by over an order of magnitude with respect to bulk water by the presence of trehalose. Our methodological approach has several important advantages with respect to conventional approaches such as the Gaussian approximation: 1), no principal restraints on the choice of the instrumental energy resolution and Q-range; 2), a single scattering law can be used to describe the dynamic behavior of hydration water on several instruments; 3), the signal/noise of the data obtained is better than in comparable quasielastic scattering experiments; 4), it is well suited to immediate comparison with complementary quasielastic scattering experiments; 5), H₂O-hydrated, perdeuterated CPC as used here is quite unique for the study of hydration water dynamics since it is available in large milligram quantities needed for neutron spectroscopy experiments. However, our approach has a high potential to be applied to study dynamics of biological systems that are available in these amounts such as hydrated proteins, DNAs or RNAs, membranes, and even entire cells.

Dynamic information that can be extracted by our approach is limited by the energy resolution and Q-ranges covered by the instruments used. Parameters, e.g., relaxation times, that are much larger (or smaller) than the instrumental resolutions can be extracted only approximately. In these cases, quasielastic experiments are advisable to complement the information.