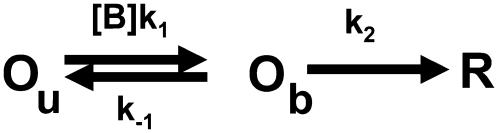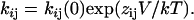On the Mechanism of TBA Block of the TRPV1 Channel

Abstract

The transient receptor potential vanilloid 1 (TRPV1) channel is a nonselective cation channel activated by capsaicin and responsible for thermosensation. To date, little is known about the gating characteristics of these channels. Here we used tetrabutylammonium (TBA) to determine whether this molecule behaves as an ion conduction blocker in TRPV1 channels and to gain insight into the nature of the activation gate of this protein. TBA belongs to a family of classic potassium channel blockers that have been widely used as tools for determining the localization of the activation gate and the properties of the pore of several ion channels. We found TBA to be a voltage-dependent pore blocker and that the properties of block are consistent with an open-state blocker, with the TBA molecule binding to multiple open states, each with different blocker affinities. Kinetics of channel closure and burst-length analysis in the presence of blocker are consistent with a state-dependent blocking mechanism, with TBA interfering with closing of an activation gate. This activation gate may be located cytoplasmically with respect to the binding site of TBA ions, similar to what has been observed in potassium channels. We propose an allosteric model for TRPV1 activation and block by TBA, which explains our experimental data.

INTRODUCTION

The first transient receptor potential (TRP) channel was identified in 1977 as a phototransduction mutant in Drosophila (1). Since then, at least 20 different TRP channels have been described (see (2) for review). The importance of TRP channels is demonstrated by the wide variety of their functions, which include responding to painful stimuli, receptor–mediated excitation, responding to a wide range of temperatures, repletion of intracellular calcium stores, and modulation of the cell cycle (for reviews see (3,4)). Despite the clear physiological importance of this protein family, little is known about its structural features.

The transient receptor potential vanilloid 1 (TRPV1) channels are activated not only by the vanilloid capsaicin, but also by noxious heat (>43°C), low pH, voltage, and various lipids (5–10).

Each subunit of the tetrameric TRPV1 channel is predicted to have six transmembrane domains with intracellular N- and C-termini and a short, pore-forming hydrophobic stretch between the fifth and sixth transmembrane domains. Similar topological features have been reported for other ion channels such as cyclic nucleotide-gated channels (CNG), the Shaker-related voltage-gated K⁺ channels (Kv), and the hyperpolarization-activated K⁺ channels (HCN) (11,12), suggesting that the overall topological features of TRPV channels are similar to those of the Kv channel superfamily. Conforming to this assertion, there is homology between the pore region of TRPV channels and the KcsA K⁺ channel (13). Some authors have generated homology models of the pore based on KcsA where some of the pore characteristics, such as the existence of a pore helix, have been confirmed (14,15). A number of the permeation characteristics of TRPV channels are also consistent with multi-ion permeation, just as in Kv channels (13,16). These results suggest that some of the functional properties of the TRPV pore may be more similar to those of Kv channels than we might have expected.

For voltage-dependent Kv and HCN channels (17–19), the activation gate has been determined to be a bundle crossing, formed by the S6 transmembrane segments, at the intracellular part of the channel. In contrast, the gate of CNG channels seems to be formed by the selectivity filter and not the bundle crossing, which undergoes a conformational change upon opening (20–22).

An important consequence of the intracellular bundle-crossing gating mechanism in Kv channels is that the gate interacts with large pore blockers like quaternary ammoniums (QAs), for which the intracellular binding site is formed by the potassium dehydration transition site (23).

The use of QA compounds for the study of K⁺ channel permeation and gating was pioneered by Armstrong (24–26). Tetraethylammonium (TEA) and its QA derivatives were found to block the ionic current only after the channel has opened, and it was proposed that QA compounds bind within the pore because the dissociation of the blockers becomes faster as the external [K⁺] is increased.

To date, many regions within the TRPV1 protein have been shown to be involved in specific functions. Nevertheless, the identity and the localization of the activation gate(s) of this channel have remained unclear. To obtain information about the nature of the activation gate(s) of the TRPV1 channel, we tested whether tetrabutylammonium (TBA) could block TRPV1 channels, and characterized the mechanism of block by this molecule. We found that TBA acts as a high-affinity channel blocker from the intracellular side in a voltage- and state-dependent fashion. Our data indicate that TBA interferes with closure of TRPV1 channels, suggesting that the activation gate is located cytoplasmically with respect to the binding site of QA ions, as with potassium channels. Finally, we propose an allosteric model for TRPV1 channel activation and block by TBA based on experimentally determined parameters and that accurately predicts our experimental data.

MATERIALS AND METHODS

Mammalian cell culture and recording

HEK293 cells expressing large T antigen were transfected with rTRPV1-pCDNA3 and pIRES-GFP (BD Biosciences, San Jose, CA) to visualize successfully transfected cells. Cell transfection was carried out with Lipofectamine (Invitrogen, Carlsbad, CA) according to manufacturer's instructions. Cells were plated in coverslips and used for recording one day after transfection. All inside-out patch clamp recordings were made using symmetrical solutions consisting of 130 mM NaCl, 3 mM HEPES (pH 7.2) and 1 mM EDTA for Ca²⁺-free conditions (27), unless otherwise stated. Osmolarity was adjusted with sucrose, and Trizma Base (Sigma-Aldrich, St. Louis, MO) was used to adjust pH for low sodium experiments.

The solutions bathing the intracellular surfaces of the patches were changed using an RSC-200 rapid solution changer (BioLogic, Claix, France).

Capsaicin (Sigma-Aldrich) stock solutions (4 mM) were prepared in ethanol, diluted to different concentrations, and applied to the intracellular surface of the patches to produce channel activation. All recordings were performed with a saturating capsaicin concentration (4 μM) unless otherwise stated.

Tetrabutylammonium chloride (TBA) (Fluka, St. Louis, MO) stock solutions were prepared with the low divalent solution described above and diluted to the final concentration with the same solution and supplemented with capsaicin.

Macroscopic currents were low-passfiltered at 2 kHz and sampled at 10 kHz with an EPC 10 amplifier (HEKA Elektronik GMBH, Pfalz, Germany). Data were acquired and analyzed with PULSE data acquisition software (HEKA Elektronik) and were plotted and analyzed with programs written using Igor Pro (Wavemetrics Inc., Portland, OR).

Pipettes were pulled from borosilicate glass, covered in Q-Dope (GC Electronics, Santa Ana, CA) and had a resistance of 2–4 MΩ. For macroscopic current recordings, the following voltage protocol was used: patches were held at 0 mV and given a pre-pulse to −120 mV for 30 ms. Voltage was then stepped from −150 to 150 mV in 10 mV increments for 100 ms and then returned back to −120 mV for 30 ms.

Block by TBA was quantified from 200 ms voltage pulses from −120 to 120 mV in 20 mV increments, in the presence of varying concentrations of TBA. We define the fraction of blocked channels, f_B as: 1−I/I_o, where I is the current in the presence of TBA and I_o is the current in the absence of TBA. The apparent dissociation constant, K_D, was estimated by fitting the dose-response relation to the Hill equation at a given voltage:

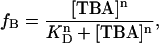(1)

where n is the Hill coefficient and [TBA] is the blocker concentration.

All recordings were performed at room temperature (19°C). Leak currents in the absence of capsaicin were subtracted from currents in the presence of capsaicin for all experiments.

Channel closure kinetics were measured using a tail-current protocol in which the patch was held at −120 mV for 20 ms, then stepped to 60 mV for 100 ms and returned to voltages from −120 to 0 mV in 20 mV increments for 100 ms. Tail currents were analyzed in this third interval. All tail-current recordings are the average of three traces to reduce noise.

Single-channel currents were recorded in inside-out patches using the same solutions as for macroscopic currents. Pipettes were pulled from borosilicate glass, covered in Q-Dope (GC Electronics) to reduce stray capacitance and fire polished to a resistance of 7–9 MΩ. Currents were filtered at 2 kHz and sampled at 5 kHz. Data were collected continuously at a fixed membrane potential of 60 mV. Event detection was carried out with the 50% threshold crossing technique (28). All-points amplitude histograms were collected and fitted with a double Gaussian function.

For determination of the open probability as a function of capsaicin concentration, we followed a method similar to that outlined in Islas and Sigworth (29). Macroscopic and single-channel openings were recorded in the same patch at 100 mV using patches that contained many channels. At low capsaicin concentrations, traces were leak subtracted with a leak template formed by the average of null sweeps. The same leak template was used to subtract the macroscopic currents. Channel openings were idealized with up to five thresholds if more than one open level was present. Idealized traces of 50–100 sweeps were ensemble-averaged to form an NP trace (open probability, P × number of channels, N). The steady-state value of the NP trace was used for plotting. To determine the absolute value of P, the number of channels in the patch was estimated from nonstationary noise analysis of 80–100 current sweeps at a saturating concentration of capsaicin, using the algorithm of Heinemann and Conti (30) to determine the variance. Mean-variance plots were then fitted to the function:

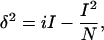where δ² is the variance, i is the single-channel current, I is the mean current, N is the number of channels and P = NP/N and P_max = I/iN (31).

The values i_noise = 6.26 ± 0.096 pA (n = 5) and maximum open probability P_noise = 0.87 ± 0.017 (n = 5), obtained from noise analysis, were comparable to those obtained from single-channel records (i_sc = 8.7 ± 1.2 pA; P_sc= 0.94) at the same voltage of 100 mV.

Bursts analysis was carried out in multi-channel patches at very low capsaicin concentrations. A burst was defined as a group of openings separated by shut periods no longer than the critical time t_crit. This critical time was chosen according to the criteria of Colquhoun and Sakmann (32), by which equal proportions of short and long closed periods are misclassified as being intra or interburst closed periods. At 10 nM capsaicin, in the absence of blocker, channel gating is simplified and two closed time constants can be observed with means of 600 μs and 110 ms. In this case t_crit = 2.3 ms. In the presence of blocker, the mean blocked durations are 3 ms and 80 ms. In this case t_crit = 7.5 ms.

Steady-state open probability (P) predictions from models were calculated according to:

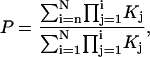where 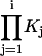is defined as the product of equilibrium constants for any pathway from state 1 to state j = i and K_j is the equilibrium constant for a transition from state j−1 to state j and K₁=1. Kinetic predictions from models were obtained by Q-matrix methods (33,34) implemented in Igor.

RESULTS

TBA blocks TRPV1 channels

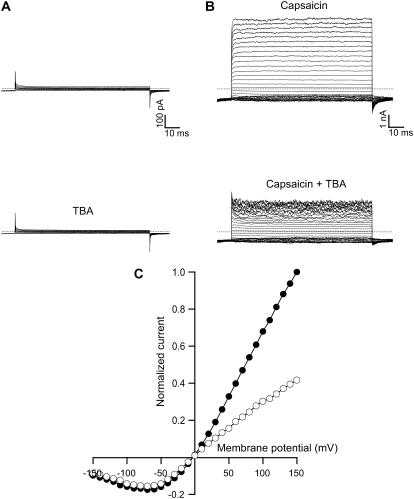
In this study, we have examined the effects of TBA on TRPV1 channels. TRPV1 channels were expressed in HEK293 cells and currents recorded in the inside-out configuration of the patch clamp technique. As shown in Fig. 1 A, under our recording conditions, endogenous currents in nontransfected HEK cells are negligible. The addition of 250 μM TBA to these patches produced a decrease of 10–30% in current.

FIGURE 1.

Block of TRPV1 currents by intracellular TBA. (A) Currents from a nontransfected cell in the absence (top panel) and presence of 250 μM TBA (lower panel). (B) Current traces without TBA (top panel) and with 250 μM TBA (lower panel) in the same patch from a cell transfected with TRPV1. The currents were elicited by stepping membrane voltage from the 0 mV holding potential to −120 mV and then to various test potentials from −150 to 150 mV in 10 mV increments (see Materials and Methods). Currents in (B) were obtained in the presence of 4 μM capsaicin and corrected for background current in the absence of agonist. The dotted lines identify the zero current levels. (C) Normalized current-voltage plots obtained from the current traces shown in B (top panel, solid symbols and lower panel, open symbols). Data were normalized to the maximum current obtained in the absence of TBA at 150 mV.

In the presence of 4 μM capsaicin, the application of depolarizing voltage pulses to patches obtained from TRPV1-transfected cells elicited outward-rectifying Na⁺ currents. (Fig.1 B). TRPV1 currents activate rapidly, as reported previously (35). The addition of 250 μM of TBA to the intracellular face of the patch effectively reduced the size of the current, presumably due to block of permeation through the channels (Fig. 1 B). Fig. 1 C shows the normalized steady-state current-voltage relation obtained from currents in B. Current blockade was more effective at depolarized potentials. This voltage dependence of block strongly suggests interaction of the blocker with some region in the pore or alternatively with some region in the protein within the membrane's electric field or a voltage–independent interaction with the voltage sensor.

Voltage dependence of block

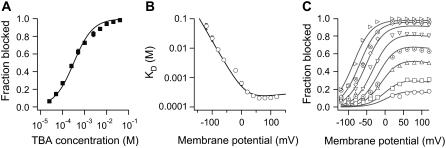
To further characterize the properties of TBA block of TRPV1 channels, we performed dose-response experiments with varying TBA concentrations at various voltages. Fig. 2 A shows the dose-response curve measured at 100 mV. We found that block is concentration-dependent with an apparent dissociation constant, K_D at 100 mV of 280 μM. The value of K_D was measured at varying voltages and plotted in Fig. 2 B to show that block indeed occurs most efficiently at positive membrane voltages. The data in Fig. 2 B have the surprising property that the value of K_D tends to a limiting value at positive voltages where a “saturation of block” seems to occur. A similar phenomenon has been previously described in Kv and IRK K⁺ channels, and it has been suggested that a plausible explanation for it is the presence of a “relief of block” mechanism where the apparent voltage dependence of K_D disappears and no more block is obtained with further depolarization, presumably due to the blocker acting as a partial permeant ion (36,37).

FIGURE 2.

TBA block characteristics. (A) Effect of TBA on the fraction of blocked channels. Average blocking dose-response as a function of TBA concentration obtained from nine patches. Block by TBA was completely reversible. The Hill equation (Eq. 1) was fitted to the data with parameters n = 0.89 and K_D = 280 μM. (B) Voltage dependence of K_D measured from five patches. The continuous line is the predicted K_D as a function of voltage from the permeant blocker model shown in Scheme 1. The rate constants used are: k₁ = 5 × 10⁵ M⁻¹s⁻¹ × exp(0.99e_oV/kT), k₋₁ = 90s⁻¹ × exp(−0.13e_oV/kT), k₂ = 163s⁻¹ × exp(0.02e_oV/kT). These rate constants were constrained to be similar to those obtained from data on TBA kinetics of block shown in Fig. 6. (C) The fraction of blocked channels as a function of voltage in the presence of TBA. Increasing concentrations are indicated by the following symbols (in μM): ○, 50; □, 100; ▵, 250; ⊕, 500; ▿, 1000; ⋄, 2500; ⊗, 5000; ▹, 10,000. Continuous lines are the predictions from the same model and parameters used in (B).

Saturation of block can also be evidenced in the voltage dependence of the fraction of blocked channels, f_B, which is also plotted as a function of voltage in Fig. 2 C. The data clearly indicate that block is voltage-dependent since f_B increases as the voltage becomes positive. Nevertheless, the fraction of blocked current does not reach a maximum value of one at depolarized voltages until very high blocker concentrations are used and instead plateaus for each TBA concentration, and no more blockade can be attained at more positive voltages. This behavior is contrary to what the canonical Woodhull model for ionic blockade would predict, which is that, regardless of the blocker concentration, sufficiently depolarized voltages should produce complete block (38).

The nature of this diminished block at high membrane potentials has not received a completely satisfactory explanation in any of the ion channels in which it has been described. As mentioned above, for its simplicity, the most common explanation has been that of a permeant blocker producing relief of block. This model postulates that an intracellularly applied blocker is in equilibrium with its binding site but can escape to the external solution and during that time interval, normal permeation occurs (39–41), effectively reducing the amount of block.

A simple model based on the permeant blocker hypothesis (42) as the one shown in Scheme 1 is able to accurately account for the shape and voltage dependence of the fraction of blocked channels (Fig. 2 B and C, continuous lines), assuming that the rate of blocker dissociation is the same as that of blocker permeation.

SCHEME 1.

Simple mechanism for relief of block.

In Scheme 1, O_u is the open unblocked channel, O_b is the open blocked channel, R is the relieved channel, [B] is the TBA molar concentration, and k₁ and k₋₁ are the rate constants for block and unblock, respectively. Finally, k₂ is the rate constant for TBA permeation, and it predicts the size of the TBA current. The k₂ rate constant is so small that even if there was TBA permeation, we would not be able to detect it. In fact, in experiments where internal Na⁺ was substituted by TBA, we did not observe measurable TBA currents (data not shown).

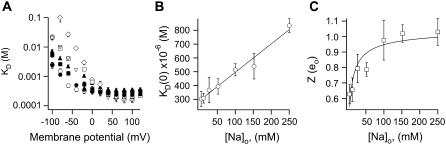
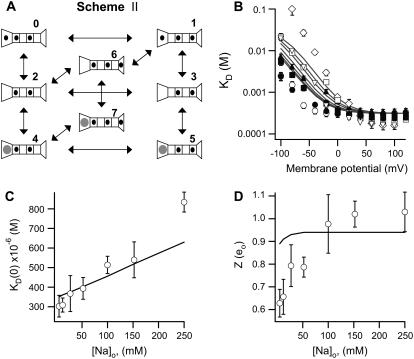
An alternative explanation for the saturation of block has been advanced, which posits that ion-ion and ion-blocker interactions in the permeation pathway lead to saturation of block without blocker permeation (43), mainly through repulsion between permeant ions and blocker molecules. To explore this possibility, we first determined whether the blocker molecule is able to interact with the permeant ion. By varying the extracellular Na⁺ concentrations, the occupancy of the ion binding sites within the channel selectivity filter is changed, which may affect the interaction of the permeant ions with the TBA molecule occupying its intracellular binding site. We measured the K_D for intracellular TBA block with 150 mM intracellular NaCl, while varying the extracellular NaCl concentration.

Fig. 3 A displays the voltage and sodium ion dependence of the K_D measured at several voltages as in Fig. 2 B. For every value of extracellular Na⁺, the behavior of the K_D is the same, with blocker affinity increasing at more positive potentials but reaching a limiting value at voltages positive to 20 mV, which reflects saturation of block at those potentials. Fig. 3 B plots the value of K_D at 0 mV as a function of sodium concentration. Fig. 3 A and B show that the K_D and, therefore the affinity of the channel for the blocker, decreases as the sodium concentration is increased, which is an expression of the “knock-off” effect described in other ion channel pore blockers (44,45) and a clear indication of an interaction between the blocker and the permeant ion.

FIGURE 3.

Ion interactions in TRPV1 channels. (A) The effect of extracellular Na⁺ on the voltage dependence of K_D, estimated from Eq. 1. Different symbols represent varying Na⁺ concentrations: ○, 5 mM; •, 12 mM; ▪, 27 mM; ▴, 52 mM; ▿, 102 mM; □, 152 mM; ⋄, 252 mM. Data were obtained from three to six patches. (B) The K_D at 0 mV is plotted as a function of extracellular Na⁺ concentration; the continuous curve is a fit of a line to the data. (C) Voltage dependence of K_D at negative voltages. The value of Z was obtained from fits of Eq. 2 to the data in (A) from −120 to −20 mV. The continuous curve is a fit to the Hill equation, with a steepness factor of 0.6 and a K_1/2 of 5 mM.

The K_D voltage-dependence in the Woodhull model is given by:

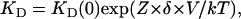(2)

where K_D (0) is the dissociation constant at 0 mV, Z ×δ is the apparent voltage dependence, and kT has its usual meaning. We obtained an estimate of the voltage dependence by fitting Eq. 2 to the curves in Fig. 3 A from −120 mV to −10 mV, where the voltage dependence behaves according to Eq. 2. We observed that the voltage dependence (the value of Z ×δ) of block increases as a function of extracellular Na⁺ concentration (Fig. 3 C), reaching a value of 0.98 ± 0.129, which in the Woodhull model would imply that TBA traverses almost all the electric field. An elegant explanation for these very high apparent voltage dependences has been advanced by Spassova and Lu (46) to account for a similar observation in inward rectifier K⁺ channels and is based on equivalent observations in voltage-gated ion channels (36,47). In this proposal, blocker binding has little voltage dependence but produces the concerted displacement of ions in the selectivity filter. This concerted movement of permeant ions and blocker molecule confers the high voltage dependence of block observed.

Taken together these two observations indicate that ion-ion and ion-blocker interactions occur in the selectivity filter of TRPV1 channels and suggest that they may be related to the saturation of block. We sought to examine whether a permeation model that includes these interactions can explain our experimental observations. The model we used is based on the permeation cycle observed in the KcsA potassium channel (48–50) and includes competition between the TBA molecule and the permeant ions as well as the concerted movements of ions induced by TBA binding (Fig. 4 A). The parameters used in simulations using Scheme 2 (Fig. 4 A) are given in Table 1. These parameters were chosen to reproduce the amount of saturation of block and the channel conductance as well as the open channel I/V curve in a range from −100 to 100 mV.

FIGURE 4.

A multi-ion permeation model explains saturation of block. (A) The permeation and block model used for simulations. There are four ion binding sites in the selectivity filter and two more sites, one on the internal cavity (left) and one on the external cavity (right). TBA (gray circles) binds in the internal cavity and does not enter the selectivity filter. The fraction of electric field (δ) traversed in each transition is partitioned as follows. Transitions among sites in the selectivity filter have a δ = 0.22, entering the internal cavity δ = 0.06, and entering the external cavity δ =0.06. There is a repulsive interaction between blocker and permeant ions and between permeant ions whenever two contiguous sites are occupied at the same time. The factor is √r with r = 700, which decreases forward rate constants by a factor 1/√r and increases backward rate constants by √r. (B) The effect of extracellular Na⁺ on the voltage dependence of K_D. The same data as in Fig. 3 A are shown with the predictions from Scheme 2 superimposed. (C) The K_D at 0 mV is plotted as a function of extracellular Na⁺ concentration; the straight line is the prediction from Scheme 2. (D) Voltage dependence of K_D at negative voltages. The value of Z was obtained from fits of Eq. 2 to the data in (B) from −120 to −20 mV. The continuous line is the prediction from Scheme 2. Parameters are given in Table 1.

TABLE 1.

Parameters of the permeation model (Scheme 2)

Rate constant k(i,j) at 0 mV*	Value
(0,1); (2,3); (4,5)	1×1010 s−1
(1,0); (3,2); (5,4)	3×1010 s−-1
(0,2); (1,3)	9.9×107 s−1
(2,0); (3,1)	7.9×109 M−1s−1
(1,6)	3×109 s−1
(6,1)	7.9×109 s−1
(6,2); (7,4)	6.3×107 s−1
(2,6); (4,7)	9.9×108 M−1s−1
(2,4); (3,5); (6,7)	4×108 M−1s−1
(4,2); (5,3); (7,6)	1×104 s−1

The voltage dependence (z_ij) of each rate constant is indicated in the legend in Fig. 4. Rate constants for transitions between states i and j are given by:

^*The numbering of states is indicated in Scheme 2 (Fig. 4).

The model is able to predict the shape of the K_D as a function of voltage, the increase of K_D at high Na⁺ concentrations (Fig. 4 B and C), and the increased voltage dependence, although the predicted increase is less than observed (Fig. 4 D). Likewise, the model predicts saturation of block without requiring permeation of the large TBA molecule.

Kinetics of TBA block

To assess the kinetics of block by TBA, we carried out single-channel recordings. As shown in Fig. 5 A (left panel), at 4 μM capsaicin and 60 mV, channel openings are rather long and the open probability is 0.92. Kinetic analysis shows that there are at least four exponential components in the distribution of open times and also four closed time exponentials (data not shown). Multiple closed and open states have been reported previously for TRPV1 channels (51). Fig. 5 A (right panel) shows the amplitude histogram fitted with a sum of two Gaussian functions. This analysis yields a single-channel current of 6 pA, which corresponds to a conductance of 100 pS. Fig. 5 B (left panel) shows a current trace from the same patch recorded in the presence of 250 μM TBA. Single-channel current is not significantly affected as evidenced by the distribution of current amplitudes (Fig. 5 B, right panel), which yields a single-channel current of 5.9 pA, and individual blocking events can be resolved. The appearance of some longer lived blocked life times suggests differences in the affinity for block among the various open states of the TRPV1 channels.

FIGURE 5.

TBA does not affect TRPV1 single-channel conductance. (A, left) Single-channel recordings of TRPV1 activated by 4 μM capsaicin at 60 mV. The symbols O and C represent the open and closed current level, respectively. The right panel shows an all-points histogram (gray line) obtained from 30 traces as in the ones on the left; superimposed is the fit to a sum of two Gaussian functions (black line). The open level amplitude is 6 pA. (B) The patch in (A) was exposed to 250 μM TBA. The current traces were recorded also at 60 mV. Individual blocking events are discernible in the current trace as short-lived shut events. The all-points histogram from 25 traces is shown on the right with the fit to a sum of two Gaussians with open amplitude of 5.9 pA.

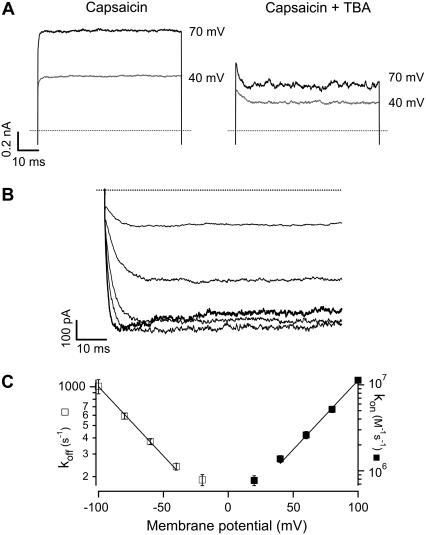
Due to the very complex kinetic behavior of the channel at high capsaicin concentrations, we did not attempt to obtain any quantitative kinetic parameters from these data. Instead, we analyzed the time courses of the onset and offset of block during activating voltage pulses. At intermediate depolarization (40 to 100 mV), there is an exponential decay of current in the presence of TBA, which suggests that the kinetics of block may be slow enough that we may be able to resolve it.

Fig. 6 A shows current traces without TBA (left panel) and with 250 μM TBA (right panel) at two different voltages in a representative patch. The onset of block can clearly be resolved in the presence of TBA at both voltages. Fig. 6 B shows the current traces at negative voltages in the presence of 2.5 mM TBA. The voltage-dependent unblocking reaction can be observed as an exponential increase of current when the channel should be closing. For a blocking reaction of the form:

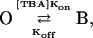where k_on is the blocker association rate constant and k_off is the blocker dissociation rate constant, the voltage-dependent time constant, τ(V) of the exponential current decay is given by:

(3)

FIGURE 6.

Kinetics of TBA block. (A) Currents recorded at the indicated membrane potential in the absence (left) and presence of 250 μM TBA (right). The onset of channel block is evidenced by the exponential current decay. (B) Recovery from channel block at negative voltages in the presence of 250 μM TBA. The patch was stepped to 60 mV and repolarized to record tail currents from −100 mV to −20 mV. The exponential increase of current is due to voltage-dependent unbinding of TBA from the channel. The trace at −100 mV is shown as a thick black line and reflects both unblocking and deactivation of the channel. (C) Voltage dependence of on- and off-rate constants. The off-rate constant k_off was obtained from fits of a single exponential to records as in (B) and for k_on, the inverse of the time constant of an exponential fitted to the current decay of records as in A (right) was plotted as a function of TBA concentration, and the slope used as an estimate of k_on. The values of k_off and k_on as a function of voltage were fitted with an exponential function of voltage (Eq. 4) with parameters: k_on(0) = 2.5 × 10⁵ M⁻¹s⁻¹, k_off(0) = 83.76s⁻¹, z_on = 0.93 and z_off = −0.63. Symbols are the mean ± SE (n = 4).

An estimate of k_on can be obtained from the slope of the inverse of τ as a function of TBA concentration at positive potentials, and an estimate of k_off was obtained from the inverse of τ at negative voltages. Fig. 6 C depicts the summary of the data obtained from several patches. The k_on (solid symbols) is a pseudo-first order rate constant with units (M⁻¹ s⁻¹). Clearly, the k_on increases at positive voltages and decreases at negative voltages. The k_off has, as expected, the opposite behavior: increases at negative voltages and decreases at positive voltages and is independent of blocker concentration (units s⁻¹). The solid lines are fits to an exponential function of voltage of the form:

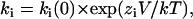(4)

where k_i(0) is the value of the corresponding rate constant at 0 mV and z_i is the partial charge associated with the reaction. We obtained the following parameters: k_on(0) = 2.5 × 10⁵ M⁻¹s⁻¹, k_off(0) = 83.76 s⁻¹, z_on = 0.93 and z_off = −0.63.

State dependence of block

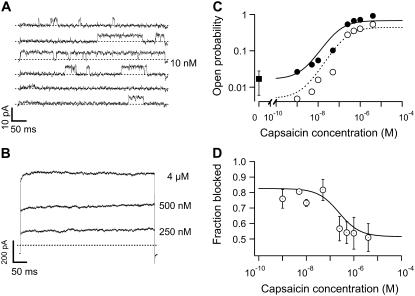
The observation of the rate of unblocking at negative potentials would suggest that the channels are unable to close until the blocker leaves the channel, an indication of a preference of the blocker for the open state. We sought to determine the state dependence of TBA block by measuring the dose response for activation of TRPV1 by capsaicin. The same membrane patches with many channels were used to measure both macroscopic currents at high concentrations of capsaicin and the opening of one or a few channels when the concentration of ligand is very small. Fig. 7 A shows a few channel openings elicited by 10 nM intracellular capsaicin and Fig. 7 B shows the macroscopic response to higher concentrations of the agonist in the same patch. The channel openings at low concentrations were identified as TRPV1 channels based on their conductance and the fact that the burst length increases with capsaicin concentration (data not shown). The openings at each concentration were idealized and averaged to form an ensemble-averaged trace, as described in the methods section. The same protocol was repeated on the same patch but in the presence of 250 μM TBA.

FIGURE 7.

State dependence of block by intracellular TBA. (A) Individual channel openings from a patch with 150 channels in the presence of 10 nM capsaicin. The open probability obtained from the ensemble-averaged idealized traces at 100 mV is 0.016. (B) Macroscopic currents elicited by the indicated concentration of capsaicin in the same patch as in (A). (C) Block of TRPV1 channels by TBA. The solid circles are the open probability in response to capsaicin obtained from dose responses as in (A) and (B). Open circles are the open probability in the presence of 250 μM TBA in the same patch. The square symbol is the value of the unliganded open probability determined from separate patches. The continuous line represents the prediction of Scheme 3 in the absence of blocker. The dotted curve is the prediction of Scheme 3, which allows block in the open state only. The parameters of the model are given in Table 2. (D) Fraction of blocked channels, f_B,, as a function of capsaicin concentration. Data were transformed according to 1−(P_B/P), where P is the open probability in the absence of blocker and P_B is the open probability with blocker. The continuous curve is the prediction of Scheme 3 with the same parameters as in C. Symbols are the mean ± SE (n = 3).

At 19°C (Fig. 7 C, solid circles) the steady-state open probability, P as a function of capsaicin concentration, could be measured down to a value smaller than 0.02. The data suggest that the value of P at low capsaicin concentrations approaches an asymptotic value that is independent of capsaicin, P_u, which should reflect the probability of unliganded openings. We carried out a direct measurement of the value of P_u at 19°C, in different multi-channel patches, and determined its value to be 0.017 ± 0.011 (n = 3).

This result is a hallmark of an allosteric mechanism of activation by the ligand (52). The allosteric behavior of TRPV1 observed in the dose-response curves is compatible with our single-channel recordings, which show the presence of multiple open states, which have been previously observed (51). Fig. 7 C also shows the value of P as a function of capsaicin in the presence of 250 μM blocker for the same patch (open circles). It is clear that TBA reduces the open probability over the whole range of agonist concentrations. Fig. 7 D shows the fraction of current blocked by TBA as a function of capsaicin concentration obtained from three different membrane patches. The fraction of blocked current seems to be almost constant over the range of open probabilities, and the fraction blocked at lower capsaicin concentrations (low open probabilities) is slightly larger than at higher capsaicin concentrations. 250 μM TBA blocks ∼50% of the current when the open probability is near 1.0, and it blocks near 75% when the open probability is near 0.02.

Taken at face value, these data would suggest that the blocker has about the same affinity for the closed and the open state, as has been observed for the blockers tetracaine and dequalinium in CNG channels (53,54). Another mechanism that displays the same behavior occurs when the blocker is able to access only the open state of the channel but becomes “trapped” when the channel closes, which would produce a slight stabilization of the closed state in the presence of the blocker. This mechanism has been demonstrated in Kv, HCN, and other potassium channels (55–57). However, similar behavior has been reported in HCN channels where the blocker ZD7288 appears to block better at positive voltages where channels are mostly closed. The explanation in this case is that the blocker binds only to open channels, but there are more than one open state, each with different blocker affinities, and ZD7288 has greater affinity for open states that occur earlier in the gating pathway (57). Given the presence of multiple open states in TRPV1, an open channel block mechanism, with the affinity of the blocker being different for each of the various open states, seems plausible. Thus, we further explore an open-state block mechanism.

TRPV1 channels are blocked by TBA in the open state

A direct consequence of open-state block without trapping is that the channel cannot close in the presence of blocker but has to unblock first to close. We examined whether this is the case in TRPV1 channels in two ways. First we tested the effect of TBA on single-channel burst kinetics, and then we measured channel closure kinetics.

Given the complexity of single-channel kinetics, we attempted to simplify the measurements by carrying out recordings in conditions where the channel should behave approximately as a two-state system, which can be accomplished at low capsaicin concentrations. Under these conditions, channel gating occurs in bursts of openings separated by long closed periods (Fig. 8 A). The classic prediction for an open-state blocker is that channels cannot close in the presence of blocker, and thus for a simple mechanism with a single open state, the burst length (B_L) in the presence of TBA should increase according to (58):

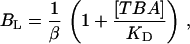(5)

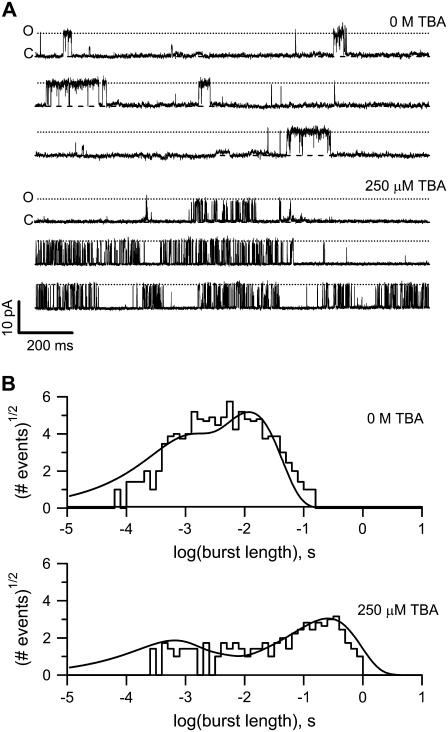
where β is the channel closing rate, K_D is the blocker dissociation constant, and [TBA] is the blocker concentration. In our case, the presence of multiple open and closed states implies that the burst length distribution has potentially many exponential components, but it is still true that if the blocker can only block in the open state, we should observe a lengthening of some components in the burst length distribution. Fig. 8 A shows single-channel current traces at 60 mV in the presence of 10 nM capsaicin and no blocker (upper panel) or with 250 μM TBA (lower panel). The burst length distribution histograms are shown in Fig. 8 B: the histogram in the presence of blocker is in the lower panel and shows a shift toward longer lived bursts as compared with the histogram in the absence of blocker (top panel). According to Eq. 5, when the concentration of blocker is equal to K_D, the burst length should double. We observed that the value of B_L increases approximately five times, presumably due to the fact that at a low capsaicin concentration the open states with higher affinity are occupied and 250 μM of TBA is a concentration beyond the microscopic K_D. This interpretation is in accordance with the data presented in Fig. 7, which shows that, at low capsaicin concentration, the value of f_B is higher, indicating that the microscopic association constant of earlier open states is also higher. These observations support an open-state block mechanism, and the model presented in the discussion, which distinguishes between open states with different TBA affinities, is able to nicely account for the distribution of B_L. Fig. 8 B (lines) shows the predicted burst length distributions from the full model in Scheme 3 using parameters in Table 2.

FIGURE 8.

Burst kinetics support an open-state block mechanism. (A) TRPV1 channel burst kinetics. Upper panel shows bursts of openings at 60 mV in the presence of 10 nM capsaicin in a patch containing ∼120 channels. The closed and open channel levels are indicated. Rare openings of a very small conductance channel are also visible. The lower panel shows traces recorded in the same patch and under the same conditions as in the upper panel but in the presence of 250 μM TBA. (B) Burst-length distributions of the patch in (A). The upper panel shows the burst-length distribution in the absence of blocker. The lower panel shows the burst length distribution in 250 μM TBA. The continuous lines are the prediction of the burst length from Scheme 3 with the parameters shown in Table 2.

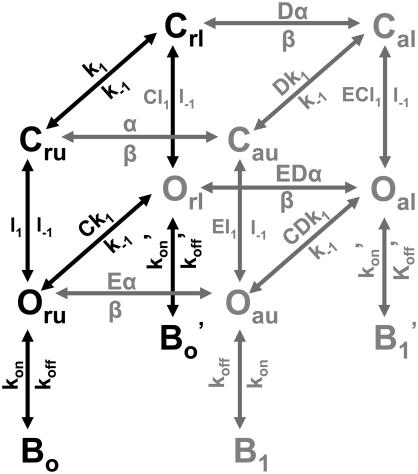
SCHEME 3.

Full model for open-state block.

TABLE 2.

Rate constants for simulations from Scheme 3

Rate constant*	Value (at 0 mV)	z(eo)
α	240 s−1	0.3
β	5300 s−1	−0.05
k1	1.05×107 M−1s−1	0.01
	273 s−1	−0.01
l1	9.6 s−1	0.05
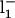	480 s−1	−0.05
kon	2.2×107 M−1s−1	0.53
koff	39 s−1	−0.55
kon′	1.25×105 M−1s−1	0.93
koff′	40 s−1	−0.63

The values of the allosteric factors are: C = 125, E = 500, D = 10.

^*The voltage dependence of an individual rate constant k_i is given by equations of the form: 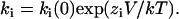k_i(0) is the value of k_i at 0 mV, V is the membrane potential in mV and kT has its usual meaning.

Another line of evidence in support of the open-state block mechanism is provided by the kinetics of channel closure. A prediction of the open-state block mechanism is that channels should reopen before closing in the presence of blocker, which would be evidenced by a slowing of tail current kinetics. In contrast, both a mechanism that allows equal access to open and closed channels and a trapping mechanism predict tail current kinetics that are not different or are even faster in the presence of blocker (59,60). To further test the open-state block mechanism, we studied the effects of TBA on TRPV1 channel-closure kinetics by determining if tail currents were slowed down in the presence of blocker.

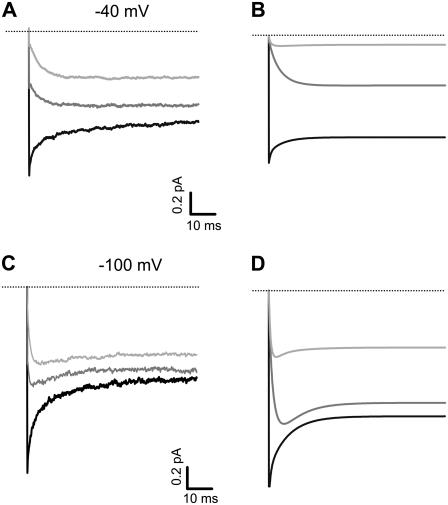
Upon repolarization, the decay of tail currents can be described with up to two exponentials (not shown). Tail currents of TRPV1 in the presence of 2.5 mM TBA show significant differences in time course. The magnitude of the tail current was reduced as a consequence of steady-state block during the depolarizing test pulse, and the time courses were significantly slower in the presence of the blocker at −100 mV, as shown in Fig. 9 C. Moreover, tail currents in the presence of TBA presented a characteristic “hook”, indicative of the blocker having to exit the channels before they can close, as was also described in Kv channels (59). At a less negative voltage (−40 mV, Fig. 9 A), where channels do not close completely, the tail current is dominated by TBA unblocking kinetics, as evidenced by the exponential growth of current as the blocker leaves open channels. These results can be neatly explained by a mechanism with the blocker having to leave the open channel before it can close. Simulations with Scheme 3 showed tail current time courses that are very similar to those experimentally observed (Fig. 9 B and D, see discussion). These results are not consistent with a state-independent blocking mechanism or a state-dependent blocking mechanism with trapping.

FIGURE 9.

Closure kinetics of TRPV1 channels are affected by TBA. Tail currents of channel activated by 4 μM capsaicin and a voltage pulse to 60 mV in the absence of blocker are shown as the black trace for a tail voltage of −40 (A) and a tail voltage of −100 mV (C). Tail currents were also recorded in the presence of 250 μM (gray traces) or 2.5 mM TBA (light gray traces) for each voltage. (B and D) Simulations of tail currents for each condition shown in (A) and (C) were performed according to the open-channel block mechanism shown in Scheme 3. The rate constants for block at 0 mV and the voltage dependences of the blocking rate constants used for tail-current modeling were obtained from measurement of blocking kinetics (k_on and k_off) as shown in Fig. 6. All model parameters are shown in Table 2. The lines of panels (B) and (D) represent the model predictions for the same conditions used in (A) and (C). The model shown here does not include any mechanism for saturation of block and thus predicts more block than observed.

DISCUSSION

In this study we demonstrate that TBA is a high affinity blocker of TRPV1 channels. TBA block occurs in a voltage-dependent fashion and shows saturation at positive voltages. The mechanism seems to be consistent with open-state block, similar to that observed in voltage-dependent (Kv) potassium channels.

Block by TBA is voltage-dependent since efficiency of block is increased as the membrane potential becomes more depolarized; however, the value of its dissociation constant reaches a minimum at potentials more positive than 20 mV. This phenomenon of saturation of block can also be observed in the voltage dependence of the fraction of blocked channels as an incomplete block at positive potentials. This deviation from the canonical predictions for a voltage-dependent blocker (Woodhull model) has been traditionally explained in terms of the blocker being a partial permeant ion (40–42). The permeant blocker model we employed predicts saturation of block even at a TBA permeation rate of ∼200 s⁻¹, which would produce extremely small currents, suggesting that TBA permeation may still be present but is immeasurably slow. As suggested by Heginbotham and Kutluay (43), transport of permeant blockers may be only detectable by radiolabeled tracer studies or some other form of direct measurement.

In any event, it seems that given the large size of TBA (∼10Å), permeation of this molecule would require a large deformation of the selectivity filter or, alternatively, the permeation pathway in TRPV1 channels being able to accommodate very large molecules. Even the largest estimate of the TRPV1 pore diameter is of 6.8 Å (13,61), which makes TBA permeation unlikely. It has been suggested that saturation of block can occur as a consequence of ion interactions between permeant ions and the blocker molecule, without having to invoke blocker permeation, and it can be observed even in simple multi-ion permeation models (43,62).

Our experiments indicate that TRPV1 channels do behave like multi-ion pores. Varying the concentration of extracellular Na⁺ yielded results that point to the presence of multi-ion interactions in TRPV1. For example, we observed a “knock-off” effect in the form of decreased affinity for TBA at higher external Na⁺ concentrations (Fig. 3). This effect is likely produced because at higher Na⁺ concentrations, the occupancy of permeant ion sites in the permeation pathway is increased, creating a competition effect with TBA, which likely occupies a nearby site in the permeation pathway. We also observed remarkably high values for the voltage dependence of TBA block, a value of z of nearly 1 and a considerable increase of this apparent voltage dependence as a function of higher Na⁺ concentration.

A similar effect has been reported in other channels including inward rectifiers and Kv channels (46,63–65). Those observations have prompted the notion that the blocking reaction may not have an intrinsically large high voltage dependence, but instead most of the voltage dependence arises as a consequence of ion-blocker repulsion and the blocker displacing one or more permeant ions in the selectivity filter, where most of the electric field decays (66). This explanation is also supported by the structure of the pore in all of the ion channel molecules for which high resolution structures are available. All of these channels have a large intracellular cavity, where quaternary ammonium blockers have been shown to bind in the KcsA channel. Calculations have shown that a very small fraction of the electrical potential difference is sensed by a blocker occupying this cavity (62,66).

To explain our data, we used a multi-ion permeation model that includes all of these features (ion-ion and ion-blocker repulsion, ion-blocker competition) and is based on permeation models derived from the known structure of potassium channels. It is worth noting that data pointing out to some multi-ion channel properties are available for TRPV6 channels (16). These authors have demonstrated the existence of an anomalous mole-fraction effect for Ca²⁺ and Na⁺ ions as well as multi-ion block by trivalent cations. The purpose of this model is to provide a simple explanation for a large set of experimental observations pertaining to block by TBA and is not meant as a definitive but as an initial explanation for the pore properties observed here as well as for saturation of block in TRPV1 channels.

The main feature of the model is that it accurately reproduces the observed saturation of block without the need to assign permeability to the TBA molecule. In the model, saturation of block occurs as a consequence of both the competition between the blocker and the first permeant ion in site 1 (Scheme 2 (Fig. 4 A)) and repulsive ion-ion interactions between permeant ions occupying sites in the selectivity filter. This later effect was first proposed by Heginbotham and Kutluay (43). Competition between Na⁺ ions and the blocker molecule is also responsible for the decreased affinity for TBA at higher Na⁺ concentrations. As shown in Fig. 4 B the model can predict qualitatively the increase in K_D as extracellular Na⁺ is increased and the increased voltage dependence of K_D at higher Na⁺ concentrations (Fig. 4 C and D). Nevertheless, the observed change in the magnitude of the apparent valence, Z, is larger than that predicted by the model. This is due to the fact that in Scheme 2 (Fig. 4 A), the blocker is able to produce the concerted displacement of two ions across almost half the membrane potential drop, but the channel is not allowed to have less than two ions at any time. Therefore, the minimum value of Z that can be expected at low Na⁺ concentration is higher than the value that we measure. In summary, this model is able to qualitatively account for a large set of experimental observations with a single set of parameters.

Our experiments varying the extracellular Na⁺ concentration did not compensate for the reduced ionic strength, in part because of the fact that these channels are permeable to a large range of organic cations that we could have used to maintain ionic strength. Nevertheless, we can obtain an estimate of the expected effects of reduced ionic strength. The fixed surface charge near the external entrance of the pore of some channels has been estimated to be in the order of −0.06 to −0.1 e_o/nm² (45,67). At our lowest Na⁺ concentration, this would represent a concentrating factor for monovalent cations of three- to fivefold and this would be reduced to ∼1.7-fold at the higher Na⁺ concentration. This concentrating effect would increase the Na⁺ occupancy of the channel and produce a slight overestimation of the effect of Na⁺ at low concentrations.

Kinetics and open-state dependence of TBA block

Block by TBA did not significantly affect the single-channel conductance of TRPV1 channels. In single-channel recordings, individual blocking events can be discerned, along with some longer events, which suggests that TBA is a blocker with intermediate kinetics and that blockade may be slow enough to be resolved in macroscopic current recordings. At depolarized voltages, current decays exponentially with a time constant that is exponentially dependent on voltage and mainly reflects the contribution of the on-rate constant for blocker association with the channel. At negative voltages, between −100 and −40 mV, the channel closes incompletely and slow enough that the exit of blocker from the channel can be evidenced as an exponential increase of current from its blocked level. This process reflects mainly the off-rate constant, which we found to be independent of blocker concentration, as expected for a true off-rate constant. We will come back to this point. The determination of the voltage dependence of on- and off-rate constants, shows that the total valence of the transition (z_on + z_off) > 1, which is in accordance to the high value of Z determined in Fig. 3 C and which we suspect is a result of ion-blocker interactions in the conduction pore.

When we measured the activation of TRPV1 by capsaicin, one observation was unavoidable: TRPV1 channels seem to be able to open in the absence of ligand. The open probability at low capsaicin concentrations approaches an asymptotic value that is independent of capsaicin concentration. In fact we were able to measure this probability of unliganded openings and found it to be 0.017 at 19°C. In their study of voltage, temperature, and capsaicin activation, Voets and colleagues (35) proposed a simple two-state model that cannot account for these observations. Instead, an allosteric mechanism, such as those proposed for BK channels (52) and HCN (68) channels, seems to be necessary. Such a mechanism is also implied by the presence of multiple open and closed states (data not shown and (51,69)).

In our experiments, the fraction of blocked current varies over the range of open probabilities, and the fraction of blocked channels is slightly larger at lower capsaicin concentrations (low open probabilities). This observation would suggest, as proposed in CNG channels (53,54,70), that the blocker can gain equal access to both open and closed channels and the higher fraction of block at lower open probabilities observed in Fig. 7 could be explained by a higher affinity of the compounds for the closed state of the channels. We attempted to measure accessibility of the blocker in closed states by looking for a slowed down activation by capsaicin after application of TBA in the closed state, but activation was not affected by exposure of closed channels to TBA. In a second mechanism, the blocker would be able to access only the open state of the channel and become “trapped” when the channel closes, a mechanism that has been demonstrated in Kv and HCN potassium channels (55–57). We attempted to measure trapping of TBA but were also unable to observe it. Trapping experiments require completely closing the channels by either negative voltages or by rapidly removing capsaicin, which is hard to achieve before TBA leaves its binding site.

A number of observations support open-state block rather than closed-state blocking or trapping. In the latter two mechanisms, the channel has to be able to close with the blocker in its binding site, which is reflected by the appearance of faster tail currents in the presence of blocker (59,60). We have observed that the channels cannot close until the blocker leaves the channel, which is reflected in our observation that tail currents become slower in the presence of TBA and at small negative voltages the tail current actually increases because at these potentials the blocker leaves the channel and visits the open state before closing. The appearance of a hook in tail currents in the presence of TBA is a particularly interesting observation since it implies that the blocker has to leave the blocked (open) channels before they can close.

Our final test for an open-state block mechanism relies on measuring single-channel burst kinetics. Our initial single-channel recordings hinted at the presence of multiple open states; so to simplify the analysis, we carried out recordings at low capsaicin concentrations in multiple channel patches. Under these conditions, channel gating occurs in bursts that include openings separated by very brief closures. Bursts are separated by longer closed periods. In the presence of TBA, the burst also includes the individual blocking and unblocking events, increasing its duration. An open-state mechanism makes the prediction that in the presence of blocker the burst length should be increased. We used a concentration very close to the macroscopic K_D of TBA, which should double the burst length, but instead we observed a fivefold increase. We think that this increase is a result of TBA being a more effective blocker at low capsaicin concentrations and therefore 250 μM TBA blocks a larger fraction of the current instead of blocking only half of it. This is also suggested from simulations of the burst length distributions derived from Scheme 3, in which the affinity of the unliganded channel is higher than that of fully liganded ones.

Overall, several lines of evidence support an open-state block of TRPV1 channels by TBA and that this block occurs with different affinities of the multiple open states present in these channels resulting in a higher affinity for the blocker at low capsaicin concentrations as shown in Fig. 7 C and D. If all the affinities of the various open states of the channel for the blocker were equal, then we would expect the fraction of current blocked to be higher at high capsaicin concentrations. In conclusion, block of TRPV1 channels by TBA is very similar to block of voltage-gated K⁺ channels by other quaternary ammonium derivatives in that it occurs in a state-dependent fashion with the blocker preferentially occupying open states and slowing channel closure kinetics.

Modeling of state-dependent block by TBA

Finally, we produced a model for TRPV1 gating which integrates the open-state dependence of block by TBA and some of the allosteric gating features of the activation by capsaicin that we observed experimentally (Scheme 3). Our model assumes that block occurs only in the open state and that the channel has multiple open states. This model is similar to the ones that have been used to explain some features of gating in TRPM8 channels (71) and is a simplified version of other more thorough models previously used to explain the presence of multiple open states in TRPV1 channels and the gating by voltage and calcium ions in calcium activated potassium BK channels (51,52).

In Scheme 3, C stands for closed and O for open channels. The suffixes r and a indicate that the voltage sensor is in the resting position and activated position, respectively, u indicates unliganded channels, and l indicates liganded channels. There are four blocked states, which are indicated by B₀, B₀′, B₁ and B₁′; the model is set up such that TBA affinity for unliganded open states is ∼100 times that of open states bound to capsaicin to account for the larger fraction of blocked channels and the burst length with TBA at low capsaicin concentrations. For example, the pathways (black) correspond to the activation by capsaicin at low voltages. The model can accurately describe a number of observations using a single set of parameters, such as the steady-state dependence of activation by capsaicin (Fig. 7 C), and can explain the steady-state dependence of block by TBA (Fig. 7 D) including the fact that the apparent affinity for the blocker is larger at low capsaicin concentrations, where states O_ru and O_au are mostly occupied. This model also explains an increased burst length in the presence of 250 μM TBA that is larger than twice that observed in the absence of blocker (Fig. 8). This is because the affinity of states O_ur and O_ua for TBA is larger than 250 μM, whereas states O_rl and O_al, which are mostly occupied at saturating capsaicin, have an affinity for blocker that is closer to 250 μM.

This model is also consistent with the existence of multiple open and closed states and predicts that tail currents should decay according to more than one exponential time course (see simulations in Fig. 9 B and D in the absence of TBA, black curves). When simulations are carried out in the presence of blocker, the model predicts the slowing down of tail currents and the presence of a “hook.” In the simulations in Fig. 9 B and D, the model predicts a larger reduction of current because it does not take into account the phenomenon of saturation of block described above.

This model can be expanded to include the effects of temperature in an allosteric fashion. It will be interesting to see if an expanded model can be used to explain gating of TRPV1 channels in detail.

Tetralkylammonium molecules such as TBA have been extensibly used to study the activation gates of voltage-gated K⁺ channels (24), where an open-state blocking mechanism of the type presented here was used as a strong indicative of the channel's activation gate being formed by a region located somewhere cytoplasmically with respect to the blocker's binding site. Although studies involving site-directed mutagenesis are required, based on the data shown in this study, we suggest that the same may be true of the location of the activation gate of TRPV1 channels.