Abstract
We developed a model of the rat ventricular myocyte at room temperature to predict the relative effects of different mechanisms on the cause of the slow increase in force in response to a step change in muscle length. We performed simulations in the presence of stretch-dependent increases in flux through the Na+-H+ exchanger (NHE) and 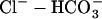 exchanger (AE), stretch-activated channels (SAC), and the stretch-dependent nitric oxide (NO) induced increased open probability of the ryanodine receptors to estimate the capacity of each mechanism to produce the slow force response (SFR). Inclusion of stretch-dependent NHE & AE, SACs, and stretch-dependent NO effects caused an increase in tension following 15 min of stretch of 0.87%, 32%, and 0%, respectively. Comparing [Ca2+]i dynamics before and after stretch in the presence of combinations of the three stretch-dependent elements, which produced significant SFR values (>20%), showed that the inclusion of stretch-dependent NO effects produced [Ca2+]i transients, which were not consistent with experimental results. Further simulations showed that in the presence of SACs and the absence of stretch-dependent NHE & AE inhibition of NHE attenuated the SFR, such that reduced SFR in the presence of NHE blockers does not indicate a stretch dependence of NHE. Rather, a functioning NHE is responsible for a portion of the SFR. Based on our simulations we estimate that in rat cardiac myocytes at room temperature SACs play a significant role in producing the SFR, potentially in the presence of stretch-dependent NHE & AE and that NO effects, if any, must involve more mechanisms than just increasing the open probability of ryanodine receptors.
exchanger (AE), stretch-activated channels (SAC), and the stretch-dependent nitric oxide (NO) induced increased open probability of the ryanodine receptors to estimate the capacity of each mechanism to produce the slow force response (SFR). Inclusion of stretch-dependent NHE & AE, SACs, and stretch-dependent NO effects caused an increase in tension following 15 min of stretch of 0.87%, 32%, and 0%, respectively. Comparing [Ca2+]i dynamics before and after stretch in the presence of combinations of the three stretch-dependent elements, which produced significant SFR values (>20%), showed that the inclusion of stretch-dependent NO effects produced [Ca2+]i transients, which were not consistent with experimental results. Further simulations showed that in the presence of SACs and the absence of stretch-dependent NHE & AE inhibition of NHE attenuated the SFR, such that reduced SFR in the presence of NHE blockers does not indicate a stretch dependence of NHE. Rather, a functioning NHE is responsible for a portion of the SFR. Based on our simulations we estimate that in rat cardiac myocytes at room temperature SACs play a significant role in producing the SFR, potentially in the presence of stretch-dependent NHE & AE and that NO effects, if any, must involve more mechanisms than just increasing the open probability of ryanodine receptors.
INTRODUCTION
Strain is a principal regulator of cardiac output. Under normal function increased diastolic filling results in an increase in cardiac output to match venous return. If the increased diastolic volume is maintained, the myocardium responds with a biphasic increase in developed tension. The initial rapid increase in developed tension is attributed to the Frank Starling mechanism and occurs independently of changes in the excitation induced [Ca2+]i transient. Rather, it is produced by the combination of length-dependent increases in both isometric tension and Ca2+ sensitivity (1). The slow force response (SFR) to stretch, which follows this initial increase, occurs over a period of 10–15 min and results in a further 20–50% increase in actively generated tension (2). Although the SFR to stretch has been recorded in organ (3), muscle (2), and myocyte (4) preparations the underlying mechanism(s) and signaling pathway(s) remain debated (5). Recently three potential hypotheses have emerged as the likely candidates to cause the SFR: 1), stretch activated flux through the Na+-H+ exchanger (NHE) (6–8), 2), increased conductance of cations through stretch-activated channels (SAC) (6), and 3), nitric oxide (NO) signaling (9).
The SFR is often (7,8,10), although not always (4), observed in the presence of increased [Na+]i. Recently the increase in [Na+]i has been attributed to an increase in NHE activity due to an increase in the rate of exchanger cycling through a stretch-activated pathway (7,8,10–12). The resulting increase in [Na+]i, in turn, enhances the [Ca2+]i influx on the Na+-Ca2+ exchanger (NCX) increasing the peak of the [Ca2+]i transient and hence developed tension (7,8,11).
SACs are reported as modulators of the action potential (13) and [Ca2+]i transient (14,15) morphology in response to stretch. Zeng et al. (16) reported that SACs in rat cardiac myocytes conduct both K+ and Na+, although not Ca2+. Hence, nonspecific cation SACs provide a potential path for Na+ into the cell following stretch, resulting in an increase in [Na+]i and the corresponding enhanced [Ca2+]i influx on NCX, as outlined above for stretch-activated NHE. Calaghan and White (6) found SACs to have a significant effect on the SFR in rat myocytes and papillary muscles. However, von Lewinski and co-workers found no effect of SACs on the slow force response in both human (8) and rabbit (11) myocardium.
Finally, NO is also a known regulator of cardiac contraction (17,18). Recently, Villa-Petroff et al. (9) found an increase in the open probability of the ryanodine receptor (RyRs) in the presence of a stretch-induced increase in NO. Villa-Petroff et al. (9) hypothesized that the increased open probability of the RyRs would cause the SFR. In this hypothesis it was postulated that NO regulation would increase the quantity of Ca2+ released from the sarcoplasmic reticulum (SR) during excitation.
This NO mediated mechanism clearly requires a functioning SR, specifically one that contains Ca2+ and releases Ca2+ during excitation. Inhibition of Ca2+ release and uptake from the SR causes a significant decrease in SFR in failing human myocardium (11) but not in rat (1,6) or rabbit (19). Calaghan and White (6) were also unable to detect any effect of NO on the SFR in rat isolated myocytes and papillary preparations when NO synthesis was inhibited by L-NAME.
A wide range of experimental data is available to quantify the electrophysiology and contraction of cardiac myocytes, much of which has been coalesced into detailed mathematical models. Models provide a means to test both the individual and combined effects of the stretch-dependent elements on the SFR. As recent experimental studies (6) and reviews (17) have postulated that a combination of stretch-dependent elements may cause the SFR.
Previous modeling studies have identified transmembrane Na+ flux as the most likely cause of the SFR to stretch (20) and quantified the effects of SACs and tension-dependent [Ca2+]i buffering on the [Ca2+]i transient (21). In both studies the model was based on the Luo Rudy guinea pig cell model (22) and compared with either rabbit (20) or rat (21) SFR experimental data.
In this study we implement a rat ventricular myocyte model at room temperature to make direct comparisons between simulations and experiments, within a framework, which maintains a consistent species focus both in model simulations and in comparisons with experimental results. The framework developed is capable of simulating the major proposals for the cause of the SFR and can be readily extended to test new hypotheses in the future. The electrophysiology is quantified by the Pandit et al. (23) rat myocyte model. The Ca2+ dynamics were replaced with the recently proposed coupled L-type Ca2+ channel-RyR (LCC-RyR) model, developed by Hinch et al. (24), which has been fitted using rat myocyte data. Active tension is calculated using the framework proposed by Niederer et al. (25), also parameterized from largely rat literature. The electrophysiology, Ca2+ dynamics, and active contraction models form a base computational representation of a cardiac cell.
To represent the stretch-dependent mechanisms, we incorporate the additional modeling elements of stretch-dependent pH regulation, SACs, and stretch-dependent increased NO production and the resulting increased Ca2+ release from the RyRs. We then estimate the relative effects of individual and combinations of stretch-dependent elements on the SFR and [Ca2+]i transient. The simulation results are then compared with experimental data to estimate the feasibility of and examine inconsistencies in the current hypothesized causes of the SFR.
METHODS
Model development
The base cardiac cell model quantifies the Ca2+ dynamics, active tension, and the membrane potential. The stretch-dependent pHi regulation, SAC conductance, and NO production modeling elements are then added. Finally the Na+-K+ pump is adapted to better represent rat experimental data and ensure the correct [Na+]i frequency response.
The model was coded in CellML (26) and all model development and simulations were performed using the freely available Cellular Open Resource (COR) (27).
Basic cell model
As noted above, the base cell model is developed by coupling the Pandit et al. (23) electrophysiology, the Hinch et al. (24) Ca2+ dynamics, and the Niederer et al. (25) contraction model. All three models have been developed to represent rat cardiac myocytes at room temperature. In this study we have used the endocardial parameter set from the Pandit et al. (23) electrophysiology model study. The Pandit et al. (23) cell model relies on common pool Ca2+ dynamics, which are incapable of representing graded Ca2+ release (28) an intrinsic property of the cardiac myocyte (29). To achieve a graded release of SR Ca2+ we replace the Ca2+ dynamics in the Pandit et al. (23) framework with the computationally efficient and biophysical LCC-RyR model from Hinch et al. (24). These electrophysiology elements have been coupled to active tension using the model of Niederer et al. (25), which accounts for the effects of Ca2+-activated contraction.
The units of all the models were converted to mm, mS, ms, mV and μA. The changes in ion concentrations in the model are calculated from a flux of ions divided by the cell volume. During an action potential the changes in [Ca2+]i are considerably greater than [Na+]i or [K+]i and hence are more sensitive to the cell volume. Thus, the myocyte and SR volumes were set to the Hinch et al. (24) Ca2+ model values as opposed to the Pandit et al. (23) electrophysiology model values. The [Ca2+]i binding to troponin C kinetics were set to the Niederer et al. (25) values as they are defined from more recent experimental measurements. To ensure that the Hinch et al. (24) model produced a Ca2+ influx comparable to the original Pandit et al. (23) model, the number of regulatory units was increased to 75,000 from 50,000. The SR leak current conductance was then reduced to 5 × 10−6ms−1 to ensure an equilibrium SR Ca2+ concentration of 700 μM. The model currents and capacitance were defined in per mm2 using 1.534 × 10−2 mm2 as the capacitive area (30) to be compatible with tissue simulations. The Na+-K+ pump [Na+]i dependence and maximum flux were also adapted to match recent experimental results from rat myocytes (31). Validation of the complete model including the additional length-dependent components is described below.
Cell/muscle length
Cell/muscle length is a parameter in both the model of contraction and the stretch-dependent model elements. In all cases length is defined by the extension ratio (λ). In the case of the contraction model, λ = 1, corresponds to a sarcomere length of ≈2 μm. However, the majority of length measurements in experiments used to quantity the stretch-dependent elements are recorded as a percentage of the length at which maximum active tension is generated, which is problematic to quantify at a sarcomere scale. To accommodate this, we define all of the stretches relative to the resting cell length or λ = 1. The significance of this assumption is tested below.
pH regulation
pHi in the cardiac myocyte is maintained through a combination of pH regulated cotransporters and exchangers. The NHE and 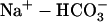 cotransporter (NBC) act as acid extruders and
cotransporter (NBC) act as acid extruders and 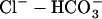 exchanger (AE) and Cl−-OH− exchanger (or equivalently the Cl−-H+ cotransporter) (CHE) act as base extruders (32). In this study pH regulation will be modeled using the six-state CHE, AE, and NBC transporter models developed by Crampin and Smith (33). A NHE model was developed that took a greater account of Na+ dependencies due to the range of [Na+]i values encountered during the SFR and the proposed importance of NHE in causing the SFR. The NHE model consists of a transporter and a regulatory component, as proposed previously by Crampin and Smith (33). The transporter component was modeled using a simplified two-state exchanger model, where α-values correspond to the forward and backward rates between the two states with 1 and 2 signifying the rates when Na+ or H+ are bound to the exchanger, respectively. The model was fit using both pHi (34) and [Na+]i (35) dependent data and making use of the thermodynamic constraint that
exchanger (AE) and Cl−-OH− exchanger (or equivalently the Cl−-H+ cotransporter) (CHE) act as base extruders (32). In this study pH regulation will be modeled using the six-state CHE, AE, and NBC transporter models developed by Crampin and Smith (33). A NHE model was developed that took a greater account of Na+ dependencies due to the range of [Na+]i values encountered during the SFR and the proposed importance of NHE in causing the SFR. The NHE model consists of a transporter and a regulatory component, as proposed previously by Crampin and Smith (33). The transporter component was modeled using a simplified two-state exchanger model, where α-values correspond to the forward and backward rates between the two states with 1 and 2 signifying the rates when Na+ or H+ are bound to the exchanger, respectively. The model was fit using both pHi (34) and [Na+]i (35) dependent data and making use of the thermodynamic constraint that 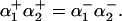 The regulatory component modeled the intracellular allosteric “proton modifier site” (36) and was represented by a simple Hill scaler.
The regulatory component modeled the intracellular allosteric “proton modifier site” (36) and was represented by a simple Hill scaler.
A complete [Na+]i and pHi dependent data set is not currently available for NHE so the model was fit using Na+ dependent data normalized by the maximum measured flux, from sheep Purkinje fibers (35) and pHi dependent data from rat (34). The model does not take account of extracellular ion dependencies as these are fixed in all simulations to pHo = 7.4 and [Na+]o = 140 mM. Transporter kinetics are described by Eq. 1,
 |
(1) |
where 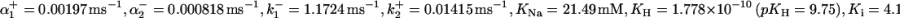 and
and 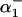 and
and 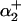 are defined in Eq. 1. The model parameters were fit using rat pHi-dependent flux data (34) with [Na+]i set to 10 mM (see Fig. 1 A) and normalized [Na+]i flux data from sheep Purkinje fibers with pHi = 6.4 (35) (see Fig. 1 B).
are defined in Eq. 1. The model parameters were fit using rat pHi-dependent flux data (34) with [Na+]i set to 10 mM (see Fig. 1 A) and normalized [Na+]i flux data from sheep Purkinje fibers with pHi = 6.4 (35) (see Fig. 1 B).
FIGURE 1.
(A) Steady-state flux across NHE as a function of pHi in rat cardiac myocytes for experimental measurements (points) (34) and fitted model simulations with pHo = 7.4, [Na+]o = 140 mM, and [Na+]i = 10 mM (line). (B) Comparison between fitted model, with [Na+]o = 140 mM, pHi = 6.4, and pHo = 7.4 (solid line) and normalized flux across the NHE recorded in sheep Purkinje fibers (solid squares) as a function of [Na+]i (35).
Change in pHi for a given proton flux (JH) (where JH comprises the sum of the JNHE, JCHE, JAE, and JNBC) was modeled using Eq. 2, where βi is the intrinsic buffering capacity.
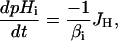 |
(2) |
where the intrinsic buffering capacity (Eq. 3) is contributed to via the two independent buffers b1 and b2:
 |
(3) |
where Cb1 = 31.2 mM, pKa1 = 6.4, Cb2 = 6.85 mM, and pKa2 = 7.48. The buffering capacity equation parameters were refit from the original values recorded by Swietach et al. (37) to account for a 50% decrease in buffering capacity at 22°C, based on the 40% decrease observed for a 10°C decrease in temperature (38). The transporter models outlined in Eq. 1 are also fitted from experimental data measured at 37°C. Che'en et al. (38) found that NHE and NBC flux have a Q10 of 2. Assuming that the Q10 value is similar for CHE and AE (39) in rat cardiac myocytes all transport fluxes were scaled to 35% of the values at 37°C to represent model fluxes at 22°C.
A simple background flux with a linear voltage dependence (Eq. 4) was added with a conductance of 4 × 10−6 mS to ensure a resting pHi consistent with a resting pHi of 7.26 in HEPES solution reported by Yamamoto et al. (34). Adding 5% CO2 caused a small drop in pHi to 7.21, which is within the experimentally measured range of no change (40) and 0.15 pH units (34). The addition of the H+ current is not based on experimental evidence, however, similar currents have been included in earlier modeling studies (41). The implications of this current and its justification are discussed in more detail in the model critique below.
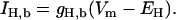 |
(4) |
The inclusion of CHE and AE results in a Cl− flux. To ensure a stable set of ionic concentrations and membrane potential within the cell model this influx of charge must be accounted for by including intracellular Cl− (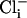 ) in the model. As both AE and CHE bring Cl− into the cell a small Cl− leak current with a conductance of 2 × 10−5 mS was added to ensure that at rest the resting membrane potential was ≈−80 mV and the reversal potential of Cl− ≈ −55 mV (42), with an extracellular Cl− concentration of 126 mM (43).
) in the model. As both AE and CHE bring Cl− into the cell a small Cl− leak current with a conductance of 2 × 10−5 mS was added to ensure that at rest the resting membrane potential was ≈−80 mV and the reversal potential of Cl− ≈ −55 mV (42), with an extracellular Cl− concentration of 126 mM (43).
 |
(5) |
NHE & AE stretch dependence
The stretch dependence of NHE was demonstrated by Alvarez et al. (7) in HEPES solution (eliminating NBC flux), by showing that stretching rat papillary muscles induced an alkolisis of 0.09 ± 0.01 pH units, which could be removed by the NHE blocker amiloride. At the same time a rise in [Na+]i of 5.5–6 mM and an increase in peak active tension was recorded, which Alvarez et al. (7) attributed to the combined effects of increased NHE activity and increased Ca2+ influx on NCX. Increased NHE flux in response to stretch has also been proposed in papillary (6,10,12,44–46), trabeculae (7,8), ventricular myocytes (6), and ventricular strip (11) preparations in human (11), ferret (44), rabbit (8), rat (6,7), and cat (45,10) preparations, suggesting that the NHE response to stretch is an intrinsic property of the myocyte and independent of species. In bicarbonate buffered solutions the cellular pH has been shown to remain constant following stretch (46). This is hypothesized to be a result of an increase in flux through AE, which compensates the increased flux through NHE (46).
The stretch responses of both NHE & AE have been shown to be the result of a protein kinase C dependent pathway (46). In this study we assume that stretch-dependent phosphorylation of AE and NHE causes an increase in flux by altering the dissociation constant of protons binding to the intracellular pHi regulatory site (Ki in Eq. 1 for NHE). We also assumed that the effects of stretch are instantaneous as the slow force response of stretch is expected to take place over a longer timescale than phosphorylation and there is little information available to quantify any time dependence.
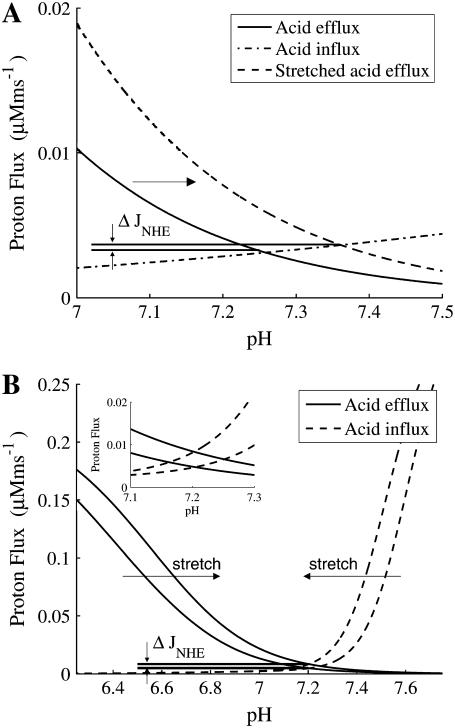
pHi is determined by the equilibrium of acid carrier flux within the “permissive zone”, as defined by Leem et al. (32). Although the fluxes are small, changes in either the acid influx or efflux will cause a shift in the pHi. The changes in pHi recorded following stretch were used to determine the changes in NHE & AE. The changes in NHE flux following stretch were constrained by the observed 0.1 increase in pHi in the absence of extracellular CO2 for a 10% stretch (7). Here we model the change in pH using the hypothesis proposed by Alverez et al. (7), that acid efflux through NHE is increased following stretch, while acting against a constant acid influx on CHE and the background proton flux (Eq. 4). Fig. 2 A shows how a 30% decrease in the dissociation constant of protons to the NHE regulatory site model causes an increase in pHi of 0.1 pH units and a 0.00054 μMms−1 increase in Na+ influx (see ΔJNHE Fig. 2 A) at steady state. The model for the change in AE flux following stretch was fit by the experimental observations of no change in pHi in 5%CO2 / 95% O2 solution, in the presence of a 30% decrease in the dissociation constant of protons to the model NHE regulatory site, as noted above. Fig. 2 B shows how a 28% increase in the dissociation constant to the AE regulatory site balances the increase in NHE flux following a 10% stretch, resulting in no change in pHi and a 0.0036 μM ms−1 increase in Na+ influx (see ΔJNHE Fig. 2 B) at steady state. Experimental results record between no change (12) and a 0.03 ± 0.01 (46) drop in pH in 5% CO2/95% O2 solution, in the absence of NHE for an 8% and 6% stretch, respectively. Here the simulated increase in AE flux, following stretch, resulted in a 0.01 pH unit drop in pH, which is within the experimentally measured results. The stretch dependence of the dissociation constants are quantified in the model by Eqs. 6 and 7 for NHE & AE, respectively:
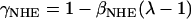 |
(6) |
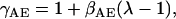 |
(7) |
where γNHE and γAE are the length-dependent scalers of the binding affinities for NHE & AE, respectively, and βNHE = 2.804 and βAE = 2.5 are the strain coefficients of NHE & AE, respectively.
FIGURE 2.
(A) Change in acid flux following 10% stretch in HEPES buffered solution (no AE or NBC). Solid and dash-dotted lines show the acid efflux and influx as functions of pHi before stretch, respectively. Following 10% stretch, the flux through NHE increases shifting the acid efflux curve to the right from the solid line to the dashed line. Resulting in a 0.1 pH unit increase in pHi and an increase in flux through NHE of ΔJNHE = 0.00054 μM ms−1. (B) Change in acid flux following a 10% stretch in 5% CO2 bicarbonate buffered solution. Solid lines and dashed lines are the acid efflux and influx as functions of pHi, respectively. Following a 10% stretch, acid efflux shifts right and acid influx shifts left as indicated by the arrows. An enlargement of the change in intersection of the acid influx and efflux is shown in the figure inset. Stretch results in an increase in NHE flux of ΔJNHE = 0.0036 μM ms−1 and no change in pHi.
Stretch-activated channels
Stretch-activated channels have been reported in isolated myocytes (16), multicellular (47), and whole heart preparations (48). Models for stretch-activated channels have been proposed by Zeng et al. (16) for rat myocytes and Kohl and Sachs (49) and Healy and McCulloch (50) for guinea pig myocytes. Recently Li et al. (51) have reported that the stretch-dependent currents in rat myocytes are the result of a stretch-activated K+ specific current (IKo) and a nonspecific stretch activated channel (Ins). Healy and McCulloch characterized IKo for guinea pig myocardium, using an adaptation of the IKp current (52) and modeled Ins with a linear current voltage relationship (16). In this study we apply the same method, fitting the conductance and length dependence of Ins and IKo for the rat myocyte using I-V curves recorded at 22°C during a 10% regional strain by Li et al. (51). Subsequently, we separated Ins into Na+ and K+ components as proposed by Li et al. (51) (see Eq. 9). The relative conductance of Na+ and K+ through SACs (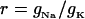 ) can be estimated given the reversal potential of Ins (
) can be estimated given the reversal potential of Ins (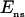 ) of −10 mV and the reversal potential of Na+ and K+ (53), which are ≈65 and ≈−85 mV, respectively, using Eq 8:
) of −10 mV and the reversal potential of Na+ and K+ (53), which are ≈65 and ≈−85 mV, respectively, using Eq 8:
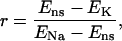 |
(8) |
giving r = 1. The resulting cation SAC current is defined by:
 |
(9) |
The stretch-dependent K+ specific current (Eq. 10) is defined by:
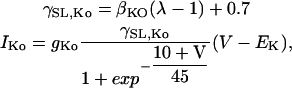 |
(10) |
where λ is the extension ratio, gns and gKo are equal to 4.1 × 10−7 mS and 1.2 × 10−6 mS, respectively, and βns = 10 and βKO = 3 are the strain coefficients for nonspecific SACs and K+ SACs, respectively. The strain dependence of the conductance, 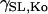 and
and 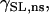 was fit with a linear function to the experimentally recorded I-V curve, recorded at two strain points, 0 and 10% (51). The background K+ current was substituted for IKo, because at resting membrane potential IKo was approximately equal to the background K+ current and IKo was not included in the original Pandit et al. (23) cell model. The resulting model produces a current of Ins = −3.795 pA mm−2 and IKo = 0.0416 pA mm−2 with 10% strain and Vm = −80 mV.
was fit with a linear function to the experimentally recorded I-V curve, recorded at two strain points, 0 and 10% (51). The background K+ current was substituted for IKo, because at resting membrane potential IKo was approximately equal to the background K+ current and IKo was not included in the original Pandit et al. (23) cell model. The resulting model produces a current of Ins = −3.795 pA mm−2 and IKo = 0.0416 pA mm−2 with 10% strain and Vm = −80 mV.
Nitric oxide dependence of ryanodine receptors
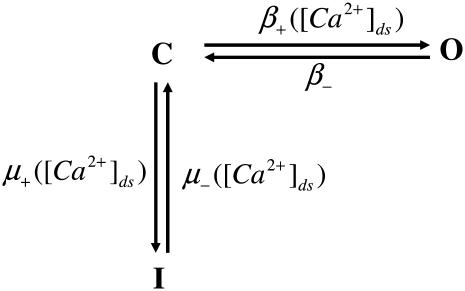
Increased NO production has been recorded following stretch (9). Villa Petroff et al. (9) proposed that NO acts as a secondary messenger of stretch by selectively increasing the open probability of the RyRs (9). Although NO has been found to act on other SR Ca2+ handling mechanisms, namely L-type Ca2+ channels and SERCA and through cGMP pathways (54), these were all ruled out by Villa Petroff et al. (9). Villa-Petroff et al. (9) found that a 7% and 12% stretch caused an approximate twofold and fourfold increase in Ca2+ spark frequency. In the model proposed in this study, Hinch et al. (24) represent Ca2+ release from the RyRs as a three-state model (see Fig. 3). We assume that the increased Ca2+ spark frequency is a result of an increased probability of a RyR shifting from the closed (C) to the open (O) state in the quiescent model, because only a small proportion of RyRs are in the inactivated (I) state when the cell is in a quiescent state. Solving for the quiescent steady-state RyR model, such that [Ca2+]ds ≈ [Ca2+]i, gives Eq. 11.
 |
(11) |
such that
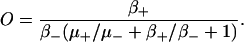 |
(12) |
FIGURE 3.
Schematic of RyR model from the Hinch et al. (24) Ca2+ model. The model has three states: closed (C), open (O), and inactivated (I). The opening rate (β+) between C and O and both activation (μ+) and inactivation (μ−) rates between I and C are [Ca2+]ds dependent. The closing rate (β−) between O and C is constant.
Simplifying gives, O ≈ β+/β− as β+ ≪ β− and μ+ ≪ μ−. The fraction of RyRs in the open state in the quiescent cell was increased by decreasing the RyR rate of closing (β−) because NO has been reported to predominantly affect active tension relaxation (55) although similar results are achieved in the simulations described below by altering the opening rate of RyRs (results not shown). The decrease in β− is modeled by reducing the RyR proportion of time closed in the active mode by a strain dependent scaler γNO (see Eq. 13), with a strain coefficient of βRyR = −6.47, such that a strain of 7% and 12% induce an increase in the proportion of RyRs in the open state by a factor of 1.83 and 4.48, respectively, effectively close to the Villa Petroff (9) data.
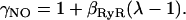 |
(13) |
Sodium potassium pump
The Na+-K+ pump (NaK) model in the Pandit cell model (23) is taken from a guinea pig model (22) and scaled to balance the flux of Na+ and K+ to achieve a resting [Na+]i concentration of 10.7 mM. The model is based on guinea pig data and has a near linear (Hill coefficient 1.5) dependence on [Na+]i. Recent experimental results from Despa et al., (31) found that the NaK pump is highly dependent on [Na+]i in rat, with a Hill coefficient of 4.0, although the binding affinity of [Na+]i remains the same. Considering this, the Hill coefficient of NaK was increased to 4.0, although higher than previous values (3.0) (56), the Hill coefficient is taken directly from a fit to recent experimental data and so was not changed. The maximum flux was increased to 9.5 μA/mm2 to fit the model [Na+]i-frequency response to data from Despa et al. (31) (see Fig. 4).
FIGURE 4.
Plot of [Na+]i as a function of frequency. Experimental data (points) taken from Despa et al. (60). Maximum flux through NaK was fitted to achieve model [Na+]i response (dashed line).
RESULTS
Model validation
The rat electrophysiology model described here is an ensemble of models. Many of the model components used here have been previously verified. The ensemble model's stability over prolonged periods is essential for modeling the slow force response, which takes place over ≈15 min. In the quiescent state there are no changes in [Na+]i, [K+]i, [Ca2+]i, and Vm over any time period and over 20 min of pacing at 1Hz [Na+]i, [K+]i, [Ca2+]i, and Vm changed by <0.1%.
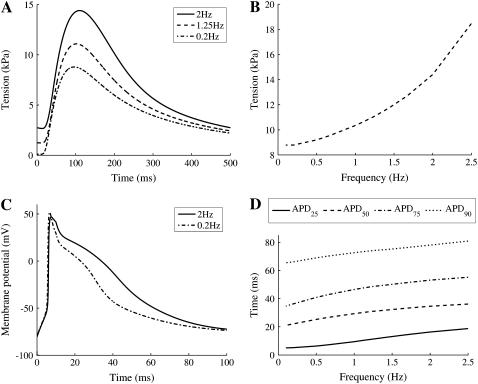
To ensure that the model components were coupled appropriately the maximum tension and action potential duration were calculated as functions of frequency. The final model exhibits nontrivial frequency responses, which are qualitatively similar to those of rat, with both measures of action potential duration and peak active tension increasing with frequency. Fig. 5, A and B, show tension traces at 2, 1.25, and 0.2 Hz and the peak tension as a function of pacing frequency, respectively. As both figures demonstrate, the peak tension increases with pacing frequency as observed experimentally at room temperature and physiological [Ca2+]o (1 mM) (57). Fig. 5, C and D, show simulated action potentials at 0.2 and 2 Hz and the action potential durations at 25%, 50%, 75%, and 90%, respectively. The model exhibits increasing values for all measures of action potential duration, qualitatively matching additional rat experimental data (58).
FIGURE 5.
(A) Model simulations of tension transient with no strain (λ = 1), at 0.2 Hz (dash-dotted line), 1.25 Hz (dashed line), and 2 Hz (solid line). (B) Increase in peak tension with pacing frequency between 0.1 and 2 Hz with no strain (λ = 1). (C) Model simulations of action potential, at 0.2 Hz (dash-dotted line) and 2 Hz (solid line). (D) The time taken for 90% (APD90, dotted line), 75% (APD75, dash-dotted line), 50% (APD50, dashed line), and 25% (APD25, solid line) repolarization with pacing frequency between 0.1 and 2 Hz.
Slow force response
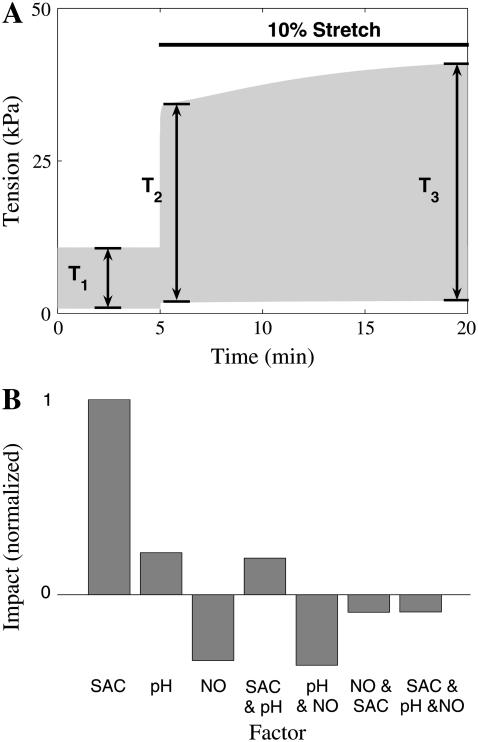
SFR simulations were performed after the cell reached a steady state at 1 Hz pacing frequency, in 5% CO2 and λ = 1. Steady state was defined by constant [Na+]i and [K+]i over a period of 20 min. The cell was then paced for 5 min at resting length (λ = 1) and then stretched by 10% (λ = 1.1) for 15 min. Fig. 6 A shows an example simulation, where SACs are present. The force response to stretch was separated into a Frank Starling effect and SFR. The Frank Starling effect was defined as the percentage change in tension between before the stretch and 10 s after the stretch was applied ((T2 − T1)/T1 from Fig. 6 A). The SFR was taken as the percentage change in tension between 10 s and 15 min after the stretch was applied
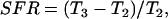 |
(14) |
where T2 and T3 are defined in Fig. 6 A.
FIGURE 6.
(A) Example tension trace from SFR simulation, in the presence of SACs. Cell is paced at 1 Hz at rest (λ = 1) after 5 min a 10% stretch (λ = 1.1) is applied for 15 min. T1, T2, and T3 are the active tension before, 10 s after, and 15 min after stretch, respectively. (B) Impact of individual and combinations of SACs (SAC), stretch-dependent NHE & AE (pH), and increased open probability of RyRs due to stretch released NO (NO) on the SFR, as determined from a factorial experiment design. The impact of each factor or combination was normalized against the maximum impact (in this case SAC).
Applying a step in extension ratio in the presence of different model permutations of the three stretch-dependent elements computationally isolates which individual mechanism or combination of mechanisms are capable of reproducing the experimentally observed SFR. A factorial set of experiments was performed using the model as defined in Table 1. The resulting impact of each individual factor or combinations of factors on the SFR was calculated from the results in Table 1 (59). Fig. 6 B shows the impact of the different factor combinations relative to the maximum impact (in this case SACs). The SACs are the only stretch-dependent element that was capable of reproducing a SFR consistent with experimental observations, with stretch-dependent pH having only 37% of the impact of SACs and NO-induced changes in RyR open probability having a negative effect (see Fig. 6 B).
TABLE 1.
SFR factorial experiment design
| Experiment | PH | SAC | NO | SFR (%) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0.00 |
| 2 | 1 | 0 | 0 | 0.87 |
| 3 | 0 | 1 | 0 | 32.03 |
| 4 | 1 | 1 | 0 | 49.16 |
| 5 | 0 | 0 | 1 | 0.00 |
| 6 | 1 | 0 | 1 | 13.51 |
| 7 | 0 | 1 | 1 | −0.01 |
| 8 | 1 | 1 | 1 | 24.17 |
Each experiment includes a combination of the stretch-dependent SAC, NO, and pH modeling elements as indicated by a 1 (present) or 0 (absent) and the resulting SFR as defined by Eq. 14.
Calcium response to stretch
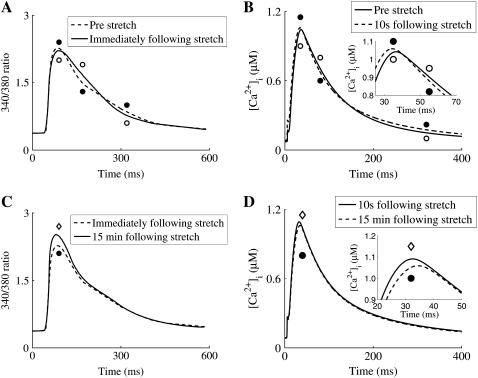
The factorial analysis above found that SACs were the single-most significant factor in causing the SFR. Although this suggests that SACs play a role in generating the SFR, it does not rule out NO-induced opening of the RyRs or increased flux through NHE & AE as complementary mechanisms because the SFR was still significant when either pH or both pH and NO stretch-dependent elements were included in the presence of SACs (see Table 1). As a further test of which mechanisms are involved in SFR we compared simulated [Ca2+]i transients before, 10 s after, and 15 min after a 10% stretch, with experimental results from Kentish and Wrzoesk (1). The factorial analysis identified combinations 3, 4, and 8 from Table 1 as being capable of inducing a SFR > 20%. Fig. 7 shows an example comparison of [Ca2+]i transients for model simulations in the presence of SACs and stretch-dependent NHE & AE. Model simulations show a 5% increase in [Ca2+]i during the course of the stretch compared to an 11% increase observed by Kentish and Wrzoesk (1). It is important to note that this quantitative comparison is made with the only single furo-2 trace that was available for comparison.
FIGURE 7.
Example comparison of [Ca2+]i between model simulations in the presence of stretch-dependent NHE & AE and SACs and experimental results from Kentish and Wrzosek (1). (A) 340:380 ratio (a measure of [Ca2+]i) transients prestretch (solid line and open circles) and immediately after stretch (solid line and solid circles). (B) Simulation [Ca2+]i transients prestretch (solid line and open circles) and 10 s after stretch (solid line and solid circles); inset shows enlargement of crossover of transients at the peak. (C) 340:380 ratio transients immediately after stretch (solid line and solid circles) and 15 min after stretch (solid line and open diamonds). (D) Simulation [Ca2+]i transients 10 s after stretch (solid line and solid circles) and 15 min after stretch (solid line and open diamonds) inset shows enlargement of transients at the peak.
Fig. 8 compares the [Ca2+]i transient of these stretch-dependent element combinations with results from Kentish and Wrzoesk (1).
FIGURE 8.
Comparison between simulation indices of [Ca2+]i transients (plots b, d, f, and h) and experimental indices of 340:380 ratio (a measure of [Ca2+]i) transients (1) (plots a, c, e, and g) before stretch, 10 s after a 10% strain, and 15 min after a 10% strain. Model simulations contain four combinations of the stretch-dependent elements: SACs (SAC, dashed line and open squares), SACs and stretch-dependent NHE & AE (SAC & pH, dash-dotted line and solid squares), SACs and stretch-dependent NO effects (SAC & NO dotted line and open diamonds), and SACs and stretch-dependent NO and NHE & AE effects (SAC & NO & pH, solid line and solid diamonds). (A and B) Peak measure of [Ca2+]i. (C and D) Time to peak. (E and F) Time for the transient to fall to half of its maximum amplitude (RT50). (G and H) Time for the transient to fall to 10% of its maximum amplitude (RT90).
The inclusion of the SACs modeling element resulted in [Ca2+]i transients that qualitatively matched experimental results. However, in the presence of NO effects both the peak [Ca2+]i, time to peak [Ca2+]i, and RT50 times were notably different from experimental results. The stretch dependence of NHE & AE caused nominal changes in the [Ca2+]i transient, which is interesting to contrast with previous experimental studies that found that inhibition of NHE attenuated the increase in [Ca2+]i associated with SFR (6).
NHE & AE
Surprising, in the context of the comparisons between experimental data and the results in Fig. 7, is that the stretch dependence of NHE & AE caused only nominal changes in the SFR and the [Ca2+]i transient. Increased NHE activity is consistently attributed with causing the SFR in experimental results, primarily due to the removal or reduction of the SFR when NHE is blocked by amiloride or cariporide. To test the effects of blocking NHE on the SFR we compared simulated SFR values calculated with normal and inhibited NHE and including SAC or SAC and pH stretch-dependent elements. In NHE inhibited simulations NHE was inhibited for the duration of the experiment. In both normal and NHE inhibited simulations the cell was paced at 1 Hz at resting length (λ = 1) in the presence of 5% CO2 until it reached a steady state. SFR values were then calculated after 15 min of stretch as described above.
Fig. 9 compares simulated control and NHE inhibited SFR values in the presence of SACs and SACs and NHE & AE stretch-dependent elements. We observe a 32% and 56% decrease in SFR after NHE inhibition in models containing SAC and SAC, and NHE & AE stretch-dependent elements, respectively.
FIGURE 9.
SFR following 10% stretch for 15 min for models containing SACs (SAC) and SACs and stretch-dependent NHE & AE (pH) in the presence (control) and absence (NHE inhibition) of NHE.
Sensitivity
In this study we have added background Cl− and H+ fluxes, increased the number of LCC-RyR units, and added stretch dependencies to NHE & AE, and stretch-activated channels. The sensitivity of the SFR model results to each of these modeling element was quantified by the change in peak [Ca2+]i, [Na+]i, and the SFR in the presence of SACs and pH stretch-dependent elements, after a 10% perturbation in key parameters, as shown in Table 2. The sensitivity of model results to the strain dependence of the stretch-dependent elements was also tested in simulations containing each relevant stretch-dependent element individually. Results are shown in Table 3. Simulations were performed at described above with all measurements taking place 15 min after a 10% strain (λ = 1.1) was imposed.
TABLE 2.
Model parameter sensitivity
| Parameter | Value | SFR (%) | Peak [Ca2+]i (%) | Δ[Na+]i (%) |
|---|---|---|---|---|
| βAE | 2.75 | 0.78 | 0.16 | 0.74 |
| βNHE | 3 | 2.54 | 0.52 | 2.64 |
| βKo | 3.3 | 0.14 | −0.02 | 0.03 |
| βSAC | 11 | 10.61 | 2.74 | 9.81 |
| gCl | 2 × 10−5 | −0.22 | 0.01 | −1.04 |
| gH | 4.4 × 10−6 | 0.29 | 0.11 | −0.54 |
| N | 82,500 | −10.39 | 14.87 | 1.81 |
Percent change in peak [Ca2+]i and [Na+]i and change in SFR with 10% increase in each of the added or altered parameters in model simulation containing SACs and pH stretch-dependent elements.
TABLE 3.
Stretch dependence sensitivity
| Parameter | Value | SFR (%) | Peak [Ca2+]i (%) | Δ[Na+]i (%) |
|---|---|---|---|---|
| βAE and βNHE | 2.75 and 3 | 0.18 | 0.16 | 0.87 |
| βKo and βSAC | 3.3 and 11 | 7.89 | 2.46 | 3.47 |
| βNO | 7 | −0.16 | 0.84 | 1.24 |
Percent change in peak [Ca2+]i and [Na+]i and change in SFR with 10% increase in length dependence of the stretch-dependent elements solely in the presence of the relevant element.
DISCUSSION
The source of the SFR is currently debated. Experimental studies have reported conflicting results on the cause of SFR, finding SACs, stretch-dependent NHE & AE, and stretch-dependent, NO-induced changes in RyR dynamics as potential sources of the SFR. We have employed mathematical modeling to initially characterize discrete experimental data sets for the three hypothesized mechanisms and estimate to what extent individual or combinations of these mechanisms are necessary to reproduce the SFR. We proposed three tests to characterize the capability of these elements to replicate tension and [Ca2+]i transient experimental results after stretch. The first test measured the capacity of individual and combinations of the three mechanisms to replicate experimental SFR tension results, under physiological conditions. The second test compared simulated changes in the [Ca2+]i transient after stretch with experimental results. The third test compared changes in the simulated SFR after the inhibition of NHE with experimental results.
Stretch-dependent elements involved in the SFR
In the first of the three tests to quantify the effects of the three previously proposed stretch-dependent mechanisms on the SFR we performed a factorial analysis. A factorial analysis provides an indicator of the relative impact of each, or combinations, of factors on a system metric (59). In this case the system was the cell model, the factors were the stretch-dependent elements, and the metric is the SFR as defined above by Eq. 14. Table 1 summarizes the results of the individual experiments performed in the factorial analysis and Fig. 6 B summarizes the effects of each factor and factor combination on the SFR or system metric. In the process of performing a factorial analysis the SFR values are calculated in the presence of the different permutations of the three mechanisms.
The first test identified SACs as a significant contributor to the SFR, both in individual experiments and the factorial analysis. Acting independently SACs caused a 32% SFR compared with 0.87% and 0.00% for stretch-dependent NHE & AE, and RyR dynamics, respectively (see Table 1), compared with experimental values of 20–50% (2). The factorial analysis found stretch-dependent NHE & AE has only 23.31% of the SAC impact on the SFR (see Fig. 6 B) and changes in RyR dynamics have a negative individual and synergistic impact on SFR.
The second of the three tests compared simulated [Ca2+]i transients with experimental results from Kentish and Wrzosek (1). All the models tested contained SACs and different combinations of stretch-dependent NHE & AE and stretch-dependent, NO-induced changes in RyR dynamics. All three stretch-dependent element combinations predicted an increase in peak [Ca2+]i comparable with experimental results (see Fig. 8, A and B). However, the inclusion of NO effects caused a significant drop in peak [Ca2+]i 10 s after the stretch was applied, which was not seen by Kentish and Wrzoesk (1). Simulations in the presence of NO caused an increase in the time to peak [Ca2+]i immediately after stretch; this is contrary to both experimental results and simulations in the absence of NO, which recorded a nominal decrease (see Fig. 8, C and D). Simulations in the absence of stretch-dependent NO effects compared well with experimental results, showing a monotonic decrease in RT50 immediately and 15 min after stretch. Whereas in the presence of NO effects there was an increase in RT50 immediately following stretch (see Fig. 8, E and F). All three simulations and experimental results recorded an initial increase in RT90 followed by a plateau during the SFR (see Fig. 8, G and H). Hence, of the three stretch-dependent element combinations tested, the model, which included NO-induced changes in RyR dynamics produced stretch-induced changes in the [Ca2+]i transient that were not consistent with experimental results.
The third test aimed to elucidate the importance of any stretch dependence of NHE & AE, which has been widely attributed as the cause of the SFR, as noted above. We tested the effects of blocking NHE on the SFR and the effects of model structure on the rise in [Na+]i after stretch. It is well documented that the SFR is attenuated in the presence of NHE blockers (7,8,11). Hence, we predicted that, in the absence of stretch-dependent NHE, the simulated SFR would remain unchanged when NHE was blocked. However, as Fig. 9 demonstrates, the SFR is attenuated in the presence of blocked NHE regardless of the inclusion of stretch-dependent NHE & AE in the presence of SACs; such that, in model simulations, we find that NHE alone is a significant contributor to the SFR, whereas the stretch dependence of NHE & AE is a feasible but nonessential contributor to the SFR.
Comparing model findings with experimental data
Model simulations tested three hypothesized sources of the SFR. We found that stretch-dependent NHE & AE potentially contributed to the SFR. SACs were a significant component in producing the SFR, whereas, stretch-dependent, NO-induced changes in RyR dynamics caused [Ca2+]i transients after stretch, which were not consistent with experimental measurements. However, the role of SACs in the SFR is still debated; the effects of NO on the SFR and its effects, if any, on RyRs are controversial, whereas stretch-dependent NHE regulation is consistently attributed to being the source of the SFR. We now aim to rationalize the model results on each of the three proposed mechanisms in the context of the apparently inconsistent experimental data.
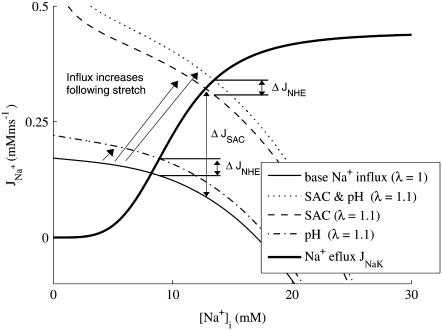
One consistent finding in SFR studies is an effect of [Na+]i. This has been attributed to increased [Ca2+]i influx on NCX (10). In concurrence with earlier modeling (20) and experimental (6) studies we find that the buildup of [Na+]i in response to stretch is the most likely path through which stretch modulated elements affect force. The route through which extracellular Na+ enters the cell is proposed to be through NHE or nonspecific SACs, as noted above. However, model simulations containing solely stretch-activated NHE & AE were incapable of causing a significant rise in [Na+]i and hence, tension, after stretch. The reason for this can be demonstrated graphically. Fig. 10 shows the total Na+ efflux (thick solid line) and influx (thin solid line) at rest (λ = 1) as a function of [Na+]i with all other state variables fixed to their values in the quiescent state. The intersection of the two curves ([Na+]i = 8.2 mM) approximates resting [Na+]i before stretch (10 mM (60)). After stretch the influx curve shifts to the right, as indicated by the arrows, for simulations including the NHE & AE (dash-dotted line), SACs (dashed line), and both (dotted line) stretch-dependent elements. It is clear from this graph that the increase in Na+ influx required to shift [Na+]i is significant, given that the efflux of [Na+]i, through NaK, has a fourth-order dependence on [Na+]i. Regardless of the inclusion of SACs the increase in Na+ influx through NHE (ΔJNHE in Fig. 10) is ≈0.0035 μM ms−1, which is insufficient to cause more than an ≈0.7 mM change in [Na+]i. This compares to the ΔJSAC of 0.023 μM ms−1, which is ∼8× larger and capable of causing an ≈4.5 mM increase in [Na+]i in the quiescent state. Hence, it appears unlikely that the increase of [Na+]i flux through stretch-dependent stimulation of NHE is sufficient to shift [Na+]i significantly in rat myocytes.
FIGURE 10.
Changes in Na+ influx and efflux in the presence of SAC and/or pH stretch-dependent elements, following stretch, in the quiescent cell. Fluxes are calculated as a function of [Na+]i with [K+]i, [Ca2+]i, [Ca2+]SR, and Vm clamped at their quiescent values of 144.19, 6.508 × 10−5, 0.6817 mM, and −79.90 mV, respectively. Na+ efflux through NaK (bold solid line), Na+ influx prestretch (solid line), and Na+ influx following 10% stretch in the presence of stretch-dependent NHE & AE (pH, dot-dashed line), stretch-dependent NHE & AE, and SAC (SAC & pH dotted line), and SACs (SAC dashed line). ΔJNHE indicates the change in Na+ flux caused by the addition of stretch-dependent NHE. ΔJSAC indicates the change in Na+ flux caused by the addition off SACs.
However, blocking NHE consistently attenuates the SFR (6,8). In experiments where NHE is blocked, the blocking agent is added 15–25 min (6,8) before stretch and the muscle is then left to reach steady state. At rest NHE makes up 25% (29% in the model) of the basal Na+ flux in rat myocytes (60), hence blocking NHE results in a drop in resting [Na+]i before stretch. In simulations performed in the absence of stretch-dependent NHE & AE, in the presence of SACs, and with NHE blocked, the final [Na+]i value after 15 min of stretch is less than if NHE were functional. Considering that NCX flux is a cubic function of [Na+]i and, hence, as [Na+]i increases, the sensitivity of NCX to [Na+]i also increases, then for the same change in [Na+]i and starting at a lower initial [Na+]i will cause a smaller increase in Ca2+ influx through NCX and hence attenuate the SFR. This can be seen in Fig. 9, where in the absence of NHE & AE stretch dependencies inhibiting NHE causes a 30% drop in SFR in the presence of SACs. Hence, the decrease in SFR observed in the presence of NHE blockers suggests that the functioning NHE provides a significant contribution to the SFR alone rather than any specific dependencies.
Another means of testing the capacity of NHE stimulation to cause the SFR and the accompanying changes in [Na+]i is to consider the change in proton concentration that occurs during the SFR. The change in pH, following stretch, recorded in the absence of bicarbonate was ≈0.1 pH units, which equates to an ∼0.02-μM increase in free proton concentration and a 2-mM increase in the concentration of protons bound to buffers in the model. Whereas [Na+]i increases by 5.5–6 mM (7) in rat and 3 mM (8) in rabbit cardiac myocytes after stretch. As NHE operates in a 1:1 (61) ratio it would be surprising if NHE was the sole source of the additional Na+, as the change in protons (2 mM) is far less than the change in [Na+]i in rat, although, similar to the increase in [Na+]i observed in rabbit.
The second pathway for Na+ into the cell is on nonspecific cation SACs. SACs are consistently reported in cardiac myocytes (13) and have been reported to carry Na+ (13,16,51,62,63) through the nonspecific cation SAC subset. However, the significance of SACs in the SFR is not unanimous across the literature. Studies by von Lewinski and co-workers (8,11) found no role for SACs in the SFR in rabbit and human myocardium. In rabbit ventricular strips von Lewinski (8) found the action potential amplitude, resting membrane potential, and action potential duration were unchanged following a 10% stretch. These observations appear inconsistent with the existence of functioning SACs, which would be expected to modulate the action potential in some form. In both studies von Lewinski and co-workers (8,11) made use of Gd3+ to block SACs, however, Gd3+ also blocks NCX (64) and Na+ channels (65), which can lead to confounding results (6). This compares with rat myocytes, where SACs were found to contribute to the SFR using the SAC blocker streptomycin (6) and the action potential adapts significantly after stretch (16,51).
Furthermore, the primary path for [Na+]i into the cell, after stretch, could be species dependent. A notable difference between rats and other species used in SFR experiments is the high resting [Na+]i value (66). The change in [Na+]i following stretch is also significantly higher in rat (5.5–6 mM) (7) than in rabbit (8) and cat (46) (≈2–3 mM) preparations. Key [Na+]i transporters, namely NCX (67), NHE (34), and NaK (60) are also different in rat and low [Na+]i species and any stretch-induced increase in [Na+]i influx will result in an increase in NaK and decrease in NHE and NCX Na+ flux, causing a net decrease in Na+ influx from the three transporters. Hence, a role for stretch-induced NHE stimulation in low [Na+]i species is not inconsistent with the findings of this study.
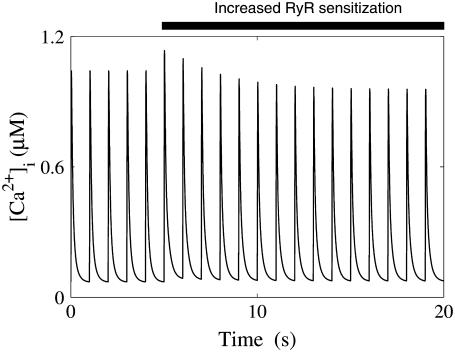
The third hypothesis tested was the stretch-dependent release of NO and the resulting increase in the open probability of RyR. As discussed above, model results are not consistent with the role of NO proposed by Villa Petroff et al. (9) in the SFR, nor are the model simulations consistent with NO effects on the RyRs in combination with either SACs, or NHE & AE stretch dependencies. The interpretation of the simulations is further confounded by experimental studies that do not provide a clear role for NO in response to stretch. Although Villa-Petroff et al. (9) found the SFR to be NO dependent, this experiment has not been able to be replicated by Calaghan and White (6) and is inconsistent with the simulation results presented here. Two of the key assumptions of this hypothesis, namely: 1), the need for a functioning SR (as defined above) to observe a SFR; and 2), NO activates the RyRs, are both contested. von Lewinski (11) found that blocking Ca2+ uptake and release from the SR with cyclopiazonic acid and ryanodine attenuated the SFR. However, in rat the SFR is still present when the SR Ca2+ release and uptake is inhibited by thapsigargin and ryanodine (6) or cyclopiazonic acid and ryanodine (1). Similar results have also been shown in the rabbit (19). SR Ca2+ content is also observed to rise during the SFR but this is not required for the SFR to occur (19). The effect of NO on RyRs is also debated; separate experimental studies have found NO to both inactivate (68) and activate (69) cardiac RyRs. Further still, increased open probability of RyRs has been shown to cause a transient increase in systolic [Ca2+]i transients (70), as a result of SR feedback mechanisms, which are captured by the model (see Fig. 11). This observation directly conflicts with the hypothesis of Villa Petroff et al. (9) and is highlighted by the inability of increased RyR open probability to cause a significant SFR (see Table 1). Hence, the role of NO, if any, in the SFR appears unlikely to solely involve the sensitization of RyRs. Casadei and Sears (17) postulated that the increase in Ca2+ influx on NCX, due to [Na+]i accumulation, in conjunction with an increase in RyR open probability may allow a sustained increase in systolic [Ca2+]i. In model simulations the addition of NO stretch-dependent effects caused a decrease in SFR after stretch regardless of the presence of other stretch-dependent elements. However, whereas the physiological effects of nitrosylation occur over a period of several minutes (9), they were assumed in the model to act instantaneously (due to limited time transient data). Hence, it is possible that a gradual modulation of RyR sensitivity may affect both the capacity of NO to cause the SFR and potential transient effects of NO on the SFR. We suggest that further experiments are required to confirm a role for stretch released NO activation of RyRs in the SFR to stretch. We suggest that such experiments could have the additional dual goals of determining the significance, if any, of gradual RyR modulation and potentially expanding the proposed hypothesis to include other Ca2+ or Na+ handling mechanisms.
FIGURE 11.
The effects of increased RyR sensitization on the [Ca2+]i transient. Initially the [Ca2+]i transient is at a steady state at a 1 Hz pacing frequency. After 5 s a 50% increase in RyR open probability was applied by decreasing the rate of closing of the RyRs by 50%.
Model critique
The model proposed here is necessarily an approximation, and thus it is important to consider the embedded limitations and assumptions. The limitations of the model and motivations for the model adaptations are now discussed. These include: 1), the structure of the [Na+]i regulation and stretch dependence of NHE model, 2), the addition of pH regulation required the development of a simplified NHE model and the inclusion of Cl− and H+ leak fluxes, 3), adding in stretch dependencies required the fitting of a rat parameter set for the Healy and McCulloch SAC model (50), representing the stretch dependence of RyR dynamics and NHE & AE fluxes, 4), the definition of strain, and 5), the challenges inherent in modeling.
One potential reason for the lack of evidence for NHE stretch dependence shown by model results may be due to assumptions about the model structure, which we now explicitly test. In the model development it was assumed that NHE flux was reduced by increased [Na+]i, whereas some experimental results find nominal inhibition at physiological concentrations of [Na+]i (35). Even though there is no experimental evidence, it is possible that CHE is also stretch dependent, which would increase the flux through NHE required to cause a 0.1 pH unit change in pH following stretch in HEPES solution, as noted above. It has also been proposed that the NaK pump has a third- (56) and not fourth-order dependence on [Na+]i, which would alter the change in [Na+]i in response to an increased [Na+]i influx on NHE. All three assumptions about the model structure attenuate the affects of a stretch-dependent NHE. Using the original model, in the presence of stretch-dependent NHE & AE and the absence of SACs, [Na+]i increased by 0.8 mM and caused an SFR of 0.87% following 15 min of stretch. If NHE inhibition by [Na+]i is removed from this model by fixing [Na+]i in Eq. 1 to the diastolic [Na+]i value at 1 Hz (11.33 mM) then the increase in [Na+]i is 0.84 mM. If CHE were also stretch dependent we would observe a greater increase in NHE flux but still no change in pHi. To model this we clamped pHi and increased the flux of NHE following stretch twofold; under these conditions [Na+]i increases by 2.52 mM causing a SFR of 12%. Thirdly, changing the [Na+]i dependence of the NaK pump model to a third-order dependence and increasing the maximum NaK flux by 5.5% to maintain the [Na+]i frequency relationship on [Na+]i, caused a 0.92-mM increase in [Na+]i. Thus, the rise in [Na+]i after stretch is only sensitive to the increase in NHE flux after stretch but doubling the increase caused a small <20% SFR, which is consistent with the study conclusion that stretch-dependent NHE & AE alone cannot replicate experimental SFR values.
To achieve resting pHi values in HEPES and bicarbonate buffered solutions in quiescent cells a background proton flux was added. Initially, combining the models of NHE, NBC, AE, and CHE resulted in a resting pHi was 7.25 and 7.38 in bicarbonate and HEPES buffered solution, respectively. Although, it was possible that metabolic pH production could reduce these high pHi values. However, taking basal metabolism as 6.3 mWg−1 (71), converting to nmol ms−1 using the scaling factors from Gibbs and Loiselle (72) and assuming ≈1:1 ratio between O2 consumption and CO2 production, results in a persistent CO2 flux of 12.6 nmol ms−1. Including this persistent flux in the model results in a decrease in pHi in HEPES solution of <0.01 pH units. Increasing the CO2 flux by a factor of 100–1.26 μM ms−1 caused pHi to drop to 7.31. As such we concluded that the deviation in model pHi from experimental results was not due to the absence of basal metabolic H+ production. During paced simulations the accumulation of lactic acid or other metabolic byproducts could also contribute to changes in pHi. However, Bountra et al. (73) found that pHi changed by ≈0.01 pH units per Hz in bicarbonate buffered solutions, which is less than the mean ± SE of the resting pH experimental measurements to which we are fitting. As such, no form of metabolic acid production was included in our model. A small voltage-dependent background leak flux was added, as in earlier modeling studies (41), with a conductance of 4 × 10−6 mS, which lowered resting pHi to 7.21 and 7.26 in bicarbonate and HEPES buffered solution, respectively. The background flux is parameterized to ensure viable resting pHi values and is not based on any experimental data. It is possible that the use of a mix of models (rat and guinea pig) creates a discrepancy in fluxes at resting pHi, which we have filled with the leak current. However, this cannot be determined until a complete data set is available for rat proton equivalent exchangers. Table 2 shows that [Na+]i, [Ca2+]i, and SFR are insensitive to the conductance of the background leak and as such demonstrate that the final conclusions of this study are independent of the leak current.
To compare a broad range of stretch-dependent mechanisms requires a standard definition of stretch. Ideally sarcomere length would be recorded in a standard preparation, however, the experimental studies that provide the multiple data sets required to parameterize the model use a variety of definitions. To accommodate the range of strain measurements and preparation types we assumed that the strain was a percentage of the reference length. To quantify the significance of this assumption, we tested the sensitivity of the SFR, [Na+]i, and peak [Ca2+]i to perturbations in the length dependence of the three stretch-dependent elements. Table 3 shows that only the length dependence of the SAC channels caused a significant change in the SFR (7.89%). Furthermore, halving the length dependence of SACs results in a SFR of 8.28%, considerably greater than either NO or pH dependent elements acting alone or in combination. Also, increasing the length sensitivity of either pH or NO effects caused effectively no change in the SFR. Hence, it appears unlikely that the study conclusions are affected by the definition of strain.
Although we have made every effort to parameterize and validate the model against a wide range of experimental data, it is important not to underestimate the complexity of biological systems. Specifically, we are cognizant, that just because the quantitative mechanism embedded in a model explains experimental data, it does not mean that this is a unique and/or correct explanation. This study uses modeling to make quantitative comparisons between different hypothesized causes of the SFR based on a set of rationalized assumptions. We have identified the SACs as the most plausible of the three stretch-dependent elements tested. This does not mean that SACs are definitely the cause of the SFR. However, based on the current experimental data available and on an established and transparently parameterized modeling framework, SACs are the most plausible cause of the SFR in rat ventricular myocytes.
Applications
The model proposed here incorporates a wide range of cellular functions including many stretch-dependent elements commonly excluded form electrophysiology cell models. The model provides a framework to test new hypotheses of the cause of the SFR based on new experimental data in the future and act as a starting point for developing coupled electromechanics models of rat cardiac myocytes. The code was written in CellML (26) and is freely available at www.cellml.org. The efficient computational form of the model means that it is suitable for single-cell and multicell simulations. The electrophysiology equations are posed to be compatible with continuum models of electrophysiology and the tension model can be used to calculate active tension fields to determine large deformation mechanics to facilitate the use of the model in coupled electromechanics simulations. This provides a means to link between cellular and whole organ spatial scales and further the goals of the IUPS physiome project (74).
SUMMARY
In this study we developed a detailed, biophysical and dynamically stable model of the rat cardiac myocyte at room temperature. The model is unique in its use of species and temperature-specific data to determine the model parameters and steady-state action potential duration, [Na+]i, and force frequency responses. The model is also capable of replicating the nontrivial changes in [Ca2+]i transients in response to stretch and changes in RyR dynamics, as highlighted in the inset of Figs. 7 B and 11, respectively.
We have compared the capacity of individual and combinations of stretch-dependent NHE & AE, SACs, and stretch-dependent, NO-induced changes in RyR dynamics to produce the SFR, the effects of these elements on the [Ca2+]i transient after stretch, and the changes in SFR after NHE inhibition. Simulations containing stretch-dependent, NO-induced RyR increased open probability were not capable of replicating both the SFR and the changes in [Ca2+]i dynamics observed after stretch. The increased flux through NHE & AE after stretch is capable of contributing to the SFR, however, NHE alone plays an important role in generating the SFR, independent of any stretch dependencies. Hence, our results predict that SACs play an important role in producing the SFR, potentially in combination with stretch-dependent NHE & AE but that the effects of NO, if any, are likely to include more than an increased open probability of RyRs.
Acknowledgments
The authors thank Professor Richard Vaughan-Jones and Dr. Pawel Swietach for helpful discussions.
S.N. thanks the New Zealand Vice Chancellors Committee (NZVCC) and the New Zealand Tertiary Education Commission (TEC) for providing funding. N.S. acknowledges support by the Marsden Fund of the Royal Society of New Zealand through grant No. 04-UOA-177 and the National Institutes of Health through the NIH multiscale grant No. RO1-EB005825-01.
References
- 1.Kentish, J. C., and A. Wrzosek. 1998. Changes in force and cytosolic Ca2+ concentration after length changes in isolated rat ventricular trabeculae. J. Physiol. (Lond.). 506:431–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Allen, D. G., and S. Kurihara. 1982. The effects of muscle length on intracellular calcium transients in mammalian cardiac-muscle. J. Physiol. (Lond.). 327:79–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Todaka, K., K. Ogino, A. Gu, and D. Burkhoff. 1998. Effect of ventricular stretch on contractile strength, calcium transient, and camp in intact canine hearts. Am. J. Physiol. 274:H990–1000. [DOI] [PubMed] [Google Scholar]
- 4.Hongo, K., E. White, J. Y. Le Guennec, and C. H. Orchard. 1996. Changes in [Ca2+]i, [Na+]i and Ca2+ current in isolated rat ventricular myocytes following an increase in cell length. J. Physiol. (Lond.). 491:609–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Calaghan, S. C., A. Belus, and E. White. 2003. Do stretch-induced changes in intracellular calcium modify the electrical activity of cardiac muscle? Prog. Biophys. Mol. Biol. 82:81–95. [DOI] [PubMed] [Google Scholar]
- 6.Calaghan, S., and E. White. 2004. Activation of Na+-H+ exchange and stretch-activated channels underlies the slow inotropic response to stretch in myocytes and muscle from the rat heart. J. Physiol. (Lond.). 559:205–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alvarez, B. V., N. G. Perez, I. L. Ennis, M. C. Camilion de Hurtado, and H. E. Cingolani. 1999. Mechanisms underlying the increase in force and Ca2+ transient that follow stretch of cardiac muscle: a possible explanation of the Anrep effect. Circ. Res. 85:716–722. [DOI] [PubMed] [Google Scholar]
- 8.von Lewinski, D., B. Stumme, L. S. Maier, C. Luers, D. M. Bers, and B. Pieske. 2003. Stretch-dependent slow force response in isolated rabbit myocardium is Na+ dependent. Cardiovasc. Res. 57:1052–1061. [DOI] [PubMed] [Google Scholar]
- 9.Petroff, M. G. V., S. H. Kim, S. Pepe, C. Dessy, E. Marban, J.-L. Balligand, and S. J. Sollott. 2001. Endogenous nitric oxide mechanisms mediate the stretch dependence of Ca2+ release in cardiomyocytes. Nat. Cell Biol. 3:867–873. [DOI] [PubMed] [Google Scholar]
- 10.Perez, N. G., M. C. C. de Hurtado, and H. E. Cingolani. 2001. Reverse mode of the Na+-Ca2+ exchange after myocardial stretch: underlying mechanism of the slow force response. Circ. Res. 88:376–382. [DOI] [PubMed] [Google Scholar]
- 11.von Lewinski, D., B. Stumme, F. Fialka, C. Luers, and B. Pieske. 2004. Functional relevance of the stretch-dependent slow force response in failing human myocardium. Circ. Res. 94:1392–1398. [DOI] [PubMed] [Google Scholar]
- 12.Cingolani, H. E., B. V. Alvarez, I. L. Ennis, and M. C. Camilion de Hurtado. 1998. Stretch-induced alkalinization of feline papillary muscle: an autocrine-paracrine system. Circ. Res. 83:775–780. [DOI] [PubMed] [Google Scholar]
- 13.Hu, H., and F. Sachs. 1997. Stretch-activated ion channels in the heart. J. Mol. Cell. Cardiol. 29:1511–1523. [DOI] [PubMed] [Google Scholar]
- 14.Han, C., P. Tavi, and M. Weckstrom. 2002. Modulation of action potential by [Ca2+]i in modeled rat atrial and guinea pig ventricular myocytes. Am. J. Physiol. 282:H1047–H1054. [DOI] [PubMed] [Google Scholar]
- 15.Belus, A., and E. White. 2003. Streptomycin and intracellular calcium modulate the response of single guinea-pig ventricular myocytes to axial stretch. J. Physiol. (Lond.). 546:501–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zeng, T., G. C. L. Bett, and F. Sachs. 2000. Stretch-activated whole cell currents in adult rat cardiac myocytes. Am. J. Physiol. 278:H548–H557. [DOI] [PubMed] [Google Scholar]
- 17.Casadei, B., and C. E. Sears. 2003. Nitric-oxide-mediated regulation of cardiac contractility and stretch responses. Prog. Biophys. Mol. Biol. 82:67–80. [DOI] [PubMed] [Google Scholar]
- 18.Belge, C., P. B. Massion, M. Pelat, and J. L. Balligand. 2005. Nitric oxide and the heart: update on new paradigms. Ann. N. Y. Acad. Sci. 1047:173–182. [DOI] [PubMed] [Google Scholar]
- 19.Bluhm, W. F., and W. Y. Lew. 1995. Sarcoplasmic reticulum in cardiac length-dependent activation in rabbits. Am. J. Physiol. 269:H965–H972. [DOI] [PubMed] [Google Scholar]
- 20.Bluhm, W. F., W. Y. Lew, A. Garfinkel, and A. D. McCulloch. 1998. Mechanisms of length history-dependent tension in an ionic model of the cardiac myocyte. Am. J. Physiol. 274:H1032–H1040. [DOI] [PubMed] [Google Scholar]
- 21.Tavi, P., C. Han, and M. Weckstrom. 1998. Mechanisms of stretch-induced changes in [Ca2+]i in rat atrial myocytes: role of increased troponin c affinity and stretch-activated ion channels. Circ. Res. 83:1165–1177. [DOI] [PubMed] [Google Scholar]
- 22.Luo, C. H., and Y. Rudy. 1994. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 74:1071–1096. [DOI] [PubMed] [Google Scholar]
- 23.Pandit, S. V., R. B. Clark, W. R. Giles, and S. S. Demir. 2001. A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys. J. 81:3029–3051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hinch, R., J. L. Greenstein, A. J. Tanskanen, L. Xu, and R. L. Winslow. 2004. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 87:3723–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Niederer, S. A., P. J. Hunter, and N. P. Smith. 2006. A quantitative analysis of cardiac myocyte relaxation: a simulation study. Biophys. J. 90:1697–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cuellar, A., C. Lloyd, P. Nielsen, M. Halstead, D. Bullivant, D. Nickerson, and P. Hunter. 2003. An overview of CellML 1.1, a biological model description language. Trans. Soc. Model. Simu. Int. 79:740–747. [Google Scholar]
- 27.Garny, A., P. Kohl, and D. Noble. 2003. Cellular open resource (COR): a public CellML based environment for modeling biological function. Int. J. Bifurcat. Chaos. 12:3579–3590. [Google Scholar]
- 28.Stern, M. D. 1992. Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 63:497–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wier, W. G., and C. W. Balke. 1999. Ca2+ release mechanisms, Ca2+ sparks, and local control of excitation-contraction coupling in normal heart muscle. Circ. Res. 85:770–776. [DOI] [PubMed] [Google Scholar]
- 30.Bondarenko, V. E., G. C. L. Bett, and R. L. Rasmusson. 2004. A model of graded calcium release and L-type Ca2+ channel inactivation in cardiac muscle. Am. J. Physiol. 286:H1154–H1169. [DOI] [PubMed] [Google Scholar]
- 31.Despa, S., and D. M. Bers. 2003. Na/K pump current and [Na]i in rabbit ventricular myocytes: local [Na]i depletion and Na buffering. Biophys. J. 84:4157–4166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Leem, C. H., D. Lagadic-Gossmann, and R. D. Vaughan-Jones. 1999. Characterization of intracellular pH regulation in the guinea-pig ventricular myocyte. J. Physiol. (Lond.). 517:159–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Crampin, E. J., and N. P. Smith. 2006. A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys. J. 90:3074–3090. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
34.Yamamoto, T., P. Swietach, A. Rossini, S.-H. Loh, R. D. Vaughan-Jones, and K. W. Spitzer. 2005. Functional diversity of electrogenic
 cotransport in ventricular myocytes from rat, rabbit and guinea pig. J. Physiol. (Lond.). 562:455–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
cotransport in ventricular myocytes from rat, rabbit and guinea pig. J. Physiol. (Lond.). 562:455–475. [DOI] [PMC free article] [PubMed] [Google Scholar] - 35.Wu, M.-L., and R. D. Vaughan-Jones. 1997. Interaction between Na+ and H+ ions on Na-H exchange in sheep cardiac Purkinje fibers. J. Mol. Cell. Cardiol. 29:1131–1140. [DOI] [PubMed] [Google Scholar]
- 36.Kinsella, J. L., P. Heller, and J. P. Froehlich. 1998. Na+/H+ exchanger: proton modifier site regulation of activity. Biochem. Cell Biol. 76:743–749. [DOI] [PubMed] [Google Scholar]
- 37.Swietach, P., and R. D. Vaughan-Jones. 2005. Relationship between intracellular pH and proton mobility in rat and guinea-pig ventricular myocytes. J. Physiol. (Lond.). 566:793–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
38.Ch'en, F. F. T., E. Dilworth, P. Swietach, R. S. Goddard, and R. D. Vaughan-Jones. 2003. Temperature dependence of Na+-H+ exchange,
 co-transport, intracellular buffering and intracellular ph in guinea-pig ventricular myocytes. J. Physiol. (Lond.). 552:715–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
co-transport, intracellular buffering and intracellular ph in guinea-pig ventricular myocytes. J. Physiol. (Lond.). 552:715–726. [DOI] [PMC free article] [PubMed] [Google Scholar] - 39.Vaughanjones, R. D. 1979. Non-passive chloride distribution in mammalian heart-muscle—microelectrode measurement of the intracellular chloride activity. J. Physiol. (Lond.). 295:83–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
40.Aiello, E. A., M. G. V. Petroff, A. R. Mattiazzi, and H. E. Cingolani. 1998. Evidence for an electrogenic
 symport in rat cardiac myocytes. J. Physiol. (Lond.). 512:137–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
symport in rat cardiac myocytes. J. Physiol. (Lond.). 512:137–148. [DOI] [PMC free article] [PubMed] [Google Scholar] - 41.Swietach, P., C. H. Leem, K. W. Spitzer, and R. D. Vaughan-Jones. 2005. Experimental generation and computational modeling of intracellular pH gradients in cardiac myocytes. Biophys. J. 88:3018–3037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bers, D. M. 2001. Excitation-Contraction Coupling and Cardiac Contractile Force, 1st Ed. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- 43.Vaughan-Jones, R. D. 1986. An investigation of chloride-bicarbonate exchange in the sheep cardiac Purkinje fibre. J. Physiol. (Lond.). 379:377–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Calaghan, S. C., and E. White. 2001. Contribution of angiotensin II, endothelin 1 and the endothelium to the slow inotropic response to stretch in ferret papillary muscle. Pflugers Arch. 441:514–520. [DOI] [PubMed] [Google Scholar]
- 45.Ennis, I. L., C. D. Garciarena, N. G. Perez, R. A. Dulce, M. C. Camilion de Hurtado, and H. E. Cingolani. 2005. Endothelin isoforms and the response to myocardial stretch. Am. J. Physiol. 288:H2925–H2930. [DOI] [PubMed] [Google Scholar]
-
46.Cingolani, H. E., G. E. Chiappe, I. L. Ennis, P. G. Morgan, B. V. Alvarez, J. R. Casey, R. A. Dulce, N. G. Perez, and M. C. Camilion de Hurtado. 2003. Influence of Na+-independent
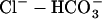 exchange on the slow force response to myocardial stretch. Circ. Res. 93:1082–1088. [DOI] [PubMed] [Google Scholar]
exchange on the slow force response to myocardial stretch. Circ. Res. 93:1082–1088. [DOI] [PubMed] [Google Scholar] - 47.Kamkin, A., I. Kiseleva, K.-D. Wagner, K. P. Leiterer, H. Theres, H. Scholz, J. Gunther, and M. J. Lab. 2000. Mechano-electric feedback in right atrium after left ventricular infarction in rats. J. Mol. Cell. Cardiol. 32:465–477. [DOI] [PubMed] [Google Scholar]
- 48.Chen, R. L., D. J. Penny, G. Greve, and M. J. Lab. 2004. Stretch-induced regional mechanoelectric dispersion and arrhythmia in the right ventricle of anesthetized lambs. Am. J. Physiol. 286:H1008–H1014. [DOI] [PubMed] [Google Scholar]
- 49.Kohl, P., and F. Sachs. 2001. Mechanoelectric feedback in cardiac cells. Philos. Trans. R. Soc. Lond. A. 359:1173–1185. [Google Scholar]
- 50.Healy, and McCulloch. 2005. An ionic model of stretch-activated and stretch-modulated currents in rabbit ventricular myocytes. Europace 7:S128–S134. 10995129. [DOI] [PubMed] [Google Scholar]
- 51.Li, X. T., V. Dyachenko, M. Zuzarte, C. Putzke, R. Preisig-Muller, G. Isenberg, and J. Daut. 2006. The stretch-activated potassium channel trek-1 in rat cardiac ventricular muscle. Cardiovasc. Res. 69:86–97. [DOI] [PubMed] [Google Scholar]
- 52.Puglisi, J. L., and D. M. Bers. 2001. Labheart: an interactive computer model of rabbit ventricular myocyte ion channels and ca transport. Am. J. Physiol. 281:C2049–C2060. [DOI] [PubMed] [Google Scholar]
- 53.Trayanova, N., W. Li, J. Eason, and P. Kohl. 2004. Effect of stretch-activated channels on defibrillation efficacy. Heart Rhythm. 1:67–77. [DOI] [PubMed] [Google Scholar]
- 54.Massion, P. B., O. Feron, C. Dessy, and J. L. Balligand. 2003. Nitric oxide and cardiac function: ten years after, and continuing. Circ. Res. 93:388–398. [DOI] [PubMed] [Google Scholar]
- 55.Shah, A. M., and P. A. MacCarthy. 2000. Paracrine and autocrine effects of nitric oxide on myocardial function. Pharmacol. Ther. 86:49–86. [DOI] [PubMed] [Google Scholar]
- 56.Smith, N. P., and E. J. Crampin. 2004. Development of models of active ion transport for whole-cell modelling: cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 85:387–405. [DOI] [PubMed] [Google Scholar]
- 57.Layland, J., and J. C. Kentish. 1999. Positive force- and Ca2+(i)-frequency relationships in rat ventricular trabeculae at physiological frequencies. Am. J. Physiol. 276:H9–H18. [DOI] [PubMed] [Google Scholar]
- 58.Schouten, V. J. A., and H. E. D. J. ter Keurs. 1991. Role of Ica and Na+/Ca2+ exchange in the force-frequency relationship of rat heart muscle. J. Mol. Cell. Cardiol. 23:1039–1050. [DOI] [PubMed] [Google Scholar]
- 59.Box, G. E. P. 1978. Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building. Wiley Series in Probability and Mathematical Statistics. Wiley, New York.
- 60.Despa, S., M. A. Islam, S. M. Pogwizd, and D. M. Bers. 2002. Intracellular [Na+] and Na+ pump rate in rat and rabbit ventricular myocytes. J. Physiol. (Lond.). 539:133–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Aronson, P. S., J. Nee, and M. A. Suhm. 1982. Modifier role of internal H+ in activating the Na+-H+ exchanger in renal microvillus membrane-vesicles. Nature. 299:161–163. [DOI] [PubMed] [Google Scholar]
- 62.Kamkin, A., I. Kiseleva, K.-D. Wagner, J. Bohm, H. Theres, J. Gnther, and H. Scholz. 2003. Characterization of stretch-activated ion currents in isolated atrial myocytes from human hearts. Pflugers Arch. 446:339–346. [DOI] [PubMed] [Google Scholar]
- 63.Bustamante, J. O., A. Ruknudin, and F. Sachs. 1991. Stretch-activated channels in heart cells: relevance to cardiac hypertrophy. J. Cardiovasc. Pharmacol. 17(Suppl 2):S110–S113. [DOI] [PubMed] [Google Scholar]
- 64.Zhang, Y. H., and J. C. Hancox. 2000. Gadolinium inhibits Na+-Ca2+ exchanger current in guinea-pig isolated ventricular myocytes. Br. J. Pharmacol. 130:485–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Li, G. R., and C. M. Baumgarten. 2001. Modulation of cardiac Na+ current by gadolinium, a blocker of stretch-induced arrhythmias. Am. J. Physiol. 280:H272–H279. [DOI] [PubMed] [Google Scholar]
- 66.Bers, D. M., W. H. Barry, and S. Despa. 2003. Intracellular Na+ regulation in cardiac myocytes. Cardiovasc. Res. 57:897–912. [DOI] [PubMed] [Google Scholar]
- 67.Cooper, P. J., M. L. Ward, P. J. Hanley, G. R. Denyer, and D. S. Loiselle. 2001. Metabolic consequences of a species difference in Gibbs free energy of Na+/Ca2+ exchange: rat versus guinea pig. Am. J. Physiol. 280:R1221–R1229. [DOI] [PubMed] [Google Scholar]
- 68.Zahradnikova, A., I. Minarovic, R. C. Venema, and L. Meszaros. 1997. Inactivation of the cardiac ryanodine receptor calcium release channel by nitric oxide. Cell Calcium. 22:447–453. [DOI] [PubMed] [Google Scholar]
- 69.Stoyanovsky, D., T. Murphy, P. R. Anno, Y.-M. Kim, and G. Salama. 1997. Nitric oxide activates skeletal and cardiac ryanodine receptors. Cell Calcium. 21:19–29. [DOI] [PubMed] [Google Scholar]
- 70.Trafford, A. W., M. E. Diaz, and D. A. Eisner. 1998. Stimulation of Ca-induced Ca release only transiently increases the systolic Ca transient: measurements of Ca fluxes and sarcoplasmic reticulum Ca. Cardiovasc. Res. 37:710–717. [DOI] [PubMed] [Google Scholar]
- 71.Loiselle, D. S., and C. L. Gibbs. 1979. Species differences in cardiac energetics. Am. J. Physiol. 237:H90–H98. [DOI] [PubMed] [Google Scholar]
- 72.Gibbs, C. L., and D. S. Loiselle. 2001. Cardiac basal metabolism. Jpn. J. Physiol. 51:399–426. [DOI] [PubMed] [Google Scholar]
- 73.Bountra, C., K. Kaila, and R. D. Vaughan-Jones. 1988. Effect of repetitive activity upon intracellular pH, sodium and contraction in sheep cardiac Purkinje fibres. J. Physiol. (Lond.). 398:341–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Hunter, P., N. Smith, J. Fernandez, and M. Tawhai. 2005. Integration from proteins to organs: the IUPS physiome project. Mech. Ageing Dev. 126:187–192. [DOI] [PubMed] [Google Scholar]