A Molecular Model for Intercellular Synchronization in the Mammalian Circadian Clock

Abstract

The mechanisms and consequences of synchrony among heterogeneous oscillators are poorly understood in biological systems. We present a multicellular, molecular model of the mammalian circadian clock that incorporates recent data implicating the neurotransmitter vasoactive intestinal polypeptide (VIP) as the key synchronizing agent. The model postulates that synchrony arises among circadian neurons because they release VIP rhythmically on a daily basis and in response to ambient light. Two basic cell types, intrinsically rhythmic pacemakers and damped oscillators, are assumed to arise from a distribution of Period gene transcription rates. Postsynaptic neurons show time-of-day dependent responses to VIP binding through a signaling cascade that activates Period mRNA transcription. The heterogeneous cell ensemble model self-synchronizes, entrains to ambient light-dark cycles, and desynchronizes in constant bright light or upon removal of VIP signaling. The degree of synchronicity observed depends on cell-specific features (e.g., mean and variability of parameters within the rhythm-generating loop), in addition to the more commonly studied effect of intercellular coupling strength. These simulations closely replicate experimental data and predict that heterogeneous oscillations (e.g., sustained, damped, and arrhythmic) arise from small differences in the molecular parameters between cells, that damped oscillators participate in entrainment and synchrony of the ensemble of cells, and that constant light desynchronizes oscillators by maximizing VIP release.

INTRODUCTION

The circadian clock is responsible for the robust regulation of a variety of physiological and behavioral processes for a diverse range of organisms, including Neurospora (1,2), Arabidopsis (3), Drosophila (4), mouse (5,6), and humans (7). Recent advances in the understanding of the molecular basis for circadian rhythms have also revealed details on the hierarchical organization of the circadian system, suggestive of robust design principles at the single-cell level (8). However, the intercellular mechanisms that allow large populations of coupled pacemaker cells to synchronize and coordinate their rhythms are not well understood. Furthermore, the experimental evidence strongly suggests that robustness in timekeeping precision only emerges in the collective behavior and not at the single-cell level (9). The study of coupled biological oscillators has attracted much attention (10,11) and is part of a broader movement toward research on complex dynamical systems (12). Such systems are intrinsically difficult to understand because the network nodes are high dimensional, the network connectivity is highly coupled across the population, and the wiring can change over time. Such complexity in network organization, however, often gives rise to surprisingly simple network performance properties (13).

In mammals, the suprachiasmatic nucleus (SCN) of the hypothalamus is a dominant circadian pacemaker that drives daily rhythms in behavior and physiology (14). Experimental studies demonstrate that SCN neurons sustain circadian rhythms without periodic input and indicate that a pacemaker within the SCN is required to drive near 24-h rhythmicity in other regions of the brain (15–17). When dispersed on multielectrode arrays, individual SCN neurons in the same culture can express firing rate rhythms with different periods (18–21). These results show that the SCN is a multioscillator system and suggest that individual SCN cells can act as autonomous circadian pacemakers. In vivo, these cells must synchronize to environmental cycles and to each other. Although intercellular communication within the SCN has been the focus of significant experimental effort, little is known about how SCN cells synchronize to each other to coordinate behavior (22–24).

Recent experimental evidence has shown that vasoactive intestinal peptide (VIP) is required for circadian synchrony in the SCN and in behavior (24). VIP, synthesized by ∼15% of the 20,000 SCN neurons, is rhythmically released from the rat SCN in vitro (25) and shifts both behavioral and SCN firing rhythms (26,27). The VIP receptor VPAC2 (encoded by the Vip2r gene) is expressed in ∼60% of SCN neurons (28). Mice overexpressing this receptor have a shorter free-running period of locomotor activity (29). VIP-deficient (30) and VPAC2-deficient (31) mice express multiple free-running circadian periods simultaneously, or shorter periods and lower-amplitude rhythms than wild-type mice (24,32). Although 70% of wild-type SCN neurons show circadian firing rhythms with similar periods and phases, a wide range of periods are observed with the 30% of mutant neurons that fire rhythmically. Daily application of a VPAC2 agonist restores rhythmicity to previously arrhythmic VIP−/− neurons and synchronizes firing rhythms of neurons within a culture (24,32). Many VIP−/− neurons that became rhythmic during daily VIP application synchronized to each other with stable phase relationships and, surprisingly, continued to oscillate for several days after VIP was removed (24), suggesting that most SCN neurons may function as damped circadian oscillators. How VIP synchronizes SCN oscillators remains unclear.

A number of mathematical models for the highly conserved circadian clock in Neurospora (33–35), Drosophila (35–39), and mammals (40,41) have been proposed. Modeling of neuron populations for the purpose of studying circadian synchronization also has received substantial attention. There is a vast literature on the synchronization of heterogeneous populations of coupled oscillators that has application to circadian rhythm generation (10,42–45). A prototypical problem involves a population of limit-cycle oscillators with natural frequencies drawn from a random distribution that are globally coupled through sinusoidal functions depending on differences between the oscillator phases. In the absence of coupling, each oscillator produces its natural frequency and a coherent overall rhythm is not observed. When the coupling weight is sufficiently large, the system exhibits a phase transition where some oscillators self-synchronize with complete synchronization observed in the limit of a large coupling weight (45).

Similar conceptual models constructed from simple differential equation models of a single oscillating neuron and phenomenological descriptions of intercellular coupling have been proposed for studying circadian rhythm generation (19,46–50). Although conceptually appealing and computationally efficient, such population models cannot be directly related to specific molecular events. Multicellular models based on more mechanistic descriptions of circadian gene regulation have been presented for Drosophila (51) and the cockroach Leucophaea maderae (52), but not for mammals. To our knowledge, multicellular models comprised of both a detailed molecular description of a single circadian neuron and its intercellular signaling are not currently available for any organism. This article represents a step toward developing a multicellular, molecular model of the mammalian circadian clock.

COMPUTATIONAL MODEL

Gene regulation model

The computational model (Fig. 1) implemented a core oscillator from a previously published gene regulation model (41) that was modified to allow the incorporation of communication between multiple cells. In the original model, each cell consisted of 16 ordinary differential equations that define a negative feedback loop in which transcription of the Period (Per) gene is activated by dimers formed from the transcription factors CLOCK and BMAL1. Our model did not include a known positive feedback loop involving REV-ERBα, which is not required for rhythm generation (41). Transcriptional activation is suppressed by a PER-CRY protein complex. Circadian rhythmicity results from accumulation and subsequent degradation of these two proteins over a period of ∼24 h. Sustained oscillations can be produced in conditions corresponding to continuous darkness or to entrainment by light-dark cycles with a period of 24 h.

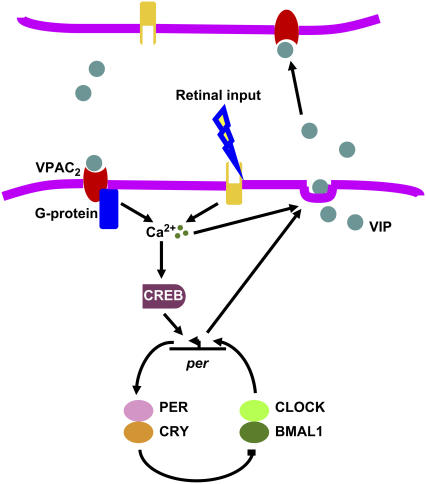
FIGURE 1.

Schematic of the mechanisms modeled to generate and synchronize circadian rhythms in the SCN. A core transcription-translation negative feedback loop provides the drive on rhythmic communication between cells and responds to synchronizing signals from neighboring cells. Within this loop, two transcription factors (CLOCK and BMAL1) form dimers to activate transcription of the Per gene. This activation is rhythmically suppressed and restored approximately every 24 h as the inhibitory PER and CRY proteins accumulate and then degrade. One hypothesized output of this clockwork is the circadian regulation of VIP release. VIP binds to the G-protein coupled receptor, VPAC2, to increase intracellular calcium and activate CREB. At specific phases in the circadian cycle, activated CREB induces Per transcription and shifts the phase of the circadian clock. Increases in intracellular calcium also mediate the phase-resetting effects of light and the release of available VIP. In a light-dark cycle, VIP was assumed to be constitutively released throughout the light phase. In constant darkness, VIP release was assumed to be controlled by intracellular Per mRNA levels.

Modeling light- and clock-controlled VIP release as entrainment pathways

Although recent experimental evidence suggests that extracellular VIP likely synchronizes individual SCN cells by changing their Per gene expression (53), how VIP influences the circadian gene circuit is not well understood. This model starts with the observations that VIP release in the SCN is circadian (25), augmented in response to light (54), and correlates with circadian rhythms in intracellular calcium elevation (55), cAMP content (56,57), and CREB-mediated gene expression (58). Entrainment of the SCN by light involves elevation of intracellular calcium, protein kinase activation, and binding of phosphorylated CREB to the promoters for Per transcription (59). Thus, we have modeled a signal transduction cascade in which VIP binds to the VPAC2 receptor to increase intracellular calcium and activate the CREB protein, which induces Per transcription to modulate the oscillator phase.

The following simplifying assumptions were invoked in developing the mathematical model:

• VIP mRNA and protein levels were not modeled explicitly and assumed to be constitutively expressed at all times.

• Signaling transduction events were fast, allowing several steps to be lumped by pseudoequilibrium assumptions. Both VIP and light acted through intracellular calcium, which then activated Per transcription through the CREB protein.

• VPAC2 receptors were expressed constitutively at the same level in all cells and were saturated when VIP was maximally released.

• The VIP release rate was sufficiently large during light to induce complete saturation of VPAC2 receptors, whereas VIP release in constant darkness was circadian with a constant phase relation to Per transcription.

Model details

During light, the VIP release rate was modeled as constant and sufficiently high to cause complete saturation of VPAC2 receptors. The following phase relationship of VIP release with Per mRNA was assumed during darkness,

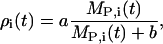(1)

where the subscript i indexes a particular cell, ρ is the extracellular concentration of VIP produced by the cell, M_P is the Per mRNA concentration, a is the maximum VIP release, and b is the saturation constant of the clock-controlled VIP release. An ensemble of individual cells was placed on a two-dimensional grid to mimic the spatial organization of circadian pacemakers. Rather than explicitly model VIP diffusion and heterogeneous network connections, empirical weight factors were used to describe the nonuniform contributions from different neurons across the network (50). The VIP concentration observed by each cell was modeled as:

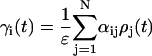(2a)

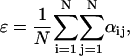(2b)

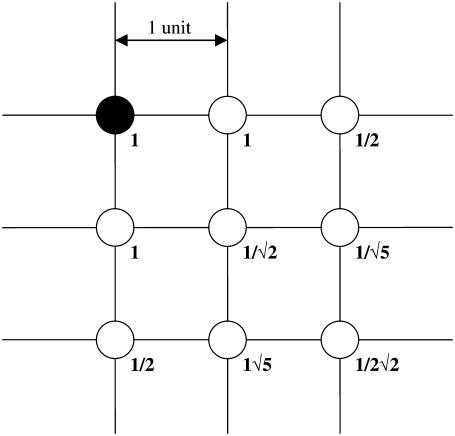
where γ_i is the local VIP concentration observed by neuron i, and α_ij is the weighted effect of neuron j on neuron i. The coupling method assumed that all cells were equally spaced on the grid. Fig. 2 illustrates the weight factors within a small system of coupled oscillators. The cell under study has a weight factor of 1 on itself. The vertically and horizontally adjacent cells are one unit away and they have weight factors of 1. The diagonally adjacent cell is √2 units away. As the weight factors are reciprocally proportional to the distances between cells, the diagonally adjacent cell has a smaller weight factor of 1/√2. Likewise, for two cells that are m units apart, the weight factor is 1/m. The VIP concentration observed by each cell was determined by summing the contribution of all cells in the population, and was scaled to a physiologically plausible value. The scale factor ɛ represents the mean of the weight factors across the population, where a value of ɛ = 56.70 for 400 cells was typical in our simulations.

FIGURE 2.

Weight factors used for the coupling of neurons placed on a two-dimensional grid. The solid circle represents the neuron of interest and has a weight factor of 1 on itself. The other weight factors are assumed to be inversely proportional to the distance away from the neuron of interest.

A simple model of receptor/ligand binding (60) was used. VIP was assumed to be a monovalent ligand that binds reversibly to the monovalent receptor VPAC2:

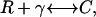(3a)

where γ denotes the VIP concentration, R denotes the VPAC2 receptor density, and C denotes the VIP/VPAC2 complex density. The total surface receptor density (R_T) was assumed to be constant:

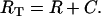(3b)

The receptor binding dynamics were assumed to be rapid with respect to the 24-h oscillation period. Therefore, the equilibrium VIP/VPAC2 complex density (C_eq) was written as:

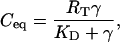(3c)

where 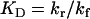represents the equilibrium dissociation constant. The extent of receptor saturation (β) was the ratio of the complex density (C_eq) to the total receptor density (R_T) and assumed the form:

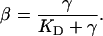(3d)

Complete receptor saturation corresponds to β = 1.

The transduction mechanism involving the receptor VPAC2, G-proteins, phospholipase C, and InsP₃ were lumped into a single step. The influx of Ca²⁺ from ligand sensitive pools was represented as ν₁β, where β was interpreted as the extent of VIP stimulus. Photic input was assumed to result in increased intracellular calcium levels. Therefore, the influx of Ca²⁺ from light-sensitive pools was represented as ν₂δ, where δ was interpreted as the extent of light stimulus and assumed values between 0 (no light) and 1 (maximum light). The influx of extracellular Ca²⁺ (ν₀) and efflux rate of cytosolic Ca²⁺ (k) were also considered. At steady state, the cytosolic calcium balance was written as:

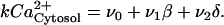(4)

The timescale of cytosolic calcium oscillations is much faster than that of gene regulation and thus was not considered.

Although the actual signaling pathways likely involve multiple secondary messengers and protein kinases (61), the model was kept as simple as possible because the scalability of the model was critical for population simulations. Likewise, more detailed models are possible for the core mammalian oscillator (40), but we elected to choose simple models that captured the essential molecular details for the synchronization phenomenon. Cytosolic Ca²⁺ influxes were assumed to be translated into intercellular communication via kinase and phosphatase activities. For simplicity, the activation of protein kinases was omitted from the model. Instead, CREB was activated via a Michaelis-Menten process by cytosolic Ca²⁺ and linearly deactivated by a generic phosphatase. The time variation of the fraction of CREB in phosphorylated form, denoted by CB*, was modeled as:

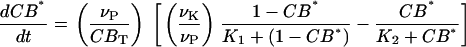(5a)

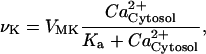(5b)

where ν_K and ν_P are the maximum rates of kinase and phosphatase activities, respectively; CB_T is the total amount of CREB; V_MK is the maximum rate of activation by Ca²⁺, and K_a, K₁, and K₂ are threshold constants.

CREB binding to the Per gene was modeled analogous as VPAC2 binding. The extent of CREB activation λ was modeled as:

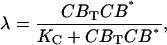(6)

where K_C is the dissociation constant. The basal and CREB-induced maximum transcription rates of Per mRNA were assumed to be additive:

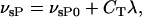(7)

where ν_sP0 is the basal transcription rate and C_T is the scaled maximum effect of the CREB-binding element on the Per gene. The maximum Per transcription rate, ν_sP, was incorporated into the kinetic equations of the gene regulation model to alter the oscillator phase, period, and amplitude of individual cells.

SIMULATION AND ANALYSIS

The resulting signaling model consisted of a single, time-dependent ordinary differential equation for phosphorylated CREB and five algebraic equations for the extent of VPAC2 saturation, the intracellular calcium concentration, the extent of CREB activation, the maximum transcription rate of Per mRNA, and the VIP release rate. A complete cell model obtained by augmenting the core oscillator with intercellular signaling was comprised of 17 ordinary differential equations plus five algebraic equations. Simulations utilized 400 cells placed on a 20 × 20 grid, resulting in a multicellular model with 6800 ordinary differential equations. The nominal parameter values for the core oscillator model were obtained from the original reference (41), whereas the parameter values associated with VIP signaling (Table 1) were chosen within biologically plausible ranges to mimic experimentally observed synchronization and desynchronization behavior.

TABLE 1.

Nominal parameter values of the VIP signaling model

Parameter	Value	Parameter	Value
vsP0	1.02 nM h−1	v2	5 nM h−1
a	10 nM	vP	1 nM h−1
b	4 nM	Ka	2.5 nM
KD	2.5 nM	VMK	8 nM h−1
RT	100 nM	K1	0.01 nM
N	100	K2	0.01 nM
k	10 h−1	CBT	1 nM
v0	0.5 nM h−1	CT	1.1 nM
v1	5 nM h−1	KC	0.3 nM

Asynchronous initial cell states were generated utilizing a previously published method developed for yeast cell population simulations (62). Cellular heterogeneities were introduced to reflect the fact that only ∼30% of SCN neurons show intrinsic rhythmicity in the absence of VIP signaling and that these rhythmic cells exhibit a broad distribution of circadian periods (24). Each model neuron was assigned a randomly perturbed value of the basal transcription rate of Per mRNA, ν_sP0, such that ∼40% of the cells produced sustained oscillations in the absence of VIP coupling. In fact, the rhythmic phenotype and level of Per mRNA have been shown to vary substantially among SCN neurons (63). The free-running periods of the intrinsic oscillators were tightly distributed around 22 h. To achieve a broader distribution of free-running periods, random perturbations were also introduced into eight kinetic parameters (k₁–k₈) associated with the core oscillation model. One major source of cell-to-cell variation in gene expression is the fluctuation in the number of regulatory proteins (64). The regulatory proteins involved in the core oscillator model are the CLOCK-BMAL1 and PER-CRY dimers. The availability of these two dimers is governed by their formation rates (determined by k₃, k₄, k₇, k₈) and their nuclear-cytoplasmic transport rates (determined by k₁, k₂, k₅, k₆). Other parameters, such as Michaelis constants and kinetic rate constants for phosphorylation, protein synthesis, and degradation were not perturbed because they are generally believed to be less variable across the cell population.

The instantaneous degree of synchrony after each oscillation cycle was measured by the synchronization index (45):

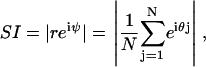(8)

where ψ is the average phase, θ_j is the phase of the j-th cell with respect to a reference cycle, N is the total number of cells, and |·| denotes the modulus. The reference cycle was chosen to be the ensemble average. The synchronization index reflects the instantaneous amplitude of the ensemble rhythm and yields values between zero (no synchronization) and one (perfect synchronization). The overall degree of synchrony over a specified time period was measured by the order parameter (50):

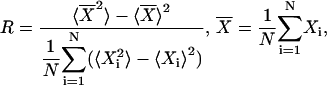(9)

where 〈 · 〉 denotes average over time, and X can be any variable of the cell model (e.g., Per mRNA level). The order parameter is the ratio of the variance of the ensemble to the average variance of the individual cells over a given time interval. This parameter quantifies the distributions of both oscillator phases and amplitudes, and ranges from zero (complete asynchrony between cells) and one (all cells oscillating exactly in phase). All R values were computed over a time period of 120 h (5 days).

RESULTS

Effect of VIP signaling

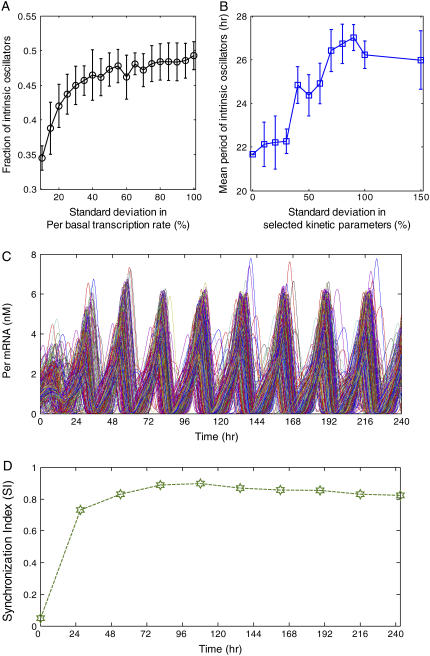
Recent experiments have shown that only ∼30% of SCN neurons produce stable rhythms in the absence of VIP signaling and that these intrinsic oscillators exhibit a wide distribution of free-running periods (24,32). To mimic these cellular heterogeneities, random perturbations were introduced into the individual neuron models via the basal transcription rate of Per mRNA (ν_sP0 in Table 1) and eight kinetic parameters (k₁ to k₈ in Table 1) of the core oscillator. We found that by setting the standard deviation in ν_sP0 to ∼10% of its mean value, we could reliably produce an uncoupled ensemble in which ∼40% of the cells were able to sustain circadian periodicity (Fig. 3 A). In addition to producing a broader distribution of free-running periods, larger perturbations in the eight kinetic parameters tended to increase the mean period of the rhythmic cells (Fig. 3 B). The increased periods observed in the coupled populations are significantly larger than those obtainable in the single cell model by perturbing the eight kinetic parameters, suggesting that the period increase is attributable to the VIP coupling mechanism. Similar results have been reported for other models of coupled biological oscillators (50,62).

FIGURE 3.

Synchronization of circadian neurons under constant darkness. The basal transcription rate of Per mRNA was subjected to a zero mean, normally distribution perturbation to obtain a desired fraction of neurons that display sustained oscillations in the absence of VIP signaling. Variations in the free-running periods of these intrinsic oscillators were generated by introducing zero mean, normally distributed perturbations to eight kinetic parameters in the core oscillator. (A) The fraction of intrinsically rhythmic cells versus the standard deviation in the Per mRNA basal transcription rate for ensembles of 100 neurons. The eight kinetic parameters were subjected to perturbation with a standard deviation of 10%. The error bars indicate the standard deviation in the rhythmic cell fraction across 10 runs. (B) The average period of the intrinsically rhythmic cells versus the standard deviation in the kinetic parameter for ensembles of 100 neurons. The Per mRNA basal transcription rate was subjected to perturbation with a standard deviation of 10%. The error bars indicate the standard deviation in the mean period across 10 runs. (C) Population synchronization dynamics of 400 circadian neurons when the Per mRNA basal transcription rate and the kinetic parameters were subjected to perturbations with a standard deviation of 10%. The population synchronized in the presence of VIP signaling despite the highly asynchronous initial state and the lack of photic input. (D) A high degree of synchrony (SI > 0.8) was obtained after three oscillation cycles (∼80 h).

An ensemble of 400 randomly perturbed neurons was placed on a 20 × 20 grid to allow proximal cells greater influence on their neighbors. We investigated the capability of this heterogeneous cell population coupled by VIP signaling to self-synchronize and produce a coherent overall rhythm under environmental conditions of constant darkness. Rapid synchronization of Per mRNA concentrations was observed despite the highly asynchronous initial state and the lack of a photic driving signal (Fig. 3 C). Within the first three days, ∼90% of the neurons became entrained to the overall rhythm produced by coupling of the inherent oscillators. The synchronization index (SI) rapidly increased during the first three days and then began to slowly approach an asymptotic value of ∼0.8 (Fig. 3 D). The kinetics of resynchronization seen here are similar to those reported for SCN neurons following removal of prolonged blockade of action potentials with tetrodotoxin (TTX) (63). The same experiments showed that measurable phase orders between cell pairs were disrupted during TTX treatment but were later restored upon TTX washout. The population model also captured this effect as measured by the synchronization index (not shown).

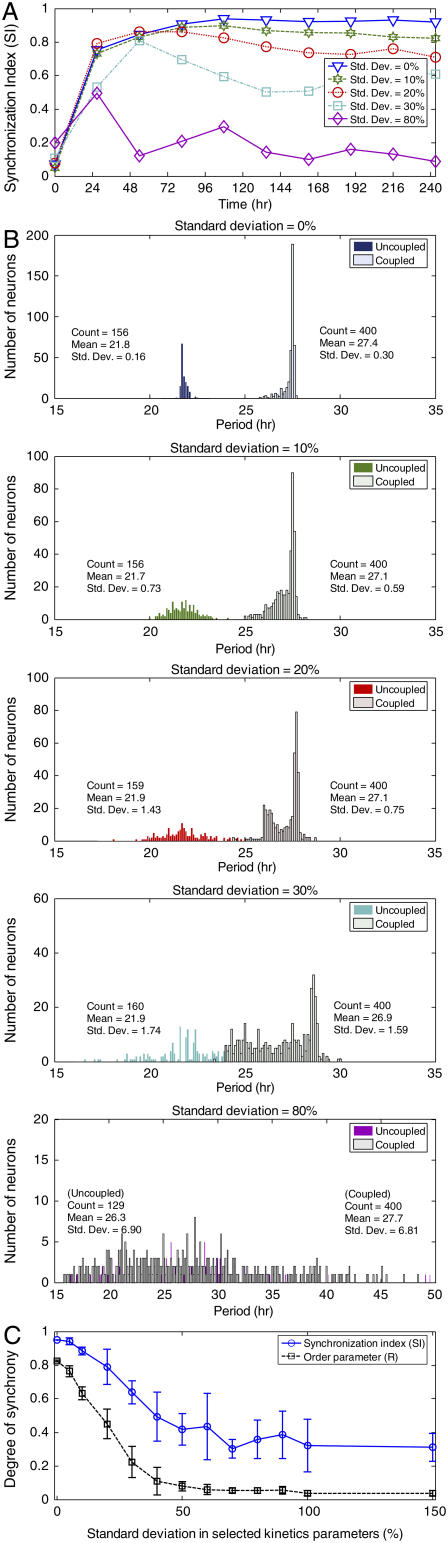
Previous theoretical studies have shown that coupled populations of heterogeneous biological oscillators exhibit a phase transition as a coupling strength parameter is increased (42–44). There exists a critical value of the coupling strength above which synchronization suddenly emerges as a collective property of the cell population. As an extension of this theoretical concept, we used our computational model to investigate the degree of synchronization achieved as a function of increasing cellular heterogeneity under constant darkness. Five cell ensembles were constructed by fixing the standard deviation of the random perturbation introduced into the basal transcription rate of Per mRNA (ν_sP0) at 10% and by varying the standard deviation (0%, 10%, 20%, 30%, and 80%) of the random perturbations introduced into the eight kinetic parameters of the core oscillator. A small standard deviation (10%) produced a modest decline in the synchronization index compared to the most homogeneous cell population (0% standard deviation in k₁–k₈ with variations only in ν_sP0, Fig. 4 A). Progressively larger perturbations (e.g., 20–30% SD) further reduced SI toward 0.6, and standard deviations greater than 50% caused SI to approach values seen in the absence of VIP signaling (<0.2). Thus, we found that perturbations that broadened the distribution of oscillator periods led to a monotonic decrease in synchrony. These observations highlight an important result of the present analysis: the degree of synchronicity observed in a heterogeneous population of oscillating cells depends on cell-specific features (e.g., mean and variability of parameters within the rhythm generating loop), in addition to the more traditional effects of intercellular coupling strength.

FIGURE 4.

Effect of random perturbations in the core oscillator on the synchronization of circadian neurons under constant darkness. Eight core oscillator parameters were subjected to zero mean, normally distributed perturbations with standard deviations of 0%, 10%, 20%, 30%, or 80%. Additionally, the basal transcription rate of Per mRNA was perturbed with a standard deviation of 10% such that ∼40% of the neurons were intrinsic oscillators. (A) The synchronization index is shown at zero time for the uncoupled population and at nine cycles for the coupled population of 400 neurons. The population failed to achieve substantial synchronization (SI > 0.6) for standard deviations >30%. (B) The distribution of periods is shown at zero time for the intrinsic oscillators in the uncoupled populations and at the ninth cycle for all cells in the coupled populations. VIP signaling increased the mean period and reduced the standard deviation of the period distribution. (C) The synchronization index (SI) at the ninth cycle and the order parameter (R) from the last five cycles versus the standard deviation in the kinetics parameters k₁–k₈ for ensembles of 100 neurons. The error bars indicate standard deviations across 10 independent runs.

Period histograms of the intrinsic oscillators were constructed for the uncoupled populations (t = 0 h) and the coupled populations following synchronization (t = 240 h) to examine the effects of VIP signaling on the period distributions (Fig. 4 B). Each case produced a slightly different number and distribution of intrinsic oscillators due to the randomization procedure used to vary the core oscillator parameters. As compared to the uncoupled case, VIP signaling increased the mean period and reduced the standard deviation of the period distribution. Smaller fractional increases in the mean period and reductions in the standard deviation were obtained as the degree of cellular heterogeneity increased. Interestingly, the 20% perturbation produced a bimodal distribution of oscillator periods. Qualitatively, the modeled populations initially resemble SCN neurons cultured at low density or in the presence of TTX where they express a wide range of periods. When allowed to communicate through VIP, the modeled neurons subsequently resemble SCN neurons cultured in explants or at high density with a narrow range of periods. Of note, prior experimental work had predicted that the period of the coupled oscillators would closely match the average period of the uncoupled oscillators (9,19,20). In contrast, the VIP-based model predicted that the period of the synchronized system, and consequently the circadian behavior, will be longer than the mean of the component oscillators. This prediction is strikingly consistent with the shortened period seen in mice lacking VIP or VPAC2 receptors (24,30,31), and motivates additional study on the period-shifting behavior of coupled oscillators. The SI at the ninth cycle and the order parameter (R) from the last five cycles were determined as a function of the standard deviation in the kinetic parameters k₁–k₈ for ensembles of 100 neurons (Fig. 4 C). The error bars indicate standard deviations across 10 independent runs. Increasing perturbation broadened both the period and amplitude distributions of the oscillators. The order parameter decreased more sharply than SI with increasing perturbation because R was also affected by variation in oscillator amplitudes.

Loss of VIP signaling

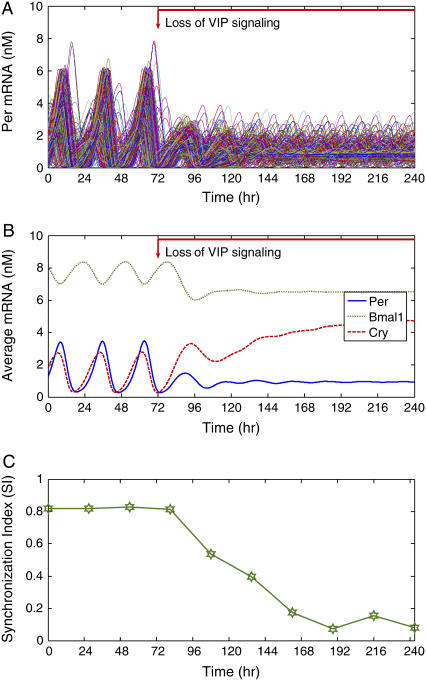
We used a 400-cell ensemble to investigate the effects of the loss of VIP signaling on synchronization dynamics and the distribution of intrinsic oscillator periods under constant darkness. Cellular heterogeneities were introduced by randomly perturbing the basal transcription rate of Per mRNA and the eight kinetic parameters in the core oscillator with 10% standard deviations. The loss of VIP signaling was simulated by setting the parameter for the extent of VPAC2 receptor saturation (β in the Table 1) to zero at t = 72 h. Nearly 60% of neurons failed to exhibit rhythmicity two cycles after VIP coupling was eliminated, and synchrony was rapidly lost in the remaining intrinsic oscillators (Fig. 5 A). mRNA concentrations were averaged across the cell ensemble to assess independently the effect of VIP signaling on synchrony among cells and the state of their pacemaker mechanism. Rhythms in Per, Bmal1, and Cry mRNAs damped out after ∼3 days, indicating either a loss of intercellular synchrony or intracellular rhythmicity (Fig. 5 B). Compared to their mean values during the initial oscillatory phase, the expression of Per and Bmal1 mRNAs decreased whereas the expression of Cry mRNA increased following the elimination of VIP signaling. Inspection of mRNA patterns in individual cells after removal of VIP coupling revealed that the rhythm amplitude was reduced in intrinsic oscillators and eliminated in nonoscillating cells. Critically, when Per and Cry were not coordinately driven in the ensemble of cells, arrhythmicity ensued. Although the coupled cell population consisted of 156 intrinsic oscillators with tightly distributed periods and a large average period, loss of VIP signaling reduced the mean period by ∼5 h and broadened the period distribution (shown in Fig. 4 B, 10% SD). The SI exhibited a sharp decrease following VIP removal and eventually settled at a small value indicating a complete loss of synchrony (Fig. 5 C). Thus, the model recapitulates findings that loss of VIP signaling leads to a loss of rhythmicity in a majority of cells and reduced synchrony within the SCN of mice (24,32), as well as a shortening of the mean circadian periodicity among the remaining rhythmic cells that is reminiscent of what has been reported for mice or SCN with disrupted VIP signaling (24,30,32).

FIGURE 5.

Effect of eliminating VIP signaling on the synchronization of 400 neurons under constant darkness. Cellular heterogeneities were introduced as in Fig. 3. The initial cell state was generated by simulating the cell ensemble until a high degree of synchrony was achieved. To mimic the loss of VIP signaling, the extent of VPAC2 saturation was set to zero at t = 72 h. (A) Approximately 60% of the neurons failed to exhibit rhythmicity after two cycles following elimination of VIP signaling. Synchrony was disrupted in the remaining 40% of rhythmic neurons. (B) When averaged across the cell population, the expression of Per and Bmal1 mRNAs decreased and the expression of Cry mRNA increased following the loss of VIP signaling. (C) The synchronization index (SI) showed that the population lost phase coherence after removal of VIP signaling.

Effect of VIP pulses

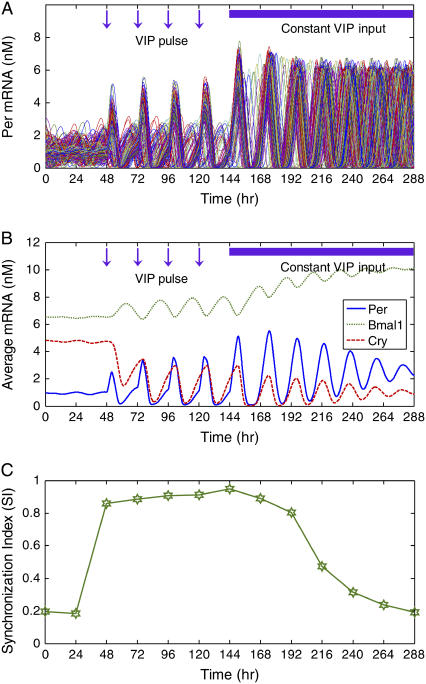
To test whether daily exposure to VIP could restore and entrain SCN rhythms, we constructed an ensemble of 400 VIP −/− neurons by setting the maximum VIP release (a) to zero. Core oscillator parameters again were subjected to random perturbations, yielding a heterogeneous population in which only ∼40% of the cells were intrinsically rhythmic. Before the initiation of VIP agonist pulses, the cell population failed to synchronize and produce a coherent overall rhythm as shown by the Per mRNA concentrations of individual cells (Fig. 6 A), as well as the ensemble averaged Per mRNA concentration (Fig. 6 B). Daily pulses of VIP agonist were simulated by increasing the extent of VPAC2 saturation (β) to its maximum value of unity for 3 h following each pulse. The 3-h duration of the agonist effect was chosen to mimic recent experiments (24) in which the agonist used had a half-life of ∼1.5 h (65). The 60% of neurons that failed to produce oscillations before the agonist pulses became rhythmic and synchronized with the inherent oscillators such that all cells were rhythmic in the VIP-treated condition. Thus, the model provided a parsimonious, entrainment-based mechanism to explain the observation that population synchrony and circadian rhythmicity can be restored to VIP-deficient SCN by daily application of a VPAC2 stimulus (24). Indeed, the model provided qualitative agreement with experiments in which daily activation of VPAC2 receptors restored rhythmicity in 40% of SCN cells and entrained the population so that 70% of SCN cells expressed synchronized circadian rhythms. When the VIP pulses were followed by a constantly high VIP level, the cells remained rhythmic with larger amplitude oscillations than observed when VIP was rhythmically released. However, constant VIP release produced a decrease in oscillation amplitude of the ensemble average, suggesting the need for experiments to determine whether a constitutive level of VIP suffices to desynchronize circadian cells without loss of rhythm amplitude. These results are in direct opposition to those obtained with simpler cell and intercellular coupling models, which predict that constant levels of the coupling agent will lead to a loss of rhythmicity in individual cells (50). The SI exhibited a rapid increase following the initiation of VIP pulses and then slowly decreased following the imposition of the constant VIP level (Fig. 6 C). The simulation results support the argument that VIP plays two roles in the SCN: to entrain pacemaking neurons and to sustain rhythms in damped oscillators.

FIGURE 6.

Effect of VIP agonist on the synchronization of 400 VIP −/− neurons under constant darkness. Cellular heterogeneities were introduced as in Fig. 3. The maximum VIP release rate was set to zero for each neuron, thereby eliminating VIP signaling. As a result, only ∼40% of the neurons displayed circadian rhythms. Daily pulses of VIP agonist were mimicked by setting the extent of VPAC2 saturation to its maximum value of unity when the agonist was applied (t = 48, 72, 96, 120, and 144 h). The agonist was assumed to be provided in excess and to have an effect that lasted 3 h. (A) Daily agonist applications induced rhythmicity in most neurons and resulted in synchronization of the cell population. Single neuron rhythmicity was maintained following the elimination of agonist pulses at t = 144 h. (B) When averaged across the cell population, the expression of Bmal1 mRNA increased and the expression of Per and Cry mRNAs was maintained constant following the removal of agonist pulses. (C) The synchronization index (SI) showed that population synchrony was slowly lost following the elimination of agonist pulses.

Entrainment to light-dark cycles

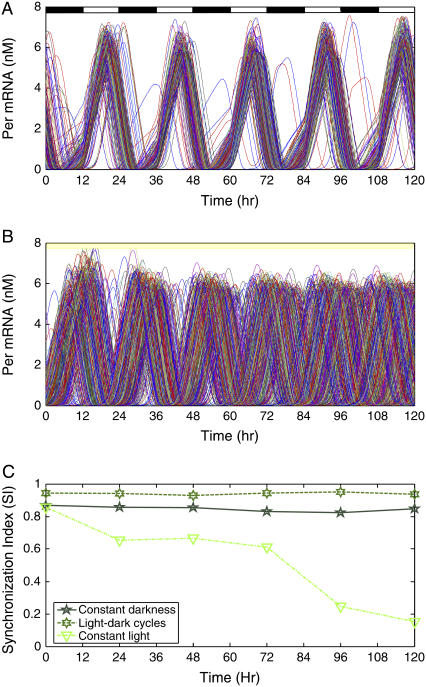
In addition to synchronizing to each other, SCN neurons must entrain to light-dark cycles to ensure accurate and robust timekeeping under varying environmental conditions. We investigated the effect of photic input on circadian synchrony and rhythmicity by exposing a heterogeneous population of 400 cells to different light schedules. Constant darkness produced a partially synchronized population in which some cells failed to synchronize with the intrinsic oscillators (R = 0.68; Fig. 3 C). The light effect was implemented by increasing the light-induced calcium stimulus (δ) to its maximum value of unity. Since VIP was released constitutively and VPAC2 receptors were saturated during light, the extent of VPAC2 saturation (β) was also increased to its maximum value of unity during the light phase. Light-dark cycles were simulated by changing these values every 12 h, with the dark phase corresponding to δ = 0 and β-values determined by Eq. 3b. Compared to constant darkness, light-dark cycles produced a more coherent overall rhythm with fewer cells that failed to synchronize (R = 0.86; Fig. 7, A and C). The Per mRNA level peaked during the late day with a period of 24 h, indicating the rhythm had entrained as seen in vivo (reviewed in Reppert and Weaver (6)). These results support the behavioral observation that entrainment to a 24-h cycle further improves the precision of the ensemble rhythm compared to free running conditions in constant darkness (cf. Herzog et al. (9)). We next simulated constant bright light by maintaining the parameters for light-induced calcium stimulus and extent of VPAC2 saturation at their elevated values. Although all neurons were rhythmic, the population failed to synchronize despite intercellular coupling by VIP signaling (R = 0.22; Fig. 7 B). The lack of synchronization produced a precipitous decline in the synchronization index (Fig. 7 C) and was accompanied by an increase in total PER protein content (not shown). These results may explain the observation that constant bright light can abolish circadian rhythms in locomotor behavior and in the ensemble activity of the SCN. Indeed, recent results showed that individual SCN cells remain rhythmic in constant light, but lose synchrony with the population (66).

FIGURE 7.

The effect of photic input on the synchronization of 400 neurons. Cellular heterogeneities were introduced as in Fig. 3. (A) Synchronization dynamics under repeated light-dark cycles implemented by imposing a square wave in the light-induced calcium stimulus. During the light phase, the VPAC2 receptors were saturated due to the constitutive release of VIP. The Per mRNA level peaked during the day, and a higher degree of synchrony was achieved than in constant darkness. (B) Synchronization dynamics under constant bright light implemented by setting the light-induced calcium stimulus and the extent of VPAC2 saturation to their maximum values. Although all the individual cells remained rhythmic, population synchrony was strongly disrupted. (C) The synchronization index (SI) showed that population synchrony was enhanced by light-dark cycles and lost during constant light.

DISCUSSION

This model for circadian synchronization of mammalian neurons provides potential molecular mechanisms for two intriguing experimental observations: individual neurons are not uniformly precise timekeepers, and “robustness” in timekeeping emerges as a property of network behavior. Random perturbations in model parameters that influenced the circadian period produced a heterogeneous cell population that behaved much like the neurons of the mammalian SCN: only ∼40% of the cells exhibited intrinsic pacemaking ability, whereas the remaining cells were damped oscillators requiring input from the pacemakers to sustain rhythmicity. When coupled by rhythmic release of VIP, each neuron adjusted its period with larger amplitude oscillations so that the network synchronized to produce a coherent circadian output. Both coupling and population heterogeneity were found to have a strong influence on the degree of synchronization, suggesting the importance of both stochastic (cell-to-cell variability) and deterministic (network architecture) phenomena in understanding multicellular synchronization. The fact that robust synchronization was achieved despite the simplified nature of the VPAC2 signal transduction model suggests that VIP might improve timekeeping precision by modulating intracellular calcium and/or CREB protein concentrations.

The kinetics of synchronization shed additional light on the robustness of the underlying mechanism: desynchronization was a slow response, extending over 3–6 days as oscillators slowly drifted out of phase, while recoupling was observed to be quite rapid, achieving convergence over 1–3 days. These dynamics parallel those seen experimentally where desynchrony was revealed after multiple days of constant bright light (66) or tetrodotoxin application (63) and resynchrony occurred rapidly, for example, by VIP pulses (24). Model parameters that showed the greatest influence on the rate of resynchronization included the maximum VIP release rate and the saturation constant of VIP binding. Thus, it is tempting to speculate that constant bright light may deplete VIP stores and that tetrodotoxin might block VIP release to blunt synchrony among circadian oscillators in the SCN.

Several aspects of the model are clearly oversimplifications of the known architecture of the SCN. For example, VIP is produced by ∼15% (not all) of SCN neurons and VPAC2 receptor activation is not known to act via a two-step cascade to activate transcription of only the Per gene (as assumed in our model). Because the model successfully captured many features of circadian rhythmicity in the SCN (e.g., VIP-dependent changes in the percentage of rhythmic, synchronized, high-amplitude circadian neurons), these simplifications may point to underlying rules. Perhaps all pacemaking neurons release VIP to produce coherent rhythms in the SCN. There may be a linear transformation from VPAC2 activation to Per transcription. Such model predictions are experimentally testable. A reasonable, but as yet untested, model assumption is that the known heterogeneity in periodicity and phasing among SCN neurons results from cell-to-cell variations in the core oscillator. This model was limited by its inability to capture cycle-to-cycle variability of individual neurons (9). Future investigations could explore the effects of daily or continuous stochastic variations in these parameters on pacemaker precision and the cooperative improvement of precision through VIP coupling.