Abstract
The rich knowledge of operon organization in Escherichia coli, together with the completed chromosomal sequence of this bacterium, enabled us to perform an analysis of distances between genes and of functional relationships of adjacent genes in the same operon, as opposed to adjacent genes in different transcription units. We measured and demonstrated the expected tendencies of genes within operons to have much shorter intergenic distances than genes at the borders of transcription units. A clear peak at short distances between genes in the same operon contrasts with a flat frequency distribution of genes at the borders of transcription units. Also, genes in the same operon tend to have the same physiological functional class. The results of these analyses were used to implement a method to predict the genomic organization of genes into transcription units. The method has a maximum accuracy of 88% correct identification of pairs of adjacent genes to be in an operon, or at the borders of transcription units, and correctly identifies around 75% of the known transcription units when used to predict the transcription unit organization of the E. coli genome. Based on the frequency distance distributions, we estimated a total of 630 to 700 operons in E. coli. This step opens the possibility of predicting operon organization in other bacteria whose genome sequences have been finished.
The advent of the genomic era has opened up the doors to the analysis of complete genome organization, especially in bacteria. The completion of many bacterial genomes has allowed the analysis of gene clusters, leading to interesting conclusions about the tendencies of genes with related functions to remain together across several genomes (1), particularly in the case of genes whose protein products physically interact (2) (understanding genes as those regions of DNA encoding separate and distinct polypeptides). The organization of genes in operons is believed to provide the advantage of coordinated regulation and production of functionally related genes. Some recent suggestions on the origin of operons emphasize the role of horizontal transfer and the advantage of transferring complete sets of genes involved in a pathway to provide a defined phenotype to the recipient bacteria (3, 4). A recent proposition states that operons might have arisen in thermophilic organisms, because the organization of genes into operons facilitates the association of functionally related protein products, thus protecting each other from thermal degradation. Such channeling of multienzyme complexes would also protect thermolabile intermediates in a pathway (5).
RegulonDB is an exhaustive database, accessible through the Internet, containing information compiled from the literature about genetic regulation and operon organization in Escherichia coli (6, 7). The present work is based on a collection of 361 known transcription units obtained from RegulonDB. This collection groups 933 genes, of which 124 are transcribed as single units, whereas the others are grouped into 237 operons with two or more cotranscribed genes. Overall, this collection represents around 25% of all genes in E. coli. Most of these genes have been classified into the functional classes defined by Monica Riley (8, 9). This classification constitutes one of the largest attempts to assign each E. coli gene a cellular function and is used and updated in the “Encyclopedia of E. coli Genes and Metabolism” or EcoCyc (10), and in the “E. coli Genome and Proteome Database” GenProtEC (11). All these data provide a substantive database to analyze and to predict the organization of transcription units at a genomic scale.
Based on this collection and on the sequence and annotations of the E. coli genome (12), we analyzed the common features shared among pairs of adjacent genes within operons, against pairs of adjacent genes representing borders between transcription units, yet transcribed in the same direction. We evaluated and demonstrated their differences in terms of distances between genes, measured in base pairs, and in terms of functional class relationships. We also showed that such differences can be used to develop a method to predict operons in the whole E. coli genome. This method might also be helpful to predict transcription unit boundaries in other prokaryotic genomes.
Data Preparation.
All of the work was performed by using ad hoc perl scripts (13). The data set from RegulonDB used in these analyses contains 361 transcription units; 237 of them are polycistronic. In this paper, we refer to the whole collection as the collection of transcription units, and to the polycistronic subset as the collection of operons. The latter was divided into the data set of pairs of adjacent genes belonging to the same operon.
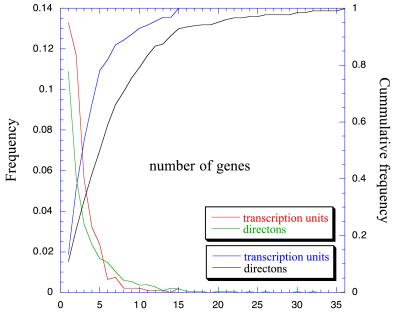
We also divided the complete M54 version of the E. coli genome into a data set of codirectional transcriptional groups. That is, we grouped together every gene transcribed in the same direction with no intervening gene transcribed in the opposite one. This was named the “directons” collection. The procedure yields a collection of 1,292 directons, 812 of which have more than one gene. The directons collection was divided into the complete data set of pairs of adjacent genes transcribed in the same direction. The number of transcription units and directons diminishes with the number of genes they contain, so that around 80% of all transcription units have fewer than five genes, whereas 80% of all directons have fewer than 10 genes (Fig. 1).
Figure 1.
Size distribution, in number of genes contained, of transcription units in RegulonDB, and size distribution of directons in the M54 version of the E. coli genome.
Then, we compared the collection of known transcription units with the collection of directons to find those directons containing transcription units with added genes at either side. Such added genes were used to construct a data set of pairs of adjacent genes at borders between transcription units, which constitutes a contrasting data set against the collection of adjacent genes in operons.
The whole operation results in a set of 572 pairs of adjacent genes in operons, a set of 346 pairs at the borders of transcription units, and a set of 3,113 total pairs of adjacent genes transcribed in the same direction.
Distance Analyses.
Distances between adjacent genes were calculated from the corresponding coordinates in the M54 version of the E. coli genome sequence. These distances represent the number of base pairs between the genes, or the number of base pairs overlapped [distance = gene2_start − (gene1_finish + 1), with gene1 and gene2 being the first and second gene in the order they occur in the genome sequence].
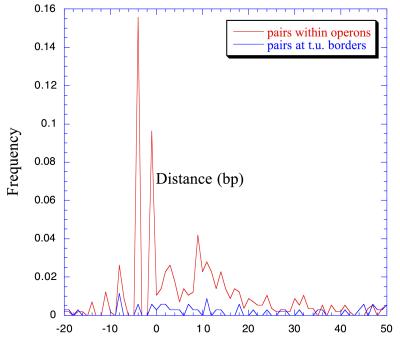
As Fig. 2 shows, there is a clear difference in distance frequency distribution between genes in the same operon and genes at the boundaries of transcription units. Genes within operons show a clear peak at short distances. The two most frequent distances are the overlaps of four bases and of one base. The former corresponds to the overlapping sequences ATGA (79 cases), GTGA (9 cases), and TTGA (1 case), in which ATG, GTG, and TTG are the start codons of the second gene in the pair, and TGA is the stop codon of the previous one. The latter most common distance corresponds to the sequences TAATG (39 cases), TGATG (15 cases), and TAGTG (1 case), with the stop and start codons sharing the middle base. There is no prevailing distance between neighboring genes that belong to different transcription units.
Figure 2.
Frequency distance distributions of pairs of adjacent genes in operons versus those of pairs of adjacent genes at the boundaries between transcription units (t.u.). There are clear differences between both distributions, with genes in operons having peaks very near to distance 0. The highest peaks correspond to the −4 and −1 overlaps.
Regulatory elements are usually located at the beginning and the end of the operon, although there are a few cases of transcription units inside operons with their own regulatory elements (eight in RegulonDB). Therefore, there may be no need for space between genes inside operons, except for that used to accommodate Shine–Dalgarno elements, although this analysis shows that such elements are easily overlapped within coding sequences. Another reason for minimal spacing between genes could be to protect mRNA from degradation by association with ribosomes (14).
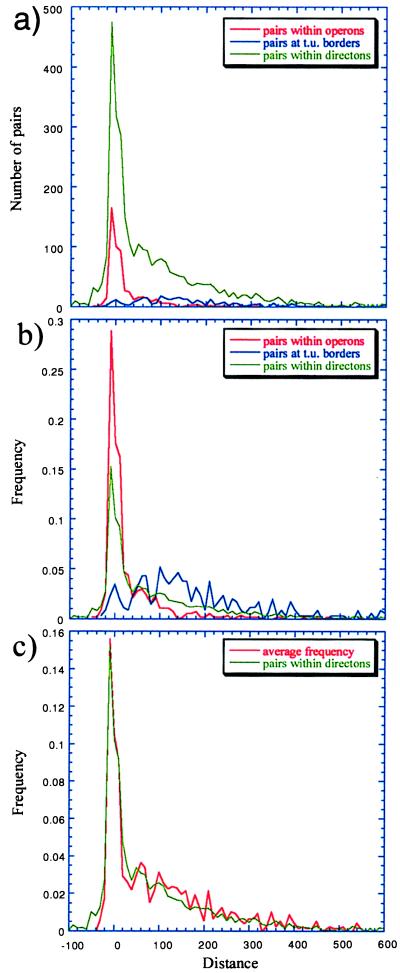
Fig. 3 shows the distance distribution, at 10-bp intervals, of all adjacent genes transcribed in the same direction of the E. coli genome, compared with that of genes within operons, and of those at the borders of transcription units. The distance distribution of the complete collection of genes transcribed in the same direction clearly shows a peak at short distances, coincident with that of the collection of genes within operons, thus indicating probable yet unidentified operons (Fig. 3a). If we observe the frequencies instead of the total number of pairs of genes for each set (Fig. 3b), the peak in operons is higher than that of the directons population. Nevertheless, as shown in Fig. 3c, the directon distance distribution overlaps nicely with the distance distribution obtained by averaging those distributions corresponding to genes within operons, and those at the borders of transcription units. This result suggests that roughly half of the total pairs of genes transcribed in the same direction would belong to operons. The result also shows that the two contrasting sets represent a good sample, because they accurately reconstruct the frequency distance distribution of all genes transcribed in the same direction, highlighting the good quality of the RegulonDB compilation. If we extrapolate from the contribution of adjacent genes in operons to each point at the peak in Fig. 3c, we can estimate a total of 629 to 643 operons in the E. coli genome. For instance, genes in operons contribute around 0.1442 to the 0.1558 value at the highest point at the peak (distances between −10 and 0 bp, Fig. 3 b and c). The contribution from genes in operons would be 0.1442/0.1558 or ≈0.9255. Now, 0.9255 × 474 (number of pairs within directons at the same point, Fig. 3a) is ≈438. One hundred sixty-five pairs of genes within operons have distances between −10 and 0 bp, and they come from a collection of 237 operons. Thus, the total operon estimate is 438 × 237/165 or ≈629]. If we extrapolate from all of the points in the curve, the estimate goes to around 700.
Figure 3.
Data used to estimate the total number of operons in the entire E. coli genome. (a) Distance distributions at 10-bp intervals. (b) Frequency distance distributions. (c) Frequency distance distributions of adjacent genes in directons versus the average of those in operons and at transcription unit (t.u.) boundaries. Notice the nice correspondence of the peaks in c, which also confirms how well the sample (operons and transcription unit borders) represents the population (directons, or total adjacent genes transcribed in the same direction). The estimated total operons, as extrapolated from these data, goes from 630 to 700.
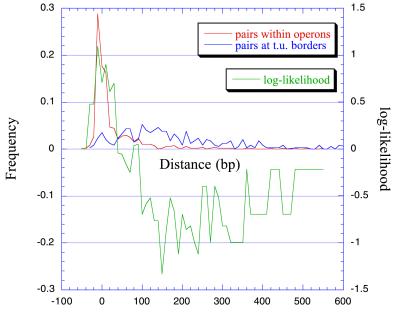
To use this information to predict the operon organization in the complete genome, we calculated distance log-likelihoods for adjacent pairs of genes to be in the same operon. Fig. 4 shows the frequency distance distributions at intervals of 10 bp of pairs of genes at operons, and of pairs at the boundaries of transcription units, as well as the log-likelihoods for each interval. The log-likelihood of a pair of neighboring genes being in the same operon as a function of distance was calculated with the formula:
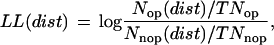 |
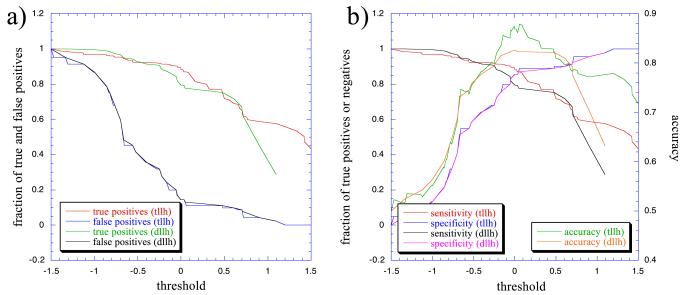
where Nop and Nnop are pairs of genes in operons and at transcriptional boundaries, respectively, at a distance [dist] (in 10-bp intervals), whereas TNop and TNnop are the total number of pairs of genes in operons and at the transcription unit boundaries, respectively. The discrimination resulting from the use of these log-likelihoods, and those described in the next section, between adjacent genes in operons and adjacent genes at the boundaries of transcription units is depicted in Fig. 5.
Figure 4.
Frequency distance distributions as obtained by adding the frequencies at 10-bp intervals, and the log-likelihoods for a pair of genes to be in an operon at each distance interval.
Figure 5.
Discrimination of known pairs of genes in operons by the use of distance log-likelihoods alone (dllh), and of distance and functional class log-likelihoods (tllh), at different thresholds. (a) Fraction of right and wrong positives at different thresholds. (b) Sensitivity (right pairs in operons detected/total pairs in operons), specificity (right pairs at borders/total pairs at borders), and accuracy (average of sensitivity and specificity) at different thresholds. The correct identifications are slightly better when functional classes are used.
Analysis of Functional Classes.
The clustering of functionally related genes in the chromosome was one of the motivations for the definition of operons in bacteria (15), and, as already mentioned, previous analyses have shown the tendency of genes to remain in clusters when their products have a related function (1). To perform a functional analysis of adjacent genes, we relied in the functional classes of Monica Riley (8, 9). In this classification, each gene is assigned a number corresponding to one of 120 functional classes.
Table 1 shows the most frequent functional classes, in pairs of genes within operons and in pairs of genes at the borders of transcription units. Four hundred eleven of 519 pairs of adjacent genes within operons with assigned functional class belong to the same class (79.2%). For instance, the most frequent functional class appearing in neighboring genes in operons is 2.72, meaning “anaerobic respiration; energy metabolism, carbon; metabolism of small molecules.” On the other hand, only 26 of 172 pairs, or 20.5%, of genes at the boundaries of transcription units share their functional class. These distributions generate a log-likelihood of 0.7192 for adjacent genes to be in an operon when they share their functional classification, and of −0.6106 if they belong to different functional classes.
Table 1.
Most frequent pairs of functional classes between adjacent genes within operons, and between those at transcription unit boundaries
| Pairs in operons
|
Pairs not in operons
|
||
|---|---|---|---|
| Functional classes | No. of pairs | Functional classes | No. of pairs |
| 2.72/2.72 | 37 | 6/51 | 5 |
| 50.3/50.3 | 32 | 40.1/40.1 | 5 |
| 40.1/40.1 | 28 | 53/58.5 | 3 |
| 53/53 | 22 | 50.3/50.3 | 3 |
| 2.71/2.71 | 22 | 40.1/40.5 | 3 |
| 52/52 | 18 | 1.1/53 | 3 |
| 1.1/1.1 | 17 | 1.1/2.72 | 3 |
| 51/51 | 16 | 1.1/1.1 | 3 |
| 1.1/53 | 13 | 9.81/53 | 2 |
| 6/6 | 9 | 60.3/60.3 | 2 |
Functional classes have a designated number as provided by Monica Riley. The numbers in this table mean: 1.1, Carbon compounds; degradation of small molecules; metabolism of small molecules. 2.71, aerobic respiration; energy metabolism, carbon; metabolism of small molecules. 2.72, anaerobic respiration; energy metabolism, carbon; metabolism of small molecules. 6, global regulatory functions; global functions. 9.81, isoleucine; amino acid biosynthesis; metabolism of small molecules. 40.1, ribosomal proteins–synthesis, modification; ribosome constituents; structural elements. 40.5, DNA–replication, repair, restriction/modification; macromolecule synthesis, modification. 50.3, surface structures; cell exterior constituents; structural elements. 51, amino acids, amines; transport of small molecules; cell processes. 52, cations; transport of small molecules; cell processes. 53, carbohydrates, organic acids, alcohols; transport of small molecules; cell processes. 58.5, osmotic adaptation; adaptation; processes. 60.3, colicin-related functions; laterally acquired elements; elements of external origin.
It is important to note that almost all of the genes in the operon data set have a defined functional class, whereas 1808, or slightly less than half of all genes in the genome, have such class description. Thus, contrary to neighbor distances between genes, which are available for all genes in the genome, the functional class provides partial information for operon prediction. Hence, the functional log-likelihood would not be a prediction parameter by itself, although, as discussed below, its addition to distance log-likelihoods improves predictions. The discrimination between pairs of genes in operons and pairs of genes at the borders of transcription units, at different thresholds, by using functional classes in addition to distance log-likelihoods is depicted in Fig. 5.
Prediction of Transcription Units in the E. coli Genome.
To test the performance of a method based on distance and functional class log-likelihoods to detect transcription units, the data set of directons was scanned, and hypothetical transcription units were generated. Pairs of contiguous genes are joined into the same operon as long as their log-likelihood score is not lower than a given threshold. Table 2 displays the number of operons and total transcription units generated at different thresholds. The best result is obtained at the same point of maximal accuracy (from Fig. 5b). At this point, the method recuperates around 75% of the set of known transcription units, although about 8% of them are generated as a result of partitioning the genome into directons. Table 3 shows the same results, but this time by using the collection of directons with known transcription units with added genes at either side. The use of distance and functional class log-likelihoods increases the rescue of complete known operons by about 10% when compared with the use of distance log-likelihoods alone (Tables 2 and 3).
Table 2.
Transcription units generated at different thresholds using the complete directons collection from the genome of E. coli
| Threshold | Transcription units
|
Operons
|
||
|---|---|---|---|---|
| Total | % of known | Total | % of known | |
| Using distance and functional class log-likelihoods | ||||
| 0.0225 | 2,646 | 73.96 | 827 | 64.14 |
| 0.0357 | 2,661 | 73.41 | 831 | 63.29 |
| 0.0493 | 2,703 | 73.96 | 814 | 63.29 |
| 0.0603 | 2,748 | 74.79 | 795 | 63.71 |
| 0.0907 | 2,751 | 74.24 | 795 | 62.87 |
| 0.0950 | 2,761 | 73.13 | 793 | 61.18 |
| 0.1639 | 2,796 | 70.08 | 784 | 56.54 |
| Using only distance log-likelihoods | ||||
| 0.0357 | 2717 | 64.54 | 842 | 51.05 |
| 0.0493 | 2784 | 65.10 | 814 | 49.37 |
| 0.4794 | 2852 | 65.37 | 791 | 48.95 |
| 0.6097 | 2976 | 63.71 | 784 | 46.41 |
| 0.7012 | 3123 | 61.50 | 717 | 42.62 |
Table 3.
Transcription units generated at different thresholds using a directons subset containing known transcription units with added genes at either side
| Threshold | Transcription units
|
Operons
|
||
|---|---|---|---|---|
| Total | % of known | Total | % of known | |
| Using distance and functional class log-likelihoods | ||||
| 0.0225 | 776 | 69.68 | 309 | 60.11 |
| 0.0357 | 788 | 69.31 | 313 | 59.57 |
| 0.0493 | 797 | 70.04 | 309 | 59.57 |
| 0.0603 | 810 | 71.12 | 305 | 60.11 |
| 0.0907 | 813 | 70.40 | 305 | 59.04 |
| 0.0950 | 820 | 69.68 | 303 | 57.98 |
| 0.1639 | 840 | 67.87 | 296 | 55.32 |
| Using only distance log-likelihoods | ||||
| 0.0357 | 816 | 59.93 | 318 | 47.34 |
| 0.0493 | 843 | 61.01 | 307 | 45.74 |
| 0.4794 | 875 | 62.09 | 301 | 46.28 |
| 0.6097 | 915 | 60.29 | 308 | 43.62 |
| 0.7012 | 968 | 58.12 | 290 | 39.89 |
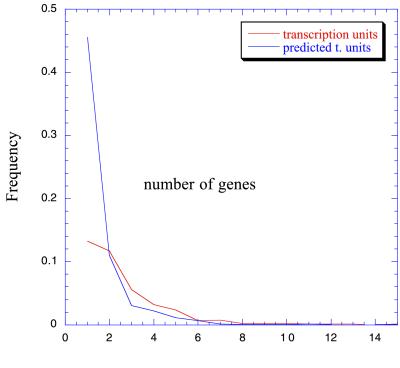
Fig. 6 displays the size of the transcription units generated at the best performing threshold (in the sense of known operons recuperated). It yields a collection of 2,748 transcription units (270 known). Among them, 795 would be operons (151 known). This distribution is shown together with that of the known transcription units from RegulonDB.
Figure 6.
Size distribution of known and predicted transcription units. As expected, the number of transcription units diminishes with their size in genes in a Poisson distribution style.
Given the constant increase in information gathered from the literature in RegulonDB, we could compare some predictions with new experimental evidence. The operon named tdcABC is a good example that highlights the power and the limitations of the method to predict transcription units. This operon has recently been shown to contain more members (16), changing the name of the operon to tdcABCDEFG. The genes tdcA and tdcB are kept together at high thresholds despite a distance of 98 bp between them (log-likelihood of 0.0493 to be in the same operon), because they belong to the same functional class (log-likelihood of 0.7192). On the other hand, despite a short distance separating gene tdcB from tdcC (21 bp, which corresponds to a log-likelihood of 0.6097 to be in the same operon), at thresholds above 0, the operon is cut, separating genes tdcB from tdcC because of their different functional class (log-likelihood of −0.6106). The functional class pair is 1.2/51, meaning “amino acids; degradation of small molecules; metabolism of small molecules”, and “amino acids, amines; transport of small molecules; cell processes,” respectively, which shows that some recategorization might improve the method, i.e., both classifications are coincident in the words “amino acids,” and both mean there is an action on “small molecules.” Genes tdcD and tdcF are kept together by distance log-likelihood alone, because the latter one does not have a functional class assigned (it is annotated as the predicted ORF yhaR). The gene tdcG is never added, because the distance between tdcF and tdcG is 65 bp, corresponding to a log-likelihood of −0.1652 to be in the same operon, and the annotation of both genes as predicted ORFs (tdcG is yahQ) does not provide the advantage of functional class comparison.
The predictions of probable operon organization here presented are based on distance distributions, and on preservation of functional class in pairs of genes within operons. Each log-likelihood estimate provides a number that can be added to log-likelihood estimates based on independent information. We therefore foresee an important space for improvement for the method. For instance, the presence of promoter regulatory motifs (17–19), ribosome binding sites (20), and terminators (21) should help in the operon identifications. Another source of improvement should come from the complement of functional assignment of genes and their products with the help of experimental work [proteome, transcriptome (22, 23), specific experiments], and that of predictive methods [homology/structure/function predictions (24–26)]. Specifically from transcriptome experiments, if the expression levels between pairs of genes in operons are more conserved than those at the borders of transcription units, then the quality of operon predictions may improve by adding the respective log-likelihood terms.
Neighboring gene distance analyses in conjunction with homologue characterization should be applicable to other bacterial genomes. These analyses will in turn provide additional regulatory, functional, and evolutionary insights. Because genes in operons have a clear tendency to share their functional classification, operon predictions may also improve and guide functional annotations in the future. The predicted transcription units will be added to the new release of RegulonDB (http://www.cifn.unam.mx/Computational_Biology/regulondb/). Work is needed in evaluating and expanding this method to predict operons in other bacterial genomes.
Acknowledgments
We acknowledge Monica Riley for providing her updated functional annotations of the E. coli genes, and Alberto Santos-Zavaleta for his work in the RegulonDB operons compilation. This work was supported by grants from Dirección General de Asuntos del Personal Académico and Consejo Nacional de Ciencia y Tecnología (Mexico) to J.C.-V., and from U.S. Department of Energy Grant DE-FG02-98ER62558.
Footnotes
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.110147297.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.110147297
References
- 1.Overbeek R, Fonstein M, D'Souza M, Pusch G D, Maltsev N. Proc Natl Acad Sci USA. 1999;96:2896–2901. doi: 10.1073/pnas.96.6.2896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dandekar T, Snel B, Huynen M, Bork P. Trends Biochem Sci. 1998;23:324–328. doi: 10.1016/s0968-0004(98)01274-2. [DOI] [PubMed] [Google Scholar]
- 3.Lawrence J G, Roth J R. Genetics. 1996;143:1843–1860. doi: 10.1093/genetics/143.4.1843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lawrence J G. Trends Microbiol. 1997;5:355–359. doi: 10.1016/S0966-842X(97)01110-4. [DOI] [PubMed] [Google Scholar]
- 5.Glansdorff N. J Mol Evol. 1999;49:432–438. doi: 10.1007/pl00006566. [DOI] [PubMed] [Google Scholar]
- 6.Huerta A M, Salgado H, Thieffry D, Collado-Vides J. Nucleic Acids Res. 1998;26:55–59. doi: 10.1093/nar/26.1.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Salgado H, Santos A, Garza-Ramos U, van Helden J, Diaz E, Collado-Vides J. Nucleic Acids Res. 1999;27:59–60. doi: 10.1093/nar/27.1.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Riley M. Microbiol Rev. 1993;57:862–952. doi: 10.1128/mr.57.4.862-952.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Riley M, Labedan B. In: Escherichia coli and Salmonella: Cellular and Molecular Biology. Neidhardt F N, Curtiss R I, Lin E C C, Ingraham J L, Low K B, Magasanik B, Resnikoff W, Riley M, Schaechter M, Umbarger E, editors. Washington, DC: Am. Soc. Microbiol.; 1996. pp. 2118–2202. [Google Scholar]
- 10.Karp P D, Riley M, Paley S M, Pellegrini-Toole A, Krummenacker M. Nucleic Acids Res. 1999;27:55–58. doi: 10.1093/nar/27.1.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Riley M. Nucleic Acids Res. 1998;26:54. doi: 10.1093/nar/26.1.54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Blattner F R, Plunkett G, 3rd, Bloch C A, Perna N T, Burland V, Riley M, Collado–Vides J, Glasner J D, Rode C K, Mayhew G F, et al. Science. 1997;277:1453–1474. doi: 10.1126/science.277.5331.1453. [DOI] [PubMed] [Google Scholar]
- 13.Wall L, Christiansen T, Schwartz R L. Programming Perl. Sebastopol, CA: O'Reilly and Associates; 1996. [Google Scholar]
- 14.Schneider E, Blundell M, Kennell D. Mol Gen Genet. 1978;160:121–129. doi: 10.1007/BF00267473. [DOI] [PubMed] [Google Scholar]
- 15.Jacob F, Monod J. J Mol Biol. 1961;3:318–356. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
- 16.Hesslinger C, Fairhurst S A, Sawers G. Mol Microbiol. 1998;27:477–492. doi: 10.1046/j.1365-2958.1998.00696.x. [DOI] [PubMed] [Google Scholar]
- 17.Rosenblueth D A, Thieffry D, Huerta A M, Salgado H, Collado–Vides J. Comput Appl Biosci. 1996;12:415–422. doi: 10.1093/bioinformatics/12.5.415. [DOI] [PubMed] [Google Scholar]
- 18.Thieffry D, Salgado H, Huerta A M, Collado–Vides J. Bioinformatics. 1998;14:391–400. doi: 10.1093/bioinformatics/14.5.391. [DOI] [PubMed] [Google Scholar]
- 19.Robison K, McGuire A M, Church G M. J Mol Biol. 1998;284:241–254. doi: 10.1006/jmbi.1998.2160. [DOI] [PubMed] [Google Scholar]
- 20.Hayes W S, Borodovsky M. Pac. Symp. Biocomput. 1998. 279–290. [PubMed] [Google Scholar]
- 21.d'Aubenton Carafa Y, Brody E, Thermes C. J Mol Biol. 1990;216:835–858. doi: 10.1016/s0022-2836(99)80005-9. [DOI] [PubMed] [Google Scholar]
- 22.Richmond C S, Glasner J D, Mau R, Jin H, Blattner F R. Nucleic Acids Res. 1999;27:3821–3835. doi: 10.1093/nar/27.19.3821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tao H, Bausch C, Richmond C, Blattner F R, Conway T. J Bacteriol. 1999;181:6425–6440. doi: 10.1128/jb.181.20.6425-6440.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhang L, Godzik A, Skolnick J, Fetrow J S. Folding Des. 1998;3:535–548. doi: 10.1016/s1359-0278(98)00069-8. [DOI] [PubMed] [Google Scholar]
- 25.Zhang B, Rychlewski L, Pawlowski K, Fetrow J S, Skolnick J, Godzik A. Protein Sci. 1999;8:1104–1115. doi: 10.1110/ps.8.5.1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rychlewski L, Zhang B, Godzik A. Protein Sci. 1999;8:614–624. doi: 10.1110/ps.8.3.614. [DOI] [PMC free article] [PubMed] [Google Scholar]