Fine structure of neural spiking and synchronization in the presence of conduction delays

Abstract

Hippocampal networks of excitatory and inhibitory neurons that produce γ-frequency rhythms display behavior in which the inhibitory cells produce spike doublets when there is strong stimulation at separated sites. It has been suggested that the doublets play a key role in the ability to synchronize over a distance. Here we analyze the mechanisms by which timing in the spike doublet can affect the synchronization process. The analysis describes two independent effects: one comes from the timing of excitation from separated local circuits to an inhibitory cell, and the other comes from the timing of inhibition from separated local circuits to an excitatory cell. We show that a network with both of these effects has different synchronization properties than a network with either excitatory or inhibitory type of coupling alone, and we give a rationale for the shorter space scales associated with inhibitory interactions.

When neurons communicate over some distance, there are conduction delays between the firing of the presynaptic neuron and the receipt of the signal at the postsynaptic cell. It is also known that cells can synchronize over distances of at least several millimeters, over which conduction delays can be significant. This raises the question of how cells can synchronize in spite of the delays. Traub et al. (1) and Whittington et al. (2) suggested that the fine structure of the spiking of some of the cells may play a part in the synchronization process for the γ frequency rhythm, found in hippocampal and neocortical systems during states of sensory stimulation. (For references, see ref. 2.) More specifically, for some models of cortical structure, they noted that the ability to synchronize in the presence of delays is correlated with the appearance of spike doublets in the inhibitory cells. The doublets appear in slice preparations when there is strong stimulation at separated sites (1, 2). In this paper, we analyze a mechanism for such synchronization, using a simplified version of equations of Traub and colleagues.

The timing of spikes within a doublet is shown to encode information about phases of local circuits in a previous cycle; the model shows how the circuit can use this information in an automatic way to bring nonsynchronous local circuits closer to synchrony. There are two independent effects in the model. The first is the response of the inhibitory (I) cells to excitation from more than one local circuit. The I-cells may produce more than one spike, whose relative timing depends on strength of excitation and recovery properties of the cell after the firing of a first spike; the latter can include effects of after-hyperpolarization or self-inhibition in a local circuit. The second effect is the response of the excitatory (E) cells to the multiple inhibitory spikes they receive from within their local circuit or other circuits. The maximal inhibition received by an E-cell can depend on the times and sizes of the inhibitory postsynaptic potentials it receives, and this affects the time until the E-cell can spike again. We show that each of the two effects is enough to allow synchronization. Together, they give the network synchronization properties that are not intuitively clear from the properties of either alone.

Previous papers have analyzed mechanisms for synchronization depending on interactions among I-cells (3–6) or E-cells (5–10). In this paper, the interactions between the local circuits include E → I and I → E. We omit the E → E connections, which are sparse in the CA1 region of the hippocampus (11), and consider only those I → I connections that are sufficiently local to be considered part of a local circuit. By considering networks with a subset of these connections, we shed light on the role of each of them in the synchronization process. In particular, we show that the different kinds of coupling work together to provide synchrony over a larger range of delays than either could do alone, and that the interaction provides a significant increase in the speed of synchronization. The I → E coupling also helps provide robustness to disruption from larger excitatory conductances, but it reduces robustness to heterogeneity. The two effects together give a rationale for the shorter space scales of the inhibitory interactions. (See Discussion.)

Our analysis considers a pair of local circuits, each having one E-cell and one I-cell; each cell represents populations of neurons. We reduce the biophysical equations for the network to a map that takes the interspike interval of the two excitatory cells to a new interspike interval after one cycle. The map does not depend on the details of the biophysical equations. (In the motivating equations in the Appendix, each cell has basic Hodgkin–Huxley-like spiking currents.) The map is derived from two subsidiary maps that encode the times that an inhibitory cell or an excitatory cell fires after receiving inputs at two different times as a function of the time difference between the inputs. From these maps, we are able to read off information about how different kinds of coupling affect stability of the synchronized state, the period of the synchronized solution, the rate of synchronization, and the response of the network to heterogeneity of the cells.

The importance of multiple spikes in the synchronization process distinguishes the mechanisms of this paper from other mechanisms of synchronization that deal with the envelope of bursting activity (3, 9) or single pulses (5–8). Indeed, the significance of the timing of individual spikes provides a new aspect of “temporal coding”; the spikes encode information about the synchronization process, rather than information directly related to sensory inputs.

Biophysical Assumptions and Reduction to Map

In the parameter ranges we use, an isolated E-cell spikes tonically. The I-cell population of a local circuit can be modeled either as excitable (does not fire without input) or tonically firing, and receiving self-inhibition (which can come from other cells of this population). In either case, the I-cell is of “type 1” (8, 12). For an excitable cell, this means that, as the cell receives increasing amounts of depolarized injected current, it becomes oscillatory through a saddle-node bifurcation. That is, the onset of repetitive firing can occur at arbitrarily low frequencies. For a tonically firing cell, it ceases oscillations with sufficient hyperpolarizing current, again through oscillations of arbitrarily low frequency. Type 1 neurons have an arbitrarily long latency to firing after stimulation.

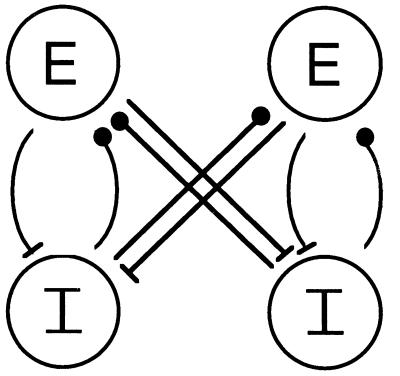
In each local circuit there is an excitatory synapse from E to I and an inhibitory synapse from I to E (see Fig. 1 and Appendix). The parameters of the synapses are chosen so that the local circuit has the following properties:

Figure 1.

Network of two coupled local circuits, each with one E and one I cell.

H1. A firing of the E-cell elicits exactly one pulse from the I-cell, providing that the latter has not fired very recently—i.e., is not in a refractory state. [This hypothesis can fail to hold if the E → I conductance is too large or takes too long to decay; in that case, a single E-cell impulse can elicit multiple I-cell spikes. We note that excitatory postsynaptic potentials to I-cells in CA1 decay quickly (13).] The time between the receipt of an excitatory pulse and the response of the I-cell depends (among other things) on the strength of the E → I connection, decreasing with increasing strength of that synapse.

H2. The E–I circuit is an oscillator: With no further input, the circuit displays a periodic rhythm, with one spike for each cell on each cycle. The period of this oscillation is determined mainly by the decay time of the I → E conductance, which is long relative to the recovery time of the I-cell, and which governs the time at which the E-cell fires after the receipt of an I-pulse. (In this parameter regime, the onsets of the E → I and I → E conductances are sufficiently fast that inhibition to the E-cell arising from a single spike of that cell prevents the occurrence of the next spike until the inhibition wears off. With other choices of time constants, it is possible to get more complicated dynamics, including bursting.)

The local circuits are coupled by adding an excitatory current to the I-cell and an inhibitory current to the E-cell, each gated by the voltage of the E-cell or the I-cell of the other circuit (Fig. 1; see Appendix). We will refer to cells of the circuit we are focusing on as the “internal” E-cell or I-cell, and the cells of the other circuit as the “external” cells. There is a conduction delay δ in each synapse between local circuits, which is taken to be fixed. If there is an absolute refractory period for the I-cell, we assume that it is smaller than δ; hence a pulse from the external E-cell spiking at the same time as the internal E-cell can (after the conduction delay) elicit a response from the internal I-cell. The value of δ is chosen small enough that the inhibitory pulse from the external I-cell in a given cycle arrives before the internal E-cell has fully recovered from the internal inhibition.

We take the spikes of each cell to be thin, so their times can be specified. The independent variable of our map will be the time between the firings of the two E-cells in a given cycle; the map produces this time on the next cycle. Synchrony corresponds to a fixed point at a time difference of zero. We assume that the system is close to synchrony; we can then use the maps to see if the dynamics brings the system closer to synchrony or further away. When the system is sufficiently close to synchrony, each E-cell fires one pulse per cycle (with further pulses halted by the inhibition), and each I-cell fires two pulses (one each in response to excitation from the external and internal E-cells).

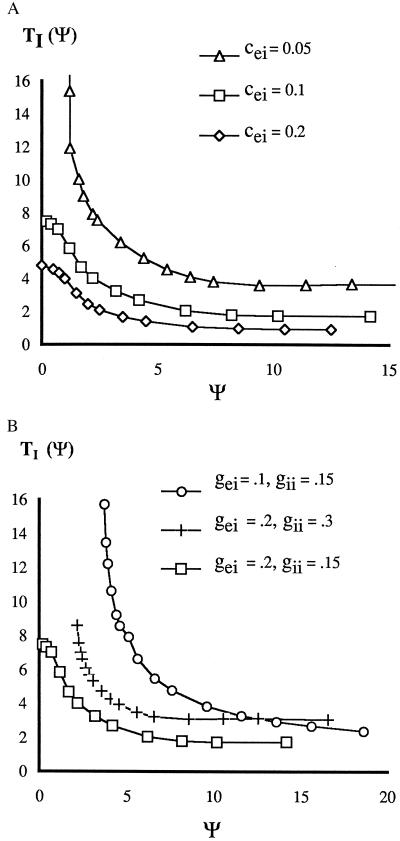
We use two preliminary maps to consider separately the effects of the response of the I-cell and that of the E-cell to their inputs. We start with T_I, which encodes the effects of the excitation to the internal I-cell from the internal and external E-cell. (If it also gets self-inhibition, we consider this to be a part of the definition of the intrinsic dynamics of the I-cell.) Let ψ be the time between the receipt by an I-cell of the excitatory pulses from the internal and external E-cells. We let T_I(ψ) be the time after the second excitatory input at which the (internal) I-cell fires next. T_I(ψ) depends on the parameters of the I-cell and the strength of the synapses onto the cell. Fig. 2A shows the dependence of T_I(ψ) on the strength c_ei of the intercircuit E → I coupling. For weak E → I coupling between circuits, the height and slope of T_I function can be arbitrarily large for small ψ, corresponding to arbitrarily long latency to firing. For sufficiently weak coupling from E → I cells, there is an absolute refractory period ψ₀ before which the I-cell will not respond to the second pulse. Increasing the self-inhibition g_ii in a local circuit introduces an absolute refractory period or increases its size. Decreasing the internal E → I coupling g_ei has a qualitatively similar effect (Fig. 2B).

Figure 2.

Latency to firing of I-cell after last received E-pulse. (A) Dependence on maximal excitatory conductance c_ei between circuits; g_ii = 0.15, g_ei = 0.2. (B) Dependence on inputs g_ei and g_ii to I cell within a circuit; c_ei = 0.1.

The map T_E encodes the effects of the timing of the inputs into the internal E-cell. Near synchrony, each I-cell displays a doublet, because of its response to the internal and external E-cells. Thus, each E-cell receives four inhibitory pulses, two each from each of the I-cells. T_E is the time after the receipt of the last pulse at which the E-cell fires next.

Let E_int, I_int denote the E- and I-cells of the internal circuit, and E_ext, I_ext those of the other circuit. Let t₁ and t₂ denote the times that the internal and external E-cells fire in some cycle. Let Δ = t₂ − t₁. Let t_ei denote the time after the E-cell fires that the I-cell of the same circuit fires, assuming no other input. (If the I-cell is modeled as an excitable cell, t_ei is the time it fires after excitation when it is fully recovered.) In terms of the map T_I, the four inhibitory pulses from I_int and I_ext are received at E_int at the following four times, with the following four paths:

1. E_int → I_int → E_int. Arrives at t₁ + t_ei.

2. E_ext → I_ext → E_int. Arrives at t₂ + t_ei + δ.

3. E_ext → I_int → E_int. Arrives at t₂ + δ + T_I(Δ + δ).

4.  E_int → I_ext → E_int. This pulse is sent from I_ext at t₁ + δ + T_I(−Δ + δ) and arrives at E_int at t₁ + 2δ + T_I(−Δ + δ).

We shall make the approximation that the effect of the first two spikes on T_E is much less important than that of the final two, and focus only on the latter. This approximation is valid because the inhibitory synapses are close to saturation after one spike. Thus, the third spike of inhibition wipes out the information from the first (both coming from the same cell), and the fourth spike does the same for spike two. Recall that T_I encodes the extra time due to partial refractoriness that an I-cell takes to fire after receiving a second pulse. Hence T_I ≥ t_ei, so that pulses 3 and 4 are the last two to arrive at E_int.

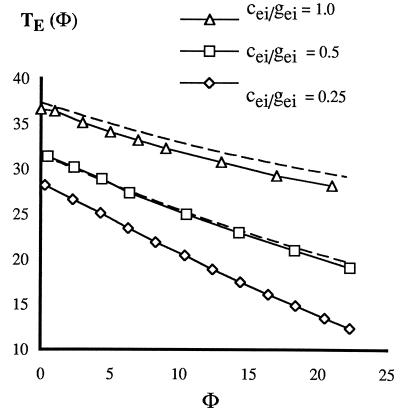
We let φ be the time between the last two spikes, so T_E = T_E(φ). T_E is defined for all φ and is a decreasing function of φ (Fig. 3). It is possible to get an analytic formula that approximates T_E and that displays its dependence on inhibitory decay time, τ, and the strength of the external and internal inhibitory synapses, as follows. The inhibitory conductance felt by the E-cell is c_iee^−t/τ + g_iee^−(t+φ)/τ, where g_ie is the conductance from the internal cell, which fires first, and c_ie is the conductance from the external one. When this quantity falls below a critical value g*, the E-cell can fire. We can get a formula for g* by noting that, if the inhibition comes only from within a circuit, the time at which the E-cell is released to fire is t_p − t_ei, where t_p is the period of the uncoupled circuit. Thus g* = g_ieexp(−t_p + t_ei). With the inhibition from both circuits, the inhibitory conductance reaches g* when t equals

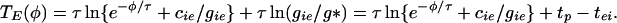1

Note that T′_E < 0 and that T_E is essentially independent of φ for large φ. Fig. 3 shows that formula 1 gives an excellent fit to the map T_E measured directly by numerically integrating the equations in the Appendix.

Figure 3.

Latency to firing of E-cell after last received I-pulse. Discrete data points are computed from equations in Appendix. The three graphs correspond (top to bottom) to c_ei/g_ei = 1.0, 0.5, 0.25. Dashed lines for the top two are computed from formula 1 with τ = 20, t_p = 25, t_ei = 1.5.

We can now specify the time t̄₁, t̄₂ at which the E_int and E_ext cells fire in the next cycle.

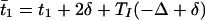2

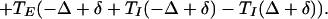A similar formula holds for E_ext with indices 1 and 2 reversed and Δ changed to −Δ. Therefore, the difference G_δ(Δ) of the time of firing of the two E-cells at the next cycle is

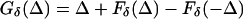3

where

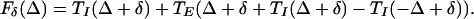4

Stability of the Synchronous Solution

Full Network.

There is a locked solution at lag Δ if G_δ(Δ) = Δ, and synchrony if Δ = 0. The synchronous solution is stable if |G′_δ(0)| < 1. From formula 3, this means that synchrony is stable if −1 < F′_δ(0) < 0. From formula 4,

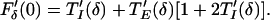5

From expression 5 we can see how the properties of the circuit affect the stability of the synchronous state. The slope of T_I can be arbitrarily large when the argument of T_I is small (as happens when the E → I coupling is weak). Thus, the analysis predicts that stability of the synchronous solution could fail for δ too small, with the stability boundary occurring for larger values of δ when the coupling is decreased.

The effect of coupling strength on the range of delays yielding synchrony was supported by simulations of the full voltage-gated equations in the Appendix. For medium coupling (c_ei = 0.1 in Fig. 2A), the slope of T_I is gentle for small values of the argument, and synchrony is stable for δ = 5. Changing c_ei to 0.05 leads to higher value of T′_I at that δ, and the analysis predicts instability, confirmed by simulation. Keeping c_ei fixed at 0.05 and increasing δ to 10, the slope of T_I decreases to where synchrony is predicted to be stable, again confirmed by simulations. In these simulations, only the external coupling is changed. Changing the internal E → I coupling has effects consistent with the changes in T_I shown in Fig. 2B. We also note that for those graphs T_I without an absolute refractory period, the slope of T_I can also be small at δ = 0. For those values of the parameter, the analysis and simulations yield stability even if there is no delay.

The I → E coupling encoded in the map T_E has a modulating effect on the synchronization process, allowing synchrony when the E → I coupling alone (encoded in T_I) would not. It is easy to check from formula 1 that −1 < T′_E(0) < 0. Thus, for a value of δ at which T′_I(δ) = −1, the value of F′_δ(0) satisfies F′_δ = −1 − T′_E(δ) > −1. Hence, stability can be attained for a larger range of δ, notably for smaller values of δ than before. This effect was checked by simulation; it was found that for parameter value c_ei = 0.1, stability can be attained for δ = 2 while T′_I(2) < −1 (Fig. 2).

Network Without I to E Coupling Between Circuits.

For such a connectivity, each E-cell gets inhibition only from the I-cell of its own circuit, and hence (near synchrony) receives two pulses of inhibition, not four. The two inputs are from spikes 1 and 3 as above, both from the internal I-cell. A variation on the above analysis can be performed to see the consequences of this change. We let T_I be the same map as before. Now φ is the time between these two inhibitory spikes, and T̄_E(φ) is the time after the second spike that E_int fires. Note that T̄_E codes how the E-cell responds to two inputs from its own local circuit.

As before, let t₁ and t₂ be the times of firing of the two E-cells in a given cycle and Δ = t₂ − t₁. Thus φ = Δ + δ − t_ei + T_I(Δ + δ). The E-cell of local circuit 1 then fires at

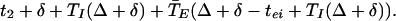6

and similarly for circuit 2. Let Ḡ_δ(Δ) be the difference in the timing of the two E-cells at the next cycle. By formula 6

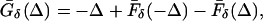7

where

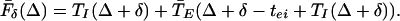8

From formulas 7 and 8, we can compare the stabilization properties of this reduced network with that of the full one. Synchrony is stable if |Ḡ′_δ(0)| < 1, i.e., −1 < F̄′_δ < 0, where

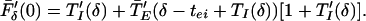9

If T′_I(δ) = −1, then F̄′_δ(0) = −1. Thus the reaction of the E-cell to the timing of the two spikes from the internal I-cell does not affect the range of delays for which synchrony is stable. This contrasts with the full network, in which the timing of the I-spikes provide an additional synchronizing mechanism, discussed in the previous section. We note that if the I → E synapse saturates after one spike, the map T̄_E is a constant. In the full network, the spikes whose times being compared come from different cells, and are therefore not subject to synaptic saturation effects.

The slope of T′_I(δ) can be very negative (Fig. 2A), and F̄′(0) is not modified much from that value by the effects of the E-cell response. When a map has a large slope at a fixed point, standard analyses show that behavior near that point is apt to be complicated—e.g., there are solutions with high period or aperiodic solutions (14). In simulations with no I → E coupling such complicated solutions were found in the parameter ranges in which T′_I(δ) is more negative than −1.

Network Without E → I Coupling Between Circuits.

In this network, each E-cell gets inhibition from the I-cells of both circuits, but the I-cell gets excitation only from its own E-cell. Thus, there are no doublets. We again let t₁ and t₂ denote the firing times of the E-cells, φ the time between the receipt of the two spikes at the E-cell, and T_E(φ) the time after the receipt of the second spike that the E-cell fires. We let t̄₁ and t̄₂ be the times at which the E-cells fire in the next cycle. Then

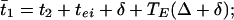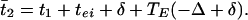10

Thus, we get t̄₂ − t̄₁ = H_δ(Δ), where

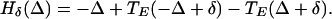11

Stability of the synchronous solution is determined by H′_δ(0), which satisfies

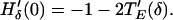12

Because −1 < T′_E < 0, the synchronous solution is always stable.

This is not the only stable fixed point, however. One can look for an antiphase solution by using the first half of expression 10 to get the time of firing of E₁ after E₂ fires. The next time for firing for E₂ is then given by the second equation of 10, with t₁ replaced by t̄₁ and −Δ by t̄₁ − t₂. Inserting the equation for t̄₁ into that for t̄₂ and subtracting the equation for t̄₁, we get that t̄₂ − t̄₁ = A(Δ) where

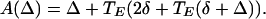13

The antiphase solution is a fixed point Δ ≠ 0 of formula 13. Because −1 < T′_E < 0, it follows that 0 < A′(Δ) < 1, so the antiphase solution is always stable. There can be a significantly large domain of attraction for the antiphase solution. Simulations show that there are initial conditions for which, with no E → I coupling, at δ = 5 the solution goes to antiphase; when the E → I coupling is added (c_ei = 0.1) the same initial conditions lead to stable synchrony.

Network Properties

Period of the Synchronous Solution.

For the network that has both E → I and I → E coupling, the period P of the synchronous solution can be deduced from formula 2 by setting Δ = 0 and subtracting t₁ to get

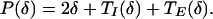14

For the network with only E → I coupling, the period is deduced from formula 6 and is

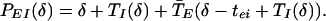15

The last term is almost constant, especially if the I → E synapse within a local circuit is close to saturation. For the network with only I → E coupling between circuits, the period comes from formula 10:

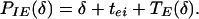16

Note that formula 14 is larger than either formula 15 or formula 16 and depends more on δ. The larger period for the fully coupled network is confirmed by simulations. One implication of this is that a fixed time lag between circuits corresponds to a smaller phase lag (fraction of period) for the fully coupled system than for either of the partially coupled ones. For larger E → I coupling, the period decreases. The periods 14–16 are also larger than the period t_p of the uncoupled circuit (with no doublets), partly because of the conduction delay δ, but also because the times T_E(δ) and T_I(δ) can be large for small δ. That the period of a coupled circuit is larger than the period of an uncoupled local circuit matches the experimental and numerical results in refs. 2, 15, and 16. The period of any of the coupled networks differs substantially from that of a network of only inhibitory neurons, whose period is determined mainly by the decay rate of the inhibition (16–19). The effect of the latter on T_E is seen in formula 1.

Rate of Synchronization.

Near synchrony, the rate of synchronization of a map Δ_t+1 = G(Δ_t) with stable fixed point Δ = 0 is governed by the size of |G′(0)|; the fastest rate occurs if G′(0) = 0, and the slowest as |G′(0)| → 1. From Eqs. 3 and 7 we see that the maximal rate occurs for F′_δ = −1/2 and F̄′_δ = −1/2 for the equations of the preceding two sections. From Eq. 5, we see that the response of the E-cell exerts a positive influence on the rate of synchronization in the two domains in which the rate would be small if there were only E → I intercircuit coupling. For small values of δ, −1 < T′_E < −1/2, depending on the size of c_ie/g_ie. With c_ie/g_ie ≈ 1, we have T′_E ≈ −1/2. Then from Eq. 5, F′_δ(0) ≈ −1/2, the optimal value for quick synchrony over a range of δ. For δ, large T′_I is small in a range where T′_E is still significant, thus helping with the synchrony (see Figs. 2 and 3). For the equations without I → E coupling, the T̄_E map does not have this effect, because T̄′_E in Eq. 9 is uniformly small.

Response to Heterogeneity.

The local circuits in a network need not be identical, and the coupling need not be exactly symmetrical. If so, exact synchrony is not a solution. Instead, one may ask how large is the deviation from synchrony for a given amount of heterogeneity, and how much heterogeneity can the network tolerate without loss of locking. The analysis of the preceding section enables us to address the first question; the second we comment on by using simulations.

The analysis of the effects of heterogeneity is independent of the kind of heterogeneity. Any asymmetry as above shows up in the equations as a difference between the maps F_δ(Δ) associated to the two circuits. Thus Eq. 3 is replaced by

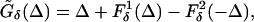17

where F_δⁱ(Δ) is approximately F_δ(Δ). Linearizing Eq. 17, the right-hand side is approximately Δ + [F_δ¹(0) − F_δ²(0)] + 2F′_δ(0)Δ. Let ɛ = [F_δ¹(0) − F_δ²(0)]. Then the fixed point, satisfying G̃_δ(Δ) = Δ, is given approximately by Δ = −ɛ/2F′_δ(0). For c_ie/g_ie = 1, T′_E(δ) ≈ −1/2 for small δ (see formula 1 or Fig. 3) and so Δ ≈ ɛ. But if c_ie/g_ie is small, then T′_E ≈ −1. Hence (from formula 5) near the stability boundary T′₁(δ) ≈ −1, F′_δ(0) is small, yielding large Δ. Thus, for small delays, it is important that the external and internal coupling strengths be comparable in size.

If there is no I to E coupling, the map with heterogeneity is a variation of formula 7, namely

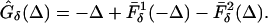18

If ɛ is now = [F̄_δ¹(0) − F̄_δ²(0)], then the linearization gives a fixed point at Δ = ɛ/2[F̄′_δ(0) + 1]. In this analysis, Δ/ɛ can be changed by scaling the variables. However, the ratio |F′_δ(0)/[F̄′_δ(0) + 1]| of the effect of heterogeneity in the network with only I → E coupling to that in the full network is independent of choices of variables. The smaller this number, the more the advantage of the reduced network in producing smaller time lags for the same heterogeneity. For δ large enough so that T′_I is ignorable (e.g., δ ≥ 6 ms) it follows from expressions 5 and 9 that this ratio is ≈|T′_E|. For c_ie = g_ie, |T′_E(δ)| ≈ e^−δ/τ[e^−δ/τ + 1], which is ≈1/2 for δ small and smaller as δ increases; this shows that the time lags for the full network are more than twice as long as for the network with no I → E coupling. The analysis is confirmed by simulations with heterogeneities up to 15% in the intrinsic frequency of the oscillators. For heterogeneities of 20% or more, synchrony can be lost, and one gets more complicated dynamics and/or suppression (20). We note that networks with I → I coupling alone have been reported to be much less robust to heterogeneity (17, 20).

Variations

Two Local Circuits, More I-Spikes per Cycle.

In the previous analysis, the reduction to the map assumed that, in each cycle, each I-cell and each E-cell produces exactly one spike in the absence of coupling between circuits. This assumption fails if the E → I coupling conductance is sufficiently increased. Simulations were done with a conductance large enough to produce a double spike in an I-cell from one excitatory postsynaptic potential. In the network with both E → I and I → E intercircuit coupling, the trajectories of the I-cells contained doublets, triplets, or even higher numbers of spikes, but the E-cells of the two networks continue to synchronize well, even in the presence of moderate heterogeneity. In the network with no I → E intercircuit coupling, the extra I-spikes disrupted synchronization. We noted that persistence of the synchronization (in the fully coupled case) occurred when the last two inhibitory postsynaptic potentials to arrive at an E-cell were from different I-cells, and in the order required by the analysis in the section on stability. (See ref. 21 for related work.)

More than Two Local Circuits.

The previous analysis dealt with just two circuits, but the effects are seen in larger arrays of local circuits as well. Simulations with arrays of five local circuits produce synchrony when the connections at the edges are modified as in ref. 1 to reflect the extra density of connections at the edges of the CA1 slice (R. Traub, personal communication).

Discussion

It has been suggested that γ-range rhythms have behavioral significance for complex motor acts (22) and sensory processing (23). The current work shows that the timing of spikes within a doublet or burst can be of major importance in the synchronization process. It helps to determine the time it takes the E-cell to overcome the inhibition. In turn, the time between the spiking of the E-cells in a given cycle determines the timing of the spikes in the next doublet.

It should be noted that it is not the doublet per se that encourages the synchronization. Rather, what is important is that the two spikes of the doublet occur in response to excitation from different local circuits. If a doublet is produced by a strong E → I synapse within a local circuit, it will not contribute to synchrony unless there is also a response from the excitation of the E-cell in the other circuit. The simulations of refs. 1 and 2 did not distinguish between these effects, but such a distinction can be made using the analytical models.

As shown above, the analytical models capture very precisely the behavior of the full biophysically based equations. There are many parameters even in the two-circuit network, and it is difficult to see from simulations alone how and why changes in some of these affect the synchronization process. The analysis provides a framework for dissecting out these effects; it shows that the behavior of the network can be understood once one has the functions T_E and T_I. Thus, the network effects of changing parameters can be understood by seeing how those parameters change the maps T_E and T_I. Using the maps, one sees many ways in which the synchronization process may be modulated to produce stable synchrony or nonsynchronous behavior.

The analysis showed that the different kinds of connections (I → E and E → I) between circuits have different synchronization properties. The two-circuit network that contains both synchronizes over a larger range of conduction delays than the network with just E → I, whereas the network with just I → E can also form stable anti-phase solutions. Thus, for synchrony in a homogeneous network, the network with both sets of connections is most robust. We have also shown that the addition of I → E connections enhances the rate of synchronization over the network with only E → I connections, and makes the network more stable to potentially desynchronizing large E → I conductances.

In a network whose local circuits are not identical, or whose coupling is not symmetric, full connectivity is not optimal, in some parameter ranges, for providing stable solutions with small time lags. If δ is relatively large, the network with both E → I and I → E connections can produce large lags; by contrast, the network with only E → I connection was shown to produce a significantly more synchronous solution for a given amount of heterogeneity.

The above results may help us to understand some of the spatial scales in cortical networks. In CA1, the excitatory pyramidal cells have axons that extend approximately 3 mm (24). Interneurons of the hippocampus, including chandelier, basket, and bistratified cells, have spatial scales about 1 mm or smaller (25). Within this smaller distance, the I → E connection can help to synchronize the local circuits that have small conduction delays between them and buffer the synchronization process against a larger set of excitatory inputs. At larger distances, with longer conduction delays, the I → E connection can become a liability when there is heterogeneity in the network.

The two-circuit problem, or even its generalization to a chain of N circuits, is still a major idealization of a network that is more of a continuum, without discrete local circuits. Simulations of networks in which the connections extend over many cells in a continuum-like manner have been done (R. Traub, personal communication), and both doublets and synchronization have been found. In addition, a more faithful network architecture would also include I → I coupling among circuits, which is critical for synchrony in the absence of phasic excitatory input to the interneurons (3–7, 16, 17, 20, 21). With many different subclasses of interneurons (25), it is likely that effects of such neurons can be felt at different space scales, providing additional mechanisms for modulating network behavior. Furthermore, the synchronization process may be influenced by thalamocortical interactions (26). The current study provides some of the building blocks for a more inclusive analysis.

ABBREVIATIONS

I-cells

inhibitory cells

E-cells

excitatory cells

Appendix

The equations for each cell are obtained from a reduction of the model of Traub and Miles for spiking (27). (The results are the same without the reduction.) The equations are

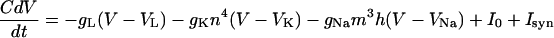with ion channels for leak, sodium, and delayed rectifier potassium. Here m = m_∞(V) = a_m(V)/[a_m(V) + b_m(V)] where a_m(V) = 0.32(54 + V)/(1 − exp[−(V + 54)/4]) and b_m(V) = 0.28(V + 27)/(exp[(V+27)/5 − 1]). The K-gate n(t) satisfies dn/dt = a_n(V)(1 − n) − b_n(V), with a_n(V) = 0.032(V + 52)/[1 − exp(−(V + 52)/5)] and b_n(V) = 0.5exp[−(57 + V)/40]. A reduction to a two-dimensional equation is obtained (28) by setting h = max(1 − 1.25n, 0). Parameter values are C = 1, g_L = 0.1, V_L = −0.67, g_Na = 100, V_Na = 50, g_K = 80, V_k = −100, I₀ = 0.5 for the I cells and I₀ = 8 for the E cells. C is measured in μF/cm², conductances in mS/cm², currents in mA/cm², voltages in mV, and time in ms.

Each synaptic current has the form g_syns(t − δ)(V − V_syn). Here g_syn = g_ii, g_ie, g_ei, c_ie, or c_ei. The subscripts denote the source and target of the synapse, the gs denote conductance within a circuit, and the cs denote conductance between the circuits, g_ii = 0.15 or 0.3, g_ei = 0.2, g_ie = 2. c_ei and c_ie were varied. δ = 0 for synapses within a local circuit. s satisfies ds/dt = AS(V̂)(1 − s) − Bs, where S(V̂) = 1 + tanh(V̂/4) and V̂ is the presynaptic voltage. For excitatory synapses, A = 20 ms⁻¹, B = 0.333 ms⁻¹, V_syn = 0; for inhibitory synapses, A = 1 ms⁻¹, B = 0.05 ms⁻¹, V_syn = −80 mV.

The maps are computed by driving a two-cell oscillating E–I circuit with another one that is at rest and stimulated at different times to elicit a spike. All simulations were done using G.B.E.’s package, XPPAUT, available from ftp://ftp.math.pitt.edu/pub/bardware. The usual method of integration is a Gear-type integrator adapted for use with delay equations. All equation files are available from G.B.E. upon request.