Expanding clinical applications of population pharmacodynamic modelling

Abstract

Population pharmacokinetics or pharmacodynamics is the study of the variability in drug concentration or pharmacological effect between individuals when standard dosage regimens are administered. We provide an overview of pharmacokinetic models, pharmacodynamic models, population models and residual error models. We outline how population modelling approaches seek to explain interpatient variability with covariate analysis, and, in some approaches, to characterize the unexplained interindividual variability. The interpretation of the results of population modelling approaches is facilitated by shifting the emphasis from the perspective of the modeller to the perspective of the clinician. Both the explained and unexplained interpatient variability should be presented in terms of their impact on the dose–response relationship. Clinically relevant questions relating to the explained and unexplained variability in the population can be posed to the model, and confidence intervals can be obtained for the fraction of the population that is estimated to fall within a specific therapeutic range given a certain dosing regimen. Such forecasting can be used to develop optimal initial dosing guidelines. The development of population models (with random effects) permits the application of Bayes’s formula to obtain improved estimates of an individual’s pharmacokinetic and pharmacodynamic parameters in the light of observed responses. An important challenge to clinical pharmacology is to identify the drugs that might benefit from such adaptive-control-with-feedback dosing strategies. Drugs used for life threatening diseases with a proven pharmacokinetic-pharmacodynamic relationship, a small therapeutic range, large interindividual variability, small interoccasion variability and severe adverse effects are likely to be good candidates. Rapidly evolving changes in health care economics and consumer expectations make it unlikely that traditional drug development approaches will succeed in the future. A shift away from the narrow focus on rejecting the null hypothesis towards a broader focus on seeking to understand the factors that influence the dose–response relationship—together with the development of the next generation of software based on population models—should permit a more efficient and rational drug development programme.

Introduction

A thorough understanding of pharmacokinetics and pharmacodynamics is the scientific foundation of clinical therapeutics. In practice, however, the selection of an appropriate dose of a drug is more often part of the art than of the science of medicine. Many analyses of dose–response data do not identify the minimum effective dose of a new drug, much less account for factors that contribute to interindividual variability in the dose–response relationship. Although population pharmacodynamic modelling methods have the potential to address these problems, the results of such analyses are often presented in a way that is difficult for most clinicians to interpret. It is therefore not surprising that population models are either viewed with considerable scepticism, or are disregarded as a form of statistical wizardry without clinical application.

Why should clinicians be interested in population pharmacokinetic and pharmacodynamic modelling? Aarons has defined population pharmacokinetics or pharmacodynamics as the study of the variability in drug concentration or pharmacological effect between individuals when standard dosage regimens are administered [1]. Clinicians are well aware of this variability in effect when a group of patients is given the same dose, and most would acknowledge that this occurs because of interindividual variability in both pharmacokinetic and pharmacodynamic factors. In contrast, few clinicians have an understanding of population pharmacodynamic modelling concepts. In the first half of this article, we provide an overview of pharmacokinetic models, pharmacodynamic models, population models and residual error models. We outline how the population modelling approaches seek to relate dose to effect, to explain some of the interpatient variability with covariate analysis, and, in some approaches, to characterize the unexplained interindividual variability. Those readers who are already familiar with these topics might wish to proceed immediately to the second section of this review, in which we consider how the clinical significance of the explained and unexplained variability can be better presented, and how population pharmacodynamic models can be applied to develop initial dosing guidelines, to adjust subsequent doses, and to improve the efficiency of the clinical drug development programme.

Pharmacokinetic models

A pharmacokinetic model describes the relationship between dose and concentrations in an individual. The structure of a pharmacokinetic model can be represented graphically by one or more boxes interconnected with arrows, which describe the rate of drug transfer between various hypothetical compartments. These models can be described mathematically by compartment volumes and clearances, rate constants, or parameters of a polyexponential equation. Although many drugs fulfill the criteria for simple one, two or three compartment models, additional complexities are frequently encountered. Following a thorough preliminary analysis of the data, an appropriate family of pharmacokinetic models is selected for evaluation. Then estimates of the pharmacokinetic parameters are obtained by fitting a model to the observed data using specialized computer software.

How useful is knowledge of these pharmacokinetic parameters to a clinician? Perhaps much less useful than we would like to believe. In the anaesthetic literature, it has been suggested that we should abandon drawing clinical conclusions from the half-lives of drugs described by multicompartment pharmacokinetic models and start thinking of recovery times using computer simulations of specific clinical scenarios [2]. Shafer & Stanski used computer simulations to illustrate that reasonable and sound clinical inferences (based on pharmacokinetic parameters) were actually totally wrong [2]. For drugs described by multicompartment pharmacokinetic models, calculation of intravenous loading doses based on the central volume of distribution (V₁ ) or the steady state volume of distribution (V_ss ) result in doses that would be judged either too small or too large by experienced clinicians [3]. In order to derive clinically useful dosing guidelines, pharmacokinetic models must be combined with pharmacodynamic models that are able to account for delays in the distribution of the drug from the plasma to its site of effect, or for delays associated with the kinetics of the physiological substances that mediate the effects of the drug.

Pharmacodynamic models

A pharmacodynamic model describes the relationship between concentration and effect in an individual. A common modelling approach is to relate a single measure of drug exposure (e.g. area under the concentration-time curve) to a single measure of drug effect (e.g. time to maximum effect). In contrast, we will focus on pharmacodynamic modelling approaches that relate the entire time course of drug concentration to the time course of drug effect. Renewed interest in the indirect nature of this relationship has been stimulated by Dayneka and colleagues’ presentation (Figure 1) of four basic models of indirect pharmacodynamic responses [4–8]. Sheiner & Verotta [7] describe a ‘general’ indirect response model linking drug concentration to effect, through an intermediate response variable (R), by means of a number of linear (L) or nonlinear (NL) functions, which may be either static (S) or dynamic (D). We have modified their equation to emphasize the link between dose (rather than concentration) to effect (Equation 1).

Figure 1.

Four basic physiologic indirect response models and differential equations describing input (k_in ) and output (k_out ) of factors controlling the response variable (R). Inhibition (IC₅₀ ) or stimulation (EC₅₀ and E_max ) of these factors occur in relation to plasma drug concentrations (C_p ). (Reprinted with permission from Dayneka et al., J Pharmacokinet Biopharm 1993; 21: 457–458[4].)

(1)

In this equation a linear function, f, is defined as one for which f (a+ b)=f (a)+f (b), and a static function as one that does not explicitly depend on time. Therefore, most pharmacokinetic models are linear dynamic (LD) functions, and the ‘E_max’ model [9] is a nonlinear static (NLS) function. This general scheme was depicted by Jusko and colleagues as shown in Figure 2 [8]. In general, a less complicated series of links adequately describes the temporal relationship between concentration and effect. For 20 years the ‘hypothetical effect compartment’ model [10–12] has been used extensively to account for the delay between drug concentration and drug effect. This model assumes that the rate of onset and offset of effect is governed by the rate of drug distribution to and from a hypothetical ‘effect site’. The effect compartment model can be viewed as a simplified instance of Equation 1, (Dose→LD→NLS→Effect), in which a linear dynamic function is used to calculate the ‘effect-site’ concentrations. These concentrations are then directly linked to the drug effect by means of a nonlinear static function (usually the ‘E_max’ model). For this reason the model is sometimes referred to as the ‘direct pharmacodynamic model’ or ‘link model.’ Some researchers have developed models to relate dose to effect without the need for concentration data [13–15].

Figure 2.

Conceptualization of multiple pharmacokinetic and pharmacodynamic determinants of drug action including distribution (rate constant, k_e0 ) to a biophase, inhibition or stimulation (H) of the production (k_in ) or removal (k_out ) of a mediator biosignal, and transduction of the response (R). (Reprinted with permission from Jusko et al., J Pharmacokinet Biopharm 1995; 23: 5–8.)

Several new and clinically helpful concepts have been derived from the effect compartment model. For instance, the apparent volume of distribution at the time of the peak effect site concentration (V_pe ) is calculated as the intravenous bolus dose divided by the plasma concentration at the time of the peak effect site concentration [16, 17]. Unlike loading dose calculations based on the central volume or the volume of distribution at steady state, calculations based on V_pe agree with doses used by experienced clinicians (Figure 3). Another new concept is the ‘context-sensitive half-time’ or ‘percentage decrement time’ [18, 19]. Computer simulations are used to show the time required for effect site concentrations to decrease by a specified percentage following infusions of different duration (Figure 4). Comparing pharmacokinetic parameters (e.g. half-lives) of different drugs will not predict the relative rates of decrease in effect site concentrations after either an intravenous bolus or a continuous infusion. In contrast, the rational selection of opioids used in anaesthesia has been facilitated by computer simulations based on the effect compartment model [19].

Figure 3.

Predicted plasma concentrations (solid line) and hypothetical effect-site (dashed line) concentrations following an intravenous bolus of 150 μg fentanyl (an opioid). The central volume of distribution (V₁ ) is calculated as the dose divided by the (predicted) plasma concentration at time zero. The volume of distribution at the time of peak effect (V_pe ) is calculated as the dose divided by the plasma concentration at the time of the peak effect site concentration. The desired effect in this example is associated with a steady state plasma concentration of 2 ng ml⁻¹. The calculated intravenous bolus dose based on V₁, V_ss and V_pe are approximately: 25 μg, 700 μg and 150 μg, respectively. The latter dose agrees with clinical practice.

Figure 4.

Simulated fentanyl plasma concentrations after steady state concentrations are maintained by a computer controlled infusion (a). The time taken for the concentration to fall by 50% is shown for a 60 min infusion (t₁ ) and for a 240 min infusion (t₂ ). Repeated simulations for infusions of varying duration are necessary to derive the 50% decrement time curve (b).

Although the hypothetical effect compartment model is often used to account for the time lag between concentration and effect, computer simulations have shown that in some cases the effect compartment model lacks parsimony, biological plausibility, and extrapolation capability [4]. Many drug responses may be considered indirect in nature, because the drug acts to stimulate or inhibit the production or loss of endogenous substances that mediate the drug effect. In these cases, indirect response models, represented by the NLS₁→R link in Equation 1, may be more appropriate. This type of model was first applied almost 30 years ago to account for the anticoagulant effects of warfarin [20, 21], and has since been used to model the effects of adrenal suppression from steroids [22–24], the cell trafficking effects of steroids [23, 25, 26], the antipyretic effects of ibuprofen [27], suppression of testosterone by the male hormonal contraceptive agent nandrolone [28] and the hypokalaemic effects of fenoterol [29]. Jusko & Ko have applied these models to published data for the muscular contraction from pyridostigmine, diuresis from frusemide, bronchodilation from terbutaline, prolactin secretion from cimetidine, and hypokalaemia from terbutaline [5]. Indirect response models are popular because they provide a reasonable description of the mechanism of action for many drugs. Chains of linear and nonlinear functions longer than Equation 1 are uncommon in the pharmacodynamic modelling literature [30]. However, the availability of concentration data for intermediary response variables (e.g. ‘R’ in Equation 1) permits a more realistic model to be developed, as demonstrated for the effect of the gonadotropin-releasing hormone antagonist antide on luteinising hormone and testosterone concentrations [31]. Unfortunately, physiological reality is often more complex than the ‘general’ indirect pharmacodynamic model (Equation 1). Additional factors that may have to be modelled include: placebo effects [32], tolerance effects [33–35], circadian rhythms [23, 31, 36], disease progression [37] and drug interactions [38].

Population models

All population analysis techniques attempt to account for the variation between individuals in terms of patient specific covariates such as age, weight, disease state, and concurrent therapy. However, even after the effects of patient covariates are considered, significant unexplained interindividual variability remains. For example, although the elderly are more sensitive to the effects of remifentanil (a new ester opioid), we still find variation in the sensitivity between individuals of the same age (Figure 5) [39]. Indeed, when the same individual is studied on different occasions, differences in pharmacokinetics and pharmacodynamic parameters are found; this is termed interoccasion variability [40]. Three approaches for determining population pharmacokinetic and pharmacodynamic model parameters are outlined below.

Figure 5.

The individual Bayesian estimates of the central volume of distribution (V₁ ), the metabolic clearance (CL₁ ), the half-time of equilibration between the blood and the effect site (t_1/2k_e0 ) and the concentration associated with 50% EEG effect (EC₅₀ ) of remifentanil. Each dot represents one patient. Some of the interindividual variability in model parameters is explained by the influence of age (lines). Considerable interindividual variability remains unexplained. (Adapted with permission from Minto et al., Anaesthesiology 1997; 86: 10–23 [39]).

Two stage approaches

The standard two stage approach can be used to determine population model parameters. In the first stage, parameter estimates are obtained for each individual, and in the second stage, the population parameter set is obtained by an average (or log-average) of the individual parameter estimates. This approach is only possible if there are sufficient data to estimate the model parameters for each individual, and if all data from each individual are described by the same structural model. An estimate of the covariance matrix describing the distribution of the parameters in the population can be obtained, although this is often not reported. The standard two stage approach has undergone several improvements, which acknowledge that the individual parameter estimates are imprecise [41].

Pooled approaches

The principal advantage of the (naive) pooled approach is its simplicity. This method involves pooling the data from all individuals to obtain an estimate of the population parameters. Although individual covariates and dosing information are taken into account, no attempt is made to characterize the distribution of the unexplained interindividual variability. Pharmacokinetic parameters estimated from balanced pharmacokinetic data using a pooled approach compared favourably with other methods [42, 43], and have performed excellently when tested prospectively [44–46]. However, the pooled approach is generally not a valid method for the analysis of pharmacodynamic data. A continuous measure of drug effect can often be described by the ‘E_max’ model. The parameter γ describes the slope of the concentration (C ) effect (E) relationship in an individual (Equation 2).

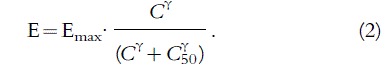(2)

The pooled approach cannot account for the fact that different patients have different C₅₀ values (the concentration at which the drug effect is 50%). Although the concentration response relationship may be quite steep in the individual, the pooled estimate of γ for the population will be much shallower (Figure 6), and will give a false sense of safety when treating the individual [41].

Figure 6.

Individual estimates of the concentration-response curves (dashed lines). The percentage response could represent the range between baseline and maximum effect for a continuous measure of effect or the probability of response for a binary measure of effect. The pooled estimate has a shallower slope (solid line).

Although the ideal measurement of drug effect is objective, noninvasive, continuous, repeatable and clinically relevant, many measures of drug effect do not meet these criteria. The most common method of analysing binary data (e.g. presence or absence of effect, presence or absence of side-effect) is logistic regression (Equation 3). In this case, the probability (P ) of drug effect is calculated as a function of concentration (C )

(3)

where C₅₀ is the concentration at which the probability of drug effect is 50%. When this approach is applied to binary data obtained from one individual, the meaning of the slope parameter (γ ) in Equation 3 is quite different from equation 2. Equation 3 implies variability in the concentration-response relationship for the individual patient, because there is a small probability of drug effect even at very low concentrations and a small probability of no drug effect even at very high concentrations. Thus γ can be considered a measure of intrapatient variability in response. When applied to population data, the naive pooled estimate of γ can be used to determine the concentration that is associated with the probability of an effect in, for example, 90% of all patients [47].

Mixed effects approaches

The nonlinear mixed effects model has been described as ‘the most satisfying, and sometimes the most satisfactory, approach to repeated measurements, at least from the regression modelling point of view’ [48]. When first introduced, the principal application of mixed effects modelling was for the analysis of sparse observational data, that is, data is obtained without controlling the independent variables of interest [49]. It has also gained popularity in therapeutic areas that normally generate sparse data, such as in the therapy of neonates and small children. As with the pooled approach, the data for all individuals are analysed simultaneously, but mixed effects models take into account both fixed and random (hence ‘mixed’) effects. An example of a fixed effect is an increased sensitivity to the effects of a drug in the elderly. Random effects are included in the model to account for the unexplained interindividual variability, as with the variation in C₅₀ shown in Figure 6. Several widely different methods are used to represent the probability distribution of these random effects and several different approximations—some of which are computationally extremely intensive—are used to linearize the model with respect to the random effects [41].

Mixed effects models have been described for continuous measures of drug effect, including both direct [39, 50, 51] and indirect [28, 29] pharmacodynamic models. Random effects models have also been described for categorical (usually binary) response data [52], and for survival-type data [53]. Sheiner [54] and Mandema [55] have presented analyses that illustrate the complexities of analysing analgesic drug trials. They have used population models (with random effects) to deal with repeated measurements, noncontinuous responses (ordered categorical and survival data), and nonrandom censoring (remedication).

The steps in the development of a mixed effects pharmacokinetic-pharmacodynamic model are summarized in Table 1, which has been adapted from several sources [56–59]. Although the use of informative graphical and statistical techniques leads to a more efficient analysis of the data, the development and evaluation of the final population model remains a lengthy process, because with each new generation of computer processor it becomes feasible to apply increasingly complex modelling approaches. The result of this labour might be a model of great beauty in the eyes of its creator; however, unless it can be applied to develop dosing guidelines and improve therapeutic outcome, the effort has been wasted.

Table 1.

Mixed effects PKPD model building^*.

Residual error models

There is always random variation of the observed values about those predicted by a model. These differences are termed residual errors, and their careful evaluation is an important part of the model building process [61]. The difficulties sometimes encountered in specifying weights for weighted nonlinear regression is largely solved by the use of extended least squares nonlinear regression, which permits the incorporation of a general parametric variance model [62]. The traditional residual error models for pharmacokinetic analyses were developed as if all sources of error have properties similar to those of assay error, whereas in reality, assay error is often only a minor part of the difference between predicted and observed concentrations. Recently, three new residual error models for population pharmacokinetic and pharmacodynamic analyses were evaluated [63]. The first model acknowledges two separate sources of residual error, replication error plus pure residual (assay) error, the second model allows for serially correlated errors, as may occur with structural model misspecification, and the third model allows a time-dependent error, as may be caused by inaccurate sample timing. Using a real data set, the use of these error models was shown to facilitate the model building process, to provide information about the sources of error, and to provide more accurate parameter estimates.

Application of population models

Even when a clinician has an excellent understanding of population modelling concepts, the results of many analyses are reported in a way that is difficult to apply to the clinical setting. The next two sections consider how the clinical significance of the explained and unexplained interindividual variability can be better presented. The final three sections consider how population pharmacodynamic models can be applied to develop initial dosing guidelines, to adjust subsequent doses, and to improve the efficiency of the clinical drug development programme.

The explained interpatient variability

All population modelling approaches provide estimates of the pharmacokinetic and pharmacodynamic parameters required to predict the response to a variety of dosing scenarios in the typical individual. Furthermore, all approaches can be used to examine the impact of that part of the interindividual variability explained by the fixed covariate effects (e.g. impact of age, weight, serum creatinine). Most often, this explained variability is expressed as formulae relating model parameters to patient covariates, as shown in Equation 4 [39].

(4)

This equation states that the total clearance (CL₁ ) is 2.6 l min⁻¹ for the typical individual aged 40 years and lean body mass (LBM) of 55 kg. Although it is relatively easy to determine the impact of changing age and LBM on clearance, it is considerably more difficult to determine their impact on the maximum effect after an intravenous bolus. The clinician cannot easily use a table of these formulae to answer clinically relevant questions, such as: If the same dose is administered to an elderly and a young patient, how much greater is the effect in the elderly patient? If the difference is clinically significant, by how much should the dose be reduced in the elderly? These questions may also relate to the drug’s side-effect profile. Thus, rather than present a table of formulae describing the statistically significant covariate effects for each of the pharmacokinetic and pharmacodynamic model parameters, the modeller should extend the analysis to evaluate the clinical impact of the covariate effects on the dose-effect relationship (Equation 1). However, we would advise caution in extrapolating beyond the range of studied patient covariates.

Clinically relevant measures of drug effect should be defined before computer simulations are used to evaluate the model. The specifics of these clinical endpoints will differ according to the nature of the drug and the disease being treated, but will generally relate to the time required to reach a specific effect, the duration of effect in relation to a specific threshold, the maximum effect, or the incidence and severity of a specific side-effect. The model can be used to determine the change in a clinically relevant endpoint when typical individuals with different covariates are administered the same dose. For example, a model describing the loss of pin prick sensation following spinal anaesthesia with plain bupivacaine was used to predict the time course of effect following a standardized intrathecal dose in each individual [50]. Based on these predictions, the duration of analgesia above the umbilicus was reported to decrease by 13 min per 10 cm increase in height. The model can also be used to determine the change in dose required to reach the same clinically relevant endpoint in typical individuals with different covariates. For example, a model describing the electroencephalographic (EEG) effects of remifentanil was used to develop dosing nomograms designed to maintain 50% maximum EEG effect at each age and LBM [60] Such analyses facilitate the clinician’s ability to assess the impact of the covariate effects on the dose–response relationship more readily than a series of formulae relating patient covariates to model parameters.

The unexplained interpatient variability

Covariate analysis is able to account for some of the interindividual variability in model parameters, but leaves considerable interindividual variability unexplained. Commonly, this unexplained variability is modelled with formulae that relate the individual’s parameters (P_i ) to the typical value of each parameter in the population (P_TV ), as shown in Equation 5 [39]

(5)

where η_i is a normally distributed random variable with mean zero and variance ω². This model results in a log normal distribution of the individual parameters. Often an approximate coefficient of variation (% CV) for each of the model parameters is reported, where the percentage CV is calculated as the square root of the variance of η_i, multiplied by 100. Most clinicians would not be aware that, based on the distribution in Equation 5, a 40% CV results in approximately a 5 fold range between the lowest and highest parameter value in the population. When presented with a table of the percentage CVs for each of the model parameters, the clinician cannot easily use this information to answer an important clinical question, such as: If the same dose is administered to every patient, what range of effects and side-effects can be expected? Thus, rather than presenting a list of percentage CVs for each of the pharmacokinetic and pharmacodynamic model parameters, the modeller should extend the analysis to evaluate the impact of this interindividual variability in model parameters on the dose-effect relationship (Equation 1).

A population model can be used to determine the expected response to an as-yet untested dosing schedule [51], although we would advise caution if extrapolating beyond the range of studied doses. A particular dosing schedule can be administered to a population of simulated patients (i.e. η_i values). The distribution of various endpoints of clinical interest can be calculated from the predicted responses [54]. Empirical Bayesian estimates of the individual’s parameters were used to predict the time course of effect to a standardized dose of intrathecal bupivacaine [50]. Based on these predictions, the time for the sensory block to reach the umbilicus, the duration of the block above the umbilicus, and the highest level of the block were determined for each individual and their distribution presented graphically (Figure 7). Population models describing the leukopaenic effects of etoposide [51] and cyclophosphamide [64] have been used to show the distribution of the white blood cell nadir times in simulated patients (Figure 8). The effect of age on the variability in response to bolus dosing and constant rate infusions of remifentanil was determined by examining the time course of the EEG effect in three simulated populations of 20, 50 and 80 year olds [60]. The authors concluded that despite pharmacokinetic and pharmacodynamic variability, age adjustment of bolus dose and infusion rates would improve the ability to achieve the therapeutic target. Knowledge of the unexplained interpatient variability in the dose–response relationship is an important index of drug safety [41]. Graphical presentation of this variability is more readily interpreted than tables that report the means and variances of model parameters.

Figure 7.

Distribution of clinically relevant endpoints based on the simulated response to an intrathecal dose of bupivacaine. T10 represents the tenth thoracic dermatome, C8 represents the eighth cervical dermatome. Duration is defined as the duration of analgesia above T10. The thick vertical line represents the median value. (Reprinted with permission from Schnider et al., Anaesthesiology 1996; 85: 502–512[50].)

Figure 8.

The distribution of white blood cell nadir times in 500 simulated individuals receiving etoposide. The continuous line is the distribution of nadir times for the model predictions; the broken line is the distribution of the simulated observed nadirs based on daily counts. (Repeated with permission from Karlsson et al., Clin Pharmacol Ther 1995; 57: 325–334[51].)

Selection of optimal initial dose

The initial dose recommendations for many new drugs are considerably greater than those ultimately found to be optimal [65]. Some modelling approaches, such as anova, ignore the dose–response relationship and, perhaps not surprisingly, can fail to identify an optimal initial dose for a new drug. The use of modelling approaches that seek to identify factors affecting the dose–response and dose-toxicity relationships, and that also seek to estimate the interindividual variability in these relationships, have the potential to address this problem.

It is commonly assumed that the dose–response curve lies to the left of the dose-toxicity curve; however, both the EC₅₀ and the slope of the dose–response curve may be the same as, lower than, or higher than the dose-toxicity curve. When the dose–response curve lies to the left of the dose-toxicity curve and when there is a relatively short delay between drug concentration and effect, the selection of the initial dose may be facilitated by cautious administration, while monitoring for both drug effect and side-effects. This careful titration of dose to ensure an adequate therapeutic response can be accomplished by skilled clinicians without the benefit of population models [3]. However, this is not possible if there are relatively long delays between dose and effect or if the dose–response curve lies to the right of the dose-toxicity curve.

Considerations affecting the selection of an optimal initial dose vary widely between the different clinical specialities. Consider the questions an anaesthetist might ask when presented with a population model for a new muscle relaxant. What dose is required to provide excellent intubating conditions within 60 s for 95% of patients? Given this dose, what is the predicted variability in duration of action? Having examined these simulations, the anaesthetist might consider that the duration of action of this dose is unacceptably long in most patients, and proceed to ask a revised set of questions. What initial dose would provide excellent intubating conditions within 90 s for 90% of patients, and how does this affect the predicted variability in duration of action? In this case, the anaesthetist is attempting to select the initial dose by balancing one clinically relevant endpoint (time to excellent intubating conditions) against another clinically relevant endpoint (duration of action) given the variability in the dose–response relationship. Consider the questions an oncologist might ask when presented with a population model, which would ideally relate drug exposure to both toxic and therapeutic endpoints (such as tumour response and survival). What dose is associated with severe toxicity in 30% of patients? What dose is associated with severe toxicity in 70% of patients? By how much is the likelihood of survival increased given the increased risk of severe toxicity? As chemotherapy doses are escalated, it might become clear that bone marrow toxicity is an inadequate endpoint for determining maximal efficacy. Such a finding would emphasize the need to develop strategies that more effectively provide bone marrow support. Alternatively, if dose escalation is not associated with a significant improvement in outcome, the selection of an initial dose causing severe toxicity in all patients would not be warranted. Figure 9 illustrates the application of a population model in the development of optimal initial dosing guidelines.

Figure 9.

Selection of optimal initial dose based on computer simulations of explained and unexplained interindividual variability. Definition of clinically relevant endpoints and of risk-benefit criteria for the therapy and disease under investigation are essential steps in the determination of the optimal initial dose. These criteria may be revised as one clinical endpoint is balanced against another, or as the risk of toxicity is balanced against the significance of therapeutic benefit.

The optimal initial dose cannot be defined if the interindividual variability in the dose–response and dose-toxicity relationships have not been estimated. Only a few investigators have applied their population models in this way. Bouillon et al. examined the concentration effect relationships of fenoterol-induced tachycardia and hypokalaemia occurring during tocolytic therapy with β₂-adrenoceptor agonists in females of childbearing age [29]. Based on the estimated interindividual variability in model parameters, they performed simulations to determine the predicted steady state heart rate and nadir in the potassium concentration for different fenoterol infusion rates. They concluded that a continuous fenoterol infusion of 2.0 μg min⁻¹ would result in a clinically acceptable distribution of adverse effects. Mandema & Stanski have derived a population pharmacokinetic-pharmacodynamic model characterizing the distribution of pain relief scores and remedication times observed in patients receiving intramuscular ketorolac, a nonsteroidal anti-inflammatory drug used for the treatment of moderate to severe postoperative pain [55]. Based on the estimated interindividual variability in model parameters, they performed simulations to determine the time of onset and the duration of adequate analgesia in 50% of the patients after each of four different doses (10, 30, 60, or 90 mg) of ketorolac. They suggested that 30 mg of intramuscular ketorolac was the optimal initial dose for postoperative pain relief, although considerations of possible drug toxicity were not included in this analysis.

Clinically relevant questions relating to the explained and unexplained variability in the population can be posed to the model, and confidence intervals can be obtained for the fraction of the population that is estimated to fall within a specific therapeutic range given a certain dosing regimen. Such forecasting can be used to develop optimal initial dosing guidelines, given knowledge of the variability in dose–response and dose-toxicity relationships, together with clinical evaluation of the relative risks and benefits associated with over-or underdosage.

Adjustment of subsequent doses

Before administering the initial dose to a patient, the most likely response can be predicted using the model parameters of the typical individual (Equation 5). If a previous covariate analysis has explained some of the interpatient variability, the prediction can be improved by adjusting the model parameters accordingly (Equation 4). Usually the actual response will differ from our best prediction, because of the unexplained interindividual variability in model parameters. We know that the dose must be reduced if the observed effect is greater than desired and must be increased if the observed effect is less than desired, but by how much? Knowledge of even a few measures of concentration or effect can be used to improve the precision of our prediction [50, 66, 67]. The Bayes approach allows us to determine the most likely model parameters for an individual by minimizing simultaneously the difference between the individual and population parameters and between the measured and predicted response [66]. This is done by acknowledging both the distribution of the population parameters and the uncertainty in the measured response. The revised (Bayes) individual parameters can then be used to calculate the dose required to achieve the desired effect in that particular individual.

Therapeutic drug monitoring and adaptive-control-with-feedback dosing strategies have mostly focused on pharmacokinetic models, which aim to target specific plasma concentrations. However, this approach ignores the wide interindividual variability in pharmacodynamics that is often present. A recent review discusses the role of therapeutic drug monitoring and adaptive control of cancer chemotherapy using feedback approaches [68]. In some instances, the need for these strategies is controversial, since there is no agreement on the meaning, or evidence for, the existence of a critical window for drug levels. In other instances, these strategies have been successful, but were considered expensive and labour intensive [69]. Few investigators have attempted to apply this approach to population pharmacodynamic models. Monitoring of zidovudine (AZT) therapy in the treatment of human immunodeficiency virus (HIV) infection would seem to be an ideal application of the Bayesian feedback approach [70]. However, it is becoming more difficult for clinical trials to demonstrate drug efficacy based on ‘hard’ clinical endpoints, such as AIDS-free time or survival time, because of the change in pattern of the disease [71, 72]. Conceivably, population models can be developed that demonstrate drug efficacy based on surrogate measures of effect, such as CD₄ T-cell levels and measures of viral load in various tissues [72, 73]. An important challenge to clinical pharmacology is to identify the drugs that might benefit from this approach [69]. Drugs used for life threatening diseases with a proven pharmacokinetic-pharmacodynamic relationship, a small therapeutic range, large interindividual variability, small interoccasion variability and severe adverse effects are likely to be good candidates.

Drug development

Sheiner, commenting on the intellectual health of the clinical drug evaluation programme, has asserted that the null hypothesis testing paradigm has led to drug trial designs and analyses that are clinically irrelevant, wasteful of the data, and excessively conservative [74]. The standard analysis strategy, and in particular the intention-to-treat analysis, can yield biased estimates of the effect of administered therapy (so-called method-effectiveness) [75]. Rather than maintaining the narrow focus on rejecting the null hypothesis—millions of dollars are spent to disprove the null hypothesis that a drug does not work—he advocates an alternative paradigm, the estimation view, which aims to ‘gather data to model and quantify nature’ [74, 76]. Sheiner asserts that clinicians must regain control over clinical trials to assure that important clinical questions are also addressed. Mixed effects modelling approaches can be applied at each phase of the clinical drug development programme [77]. Pretrial computer simulations based on population pharmacokinetic and pharmacodynamic models have been performed to evaluate candidate clinical trial designs [78, 79]. Limited sampling strategies can facilitate the completion of phase I pharmacokinetic studies in some patient groups [68]. Throughout phases II and III, systemic drug concentration data should be routinely obtained on a survey basis to help explain unusual responses, to suggest the possibility for either the presence of or lack of drug–drug interactions, and to identify other unanticipated variability, such as metabolic heterogeneity [80–83]. Recently the population approach has been successfully applied to examine the relationship between exposure to moclobemide and the occurrence of adverse events in depressed patients in phase III/IV studies [84]. Holford has evaluated the effect of tacrine and lecithin in Alzheimer’s disease using a population pharmacodynamic analysis of the combined data from five trials [85]. Using this approach it was possible to distinguish a responder population, approximately one third of patients, with a four-fold greater effect than poor responders, and that lecithin has a small additional benefit independent of tacrine. It was also possible to show that the tacrine potency was similar in all studies, but that the placebo response was different in some.

Rapidly evolving changes in health care economics and consumer expectations make it unlikely that traditional drug development approaches will succeed in the future. The integration of pharmacokinetic and pharmacodynamic principles into drug development has been proposed as a way of making it more rational and efficient [86–88]. In addition to meeting current regulatory demands, population modelling approaches provide the practising clinician with relevant information regarding dose individualization—by understanding the variability associated with the pharmacokinetics and pharmacodynamics and by identifying subpopulations with special needs—leading to safer and more efficacious drugs [89]. Although there are many reasons for clinical trial failures, many could be prevented by a more efficient trial planning process. Already several companies are developing simulation software based on population models that promise to ‘accelerate clinical development and increase the informational yield of clinical trials without compromising safety.’1 These software packages emphasize ease of use, graphical user interface, and modular design. Although these features might lessen the computer programming knowledge currently required to use existing software, the provision of the next generation of population modelling tools is only one of the important steps towards the implementation of the population approach. There must also be a shift by regulatory authorities away from the narrow focus on the null hypothesis. As well, there is a need for the education of individuals with expertise in computer programming, pharmacokinetic models, pharmacodynamic models, population models, residual error models, and nonlinear regression statistics. Such individuals must also possess the clinical insight and creative skills necessary to develop models that capture the essence of a more complex reality [90].

Conclusions

In the introduction we asked the question: why should clinicians be interested in population pharmacokinetic and pharmacodynamic modelling? We believe it is essential for clinicians to realize that population modelling approaches are more than complicated statistical models (to be ignored); they provide a powerful tool to explore factors influencing interpatient variability in the dose–response relationship, and can be applied to develop optimal dosing strategies and a more efficient new drug development programme. It is essential that improved means of presenting the results of these complicated analyses are developed. We note particularly the key role of clinicians in this regard: only clinicians are able to define the clinical endpoints that can be used to present the explained and unexplained interpatient variability; only clinicians are able to evaluate the clinical significance of potentially conflicting endpoints; and finally, only clinicians (together with their patients) are able to make clinical judgements that balance the potential risks of toxicity against the potential benefits of therapy for a particular disease process. Prepared with an understanding of population pharmacodynamic modelling concepts—together with appropriate advances in modelling software—clinicians will one day be able to apply these models themselves to answer important clinical questions that they encounter in their daily practice.