Population pharmacokinetics model and limited sampling strategy for intravenous vinorelbine derived from phase I clinical trials

Abstract

Aims

a) To characterize the pharmacokinetics of intravenous vinorelbine, b) to use a population analysis for the identification of patient covariates that might appreciably influence its disposition and c) to define a limited sampling strategy for further Bayesian estimation of individual pharmacokinetic parameters.

Methods

All data were collected from 64 patients (99 courses) entered in three different phase I trials that have been previously reported. All patients received vinorelbine as a 20 min infusion with dose levels ranging from 20–45 mg m⁻². The population pharmacokinetic model was built in a sequential manner on a subset of two-thirds of the data, starting with a covariate-free model then progressing to a covariate model using the nonlinear-mixed effect methodology. The remaining one-third of the data were used to validate several sparse sampling designs.

Results

A linear three-compartment model characterized vinorelbine blood concentrations (n = 1228). Two primary pharmacokinetic parameters (total clearance and volume of distribution) were related to various combinations of covariates. The relationship for total clearance (CL_total (l h⁻¹) = 29.2×BSA×(1−0.0090 Plt)+6.7×Wt/Cr_s) was dependent on the patient's body surface area (BSA), weight (Wt), serum creatinine (Cr_s) and platelet count before administration (Plt). The optimal limited sampling strategy consisted of a combination of three measured blood concentrations; the first immediately before the end of infusion or 20 min later, the second at either 1 h, 3 h or 6 h and the third at 24 h after drug administration.

Conclusions

A population pharmacokinetic model and a limited sampling strategy for intravenous vinorelbine have been developed. This is the first population analysis performed on the basis of a large phase I database that has identified clinical covariates influencing the disposition of i.v. vinorelbine. The model can be used to obtain accurate Bayesian estimates of pharmacokinetic parameters in situations where extensive pharmacokinetic sampling is not feasable.

Introduction

Vinorelbine is a vinca alkaloid derivative which is marketed under the brand name Navelbine® in many countries for its activity against non small cell lung and advanced breast cancer [1–5]. This semisynthetic compound differs from other vinca alkaloids in that structural modifications are on the catharantine ring instead of the vindoline ring [6]. Vinorelbine, like other vinca alkaloids, blocks cell mitosis by interfering with microtubule assembly and by inducing depolymerization of the microtubules [7]. Its relatively low neurotoxicity, compared with other vinca alkaloids, is attributed to its low affinity for axonal microtubules [8].

The pharmacokinetics of anticancer drugs are frequently affected by physiopathological factors which can explain in part the interpatient variability. Vinorelbine pharmacokinetics have been previously studied by several authors who have reported a large plasma clearance (from 0.66–1.26 l h⁻¹ kg⁻¹) and volume of distribution (from 19–75.6 l kg⁻¹) with substantial differences between studies, which might be attributed to the use of non cross-validated assays [9–16]. The basis of interpatient variability in vinorelbine pharmacokinetics was not investigated in these early phase I studies, since the number of patients in each trial was too small to develop reliable population pharmacokinetic models.

The study of patient variability has become an important issue in the characterization of a pharmacokinetics as recommended by regulatory agencies [17]. It is a major goal of the population approach to enable observational data obtained from patients during clinical trials to be used to assess the pharmacokinetic variability in patients with significant changes in pharmacokinetics and relate blood concentrations to either efficacy or/and toxicity [18].

The main goal of the current investigation was to apply a population pharmacokinetic approach to intravenous vinorelbine blood concentration, using previously acquired data. Ethical and practical constraints forbid the collection of numerous samples in phase II studies. Combining population approaches and Bayesian estimation provides an attractive opportunity to estimate individual pharmacokinetic parameters with a reduced number of samples. Therefore, our second aim was to propose optimal limited sampling strategies allowing a reasonable estimation of individual pharmacokinetic parameters for further exploration of relationships between pharmacokinetics and pharmacodynamics.

Methods

Pharmacokinetic database

Data from three phase I trials listed in Table 1 were included in this retrospective analysis. Patients with normal renal and hepatic function were being treated for various solid tumour types. All were informed about the study protocol and all gave their informed written consent before inclusion. Each study protocol was constructed in accordance with legal requirements and the Declaration of Helsinki and was approved by local Ethics Committees.

Table 1.

Phase I studies used for the population pharmacokinetic analysis.

Study [reference]	Design	1st objective	Number of patients	Number of i.v. courses	Dose (mg/m2)
[32]	Parallel groups	Maximum tolerated dose	16	1	35–45
[33]	Intra-patient escalation	Dose-linearity	20	3*	20–40
[34]	Cross-over	Bioavailability of an oral formulation	28	1	25

^*1 week wash out between courses.

All patients who took part in these phase I trials gave an average of 10 [range: 5–13] samples per individual. A total of 1228 blood vinorelbine concentrations (64 patients and 99 courses) were available for analysis. Table 2 lists the 18 (continuous and categorical) covariates that were analysed.

Table 2.

Patient characteristics.

	i.v. data set (n = 64 patients) n		Symbol	Covariate coding
Characteristics of patients
Tumour types
Gynaecological	12
Gastroenterologic	19
Lung	4
Others	35
Liver metastases	16		Mhep	0: abscence
				1: presence
	Mean±s.d.	Range
Demography
Age (years)	55±11	27–73	AGE	Numerical
Weight (kg)	66±13	39–114	Wt	Numerical
Height (cm)	168±9	150–184	Ht	Numerical
Body surface area (m2)	1.74±0.19	1.35–2.33	BSA	Numerical
Gender (M/F)	42/22		Sex	0: female
				1: male
Laboratory measurements
Serum creatinine (µm)	91±21	31–141	Crs	Numerical
Creatinine clearance* (ml min−1)	76±24	34–168	CLcr	Numerical
Total bilirubin (µm)	7.7±3.5	1–18	Bili	Numerical
Total blood protein (g l−1)	69±6	52–85	Prot	Numerical
Alanine amino transferase (IU)	30±21	4–118	SGPT	Numerical
Aspartate amino transferase (IU)	26±13	7–63	SGOT	Numerical
Alkaline phosphatase (IU)	136±137	29–952	ALP	Numerical
Lysine deshydrogenase (IU)	547±480	115–2350	LDH	Numerical
γ glutamyl transferase (IU)	80±68	12–342	GGT	Numerical
White blood cells (109/l)	6.6±4.0	1.9–37.8	WBC	Numerical
Granulocytes count (109/l)	4.5±3.4	0.9–31.7	PMN	Numerical
Platelet count (109/l)	280±108	90–594	Plt	Numerical

^*Creatinine clearance was calculated according to the Cockroft & Gault formula.

Vinorelbine assay

Blood vinorelbine concentrations were measured by a fully validated reverse-phase-high-performance liquid chromatography using ultraviolet detection after an organic liquid/liquid extraction [19]. The method allowed the determination of concentrations down to 2.5 ng ml⁻¹ with a maximal error lower than 10%. The precision of the assay measured either on the same day or on different days was less than 12%.

Population analysis

The data were analysed using the first order (F.O.) minimization algorithm implemented in NONMEM program [20] (double precision, version IV, level 2.1) running on a PC compatible computer. The first order with conditional estimation method (F.O.C.E.) was used to confirm the critical stages of model development (covariate-free and final model runs). The data were randomly split into two sets: a model building set (the so-called index set) of 39 patients (n = 65 courses which represented approximately 2/3 of the whole data) and an evaluation set of 25 patients (n = 34 courses) on which the limited sampling strategy was assessed.

From the index set, a preliminary population pharmacokinetic model was developed in three main steps:

Step 1: covariate-free model

Concentration-time data were fitted using either a two-compartment or a three-compartment model with zero order input and first order elimination from the central compartment.

For the three-compartment model, the equation was parameterized in terms of total body clearance (CL), central volume of distribution (Vc), transfer rate constants (K₂₁ and K₃₁), slope of the distribution phase (β) and volume of distribution (V). This type of structural model was used in order to obtain pharmacokinetic parameters such as terminal half-life (t_1/2) or volume of distribution of the terminal phase (V). For the two-compartment model, the equation was parameterized in terms of total body clearance (CL), central volume of distribution (Vc), transfer rate constant (K₂₁), and volume of distribution (V).

The error model describing both the interindividual and interoccasion variability in pharmacokinetic parameters was assumed to be proportional.

A covariance structure was established based on the examination of the correlation matrix from the empirical Bayes interindividual variability estimates (POSTHOC ETAs).

The residual variability was modelled with either an additive, a proportional or a slope intercept error model. As pharmacokinetic sampling was available on two to three occasions for 38 patients out of 64, interoccasion variability (random change of individual pharmacokinetic parameters between courses) could be investigated. The interoccasion variability (IOV) was estimated on clearance and V parameters (using the same OMEGA block structure as described by Karlsson & Sheiner [21]).

Step 2: Covariates screening

The relationships between the pharmacokinetic parameters of interests (CL and V) and covariates were first investigated by using both a multiple linear regression in a stepwise procedure (visual NM program [22]) and a graphical approach (plotting the POSTHOC ETAs vs covariates). Each covariate showing a significant relationship in the previous analyses (i.e. a covariate retained in the multiple linear regression and/or illustrating a pattern by the graphical approach), was then tested by the univariate NONMEM approach. The candidate covariate was evaluated by the change of the objective function value (OFV) computed using the NONMEM program. This value is proportional to minus twice the log likelihood of the data, and the difference in objective function (δ) between two hierarchical models is asymptotically χ² distributed.

When including a covariate in the model, a decrease in objective function from the base model higher than 3.8 (P<0.05) was required to confirm a statistically significant influence.

Step 3: final model

Covariates defined as relevant during the screening step, were included in a so called ‘full model’. This was evaluated by a backward elimination procedure in which each covariate was removed in turn from the ‘full model’ and the difference in OFV between the full and each reduced model was examined. An increase in OFV greater than 7.9 (P<0.005) was required to retain the covariate in the final model. Finally, the stability of the model was evaluated on the combined index and evaluation sets: parameters of the refined model (with overall data) were compared with those obtained on the index set only.

Limited sampling strategy (LSS)

Optimized sampling times were obtained using the d-optimality criterion implemented within the APIS package (version 3.04) [23]. After specifying a small number of samples m, the most informative sampling times t_i (i = 1,…,m) that allow precise estimation of the pharmacokinetic parameters are determined. This is done by using the d-optimality criterion, minimizing the volume of the confidence ellipsoid in the parameter space [24, 25]. Moreover, the minimization algorithm takes account of practical constraints like nursing hours or duration of the sampling period restricted to a short hospitalization period. Several combinations of either three or two fixed sampling times were selected close the d-optimized points and tested on the evaluation set (n = 34 courses, each being considered as an individual for the purpose of this analysis).

Individual empirical Bayes estimates of CL and t_1/2 were estimated by combining the partial individual concentration-time data with the final population model information using the POSTHOC option in the NONMEM program. For each combination, the jth individual predicted Bayesian parameter (P_pj), estimated from sparse data, was compared with the actual jth individual estimate (P_Aj: Bayesian parameter estimated from the full individual concentration-time data). To evaluate the performance of each sparse design and to compare them, the mean absolute error was computed as: MAE = ∑|[(P_pj−P_Aj)/P_Aj]|/n where n is the total number of jth individual.

Results

Population analysis

Blood vinorelbine concentrations were better fitted by a three-compartment pharmacokinetic structural model (Akaike criterion: AIC = 4802) than by a two-compartment model (AIC = 6025).

On the basis of inspection of weight residuals, a proportional error model was chosen to describe the residual variability. The covariate-free model provided precise estimates of the pharmacokinetic parameters (see Table 5) with low standard error (CV precision <11%) consistent with the non compartmental calculations.

Table 5.

Estimates and precision of the population pharmacokinetic models for intravenous vinorelbine (from all 64 patients and 99 courses). CL_tot (l h⁻¹) = θ₁·BSA·(1−θ₂·Plt)+θ₃·Wt/Cr_s.V (l) = θ₄·(1−θ₅. Plt)·(1+θ₆·Gender).

	Covariate-free model		Final model
Parameter	Estimate	Precision CV (%)	Estimate	Precision CV (%)
CL (l h−1) θ1	39.4	5
BSA θ1			29.2	7
Plat θ2			0.00090	9
Wt/Crsθ3			6.70	37
V (l) θ4	2230	6	2340	10
Plat θ5			0.000849	7
Sex θ6			0.26	31
Vc (l)	20.9	6	19.5	5
β slope (h−1)	0.218	11	0.271	6
K21 (h−1)	0.434	7	0.471	6
K31 (h−1)	0.0321	6	0.0396	10
Inter-indiviual (IIV) and inter-occasion (IOV) CV (%)
IIV CL	30	26	21	19
IOV CL	10	43	5	63
IIV V	30	25	22	26
IIV Vc	31	30	26	45
IIV β	19	42	17	37
Correlation coefficient between inter-individual estimates
CL vs V	0.98	26	0.89	23
Residual CV (%)
σ	25	17	25	17
Objective function value	6998		6779

The mean values of half-lives characterizing the pharmacokinetic profile of vinorelbine were 5.5 min, 3.1 h and 39.4 h for the first (α), second (β) and third (γ) exponential phase, respectively. The mean (±s.e. mean) population values of the total clearance, volume of distribution of the terminal phase and terminal half-life were 39.4±1.8 l h⁻¹, 2230±131 l and 39.7±2.3 h, respectively. Interindividual variability could be determined for four pharmacokinetic parameters (i.e. CL, V, Vc and β), but was close to zero for the two others ones (i.e. K₂₁ and K₃₁).

The covariance between the interindividual variability estimates of CL and V was determined since a highly significant correlation existed (r = 0.98) between these two parameters. The interindividual CV on both total clearance and V was 30%. Lower variabilities were calculated for β rate constant (CV = 19%) and terminal half-life (CV = 8%). The interoccasion variabilities (I.O.V.) were 10% and 6% for the total clearance and the volume of distribution (V), respectively. Although the I.O.V. led to a low improvement of fit (decrease in objective function value: δ = 4.2), only the I.O.V. for the clearance parameter was retained for the next steps of model building.

In step 2 of the analysis, the multiple linear regression using a stepwise procedure identified five covariates (BSA, platelet count, Cr_s, Mhep and Wt) that were related to CL.

Except for the presence or absence of liver metastases (Mhep), the univariate NONMEM analysis confirmed the relevance of the above selected covariates. Platelet count (δ = 101), body surface area (δ = 35) or weight (δ = 33), all showing a linear pattern by the graphical approach, were the most influential covariates related to vinorelbine clearance.

Based on the rationale of the Cockroft & Gault formula [26], the weight/serum creatinine (Wt/Cr_s) ratio produced a better fit than either creatinine clearance or weight or serum creatinine alone. The serum γGT decreased the OFV by 30 and age, gender, ALP, SGOT and SGPT showed a low but statistically significant improvement of fit (δ = 6–14).

As demonstrated both by the multiple linear regression analysis and the univariate NONMEM approach, body surface area and platelet count were significantly correlated with V. A linear pattern was the most appropriate to model the influence of these covariates. However, the best fit (δ = 125) was obtained when gender was related to V the mean value of which was significantly higher in males than in females. Table 3 lists the candidate covariates selected during the screening step.

Table 3.

Patients covariates identified in the screening step and in the final population pharmacokinetic model for intravenous vinorelbine.

Parameter	Screening of covariates	Final population model
CLtot	Plt, BSA, Wt/Crs, creatinine clearance, γGT, age, gender, ALP, SGOT, SGPT	BSA*, Wt/Crs, Plt
V	Plt, BSA, Gender	Plt, Gender

^*BSA was only kept into the final model developed from the entire data set.

The final set of covariates was obtained via step 3. Most of the covariates removed during the backward elimination procedure produced a significant increase (δ>15) in the OFV. BSA was no longer relevant since it did not generate a significant increase (δ = 5) in OFV when deleted.

Platelet count and Wt/Cr_s ratio for clearance, platelet count and gender for V remained the most influential covariates (Table 3).

From the index data set (two thirds of the data) the structure of the population model was

$$\text{CL} (\text{l} {\text{h}}^{-1})={\theta }_1(1-{\theta }_2 \text{Plt})+{\theta }_3 \text{Wt}/{\text{Cr}}_{\text{s}}$$

$$V \left(\text{l}\right)={\theta }_4(1-{\theta }_5 \text{Plt})\cdot (1+{\theta }_6 \text{Gender}).$$

The objective function was reduced from 4684 (covariate-free model) to 4376 (model with covariates).

The population model was assessed on the combined index and evaluation sets (n = 64 patients and 99 courses). Parameters obtained from this refined model (data not shown) were similar to those computed on the index set only, emphasizing the stability of the population model.

Limited sampling strategy

To reduce clinical constraints and given that the variability in terminal half-life was very low (CV = 8%), it was reasonable to limit the last sampling time to 24 h. As a result, the d-optimized sampling times were: end of the infusion, 20 min after the end of the infusion (40 min after the start), 1.2 h, 6.3 h, 14.9 h and 24 h after the start of infusion. Excluding the time point at 14.9 h (which would require a blood collection during the night), nine combinations of either three or two fixed sampling times were selected within 1 h after the start of the infusion, between 1–6 h and at 24 h (see Table 4 for the design of each combination). Each sparse data design was simulated using the validation set (n = 34 courses), and bias and precision were then calculated.

Table 4.

Precision of the limited sampling designs assessed on validation set.

Design number	Timing of samples (h)	CL	MAE (%) t1/2
Three blood samples
1	end inf*, 1 and 24 h	8.0	11.5
2	0.67**, 1 and 24 h	8.7	11.6
3	end inf, 3 and 24 h	6.8	11.0
4	0.67, 3 and 24 h	7.7	10.2
5	end inf, 6 and 24 h	8.4	11.7
6	0.67, 6 and 24 h	8.0	10.2
Two blood samples
7	1 and 24 h	8.2	12.0
8	3 and 24 h	8.3	13.8
9	6 and 24 h	8.5	12.9

^*end inf: is actually collected just before the end of infusion (corresponding to 20 min after infusion start).

^**00.67 h corresponds to 20 min after the end of infusion.

MAE = Mean absolute error.

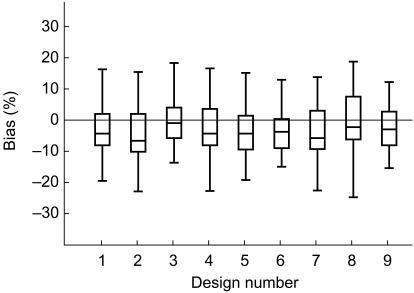
Individual Bayesian clearance was estimated with an absolute prediction error below or close to 20%. The mean absolute error (see Table 4) ranged from 6.8 to 8.7% and from 10.2 to 13.8% for the total body clearance and terminal half-life, respectively. On inspection of the box plot representation of the prediction error (Figure 3) calculated for the total body clearance, a slight negative bias appeared for each sparse sampling design. However, this bias was very low and the 95% confidence intervals of the medians were close to or included the null value.

Figure 3.

Box plots of the clearance bias calculated from limited sampling designs. Design numbers are explained in Table 4.

The best predictive performance (lowest bias and greatest precision) was obtained with the limited sampling design number 3 (i.e. samples immediately before the end of the infusion, 3 h and 24 h after the start of the infusion). The median bias was −2.1% (not significantly different from zero) and the 25th and 75th percentiles of the prediction error were −6.7 and +2.8%, respectively.

Final model development

In order to capture the influence of all covariates, the analysis was carried out on the overall data (index and evaluation sets). Patient characteristics removed previously (BSA, age, gender and liver enzymes) during the model building process from the index set were again included in the model in turn. Only BSA was eventually retained in the final model and confirmed to be relevant even after the use of a new backward elimination procedure. The final population model for intravenous vinorelbine (which included overall index and evaluation sets) was as follows:

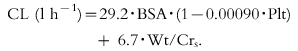(1)

$$V\left(\text{l}\right)=2340\cdot \mathrm{(1}-0.00085\cdot \text{Plt)}\cdot \mathrm{(1}+0.26\cdot \text{Gender})\text{.}$$ (2)

The estimates (with their respective precision) of this model are reported in Table 5. Intersubject and interoccasion variabilities in vinorelbine clearance decreased from 30% (covariate-free model) to 21% (final model) and from 10% to 5%, respectively. The residual variability was 25%.

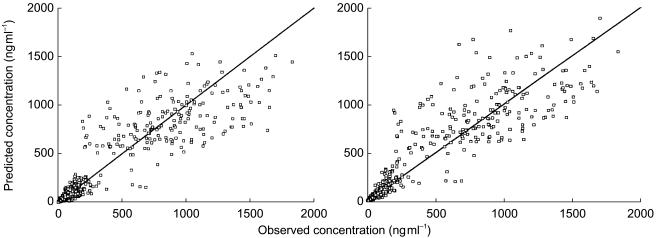
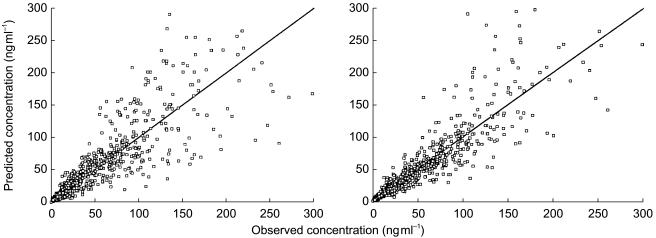
The improvement of fit from the covariate-free model to the final model is illustrated in Figures 1 and 2. Whatever the scale of the representation, the blood concentrations were better predicted using typical parameters including the covariates than with the covariate-free parameters. In addition, the covariates integrated into the final model were the same as those selected during the screening step by the multiple linear regression analysis (two stage approach).

Figure 1.

Observed and model-predicted blood vinorelbine concentrations from the overall data (n = 64 patients and 99 courses) in (a) covariate and (b) covariate-free population models for intravenous vinorelbine. The lines of identity are shown.

Figure 2.

Observed and model-predicted blood vinorelbine concentrations from the overall data (n = 64 patients and 99 courses) in (a) covariate-free and (b) covariate population models for intravenous vinorelbine. A zoom was made on blood concentrations up to 300 ng ml⁻¹. The lines of identity are shown.

Discussion

Population pharmacokinetic analysis

Population approaches to pharmacokinetic modelling are increasingly used and promoted in the area of anticancer drug development [17]. Amongst the advantages of this methodology, is its ability to quantitatively assess the influence of patients’ covariates on drug disposition.

No previous report has defined, on a large number of patients, the extent to which demographic variables or other covariates could influence the disposition of vinorelbine. Only two analyses have been performed and on a small number of patients (n≤12) to either establish a limited sampling strategy [27] or to examine the effect of age on vinorelbine pharmacokinetics [28]. Such approaches did not yield a relevant population model because of the relatively high interpatient variability on clearance and volume of distribution.

In the present work, undertaken on a much larger number of datasets involving courses of treatment, several covariates were demonstrated to influence vinorelbine pharmacokinetics. When taking account of these covariates, unexplained interpatient variabilites in clearance and volume of distribution decreased from 30% (covariate-free model) to about 20% (final model). The intrapatient variability decreased from 10% to 5%.

The platelet count before administration and BSA were the most influential covariates correlating with clearance. Platelet count was also significantly correlated with the volume of distribution (V). Such a relationship could be attributed to the high affinity of vinorelbine for platelets (78% bound) as demonstrated in vitro by Urien et al.[29]. The physiological consequence of this observation is difficult to interpret. This suggests that a higher vinorelbine blood concentrations might be observed in patients with high platelet counts and consequently the drug might produce substantial effects in haematological cell lines or on the target tumour. However, the magnitude of the influence of platelet count on blood vinorelbine clearance, even if significant, is relatively small. An increase of 50% in platelet count would produce an increase of 15% in vinorelbine blood concentrations. Since thrombocytopenia is not a limiting toxicity for vinorelbine, variation in platelet count after repeated drug administration is not likely to occur. Therefore, differences in clearance associated with platelet count variations are unlikely between courses of chemotherapy.

From the model building set, body surface area was removed from the clearance equation after the backward elimination procedure.

Despite the obvious strong correlation between weight and BSA (BSA was calculated on the basis of patient weight and height according to the Dubois formula [30]), BSA was re-entered into the final clearance equation and was confirmed to be relevant from the overall dataset. This finding demonstrated that BSA and the weight/Cr_s ratio do not act in the same way to cause the variability in pharmacokinetics of vinorelbine.

The direct relationship between BSA and clearance shown by the first part of the equation 1 supports the clinical practice of dose normalization to BSA recommended for vinorelbine. The second term in the clearance equation 1 might be a function of the renal clearance of vinorelbine, since the weight/Cr_s ratio is a surrogate for creatinine clearance. Calculated from the mean covariate values, the weight/Cr_s accounted for 13% of the total clearance of vinorelbine, which is in agreement with others who have reported that the urinary excretion of unchanged drug is 11% [10] to 14% [31] of the administered dose.

Increased serum creatinine is a common feature in patients with impaired renal function. However, as not much vinorelbine is eliminated via the urine, a decrease in renal function should have little effect on the elimination of vinorelbine from the body. According to equation 1, a patient with a serum creatinine of 500 µm (more than 5-fold higher than the mean value) and weighing 40 kg will have a total body clearance of 38 l h⁻¹ (i.e. only 10% less than average).

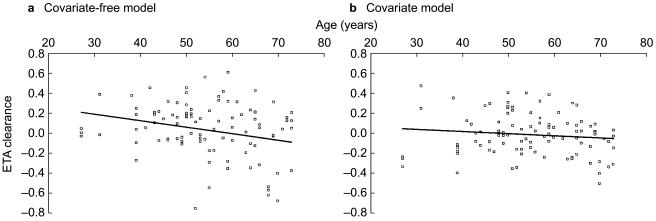
Using a database of 12 elderly patients aged 66–79 years, Gauvin et al.[28], found a direct effect of age on clearance. In the present work, nine patients were older than 65 years and 55 patients were between 27–65 years. The overall age range was therefore wide (27–73 years) and included elderly patients, increasing dramatically the power of the analysis of this covariate. In contrast to Gauvin et al.[28] a very small effect of age was found following univariate NONMEM analysis (Figure 4a). From 55 years (the mean population value) to 80 years, there was only an estimated 10% reduction in total clearance. The small effect of age on vinorelbine pharmacokinetics might be mediated through the influence of the former on renal function.

Figure 4.

Graphs showing the relationship between residuals on clearance (ETA) and age using (a) the covariate-free and (b) the final population model. The tendency observed using the covariate-free model disappeared when all the other relevant covariates were integrated. Linear regression shown.

When including all the covariates (particularly the weight/creatinine ratio) into the final model, age no longer had an influence (Figure 4b). Similarly, the presence of liver metastases in 18 patients did not affect vinorelbine clearance in our population. Robieux and colleagues [14] studied vinorelbine pharmacokinetics in patients with liver metastases, and they demonstrated significant correlations between vinorelbine plasma clearance and the monoethylglycinexylidide test, prothrombin time, albuminaemia and bilirubinaemia. In accordance with our results, hepatic transaminases and γGT did not contribute to the variability in vinorelbine pharmacokinetics. Moreover, these authors showed that the effect of hepatic metastases could only be detected in patients presenting with more than 75% of their liver volume replaced by tumour.

Limited sampling strategy

AUC(0,∞) is highly correlated with both white blood cell and absolute neutrophil count depletion after administration of intravenous vinorelbine [32]. However, the accurate determination of AUC(0,∞) requires a large number of samples when using a classical model independent approach. PK/PD investigations cannot be performed in phase II studies when intensive sampling is not possible. Therefore, identification of several optimal but limited sampling strategies is an attractive prospect. The present work assessed several sparse sampling schedules compatible with clinical practice and patient comfort.

The best limited sampling design required three samples, one immediately before the end of infusion, one 3 h and one 24 h later. Other sparse data designs, also requiring three measured concentrations gave acceptable results in the determination of individual Bayesian AUC(0,∞). An accurate estimation of the terminal half-life of 40 h was also obtained which is in accordance with previously published work [10, 31, 33].

The sparse data designs with only two measures of concentration (3 h or 6 h and 24 h after dosing) gave good predictive performances. Sabot and colleagues [27], using plasma concentrations from eight patients who received i.v. vinorelbine, suggested sampling at either 1–6–24 h or 6–24 h. However, even if statistically acceptable, these schedules could yield very inaccurate predictions of the early phase (t_1/2,_α ranging from 4 to 11 min) of the blood curve if drug administration is not strictly controlled (e.g. if the infusion rate is irregular or if the duration of infusion changes). A sampling time immediately before or in the early minutes after the end of infusion is then highly recommended.

In summary, the present work described a population model for vinorelbine pharmacokinetics derived from three phase I studies. The inclusion of a database of 64 patients allowed the identification of a set of covariates that could influence vinorelbine pharmacokinetics. The development and validation of an optimal limited sampling design will foster further analyses leading to a better understanding of intravenous vinorelbine pharmacokinetics.