Abstract
Aims
E7070 is a novel, sulphonamide anticancer agent currently under clinical development for the treatment of solid tumours. The aim of this study was to develop and validate limited sampling strategies for the prediction of E7070 exposure in two different treatment schedules for phase II studies using the Bayesian estimation approach.
Methods
Data from two phase I dose finding studies were used in which E7070 was administered either as a single 1 h infusion or as a daily 1 h infusion for 5 days. Plasma concentration-time data from 75 patients were randomly divided into an index data set, used for the development of the strategies, and a validation data set. Population pharmacokinetic parameters were derived on the basis of the index data set. The D-optimality algorithm was used for the selection of optimal time points for both treatment schedules. The developed strategies were compared by assessment of their predictive performance of exposure, expressed as AUC (area under the plasma concentration vs time curve), in the validation data set.
Results
The developed population pharmacokinetic model comprised three compartments, with saturable distribution to one peripheral compartment and both linear and saturable elimination from the central compartment. For the 1 h infusion, a four sample strategy was selected which resulted in unbiased and accurate predictions of AUC (bias 0.74%, precision 13%). A five sample strategy was generated for the daily times five schedule yielding unbiased (bias 3.2%) and precise (12% precision) predictions of AUC.
Conclusions
Optimal sampling strategies were developed and validated for estimation of E7070 exposure in two different treatment schedules. Both schedules enabled accurate and unbiased predictions of AUC.
Keywords: D-optimality, E7070, limited sampling, pharmacokinetics, population pharmacokinetics
Introduction
E7070 (N-(3-chloro-7-indolyl)-1,4-benzenedisulphonamide) is a novel sulphonamide currently under clinical investigation for the treatment of solid tumours. Sulphonamides have shown a wide variety of pharmacological activity, such as antibacterial, antidiabetic and antithyroid [1]. Continuing research with sulphonamide-based compounds has led to the discovery of compounds with antiproliferative activity. E7070 is one of those compounds and it has shown potent antitumour activity both in vitro (using human cell lines) and in vivo with human tumour xenografts, e.g. HCT116 colon carcinoma and LX-1 nonsmall cell lung carcinoma. It has been suggested that E7070 exerts its antitumour activity by inhibiting the activation of cyclin dependent kinase 2 and cyclin E, which results in a blockade of the transition of the G1 to S phase in the cell cycle [2, 3].
Based on the promising results from preclinical studies, a phase I clinical program was conducted with E7070 administered at four different treatment schedules [4–8]. For each of these the maximum tolerated dose and the dose-limiting toxicities (DLT) have been identified. The DLTs included neutropaenia and thrombocytopaenia. Other adverse events were fatigue, alopecia and local reactions at the site of drug administration. E7070 has shown antitumour activity and stabilization in studies in patients with uterine sarcoma, breast, endometrial, and renal carcinoma. During all four phase I studies, extensive pharmacokinetic sampling was performed in all patients. In all studies, noncompartmental pharmacokinetic analysis demonstrated that, with increasing doses, there are disproportionately larger increases in exposure to E7070 as expressed as AUC (area under the plasma concentration vs time curve) and that this effect is independent of the treatment schedule [4–8].
Currently, phase II clinical studies are ongoing with E7070 to determine further its antitumour activity in different tumour types, including colorectal and nonsmall cell lung cancer. Two different treatment regimens will be applied in these phase II studies: a single 1 h infusion and a 1 h infusion administered daily for 5 consecutive days. During the phase II studies, the complex pharmacokinetic behaviour of E7070 will be assessed further in a large number of patients. Furthermore, the relationship between pharmacokinetics and pharmacodynamics (i.e. tumour response and side-effects) will be investigated. Extensive pharmacokinetic sampling during the phase II studies is impractical. Therefore, optimal sampling strategies are often applied to reduce the number of samples necessary to estimate the pharmacokinetic parameters with adequate accuracy and precision.
Several techniques have been described for the development of optimal sampling strategies. An approach that is commonly applied in oncology is a multivariate linear regression procedure [9–11], which relates the pharmacokinetic parameters of interest to plasma concentrations at certain time points. In this way, one or more time points are selected for the limited sampling strategy that most accurately predict the pharmacokinetic parameter. However, this approach has several disadvantages. It can only be applied for compounds that display linear pharmacokinetics. Furthermore, it requires exact timing of both the infusion and sampling times and is developed for the prediction of only one pharmacokinetic parameter. Bayesian estimation is a second, more flexible approach to obtain individual pharmacokinetic parameter estimates [12, 13]. With this method, individual parameters are obtained on the basis of individual plasma concentration time data and a priori established population pharmacokinetic parameters. Optimal sampling can be selected by application of the D-optimality criterion [14].
The aim of the present study was to develop and validate limited sampling strategies for the prediction of the individual's exposure to E7070 using the Bayesian estimation approach. These strategies were developed for both treatment schedules that are being used in the phase II studies, the 1 h infusion and the five daily dose schedule.
Methods
Patients and pharmacokinetic studies
The development and validation of the optimal sampling strategies was performed using pharmacokinetic data from two phase I dose finding studies which were conducted with E7070. In the first study, E7070 was administered as a 1 h intravenous infusion, every 3 weeks and 40 patients were treated at 8 different dose levels between 50 and 1000 mg m−2. The second study involved a 1 h intravenous infusion of E7070 daily for 5 days, every 3 weeks. A total of 35 patients were treated on this schedule with doses ranging from 10 to 200 mg m−2 day−1. In both studies, serial blood sampling was performed during the first treatment cycle in order to characterize the pharmacokinetic profile of E7070 with each treatment regimen. With the 1 h infusion study, samples were taken at 17 time points: pretreatment, at 30 min after the start of infusion, at the end of infusion and at 10 and 30 min and 1, 2, 4, 6, 8, 12, 24, 36, 48, 72, 96 and 120 h after the end of infusion. Both day 1 and day 5 of treatment cycle 1 were sampled in the multiple dose study. On day 1, 11 samples were taken: pretreatment, at 30 min after the start of infusion, at the end of infusion and at 10 and 30 min and 1, 2, 4, 6, 8, and 12 h after the end of infusion. On day 5 and later days, 15 samples were taken: pretreatment (i.e. 23 h after the end of the 4th administration), at the end of infusion and at 10 and 30 min and 1, 2, 4, 6, 8, 12, 24, 36, 48, 72, 96 and 168 h after the end of infusion. Furthermore, samples were taken at times of peak and trough concentrations on the intervening days.
High performance liquid chromatography with u.v.-detection was used for the quantification of E7070 in plasma (NOTOX, 's Hertogenbosch, The Netherlands). The method was linear between 0.02 and 0.50 µg ml−1 with a lower limit of quantification of 25 ng ml−1. The within-batch and between-batch accuracy and precision were < 18.8%. Briefly, 0.5 ml plasma was supplemented with 1.0 ml of 0.1 m phosphate buffer (pH 5.0), and vortex mixed for 5 s. After the addition of 3 ml diethylether, the container was shaken for 10 min prior to centrifugation at 1500 g for 5 min. The upper layer was pipetted off and added to 200 µl (99:1 v/v) diethylether/glycerol. The organic phase was evaporated to dryness under a nitrogen-stream at 30 °C over approximately 20 min. This residue was dissolved in 200 µl end solution. A 100 µl aliquot of this solution was injected onto the chromatographic system.
The 75 patients were randomly divided into an index data set, which was used for the development of the limited sampling strategies, and a second data set, used for the validation of the derived schedules. Patients from both studies were equally divided among the index and the validation data set. All patients gave written informed consent and the study protocols were approved by the Medical Ethics Committee in all study centres.
Development of limited sampling strategies
Development of a population pharmacokinetic model
A population pharmacokinetic model was developed to describe the pharmacokinetic profile of E7070 in both treatment regimes. Non-compartmental analyses for both studies revealed that AUC increased disproportionately with dose [4, 5]. In Figure 1, typical plasma concentration time profiles are shown for two patients treated with E7070 in the 1 h infusion or with the 5 day regimen. The bell-shaped terminal phase of the curve indicates that the pharmacokinetics of E7070 are nonlinear in both treatment schedules. As a result, several multicompartmental, nonlinear models were evaluated, including nonlinear distribution and elimination. The pharmacokinetic models were fitted to the index data set using the NONMEM program (double precision, version V. level 1.1) [15], with the NMTRAN preprocessor and the PREDPP package (ADVAN6), operating on an MS-DOS computer. The models developed were compared using the objective function value, a goodness-of-fit criterion provided by NONMEM. Discrimination between hierarchical models was determined with the log-likelihood ratio test [15]. A P value of 0.001 representing a decrease in objective function of 10.8 was considered statistically significant. For nonhierarchical models the objective function value can not be used for formal testing, but a decrease in objective function of 10.8 units between models with the same number of parameters was considered a real difference in goodness-of-fit.
Figure 1.
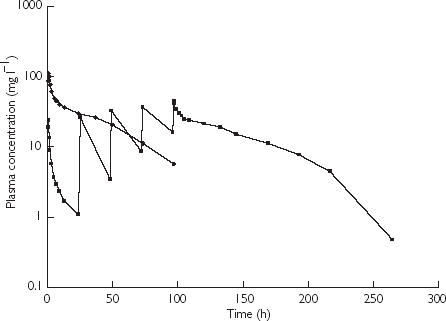
Typical plasma concentration time profiles in patients treated with E7070 in a single1 h infusion and a 1 h infusion daily for 5 days at 700 mg m−2 (♦) and 160 mg m−2 day−1 (▪), respectively.
The model that most accurately described the data comprised 3 compartments with saturable distribution to one peripheral compartment and two parallel pathways of elimination, namely a saturable and a linear route of elimination (Figure 2) [16, 17]. Saturable elimination was modelled using the Michaelis-Menten equation described by the maximal elimination capacity expressed as amount per unit time denoted as Vmax (mg h−1) and the Km (mg l−1) which is the concentration at which the elimination rate is half-maximal. Saturable distribution was modelled in an analogous manner, defining Dmax (mg h−1), the maximal distribution capacity expressed as amount per unit time and Dm (mg l−1), the concentration at which the distribution rate is half-maximal [16, 17]. Linear elimination from the central compartment was denoted by the elimination rate constant K10 (h−1). Other basic pharmacokinetic parameters were V (l), the volume of distribution of the central compartment and the intercompartmental rate constants K21 (h−1), K13 (h−1) and K31 (h−1). Interindividual variability for the PK parameters was modelled using a proportional error model assuming constant coefficients of variation. For example, variability in V was estimated using:
where Vi represents the V of the ith individual, Vpop is the population value and η is the interindividual random effect with mean 0 and variance ω2. The difference between the jth measured concentration in the ith individual (Cobsij) and its respective prediction (Cpredij) was modelled with a combined additive-proportional error model:
where ɛ is an independent random variable with mean 0 and variance σ2. The first-order method (FO) [15] was used throughout the analyses.
Figure 2.
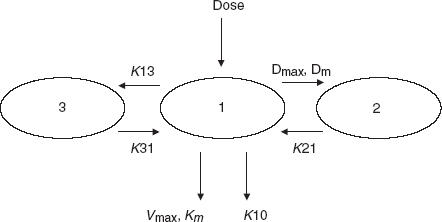
Population pharmacokinetic model for E7070.
Selection of optimal time points
The optimal sampling times were determined using the D-optimality algorithm, as implemented in the software package ADAPT II (release 4, 1997) [18] using the parameter estimates obtained in the population analysis with the index set. As AUC is not a primary model parameter, estimates of those parameters were optimized that have a strong influence on AUC. In this context, V and Vmax were important parameters. Nevertheless, the design was optimized for all model parameters separately and for different combinations of these parameters. Therefore, different numbers of parameters were to be optimized with each design. It appeared that this resulted in comparable sampling times for all combinations. Several sampling schemes were constructed for both treatment regimens, based on the optimal sampling times generated by D-optimality. Furthermore, it was accepted that the sampling schemes should be practically feasible in the phase II studies and therefore the strategies were designed to provide sampling times within a time window up to 168 h after the start of infusion for the 1-h schedule or up to 168 h after the start of the fifth administration (i.e. 264 h after the first administration) for the 5 day schedule. A sample at the end of the infusion was included in all schedules. The sampling schedules developed were validated using the plasma concentration-time data of the validation data set. Individual Bayesian estimates of AUC were generated using the values of the population pharmacokinetic parameters for both the fixed and random effects of the index data set and the plasma concentrations of the validation set at the optimal time points generated with D-optimality using the POSTHOC option in NONMEM. As E7070 displays nonlinear pharmacokinetics, AUC cannot be calculated using the equation: AUC = dose/CL. Therefore, AUC values were estimated using NONMEM, with the use of a fourth hypothetical compartment, as described previously [19]. The change of the amount in this compartment (A(4)) over time (t) in this compartment was described by the following differential equation:
where C(1) represents the concentration of E7070 in the central compartment. Integration of this equation yields the AUC which accumulates over time. Extrapolation to infinity was accomplished by extending the AUC up to a very late time point (e.g. 15.00 h), at which E7070 was no longer present in the body.
Determination of pharmacokinetic reference parameters
Reference individual values of AUC for all patients in the validation data set were generated using the complete plasma concentration time profile. The development of the population pharmacokinetic model indicated that the nonlinear pharmacokinetic behaviour of E7070 was described by a three compartment model with nonlinear distribution as well as both linear and nonlinear elimination from the central compartment. The individual AUC values were obtained by fitting the developed model to the individual data from all patients, using a fourth hypothetical compartment, as described above. For several patients, the individual data were not sufficient for the estimation of all parameters of the developed population model. In those cases, other three compartment models were applied: a linear three compartment model, a model with nonlinear elimination or a model with parallel linear and nonlinear elimination. Residual variability was modelled using a proportional error model or a combined additive and proportional error model. Discrimination between the models was based on the objective function value.
Comparison of the strategies
The validation of the limited sampling strategies was conducted on a data set distinct from the index data set. The predictive performance of the various strategies was evaluated using the mean relative prediction error (%MPE) and the corresponding 95% confidence interval (CI) as a measure of bias and the root mean squared relative prediction error (%RMSE) and the corresponding 95% CI as a measure of precision [20]. The %MPE and MSE (mean squared error) and the corresponding standard errors are given by:
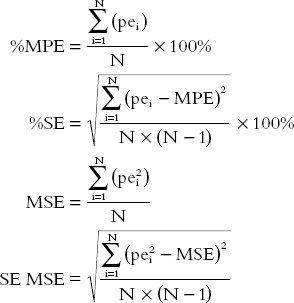 |
in which N is the number of pairs of true with predicted values and pei is the relative prediction error for each pair[ln(AUCpredicted) – ln(AUCtrue value)]. The %RMSE is calculated as the square root of the MSE, multiplied by 100% and the corresponding 95% CI is defined as the square root of the endpoints of the 95% CI of the MSE, multiplied by 100%. The sampling schedule is considered to be optimal when it yields predictions of the parameter of interest that are highly precise (% RMSE < 15%) and without statistically significant bias.
Results
Patients and pharmacokinetic studies
In total, data from 75 patients were available for these analyses. The index data set consisted of 37 patients (20 and 17 patients from the 1 h and 5 day schedule, respectively), resulting in 819 observed plasma concentrations. The validation data set comprised 38 patients (20 and 18 patients, respectively), containing 829 observed plasma concentrations.
Population pharmacokinetic model
The data of the index set could be adequately described by a three compartment model with saturable distribution to one peripheral compartment and a saturable and linear two pathway elimination from the central compartment. The results of the fit are summarized in Table 1. Pharmacokinetic modelling of the validation data set and of the combined data set yielded comparable estimates of all parameters (Table 1), indicating the stability of the model. All structural parameters were estimated with an acceptable coefficient of variation (5.2–23% and 5.4–40% for the index and validation data set, respectively). In both the index and validation data set interindividual variability could be quantified for all pharmacokinetic parameters except for Km and K31. This should not be interpreted as an absence of variability but simply that the data do not contain enough information to quantify these parameters. Interindividual variability was considerable for Dm, being 130% and 88% for the index and validation data set, respectively. Residual variability consisted of an additive error of 0.015 mg l−1 for the index set and 0.021 mg l−1 for the validation set. The proportional errors were 13% and 15%, respectively.
Table 1.
Population pharmacokinetic parameters of E7070.
| Total data set (n = 75) Estimate (CV%) | Index data set (n = 37) Estimate (CV%) | Validation data set (n = 38) Estimate (CV%) | |
|---|---|---|---|
| Parameter | |||
| V (l) | 6.3 (3.8) | 6.4 (5.2) | 6.3 (5.4) |
| Dmax (mg h−1) | 41 (16) | 47 (21) | 31 (30) |
| Dm (mg l−1) | 3.9 (16) | 4.3 (18) | 2.7 (40) |
| K21 (h−1) | 0.12 (14) | 0.11 (19) | 0.10 (20) |
| K13 (h−1) | 1.1 (7.3) | 1.1 (11) | 1.0 (9.9) |
| K31 (h−1) | 0.51 (7.5) | 0.57 (11) | 0.44 (11) |
| Km (mg l−1) | 0.52 (20) | 0.75 (23) | 0.31 (30) |
| Vmax (mg h−1) | 3.1 (12) | 4.2 (6.4) | 2.7 (17) |
| K10 (h−1) | 0.036 (16) | 0.029 (22) | 0.037 (16) |
| Interindividual variability (%) | |||
| V | 26 (18) | 24 (29) | 27 (24) |
| Dmax | 37 (56) | 39 (62) | 35 (81) |
| Dm | 100 (38) | 130 (38) | 88 (56) |
| K21 | 60 (25) | 56 (24) | 59 (56) |
| K13 | 26 (36) | 26 (58) | 21 (47) |
| Vmax | 48 (40) | 56 (65) | 44 (57) |
| K10 | 62 (42) | 65 (57) | 49 (57) |
| Residual variability | |||
| Proportional error (%) | 15 (6.1) | 13 (9.8) | 15 (6.7) |
| Additive error (mg l−1) | 0.021 (17) | 0.015 (29) | 0.021 (20) |
CV = coefficient of variation.
Determination of pharmacokinetic reference parameters
Individual reference values of AUC for the validation data set were estimated using individual fitted curves with NONMEM. The developed population model could be fitted to nine curves. A three compartment model with both linear and nonlinear elimination was fitted to five curves. A three compartment model with nonlinear elimination was fitted to nine curves, the other 15 curves were described using a linear three compartment model.
Optimal sampling strategies
For the 1 h infusion, optimal time points proved to be samples at 1, 1.5, 7, 25, 97 and 168 h after the start of the infusion. Several strategies, which would be practical in view of the phase II studies, were derived from these optimal time points (see Table 2). A sample at the end of the infusion, i.e. 1 h, was included in all sampling strategies. From all patients in the validation data set, samples were selected closest to the optimal time points. In the validation data set, samples at 168 h after start of treatment were only available for three patients from the 1 h infusion study. Therefore, this time point could not be evaluated. The predictive performance of the developed strategies is summarized in Table 3. A sampling schedule based on two time-points (schedule 1) resulted in 8.4% overestimated predictions of AUC, although this bias was not statistically significant. However the predictions were imprecise (precision 43%). Addition of a third sample improved both bias and precision (schedules 2–4). A strategy based on five samples yielded the best predictive performance of all schedules tested. However, a sample at 7 h appeared to be not practical in the phase II studies. Therefore, a four point sampling schedule with samples at 1, 1.5, 25 and 97 h after start of the infusion was considered to be the optimal strategy. The resulting predictions of AUC were very adequate with a statistically insignificant bias of 0.74% and 13% precision. In Figure 3a, the predicted values of AUC using this model are plotted against the reference values.
Table 2.
Optimal sampling strategies for the 1 h infusion.
| Strategy | Number of samples | Sampling times after start of infusion | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 1 h | 1.5 h | |||
| 2 | 3 | 1 h | 1.5 h | 7 h | ||
| 3 | 3 | 1 h | 1.5 h | 25 h | ||
| 4 | 3 | 1 h | 1.5 h | 97 h | ||
| 5 | 4 | 1 h | 1.5 h | 7 h | 25 h | |
| 6 | 4 | 1 h | 1.5 h | 7 h | 97 h | |
| 7 | 4 | 1 h | 1.5 h | 25 h | 97 h | |
| 8 | 5 | 1 h | 1.5 h | 7 h | 25 h | 97 h |
Table 3.
Predictive performance for the different sampling strategies of E7070 AUC for the 1 h infusion.
| Strategy | Number of samples | % Bias (95% CI) | % Precision (95% CI) |
|---|---|---|---|
| 1 | 2 | 8.4 (−12, 29) | 43 (28, 54) |
| 2 | 3 | 4.8 (−11, 21) | 33 (24, 41) |
| 3 | 3 | 4.9 (−5.1, 15) | 22 (16, 26) |
| 4 | 3 | 6.7 (−4.9, 19) | 26 (8.9, 35) |
| 5 | 4 | 3.8 (−5.9, 14) | 21 (15, 25) |
| 6 | 4 | 1.2 (−6.9, 9.3) | 17 (0, 24) |
| 7 | 4 | 0.74 (−5.6, 7.1) | 13 (5.6, 18) |
| 8 | 5 | −0.67 (−5.6, 4.3) | 10 (7.1, 13) |
CI = confidence interval.
Figure 3.
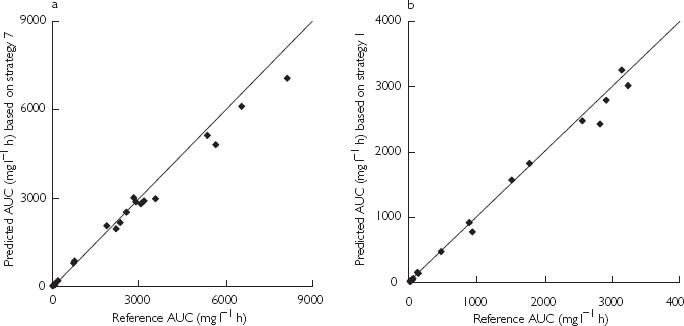
Predicted values of AUC using the optimal sampling strategies vs reference values of AUC for after a single 1 h infusion schedule (panel a) and after a 1 h infusion daily for 5 days (panel b). The solid line represents the line of identity.
The optimal time points selected for the 1 h infusion 5 day schedule included samples at 97 h, 97.5, 103, 120, 168, 192 and 264 h after the start of the first infusion. Furthermore, samples were included at 1 h after the start of the first infusion (1 h) and a sample just prior to the fifth infusion. Several sampling strategies composed from these time points were evaluated and are listed in Table 4. The predictive performance of the corresponding models is presented in Table 5. A strategy including all selected time points (i.e. 9 samples) showed the best predictive performance, although all strategies tested appeared to yield unbiased and precise predictions of AUC. It appeared that samples at 1, 103, 120 and 192 h were not essential for an accurate prediction of AUC with this schedule. A five point strategy with samples at 96, 97, 97.5, 168 and 264 h after the start of the first infusion was selected to be the optimal sampling schedule for the multiple dosing regimen. This strategy demonstrated good predictive performance (bias 3.2% and precision 12%) and could be easily implemented in the phase II study protocols. Figure 3b presents a plot of the predicted values of AUC using this strategy against the reference values.
Table 4.
Optimal sampling strategies for the 1 h infusion of E7070 daily for 5 days schedule.
| Strategy | Number of samples | Sampling times after start of infusion | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 96 h | 97 h | 97.5 h | 168 h | 264 h | ||||
| 2 | 6 | 1 h | 96 h | 97 h | 97.5 h | 120 h | 192 h | |||
| 3 | 6 | 1 h | 96 h | 97 h | 97.5 h | 120 h | 168 h | |||
| 4 | 6 | 96 h | 97 h | 97.5 h | 120 h | 168 h | 264 h | |||
| 5 | 6 | 1 h | 96 h | 97 h | 97.5 h | 168 h | 264 h | |||
| 6 | 7 | 1 h | 96 h | 97 h | 97.5 h | 103 h | 120 h | 168 h | ||
| 7 | 7 | 1 h | 96 h | 97 h | 97.5 h | 103 h | 120 h | 168 h | 192 h | 264 h |
| 8 | 9 | 1 h | 96 h | 97 h | 97.5 h | 120 h | 168 h | 264 h | ||
Table 5.
Predictive performance for the different sampling strategies for prediction of E7070 AUC for 1 h infusion daily for 5 days.
| Strategy | Number of samples | % Bias (95% CI) | % Precision (95% CI) |
|---|---|---|---|
| 1 | 5 | 3.2 (−2.6, 9.0) | 12 (6.4, 15) |
| 2 | 6 | 3.6 (−3.1, 10) | 14 (3.8, 19) |
| 3 | 6 | 2.1 (−4.4, 8.6) | 13 (0, 18) |
| 4 | 6 | 2.6 (−2.3, 7.6) | 10 (4.6, 13) |
| 5 | 6 | 1.5 (−5.5, 8.5) | 14 (2.9, 19) |
| 6 | 7 | −0.52 (−5.8, 4.7) | 10 (0, 16) |
| 7 | 7 | 1.5 (−5.5, 8.5) | 14 (2.9, 19) |
| 8 | 9 | 0.43 (−5.1, 5.9) | 11 (0, 17) |
CI = confidence interval.
Discussion
The present study focused on the development and validation of limited sampling strategies for the prediction of E7070 AUC in cancer patients. The AUC value is considered a measure of total exposure to the drug and is often used in oncology in relation to efficacy and toxicity [21]. Furthermore, the Bayesian method used allows the estimation of other potentially important parameters, such as the maximum concentration or the time above a certain threshold concentration. The limited sampling strategies developed here will be applied in phase II studies that utilize two different treatment schedules, a 1 h infusion schedule and a 1 h infusion daily for 5 days. Complete plasma concentration profiles of the patients in two phase I studies were used for the development and validation of the sampling strategies.
For the estimation of individual pharmacokinetic parameters using the Bayesian approach, pharmacokinetic parameters of the study population need to be established a priori. A population pharmacokinetic model was developed using the index data set, comprising data from 37 patients treated on either infusion schedule. The pharmacokinetic model which most accurately described the data consisted of three compartments with saturable distribution to one of the peripheral compartments and both a linear and a saturable pathway of elimination [16]. Interindividual variability could be quantified for all parameters except for K31 and Km. Modelling of the data of the 38 patients in the validation set and of the total data set (n = 75) yielded parameter estimates that were essentially equal to those of the index set, indicating that the developed population model was sufficiently robust. Furthermore, the model accurately described the individual pharmacokinetic profile, as residual variability was small, the proportional error being 13% and 15% for the index and validation data set, respectively. The additive component of the residual variability in both data sets was near the lowest observed concentration (i.e. 0.015 and 0.016 mg l−1, respectively), but inclusion of this parameter in the model significantly improved the fit to both data sets.
A Bayesian approach for optimal sampling has the advantage of being able to obtain a full pharmacokinetic profile using a sparse data set. Furthermore, there is no need for the infusion times or sampling times to be exact. The D-optimality criterion is the most often used design criterion for nonlinear models and it was used in the present study for the determination of the optimal time points within a certain time window. However, this criterion does not take into account prior knowledge of the parameter distributions [14, 22]. The efficiency of the design procedures could be improved by incorporating this prior information [22]. However, to our knowledge, software incorporating prior knowledge is not commercially available.
In the present study, optimal sampling strategies were developed and validated for the prediction of E7070 AUC with two treatment regimens. With the 1 h infusion, a four point model was selected. However, the D-optimality criterion indicated that inclusion of a sample at 168 h, would improve the predictions. The benefit of this sample could not be evaluated, as too few samples were available at this time point. However, inclusion of a sample at 264 h (i.e. 168 h after the start of the 5th administration) improved AUC predictions for the 5 day schedule. Furthermore, it is likely that a sample taken at a late time point of approximately 1 week after treatment could improve the determination of Vmax, which influences the AUC value. Therefore, the inclusion of this data point in the model was recommended. The developed sampling schedules for the treatment regimens appeared to yield very accurate predictions of AUC although the requirement for five samples is considerable. However, in view of the complex pharmacokinetic properties of E7070 with both saturable distribution and elimination, this number of samples seems to be necessary. Furthermore, these five point sampling strategies will not only enable the prediction of AUC in the phase II studies, but will also allow the description of the full pharmacokinetic profile of E7070 using Bayesian estimation. Moreover, the proposed sampling times could easily be incorporated into the study protocols.
In conclusion, we have developed and validated limited sampling strategies for the prediction of total exposure to E7070, expressed as AUC. For both treatment schedules, the strategies provided accurate and precise predictions of AUC and will facilitate pharmacokinetic monitoring during phase II studies. As the pharmacokinetics of E7070 are very complex, further characterization of its full pharmacokinetic profile in larger numbers of patients is essential, and this will enable investigation of the relationships between response or toxicity and exposure to the drug.
References
- 1.Owa T, Okachi T, Yoshimatsu K, et al. A focused compound library of novel N-(7-indolyl) benzenesulfonamides for the discovery of potent cell cycle inhibitors. Bioorg Med Chem Lett. 2000;10:1223–1226. doi: 10.1016/s0960-894x(00)00219-5. [DOI] [PubMed] [Google Scholar]
- 2.Owa T, Yoshino H, Okauchi T, et al. Discovery of novel anti-tumor sulfonamides targeting G1 phase of the cell cycle. J Med Chem. 1999;42:3789–3799. doi: 10.1021/jm9902638. [DOI] [PubMed] [Google Scholar]
- 3.Fukuoka K, Usuda J, Fukumoto H, et al. Mechanism of action of a novel sulfonamide antitumor agent, E7070. Proc Am Assoc Cancer Res. 2000;41:59. [Google Scholar]
- 4.Raymond E, ten Bokkel Huinink WW, Taied J. Phase I and pharmacokinetic study of E7070, a new chloro-indolysulfonamide, given as a 1-hour infusion every 3 weeks in patients with advanced solid tumors. Proc Am Assoc Cancer Res. 2000;41:611. [Google Scholar]
- 5.Punt CJA, Fumoleau P, van de Walle B, Faber MN, Ravic M, Campone M. Phase I and pharmacokinetic study of E7070, a novel sulfonamide, given at a daily times five schedule in patients with advanced solid tumors. A study by the EORTC-Early Clinical Studies Group (ECSG) Ann Oncol. 2001;12:1289–1293. doi: 10.1023/a:1012287111922. [DOI] [PubMed] [Google Scholar]
- 6.Droz JP, Roch H, Zanetta S, et al. Phase I trial of five-days continuous infusion E7070 [N (3-chloro-7-indoly) -1,4-bezene-disulfonamide] in patients with solid tumors. Proc Am Assoc Cancer Res. 2001;41:609. [Google Scholar]
- 7.Dittrich C, Dumez H, Calvert H. Phase I and pharmacokinetic study of E7070 in patients with solid tumors as single IV infusion, weekly x 4, q 6 weeks. Proc Am Assoc Cancer Res. 2001;41:609. [PubMed] [Google Scholar]
- 8.Raymond E, Fumoleau P, Roché H, et al. Combined results of 4 phase I and pharmacokinetic studies of E7070, a novel chloroindoly-sulphonamide inhibiting the activation of cdk2 and cyclin E. Clin Cancer Res. 2000;6:4529s. [Google Scholar]
- 9.Jodrell DI, Murray LS, Hawtof J, Graham MA, Egorin MJ. A comparison of methods for limited-sampling strategy design using data from a phase I trial of the anthrapyrazole DuP-941. Cancer Chemother Pharmacol. 1996;37:356–362. doi: 10.1007/s002800050397. [DOI] [PubMed] [Google Scholar]
- 10.Sørensen BT, Stömgren A, Jakobsen P, Jakobsen A. A limited sampling method for the estimation of the carboplatin area under the curve. Cancer Chemother Pharmacol. 1993;31:324–327. doi: 10.1007/BF00685679. [DOI] [PubMed] [Google Scholar]
- 11.Van Warmerdam LJC, ten Bokkel Huinink WW, Maes RAA, Beijnen JH. Limited sampling models for anticancer agents. J Cancer Res Clin Oncol. 1994;120:427–433. doi: 10.1007/BF01240143. [DOI] [PubMed] [Google Scholar]
- 12.Baille P, Bruno R, Schellens JHM, et al. Optimal sampling strategies for Bayesian estimation of docetaxel (Taxotere) clearance. Clin Cancer Res. 1997;3:1535–1538. [PubMed] [Google Scholar]
- 13.Thomson AH, Whitting B. Bayesian parameter estimation and population pharmacokinetics. Clin Pharmacokinet. 1992;22:447–467. doi: 10.2165/00003088-199222060-00004. [DOI] [PubMed] [Google Scholar]
- 14.D’Argenio DZ. Optimal sampling times for pharmacokinetic experiments. J Pharmacokinet Biopharm. 1981;9:739–756. doi: 10.1007/BF01070904. [DOI] [PubMed] [Google Scholar]
- 15.Beal SL, Boeckman AJ, Sheiner LB. NONMEMUser's Guide, Part V. San Francisco: University of California at San Francisco; 1988. [Google Scholar]
- 16.van Kesteren Ch, Mathôt RAA, Raymond E, et al. Population pharmacokinetic analysis of the novel anti-cancer agent E7070 in three phase I clinical studies using non-linear mixed effects modeling (NONMEM) Proc Am Soc Clin Oncol. 2001;20:93a. [Google Scholar]
- 17.Karlsson MO, Molnar V, Freijs A, et al. Pharmacokinetic models for the saturable distribution of paclitaxel. Drug Metab Dispos. 1999;27:1220–1223. [PubMed] [Google Scholar]
- 18.D’Argenio DZ, Schumitzky A. Biomedical Simulations Resource. Los Angeles: University of Southern California; 1997. ADAPT II Users Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. [Google Scholar]
- 19.Kerbusch T, De Kraker J, Mathôt RAA, Beijnen JH. Population pharmacokinetics of ifosfamide and its dechloroethylated and hydroxylated metabolites in children with malignant disease: a sparse sampling approach. Clin Pharmacokinet. 2001;40:615–625. doi: 10.2165/00003088-200140080-00005. [DOI] [PubMed] [Google Scholar]
- 20.Sheiner LB, Beal SL. Some suggestions for measuring predictive performance. J Pharmacokinet Biopharm. 1981;9:503–512. doi: 10.1007/BF01060893. [DOI] [PubMed] [Google Scholar]
- 21.van den Bongard HJGD, Mathôt RAA, Beijnen JH, et al. Pharmacokinetically guided administration of chemotherapeutic agents. Clin Pharmacokinet. 2000;39:345–367. doi: 10.2165/00003088-200039050-00004. [DOI] [PubMed] [Google Scholar]
- 22.Merlé Y, Mentré F, Mallet A. Designing an optimal experiment for Bayesian estimation: application to the kinetics of iodine thyroid uptake. Stat Med. 1994;13:185–196. doi: 10.1002/sim.4780130209. [DOI] [PubMed] [Google Scholar]


