BLAT—The BLAST-Like Alignment Tool

Abstract

Analyzing vertebrate genomes requires rapid mRNA/DNA and cross-species protein alignments. A new tool, BLAT, is more accurate and 500 times faster than popular existing tools for mRNA/DNA alignments and 50 times faster for protein alignments at sensitivity settings typically used when comparing vertebrate sequences. BLAT's speed stems from an index of all nonoverlapping K-mers in the genome. This index fits inside the RAM of inexpensive computers, and need only be computed once for each genome assembly. BLAT has several major stages. It uses the index to find regions in the genome likely to be homologous to the query sequence. It performs an alignment between homologous regions. It stitches together these aligned regions (often exons) into larger alignments (typically genes). Finally, BLAT revisits small internal exons possibly missed at the first stage and adjusts large gap boundaries that have canonical splice sites where feasible. This paper describes how BLAT was optimized. Effects on speed and sensitivity are explored for various K-mer sizes, mismatch schemes, and number of required index matches. BLAT is compared with other alignment programs on various test sets and then used in several genome-wide applications. http://genome.ucsc.edu hosts a web-based BLAT server for the human genome.

Some might wonder why in the year 2002 the world needs another sequence alignment tool. The local alignment problem between two short sequences was solved by the Smith-Waterman algorithm in 1980 (Smith and Waterman 1981). The FASTA (Pearson and Lipman 1988) and the BLAST family of alignment programs including NCBI BLAST (Altschul et al. 1990, 1997), MegaBLAST (Zhang et al. 2000), and WU-BLAST (Altschul et al. 1990; Gish and States 1993; States and Gish 1994) provide flexible and fast alignments involving large sequence databases, and are available free on many web sites. Sim4 (Florea et al. 1998) does a fine job of cDNA alignment. The SAM program (Karplus et al. 1998) and PSI-BLAST (Altschul et al. 1997) slowly but surely find remote homologs. Gotoh's many algorithms robustly deal with gaps (Gotoh 1990, 2000). SSAHA (Ning et al. 2001) maps sequence reads to the genome with blazing efficiency.

In the process of assembling and annotating the human genome, I was faced with two very large-scale alignment problems: aligning three million ESTs and aligning 13 million mouse whole-genome random reads against the human genome. These alignments needed to be done in less than two weeks' time on a moderate-sized (90 CPU) Linux cluster in order to have time to process an updated genome every month or two. To achieve this I developed a very-high-speed mRNA/DNA and translated protein alignment algorithm.

The new algorithm is called BLAT, which is short for “BLAST-like alignment tool.” BLAT is similar in many ways to BLAST. The program rapidly scans for relatively short matches (hits), and extends these into high-scoring pairs (HSPs). However, BLAT differs from BLAST in some significant ways. Where BLAST builds an index of the query sequence and then scans linearly through the database, BLAT builds an index of the database and then scans linearly through the query sequence. Where BLAST triggers an extension when one or two hits occur in proximity to each other, BLAT can trigger extensions on any number of perfect or near-perfect hits. Where BLAST returns each area of homology between two sequences as separate alignments, BLAT stitches them together into a larger alignment. BLAT has special code to handle introns in RNA/DNA alignments. Therefore, whereas BLAST delivers a list of exons sorted by exon size, with alignments extending slightly beyond the edge of each exon, BLAT effectively “unsplices” mRNA onto the genome—giving a single alignment that uses each base of the mRNA only once, and which correctly positions splice sites.

BLAT is available in several forms. Since building an index of the whole genome is a relatively slow procedure, a BLAT server is available which builds the index and keeps it in memory. A BLAT client can then query the index through the server. The client/server version is especially suitable for interactive applications, and is available via a web interface at http://genome.ucsc.edu. A stand-alone BLAT is also available, which is more suitable for batch runs on one or more CPUs. Both the client/server and the stand-alone can do comparisons at the nucleotide, protein, or translated nucleotide level.

RESULTS

BLAT is currently used in three major applications in conjunction with http://genome.ucsc.edu. BLAT is used to produce the human EST and mRNA alignments. The human EST alignments compared 1.75 × 10⁹ bases in 3.73 × 10⁶ ESTs against 2.88 × 10⁹ bases of human DNA and took 220 CPU hours on a Linux farm of 800 MhZ Pentium IIIs. BLAT was used in translated mode to align a 2.5× coverage unassembled whole-genome shotgun of the mouse versus the masked human genome. This involved 7.51 × 10⁹ bases in 1.33 × 10⁷ reads and took 16,300 CPU hours. The client/server version of BLAT is used to power untranslated and translated interactive searches on http://genome.ucsc.edu. Researchers all over the world use BLAT to perform thousands of interactive sequence searches per day. The nucleotide server has sustained over 500,000 search requests per day from program-driven queries. We do ask those researchers who are doing more than a few thousand program-driven queries to obtain a copy of BLAT to use on their own servers. The nucleotide server is not as efficient as the stand-alone program, since to save memory it does not keep the genome in memory, only the index. The index uses approximately 1 gigabyte on unmasked DNA in untranslated mode, and approximately 2.5 gigabytes on masked DNA in translated mode. The translated mode server by default is less sensitive than the default stand-alone settings. It requires three perfect amino acid 4-mers to trigger an alignment. The untranslated server usually responds to a 1000-base cDNA query in less than a second. The translated server usually responds to a 400-amino acid protein query in <5 sec.

Evaluating mRNA/DNA Alignments

As a test of BLAT, I remapped 713 mRNAs corresponding to genes that the Sanger Centre has annotated on chromosome 22 (Dunham et al. 1999) back to chromosome 22 with BLAT and with Sim4 (Florea 1998). When BLAT produced multiple alignments for an mRNA, only the highest scoring alignment was kept. In 99.99% of the annotated bases, the BLAT alignment agreed with the Sanger annotations. There were 107 bases in 10 genes where there was disagreement. In five of the 10 genes, the disagreement was only in the placement of nonstandard splice sites. In two cases, BLAT did not find small (<32-base) initial exons. In one case, an exon of six bases was present and aligning fully, but in a different place than annotated (where it also aligned fully, but with better flanking splice sites). In one case, BLAT positioned an intron to conform with the consensus sequence on the wrong strand. That is, the gap corresponding to the intron was positioned to have CT/AC rather than GT/AG ends. The final case was a 38-base sequence that BLAT was unable to place because the middle contained some degenerate sequence. The BLAT alignments were done at the default settings and took 26 sec.

The Sim4 alignments of the same data took 17,468 sec (almost 5 h). They agreed with the Sanger annotations in 99.66% of the bases. There were disagreements between the Sim4 alignments and the Sanger annotations from various causes in 52 of the genes. Most of these disagreements were small.

Evaluating Mouse/Human Translated Alignments

Though the translated modes of BLAT are relatively new, they are quick and effective. The translated mode of BLAT was inspired by the Exofish research at Genoscope (Roest Crollius et al. 2000). Exofish showed that a TBLASTX run using an identity matrix (where matches were weighted +15 and mismatches −12 for all amino acids) and a word size of 5 was quite effective in aligning coding regions conserved between Homo sapiens and Tetraodon nigroviridis. For human and mouse it has been shown that gapless alignments are in many ways preferable to gapped alignments for detecting coding regions (Wiehe et al. 2001). Table 1 shows the timings of BLAT and WU-TBLASTX run on a modest-sized data set at gapless Exofish-like settings. BLAT runs much faster, making it feasible to compare vertebrate genomes quickly enough to keep up with the vast output of today's sequencing centers.

Table 1.

Timing of BLAT vs. WU-TBLASTX on a Data Set of 1000 Mouse Reads and a RepeatMasked Human Chromosome 22

Method	K	N	Matrix	Time
WU-TBLASTX	5	1	+15/−12	2736 s
WU-TBLASTX	5	1	BLOSUM62	2714 s
BLAT	5	1	+2/−1	61 s
BLAT	4	2	+2/−1	37 s

The first WU-TBLASTX run was performed using the settings used in Exofish. The second WU-TBLASTX run was performed using the settings B = 9000 V = 9000 hspmax = 4 topcomboN = 1 W = 5 E = 0.01 Z = 3000000000 nogaps filter = xnu + seg. The K column indicates the size of the perfectly matching hit that serves as a seed for an alignment. The N column indicates how many hits in a gapless 100-amino acid window were required to trigger a detailed alignment. The Matrix column describes the match/mismatch scores or the substitution score matrix used. 

Pankaj Agarwal provided a WU-TBLASTX alignment of 13 million mouse genomic reads versus human chromosome 22 run under a gapless setting that should theoretically be somewhat more sensitive than the matrix used for the Exofish settings because of the use of the BLOSUM62 matrix (P. Agarwal, pers. comm.). Table 2 shows a comparison between this alignment and a translated BLAT alignment done at the indicated setting. The results were quite comparable in sensitivity.

Table 2.

Sensitivity of WU-TBLASTX and BLAT Applied to 13 Million Mouse Shotgun Reads and Human Chromosome 22

Method	% Chr 22	% RefSeq bases	Enrichment	% RefSeq exons
WU-TBLASTX	2.67%	81.7%	31x	84.5%
BLAT	2.89%	80.8%	28x	86.7%

The “% Chr22” column shows the percentage of chromosome 22 covered by the alignments (genomic density). The next column is the percentage of bases inside of human RefSeq coding sequences covered by the alignments (RefSeq coding density). “Enrichment” is the ratio of the RefSeq coding density compared to genomic density. Higher levels of enrichment indicate more specificity at the base level. The last column shows the percentage of RefSeq coding exons where any part of the exon is covered by an alignment. WU-TBLASTX was run with the parameters described in the second row of Table 1. BLAT was run with using a pair-of-4-mers seed and a score cut off of 30. At these settings, BLAT touches slightly more exons, but WU-TBLASTX covers slightly more bases in exons. 

Other Usage Information

BLAT can also be used in translated mode to align proteins or mRNA from one species against genomic DNA of another species. In translated mRNA/translated DNA mode, BLAT has to align only one strand of the query sequence, speeding it up by a factor of two. In this mode it also becomes more tolerant of intron-induced gaps. BLAT can do protein–protein alignments as well, but it is not likely to be the tool of choice for these. The protein databases are still small enough that BLASTP can handle them easily, and BLASTP is more sensitive than BLAT.

BLAT can handle very long database sequences efficiently. It is more efficient at short query sequences than long query sequences. It is not recommended for query sequences longer than 200,000 bases. It is not necessary to mask the DNA for untranslated BLAT searches. Translated searches generally produce much quicker, cleaner results if the sequence is masked for repeats and low complexity sequence.

METHODS

Algorithm

All fast alignment programs that I am aware of break the alignment problem into two parts. Initially in a “search stage,” the program detects regions of the two sequences which are likely to be homologous. The program then in an “alignment stage” examines these regions in more detail and produces alignments for the regions which are indeed homologous according to some criteria. The goal of the search stage is to detect the vast majority of homologous regions while reducing the amount of sequence that is passed to the alignment stage.

Searching With Single Perfect Matches

A simple and reasonably effective search stage is to look for subsequences of a certain size, k, which are shared by the query sequence and the database. In many practical implementations of this search, every K-mer in the query is compared against all nonoverlapping K-mers in the database. Let's examine the number of homologous regions that are missed, and the number of nonhomologous regions that are passed to the alignment stage using these criteria. First, we'll need some definitions:

K: The K-mer size. Typically this is 8–16 for nucleotide comparisons and 3–7 for amino acid comparisons.

M: The match ratio between homologous areas. This would be typically about 98% for cDNA/genomic alignments within the same species, about 89% for protein alignments between human and mouse.

H: The size of a homologous area. For a human exon this is typically 50–200 bases.

G: The size of the database—3 billion bases for the human genome.

Q: The size of the query sequence.

A: The alphabet size; 20 for amino acids, 4 for nucleotides.

Assuming that each letter is independent of the previous letter, the probability that a specific K-mer in a homologous region of the database matches perfectly the corresponding K-mer in the query is simply:

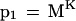1

It is convenient to introduce a term that counts the number of nonoverlapping K-mers in the homologous region:

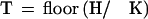2

The probability that at least one nonoverlapping K-mer in the homologous region matches perfectly with the corresponding K-mer in the query is:

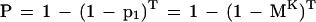3

The number of nonoverlapping K-mers that are expected to match by chance, assuming that all letters are equally likely to occur is:

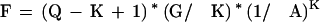4

Tables 3 and 4 show P and F values for various levels of sequence identity and K-mer sizes. For EST alignments we might want the search phase to find at least 99% of sequences that have 5% or less sequencing noise. Looking at Table 3, to achieve this level of sensitivity using this simple search method, we would need to choose a K of 14 or less. A K of 14 results in 399 regions passed on to the alignment phase by chance alone. Any smaller K would pass significantly more. Mouse and human sequences average 89% identity at the amino acid level (Makalowski and Boguski 1998). Looking at Table 4, to compare a translated mouse read and find at least 99% of the sequences at this level of identity we would need a K of 5 or less, which would result in 62,625 sequences passed on to the alignment stage. Depending on the cost of the alignment stage, these simple search criteria may or may not be suitable. Comparing mouse and human coding sequences at the nucleotide level, where there is on average 86% base identity (Makalowski and Boguski 1998), requires us to reduce our K to 7 to find at least 99% of the sequences. This results in 13,078,962 regions passed to the alignment stage, which would probably not be practical.

Table 3.

Sensitivity and Specificity of Single Perfect Nucleotide K-mer Matches as a Search Criterion

	7	8	9	10	11	12	13	14
A. 81%	0.974	0.915	0.833	0.726	0.607	0.486	0.373	0.314
83%	0.988	0.953	0.897	0.815	0.711	0.595	0.478	0.415
85%	0.996	0.978	0.945	0.888	0.808	0.707	0.594	0.532
87%	0.999	0.992	0.975	0.942	0.888	0.811	0.714	0.659
89%	1.000	0.998	0.991	0.976	0.946	0.897	0.824	0.782
91%	1.000	1.000	0.998	0.993	0.981	0.956	0.912	0.886
93%	1.000	1.000	1.000	0.999	0.995	0.987	0.968	0.957
95%	1.000	1.000	1.000	1.000	0.999	0.998	0.994	0.991
97%	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.999
B. K	7	8	9	10	11	12	13	14
F	1.3e+07	2.9e+06	635783	143051	32512	7451	1719	399

(A) Columns are for K sizes of 7–14. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected as calculated from equation 3 assuming a homologous region of 100 bases. The larger the value of K, the fewer homologies are detected. 

(B) K represents the size of the perfect match. F shows how many perfect matches of this size expected to occur by chance according to equation 4 in a genome of 3 billion bases using a query of 500 bases. 

Table 4.

Sensitivity and Specificity of Single Perfect Amino Acid K-mer Matches as a Search Criterion

K	3	4	5	6	7
A. 71%	0.992	0.904	0.697	0.496	0.317
73%	0.996	0.931	0.752	0.560	0.374
75%	0.998	0.952	0.803	0.625	0.436
77%	0.999	0.969	0.850	0.689	0.503
79%	0.999	0.981	0.890	0.752	0.574
81%	1.000	0.989	0.924	0.810	0.646
83%	1.000	0.994	0.950	0.862	0.718
85%	1.000	0.997	0.970	0.906	0.787
87%	1.000	0.999	0.984	0.942	0.850
89%	1.000	1.000	0.993	0.968	0.903
91%	1.000	1.000	0.997	0.985	0.945
93%	1.000	1.000	0.999	0.995	0.975
B. K	3	4	5	6	7
F	4.2e+07	1.6e+06	62625	2609	112

(A) Columns are for K sizes of 3–7. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected as calculated from equation 3 assuming a homologous region of 33 amino acids. (B) K represents the size of the perfect match. F shows how many perfect matches of this size are expected to occur by chance according to equation 4 in a translated genome of 3 billion bases using a query of 167 amino acids (corresponding to 500 bases). 

Searching With Single Almost Perfect Matches

What if instead of requiring perfect matches with a K-mer to trigger an alignment, we allow almost perfect matches, that is, hits where one letter may mismatch? The probability that a nonoverlapping K-mer in a homologous region of the database matches almost perfectly the corresponding K-mer in the query is:

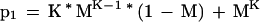5

As with a single perfect hit, the probability that any nonoverlapping K-mer in the homologous region matches almost perfectly with the corresponding K-mer in the query is:

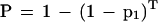6

Whereas the number of K-mers which match almost perfectly by chance are:

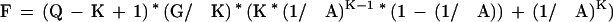7

Tables 5 and 6 show P and F for various levels of sequence identity and K-mer sizes. For the purposes of EST alignments, a K of 22 or less would pass through over 99% of the truly homologous regions while on average passing less than one chance match through to the aligner. With a reasonably fast alignment stage, it would be feasible to look for mouse/human homologies at the nucleotide level using this technique. A K size of 12 detects over 99% of the mouse homologies, and requires checking 275,671 alignments. At the amino acid level, a K size of 8 has the desired sensitivity and requires checking only 374 alignments.

Table 5.

Sensitivity and Specificity of Single Near-Perfect (One Mismatch Allowed) Nucleotide K-mer Matches as a Search Criterion

	12	13	14	15	16	17	18	19	20	21	22
A. 81%	0.945	0.880	0.831	0.721	0.657	0.526	0.465	0.408	0.356	0.255	0.218
83%	0.975	0.936	0.904	0.820	0.770	0.649	0.591	0.535	0.480	0.361	0.318
85%	0.991	0.971	0.954	0.900	0.865	0.767	0.719	0.669	0.619	0.490	0.445
87%	0.997	0.990	0.983	0.954	0.935	0.867	0.833	0.796	0.757	0.634	0.591
89%	1.000	0.997	0.995	0.984	0.976	0.939	0.920	0.897	0.872	0.775	0.741
91%	1.000	1.000	0.999	0.996	0.994	0.979	0.971	0.962	0.950	0.890	0.869
93%	1.000	1.000	1.000	0.999	0.999	0.996	0.994	0.991	0.988	0.963	0.954
95%	1.000	1.000	1.000	1.000	1.000	1.000	0.999	0.999	0.999	0.994	0.992
97%	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
B. K	12	13	14	15	16	17	18	19	20	21	22
F	275671	68775	17163	4284	1070	267	67	17	4.2	1.0	0.3

(A) Columns are for K sizes of 12–22. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected as calculated by equation 6 assuming a homologous region of 100 bases. (B) K represents the size of the near-perfect match. F shows how many perfect matches of this size expected to occur by chance according to equation 7 in a genome of 3 billion bases using a query of 500 bases. 

Table 6.

Sensitivity and Specificity of Single Near-Perfect (One Mismatch Allowed) Amino Acid K-mer Matches as a Search Criterion

	4	5	6	7	8	9
A. 71%	1.000	0.992	0.946	0.823	0.725	0.515
73%	1.000	0.995	0.965	0.867	0.785	0.586
75%	1.000	0.998	0.978	0.905	0.840	0.657
77%	1.000	0.999	0.987	0.935	0.886	0.727
79%	1.000	0.999	0.993	0.959	0.924	0.791
81%	1.000	1.000	0.997	0.976	0.952	0.849
83%	1.000	1.000	0.999	0.987	0.973	0.897
85%	1.000	1.000	0.999	0.994	0.986	0.936
87%	1.000	1.000	1.000	0.997	0.994	0.964
89%	1.000	1.000	1.000	0.999	0.998	0.982
91%	1.000	1.000	1.000	1.000	0.999	0.993
93%	1.000	1.000	1.000	1.000	1.000	0.998
B. K	4	5	6	7	8	9
F	1.2E+08	6.0E+06	300078	14985	749	37

(A) Columns are for K sizes of 4–9. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected. (B) K represents the size of the near-perfect match. F shows how many perfect matches of this size expected to occur by chance in a translated genome of 3 billion bases using a query of 167 amino acids. 

Searching With Multiple Perfect Matches

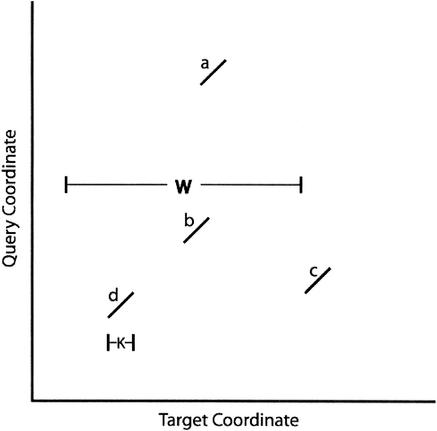
Another alternative search method is to require multiple perfect matches that are constrained to be near each other. Consider a situation where the K size is 10 and there are two hits—one starting at position 10 in the query and 1010 in the database, and another starting at position 30 in the query and 1030 in the database. These two hits could easily be part of a region of homology extending from positions 10–39 in the query and 1010–1039 in the database. If we subtract the query coordinate from the database coordinate, we get a “diagonal” coordinate. Consider the search criteria that there must be N perfect matches, each no further than W letters from each other in the target coordinate, and have the same diagonal coordinate (Fig. 1). For N = 1, the probability that a nonoverlapping K-mer in a homologous region of the database matches perfectly the corresponding K-mer in the query is simply as before:

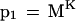8

The probability that there are exactly n matches within the homologous region is

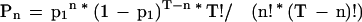9

And the probability that there are N or more matches is the sum:

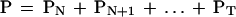10

The number of sets of N perfect matches that occur by chance is a little complex to calculate. For N = 1 it is easy:

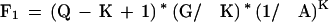11

The probability of a second match occuring within W letters after the first is

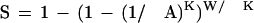12

because the second match can occur with any of the W/K nonoverlapping K-mers in the database within W letters after the first match. We can extend this reasoning to consider the chance that the N^th match is within W letters after the (N − 1)^th match, which gives the more general relationship

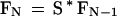13

which can be solved as

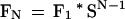14

where F_N represents the number of chance matches of N K-mers each separated by no more than W from the previous match.

Figure 1.

A pair of hits and two other hits. The hits a, b, c, and d are all K letters long. Hits d and b have the same diagonal coordinate and are within W letters of each other. Therefore they would match the “two perfect K-mer” search criteria.

Tables 7 and 8 show the sensitivity and specificity for N values of 2 and 3 and various values of other parameters which approximate cDNA or mouse/human alignments.

Table 7.

Sensitivity and Specificity of Multiple (2 and 3) Perfect Nucleotide K-mer Matches as a Search Criterion

	2,8	2,9	2,10	2,11	2,12	3,8	3,9	3,10	3,11	3,12
A. 81%	0.681	0.508	0.348	0.220	0.129	0.389	0.221	0.112	0.051	0.021
83%	0.790	0.638	0.475	0.326	0.208	0.529	0.339	0.193	0.099	0.045
85%	0.879	0.762	0.615	0.460	0.318	0.676	0.487	0.313	0.180	0.093
87%	0.942	0.866	0.752	0.611	0.461	0.809	0.649	0.470	0.305	0.177
89%	0.978	0.940	0.868	0.761	0.625	0.910	0.801	0.648	0.476	0.314
91%	0.994	0.980	0.947	0.884	0.787	0.969	0.914	0.815	0.673	0.505
93%	0.999	0.996	0.986	0.962	0.912	0.993	0.976	0.933	0.851	0.722
95%	1.000	1.000	0.998	0.993	0.979	0.999	0.997	0.987	0.961	0.902
97%	1.000	1.000	1.000	1.000	0.999	1.000	1.000	0.999	0.997	0.987
B. N,K	2,8	2,9	2,10	2,11	2,12	3,8	3,9	3,10	3,11	3,12
F	524	27	1.4	0.1	0.0	0.1	0.0	0.0	0.0	0.0

(A) Columns are for N sizes of 2 and 3 and K sizes of 8–12. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected as calculated by equation 10. (B) N and K represent the number and size of the near-perfect matches, respectively. F shows how many perfect clustered matches expected to occur by chance according to equation 14 in a translated genome of 3 billion bases using a query of 167 amino acids. 

Table 8.

Sensitivity and Specificity of Multiple (2 and 3) Perfect Amino Acid K-mer Matches as a Search Criterion

	2,3	2,4	2,5	2,6	2,7	3,3	3,4	3,5	3,6	3,7
A. 71%	0.945	0.643	0.297	0.126	0.044	0.945	0.643	0.297	0.126	0.044
73%	0.965	0.712	0.363	0.167	0.063	0.965	0.712	0.363	0.167	0.063
75%	0.978	0.776	0.436	0.218	0.089	0.978	0.776	0.436	0.218	0.089
77%	0.987	0.833	0.514	0.280	0.123	0.987	0.833	0.514	0.280	0.123
79%	0.993	0.882	0.596	0.353	0.169	0.993	0.882	0.596	0.353	0.169
81%	0.997	0.922	0.678	0.435	0.226	0.997	0.922	0.678	0.435	0.226
83%	0.999	0.952	0.757	0.526	0.298	0.999	0.952	0.757	0.526	0.298
85%	0.999	0.973	0.829	0.622	0.385	0.999	0.973	0.829	0.622	0.385
87%	1.000	0.987	0.889	0.719	0.485	1.000	0.987	0.889	0.719	0.485
89%	1.000	0.995	0.936	0.809	0.596	1.000	0.995	0.936	0.809	0.596
91%	1.000	0.998	0.969	0.886	0.712	1.000	0.998	0.969	0.886	0.712
93%	1.000	1.000	0.988	0.944	0.823	1.000	1.000	0.988	0.944	0.823
B. N,K	2,3	2,4	2,5	2,6	2,7	3,3	3,4	3,5	3,6	3,7
F	171875	245	0.4	0.0	0.0	708	0.0	0.0	0.0	0.0

(A) Columns are for N sizes of 2 and 3 and K sizes of 3–7. Rows represent various percentage identities between the homologous sequences. The table entries show the fraction of homologies detected. (B) N and K represents the number and size of the perfect matches, respectively. F shows how many perfect clustered matches expected to occur by chance in a translated genome of 3 billion bases using a query of 167 amino acids. 

Selecting Initial Match Criteria

Both single imperfect matches and multiple perfect matches have a significant advantage over single perfect matches. They drastically reduce the number of alignments which must be checked to achieve a given level of sensitivity, as shown in Tables 9 and 10. The multiple-perfect match criteria can be modified to allow small insertions and deletions within the homologous area by allowing matches to be clumped if they are near each other rather than identical on the diagonal coordinate. This improves real-world sensitivity at the expense of increasing the number of alignments that must be done. Allowing a single insertion or deletion increases the alignments by a factor of three, whereas allowing two increases the alignments by a factor of five. In general, two perfect matches with the appropriate K size give specificity for a given level of sensitivity similar to that given by three or more perfect matches. The near-perfect match criterion overall is similar to the two perfect match criteria. The near-perfect criterion cannot accommodate insertions or deletions, but it has superior performance on finding small regions of homology (Table 11). For finding coding exons in mouse/human alignments, whichever strategy is used, greater specificity is seen at the amino acid rather than the nucleotide level.

Table 9.

EST Alignment Choices

	K	F
1 Perfect	14	399
Near-Perfect	22	0.3
2 Perfect	11	0.1
3 Perfect	9	0.0

Maximum K sizes and number of chance matches passed to the alignment stage when searching for 100 bases of 95% homology with at least a 99% chance of detecting the homology. These values reflect our targets for EST alignments. 

Table 10.

Mouse/Human Alignment Choices

	K	F	F Translated
1 Perfect-DNA	7	13,078,962
1 Perfect-AA	5	62,625	187,875
Near-perfect-DNA	12	275,671
Near-perfect-AA	8	749	2,247
2 Perfect DNA	6	237,983
2 Perfect AA	4	245	734
3 Perfect DNA	5	109,707
3 Perfect AA	3	708	2,123

Assuming 86% base identity and 89% amino acid identity, this table shows the maximum K sizes and number of chance matches passed to the alignment stage when searching for regions of 100 bases (or 33 amino acids) with at least a 99% chance of detecting the homology. These values reflect our targets for human/mouse alignments. For translated DNA sequences, the F value is multiplied by six to reflect three reading frames on both strands of the query. Even with this multiplication, the specificity for a given sensitivity is several orders of magnitude greater in the amino acid rather than the nucleotide domain. 

Table 11.

Homology Size (In Nucleotides) vs. Sensitivity for Four Search Criteria as Applied to Mouse/Human Comparisons Assuming 86% Nucleotide Identity and 89% Amino Acid Identity

	20	30	40	50	60	70	80	90	100	110	120	130
A	0.625	0.805	0.881	0.927	0.962	0.977	0.986	0.993	0.995	0.997	0.999	0.999
B	0.000	0.394	0.687	0.851	0.932	0.932	0.970	0.987	0.995	0.998	0.999	0.999
C	0.483	0.733	0.862	0.929	0.963	0.965	0.981	0.990	0.995	0.997	0.999	0.999
D	0.000	0.783	0.783	0.953	0.953	0.953	0.990	0.990	0.998	0.998	1.000	1.000

The median size of a human exon is 120 bases (International Human Genome Sequencing Consortium 2001). A, perfect 5 base amino acid match; B, two perfect 4-base amino acid matches within 100 amino acids and on diagonal; C, near-perfect 12 nucleotide match; D, near-perfect 8 amino acid match. 

Since single-base insertions or deletions are relatively common artifacts of the sequencing process, nucleotide BLAT uses the two perfect 11-mer match criteria by default. Table 12 shows actual alignment times for nucleotide BLAT on a collection of ESTs at various settings. For protein matches, the default criterion is a single perfect 5 for the stand-alone program. This is because the extension phase of protein BLAT is extremely quick in the stand-alone program, so the false positives generated by this approach have relatively little cost. The client/server protein BLAT uses three perfect 4-mers by default because in the client/server version, a portion of the genome must be loaded from disk for each false positive, a relatively time-consuming operation. As a result, the client/server protein BLAT is somewhat less sensitive than the stand-alone version.

Table 12.

Alignment Times in Seconds of 10,000 ESTs (Average Size 380 Bases) Against Human Genomic Sequence Using Various K Sizes and N Sizes

K	N	2×106	2×107	2×108
10	2	3.9	35.6	680.1
10	3	3.2	21.4	348.7
11	2	2.4	8.1	92.4
11	3	2.3	6.5	61.8
12	2	3.9	7.0	39.9
12	3	3.7	6.4	33.8

The 2 × 10⁶ genomic sequence is ctg12414, which is 2,034,363 bases long and was taken from the December 2000 UCSC human genome assembly (http://genome.ucsc.edu). The 2 × 10⁷ genomic sequence is ctg15424 and is 20,341,418 bases long. The 2 × 10⁸ column is chromosome 4 and is 200,175,155 bases long. The two major components of the run-time are the time it takes to bin and sort the K-mer hits (clumping is almost instantaneous after sorting), and the time it takes to extend the clumps into alignments. The bin/sort time depends on the number of hits, which is proportional to 4^−K. The bin/sort time is somewhere between O(n) and O(n log n). The extend time is linear with respect to the number of clumps. 

Clumping Hits and Identifying Homologous Regions

To implement the match criteria, BLAT builds up an index of nonoverlapping K-mers and their positions in the database. BLAT excludes K-mers that occur too often from the index, as well as K-mers containing ambiguity codes and optionally K-mers that are in lowercase rather than uppercase. BLAT then looks up each overlapping K-mer of the query sequence in the index. In this way, BLAT builds a list of “hits” where the query and the target match. Each hit contains a database position and a query position. The following algorithm is used to efficiently clump together multiple hits. The hit list is split into buckets of 64k each, based on the database position. Each bucket is sorted on the diagonal (database minus query positions). Hits that are within the gap limit are bundled together into proto-clumps. Hits within proto-clumps are then sorted along the database coordinate and put into real clumps if they are within the window limit on the database coordinate. To avoid missed clumps near the 64k bucket boundary, unclumped hits and clumps that are within the window limit are tossed into the next bucket for additional clumping opportunities. The sorting algorithm mSort, which is related to qSort, is used. The bucketing tends to keep N relatively small.

Clumps with less than the minimum number of hits are discarded, and the rest are used to define regions of the database which are homologous to the query sequence. Clumps which are within 300 bases or 100 amino acids in the database are merged together. Five hundred additional bases are added on each side to form the final homologous region.

Searching for Near Perfect Matches

BLAT has an option to allow one mismatch in a hit. This is implemented by scanning the index repeatedly for each K-mer in the query. Every possible K-mer that matches in all but one position, as well as the K-mer that matches at every position, is looked up. In all, K*(A − 1) + 1 lookups are required. For an amino-acid search with K = 8, this amounts to 153 lookups. Because a straight index of 8-mers would require 20⁸ index positions or about 100 billion bytes, it is necessary to switch to a hashing scheme rather than an indexing scheme, further cutting efficiency. As a consequence, for a given level of sensitivity, the near-perfect match criterion runs 15× more slowly than the multiple-perfect match criterion in BLAT (Table 13). The near-perfect match criterion seems best suited for programs that hash the query sequence rather than the database. A query sequence is sufficiently small that each possible nearly matching K-mer could be hashed, and therefore the index would not have to be scanned repeatedly.

Table 13.

The Relative Sensitivity and Specificity of BLAT at Various Settings With and Without a Best-Match Filter

All nonhuman mRNA alignments		Near perfect	CPU days	% genome	% RefSeq	Enrichment
K	N
5	1	no	8.69	0.90%	69%	77x
4	2	no	6.06	0.83%	68%	81x
8	1	yes	95.25	0.86%	69%	80x
Only the best alignment for each mRNA		Near perfect	CPU days	% Genome	% RefSeq	Enrichment
K	N
5	1	no	8.69	0.70%	67%	95x
4	2	no	6.06	0.66%	65%	99x
8	I	yes	95.25	0.68%	66%	97x

The human genome (August 2001 freeze UCSC assembly http://genome.ucsc.edu) was aligned against a collection of 86,000 nonhuman mRNA sequences totaling 123,000,000 bases taken from Genbank. The CPU days were measured on 800 MhZ Pentiums. The percentage genome column shows what percent of bases in the human genome are part of gapless alignments with the mRNAs. The percentage RefSeq shows the percentage of coding bases in human RefSeq-defined genes (from the database at http://genome.ucsc.edu) which are part of a gapless alignment. Enrichment is the ratio of the RefSeq coding density inside of the alignments compared to coding density in the genome as a whole. Higher levels of enrichment indicate greater specificity. Also shown are the same statistics when only the single best place that a nonhuman mRNA aligns was considered. 

Alignment Stage

The alignment stage performs a detailed alignment between the query sequence and the homologous regions. For historical reasons, the alignment stage for nucleotide and protein alignments is quite different. Both have limitations, and are good candidates for future BLAT upgrades. On the other hand, both are quite useful in their present form for sequences which are not too divergent.

Nucleotide Alignments

The nucleotide alignment stage is based on a cDNA alignment program first used in the Intronerator (http://www.cse.ucsc.edu/∼kent/intronerator) (Kent and Zahler 2000). The algorithm starts by generating a hit list between the query and the homologous region of the database. Because the homologous region is much smaller than the database as a whole, the algorithm looks for relatively small, perfect hits. If a K-mer in the query matches multiple K-mers in the region of homology, the K-mer is extended by one repeatedly until the match is unique or the K-mer exceeds a certain size. The hits are then extended as far as possible allowing no mismatches, and overlapping hits are merged. The extended hits that follow each other in both query and database coordinates are then linked together into an alignment. If there are gaps in the alignment on both the query and database side, the algorithm recurses to fill in these gaps. Because the gaps are smaller than the original query and database sequences, a smaller k can be used in generating the hit list. This continues until either the recursion finds no additional hits, or the gap is five bases or less. At this point, extensions through Ns, extensions that allow one or two mismatches if followed by multiple matches, and finally extensions that allow one or two insertions or deletions (indels) followed by multiple matches are pursued. For mRNA alignments, it is often the case that there are several equivalent-scoring placements for a large gap in the query sequence. Generally such gaps correspond to an intron. Such gaps are slid around to find their best match to the GT/AG consensus sequence for intron ends.

The nucleotide alignment strategy works well for mRNA alignments and the type of alignments needed for genomic assembly. In these cases, the sequence identity is typically 95% or better. The strategy starts to break down when base identity is below 90%, and is therefore not suitable for most cross-species alignments.

Protein Alignments

The protein alignment strategy is simpler. The hits from the search stage are kept and extended into maximally scoring ungapped alignments (HSPs) using a score function where a match is worth 2 and a mismatch costs 1. A graph is built with HSPs as nodes. If HSP A starts before HSP B in both query and database coordinates, an edge is placed from A to B. The edge is weighted by the score of B minus a gap penalty based on the distance between A and B. In the case where A and B overlap, a “crossover” point is selected which maximizes the sum of the scores of A up to the crossover and B starting at the crossover, and the difference between the full scores and the scores just up to the crossover is subtracted from the edge score. A dynamic program then extracts the maximal-scoring alignment by traversing this graph. The HSPs in the maximal-scoring alignment are removed, and if any HSPs are left the dynamic program is run again.

The major limitation of this protein alignment strategy is that if there is an indel, part of the alignment will be lost unless the search stage manages to find both sides of the indel. For the translated mouse versus translated human genome job, which was the major motivation for protein BLAT, this limitation is not as serious as it would be when searching for more distant homologs. Indeed in the translated mouse/translated human case, this limit on indels is actually useful in some ways as it reduces the amount of pseudogenes which are found by BLAT more than it reduces the amount of genes found. Even so, in the future we hope to replace this simplistic extension phase with a banded (only small gaps allowed) Smith-Waterman algorithm (Chao et al. 1992).

Stitching and Filling In

It is often the case that the alignment of a gene is scattered across multiple homologous regions found in the search phase. These alignments are stitched together using a minor variation of the algorithm used to stitch together protein HSPs. For DNA alignments at this stage, the gap penalty is equal to a constant plus the log of the size of the gap. For mRNA/genomic alignments, if after stitching there are gaps left between aligning blocks in both the database and query sequence, the nucleotide alignment algorithm is called on the gap to attempt to fill it in. This gives BLAT a chance to find small internal exons that are further away than 500 bases from other exons, and which are too small to be found by the search stage.

Since the sort time is O(N logN), that is, proportional to N times log N, where N is the number of hits to be sorted, and the dynamic program time is O(N²) where N is the number of HSPs, an additional step is necessary to make BLAT efficient on longer query sequences. Untranslated nucleotide queries longer than 5000 bases and translated queries longer than 1500 bases are broken into subqueries that have approximately 250 bases of overlap. Each subquery is aligned as above, and the resulting alignments are stitched together. Currently this subdividing and stitching is only available for the stand-alone BLAT, not the client/server version.

DISCUSSION

As shown above, BLAT is a very effective tool for doing nucleotide alignments between mRNA and genomic DNA taken from the same species. It is more accurate and orders of magnitude faster than Sim4. Sim4 in turn is more accurate and orders of magnitude faster than other published tools such as est_genome (Mott 1997; Florea et al. 1998). Although the alignment strategy BLAT uses for nucleotide alignments becomes less effective below 90% sequence identity, it efficiently “unsplices” mRNA, and accommodates the level of sequence divergence introduced by sequencing error. BLAT is able to unsplice all the human mRNA in GenBank, including the ESTs, in less than a day on a 100-CPU computer cluster. Since the human, mouse, and other large genome projects are updating sequences at a rapid rate, and GenBank continues to grow at a rapid rate, rapid alignment is needed to keep genome annotations in synchrony with improving genome assemblies.

BLAT working in translated mode is capable of rapidly aligning data across vertebrate species without significant compromise. While TBLASTX can be configured to be more sensitive than BLAT, at settings commonly used for mammal–mammal comparisons, BLAT runs approximately 50 times faster. Even using BLAT, an alignment of public mouse whole-genome shotgun data took 12 days on our 100-CPU cluster. It would be difficult to keep the mouse–human homology information up to date with a slower tool.

High-speed alignment programs have two major stages—a search stage that uses a heuristic to identify regions likely to be homologous, and an alignment stage that does detailed alignments of the previously defined homologous regions. To get adequate speed when operating at the scale of whole genomes, the search stage is crucial. An index of some sort is key to an efficient search stage. BLAT indexes the database rather than the query sequence. This more than anything is responsible for the relatively high speed of BLAT compared to Sim4 or TBLASTX. Rather than having to linearly scan through a database of gigabases of sequence looking for index matches, BLAT only has to scan through a relatively short query sequence. The program SSAHA indexes the database in a manner very similar to that of BLAT, and is an extremely effective tool for aligning genomic regions from the same organism against each other. Currently SSAHA does not implement unsplicing logic, and always uses a single perfect match as a seed.

The challenge to indexing the database is twofold: the size of the index and the time it takes to generate the index. Fortunately, computers with several gigabytes of RAM have become affordable and commonplace in the last few years, so the size of the index is not the problem it once was. By making the index relatively efficient (only four bytes per index entry vs. eight in the published version of SSAHA), and only indexing nonoverlapping words, BLAT is able to index the human genome at the nucleotide level in 0.9 gigabytes and to index a RepeatMasker masked, translated human genome in 2.5 gigabytes. The index does take some time to generate: 30 min for a translated index of the human genome. Fortunately the index is not generated often. In batch mode, BLAT generates the index once at the start of processing a batch of typically hundreds of thousands of query sequences. In interactive client/server mode, the genome only has to be generated once for each genome assembly. The typical user simply pastes in a sequence to a web form, and quickly receives an alignment in response.

How an index is used is also important to the speed of an alignment algorithm. Triggering an alignment for each match to the index is not always the optimal strategy. For a sensitive search, it is desirable to index relatively small K-mers. However, small K-mers will return many false positives, potentially creating a bottleneck in the alignment stage if the alignment stage is computationally expensive. Requiring multiple nearby matches or using longer K-mers but tolerating a mismatch as search criteria both have much greater specificity for a given level of sensitivity than the criterion of a single perfect match. BLAT implements a very quick algorithm for finding multiple nearby perfect matches, which allows the search stage to be specific enough that the genome itself can be kept on disk and only the index kept in RAM in memory in the client/server mode.

The BLAT software in source and executable form is available without charge for nonprofit, academic, and personal uses. Nonexclusive commercial licenses are available from the author. The software can be downloaded from the source and executable links at http://www.soe.ucsc.edu/∼kent.