Abstract
We compare several commonly used expression-based gene clustering algorithms using a figure of merit based on the mutual information between cluster membership and known gene attributes. By studying various publicly available expression data sets we conclude that enrichment of clusters for biological function is, in general, highest at rather low cluster numbers. As a measure of dissimilarity between the expression patterns of two genes, no method outperforms Euclidean distance for ratio-based measurements, or Pearson distance for non-ratio-based measurements at the optimal choice of cluster number. We show the self-organized-map approach to be best for both measurement types at higher numbers of clusters. Clusters of genes derived from single- and average-linkage hierarchical clustering tend to produce worse-than-random results.
[The algorithm described is available at http://llama.med.harvard.edu, under Software.]
The widespread use of DNA microarray technology (Eisen and Brown 1999) to perform experiments on thousands of gene fragments in parallel has led to an explosion of expression data. To handle such huge amounts of data on entities whose interrelationships are poorly understood, exploratory analysis and visualization techniques are essential (DeRisi et al. 1997; Michaels et al. 1998; Wen et al. 1998). Clustering (the assignment of each of a large number of items to one of a much smaller number of classes) is one widely used technique. The science of clustering has long been under development (Everitt 1980), and there are many techniques. Hierarchical clustering (encompassing single-, complete-, and average-linkage variants), k-means clustering, and self-organized maps (SOM) are the most widely used in analysis of gene-expression data (for reviews, see Gerstein and Jansen 2000; Quackenbush 2001). In addition to these long-established algorithms, new ones have been developed specifically for analysis of gene-expression data (Getz et al. 2000; Lazzeroni and Owen 2000; Shamir and Sharan 2000; Ben-Hur et al. 2002; Sinkkonen and Kaski 2002). The availability of free software tools (Angelo 1999; Eisen 1999) implementing the hierarchical and SOM algorithms has made them very easy to apply, often to good scientific and visual effect (Eisen et al. 1998; Golub et al. 1999; Tamayo et al. 1999; Gasch et al. 2000).
An underlying assumption is that by clustering genes based on similarity of their expression patterns in a limited set of experiments, we can establish guilt by association—that is, genes with similar expression patterns are more likely to have similar biological function. Clustering does not provide proof of this relationship, but it does provide suggestions that help to direct further research. It is clear that clustering by expression pattern does not provide the best possible grouping of genes by biological function. It is easy to construct examples in which genes known to share similar functions end up in different clusters, particularly when they relate to molecular function or catalytic activity rather than to cellular role or pathway. However, as long as clustering by expression pattern is used as a means to group by putative biological function, it is meaningful to ask which method performs best. With this goal in mind, how might we compare two clustering results derived from the same expression data set? Different clustering results might be obtained from different clustering algorithms, or from different choices within a clustering algorithm. The latter choices might include algorithm parameters (e.g., number of clusters), the method of calculating distance between two gene expression vectors (e.g., Euclidean or Pearson correlation), or different ways of preprocessing data (e.g., the log transformation).
We illustrate our approach of making clustering method choices by examining the choice of cluster number. For most methods of clustering, the user must specify the number of clusters, and often quickly wonders, “What is the true number of clusters?” Many data-centric techniques have been applied to this problem, with conclusions based on which number of clusters achieves the best balance of data point dispersion within and between clusters, but none has proven robust across diverse data types (Everitt 1980). Although there have been some recent attempts to develop data-centric figures of merit that are specific to gene expression data (Lukashin and Fuchs 2001; Yeung et al. 2001; Ben-Hur et al. 2002), generic (Fraley and Raftery 1998), or use information beyond the expression data itself (Jakt et al. 2001), it seems likely that there is no single true number of clusters for gene expression data. We should perhaps ask, “What choice of cluster number would be most useful?”
When the objective of clustering is to bring genes of similar function together, we assert that the best method of clustering a particular data set is that which has the strongest tendency to bring genes of similar function together when applied to diverse expression data sets. With this in mind, we should instead ask, “What choice of number of clusters generally yields the most information about gene function (where function is known)?” For other clustering choices, we might ask, “Which distance measure generally yields the most information about gene function (where function is known)?” Present annotation databases are necessarily incomplete and evolving, but nonetheless represent the best computable summary of our present state of knowledge.
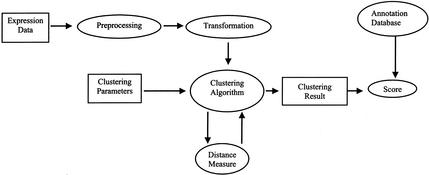
We propose a figure of merit based on the information jointly held by the functional annotation and cluster membership of all the genes clustered. We apply this method to a variety of common clustering choices. Figure 1 illustrates our approach. An implementation of the algorithm for computing the figure of merit is accessible at http://llama.med.harvard.edu as a CGI-based Web application, into which users may upload their clustered data and receive a score.
Figure 1.
Schematic of dataflow in clustering and evaluation.
RESULTS
We evaluated clustering algorithm choices based on the premise that the best clustering algorithm for expression data is that which tends to bring genes of similar function together, where function is known. Specifically, we investigated choice of number of clusters, choice between various methods of calculating dissimilarity in expression between genes (distance measures), and commonly used clustering algorithms. Given the great variety of normalization schemes that have been proposed, it was not feasible to include them in the present study, but this would make an excellent topic for further study.
Particular clustering results were evaluated by examining the relationship between clusters produced and the known attributes of the genes in those clusters, as annotated with a controlled vocabulary for gene attributes. We used the Saccharomyces Genome Database (SGD) annotation of S. cerevisiae genes with the gene ontology developed by the Gene Ontology Consortium (GO; Ashburner et al. 2000; Issel-Tarver et al. 2001).
In examining choice of cluster number, we addressed two questions: “Which clustering algorithm variants best group genes by function using expression data?” and “Given a clustering algorithm, is there an optimal number of clusters, k?”, where optimality in each case is evaluated according to existing annotation.
We devised a figure of merit, z-score, based on mutual information between a clustering result and SGD gene annotation data. The z-score indicates relationships between clustering and annotation, relative to a clustering method that randomly assigns genes to clusters. A higher z-score indicates a clustering result that is further from random. This z-score is plotted for clustering results as a function of number of clusters, k, to compare algorithms at all choices of k, and to establish an optimal value for k. We examined all cluster numbers from 2 to 100.
We also compared the following distance measures on expression data sets using k-means clustering: Euclidean, 3-norm, Manhattan or city-block, Hausdorff, and Pearson correlation. The first four are special cases of a general class of distance measures, the n-norm, defined for two d-dimensional vectors a and b, as
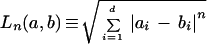 |
Manhattan distance is the common name for the 1-norm, Euclidean distance is the common name for the 2-norm. The Hausdorff distance, in which the maximum distance along any single dimension is used as the distance between the two vectors, is the ∞-norm. Pearson distance is defined as dP ≡ 1 − r, where r is the correlation coefficient. Genes that are highly positively correlated are considered similar to each other, with decreasing similarity as the correlation declines and becomes negative. Euclidean and Pearson correlation distances are common choices for clustering expression data. Some researchers report that higher n-norms may be better at clustering vectors of higher dimensionality (such as the 175-dimensional Gasch data set). Hausdorff distance was included as a negative control, because we did not expect it would be a good distance.
In addition, we compared the performance of Cluster (Eisen 1999), software that implements many clustering algorithms, of which we examined only the results produced by the hierarchical clustering, and GeneCluster (Angelo 1999), which implements self-organized maps. To obtain a comparable clustering result from hierarchical methods, genes were partitioned into disjoint clades by cutting branches at a given distance from the root. For SOM clustering, the user must not only specify k, the number of clusters, but also the layout of these clusters in a two-dimensional grid (e.g., eight clusters in a 2 × 4 grid). For a given k, we chose the most square-like layout, that is, that which minimizes the ratio of perimeter length to area.
We examined four publicly available yeast data sets. Two of these cover the well-known cell cycle data sets collected using ratio-based (i.e., two-color cDNA) and non-ratio-based (e.g., Affymetrix) array technologies. Two non-cell-cycle data collections were also examined, one ratio-based and one non-ratio-based. All data sets contain ∼3000 genes, after filtering out genes with insufficient variability. These data sets are summarized in Table 1.
Table 1.
Four Data Sets Analyzed, Representing Both Affymetrix- and Two-Color cDNA Microarrays, Cell Cycle and Non-Cell Cycle Data Sets
| Name | Ratio based? | # of genes | # of points | Description |
|---|---|---|---|---|
| Cho | No | 3000 | 15 | Two cell cycles, two of original timepoints—dropped because of unreliability |
| CJRR (Cohen et al. 2002; Jelinsky et al. 2000; Robertson et al. 2000; Roth et al. 1998) | No | 3000 | 52 | YAP1/2 knockouts with peroxide and cadmium added, yeast A kinase TPK1/2/3 mutants, chemical and damaging agents, galactose, heat shock, and mating type |
| Gasch | Yes | 3000 | 175 | Various conditions: temperature shock; exposure to H2O2, menadione, diamide, and DTT; osmotic shock; amino acid starvation; nitrogen depletion; stationary phase |
| Spellman | Yes | 3000 | 75 | Cultures synchronized in cell cycle by three independent methods |
The Cho data set consists of 15 time points covering two complete cell cycles, and collected in a non-ratio format (Cho et al. 1998). The CJRR data set is a diverse (non-cell-cycle) collection of non-ratio-based data from 52 experiments covering YAP1/2 knockouts (Cohen et al. 2002); chemical and physical damaging agents (Jelinsky et al. 2000); galactose response, heat shock, and mating type (Roth et al. 1998); and yeast A kinase TPK1/2/3 mutants (Robertson et al. 2000), all of which were obtained through ExpressDB (Aach et al. 2000). The Gasch data set is a large collection of 175 non-cell-cycle experiments, in ratio format (Gasch et al. 2000). Details of these data sets are summarized in Table 1. The Spellman data set is a ratio-based cell cycle time course (Spellman et al. 1998).
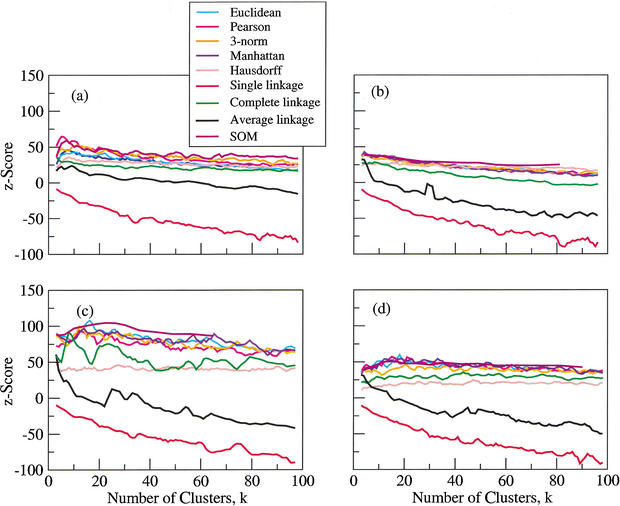
The results are shown in Figure 2. For all data sets, we show scores for k-means clustering performed with the five above-mentioned distance metrics (Euclidean, Pearson correlation, 3-norm, Manhattan, and Hausdorff), three hierarchical clustering methods (single, complete, and average linkage, all using the uncentered Pearson correlation distance—the default—which is similar to the centered Pearson correlation distance, because the data have all been median-centered), and self-organized maps (SOM). Each curve is a three-point moving average of the original data.
Figure 2.
Four data sets clustered using k-means, hierarchical, and self-organized map algorithms. The horizontal axis shows the number of clusters desired, and the vertical axis shows z-scores. Data sets are (a) Cho, (b) CJRR, (c) Gasch, and (d) Spellman.
In the Cho data set (Fig. 2a), the performance of single-linkage hierarchical clustering is worse than random, and average linkage fares little better. Complete-linkage hierarchical clustering is equal to or only slightly worse than that of the remaining algorithms, but is everywhere better than random. SOM appears to perform about as well as k-means-based methods, but does not show the falloff in score with increasing k that is characteristic of the k-means and hierarchical methods. If we examine the k-means-based methods in detail, the following conclusions can be drawn. For this data set, the best of the five k-means distance metrics examined here were Pearson correlation distance and 3-norm distance, with Pearson correlation distance winning at low k-values, and 3-norm distance winning for k > 35. It is worth noting that the best distance measures showed the optimal k-value (k*) to lie between 7 and 10. The Manhattan and Euclidean metrics perform almost as well as 3-norm, which is perhaps not surprising, given the close functional similarity between all three metrics. Hausdorff distance was the worst performing among the k-means methods for this data set.
The CJRR data set (shown in Fig. 2b) shows k* to be <10 for all clustering methods. Many of the characteristics observed for the other data sets hold true here also: the poor performance of single- and average-linkage clustering; the fact that complete-linkage hierarchical clustering outperforms both single and average linkage, but never quite matches up to any of the nonhierarchical methods; and the poorer performance of almost all methods for higher k-values. It is worth noting that Hausdorff distance shows a much less pronounced falloff with increasing k-values and surpasses the other distance metrics for high k (>55). Once again, SOM appears to perform about as well as the best k-means-based methods at low cluster number, without showing as pronounced a falloff in score with increasing k.
The Gasch data set is shown in Figure 2c. Once again, single- and average-linkage hierarchical clustering are the worst performers. Complete linkage and k-means/Hausdorff are the next poorest performers. The k-means-based metrics Euclidean, Pearson, Manhattan, and 3-norm all perform similarly to one another. SOM appears to be the best algorithm for this data set over a wide range of k-values. However, the best result at any k* was obtained from Euclidean distance. SOM and all the k-means variants except for Hausdorff show more or less monotonically decreasing scores with increasing k. Whereas the Cho and CJRR datasets have a maximum z-score of ∼50, this data set has a maximum score of nearly 100, indicating that clustering genes by this data set (which consists of responses to a wide range of conditions) yielded significantly better grouping according to function than can be obtained by using the other data sets. It is reasonable that data collected over a wide range of conditions should yield results that cluster better according to function, as has been suggested elsewhere (Eisen et al. 1998).
The Spellman data set is shown in Figure 2d. Single and average linkage are generally worse than random. Hausdorff with k-means and complete-linkage hierarchical clustering perform much better than random and show no significant decrease with increasing k-value, but underperform the remaining k-means distance metrics. Manhattan, Euclidean, and Pearson correlation distance perform comparably for all k-values, and 3-norm underperforms at low k-values, but catches up at higher k-values. SOM is slightly worse than the best k-means-based methods at most k-values, and does slightly better at higher k-values.
In all the data sets (Fig. 2), the most striking observation is that single-linkage hierarchical clustering performs significantly worse than all the others. In fact, it gave worse-than-random (a uniformly negative z-score) performance for all data sets over a wide range of cluster numbers. Average-linkage hierarchical clustering is also rather poor, scoring significantly lower than the other methods, and worse than random for cluster numbers above some modest value. The best hierarchical clustering result is complete linkage, and although it is always significantly better than random, it never consistently performs better than the commonly used k-means-based clustering algorithms.
Hausdorff distance was originally chosen as a straw man distance measure, and was never expected to perform particularly well, because it throws away much of the information about the vectors it compares, keeping only the magnitude of the difference in a single dimension. This expectation is borne out by the results in that it achieves a score lower than three other distance metrics used for k-means clustering algorithms. However, it is worth noting that even this metric performs significantly better than random. Because it does not fall off as rapidly with increasing k as other k-means distance measures, it begins to outperform them at higher k.
DISCUSSION
We studied two ratio-based and two Affymetrix-based data sets. By ranking the methods used for each data set, our results indicate that Pearson correlation distance performs better than or equal to other measures used, when applied to non-ratio-style data. For ratio-style data, we find that Euclidean distance is better than or equal to the other measures. Ratio-style data are log-transformed prior to clustering, to equalize the effects of up- and down-regulation. This also compresses the scale of variation, and Euclidean distance may be more robust than Pearson correlation to such processing. Most researchers have chosen Euclidean distance on standardized data or Pearson correlation distance for no other reason than that it seemed obvious, was simple to compute, and because they have had no rationale for choosing anything more complicated. This is the first demonstration that clearly vindicates these choices.
Because the shortcomings of the single-linkage hierarchical clustering method have long been known (Everitt 1980), it is no surprise that this method performs poorly. (Using a data-driven approach on the Cho data set and others, and with a different figure of merit, Yeung et al. [2001] have shown that single-linkage clustering was close to random, and significantly worse than other common algorithms, including k-means.) However, at first glance it is surprising that it performs less well than random assignment of genes to clusters. More surprising is that average-linkage clustering not only performs poorly, but is significantly worse than complete linkage, because average linkage is generally considered to be better than both single and complete linkage. The structures of complete- and average-linkage trees often appear to have similar topology, but the scores obtained here indicate that the branching choices near the root node are much more meaningful in the context of functional annotation for complete- than for average-linkage trees.
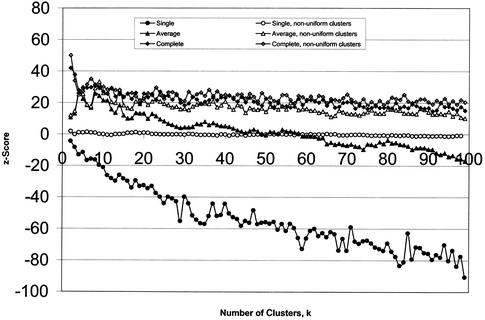
To understand how a clustering method can score worse than random, we note that single-linkage hierarchical clustering tends to produce one single large clade and several singletons. This division necessarily separates genes that have attributes in common. On the other hand, the single clade will contain most genes, yielding almost no information. With random assignment to clusters of uniform size, we can expect that sometimes by chance a cluster will contain all genes possessing a single attribute. Thus, random assignment can do better than single-linkage hierarchical clustering. Figure 3 compares single- and complete-linkage z-scores calculated using random assignment to clusters of uniform size (as used in the rest of this paper) and also using random assignment to clusters of the size produced by the clustering algorithm itself. The latter tends to subtract the effects of the uneven cluster sizes generated by the algorithm. After the effect of cluster sizes is removed, single linkage still performs on a par with random assignment, whereas complete linkage performs better, although not as well as average linkage. It might be argued that using randomly chosen cluster sizes would be less biased. However, with no prior knowledge of cluster membership, there is no a priori reason to adopt nonuniform cluster sizes. Uniform cluster sizes should be considered the default because this allows for the greatest mutual information with another variable or set of variables with unknown entropy. (See the Methods section for further discussion of mutual information.) Furthermore, certain algorithms have a known tendency to produce clusters of uneven size, even when the data do not warrant it (Everitt 1980). Such algorithms are rightly penalized.
Figure 3.
Hierarchical single- and average-linkage clustering results, scored against random assignment to clusters of uniform size (solid symbols), and random assignment to clusters of the same size as the clades obtained by hierarchical clustering (open symbols). For single linkage (circles), the difference is strongest, reflecting the strong tendency of that algorithm to produce nonuniformly sized clusters (indicated by the negative scores of the solid circles) that do not contain any functional information (evidenced by the open circles, which show that even taking account for the cluster sizes produced, the score is equivalent to random assignment). The scores for complete linkage show little difference (open and solid diamonds are almost on top of each other), indicating that the cluster sizes returned by this algorithm are indicative of actual clusters in the data. Average linkage occupies the middle ground (triangles).
Why do SOMs outperform the k-means-based algorithms examined here at higher k? It may be because of the ability of SOMs to discriminate between similar clusters. Using the analogy of the entomologist's drawer, Tamayo et al. (1999) indicate that clusters that lie adjacent on the two-dimensional grid tend to be similar. Perhaps the ability of SOMs to distinguish similar but distinct is superior to that of k-means. This remains an open question.
Supervised learning algorithms for prediction of gene function on the basis of expression data have been developed (Brown et al. 2000). Although training such algorithms can be computationally expensive, and frequent updates are required as additional annotation becomes available, supervised approaches may well outperform unsupervised ones such as those examined here. But from a pragmatic perspective, clustering algorithms are at present more readily accessible and usable by experimental biologists than supervised learning methods. Perhaps more importantly, supervised learning algorithms are not useful when the training set of known genes of a given function is small, whereas clustering may even be useful in discovering a group of coexpressed genes all holding the same previously undescribed function. We expect that an optimized clustering methodology will continue to be useful, despite expected future advances in supervised learning from expression data.
METHODS
GO defines three distinct ontologies (called biological process, molecular function, and cellular component) and represents each as a directed acyclic graph (DAG), consisting of directed edges and vertices, such that each vertex may be descended from several others. Annotation of a gene with a descendant attribute implies that the gene holds all ancestor attributes. We have parsed annotation from SGD of S. cerevisiae genes with GO attributes in such a way that attributes are inherited through the hierarchy, producing a table of ∼6300 genes and ∼2000 attributes in which a 1 in position (i,j) indicates that the gene i is known to possess attribute j, and a 0 indicates our lack of knowledge about whether gene i possesses attribute j. In other words, absence of annotation is not the same as absence of function.
With this gene-attribute table, we construct a contingency table for each cluster–attribute pair (Press et al. 1986; Cover and Thomas 1991; Schneider 2000), from which we compute the entropies for each cluster–attribute pair (HAiC), for the clustering result independent of attributes (HC), and also for each of the NA attributes in the table independent of clusters (HAi). Using the definition of mutual information between two variables X and Y, MI(X,Y) ≡ H(X) + H(Y) − H(X,Y), and assuming both absolute and conditional independence of attributes, we expand the total mutual information as a sum of mutual information between clusters and each individual attribute. We compute the total mutual information between the cluster result C and all the attributes Ai as:
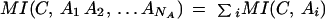 |
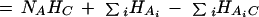 |
where summation is over all attributes i (Press et al. 1986).
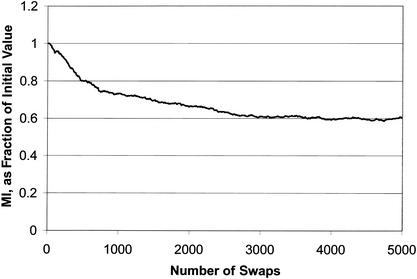
To illustrate some important characteristics of how this parameter changes as the degree of correlation between function and cluster membership is changed, we performed the following experiment on data that have already been shown to contain clusters enriched for biological function (Tavazoie et al. 1999). Beginning with downloaded supplementary data, in which some 3000 genes are combined into 30 clusters, we repeatedly chose two clusters at random, swapped one gene chosen at random from the first cluster with another randomly chosen from the second cluster, and recomputed MI. In this way, the cluster sizes were held constant, but we slowly destroyed the degree of correlation between membership in a cluster and possession of particular attributes. The results are shown in Figure 4. For simplicity, the mutual information is shown normalized to its initial value.
Figure 4.
Mutual information (MI) as a function of number of gene pairs swapped between clusters. At each permutation, two genes are chosen at random from each of two randomly chosen clusters (there are 30 clusters in all). The genes are swapped, and the MI (between cluster membership and attribute possession) is recomputed. For convenience, the MI is shown as a fraction of its initial value. It is clear that MI decreases monotonically as the genes are swapped, illustrating that it is a good gauge of the quality of the clusters. It does not fall to zero because even with random assignment of genes to clusters, it is likely that genes will coincidentally end up in the same cluster. (Clusters taken from Tavazoie et al. 1999.)
Two characteristics are evident. Firstly, as expected, MI decreases as the clusters become increasingly disordered with respect to function. Secondly, after a large enough number of random swaps, MI reaches a non-zero baseline value, reflecting the fact that even for data chosen at random, when the number of clusters is much smaller than the number of genes, there is some degree of mutual information between membership in a particular cluster and possession of certain attributes.
We score a partitioning as follows: (1) Compute MI for the clustered data (MIreal), using the attribute database derived from GO/SGD; (2) Compute MI again, for a clustering obtained by randomly assigning genes to clusters of uniform size (MIrandom), repeating until a distribution of values is obtained; (3) Compute a z-score for MIreal and the distribution of MIrandom values (with mean MIrandom and standard deviation srandom) according to z = (MIreal − MIrandom)/srandom. The z-score can then be interpreted as a standardized distance between the MI value obtained by clustering and those MI values obtained by random assignment of genes to clusters. The larger the z-score, the greater the distance, and higher scores indicate clustering results more significantly related to gene function.
Clusters to which genes were randomly assigned were chosen to be as nearly uniform in size as possible, so that some of the success of a clustering algorithm relative to random may derive from producing nonuniform cluster size distributions. Uniform cluster sizes yield the highest value of HC, which allows for the highest possible MI(C,X) for some variable X of unknown entropy H(X), because 0 ≤ MI(C,X) ≤ min(HC,H(X)).
Preparation of the Database
It is reasonable to assume that those using clustering methods are seeking a fine structure, rather than a broad one. For example, in cell cycle data, genes might be broadly classified according to the phase of the cell cycle in which they peak, yielding perhaps no more than five clusters, corresponding to early G1, late G1, S, G2, and M phases (Cho et al. 1998; Yeung et al. 2001). Certainly, this is a correct answer, but it yields little new knowledge. It would be more useful to find those (probably small) groups of genes sharing rather specific biological functions (e.g., see Fig. 1 of Eisen et al. 1998, in which several clusters of genes, varying in size from 5 through 27, are found to be significantly related in biological function). On the other hand, it is no help to classify each gene into its own cluster. Many properties are desirable in an annotation database to improve assessment of relatedness between clustering results and annotation.
- 1.
The database should contain few attributes that are shared among all or most genes, because these will not be useful in clustering in a meaningful way. However, we have found that removing such shared attributes has no effect on the overall ranking of the clustering techniques considered. (Excluding attributes held by >200 genes removed only ∼2% of attributes.) It also does little to improve the computational speed of the algorithm used to evaluate the figure of merit; therefore, we did not filter the attributes on this basis.
- 2.
The database should contain few attributes that are shared among only a handful of genes because, having low individual entropy, these attributes will make little contribution to the overall mutual information. To accomplish this, we filtered out attributes that are held by fewer than Nmin = 10 genes, which removes ∼75% of all attributes. This restriction may shift the optimal number of clusters to be slightly higher, although our conclusions are robust to this restriction as discussed below. Although the absolute scores for the algorithms varied with Nmin, the relative rankings did not. The above value was used for computational reasons.
- 3.
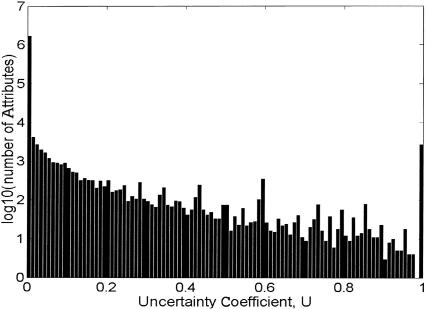
Attributes in the database should be as independent as possible, because we would like to avoid overweighting attributes that have many ancestors, or descendents assigned to highly overlapping gene sets. We measured independence using the uncertainty coefficient (see Fig. 5), defined as U = MI/max(MI), where MI is the mutual information between two attributes. This quantity has the useful property that it varies between zero and unity, with values close to zero indicating that possession of one attribute reveals little about possession of the other, whereas values close to unity indicate that a gene possessing either attribute is also likely to have the other. One way to think of this is that for high U-values, possession of either at tribute removes a large amount ofuncertainty about possession of the other. For low U-values, knowledge of either removes little uncertainty about the other. If any two attributes are shared by substantially the same collection of genes, one of the attributes should be excluded from the database to avoid counting essentially the same attribute twice. To accomplish this, we filtered out one of any pair of attributes that had a pairwise uncertainty coefficient U>Umax = 0.8.
Figure 5.
U for all attribute pairs, after removing one of each pair with U > 0.9999. Histogram showing uncertainty coefficient between all pairs of attributes, after removing one of each pair with U > 0.9999. When a pair of attributes has U = 0, there is no correlation between possession of one attribute by a gene, and possession of the other. When U = 1.0, they are completely correlated: if a gene has one attribute, it will certainly also have the other.
Sensitivity to Attribute Filtering Process
We have already described the algorithm and parameters used to reduce the database from the complete annotated genome to a subset of relatively independent attributes that are neither too general (e.g., intracellular) nor too specific (e.g., para-aminobenzoic acid [PABA] synthase) to be useful in finding meaningful clusters (see Table 2). We have acknowledged that we are biasing optimal cluster number in this manner. How sensitive are the results to the particular parameter values we choose (Nmin, Nmax, Umax)? We have constructed several databases, based on a variety of choices for Nmin and Umax. We find that although the particular scores obtained do change with differing choice of these parameters, the basic shape (location of the peak, rolloff at higher k-values, ranking of clustering methods) does not. Also, the relative success of different distance measures is insensitive to the parameters used to filter the attribute database.
Table 2.
Gene Ontology Consortium Attributes Ranked in Descending Order by the Number of Genes That Possess Each Attribute
| GO accession number | Number of genes hit | GO name |
|---|---|---|
| GO:0008151 | 2593 | Cell growth and maintenance |
| GO:0008152 | 1920 | Metabolism |
| GO:0005622 | 1837 | Intracellular |
| GO:0005623 | 1820 | Cell |
| : | : | : |
| GO:0000034 | 1 | Para-aminobenzoic acid (PABA) synthase |
| GO:0004482 | 1 | mRNA (guanine-N7)-methyltransferase |
Expression-Data Preprocessing Steps
First of all, missing expression-data values were imputed, using the KNNimpute program (Troyanskaya et al. 2001) with default parameters (15 nearest neighbors). Ratio-style data were then log-transformed, and arrays were median-normalized, to account for interarray differences. Each gene was median-centered, and ranked by standard deviation across arrays. The top 3000 genes in this ranking were selected for clustering and standardized across all arrays, so that each gene's expression profile had zero median and unit variance.
Software Implementation
We implemented the k-means algorithm with several different distance measures in the Perl programming language (Wall et al. 2000). Although this algorithm has been implemented for gene clustering, it has not been available in a form that allowed user-defined distance measures to be easily substituted in. Numerical performance was improved by up to two orders of magnitude through use of C code for the core algorithm, written in-house and interfaced with Perl using SWIG (Beazley et al. 1998; Beazley 2001) and the Perl Data Language extension (Soeller and Lukka 1997). GeneCluster (Angelo 1999) and Cluster (Eisen 1999) were obtained from their respective Web sites. Hierarchical trees from Cluster were cut into groups based on distance from the root, again using in-house C code glued to Perl with SWIG.
WEB SITE REFERENCES
http://genome-www.stanford.edu/Saccharomyces/; Saccharomyces genome database.
http://llama.med.harvard.edu/∼fgibbons; ClusterJudge algorithm.
http://pdl.perl.org/; Perl data language user guide.
http://www.lecb.ncifcrf.gov/∼toms/paper/primer; Information Theory Primer.
Acknowledgments
We thank G. Berriz, O. King, J. White, P. D'haeseleer, and P. Kharchenko for helpful discussions. We are grateful to G. Berriz, D. Goldberg, O. King, S. Wong, and S. Komili for critical reading of the manuscript. We believe this paper was improved by taking account of the suggestions of the anonymous referees, and we thank them. This work was supported in part by the Howard Hughes Medical Institute Biomedical Research Support Program for Medical Schools.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL froth@hms.harvard.edu; FAX (617) 432-3557.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.397002.
REFERENCES
- Aach J, Rindone W, Church GM. Systematic management and analysis of yeast gene expression data. Genome Res. 2000;10:431–445. doi: 10.1101/gr.10.4.431. [DOI] [PubMed] [Google Scholar]
- Angelo M. GeneCluster. Cambridge, MA: Whitehead/MIT Center for Genome Research; 1999. http://www.genome.wi.mit.edu/cancer/software/software.html ; http://www.genome.wi.mit.edu/cancer/software/software.html. . [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene ontology: Tool for the unification of biology. Nat Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beazley DM. SWIG User's Manual v.1.3; 2001. http://www.swig.org http://www.swig.org. . [Google Scholar]
- Beazley DM, Fletcher D, Dumont D. O'Reilly Perl Conference 2.0. 1998. Perl extension building with SWIG.http://www.swig.org/papers/Per198/swigperl.pdf San Jose, CA; http://www.swig.org/papers/Per198/swigperl.pdf. . [Google Scholar]
- Ben-Hur A, Elisseeff A, Guyon I. A stability based method for discovering structure in clustered data. In: Altman RB, et al., editors. Pacific Symposium in Biocomputing. Kauai, HI: World Scientific; 2002. pp. 6–17. [PubMed] [Google Scholar]
- Brown P, Grundy WN, Lin D, Cristianini N, Sugnet CW, Furey TS, Jr, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci. 2000;97:262–267. doi: 10.1073/pnas.97.1.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
- Cohen BA, Pilpel Y, Mitra RD, Church GM. Discrimination between paralogs using microarray analysis: Application to the Yap1p and Yap2p transcriptional networks. Mol Biol Cell. 2002;13:1608–1614. doi: 10.1091/mbc.01-10-0472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. In: Elements of information theory. Schilling DL, editor. New York: Wiley-Interscience; 1991. [Google Scholar]
- DeRisi JL, Iyer VR, Brown PO. Exploring the metabolic and genetic control of gene expression on a genomic scale. Science. 1997;278:680–686. doi: 10.1126/science.278.5338.680. [DOI] [PubMed] [Google Scholar]
- Eisen, M. 1999. Cluster. http://rana.lbl.gov.
- Eisen MB, Brown PO. DNA arrays for analysis of gene expression. Methods Enzymol. 1999;303:179–205. doi: 10.1016/s0076-6879(99)03014-1. [DOI] [PubMed] [Google Scholar]
- Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everitt B. Cluster analysis, 1st ed. London: Heinemann; 1980. [Google Scholar]
- Fraley C, Raftery AE. How many clusters? Which clustering method? Answers via model-based cluster analysis. Comput J. 1998;41:578–588. [Google Scholar]
- Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO. Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein M, Jansen R. The current excitement in bioinformatics—analysis of whole-genome expression data: How does it relate to protein structure and function? Curr Opin Struct Biol. 2000;10:574–584. doi: 10.1016/s0959-440x(00)00134-2. [DOI] [PubMed] [Google Scholar]
- Getz G, Levine E, Domany E. Coupled two-way clustering analysis of gene microarray data. Proc Natl Acad Sci. 2000;97:12079–12084. doi: 10.1073/pnas.210134797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- Issel-Tarver L, Christie KR, Dolinski K, Andrada R, Balakrishnan R, Ball CA, Binkley G, Dong S, Dwight SS, Fisk DG, et al. Saccharomyces genome database. Methods Enzymol. 2002;350:329–346. doi: 10.1016/s0076-6879(02)50972-1. [DOI] [PubMed] [Google Scholar]
- Jakt LM, Cao L, Cheah KSE, Smith DK. Assessing clusters and motifs from gene expression data. Genome Res. 2001;11:112–123. doi: 10.1101/gr.148301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelinsky S, Estep P, Church GM, Samson L. Regulatory networks revealed by transcriptional profiling of damaged Saccharomyces cerevisiae cells: RPN4 links base excision repair with proteosomes. Mol Cell Biol. 2000;20:8157–8167. doi: 10.1128/mcb.20.21.8157-8167.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazzeroni L, Owen A. Plaid models for gene expression data. Statistica Sinica. 2000;12:61–86. [Google Scholar]
- Lukashin AV, Fuchs R. Analysis of temporal gene expression profiles: Clustering by simulated annealing and determining the optimal number of clusters. Bioinformatics. 2001;17:405–414. doi: 10.1093/bioinformatics/17.5.405. [DOI] [PubMed] [Google Scholar]
- Michaels GS, Carr DB, Askenazi M, Furman S, Wen X, Somogyi R. Cluster analysis and data visualization of large-scale gene expression data. In: Altman RB, et al., editors. Pacific Symposium in Biocomputing. Kauai, HI: World Scientific; 1998. pp. 42–53. [PubMed] [Google Scholar]
- Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical recipes. 1st ed. Cambridge, UK: Cambridge University Press; 1986. [Google Scholar]
- Quackenbush J. Computational analysis of microarray data. Nat Rev Genet. 2001;2:418–427. doi: 10.1038/35076576. [DOI] [PubMed] [Google Scholar]
- Robertson LS, Causton HC, Young RA, Fink GR. The yeast A kinases differentially regulate iron uptake and respiratory functions. Proc Natl Acad Sci. 2000;97:5984–5988. doi: 10.1073/pnas.100113397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth FP, Hughes JD, Estep PW, Church GM. Finding DNA regulatory motifs within unaligned noncoding sequences clustered by whole-genome mRNA quantitation. Nat Biotech. 1998;16:939–945. doi: 10.1038/nbt1098-939. [DOI] [PubMed] [Google Scholar]
- Schneider TD. Information theory primer. 2000. http://www.lecb.ncifcrf.gov/∼toms/paper/primer http://www.lecb.ncifcrf.gov/∼toms/paper/primer. . [Google Scholar]
- Shamir R, Sharan R. CLICK: A clustering algorithm with applications to gene expression analysis. Proc Int Conf Intell Syst Mol Biol. 2000;8:307–316. [PubMed] [Google Scholar]
- Sinkkonen J, Kaski S. Clustering based on conditional distributions in an auxiliary space. Neur Comput. 2002;14:217–239. doi: 10.1162/089976602753284509. [DOI] [PubMed] [Google Scholar]
- Soeller C, Lukka T. Perl data language user guide. 1997. http://pdl.perl.org/ http://pdl.perl.org/. . [Google Scholar]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitarbeewan S, Dmitrovsky E, Lander ES, Golub TR. Interpreting patterns of gene expression with self-organizing maps: Methods and application to hematopoietic differentiation. Proc Natl Acad Sci. 1999;96:2907–2912. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281–285. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein, Altman RB. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- Wall L, Christiansen T, Orwant J. Programming Perl. 3rd ed. Sebastopol, CA: O'Reilly & Associates; 2000. [Google Scholar]
- Wen X, Fuhrman S, Michaels G, Carr D, Smith S, Barker J, Somogyi R. Large-scale temporal gene expression mapping of central nervous system development. Proc Natl Acad Sci. 1998;95:334–339. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung KY, Haynor DR, Ruzzo WL. Validating clustering for gene expression data. Bioinformatics. 2001;17:309–318. doi: 10.1093/bioinformatics/17.4.309. [DOI] [PubMed] [Google Scholar]