Abstract
The completion of the human genome project and the construction of single nucleotide polymorphism (SNP) maps have lead to significant efforts to find SNPs that can be linked to pathophysiology. In silico models of complete biochemical reaction networks relate a cell's individual reactions to the function of the entire network. Sequence variations can in turn be related to kinetic properties of individual enzymes, thus allowing an in silico model-driven assessment of the effects of defined SNPs on overall cellular functions. This process is applied to defined SNPs in two key enzymes of human red blood cell metabolism: glucose-6-phosphate dehydrogenase and pyruvate kinase. The results demonstrate the utility of in silico models in providing insight into differences between red cell function in patients with chronic and nonchronic anemia. In silico models of complex cellular processes are thus likely to aid in defining and understanding key SNPs in human pathophysiology.
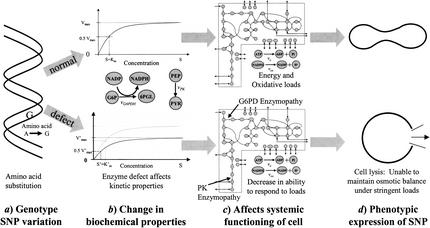
The Human Genome Project (HGP) is now essentially complete. One result of the HGP is the definition of single nucleotide polymorphisms (SNPs) and their effects on the development of human disease. Although the number of SNPs in the human genome is expected to be a few million, it is estimated that only 100,000 to 200,000 will effectively define a unique human genotype. A subset of these SNPs is believed to be “informative” with respect to human disease (Syvanen 2001). Many of these “informative” SNPs will fall into coding regions while others will be found in regulatory regions. The human genotype-phenotype relationship is very complex and it will be hard to determine the causal relationship between sequence variation and physiological function. One way to deal with this intricate relationship is to build large-scale in silico models of complex biological processes (Fig. 1). Defects or alterations in the properties of a single component in complex biological processes can be put into context of the rest by using an in silico model. In this work, recent data on SNPs in key red blood cell enzymes (Fig. 1a) and corresponding alterations in their kinetic properties (Fig. 1b) were used in an in silico red blood cell model (Fig. 1c) to calculate the overall effect of SNPs on whole cell function (Fig. 1d).
Figure 1.
A schematic depiction of the genotype-phenotype relationship; from sequence variation (a) to changes in biochemical function (b) to network properties (c) to overall physiological function (d). The upper path signifies a normal pathological situation. The DNA sequence codes a nondeficient enzyme that catalyzes the glucose-6-phosphate dehydrogenase or pyruvate kinase reactions normally resulting in homeostatic red blood cell metabolism with the cell assuming its traditional biconcave shape. The lower path represents a pathological situation, a defect in the DNA sequence that leads to a metabolic enzyme with altered catalytic activity. The result is a loss in the cell's ability to respond to oxidative and/or energy loads, hence an inability to maintain osmotic balance and stability that ultimately results in lysis–the phenotypic expression of the genetic defect.
Erythrocyte metabolism has been extensively studied. Over the years, a series of mathematical models of increasing scope and detail of erythrocyte metabolism have been formulated and they have been used to describe the red blood cell's integrated metabolic functions (Rapoport and Heinrich 1975; Heinrich et al. 1977; Schauer et al. 1981; Joshi and Palsson 1989; Mulquiney and Kuchel 1999). Such models can be used to describe the consequences of altered kinetic constants on red blood cell function (Heinrich et al. 1977; Holzhütter et al. 1985; Schuster 1995; Jacobasch and Rapoport 1996; Martinov et al. 2000). The study of variations in the kinetic properties of red blood cell enzymes is not merely an academic study of the quality of a mathematical model, but has real utility in the clinical diagnosis and treatment of enzymopathies and can provide a link to the underlying sequence variation (Fig. 1). Here, an in silico model is used to study SNPs in two of the most frequent red blood cell enzymopathies: glucose-6-phosphate dehydrogenase (G6PD) and pyruvate kinase (PK).
RESULTS
For both enzyme deficiencies, clinical data was obtained from the published literature to determine measured values for the various kinetic parameters (Vmaxs, Kms, Kis) associated with each clinically diagnosed variant. These numerical values were then used in the in silico model (Jamshidi et al. 2001) and sensitivities to various oxidative and energy loads (above normal, baseline values) were simulated. The results are interpreted with respect to the genetic basis of the enzymopathy in an attempt to establish a direct link between the genotype and phenotype (Fig. 1).
G6PD Deficiency
G6PD catalyzes the first step in the oxidative branch of the pentose pathway (Fig. 1c) and is thus of critical importance in maintaining the red blood cell's resistance to oxidative stresses. G6PD has been studied extensively since its initial discovery and characterization in the early 1960's (Kirkman 1960; Kirkman 1962; Thorburn and Kuchel 1985; Kirkman and Gaetani 1986). It is the most common erythrocyte enzymopathy, affecting ∼400 million people worldwide. The World Health Organization (WHO) has standardized methods by which to describe these deficiencies, and over 400 different biochemical variants have been described based on the biochemical properties (e.g., electrophoretic mobility, Vmax, etc.) of the enzymes (Beutler 1990). Four classes have been defined ranging from class I (chronic nonspherocytic hemolytic anemia) to class IV (no deficiency) grading the level of hemolytic anemia observed in patients having G6PD deficiencies (Beutler and Yoshida 1988; Beutler 1990; Jacobasch and Rapoport 1996).
G6PD deficiency is a sex-linked trait. The G6PD gene is located in position Xq28 in the long arm of the X chromosome, with 13 exons and 12 introns spanning 20 kb (Yoshida 1986; Beutler 1990; Jacobasch and Rapoport 1996). As a monomer, G6PD is a 59-kD protein, 515 amino acids long. It is active in the tetrameric (in acid) or dimeric (in base) forms (Adediran 1996). The monomer has two domains, an N-terminal domain (amino acids 27–200) and a β+α domain. The N-terminal domain contains a β-α-β dinucleotide (NADP) binding site (amino acids 38–44). The α-helix links the two domains and contains a highly conserved substrate-binding site (amino acids 198–206). The quaternary structure of the enzyme is important for its stability and its ability to maintain normal activity. Normal G6PD requires low concentrations of NADP to maintain its integrity (Beutler 1986). Thus, NADP serves two functions; it stabilizes the dimer and serves as a substrate. The same domain is believed to be responsible for structural stability and catalytic activity (Hirono et al. 1989).
G6PD from normal patients and patients with hemolytic anemia have been characterized on the molecular level. A total of 61 G6PD class I variants have been described at the molecular level. Of the 61 class I chronic variants, 55 are the result of SNPs involving amino-acid changes, five result from frame deletions and one results from a splicing defect (Fiorelli et al. 2000).
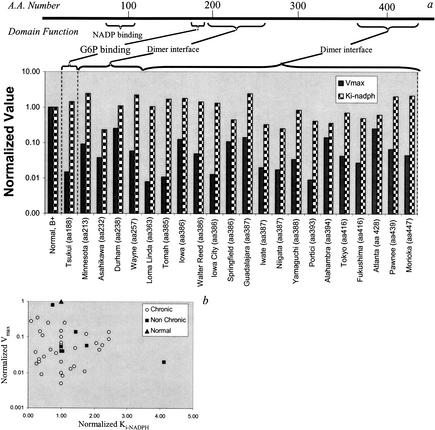
Clinically diagnosed SNPs cluster around important, active regions of G6PD enzyme including the dimer interface and substrate-binding sites (Fig. 2a). Numerical values of G6PD kinetic parameters were varied in silico to determine the sensitivity of red blood cell metabolic functions to these changes in enzyme function. The most sensitive parameters were found to be Vmax and Ki-NADPH. The NADPH/NADP ratio proved to be the most informative indicator of metabolic status as it was the most sensitive to changes in these two parameters and it gives an indication as to the oxidative state of the cell (Kirkman et al. 1975).
Figure 2.
The location of SNPs in the glucose-6-phosphate dehydrogenase (G6PD) protein. (a) The G6PD variants for which there is full molecular characterization available, are shown with their corresponding parameter values and amino-acid location of the single nucleotide polymorphism (SNP). Note that the SNPs are located in critical regions of the protein. (b) Shows that there is no obvious correlation between the altered numerical values for the two kinetic parameters in either the chronic or nonchronic cases.
For each documented variant, there appears to be no direct correlation between Vmax and Ki-NADPH (Fig. 2b). Clinically, G6PD deficiencies are broken down into two main categories: chronic and nonchronic hemolytic anemia. Chronic cases show clinical symptoms and are very sensitive to the environment. Nonchronic cases appear normal under homeostatic conditions but can experience problems when subjected to large oxidative stresses (Jacobasch and Rapoport 1996). For this study, kinetic data for 12 chronic and 8 nonchronic cases from Yoshida and 19 chronic cases from Fiorelli were used (Yoshida 1986; Fiorelli et al. 2000). The G6PD variant data used from the references were characterized according to the WHO standards defined in Betke et al. (1967).
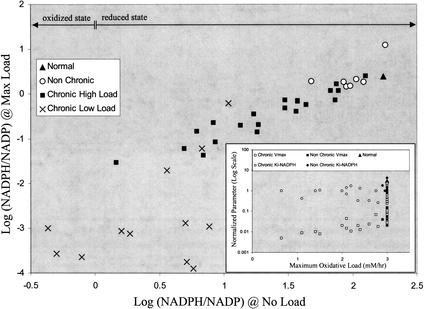
Under normal conditions (i.e., oxidative load, vox = 0), there are differences between the chronic and nonchronic groups, with the chronic group having a somewhat lower homeostatic steady-state NADPH/NADP ratio than the nonchronic group (data not shown). When subjected to an oxidative load (vox > 0), noticeable differences between the two groups (chronic and nonchronic) appear (Fig. 3). The NADPH/NADP ratio at the maximum tolerated oxidative load (vox = max value) correlates with this ratio in the unstressed situation (vox = 0). The group of chronic hemolytic anemia patients is clearly separated from the normal and nonchronic group. A number of the chronic cases can only withstand a very modest oxidative load. Of the variant cases studied, a handful has been characterized at the molecular (amino acid) level (Table 1). Of the cases considered, most of the single-base changes in the chronic (class I) variants occur at or near the dimer interface (exons 10,11 and 6,7) or near the NADP binding site, leading to an impaired ability to respond to systemic oxidative challenges.
Figure 3.
The ability of glucose-6-phosphate dehydrogenase (G6PD) variants to respond to oxidative load based on in silico red blood cell model results. The NADPH/NADP is plotted for maximum load (vox = max value tolerated) versus no oxidative load (vox = 0) for each G6PD variant. The nonchronic cases cluster near the normal case and can sustain a maximum oxidative load of near normal (3 mM/h). The chronic cases can be split into two categories, those that can sustain a near-normal load (chronic high load) and those who are well below normal (chronic low load). The horizontal arrows demarcate two regions: an oxidized state (Log [NADPH/NADP] < 0) where the majority of the cofactor is in the form of NADP and a reduced state (Log [NADPH/NADP] > 0) where the majority of the cofactor is in the form of NADPH. For G6PD enzymopathies, the oxidized state is prevalent, while the reduced state is found in normal individuals (Kirkman et al. 1975). The insert shows no clear correlation between Vmax, Ki-NADPH, and the cell's ability to withstand oxidative loads.
Table 1.
Molecular Characterization of Specific SNPs for Selected Cases of G6PD Variants Including DNA Sequence Change, Corresponding Amino-Acid Change, and Result
| Variant | Type | Nucleotide change | Amino-acid change | Result |
|---|---|---|---|---|
| B+ | normal | none | none | |
| A+ | nonchronic | 376 A→G | Asn→Asp | polar to acidic |
| A− | nonchronic | 376 A→G | Asn→Asp | polar to acidic |
| 202* G→A | Val→Met | nonpolar to nonpolar | ||
| Mediterranean | nonchronic | 563 C→T | Ser→Phe | polar to nonpolar |
| Tsukui | chronic | 561-563 del | 188/189 del | – |
| Minnesota | chronic | 637 G→T | 213 Val→Leu | nonpolar to nonpolar |
| Asahikawa | chronic | 695 G→A | 232 Cys→Tyr | slightly polar to nonpolar |
| Durham | chronic | 713 A→G | 238 Lys→Arg | basic to basic |
| Wayne | chronic | 769 C→G | 257 Arg→Gly | basic to nonpolar |
| Loma Linda | chronic | 1089 C→A | 363 Asn→Lys | polar to basic |
| Tomah | chronic | 1153 T→C | 385 Cys→Arg | slightly polar to basic |
| Iowa | chronic | 1156 A→G | 386 Lys→Glu | basic to acidic |
| Walter Reed | chronic | 1156 A→G | 386 Lys→Glu | basic to acidic |
| Iowa City | chronic | 1156 A→G | 386 Lys→Glu | basic to acidic |
| Springfield | chronic | 1156 A→G | 386 Lys→Glu | basic to acidic |
| Guadalajara | chronic | 1159 C→T | 387 Arg→Cys | basic to slightly polar |
| Iwate | chronic | 1160 G→A | 387 Arg→His | basic to acidic/basic |
| Niigata | chronic | 1160 G→A | 387 Arg→His | basic to acidic/basic |
| Yamaguchi | chronic | 1160 G→A | 387 Arg→His | basic to acidic/basic |
| Portici | chronic | 1178 G→A | 393 Arg→His | basic to acidic/basic |
| Alhambra | chronic | 1180 G→C | 394 Val→Leu | nonpolar to nonpolar |
| Tokyo | chronic | 1246 G→A | 416 Glu→Lys | acidic to basic |
| Fukushima | chronic | 1246 G→A | 416 Glu→Lys | acidic to basic |
| Atlanta | chronic | 1284 C→A | 428 Tyr→End | – |
| Pawnee | chronic | 1316 G→C | 439 Arg→Pro | basic to nonpolar |
| Morioka | chronic | 1339 G→A | 447 Gly→Arg | nonpolar to basic |
All data comes from Yoshida and Lin (1973); Vulliamy et al. (1988); Beutler (1990); Au et al. (2000); Fiorelli et al. (2000).
Most, but not all of the A variants have an amino-acid 202 mutation; some have the second mutation at another site.
PK Deficiency
Pyruvate kinase (PK) is a key glycolytic regulatory enzyme. There have only been ∼400 documented variants since PKs first description in 1961 (Tanaka and Zerez 1990; Jacobasch and Rapoport 1996; Zanella and Bianchi 2000). PK accounts for 90% of the enzyme deficiencies found in red blood cell glycolysis (Jacobasch and Rapoport 1996). It is autosomal recessive where clinical manifestations appear only in compound heterozygotes (two mutant alleles). There are four isozymes: L, R, M1, and M2, with the R type being exclusive to red blood cells. PK is encoded by the PK-LR gene on chromosome 1q21. The kinetics of the enzyme have been extensively studied (Otto et al. 1974). PK activity is regulated by F6P, ATP, Mg, and MgATP. Anemic heterozygotes have 5–40% of normal PK activity.
Active PK exists as a tetramer of four 60 kD subunits. There are four domains: A [a (αβ)8 barrel], B (a small β barrel), the C-terminal, and the N-terminal with a helix-turn-helix motif. The amino-acid sequence of PK is highly conserved. Based on PK studies of the rabbit, Escherichia coli, and yeast, the PEP and cation binding sites are in the cleft between the A and B domains, close to the sixth and eighth loops of the (αβ)8 barrel. PK exhibits 222 symmetry, and there are two states for the tetramer, the low-affinity, tight (T) conformation and the high-affinity, relaxed (R) conformation. The PEP and Mg2+ binding sites are in the cleft between the A and B domains close to the sixth and eighth loops of the (αβ)8 barrel. The FDP binding site is in the C domain. The enzyme is stabilized by the interaction between the A and C domains of opposing subunits (Zanella and Bianchi 2000). While the crystal structure of human R-type PK has not yet been explicitly determined, it shares sequence homology with feline PK, whose crystal structure has been determined. Given this information along with computer simulation studies, it has been determined that some of the PK SNPs leading to severe hemolytic anemia are not in the catalytic sites. Some of these mutations are believed to occur at subunit interfaces (Solinge et al. 1997).
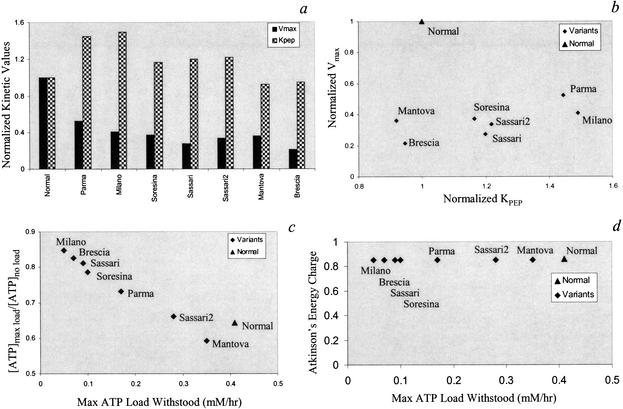
Unlike for G6PD, the characterized PK SNPs are scattered throughout the protein coding region and do not appear to cluster near the corresponding active site of the enzyme (Zanella and Bianchi 2000). A summary of the PK variants is presented in Table 2. The biochemical data used for the PK variants from these references were characterized according to the protocols described by Miwa et al. (1979). The documented kinetic values for the main kinetic parameters Vmax and KPEP are shown (Fig. 4a). Similar to the G6PD variants, there is not a clear correlation between changes in the numerical Vmax and KPEP amongst the PK variants (Fig. 4b). Although changes in KADP are also documented for each variant and accounted for in the simulations, increases or decreases in its value did not significantly affect the red blood cell's steady-state metabolite concentrations or its ability to withstand energy loads (data not shown). Changes in KPEP and Vmax influence the concentration of ATP and 2,3DPG most significantly. When increased energy loads (ve >0) are applied in silico, differences between the variants are observed. The ratio between the ATP concentration at maximum tolerated load (ve = max value) and the ATP concentration in the unchallenged state (ve = 0) varies approximately linearly with the maximum tolerated load when all the variants are evaluated (Fig. 4c). Thus, the variants that tolerated the lowest maximum load have an [ATP]max/[ATP]no load ratio close to unity indicating their sharply diminished ability to deviate from the nominal homeostatic state. Interestingly, the computed energy charge [EC = (ATP + ½ADP)/(ATP+ADP+AMP)] (Atkinson 1977) stays relatively constant (Fig. 4d). This result indicates that red blood cell metabolism strives to maintain its EC within the tolerated load range, thus allowing for an energetically consistent metabolic function.
Table 2.
Molecular Characterization of Specific SNPs for PK Variants Including DNA Sequence Change, Corresponding Amino-Acid Change, and Result
| Variant | Nucleotide change | Amino acid change | Result |
|---|---|---|---|
| Sassari | 514 G→C | Glu→Gln | acidic to slightly polar |
| Parma | not characterized | – | – |
| 1456 C→T | Arg→Trp | basic to nonpolar | |
| Soresina | 1456 C→T | Arg→Trp | basic to nonpolar |
| 1552 C→A | Arg→Ser | basic to slightly polar | |
| Milano | 1456 C→T | Arg→Trp | basic to nonpolar |
| Brescia | 1042-1044 del | Lys deleted | basic deleted |
| 1456 C→T | Arg→Trp | basic to nonpolar | |
| Manatova | 1168 G→A | Asp→Asn | acidic to slightly polar |
All data obtained from Solinge et al. (1997); Zanella and Bianchi (2000).
Figure 4.
The ability of pyruvate kinase (PK) variants to respond to energy load. (a) The numerical values for Vmax and KPEP for the documented PK cases. (b) There is no obvious correlation between the two kinetic parameters amongst the variants studied. (c) As the maximum tolerated ATP load decreases, the ratio of the cells [ATP] at maximum load versus at no load increases resulting in a near linear relationship. (d) The energy charge remains near constant despite the significant drop in the each variant's ability to withstand an ATP load.
DISCUSSION
With the HGP effectively complete and the amount of sequence variation information growing, the need to define the consequences of such variations on physiological function is brought to the forefront. Here, we use the human red blood cell to show that an in silico model can be used to aid in this process.
Sequence variations in coding regions for metabolic enzymes can lead to altered kinetic properties. The kinetic properties of enzymes are described by many parameters, and a single SNP can alter one or many of these parameters. For the variants of G6PD and PK considered here, there appears to be no clear relationship between their kinetic parameters as a function of sequence variation. Thus, consequences of sequence variations on the function of a gene product must be fully evaluated to get a comprehensive assessment of the altered biochemical function.
The consequences of many simultaneously altered enzyme properties must in turn be evaluated in terms of the function of the enzyme in the context of the reaction network in which it participates. The assessment of sequence variation on biochemical and kinetic properties of enzymes may seem difficult and this challenge is currently being addressed (Yamada et al. 2001), but the assessment of sequence variation on entire network function is even more complicated. This highly complex and intricate relationship between sequence variation and network function can be studied through the use of a computer model. Here, we have shown that a large number of variants in red blood cell G6PD and PK can be systematically analyzed using an in silico model of the red blood cell. Correlations between sequence variation and predicted overall cell behavior is established, and in the case of G6PD, it in turn correlates with the severity of the clinical conditions.
The red blood cell in silico model has been developed through successive iterations over the past 30 years (Rapoport and Heinrich 1975; Heinrich et al. 1977; Schauer et al. 1981; Holzhütter et al. 1985; Joshi and Palsson 1989; Mulquiney and Kuchel 1999). Building in silico models of complex biological processes has therefore proven to be a difficult task. This challenge may now be more manageable given the development of data-driven constraints-based models (Schilling et al. 1999; Palsson 2000). We thus may be entering an era where in silico biology will develop computer representations of complex biological processes, and these in silico models may then, in turn, aid in the analysis, interpretation, and even prediction of intricate genotype-phenotype relationships, both for normal physiological and pathophysiological conditions.
METHODS
The metabolic network of the mature erythrocyte is composed of glycolysis, the pentose phosphate shunt, the 2,3-diphosphoglycerate (2,3DPG) shunt, and the nucleotide salvage pathway. Glycolysis produces ATP by substrate-level phosphorylation to drive the Na/K pump that enables the cell to maintain osmotic balance and its biconcave shape. The pentose phosphate pathway produces NADPH to keep glutathione in the reduced state and allows the cell to counteract oxidative loads (via oxygen radicals, superoxides, etc.). The two enzyme deficiencies considered here involve key fluxes in these two key metabolic pathways.
Simulation studies with a model of red blood cell metabolism were performed on a PC using Mathematica (Wolfram Research; Jamshidi et al. 2001). The model includes glycolysis, the pentose-phosphate pathway, the Rapoport-Leubering (2–3DPG) shunt, nucleotide synthesis and degradation reactions, the ATPase pump, equilibrium expressions accounting for magnesium complexing, and osmotic and electroneutrality balances. This in silico model is composed of 41 differential and algebraic equations that must be solved simultaneously (Joshi and Palsson 1989; Joshi and Palsson 1990; Lee and Palsson 1991).
Although the model can compute dynamic metabolic responses, here we focus solely on the steady-state solutions. The numerical value for any kinetic parameter in the model can be varied and the resulting steady state calculated. If the numerical value of a kinetic parameter is varied too far from its normal value, a point will be reached where there is no solution to the system of equations and the in silico cell is not able to reach a steady state. This point corresponds to uncontrolled cell swelling and lysis.
Loads on energy (ve) and redox (vox) metabolism are simulated in silico by assigning increased fluxes to the following nonspecific conversions of cofactors to simulate elevated metabolic loads (Fig. 1c),
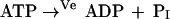 |
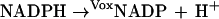 |
which are zero in the normal physiological state. When ve or vox have reached values that lead to cell lysis, they are scored as the maximum flux loads sustainable by the cell. This maximum will vary with the numerical values of the kinetic parameters that in turn may be influenced by SNPs.
Acknowledgments
This work is funded by National Science Foundation (Graduate Research Fellowship to S.J.W. BES01–20363, BES98–14092, and MCB98–73384) and the National Institutes of Health (GM57089).
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL palsson@ucsd.edu; FAX (858) 822-3120.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.329302.
REFERENCES
- Adediran SA. Kinetic and thermodynamic properties of two electrophoretically similar genetic variants of human erythrocyte glucose-6-phosphate dehydrogenase. Biochimie. 1996;78:165–170. doi: 10.1016/0300-9084(96)89501-0. [DOI] [PubMed] [Google Scholar]
- Atkinson DE. Cellular energy metabolism and its regulation. New York: Academic Press; 1977. [Google Scholar]
- Au SW, Gover S, Lam V, Adams MJ. Human glucose-6-phosphate dehydrogenase: The crystal structure reveals a structural NADP molecule and provides insights into enzyme deficiency. Structure. 2000;8:293–303. doi: 10.1016/s0969-2126(00)00104-0. [DOI] [PubMed] [Google Scholar]
- Betke KBE, Brewer GJ, Kirkman HN, Luzzatto L, Motulsky AG, Ramot B, Siniscalco M. Standardization of procedures for the study of glucose-6-phosphate dehydrogenase. Report of a WHO scientific group. WHO Tech Rep Ser. 1967;Ser:366. [PubMed] [Google Scholar]
- Beutler E. Red cell metabolism. Edinburgh, England; New York: Churchill Livingstone; 1986. [Google Scholar]
- Beutler E. The genetics of glucose-6-posphate dehydrogenase deficiency. Semin Hematol. 1990;27:137–164. [PubMed] [Google Scholar]
- Beutler E, Yoshida A. Genetic variations of glucose-6-phosphate dehydrogenase: A catalog and future prospects. Medicine. 1988;67:311–334. doi: 10.1097/00005792-198809000-00003. [DOI] [PubMed] [Google Scholar]
- Fiorelli G, Martinez di Montemuros F, Domencia Cappellini M. Chronc non-spherocytic haemolytic disorders associated with glucose-6-phosphate dehydrogenase variants. Baillieres Clin Haematol. 2000;13:35–55. doi: 10.1053/beha.1999.0056. [DOI] [PubMed] [Google Scholar]
- Heinrich R, Rapaport SM, Rapaport TA. Metabolic regulation and mathematical models. Prog Biophys Mol Biol. 1977;32:1–82. [PubMed] [Google Scholar]
- Hirono A, Kuhl W, Gelbart T, Forman L, Fairbanks VF, Beutler E. Identification of the binding domain for NADP of human glucose-6-phosphate dehydrogenase by sequence analysis of mutants. Proc Natl Acad Sci. 1989;86:10015–10017. doi: 10.1073/pnas.86.24.10015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzhütter HG, Jacobasch G, Bisdorff A. Mathematical modelling of metabolic pathways affected by an enzyme deficiency. A mathematical model of glycolysis in normal and pyruvate-kinase-deficient red blood cells. Eur J Biochem. 1985;149:101–111. doi: 10.1111/j.1432-1033.1985.tb08899.x. [DOI] [PubMed] [Google Scholar]
- Jacobasch G, Rapoport SM. Hemolytic anemias due to erythrocyte enzyme deficiencies. Mol Aspects Med. 1996;17:143–170. doi: 10.1016/0098-2997(96)88345-2. [DOI] [PubMed] [Google Scholar]
- Jamshidi N, Edwards JS, Fahland T, Church GM, Palsson BØ. Dynamic simulation of the human red blood cell metabolic network. Bioinformatics. 2001;17:286–287. doi: 10.1093/bioinformatics/17.3.286. [DOI] [PubMed] [Google Scholar]
- Joshi A, Palsson BØ. Metabolic dynamics in the human red cell. Part I–A comprehensive kinetic model. J Theor Biol. 1989;141:515–528. doi: 10.1016/s0022-5193(89)80233-4. [DOI] [PubMed] [Google Scholar]
- Joshi A, Palsson BØ. Metabolic dynamics in the human red cell. Part IV–Data prediction and some model computations. J Theor Biol. 1990;142:69–85. doi: 10.1016/s0022-5193(05)80013-x. [DOI] [PubMed] [Google Scholar]
- Kirkman HN. Different enzymic expressions of mutants of human glucose-6-phosphate dehydrogenase. Proc Natl Acad Sci. 1960;46:938–944. doi: 10.1073/pnas.46.7.938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkman HN. Glucose-6-phosphate dehydrogenase from human erythrocytes. I. Further purification and characterization. J Biol Chem. 1962;237:2364–2370. [PubMed] [Google Scholar]
- Kirkman HN, Gaetani GF. Regulation of glucose-6-phosphate dehydrogenase in human erythrocytes. J Biol Chem. 1986;261:4033–4038. [PubMed] [Google Scholar]
- Kirkman HN, Gaetani GD, Clemons EH, Mareni C. Red cell NADP+ and NADPH in glucose-6-phosphate dehydrogenase deficiency. J Clin Inves. 1975;55:875–878. doi: 10.1172/JCI107998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee I-D, Palsson BØ. A comprehensive model of human erythrocyte metabolism: Extensions to include pH effects. Biomedica Biochimica Acta. 1991;49:771–789. [PubMed] [Google Scholar]
- Martinov MV, Plotnikov AG, Vitvitsky VM, Ataullakhanov FI. Deficiencies of glycolytic enzymes as a possible cause of hemolytic anemia. Biochim Biophys Acta. 2000;1474:75–87. doi: 10.1016/s0304-4165(99)00218-4. [DOI] [PubMed] [Google Scholar]
- Miwa S, Boivin P, Blume KG, Arnold H, Black JA, Kahn A, Staal GE, Nakashima K, Tanaka KR, Paglia DE, et al. Recommended methods for the characterization of red cell pyruvate kinase variants. International Committee for Standardization in Haematology. Brit J Haematol. 1979;43:275–286. doi: 10.1111/j.1365-2141.1979.tb03751.x. [DOI] [PubMed] [Google Scholar]
- Mulquiney PJ, Kuchel PW. Model of 2–3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed kinetic equations: Computer simulation and metabolic control analysis. Biochem J. 1999;342:597–604. [PMC free article] [PubMed] [Google Scholar]
- Otto M, Heinrich R, Kuhn B, Jacobasch G. A mathematical model for the influence of frutose-6-phosphate, ATP, potassium, ammonium, and magnesium on the phosphofructokinase from rat erythrocytes. Eur J Biochem. 1974;49:169–178. doi: 10.1111/j.1432-1033.1974.tb03822.x. [DOI] [PubMed] [Google Scholar]
- Palsson BØ. The challenges of in silico biology. Nat Biotech. 2000;18:1147–1150. doi: 10.1038/81125. [DOI] [PubMed] [Google Scholar]
- Rapoport TA, Heinrich R. Mathematical analysis of multienzyme systems. I: Modelling of glycolysis of human erythrocytes. Biosystems. 1975;7:120–129. doi: 10.1016/0303-2647(75)90049-0. [DOI] [PubMed] [Google Scholar]
- Schauer M, Heinrich R, Rapoport SM. Mathematische modellierung der glykolyse und des adeninnukleotidstoffwechsels menschlicher erythrozyten. Acta Biological er Medica Germanica. 1981;40:1659–1682. [PubMed] [Google Scholar]
- Schilling CH, Edwards JS, Palsson BØ. Towards metabolic phenomics: Analysis of genomic data using flux balances. Biotechnol Prog. 1999;15:288–295. doi: 10.1021/bp9900357. [DOI] [PubMed] [Google Scholar]
- Schuster R, Holzutter HC. Use of mathematical models for predicting the effect of large scale enzyme activity alterations: Applications to enzyme deficiencies of red blood cells. Eur J Biochem. 1995;229:403–418. [PubMed] [Google Scholar]
- Solinge WWv, Kraaijenhagen RJ, Rijksen G, van Wijk R, Stoffer BB, Gajhede FCNM. Molecular modeling of human red blood cell pyruvate kinase: Structural implications of a novel G-1091 to A mutation causing severe nonspherocytic hemolytic anemia. Blood. 1997;90:4987–4995. [PubMed] [Google Scholar]
- Syvanen A. Accessing genetic variation: Genotyping single nucleotide polymorphisms. Nat Rev Genet. 2001;2:930–942. doi: 10.1038/35103535. [DOI] [PubMed] [Google Scholar]
- Tanaka KR, Zerez CR. Red cell enzymopathies of the glycolytic pathway. Semin Hematol. 1990;27:165–185. [PubMed] [Google Scholar]
- Thorburn DR, Kuchel PW. Regulation of the human-erythrocyte hexose-monophosphate shunt under conditions of oxidative stress. A study using NMR spectroscopy, a kinetic isotope effect, a reconstituted system and computer simulation. Eur J Biochem. 1985;150:371–386. doi: 10.1111/j.1432-1033.1985.tb09030.x. [DOI] [PubMed] [Google Scholar]
- Vulliamy TJ, D'Urso M, Battistuzzi G, Estrada M, Foulkes NS, Martini G, Calabro V, Poggi V, Giordano R, Town M, et al. Diverse point mutations in the human glucose-6-phosphate dehydrogenase gene cause enzyme deficiency and mild or severe hemolytic anemia. Proc Natl Acad Sci. 1988;85:5171–5175. doi: 10.1073/pnas.85.14.5171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada K, Chen Z, Rozen R, Matthews RG. Effects of common polymorphisms on the properties of recombinant human methylenetetrahydrofolate reductase. Proc Natl Acad Sci. 2001;98:14853–14858. doi: 10.1073/pnas.261469998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida A. Glucose-6-Phosphate Dehydrogenase. Orlando, FL: Academic Press; 1986. Kinetics and molecular abnormalities of human G6PDH variants; pp. 493–502. [Google Scholar]
- Yoshida A, Lin M. Regulation of glucose-6-phosphate dehydrogenase activity in red blood cells from hemolytic and nonhemolytic variant subjects. Blood. 1973;41:877–891. [PubMed] [Google Scholar]
- Zanella A, Bianchi P. Red cell pyruvate kinase deficiency: From genetics to clinical manifestations. Ballieres Clin Hematol. 2000;13:57–81. doi: 10.1053/beha.1999.0057. [DOI] [PubMed] [Google Scholar]