Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2002 Dec;12(12):1943–1949. doi: 10.1101/gr.655102

Generalized Gap Model for Bacterial Artificial Chromosome Clone Fingerprint Mapping and Shotgun Sequencing

Michael C Wendl 1,2, Robert H Waterston 1
PMCID: PMC187573  PMID: 12466299

Abstract

We develop an extension to the Lander-Waterman theory for characterizing gaps in bacterial artificial chromosome fingerprint mapping and shotgun sequencing projects. It supports a larger set of descriptive statistics and is applicable to a wider range of project parameters. We show that previous assertions regarding inconsistency of the Lander-Waterman theory at higher coverages are incorrect and that another well-known but ostensibly different model is in fact the same. The apparent paradox of infinite island lengths is resolved. Several applications are shown, including evolution of the probability density function, calculation of closure probabilities, and development of a probabilistic method for computing stopping points in bacterial artificial chromosome shotgun sequencing.

Complete DNA sequences are critical resources for biomedical research. Motivated both by the need for such information and by enabling advances in technology, sequencing efforts continue to expand dramatically. Several “model” organisms have already been completed (e.g., Johnston et al. 1997; The Caenorhabditis elegans Sequencing Consortium 1998; Adams et al. 2000; The Arabidopsis Genome Initiative 2000), and draft versions of the human genome have recently been announced (International Human Genome Sequencing Consortium [IHGSC] 2001; Venter et al. 2001). Numerous additional projects are either planned or underway.

There are a number of views regarding optimal strategies toward sequencing. Experience derived from recent human projects (IHGSC 2001; McPherson et al. 2001) confirms that a fingerprint approach based on bacterial artificial chromosome (BAC) clones (Shizuya et al. 1992) is effective for large genomes. Conversely, small genomes can usually be sequenced directly using the random shotgun method (e.g., Heidelberg et al. 2000). The seminal work of Lander and Waterman (1988) provided the first step toward a fundamental theoretical basis for these two important procedures. In particular, the Lander and Waterman (L-W) theory permits calculation of the expected number of gaps as a function of the number of clones or subclones processed and the resolution for detecting overlaps (Fig. 1). Because project completion basically depends on the number of outstanding gaps (Roach et al. 1999), this statistic is useful both in planning and troubleshooting and remains one of scientists' standard analytical tools (Myers 1999).

Figure 1.

Figure 1

Open in a new tab

Schematic representation of fingerprint mapping and shotgun sequencing. Crossbars represent average amount of overlap required for detection. Some predicted gaps will be genuine as in (a) for which no clone spans the region, whereas others will be falsely predicted as in (b) because of insufficient detection resolution.

Mathematical descriptions of mapping and sequencing are rooted in classical theories of probabilistic coverage processes (Kendall and Moran 1963; Solomon 1978). These early results are idealized in the sense that they do not consider biologically relevant parameters, such as detection resolution for clone overlaps. The L-W theory was the first practical advance in this regard. The L-W model posits a simple geometric coverage process from which expected values are deduced. Conversely, Roach (1995) proposes a process governed by a binomial distribution and argues that the geometric model is valid only for limited coverage. Wendl et al. (2001) cast some doubt on this conclusion by showing that L-W results can be obtained independently of a geometric assumption, but they did not further resolve the discrepancy. Other idealized results have been developed, for example, the probability of closure in which the alphabet of nucleotide bases is infinite (Derrida and Fink 2002). The text by Hall (1988) discusses some related problems.

Here, we formulate a rigorous extension to L-W theory. This work was motivated by three concerns. First, L-W theory is based on the assumption of vanishing clone size. This simplification is actually embedded in all the standard models discussed previously, in which it is invoked in equivalent forms of infinite genome size or a continuum representation of the problem rather than a discrete one. The degree to which projects such as BAC fingerprinting small genomes (e.g., Tomkins et al. 2001) violate the vanishing clone length assumption is unclear. Second, there are apparent theoretical discrepancies with other models, especially the well-known paradox of infinite island lengths (Roach 1995). Finally, L-W theory does not support descriptive statistics beyond the expected value. The current generalization fully resolves each of these issues. We show several example applications that give a more accurate and comprehensive gap characterization of mapping and sequencing than has previously been available.

RESULTS

A combinatorially exact distribution describing gaps appears in equation 4. Variables L and G denote clone and project lengths, respectively, T specifies the average length of overlap required for detection, and N represents the number of clones processed. Statistics are characterized by the moment-generating function in equation 5, from which are derived expected number and variance of gaps in equations 6 and 7. Higher moments can be derived in a straightforward fashion from equation 5. Corresponding approximate results appear in equations 9 through 12. We quantify errors arising in the latter set of equations and show that they are equivalent to models by Lander and Waterman (1988) and Roach (1995).

Error Quantification for Approximate Models

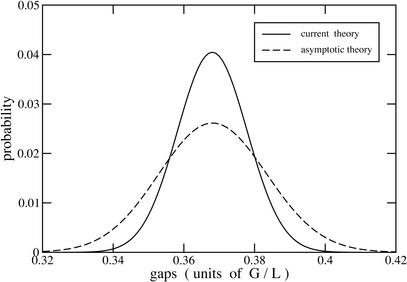
The approximate model is obtained by invoking two simplifications with respect to equation 3. First, asymptotic approximation is used, that is, (1 − α)N → e−αN, where α = (L − T)/G is small (Seed 1982; Torney 1991; Marr et al. 1992). Second, gap limits are not established as in equation 3. Finite probabilities are therefore permitted for numbers of gaps in excess of the physical maximum, int (G/L). In general, the resulting probability density given by equation 9 is artificially disperse compared with the combinatorially exact result in equation 4 (Fig. 2). Consequently, approximation is only valid when clone length is “small enough” compared with project size.

Figure 2.

Figure 2

Open in a new tab

Representative probability density functions for a hypothetical mapping project (L/G = 0.001, T/L = 0) at 1× coverage.

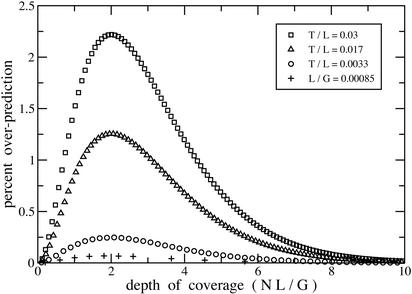
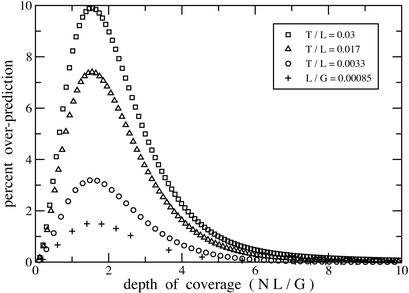
Current mapping and sequencing projects encompass L/G ratios that vary over five orders of magnitude, with the maximum being of order 10−2 for certain fingerprint projects (Table 1). Exact theory is difficult to compute for low L/G, whereas approximate theory is not valid for high L/G. Delineating values for which each is appropriate is therefore useful. Figure 3 shows error evaluation for the expected number of gaps in a set of projects having 0.00085 ≤ L/G ≤ 0.03 (Zhu et al. 1999; Chang et al. 2001). Predictably, the worst case is that in which relative clone size is largest. Yet, even at this extreme, the maximum error is only on the order of 2%. Asymptotic theory is therefore a remarkably robust predictor of expected gaps. Figure 4 shows the corresponding error evaluation for standard deviation of the gap distribution. Here, error is more sensitive, being about five times as large as that of the expected value. A 2% error limit indicates applying the exact model for BAC shotgun sequencing and small genome fingerprinting (Table 1).

Table 1.

Representative Fingerprint Mapping and Shotgun Sequencing Projects

Project description Approximate L/G Reference
Whole genome shotgun 1.8 × 10−7 Venter et al. (2001)
 sequencing of complex  organisms 4.6 × 10−6 Adams et al. (2000)
BAC clone fingerprinting  of large genomes 6.0 × 10−5 McPherson et al. (2001)
Bacterial whole genome 1.4 × 10−4 Heidelberg et al. (2000)
 shotgun sequencing 2.6 × 10−4 Fleischmann et al. (1995)
BAC clone fingerprinting 7.7 × 10−4 Mozo et al. (1999)
 intermediate-size genomes 8.5 × 10−4 Chang et al. (2001)
BAC shotgun sequencing 3.0 × 10−3 IHGSC (2001)
BAC clone fingerprinting 3.3 × 10−3 Martin et al. (2002)
 small genomes 1.1 × 10−2 Dewar et al. (1998)
1.7 × 10−2 Tomkins et al. (2001)
2.1 × 10−2 Diaz-Perez et al. (1997)
3.0 × 10−2 Zhu et al. (1999)
Open in a new tab

BAC, bacterial artificial chromosome. 

Figure 3.

Figure 3

Open in a new tab

Parametric characterization of how asymptotic theory overpredicts expected value of gaps. Ordinate is scaled by the maximum exact expected value for each project.

Figure 4.

Figure 4

Open in a new tab

Parametric characterization of how asymptotic theory overpredicts standard deviation of gaps. Ordinate is scaled as in Figure 3.

Unification of Previous Models

Equations 3 through 12 resolve a long-standing controversy between two established theories. The Lander and Waterman (1988) model can be considered the standard: It is widely applied and characterizes the expected number of islands and their expected lengths via the simple expressions N e−αN and G(eαN − 1)/N. Roach (1995) developed an alternative model, which is thought to be fundamentally different from the L-W model. Roach asserts that L-W results are inconsistent at higher coverages. In particular, expected island length is unbounded and exceeds that of the project itself for coverage depths above approximately 6× to 8×. This trend appears in the original Lander and Waterman article, although it is not discussed per se. It is then argued by Roach that the fundamental basis of the L-W theory is not valid in this range. Kupfer et al. (1995) have raised similar concerns. Consequently, many investigators resort exclusively to the Roach model when coverages of interest exceed 5× (Smith et al. 1997; Yamada et al. 2000).

If a slightly modified interpretation is applied to one of the L-W results, we show that not only is this assertion incorrect but that the Lander and Waterman (1988) and Roach (1995) models are basically identical and both consistent. The paradox of unbounded island length is really a matter of correctly characterizing limiting behavior and can be resolved as follows. Although investigators usually regard gap number and island number as equal, the latter must converge to one greater than the former in the limit of closure, that is

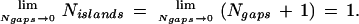graphic file with name M1.gif 1

Suppose that we increment the L-W expression for the expected number of islands by 1 to obtain the correct limiting behavior as closure is approached. Although not as important for practical calculations, let us also replace N with N − 1 to obtain the correct behavior at project initiation, that is, the first clone yields exactly 1 island. The result is N e−α(N − 1) + 1 − ε, where ε = e−α(N − 1) is a small quantity that quickly vanishes. This expression is identical within ε to E〈I〉 + 1, where E〈I〉 is given by equation 11. Because equation 11 represents the expected value of gaps, the Lander and Waterman (1988) result above should be more properly regarded as the number of gaps rather than the number of islands. In this context, the model is fully consistent and limiting behavior is correct. For example, the quotient of bases covered, G(1 − e−αN), and number of islands (with correct end-limiting behavior) yields a more reasonable L-W approximation for expected island length

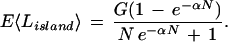graphic file with name M2.gif 2

Equation 2 correctly converges to the project length G.

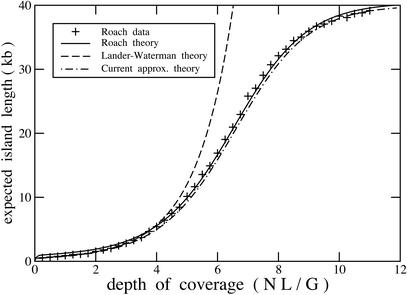
Furthermore, equation 11 is derived from equation 9, which is essentially the same density function given by Roach (1995), that is, a binomial distribution based on the probability of a gap. The Lander and Waterman (1988) and Roach (1995) models are thus fundamentally equivalent, although Roach provides the underlying density function that did not appear in the Lander and Waterman article. Differences in appearance of the equations between the two articles are second-order and can be neglected for practical calculations. Specifically, Roach (1995) uses N − 1 rather than N but does not explicitly use exponentiation. Strictly speaking, his result remains asymptotic because gap limits are not rigorously established as in equation 3. This leads to a one-term approximation of equation 4. To illustrate the equivalency, we repeat a case study by Roach (1995) that compares expected island lengths for a shotgun sequencing project (Fig. 5). Whereas original L-W theory diverges, equation 2 duplicates results obtained by Roach within the second-order differences mentioned above. Amending limiting behavior as we have described here promises to resolve similar anomalies in other models (Arratia et al. 1991; Port et al. 1995).

Figure 5.

Figure 5

Open in a new tab

Repeat of a case study by Roach (1995) that compares expected island length for a shotgun sequencing project having G = 40,000, L = 500, and T = 20. Crosses represent average values derived from a series of Monte Carlo simulations performed by Roach (1995). Coordinate axes are scaled exactly as in Roach (1995).

DISCUSSION

Past work has largely focused on expected value of gaps, islands, and so forth. Here we broaden these results by several example calculations using both our combinatorially exact and asymptotically approximate models.

Evolution of Gaps

The process by which gaps evolve in a project can be examined by plotting probability density as a function of coverage depth N L/G (Fig. 6). Dispersion is minimal at the outset, which is expected, given that the number of possible arrangements for a limited number of clones is relatively small. Distributions are not symmetric. As a project progresses toward 1× coverage, distributions rapidly become disperse and symmetric. It is in this region that theoretical predictions for expected gaps are most likely to differ from results obtained in the laboratory. The shape remains almost constant for several increments in coverage. As deeper coverage is reached, for example, 5× in this case, distributions start to contract and become asymmetric. The trend becomes more exaggerated as closure is approached. Dispersion also increases with L/G as characterized by the quotient of maximum σ to maximum E〈I〉 (Fig. 7). In general, this implies that estimates of the expected number of gaps are more likely to reflect actual laboratory observations for smaller L/G.

Figure 6.

Figure 6

Open in a new tab

Evolution of probability density function for a hypothetical project (L/G = 0.001, T/L = 0) up to 5× coverage as evaluated by equation 4. Arrows indicate whether the average number of gaps is increasing (→) or decreasing (←) for each distribution.

Figure 7.

Figure 7

Open in a new tab

Dispersion of probability density function characterized by the quotient of maximum standard deviation and maximum expected gaps.

Closure Probabilities

Although it is not a rigorous indicator, some estimate of the difficulty of a project can be obtained by examining the probability of closure, that is, the absence of gaps. Straightforward simplification of equations 4 and 9 yields p(0, N). It is clear from Figure 8 that closure is approached faster for projects having larger L/G values. Maximizing clone length (or sequencing read length) is therefore critical. Similar behavior has been noted previously for random subcloning by Roach (1995) using the Flatto and Konheim (1962) theory and for pairwise end sequencing using computer simulation (Roach et al. 1995). In our opinion, idealized models that predict lower coverages, for example, 15× for shotgun sequencing a typical human chromosome of 108 bases (Derrida and Fink 2002), are incorrect. Trends in Figure 8 approximately follow (1 − e−NL/G)N, as shown by equation 9, which penalizes short clones because N must be larger to attain a given coverage. This reflects the fact that larger clones are more effective at closing gaps than smaller ones and explains why BAC clones can be shotgunned to within a few gaps, whereas whole genome shotgun projects retain many gaps at the same coverage. These expectations extrapolate in large degree to fingerprinting as well. For example, projects having L/G of 3.3 × 10−3 (Martin et al. 2002) or above reach a probability of closure of 99% or higher by 13× coverage. In practice, some bias will likely exist, meaning that a small number of gaps must still be closed by directed means.

Figure 8.

Figure 8

Open in a new tab

Probability of closure as a function of depth of coverage for various projects: 1. Zhu et al. (1999); 2. Dewar et al. (1998); 3. Fleischmann et al. (1995); 4. McPherson et al. (2001); 5. Adams et al. (2000); 6. Venter et al. (2001). Abbreviations “f.p.” and “w.g.s.” represent fingerprint mapping and whole genome shotgun sequencing projects, respectively. Cases 1 and 2 were evaluated using equation 4, whereas the remaining cases were determined using equation 9.

BAC Shotgun Sequencing

The concept of closure probability can also be applied to deriving probabilistic stopping points in BAC clone shotgun sequencing. Current practice uses a simple linear scale: 5× coverage is considered a “half shotgun” and 10× coverage is a “full shotgun.” However, these figures do not take into account clone size or the average read length obtained from sequencing reactions. Roach (1995) proposed a criterion based on the expected cost for incrementally closing a gap, but the scale increases exponentially near closure. A more systematic method unaffected by the exponential problem can be defined according to confidence levels, for example, a 90% confidence of closure. BAC clone length is typically on the order of 150 kb (IHGSC 2001) but can average as low as 58 kb (Diaz-Perez et al. 1997) or show significantly higher values, for example, 235 kb for some human clones (Wendl et al. 2001). Read length is generally in the range of 500 to 800 base pairs in a large-scale production environment. Figure 9 shows that reasonable stopping points vary between about 8.5× and 12× coverage and decrease approximately linearly with read length. “Full shotgun” of a typical 150-kb BAC coincides with 10× coverage for an average read length of 650 bases and a 90% confidence level of closure. Longer clones, lower read lengths, or higher confidence values would require additional coverage beyond 10×.

Figure 9.

Figure 9

Open in a new tab

Stopping points for bacterial artificial chromosome (BAC) shotgun sequencing based on confidence levels for closure of 90% and 95%. Short clones averaging 58 kb (Diaz-Perez et al. 1997) were evaluated using equation 4, whereas “typical clones” of 150 kb (IHGSC, 2001) and longer clones of 235 kb (Wendl et al. 2001) were determined using equation 9.

METHODS

We briefly describe assumptions used in modeling BAC clone mapping and shotgun sequencing and then construct a theory describing evolution of gaps for these processes.

Assumptions

The following assumptions collectively represent what is possible in the laboratory regarding implementation of BAC clone and subclone libraries. Well-made libraries would be expected to display characteristics reasonably close to these.

First, we make the conventional assumption of a uniform clone distribution. Techniques used for BAC clone libraries enable a high degree of uniformity (Osoegawa et al. 1998, 2000; Cheung et al. 2001; Osoegawa et al. 2001), and subclone libraries are usually created by mechanical means, which are not significantly biased (e.g., sonication). We assume that cloning biases are small or can be minimized. Second, we make the standard assumption of a constant clone length L. Although length variability is largely governed by fractionation protocols, it is typically small in practice (Osoegawa et al. 1998). Third, chimerism is low in a well-made library, for example, less than 1% for BACs (Osoegawa et al. 2000), so it is ignored. Fourth, end effects are neglected because they are genome and project specific. Although they have little influence on large projects(Arratia et al. 1991; Balding and Torney 1991; Ewens et al. 1991), they can have a small biasing effect on fingerprint mapping if L/G is comparatively large. Conversely, for circular architectures found in bacterial fingerprint projects (Tomkins et al. 2001), the assumption is identically satisfied. Some models account for end effects on a linear representation of the DNA target; however, this is spurious for genomes with more than one chromosome. One would have to properly model all chromosome-specific end effects. Lacking such genome-specific considerations, the appropriate configuration is a circular DNA target. Last, we assume that overlap detection can be adequately modeled using the simple threshold constant T used by previous theories (Lander and Waterman 1988; Roach 1995). This parameter can be thought of as an expected value required for an overlap to be detected.

Theoretical Development

Let N be the number of clones that have been processed in a fingerprint mapping or shotgun sequencing project and I be a random variable representing the number of gaps i among these N clones. Following Lander and Waterman (1988) and Roach (1995), we define the effective clone length as α = (L − T)/G. This expression accounts for the penalty involved in not detecting an actual overlap. That is, if a real overlap is less than T, a gap is assumed. No restrictions are imposed on clone size except 0 < L/G < 1. In other words, we do not explicitly invoke the asymptotic approximation.

We begin by deriving probabilities of gaps immediately following particular sets of clones. Let the target DNA segment be represented by a circle of unit circumference so that each of the N clones contributes a fractional coverage α. A gap occurs when the starting positions of two clones are greater than α apart. Following Solomon (1978), we can infer the probability of gaps following particular sets of clones by applying a geometric translation operator to each set. For example, the probability of a gap immediately following any one specific clone of the N clones is f(1) = (1 − α)N − 1. For gaps following any two particular clones, the probability is f(2) = (1 − 2α)N − 1. Generalizing this procedure for m specific clones leads to

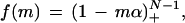graphic file with name M3.gif 3

where the “plus” notation (Siegel 1979) is defined as (j)+ = max (0, j). This restriction arises from the fact that the number of gaps is bounded by the minimum number of clones required to cover the project exactly one time. In other words, there can be, at most, a tiny gap between each clone as 1× coverage is approached. The probability of a number of gaps greater than this value is zero. Results from equation 3 are biased upward as T increases because gaps are presumed when overlaps are too small to be detected.

Next, we must account for the various ways these gap arrangements can be realized. For example, in the case of m = 2, gaps could follow the first and second clones, the first and third clones, and so forth. Stevens' Theorem (Stevens 1939; Solomon 1978) can be applied directly for this calculation. We thus obtain the probability density function for i gaps distributed among N clones

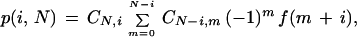graphic file with name M4.gif 4

where Cj,k is the binomial coefficient for j gaps taken k at a time. By applying the definition of the moment-generating function (Ross 2000), we obtain

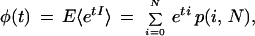graphic file with name M5.gif 5

from which all moments of interest can be derived.

The standard gap statistic provided by previous models is the expected number of gaps E〈I〉 resulting from N clones. Evaluating the first moment E〈I〉 = φ‘(0), we obtain

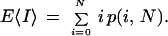graphic file with name M6.gif 6

This result is more general than corresponding expressions given by Lander and Waterman (1988) and Roach (1995) because it can be applied with larger L/G ratios. Variance is a useful measure of dispersion and can be computed as a combination of the first and second moments σ2 = E〈I2〉 − (E〈I〉)2. Evaluation of E〈I2〉 = φ"(0) from equation 5 along with some algebraic manipulation shows

graphic file with name M7.gif 7

Standard deviation σ is obtained by taking the square root of equation 7. Higher moments such as skewness and kurtosis could be derived by similar operations.

These equations become progressively more difficult to evaluate as L/G decreases. Specifically, N becomes very large for coverages of interest, making the ranges of both the summations and the binomial coefficients correspondingly large. Moreover, full precision of the binomial coefficients must be retained, otherwise round-off error quickly destabilizes the calculation. Here, we use Perl, which implements arbitrary precision integer and floating point object classes (Wall et al. 2000). In most cases, we do not evaluate the equations “exactly,” that is, over the entire distribution such that the total probability is identically 1. Instead, we truncate computations for the moments in equations 6 and 7 such that the total probability is at least 0.9998. This dramatically reduces computational time without significant loss of accuracy.

Asymptotic Approximation

When L/G is small enough, one can invoke the so-called asymptotic approximation (Seed 1982; Torney 1991; Marr et al. 1992), whereby (1 − α)N → e−αN for suitable α and N. In this case, the specific probability in equation 3 follows the limit [1 − (i + m)α]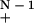Inline graphic → e−α(i + m)(N − 1). Let b = e−α(N − 1), then equation 4 becomes

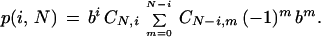graphic file with name M9.gif 8

The summation in equation 8 is simply an expansion of (1 − b)N − i. Thus, the density function in equation 4 reduces to the binomial distribution

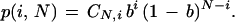graphic file with name M10.gif 9

Following equation 5, we substitute this expression to obtain the moment-generating function, which can be simplified via the Binomial Theorem to obtain

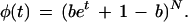graphic file with name M11.gif 10

Equation 10 is the well-known generating function for a binomial distribution having a Bernoulli “success” probability of b (Ross 2000). Deriving the appropriate moments, we find the expected value to be

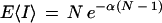graphic file with name M12.gif 11

and the variance to be

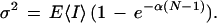graphic file with name M13.gif 12

Higher moments can be derived in a straightforward fashion by succeeding derivatives of φ(t).

Availability

Programs implementing the theory developed in this article are written in Perl and are freely available from the authors. The Perl language itself and necessary modules used here are freely available at www.cpan.org on the World Wide Web.

Acknowledgments

We thank Drs. Warren Gish and Gary Stormo of the Washington University Genetics Department for reviewing draft manuscripts and Drs. Marco Marra of the British Columbia Cancer Research Centre and John Wallis of the Washington University Genome Sequencing Center for informative discussions. This work was supported by a grant from the National Human Genome Research Institute (HG02042)

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Footnotes

Genome Sequencing Center, Box 8501, 4444 Forest Park Blvd., Saint Louis, MO 63108. E-MAIL mwendl@watson.wustl.edu.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.655102.

REFERENCES

  1. Adams MD, Celniker SE, Holt RA, Evans CA, Gocayne JD, Amanatides PG, Scherer SE, Li PW, Hoskins RA, Galle RF, et al. The genome sequence of Drosophila melanogaster. Science. 2000;287:2185–2195. doi: 10.1126/science.287.5461.2185. [DOI] [PubMed] [Google Scholar]
  2. Arratia R, Lander ES, Tavaré S, Waterman MS. Genomic mapping by anchoring random clones: A mathematical analysis. Genomics. 1991;11:806–827. doi: 10.1016/0888-7543(91)90004-x. [DOI] [PubMed] [Google Scholar]
  3. Balding DJ, Torney DC. Statistical analysis of DNA fingerprint data for ordered clone physical mapping of human chromosomes. Bull Math Biol. 1991;53:853–879. doi: 10.1007/BF02461488. [DOI] [PubMed] [Google Scholar]
  4. Chang YL, Tao Q, Scheuring C, Ding K, Meksem K, Zhang H-B. An integrated map of Arabidopsis thaliana for functional analysis of its genome sequence. Genetics. 2001;159:1231–1242. doi: 10.1093/genetics/159.3.1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cheung VG, Nowak N, Jang W, Kirsch IR, Zhao S, Chen XN, Furey TS, Kim UJ, Kuo WL, Olivier M, et al. Integration of cytogenetic landmarks into the draft sequence of the human genome. Nature. 2001;409:953–958. doi: 10.1038/35057192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Derrida, B. and Fink, T.M.A. 2002. Sequence determination from overlapping fragments: A simple model of whole-genome shotgun sequencing. Phys. Rev. Lett. 88: art. no. 068106. [DOI] [PubMed]
  7. Dewar K, Sabbagh L, Cardinal G, Veilleux F, Sanschagrin F, Birren B, Levesque RC. Pseudomonas aeruginosa PAO1 bacterial artificial chromosomes: Strategies for mapping, screening, and sequencing 100 kb loci of the 5.9 Mb genome. Microb Comp Genomics. 1998;3:105–117. doi: 10.1089/omi.1.1998.3.105. [DOI] [PubMed] [Google Scholar]
  8. Diaz-Perez SV, Alatriste-Mondragon F, Hernandez R, Birren B, Gunsalus RP. Bacterial artificial chromosome (BAC) library as a tool for physical mapping of the archaeon Methanosarcina thermophila TM-1. Microb Comp Genomics. 1997;2:275–286. doi: 10.1089/omi.1.1997.2.275. [DOI] [PubMed] [Google Scholar]
  9. Ewens WJ, Bell CJ, Donnelly PJ, Dunn P, Matallana E, Ecker JR. Genome mapping with anchored clones: Theoretical aspects. Genomics. 1991;11:799–805. doi: 10.1016/0888-7543(91)90003-w. [DOI] [PubMed] [Google Scholar]
  10. Flatto L, Konheim AG. The random division of an interval and the random covering of a circle. SIAM Rev. 1962;4:211–222. [Google Scholar]
  11. Fleischmann RD, Adams MD, White O, Clayton RA, Kirkness EF, Kerlavage AR, Bult CJ, Tomb JF, Dougherty BA, Merrick JM, et al. Whole-genome random sequencing and assembly of H. influenzae rd. Science. 1995;269:496–512. doi: 10.1126/science.7542800. [DOI] [PubMed] [Google Scholar]
  12. Hall P. Introduction to the theory of coverage processes. New York, NY: John Wiley & Sons; 1988. [Google Scholar]
  13. Heidelberg JF, Eisen JA, Nelson WC, Clayton RA, Gwinn ML, Dodson RJ, Haft DH, Hickey EK, Peterson JD, Umayam L, et al. DNA sequence of both chromosomes of the cholera pathogen Vibrio cholerae. Nature. 2000;406:477–483. doi: 10.1038/35020000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. International Human Genome Sequencing Consortium Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
  15. Johnston M, Hillier L, Riles L, Albermann K, Andre B, Ansorge W, Benes V, Bruckner M, Delius H, Dubois E, et al. The nucleotide sequence of Saccharomyces cerevisiae chromosome XII. Nature. 1997;387:87–90. [PMC free article] [PubMed] [Google Scholar]
  16. Kendall MG, Moran PAP. Geometrical probability. New York, NY: Hafner Publishing Company; 1963. [Google Scholar]
  17. Kupfer K, Smith MW, Quackenbush J, Evans GA. Physical mapping of complex genomes by sampled sequencing: A theoretical analysis. Genomics. 1995;27:90–100. doi: 10.1006/geno.1995.1010. [DOI] [PubMed] [Google Scholar]
  18. Lander ES, Waterman MS. Genomic mapping by fingerprinting random clones: A mathematical analysis. Genomics. 1988;2:231–239. doi: 10.1016/0888-7543(88)90007-9. [DOI] [PubMed] [Google Scholar]
  19. Marr TG, Yan X, Yu Q. Genomic mapping by single copy landmark detection: A predictive model with a discrete mathematical approach. Mamm Genome. 1992;3:644–649. doi: 10.1007/BF00352482. [DOI] [PubMed] [Google Scholar]
  20. Martin SL, Blackmon BP, Rajagopalan R, Houfek TD, Sceeles RG, Denn SO, Mitchell TK, Brown DE, Wing RA, Dean RA. MagnaportheDB: A federated solution for integrating physical and genetic map data with BAC end derived sequences for the rice blast fungus Magnaporthe grisea. Nucleic Acids Res. 2002;30:121–124. doi: 10.1093/nar/30.1.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. McPherson JD, Marra M, Hillier L, Waterston RH, Chinwalla A, Wallis J, Sekhon M, Wylie K, Mardis ER, Wilson RK, et al. A physical map of the human genome. Nature. 2001;409:934–941. doi: 10.1038/35057157. [DOI] [PubMed] [Google Scholar]
  22. Mozo T, Dewar K, Dunn P, Ecker JR, Fischer S, Kloska S, Lehrach H, Marra M, Martienssen R, Meier-Ewert S, et al. A complete BAC-based physical map of the Arabidopsis thaliana genome. Nat Genet. 1999;22:271–275. doi: 10.1038/10334. [DOI] [PubMed] [Google Scholar]
  23. Myers G. Whole-genome DNA sequencing. Comput Sci Eng. 1999;1:33–43. [Google Scholar]
  24. Osoegawa K, Woon PY, Zhao B, Frengen E, Tateno M, Catanese JJ, de Jong PJ. An improved approach for construction of bacterial artificial chromosome libraries. Genomics. 1998;52:1–8. doi: 10.1006/geno.1998.5423. [DOI] [PubMed] [Google Scholar]
  25. Osoegawa K, Tateno M, Woon PY, Frengen E, Mammoser A G, Catanese JJ, Hayashizaki Y, de Jong PJ. Bacterial artificial chromosome libraries for mouse sequencing and functional analysis. Genome Res. 2000;10:116–128. [PMC free article] [PubMed] [Google Scholar]
  26. Osoegawa K, Mammoser AG, Wu C, Frengen E, Zeng C, Catanese JJ, de Jong PJ. A bacterial artificial chromosome library for sequencing the complete human genome. Genome Res. 2001;11:483–496. doi: 10.1101/gr.169601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Port E, Sun F, Martin D, Waterman MS. Genomic mapping by end-characterized random clones: A mathematical analysis. Genomics. 1995;26:84–100. doi: 10.1016/0888-7543(95)80086-2. [DOI] [PubMed] [Google Scholar]
  28. Roach JC. Random subcloning. Genome Res. 1995;5:464–473. doi: 10.1101/gr.5.5.464. [DOI] [PubMed] [Google Scholar]
  29. Roach JC, Boysen C, Wang K, Hood L. Pairwise end sequencing: A unified approach to genomic mapping and sequencing. Genomics. 1995;26:345–353. doi: 10.1016/0888-7543(95)80219-c. [DOI] [PubMed] [Google Scholar]
  30. Roach JC, Siegel AF, van den Engh G, Trask B, Hood L. Gaps in the human genome project. Nature. 1999;401:843–845. doi: 10.1038/44684. [DOI] [PubMed] [Google Scholar]
  31. Ross SM. Introduction to probability models. 7th edition. San Diego, CA: Academic Press; 2000. [Google Scholar]
  32. Seed B. Theoretical study of the fraction of a long-chain DNA that can be incorporated in a recombinant DNA partial-digest library. Biopolymers. 1982;21:1793–1810. doi: 10.1002/bip.360210909. [DOI] [PubMed] [Google Scholar]
  33. Shizuya H, Birren B, Kim UJ, Mancino V, Slepak T, Tachiiri Y, Simon M. Cloning and stable maintenance of 300-kilobase-pair fragments of human DNA in Escherichia coli using an F-factor-based vector. Proc Natl Acad Sci. 1992;89:8794–8797. doi: 10.1073/pnas.89.18.8794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Siegel AF. Asymptotic coverage distributions on the circle. Ann Probability. 1979;7:651–661. [Google Scholar]
  35. Smith DR, Richterich P, Rubenfield M, Rice PW, Butler C, Lee HM, Kirst S, Gundersen K, Abendschan K, Xu QX, et al. Multiplex sequencing of 1.5 Mb of the Mycobacterium leprae genome. Genome Res. 1997;7:802–819. doi: 10.1101/gr.7.8.802. [DOI] [PubMed] [Google Scholar]
  36. Solomon H. Geometric probability. Philadelphia, PA: Society for Industrial and Applied Mathematics; 1978. [Google Scholar]
  37. Stevens WL. Solution to a geometrical problem in probability. Ann Eugen. 1939;9:315–320. [Google Scholar]
  38. The Arabidopsis Genome Initiative Analysis of the genome sequence of the flowering plant Arabidopsis thaliana. Nature. 2000;408:796–815. doi: 10.1038/35048692. [DOI] [PubMed] [Google Scholar]
  39. The C. elegans Sequencing Consortium. Genome sequence of the nematode C. elegans: A platform for investigating biology. Science. 1998;282:2012–2018. doi: 10.1126/science.282.5396.2012. [DOI] [PubMed] [Google Scholar]
  40. Tomkins JP, Wood TC, Stacey MG, Loh JT, Judd A, Goicoechea JL, Stacey G, Sadowsky MJ, Wing RA. A marker-dense physical map of the Bradyrhizobium japonicum genome. Genome Res. 2001;11:1434–1440. doi: 10.1101/gr.185001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Torney DC. Mapping using unique sequences. J Mol Biol. 1991;217:259–264. doi: 10.1016/0022-2836(91)90540-m. [DOI] [PubMed] [Google Scholar]
  42. Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, Sutton GG, Smith HO, Yandell M, Evans CA, Holt RA, et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
  43. Wall L, Christiansen T, Orwant J. Programming Perl. 3rd edition. Sebastopol, CA: O’Reilly & Associates, Inc.; 2000. [Google Scholar]
  44. Wendl MC, Marra MA, Hillier LW, Chinwalla AT, Wilson RK, Waterston RH. Theories and applications for sequencing randomly selected clones. Genome Res. 2001;11:274–280. doi: 10.1101/gr.133901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yamada K, Ogawa H, Tamiya G, Ikeno M, Morita M, Asakawa S, Shimizu N, Okazaki T. Genomic organization, chromosomal localization, and the complete 22 kb DNA sequence of the human GCMa/GCM1,a placenta-specific transcription factor gene. Biochem Biophys Res Commun. 2000;278:134–139. doi: 10.1006/bbrc.2000.3775. [DOI] [PubMed] [Google Scholar]
  46. Zhu H, Blackmon BP, Sasinowski M, Dean RA. Physical map and organization of chromosome 7 in the rice blast fungus Magnaporthe grisea. Genome Res. 1999;9:739–750. [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES