Neural signature of fictive learning signals in a sequential investment task

Abstract

Reinforcement learning models now provide principled guides for a wide range of reward learning experiments in animals and humans. One key learning (error) signal in these models is experiential and reports ongoing temporal differences between expected and experienced reward. However, these same abstract learning models also accommodate the existence of another class of learning signal that takes the form of a fictive error encoding ongoing differences between experienced returns and returns that “could-have-been-experienced” if decisions had been different. These observations suggest the hypothesis that, for all real-world learning tasks, one should expect the presence of both experiential and fictive learning signals. Motivated by this possibility, we used a sequential investment game and fMRI to probe ongoing brain responses to both experiential and fictive learning signals generated throughout the game. Using a large cohort of subjects (n = 54), we report that fictive learning signals strongly predict changes in subjects' investment behavior and correlate with fMRI signals measured in dopaminoceptive structures known to be involved in valuation and choice.

Neuroimaging experiments have begun to identify dynamic neural responses related to economic instincts including risk, gains, losses, and errors in reward expectations (1–8). Using interpersonal economic exchanges with humans and computers, even fairness, deviations from fairness, and revenge responses have produced an array of consistent neural correlates (9–12). Using event-related fMRI and a sequential investment game, we probe a formerly underappreciated signal type, a fictive learning error, predicted by a natural extension of a reinforcement learning model called Q-learning (13, 14). These signals are an augmentation to reinforcement learning models now used widely to design and interpret neuroimaging experiments in a range of reward-learning and economic decision-making tasks (Fig. 1A) (for a review, see ref. 15). We begin by introducing fictive learning signals in relation to reward error models based on experience, identify their connection to an older model of regret-based choice, and justify the elements of our sequential decision-making game given to human subjects.

Fig. 1.

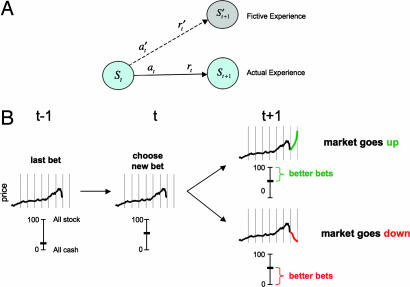
Schematic of the idea of a fictive error and task design. (A) At time t, an agent in state S_t transitions to a new state S_t+1 by taking action a_t and observes a reward r_t. However, the agent also observes other rewards r′_t that could have been received had alternative actions a′_t been chosen. (B) The figure under time t − 1 shows the state of the task immediately after a snippet of market has been revealed. At time t the subject makes a new allocation between cash and stock (in this case increasing the bet). When the market goes up, bigger investments are immediately revealed as better choices, generating the fictive error “best choice − actual choice.” Likewise for market drops, smaller investments would have been better.

Experiments examining the neural basis of valuation have identified midbrain dopaminergic systems as central players for reward processing and for the valuations that underlie reward processing and reward-guided choice (1–8, 16–22). This work associates transient modulations in the activity of midbrain dopamine neurons with reward prediction error signals (3–7, 16–18), and has equated reward prediction errors with the temporal difference (TD) error term that guides learning and action choice in actor-critic models (6, 15).

One formulation of this model, called Q-learning, depicts the TD error term δ_t as

where r(a) is the reward obtained for choosing action a, Q(S_t, a) is the value of action a in state S_t,

is the maximum of the Q values over all actions available from state S_t, and γ is a discount factor (Fig. 1A) (13, 14). It is this error signal that guides the learning of the value of states and actions based on actions actually taken (23). The general idea is illustrated in Fig. 1A. The animal is in a state S_t at time t, chooses some action to leave the state, ends up in a new state S_t+1 at time t + 1, and observes some reward r that depends on the action chosen. At such transitions, the TD error can inform the system about which output states, and consequently which actions, should yield the best average long-term returns. This framework has now been used extensively to understand a wide range of reward processing and valuation experiments in humans (15, 20).

Reinforcement learning models like the Q-learning model above focus on updating stored internal values based solely on the direct experience of the learner as indicated in Fig. 1A (solid arrow); however, once an action is taken, it is often the case that information becomes available that shows that another action (among those not taken; dashed arrow) would have been more valuable. It is these “could have been” actions that provide extra criticism for updating the values of states and actions (i.e., the Q values); and just like the reward prediction errors associated with actual experience, there should be analogous learning signals associated with the actions not taken: fictive learning signals.

In this article, we use a sequential gambling task that probes the ongoing difference between “what could have been acquired” and “what was acquired.” Fig. 1B shows the outline of events in the task. At time t, the player makes a new investment allocation (bet) by moving a centrally placed slider bar to the new bet, and at time t + 1, the next snippet of market information is displayed (Fig. 1B). Two outcomes are possible at that moment: (i) the market goes up and all bets higher than the bet placed are better because they would have accrued greater gains or (ii) the market goes down and all bets lower than the bet placed are better because they all would have accrued smaller losses.

At each decision point, bets can be set anywhere from 0% to 100% in increments of 10%. Each player plays 10 different markets and makes 20 decisions per market arranged at regular intervals as depicted in Fig. 1B. Fig. 1B displays the important design features of the game to clarify when the fictive error signal is expected to change; the exact visual arrangement is shown in Fig. 2A, and a time-line is shown in Fig. 2B. After each choice, the natural learning signal for criticizing the choice (the bet) is the difference between the best return that “could have been” obtained and the actual return, that is, the fictive error signal.

Fig. 2.

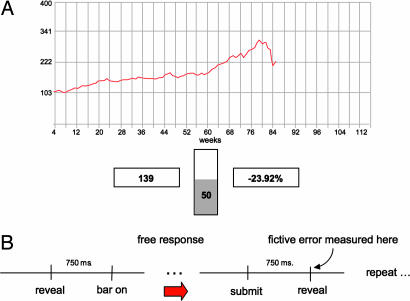
Experiment screen and time line. (A) Screen like that seen by subject (the background was dark in the scanner). The subject has just lost 23.92% (right box), has a portfolio worth $139 (left box), has 50% invested in the market (middle bar), and has nine choices remaining (from examining the screen). (B) Time-line of experiment. After the market outcome is revealed, the middle bar (which indicates the bet size) is grayed out, and a new bet cannot be submitted. The bar is illuminated 750 ms later, and the subject has a free response period to submit a new bet. After the new bet is submitted, the next snippet of market is revealed 750 ms later. The major regressors (including the fictive error) used in the fMRI analysis are time-locked to this event.

We now define the fictive error signal in this task and note here that it is strongly related to a term in the “regret-based” theory of decision-making under uncertainty proposed by Bell, Loomes, and Sugden in 1982 (24, 25). We avoid calling the signal regret because this term has a much broader, multidimensional meaning than we imply by fictive error (26).

Let the fractional change in the market (price) at time t be r_t, and let the concurrent time series of bets be b_t. At each time t, the amount gained due to the subject's choice is b_t · r_t⁺ for positive fractional changes in the market r_t⁺, that is, r_t⁺ = (p_t − p_t−1)/(p_t) > 0, where p_t is the market price at time t. The amount lost is b_t · r_t⁻ for similarly defined negative fractional changes in the market r_t⁻. After a decision, we take the fictive error to be the difference between the best outcome that could have been achieved and the actual gain or loss. After an “experiential” gain, the fictive error is f_t⁺ = 1 · r_t⁺ − b_t · r_t⁺; the best bet would have been 100%, i.e., all invested. After an “experiential” loss, the associated fictive error is f_t⁻ = 0 · r_t⁻ − b_t · r_t⁻; the best bet would have been 0%, i.e., all “cashed out.”

Results

Fifty-four healthy subjects (31 male, 23 female; ages 19–54) were scanned while performing the investment task outlined in Fig. 1B and Fig. 2. All players were initially endowed with $100. Each subject played 20 markets and made 20 decisions per market. The markets were presented in one of two conditions: (i) “Live,” where the subject made money, and (ii) a condition called “Not Live,” which controlled for visuomotor aspects of the task. Half the markets were played live and half not live, and these conditions occurred in a randomized order for each subject. For all markets used in this task, the price histories were taken from actual historical markets [see supporting information (SI) Fig. 7 and SI Data Set for market details].

To determine the impact of the fictive error (f_t⁺ = 1 · r_t⁺ − b_t · r_t⁺) on the subjects' behavior, we performed multiple regression analysis on the behavioral data and found that the fictive error over gains emerges quite naturally as an important behavioral signal determining the next bet. We regressed the next bet b_t+1 against the previous bet b_t, the previous market broken up into positive and negative parts (r_t⁺ and r_t⁻, respectively), and the return of the investor separated into gains and losses (b_t · r_t⁺ and b_t · r_t⁻):

The results of this multiple regression are shown in Table 1(see SI Table 2 for an alternative regression, SI Data Set for statistics on subjects' performance, and SI Appendix for experience-related and reaction time data). The only term that does not emerge with a significant effect on the next bet is loss b_t · r_t⁻.

Table 1.

Behavioral regression

Coefficient	Estimate	SE	t value	p value
c	−0.026	0.013	−2.11	0.023
b̃t	0.582	0.031	18.9	0.000
rt+	5.56	0.651	8.54	0.000
rt−	−3.76	0.529	−7.09	0.000
bt · rt+	−2.91	1.16	−2.51	0.006
bt · rt−	−1.55	1.23	−1.26	0.105

Results of linear multiple regression of b̃_t+1, normalized next bet, on indicated variables: b̃_t is normalized previous bet, r_t⁺ = max(r_t, 0), where r_t is the previous market return, r_t⁻ = max(−r, 0), and b_t is the unnormalized previous bet. b_t · r_t⁺ is the actual investor return for the positive market case, and similarly for b_t · r_t⁻. Random effects over subjects, n = 54.

Not surprisingly, the three first-order terms (b_t, r_t⁺, and r_t⁻) significantly predict the next bet b_t+1: the last bet b_t, positive changes in the market r_t⁺, and negative changes in the market r_t⁻. These effects are modulated by a negative contribution from b_t · r_t⁺ (gain).

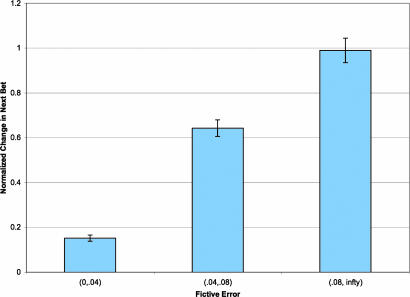
Consequently, the multiple regression results show that the next bet can be explained by a weighted sum of (i) the last market (positive and negative) and (ii) a term proportional to (r_t⁺ − b_t · r_t⁺), which is exactly the fictive error over gains f_t⁺ = 1 · r_t⁺ − b_t · r_t⁺, as defined previously. This influence of the fictive error on the next bet is depicted graphically in Fig. 3 for small, medium, and large values of the fictive error (see SI Fig. 8 for scatterplot).

Fig. 3.

Influence of fictive error signal on behavior. Barplot of the average normalized change in next investment versus the level of the fictive error. Changes in investment were converted into z-scores within each subject. The fictive error signal was binned into three levels [(0.00, 0.04), (0.04, 0.08), (0.08, ∞)] for the figure (see SI Fig. 8 for a scatterplot). Error bars are standard errors.

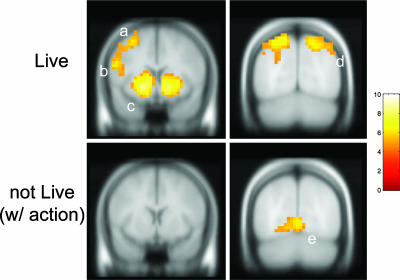
These behavioral findings were paralleled by strong hemodynamic responses for these same variables. We found clear neural correlates for the influence of the market, experiential errors, and fictive errors by using these quantities to construct regressors that modulate a standard hemodynamic response time-locked to the market reveal events (see Methods for complete listing of the regressors used). We present first the results for the fictive error f_t⁺ regression (Fig. 4). In the live condition, significant activation is seen for the f_t⁺ regressor in ventral caudate, ventral putamen, and posterior parietal cortex (PPC) (see SI Appendix for activation tables). No significant activation is seen either in the striatum or PPC in the not live case for the analogous regressor r_NL⁺, showing that the activity in the striatum and PPC is not related to the visual display (the activation for r_t⁺ is not central to our argument, but see SI Fig. 9).

Fig. 4.

Brain responses to fictive error signal. (Upper) SPM t-statistic map for the fictive error regressor (f_t⁺) showing activation in motor strip (a), inferior frontal gyrus (b), caudate and putamen (c), and PPC (d). Threshold: p < 1 × 10⁻⁵ (uncorrected); cluster size ≥5. Slices defined by y = 8 and y = −72. Random effects over subjects, n = 54. (Lower) SPM t-statistic map for the positive market return (r_NL⁺) regressor in the “Not Live” condition showing no activation in the striatum but strong activation in the visual cortex (e). Threshold: p < 1 × 10⁻⁵ (uncorrected); cluster size ≥5. Slices defined by y = 8 and y = −72. Random effects over subjects, n = 54.

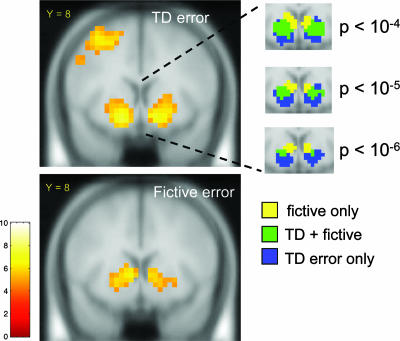
TD errors in decision-making tasks have been studied in depth, and fMRI studies have consistently shown TD error activation in striatum (3–7, 15, 20). We thus focus here on the striatal activation and whether we can separate striatal responses due to TD errors (experiential errors) from those due to fictive errors. In this investment game there are several forms that a TD error might take. We used the TD error signal generated by the difference of the investor return and investment size (reward − expected reward). This regressor is a model-free version of a TD signal where the bet is taken as the proxy for expected reward. To address colinearity issues, we simultaneously included the TD error and the orthogonalized fictive error signal in the model with both regressors time-locked to the moment when the new market value was revealed. Fig. 5 shows that the fictive error signal produces responses in the ventral caudate not explained by the TD error signal, as well as a significant response in bilateral PPC. The finding in the dorsal striatum agrees with previous work showing activation in the dorsal striatum in instrumental conditioning tasks (6, 27, 28). The fictive error strongly influences the next bet and the associated brain response in the dorsal striatum is consistent with this prior work dissociating TD errors in passive tasks (ventral striatum) from those in active, instrumental tasks (dorsal striatum) (6).

Fig. 5.

Basic TD regressor and fictive error signal. SPM t-statistic maps of the basic TD regressor (Upper) and the fictive error signal (Lower) showing activation in the striatum associated with each. The fictive error regressor is orthogonalized with respect to the TD regressor. Threshold: p < 1 × 10⁻⁵ (uncorrected); cluster size ≥5. Random effects over subjects, n = 54. (Insets) Separate colored-coded activations for fictive error only, TD error only, and the overlap region of the two. These activations are shown at three levels of significance and suggest that activations to fictive error only may be segregated to the ventral caudate.

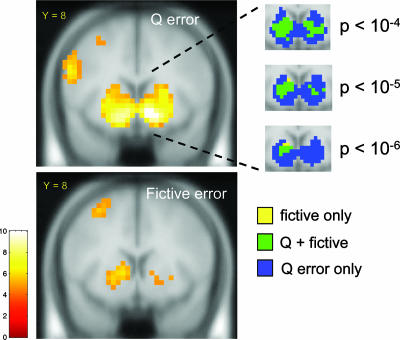
To further substantiate our behavioral findings in the multiple regression analysis above, we fit a Q-learning model to the behavioral data using a tabular representation of states and actions (see Methods for details). This analysis augments the multiple regression analysis by framing the sequential decision task as a learning problem and not merely a series of decisions explained by a set of reasonable variables. Fig. 6 displays the thresholded t-maps of the TD error from the Q-learning model and the orthogonalized fictive error signal. These behavioral and neural results support the conclusion that the fictive error signal over gains f_t⁺ = 1 · b_t − b_t · r_t⁺ significantly modulates investor behavior and has a robust neural correlate in the ventral caudate that is distinguishable from a standard experiential (TD) error.

Fig. 6.

Q-learning TD regressor and fictive error signal. SPM2 t-maps of the Q-learning TD regressor (Upper) and the fictive error signal (Lower) again showing activation in the ventral striatum associated with the TD error, and in the ventral caudate for the fictive error. The fictive error regressor is orthogonalized with respect to the TD regressor. Threshold: p < 1 × 10⁻⁵ (uncorrected); cluster size ≥5. Random effects over subjects, n = 54. (Insets) Separate colored-coded activations for fictive error only, TD error only, and the overlap region of the two. The area of overlap is larger for the Q-learning model and fictive error than for the TD regressor and fictive error (see Fig. 5).

Discussion

Our analysis shows that the fictive error signal f_t⁺ is an important determinant of choice behavior in a sequential decision-making game and has a clear neural correlate in the ventral caudate. Learning signals based on experiential rewards mediated by the dopamine system have been studied extensively (3–7, 16–18, 21, 22, 29, 30). The experiential rewards that activate these circuits range from primary rewards, to money, to more abstract constructs such as trust and revenge (11, 12). From these results it is clear that abstract concepts of reward can harness the dopamine system. The fictive error differs in that it involves rewards not received from actions not taken. From a biological perspective, this generalization is compelling: more information is preferable to less, assuming that the cost of getting and storing the information is not too high.

Our fictive error signal is regret operationalized as in Bell, Loomes, and Sugden (24, 25). These authors developed a theory of choice that formalized the impact of the emotion of regret by adding a term to the standard von Neumann–Savage expected utility theory (EUT) that explicitly quantified the comparison of the outcomes obtained to outcomes foregone. Loomes, Sugden, and Bell's theory accounts for many of the anomalies described earlier by the prospect theory of Kahneman and Tversky (30). A large psychological literature chronicles the impact of counterfactuals, specifically regret, as well as emotions on choice (26, 32, 33). We stress that the signal described above may or may not have anything to do with the feeling of regret and that our definition of a fictive error signal is defined as a function of two measurable quantities and is correlated with a (possibly covert, i.e., unconscious) signal in the brain.

Related concepts such as counterfactuals and regret have been studied behaviorally and in fMRI experiments (1, 8, 34–36). Breiter et al. (1) report activity related to counterfactual processing (disappointment) in a passive gambling task. Camille et al. (34) report on the lack of the influence of regret in orbitofrontal patients in a two-choice gambling game. Coricelli et al. (35) use a similar two-choice paradigm in normal subjects in an fMRI study and report activity in the orbitofrontal cortex associated with regret. Kuhnen and Knutson (8) use a three-choice task and report activity correlated with the difference between the obtained outcome and the outcome of the other risky choice in bilateral caudate. Camerer and Ho (36) use knowledge of rewards from actions not taken in their EWA (experience weighted attractions) model. In this model, actions are taken according to probabilities that depend on attractions that are updated after choices are made. The attractions are updated by adding a fraction of the reward that was received (in the case of the chosen action) or could have been received (in the case of the actions not taken). EWA has been successful in modeling behavior in a multitude of games from experimental economics (36, 37). Although EWA uses counterfactual information to update attractions, it does not explicitly include a term comparing the foregone reward with the actual reward.

Our result also adds to the evidence pointing to a special role for the caudate in decision-making in trial-and-error tasks involving a diverse range of rewards, even including rewards associated with social exchange (6, 11, 27, 28). Broadly, these previous studies have reported caudate activation related to the presentation of cues and receipt of reward in instrumental tasks. Indeed, in O'Doherty et al. (6) there was no activation in the caudate in the purely passive condition, providing evidence for a dorsal/ventral dissociation between actor and critic. The fictive error can be related to an extended version of the actor–critic architecture introduced by Rosenstein and Barto (38), who combine reinforcement and supervised learning in the actor's error signal in the actor–critic structure. We interpret the fictive error as the report of an “endogenous supervisor.” More formally (following ref. 38 closely), if we denote the actor's policy by π^a(θ), where θ is a vector of parameters, then the actor's policy parameter update is given by

Here, k ∈ [0,1] is a parameter that measures the relative weight of the reinforcement versus supervised aspects of learning, Δ^RL is the standard reinforcement learning update, and Δ^SL is the supervised learning error term that can be related to the fictive error (see SI Appendix) by using steepest descent:

The first term on the right is the fictive error of this article, and the second term is identical to loss, because “shorting” (negative bets) was not allowed.

Redish (39) captures (stylistically) several interesting aspects of cocaine addiction using a maneuver related to the “endogenous supervisor.” He adds a term to the TD update equation for the critic that models the synaptic dopamine concentration increase caused by cocaine. It is intriguing to speculate that fictive error signals in the actor might have similar effects and underlie components of compulsive gambling (40).

While we focused on the striatal activation in this work, the activation in PPC associated with the fictive error signal overlaps the activations in humans associated with delayed saccades in PPC (identified as intraparietal sulcus 2, IPS2) found in Schluppeck et al. (41). The homologous area of PPC in non-human primates, LIP, has been implicated in decision-making (42–44). The IPS2 activation in our task was not present in the not live visual control condition, suggesting that IPS2 may play a role in humans similar to that of LIP in non-human primates.

There is now ample evidence for experiential signals encoded by the dopamine system in the form of TD errors. In this article, we have shown evidence for a type of signal, a fictive error signal, that, in our experiment, drives choice behavior and has a neural correlate in the ventral caudate. It seems likely that situating fictive error signals within the framework of machine learning models will provide additional insight into normal human behavior as well as into diseases of decision-making.

Methods

Task Description.

Subjects were scanned in accordance with a protocol approved by the Baylor College of Medicine institutional review board. Exclusion criteria were claustrophobia, DSM-IV Axis I or II diagnosis, pregnancy, medications other than contraceptives, contraindications to MRI (metal objects in body), active medical or neurological disorder, and history of alcohol or drug dependence. The subjects were between 19 and 54 years old (31 males, 23 females). One recruited subject started the scanning but did not finish. After being read the task instructions (SI Text), the subjects were placed into the scanner (Allegra 3T; Siemens) and performed the following task. Two conditions, “Live” and “Not Live,” alternated, with the “Not Live” condition appearing first. During the “Live” condition, subjects made investment decisions, and in the “Not Live” condition, they made visual discriminations. In both conditions, price histories of actual historical market prices were shown to the subjects (Market data: weekly closing prices from EconStats; see SI Fig. 7 and SI Data Set for market graphs and summary statistics). At the beginning of a “Live” block, an initial 10-unit segment of price history was presented. Each unit represented four actual weeks of price history. The visual display represented each unit by the four weekly price points. The prices were normalized to 100, so that the initial price was 100. A subject then used a button box activated by one hand to move a slider bar depicted on the screen to indicate her percentage allocation to the market. At 0%, none of the initial $100 endowment would be allocated to the market; at 100%, all would be subject to market fluctuations. The slider moved in increments of 10%. After deciding her allocation, the subject used a button box activated by her other hand to submit the decision using another button box. The hand assignments were balanced over subjects. After a delay of 750 ms, the next unit of price history appeared on the screen (the previous history remained displayed, but the history was recentered to prevent telegraphing unintended information about the market), the portfolio value was updated, and the percentage profit/loss was displayed. After a delay of 750 ms, the slider bar changed from gray to red, indicating the free response time for the portfolio allocation decision (Fig. 2B). The process then repeated. Note that subjects' portfolios were automatically rebalanced after each return to retain the previously selected asset allocation. Additionally, this allocation was displayed on the slider bar before the next decision, for a total of 20 allocation decisions per round. At the end of the “Live” round, the screen briefly disappeared, and a screen displaying “Not Live” announced the beginning of the “Not Live” condition. During this condition the screen and events were similar in appearance, but a visual discrimination decision was made rather than an asset allocation decision: the subject used the same slider bar to answer whether the current price was higher or lower than the price two-segments previous. This was also repeated for 20 choices. Each subject saw a grand total of 10 “Live” and 10 “Not Live” markets. The 20 historical markets were divided into two groups of similar characteristics. Subjects were approximately balanced (26 for group A, 28 for group B) across the two groups of markets for the “Live” condition; the order of the markets for any particular subject was random.

Image Acquisition and Preprocessing.

High-resolution T1-weighted scans were acquired by using an MPRage sequence (Siemens). Functional run details: echo-planar imaging, gradient recalled echo; repetition time (TR) = 2,000 ms; echo time (TE) = 40 ms; flip angle = 90°; 64 × 64 matrix, 26 4-mm axial slices, yielding functional 3.4 mm × 3.4 mm × 4.0 mm voxels. Preprocessing of functional imaging data was performed with SPM2 (Wellcome Department of Imaging Neuroscience). Motion correction to the first functional scan was performed by using a six-parameter rigid-body transformation (45). The average of the motion-corrected images was coregistered to each individual's structural MRI by using a 12-parameter affine transformation. Slice timing artifact was corrected, after which images were spatially normalized to the MNI template (46) by applying a 12-parameter affine transformation, followed by a nonlinear warping using basis functions (47). Images were then smoothed with an 8-mm isotropic Gaussian kernel and high-pass-filtered in the temporal domain (filter width 128 sec).

Statistical Analyses.

Behavioral analysis and definitions.

The time series of investments and market returns were extracted for each subject. The subjects' investments were z-normalized within subject. The following multivariate regression was then performed in R (The R Foundation for Statistical Computing; function lme, random effects over subjects, n = 54):

Here, b̃_t is the within-subject z-scored bet. The other terms have been defined in the main text. The initial reveal, first reveal, and final reveal data were excluded from the regression because for the initial reveal there is no preceding investment decision, for the first reveal the investment decision was in a different context (i.e., no previous investment), and for the final reveal there is no immediately following investment decision. The results are shown in Table 1.

General linear model analysis.

Visual stimuli and motor responses (see SI Appendix for complete list of regressors) were entered in a general linear model (48) as separate regressors constructed by convolving punctate events at the onset of each stimulus or motor response with the fixed hemodynamic response function implemented within SPM2. Additional regressors were constructed from the markets or from behavioral data. For example, the fictive error regressor was formed by multiplying (point-wise in time) the live reveal (punctuate) regressor by r_t⁺(1 − b_t). The basic TD regressor was constructed as follows. At live reveal t, the z-normalized subject return was defined as r̃_t = (r_t − mean(r))/(stdev(r)), where the mean and standard deviation is taken over the subject returns already experienced. The subject's z-normalized investment b̃_t was defined similarly. The basic TD regressor was then defined as TD_t = r̃_t − b̃_t. As in the case of the behavioral data, the initial and first reveal data and the final l reveal data were omitted from the regressors. Orthogonalization of the fictive error regressor with respect to the TD error regressor was accomplished by subtracting the orthogonal projection of the fictive error onto the TD error from the fictive error regressor. SPM2 beta maps were constructed for regressors of interest and then entered into a random-effects analysis by using the one sample t test function.

Dynamic Choice Models: Q-Learning.

A Q-learning model (13, 14) was estimated by using a tabular representation of the state space and actions. The state space Ω was taken to be a product of a discrete representation of the last market return (6 categories: (−100, −0.05], (−0.05, −0.025], (−0.025, 0], (0, 0.025], (0.025, 0.05], (0.05, 100]), and the previous investment (11 categories). The space of actions A was taken to be the set of possible investments (0, 0.1, 0.2, …, 0.8, 0.9, 1). The reward R after making an investment α was α × r, where r was the market return. The Q values were updated according to

Here, γ = 0.99 is the discount parameter, and c₁ is the learning rate (this TD was used for the regressor mentioned in above). The choice probabilities were then obtained from the Q values by the Boltzmann distribution

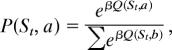where β = 1/T is the inverse temperature, which measures how concentrated the distribution is about the maximal Q value. The initial Q values were all taken to be zero, and the likelihood of each subject's choices was maximized over the learning rate and temperature by subject.

Abbreviations

PPC

posterior parietal cortex

TD

temporal difference.