Electrophoresis of individual microtubules in microchannels

Abstract

We use micrometer-sized fluidic channels to confine and measure electrophoresis of freely suspended individual microtubules. We measure orientation-dependent velocities of microtubules and the electro-osmotic flow mobility in our channels to infer the anisotropic electrophoretic mobility of microtubules under physiological conditions. We discuss the difference between electrophoresis and purely hydrodynamic motion and its implications for interpreting mobility measurements. We show that the mobility anisotropy is a factor of 0.83, clearly different from the well known anisotropy factor of 0.5 in Stokes drag coefficients for cylindrical objects. We also show that the velocity is independent of microtubule length, which would be different for hydrodynamic motion. We demonstrate that the electric force on the counterions has important consequences for the interpretation of electrophoresis experiments and that ignoring this can lead to an underestimation of the effective charge by orders of magnitude. From the electrophoresis measurements, we calculate an effective surface-charge density of −36.7 ± 0.4 mC/m² for microtubules. Electrophoretic measurements of subtilisin-digested microtubules, which have the negatively charged C termini on the outer surface removed, show a 24% decrease in mobility and, correspondingly, in surface charge, but no change in anisotropy.

The electrophoretic mobility of molecules is a fundamental property, that relates a molecule's velocity to an external electric field. In ensemble electrophoresis measurements, such as gel electrophoresis or dynamic light scattering, the differences between individual molecules are obscured. To overcome this limitation, individual molecules can be made visible by fluorescent labeling, and their electrophoretic motion can be imaged using fluorescence microscopy (1), provided that the motion of the molecules is confined within the focal plane of the objective. Microfabricated slit-like fluidic channels form an excellent system to confine and observe the electrophoretic motion of individual fluorescently labeled biomolecules, such as microtubules (2), actin filaments, or virus particles (3).

Here, we present measurements of the electrophoretic mobility of individual microtubules in micrometer-sized fluidic channels. Microtubules are stiff cylindrical biopolymers with a diameter of 25 nm and lengths of several micrometers. Their high persistence length (≈1–5 mm) makes them a good model system for other rod-like particles such as very short DNA molecules or tobacco mosaic viruses. The electrophoretic mobility of cylindrical colloidal particles was predicted long ago to be anisotropic (4), which was only recently confirmed experimentally (2).

Here, we present an extensive study of the microtubule anisotropic mobility. This is not only interesting from a fundamental colloid science point of view. The mobility also determines the force that is applied, for example, in bionanotechnological applications, where electric fields bend and steer microtubules (2) or actin filaments (5) that are propelled by molecular motors. Finally, the mobility of a biomolecule is a measure of its effective charge.

We start with a brief summary of the theoretical framework of electrophoresis. This reiterates some original work from 1933 (6), because electrophoretic experiments are often incompletely interpreted, neglecting the effect of the counterions. We show that this has led to orders-of-magnitude underestimates for the effective charge. Combined with measurements of the electrophoretic mobility of individual microtubules, we aim to give a compact theoretical description and experimental demonstration of the differences between electrophoretic and purely hydrodynamic motion.

Theoretical Framework

The charge of a colloidal particle in an electrolyte is screened by counterions that are organized in a double layer structure. The first layer of ions is confined to the surface in the Stern layer, whereas the diffuse layer reflects a balance between electrostatic attraction and entropic repulsion and is described by Poisson–Boltzmann theory. As a result, the space charge density ρ decays exponentially with the Debye length ${\lambda }_D=\sqrt{k_{b}T\epsilon /{\displaystyle {\sum }_i{z}_i^2{e}^2{n}_i}}$, where k_b is Boltzmann's constant, T is temperature, ε is the solvent's dielectric constant, and e is the electron charge. The summation runs over all ion species i with valence z_i and number density n_i.

The presence of the counterions makes electrophoretic motion markedly different from purely hydrodynamic motion caused by nonelectric forces. The main difference is that an electric field exerts force both on the object and on the surrounding fluid via the counter ions, the so-called retardation effect, whereas in gravitational or magnetic sedimentation of colloids, the externally applied force acts only on the object. This difference has been pointed out by several authors (4, 6, 7), but despite this, force balance in electrophoresis is often incompletely stated in terms of the electric force on the particle and Stokes hydrodynamic friction (3, 8, 9), thereby neglecting the retardation effect.

In the following, we first demonstrate the importance of the retardation effect by comparing the fluid motion around a sphere both in electrophoretic and hydrodynamic motion (6). Then, we describe the electrophoresis of cylinders while allowing for a deformation of the ionic double layer by the external field, the so-called relaxation effect.

Fluid Motion Around a Sphere.

Following Henry's (6) key arguments, we solve the fluid velocity u around a spherical insulating particle of radius R, and uniformly distributed charge Q [detailed steps are given in supporting information (SI) Appendix]. The particle moves with velocity v by an electric field E (Fig. 1b). It is assumed that inertial terms can be neglected and that the potential due to the external electric field, V, can be superimposed on the potential in the double layer ψ. Implicit in this assumption is that the ionic double layer is not distorted. By imposing a velocity −v on the system, the particle is at rest and the fluid at infinity moves with −v. Under these conditions, the fluid motion is described by the Navier–Stokes equation

with η the viscosity of the fluid and p the hydrostatic pressure.

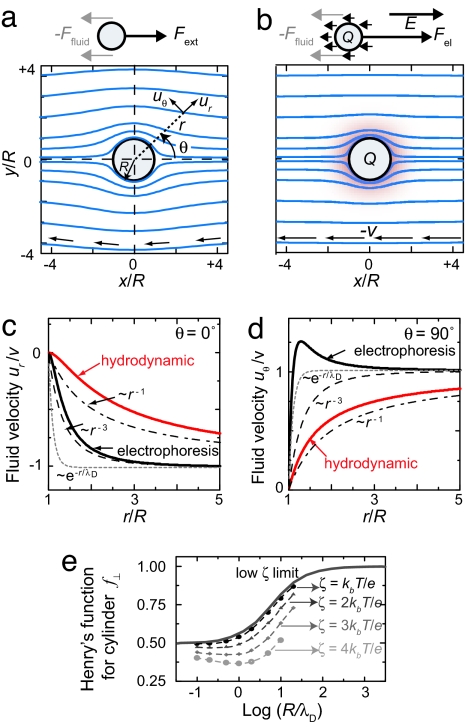
Fig 1.

Hydrodynamic vs. electrophoretic motion. (a) Calculated flow lines around a particle that is moved by an external (nonelectric) force. The fluid has a long-range perturbation. (b) During electrophoresis (R/λ_D = 10), the fluid is only perturbed within a much smaller distance around the particle. (c) Velocity decay in front of the particle for electrophoretic and hydrodynamic motion. The fluid disturbance in electrophoretic motion decays approximately as r⁻³ (dashed line), which is longer range than the exponential Debye–Hückel decay (dotted line). In hydrodynamic motion the fluid disturbance decays much slower, ∝ r⁻¹ (dash-dotted line). (d) Velocity decay perpendicular to the particle motion (lines are as in c). (e) Numerically calculated values (symbols) (4, 27) of Henry's function f_⊥ for a cylinder (Eq. 7) as a function of R/λ_D for 4 different values of ζ. Dashed lines are guides to the eye. The solid line is the limit of Henry's function for low ζ and no relaxation effect (11).

It is assumed that a no-slip plane exists for the particle. The fluid between the surface and the no-slip plane is stationary with respect to the particle and the charge contained within the no-slip plane is effectively part of the objects charge. The potential at the no-slip plane, ζ, is denoted the zeta potential.

The solution of Eq. 1 describes the fluid motion with respect to the sphere's origin, in polar coordinates

The functionals U_r (ψ, r, E) and U _θ (ψ, r, E) represent the long-range fluid disturbance due to the electric forces on the counterions, and they depend on the local electrostatic potential ψ (explicit form in Eqs. 14 and 15 in SI Appendix.

We calculate the resulting particle velocity v from the force balance on the sphere. The total force exerted by the fluid, found from integrating all the viscous and pressure forces around the sphere, is

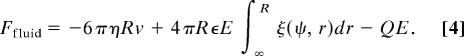Here ξ(ψ, r) is a functional of the particle's electrostatic potential (explicit form in Eq. 16 in SI Appendix). Interestingly, the external force on the particle F_el = +QE exactly cancels the last term in Eq. 4, and force balance (F_fluid + F _el = 0) thus yields the velocity of the particle as

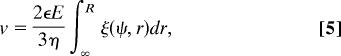which does not depend explicitly on the object's total charge Q, but rather on ζ potential and λ_D through the integral term. Eq. 5 allows to evaluate the velocity, provided the electrostatic potential ψ is known.

Hydrodynamic Versus Electrophoretic Motion.

We now present explicit solutions to the fluid flow problem so as to arrive at a simple physical picture of the differences between electrophoretic and hydrodynamic motion in the length scales of the fluid disturbance. For purely hydrodynamic motion of a uncharged particle (ψ = 0, U_r = U_θ = 0), the fluid motion (Eqs. 2 and 3) reduces, as expected, to the long-range Stokes profile around a sphere. In Fig. 1a, we display the flowlines around the particle, which are curved around the particle up to distances > 4R.

For the fluid motion around a sphere during electrophoresis, we evaluate Eqs. 2 and 3 for a Debye–Hückel ionic atmosphere (ψ(r)=ζR/re^{−(r−R)/λ_D}). Fig. 1b visualizes the flow lines, which, in contrast to hydrodynamic motion, are almost undisturbed by the particle. In electrophoresis, the additional long-range fluid disturbance caused by the motion of the counterions exactly cancels the long-range fluid disturbance induced by the particle motion.

We quantify the length scale of the fluid perturbations in Fig. 1 c and d, where we plot the velocity in front of the particle, u_r (r, θ = 0°) (Fig. 1c), and perpendicular to the particle, u_θ (r, θ = 90°) (Fig. 1d) as a function of distance. In hydrodynamic motion the velocity decays to its undisturbed velocity, −v, much slower (∝ r⁻¹) than in electrophoresis, which decays approximately as ∝r⁻³, in accordance with the argument presented by Long and Ajdari (10).

The electric force on the counterions has consequences for the interpretation of electrophoresis experiments. In hydrodynamic motion under external force F_ext, the fluid is sheared over a distance of order ≈R (Fig. 1a). Force balance (Eq. 4, with ψ = 0) gives the well known result that velocity is inversely proportional to the Stokes drag coefficient, 6πηR. On the other hand, in electrophoretic motion the long-range fluid motions of the sphere and the counterions exactly cancel and the fluid is sheared over a much shorter distance. The restraining force is thus significantly increased compared to Stokes drag. Conversely, to move an object with the same velocity v in electrophoresis, the electrical force that is needed to compensate the fluid forces (Eq. 4) is much higher than in hydrodynamic motion (Fig. 1a vs. b). Stating force balance in electrophoresis merely in terms of the electric force (QE) and the hydrodynamic stokes drag of the object (6πηR) will thus typically lead to an underestimate of the restraining force and thus of the object's charge Q that can be very significant, as we will show.

Electrophoresis of a Cylinder.

Experimentally, we study electrophoresis of cylindrical geometries that are predicted to have an orientation-dependent mobility. Under the same assumptions as for the spherical particle (ignoring relaxation effects), the mobility of infinitely long cylinders oriented axially along the electric field is given by the Smoluchowski equation (6)

For transverse orientations of the cylinder to the electric field, the electrophoretic mobility, μ_⊥, is given by (6, 11)

Here f_⊥ is Henry's function for a cylinder and depends on ζ and R/λ_D. For low ζ (using the linearized Poisson–Boltzmann equation) and ignoring relaxation, f_⊥ increases monotonically from 1/2 for R ≪ λ_D toward 1 for R ≫ λ_D (Fig. 1e).

At higher ζ potential, two assumptions break down: (i) The linearisation of the Poisson–Boltzmann is invalidated, and (ii) the relaxation effect becomes important. During electrophoresis, the ionic double layer is continuously destroyed behind the migrating object and rebuilt in front of it. The finite mobility of the ions leads to cylindrically asymmetric ρ(r, θ) and ψ(r, θ), which leads to a decrease in f_⊥ for moderate values of R/λ_D (4, 12). For μ_⊥, the effects of relaxation and high ζ potential have been calculated by numerical methods for spherical (12) and cylindrical (4, 13) geometries, which are shown in Fig. 1e. The decrease in f_⊥ with increasing ζ reflects mainly the effect of relaxation, whereas the nonlinearity of the Poisson–Boltzmann equation only has a small effect (12). For μ_‖, Stigter (13) argues that Eq. 6 is still a good approximation for finite-length cylinders, as long as the length of the cylinder is large compared to λ_D.^† Experimental values of the ζ potentials presented below will be <2k_bT/e.

Experimental Results

We observe electrophoretic motion of fluorescently labeled microtubules in 50 × 1 μm² slit-like channels that are fabricated (details in SI Appendix) between 5 mm spaced entrance reservoirs in glass substrates (Fig. 2 a and b). The entire channel is coated with casein to prevent interactions between channel walls and microtubules.

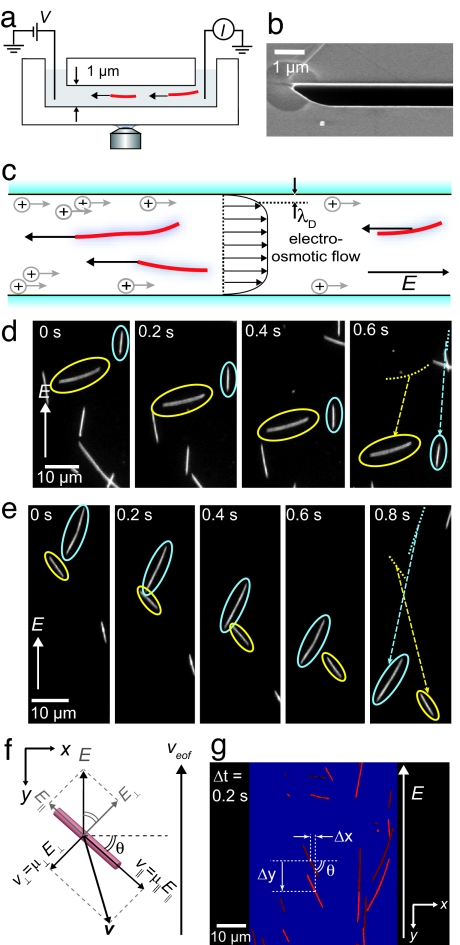
Fig. 2.

Experimental geometry. (a) Electrophoretic motion of microtubules in channels is observed using fluorescence microscopy. (b) Scanning-electron microscope image of a part of the cross-section of a channel. (c) The velocity of microtubules is a superposition of their electrophoretic velocity and an EOF velocity. (d and e) Fluorescence of electrophoresis (E = 4 kV/m) of individual microtubules. (d) A microtubule oriented axially along the electric field moves faster than a microtubule oriented perpendicular to the field. (e) Microtubules can have a velocity that is not collinear with E. (f) Diagram of the velocity components of a microtubule oriented under an angle θ with E along the y axis. The electric field has components axially (E_‖) and perpendicular (E_⊥) to the microtubule. The anisotropic mobility results in net velocity v that is not collinear with E. (g) Overlay of two images taken at a 0.2-s interval. For each microtubule, the average orientation θ and center-of-mass displacements in the x and y directions, Δx and Δy respectively, are determined.

The measured velocity of microtubules is a superposition of their electrophoretic velocity and any fluid velocity in the microchannel. Because of the negative surface charge of our glass channels, the electric field induces an electro-osmotic flow (EOF) along the direction of the electric field (Fig. 2c). The EOF velocity of magnitude μ_EOFE is homogeneous over the cross-section of the channel except within a distance λ_D = 0.7 nm of the channel walls. The EOF-mobility μ_EOF is given by the Schmoluchowski result (Eq. 6) with substitution of the ζ-potential of the glass, ζ_SiO2. [Eq. 6 describes the relative motion between a charged surface and the fluid and therefore equivalently applies to electrophoresis and EOF.] We first present measurements of the combined EOF- and electrophoretically driven motion of microtubules, followed by measurements of the EOF velocity in our channels.

Electrophoresis of Microtubules.

Fig. 2 d and e shows two representative series of time-lapse camera images of the electrophoretic motion of microtubules. Fig. 2d shows the displacements of two microtubules in perpendicular and axial orientations to E. After 0.6 s, the perpendicular microtubule has clearly moved over a shorter distance than the axially oriented microtubule. Fig. 2e shows the displacements of two microtubules that are not oriented axially or perpendicularly to the electric field, but under approximately equal, opposite angles to E. Both microtubules show a displacement that is not collinear with E. Instead, the velocity of each filament is oriented slightly toward its axis. The displacements of both microtubules in the direction of the electric field are approximately equal in this case.

The direction and magnitude of the electrophoretic velocity of a microtubule are observed to depend on orientation with respect to the electric field. This orientation-dependent velocity is a hallmark of the predicted anisotropic mobility of a cylindrical particle (Eqs. 6 and 7). In Fig. 2f, we show a diagram of a microtubule oriented under an angle θ with the x axis and the electric field along the y axis. The velocity of the microtubule, v, is not collinear with the driving field, but instead has a component perpendicular to E. The EOF also contributes a velocity to the microtubule in the y direction. From Fig. 2f, we thus express the velocity in the x direction, v_x, and y direction, v_y, in terms of the anisotropic and EOF mobilities

To determine the anisotropic mobilities, we measure the θ-dependent displacements of a large number of microtubules in the x and y directions between consecutive frames (Fig. 2g). Fig. 3 a and b displays experimental results for the orientation-dependent v_x and v_y at E = −4 kV/m. In accordance with Fig. 2 d and e, microtubules oriented with 0 < θ < 90° have a positive velocity perpendicular to E, whereas microtubules in the opposite orientation, 90° < θ < 180°, move in the negative x direction. From Fig. 3b, we confirm that microtubules oriented perpendicular to E have lower v_y than microtubules with axial orientations to the field. The solid lines in Fig. 3 a and b are fits of Eqs. 8 and 9 to the data. These equations clearly describe the observed orientation dependence very well. The fitted amplitude [A = (μ_‖−μ_⊥) E] and offset [B = (μ_⊥ + μ_EOF) E] contain information about the mobilities (Eqs. 8 and 9).

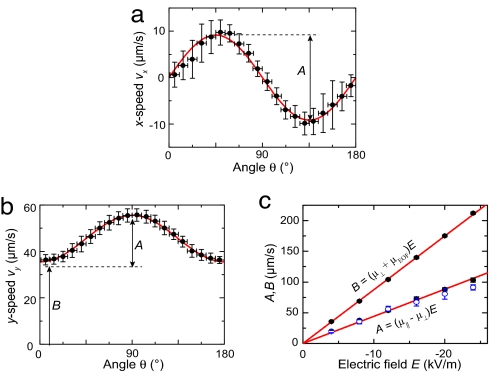
Fig. 3.

Electrophoresis. (a) Measured v_x as function of orientation θ at E = −4 kV/m (mean ± standard deviation of 9° bins, n = 4,570). The solid line is a fit to Eq. 8. (b) θ-dependent v_y (same E), with a fit to Eq. 9. (c) Fitted values of B (from b) and A (from a and b) as function of E. From the fits, we find (μ_‖ − μ_⊥) = (−4.42 ± 0.12) × 10⁻⁹ m²/Vs, and (μ_⊥ + μ_EOF) = (−8.75 ± 0.04) × 10⁻⁹ m²/Vs.

We measured orientation-dependent velocities for different electric fields ranging up to 24 kV/m. Fig. 3c displays the values of A and B as a function of the electric field. From the linear v − E relation, we infer that we can safely use the linear superposition of parallel and axial components of the velocity (Fig. 2f). Any coupling between the relaxation effect in the perpendicular direction (∝ E) and the electric field in the axial direction would induce a response ∝ E² as well as a torque on the microtubules. The absence of any alignment (Fig. 2 d and e) and the linear response in E (Fig. 3c) indicate that coupling is negligible and justify the use of Eqs. 8 and 9 up to the field strengths used.

EOF.

To separate the electrophoretic and EOF contributions to the observed microtubule velocities, we measure the velocity of the EOF in our channels using a current-monitoring method (14). The reservoirs at the ends of the channel are each filled with solutions of slightly different resistivity (ρ₁/ρ₂ ≈ 0.9) (Fig. 4a). Applying a voltage induces an EOF that replaces the buffer solution in the channel. Depending on flow direction, the monitored channel resistance will linearly increase or decrease until the total channel is filled with solution from one of either reservoirs. The EOF velocity is obtained from dividing the channel length ΔL by the average time interval of the conductivity change Δt. We used the same buffer as in the electrophoresis experiments.

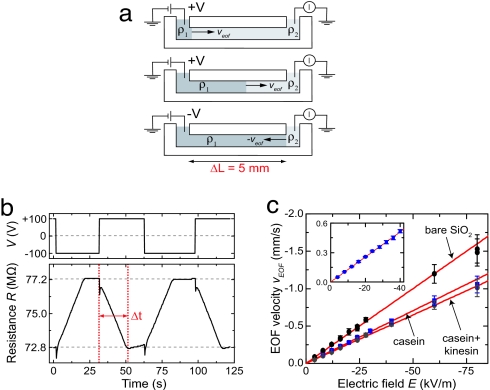
Fig. 4.

EOF. (a) Schematic of current-monitoring method for measurement of the EOF velocity. (b) Typical measurement (E = 20 kV/m). The channel resistance (Lower) changes over Δt ≈ 20 s upon changes of voltage (Upper). (c) Measured EOF velocities in a single channel with different surface coatings as function of E. From the fits we find μ_EOF = (+ 2.00 ± 0.04) × 10⁻⁸ m²/Vs, (+ 1.41 ± 0.01) × 10⁻⁸ m²/Vs, and (+1.29 ± 0.01) × 10⁻⁸ m²/Vs for the untreated channel (bare SiO₂), the casein-coated, and the casein–kinesin-coated channel, respectively. (Inset) Measurements for the channel that was used in the electrophoresis experiments.

Fig. 4b shows a typical measurement of the change in channel resistance with time. Initially, at t = 0 s, the resistance of the channel is 72.8 MΩ. Then, t = 2 s, we induce an EOF by applying a voltage difference of −100 V over the 5-mm-long channel. As a result, the channel resistance increases until it reaches a steady value of 77.2 MΩ at t = 22 s. After again reversing the polarity of the voltage, on t = 32 s, the channel resistance decreases until it has returned to its original value (t = 52 s).

Measured EOF velocities as function of E are shown in Fig. 4c. To determine the effect of protein absorption, we show EOF velocities measured in a single channel with different surface coatings. From the slope of the fits, we determine that μ_EOF = (+1.28 ± 0.01) × 10⁻⁸ m²/Vs in the casein-coated channel that we used in the electrophoresis experiments (Fig. 4c Inset).

Discussion

We now determine the electrophoretic mobilities of the microtubules by substraction of the EOF mobility. From the data in Figs. 3c and 4c, we calculate the electrophoretic microtubule mobilities for axial and perpendicular orientations to the electric field as μ_‖= (−2.59 ± 0.02) × 10⁻⁸ m²/Vs and μ_⊥ = (−2.15 ± 0.01) × 10⁻⁸ m²/Vs, respectively. This finding is in good agreement with previous bulk measurements of the average mobility (8, 15). We calculate that the anisotropy μ_⊥/μ_‖ = 0.83 ± 0.01.

Electrophoretic Motion Is Not Described by Stokes Drag.

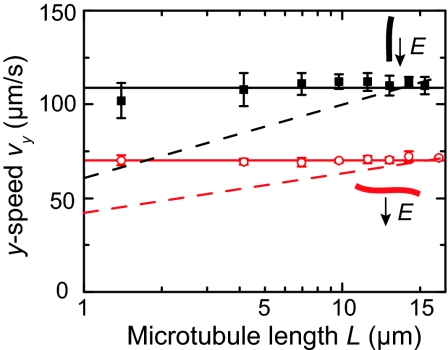
Our experimental results illustrate that electrophoretic motion indeed differs significantly from purely hydrodynamic motion. First, we note that the measured velocity anisotropy of 0.83 ± 0.01 is clearly different from the well known anisotropy of 0.5 in Stokes-drag coefficients for long cylinders. Moreover, Fig. 5 displays the measured electrophoretic velocities of microtubules as a function of their length. We do not observe any significant length dependence of the measured v_y, for neither perpendicular (θ = 0°) nor parallel (θ = 90°) orientations of microtubules to the electric field. The length-independent electrophoretic velocity of microtubules is in agreement with Eqs. 6 and 7, but in clear contrast with a Stokes description.

Fig. 5.

Measured length dependence of the electrophoretic motion of microtubules for perpendicular orientation (open circles) and for axial orientations (filled squares) to the electric field (E =−8 kV/m). The solid lines are guides to the eye. The dotted lines show the expected length dependence of the purely hydrodynamic motion [≈ln(L/R)] for cylinders (R = 12.5 nm).

If electrophoretic motion of microtubules were a balance of electric (∝ QE) and Stokes-drag forces (∝ cLv) we would expect a length dependence, because the Stokes-drag coefficient c for a cylinder is itself dependent on L (16) (Eqs. 17 and 18 in SI Appendix). This applies for cylinders far from a surface, which is a good approximation to our experimental situation (Fig. 7 in SI Appendix). Fig. 5 shows the expected length dependence for cylinder motion that would result from a balance between electric and Stokes drag forces (dashed lines). The clear deviation of the experimental data from the simulated data [≈ln(L)] shows the inadequacy of the Stokes treatment of electrophoresis.

Effective Surface-Charge Density σ_eff.

From the EOF mobility measurements (Fig. 4c), we deduce the ζ potential (Eq. 6) of the channel walls. For the untreated channel wall, we calculate ζ = −25.1 ± 0.05 mV. For the protein-coated channels, we find values ζ = −19.0 ± 0.1 mV, and ζ = −17.3 ± 0.1 mV for the casein and casein–kinesin-coated channels, respectively. We determine the effective surface-charge density σ_eff of the channels from the Grahame equation, which relates the ζ potential to σ_eff (17)

For the bare channel, we find σ_eff = −27.5 ± 0.5 mC/m², which corresponds well with streaming current measurements (18).

Similarly, for microtubules, we infer, directly from the value of μ_‖ that ζ = −32.6 ± 0.3 mV, corresponding to σ_eff = −36.7 ± 0.4 mC/m². Note that the measured mobility anisotropy provides a second independent estimate for the value of ζ. For a perfect cylinder, the anisotropy μ_⊥/μ_‖ equals the Henry factor f_⊥, from which we derive the ζ potential through Fig. 1e. In this way, we find a similar value ζ = −39 ± 6 mV, but this method is less accurate because the uncertainty in the anisotropy amplifies the error in ζ. Nevertheless, it is interesting that the two different methods yield similar values of ζ. The measurement of μ_‖ reflects a measure of the ζ potentials of both the inner and outer surfaces of the cylindrical microtubule, whereas the value of μ_⊥ only reflects the ζ potential of the outer surface. The agreement between the two methods for calculating ζ thus indicates that the inner- and outer-surface ζ potentials are comparable.

Effective Tubulin–Dimer Charge Q_eff.

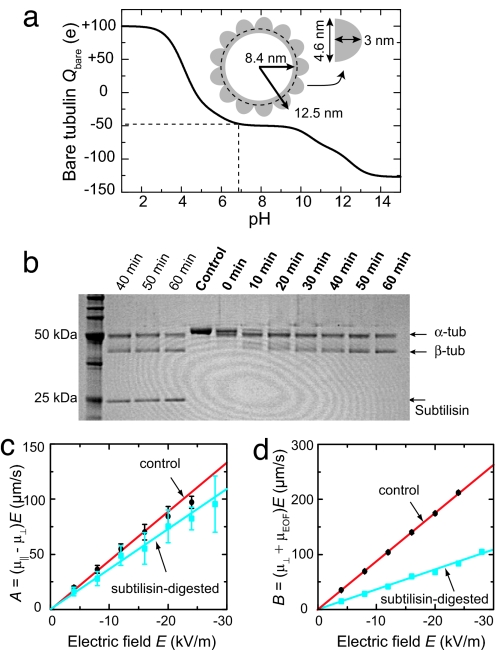
To calculate the effective charge per tubulin dimer Q_eff from σ_eff, we compute the solution-exposed surface of the tubulin dimer. Microtubules are composed of 13 protofilaments that associate laterally into a cylinder. The protofilaments consist of head-to-tail associated dimers of α- and β-tubulin. The dimensions of the cross-section, derived from an axial projection of the electron-density map of the microtubule (19, 20), are shown in Fig. 6a. For a 13-protofilament microtubule, we calculate that the solution-exposed outer surface of the tubulin dimer is 67 nm², whereas the inner surface is 33 nm². From the measured σ_eff, we then calculate Q_eff = −23 ± 0.2 e per dimer, assuming homogeneous charge distributions on the microtubule's inner and outer surfaces.

Fig. 6.

Tubulin digestion. (a) Calculated Q_bare per dimer from sequence data. At pH 6.9, the calculated Q_bare is −47 e per dimer. (Inset) Cross-section dimensions of a microtubule constructed from an axial projection of the microtubule electron-density map (20). The 13 protofilaments are displayed as half-ellipsoids of 4.6 nm width and 3.0 nm height, around a 1.1-nm-thick cylinder of inner radius of 8.4 nm. (b) Denaturing SDS/PAGE of digested microtubules. “Control” shows untreated centrifuged microtubules in a single band. The subsequent lanes show the results for subtilisin-treated microtubules for different digestion times, obtained after centrifugation. Subtilisin is present at the 25-kDa band before centrifugation (first three lanes). (c) Amplitude of measured v_x(θ) and v_y(θ) of digested microtubules as function of E. “Control” is from Fig. 3c for undigested microtubules. (d) Offset of measured v_y(θ) of digested microtubules for different Es.

This value of the effective charge is higher than we previously calculated (2), because we use a more accurate model for the microtubule outer surface here (undulated surface instead of a smooth cylinder), and because we include the inner surface of the microtubule. The rationale for the latter is that the screening length is much smaller than the inner radius of the microtubules. The fluid can thus flow unhindered through the microtubule and according to the Smoluchowski result, the mobility is only dependent on the potential at the no-slip plane.

We compare the value of Q_eff to the bare charge of the tubulin dimer as calculated from the amino acid sequence (21, 22). Fig. 6a displays the calculated pH-dependent bare dimer charge Q _bare in a range of pH = 1–14, obtained from a summation over all charged amino acids (Eq. 20 and Table 1 in SI Appendix). At the pH = 6.9 of our experiments, we calculate Q_bare = −47 e per dimer. We find that the value of Q_eff from our experiments constitutes ≈50% of the calculated bare charge. We attribute this lower value to screening. Q_eff is the sum of the bare microtubule charge and the counterion charge contained within the no-slip plane. Our result suggest that 50 % of the counterion charges are strongly bound to, and move with, the microtubule under the electric field strengths used.

For comparison, reports of Q_eff that ignore the retardation effect yielded values varying from −0.2 (8) to −3 × 10⁻⁴e per dimer (9). Clearly, the restraining force of the counterions can be so large that, depending on the experimental conditions, ignoring it can lead to an underestimation of the effective charge up to 5 orders of magnitude.

The value of Q_eff that we infer from the experimentally determined ζ potential relies on three assumptions. First, by speaking of the ζ potential, we implicitly assume the existence of a no-slip plane, which is a widely used but theoretical entity. Second, by calculating σ_eff from ζ, we assume the validity of the mean-field Poisson–Boltzmann equation. However, under our experimental conditions, λ_D is of the same order of magnitude as the hydrated-ion diameter, and finite ion-size effects can be expected to play a role. Third, the value of Q_eff depends on the solution-exposed surface area that we use for the tubulin dimer. In the extreme limit of modeling the microtubule as a solid cylinder the exposed area is reduced by 50%. We expect that the latter assumption forms the largest contribution to the uncertainty in our estimate for Q_eff. Despite the above considerations, we believe that our method provides a fair estimate of the protein charge, unlike the reports that make orders-of-magnitude systematic errors by ignoring the retardation effect.

Charge Modification by Digestion.

We also probed the effect of charge reduction on the the mobility of microtubules. The α and β subunits consist of 450 and 445 amino acids, respectively, each with a molecular mass of ≈50 kDa (21, 22). The subunits exhibit globular folding with their C termini, which are relatively rich in acidic groups, exposed to the outer surface of the microtubule (23).

We modified the charge of the tubulin dimer by removing part of the subunits C termini by proteolytic digestion using subtilisin (24). Subtilisin cleavage occurs with high efficiency (94%) at positions Asp-438 and Gln-433 for α- and β-tubulin, respectively (25), thereby removing a fragment of 13 amino acids, of which 8 are acidic, from each monomer. We expect Q_bare = −30 e per dimer after digestion, i.e., a reduction of 36%.

We performed subtilisin digestion on taxol-stabilized microtubules of the same batch as we used before, for different periods of time. Fig. 6b shows the progression of the digestion reaction. For undigested microtubules (control), the α and β show a single band at ≈50 kDa. After subtilisin digestion, the original tubulin band disappears, and two bands start to appear of a slightly lower apparent molecular weight, indicative of tubulin digestion (26). The digestion of α-tubulin is faster than the digestion of β-tubulin (26). Within the resolution of the gel, digestion is complete after 60 min. Microtubules treated for 60 min with subtilisin were still intact and used in electrophoresis experiments.

We measured the orientation-dependent velocity of digested microtubules for different electric fields. The experiments are performed in the same channel as used for the undigested microtubules. Fig. 6 c and d present the fitted amplitudes and offsets of the v_x and v_y data as a function of electric field for digested microtubules. The subtilisin-digested microtubules have significantly reduced velocities compared to undigested microtubules. From the linear fits, we determine μ_‖ = −2.00 ± 0.02 × 10⁻⁸ m²/Vs, and μ_⊥ = −1.64 ± 0.01 × 10⁻⁸ m²/Vs for digested microtubules.

We find that the mobility of the digested microtubules has been reduced significantly, as expected from the large reduction in charge residing on the outer surface of the microtubule. It is interesting that the values of μ_‖ and μ_⊥ have been reduced by the same amount, by 23 ± 2 % and 24 ± 1 %, respectively, and that the anisotropy is thus not different for the digested microtubules. From Fig. 1e, we expect an increase of f_⊥(ζ) from 0.83 to 0.86 upon a 23% reduction in surface charge. However, these numerical results apply to homogeneously charged cylinders and it remains a theoretical challenge to describe inhomogeneous charge distributions on open cylinders. Our experimental results can serve as input for further theoretical investigations in the mobility of composite cylindrical objects with different inner and outer surface potentials.

Conclusions

We used microfabricated fluidic channels to measure the electrophoretic motion of individual microtubules, which, with their cylindrical shape, constitute an important basic geometry. Together with measurements of the EOF velocity in our channels, we determined the electrophoretic mobility. These measurements experimentally demonstrated two important differences with purely hydrodynamic motion of cylindrical filaments. (i) The mobility is independent of microtubule length, in contrast to the length-dependent hydrodynamic drag. (ii) The electrophoretic mobility is anisotropic, with microtubules oriented perpendicular to the electric field moving a factor of 0.83 slower than for axial orientations. This is markedly different from hydrodynamic motion, where the drag anisotropy is a factor of 0.5. We have argued that these differences are due to the motion of the counterions, which makes the fluid perturbations much shorter range than in hydrodynamic motion, and that this has important implications in the interpretation of electrophoresis measurements. Although understood long ago, these results are often neglected in recent electrophoresis experiments, which leads to order-of-magnitude underestimations of the effective charge.

From the mobility measurements we inferred Q_eff = −23 ± 0.2 e per tubulin dimer. We also measured the electrophoretic mobility of subtilisin-treated microtubules that had their highly negatively charged C termini removed by digestion. We measured a 23% reduction in mobility, but no change in anisotropy.

Enclosed microfluidic channels form an excellent system to measure electrophoretic motion of individual biomolecules. From these experiments we gained valuable insights into fundamental electrophoretic properties of colloidal cylinders and obtained measurements of the effective charge of individual biomolecules.

Abbreviation

EOF

electro-osmotic flow.