Shear-induced unfolding triggers adhesion of von Willebrand factor fibers

Abstract

von Willebrand factor (VWF), a protein present in our circulatory system, is necessary to stop bleeding under high shear-stress conditions as found in small blood vessels. The results presented here help unravel how an increase in hydrodynamic shear stress activates VWF's adhesion potential, leading to the counterintuitive phenomena of enhanced adsorption rate under strong shear conditions. Using a microfluidic device, we were able to mimic a wide range of bloodflow conditions and directly visualize the conformational dynamics of this protein under shear flow. In particular, we find that VWF displays a reversible globule-stretch transition at a critical shear rate γ̇_crit in the absence of any adsorbing surface. Computer simulations reproduce this sharp transition and identify the large size of VWF's repeating units as one of the keys for this unique hydrodynamic activation. In the presence of an adsorbing collagen substrate, we find a large increase in the protein adsorption at the same critical shear rate, suggesting that the globule unfolding in bulk triggers the surface adsorption in the case of a collagen substrate, which provides a sufficient density of binding sites. Monitoring the adsorption process of multiple VWF fibers, we were able to follow the formation of an immobilized network that constitutes a “sticky” grid necessary for blood platelet adhesion under high shear flow. Because areas of high shear stress coincide with a higher chance for vessel wall damage by mechanical forces, we identified the shear-induced increase in the binding probability of VWF as an effective self-regulating repair mechanism of our microvascular system.

Our circulatory system is exposed to an amazingly wide span of shear rates, ranging from 1 to 10⁵ s⁻¹ (1). This range calls for adhesion mechanisms during blood clotting that are different for different regimes of shear rates. At small shear rates, which are found in rather wide vessels, objects such as vesicles or cells bind to vessel walls once the contact area and the adhesion strength is large enough (2). At high shear rates, which are found in small arteries, hydrodynamic lift forces inhibit formation of a sufficiently large contact area, which makes adsorption of soft objects from the blood onto vessel walls increasingly difficult. In fact, theoretical analyses predict that adhering compact and soft objects (such as vesicles or platelets) will roll and detach from a surface at a particular shear stress and, more importantly, will remain unbound if the shear rate is increased further (3, 4). Experiments on leukocyte adhesion confirmed these theoretical predictions quite nicely (2). However, the experimental finding for blood platelet adhesion in small arteries contradicts this scenario: von Willibrand factor (VWF)-mediated platelet adhesion, which is necessary to stop bleeding in small vessels, is strongly enhanced under high shear-flow conditions (5). Therefore, this example of shear-induced adsorption must be explained by a distinct mechanism. Under normal conditions, the glycoprotein VWF assembles into multimeric polymers that, when stretched, can reach a length of up to 100 μm (6). The repeating unit is unusually large (≈70-nm long axis, 10-nm short axis) (7) and represents a dimer containing 5,100 aa (8). A number of recent studies on VWF suggest that a conformational transition, presumably triggered by an increase in shear, may be necessary for the initiation of platelet adhesion (5, 9–11). Former studies on the dynamics of uncollapsed biopolymers in good solvent conditions predict mechanically induced transitions for shear rates in the range of a few 10 s⁻¹ (12). In contrast, typical shear rates in small arteries, where procoagulatory activity of VWF is predominant, are in the range of 1,000 s⁻¹. Until now, there have been no studies of which we are aware that mimic the hydrodynamic conditions of our microcirculatory system and directly monitor the conformational dynamics of unbound and conformationally unrestricted VWF when exposed to shear flow. Therefore, the origin of VWF's peculiar hydrodynamic behavior and related function remained unclear on both dynamical and molecular grounds.

Here, we unravel VWF's response to hydrodynamic stress by exploiting a microfluidic flow chamber incorporated directly on a chip. We found that the application of unusually high shear flows (>1,000 s⁻¹) results in an abrupt elongation of VWF fibers in solution. Computer simulations clearly indicate that the molecular origin of VWF's extraordinarily response to mechanical stress can be tracked back to its extremely large repeating unit size. The conformational transition takes place in a reversible manner and on very short time scales. It must therefore not be mistaken with protein denaturation. The results presented here comprise a thorough investigation of VWF's behavior under strong shear flow and enable us to bridge the gap between physical forces, physiological function, and VWF-related diseases.

Results and Discussion

Shear-Induced Stretching.

VWF was diluted in PBS (including 1 mM Mg and 1 mM Ca) that was then spread over the hydrophilic track of the flow chamber chip described in Materials and Methods (Fig. 1). Images of VWF at concentrations typical for human blood (c ≈ 2 μg/ml) are presented in Fig. 2. At shear rates of γ̇_crit ≈ 10–1,000 s⁻¹, the biopolymer exhibits a compact conformation (Fig. 2a Left). The size of the VWF globules was estimated within our fluorescence setup to be d ≈ 2 μm, clearly showing that it consists of more than one repeating unit. This compact conformation remains unchanged as long as the shear rate is maintained below a certain (critical) value γ̇_crit ≈ 5,000 s⁻¹. Increasing the shear rate above γ̇_crit induces a shape transformation of the VWF fibers from a collapsed conformation to a stretched conformation with a length, l, of ≈15 μm (Fig. 2a Right). Fig. 2b shows that this transition is reversible, because the protein immediately relaxed to its compact conformation when the flow was turned off (at time t = 0 ms).

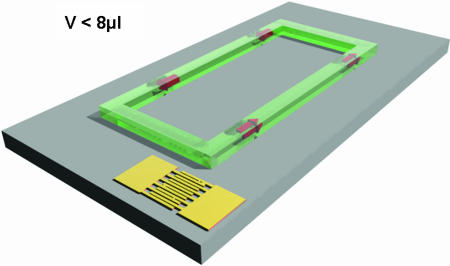
Fig. 1.

The planar microfluidic device. The blood vessel is modeled by a planar hydrophilic track on an otherwise hydrophobic piezoelectric substrate. A surface acoustic wave, excited electrically, eventually interacts with the confined liquid at the solid–liquid interface and drives the liquid to flow (acoustic streaming). The surface wave basically acts as a localized pump, because its mechanical energy is absorbed by the liquid over only a few micrometers. Due to the small scales of this microfluidic system, it creates a homogenous laminar flow (low Reynold's number) along the channel, mimicking the blood flow in arteries or capillaries.

Fig. 2.

Dynamic conformational change of VWF under shear. (a) Cartoon (Upper) and selected fluorescence (Lower) images of a video sequence (SI Movie 1, acquired at 25 frames per second) of VWF below and above the critical shear rate of a few thousand s⁻¹. Above γ̇_crit, the protein is in an elongated conformation. The little yellow spots on the protein are meant to represent a variety of known binding sites. To assure that only unbound VWF was detected, the focus of the microscope was set ≈10 μm above the surface of the chip in the middle of the channel. (b) Relaxation of VWF. Selected fluorescence images of a video sequence (SI Movie 1, acquired at 25 frames per second). Once the hydrodynamic shear force is reduced below γ̇_crit at 0 ms, the protein immediately relaxes back to its compact state. The unfolding process is reversible and presumably does not include protein denaturation.

The abrupt nature of the transition can also be seen as a sudden increase in the average extension of the fibers as a function of shear rate, as shown in Fig. 3. These features (reversibility and critical stretching) make VWF a mechanically switchable protein, which, as will be shown, is crucial to its ability to stop bleeding.

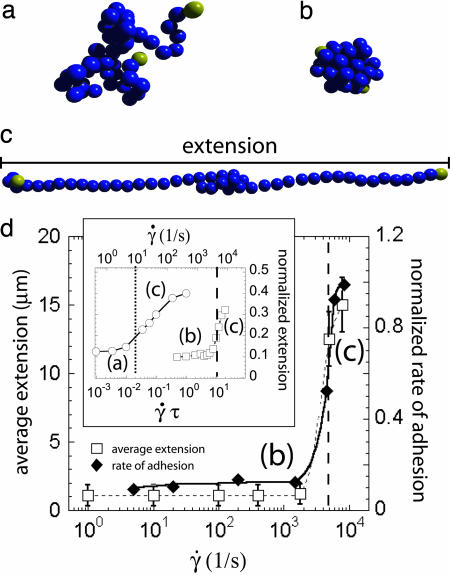
Fig. 3.

Typical polymer configurations, coiled (a), collapsed (b), and stretched (c), observed at different solvent conditions and different values of the shear rate [images were selected from our computer simulation (SI Movie 2)]. (d) The experimentally determined average extension (open squares) and the normalized rate of adhesion (filled diamonds) of VWF multimers as a function of the shear rate (SI Movie 3). The vertical dashed line is located at the critical shear rate, and the letters denote the type of prevalent polymer conformation as illustrated in the sketches. (Inset) Simulation results for the normalized extension (equal to the average extension divided by the contour length) of a 50-mer as a function of the dimensionless shear rate γ̇τ (lower scale) and the physical shear rate γ̇ using a monomer size a = 80 nm and a viscosity η = 1 cP (upper scale). The coiled (open circles) and the collapsed (open squares) polymers have an attractive contact potential depth of ΔU = 0.416 and ΔU = 2.08 (in units of k_BT), respectively. The vertical dotted and dashed lines correspond to the shear rates at which the coiled and collapsed polymers start exhibiting strong elongations, respectively, as determined by a maximum in the higher-order cumulants. The lines joining the data points are just to guide the eye.

The fact that the transition occurs at such a high shear rate cannot be understood from previous studies on linear chains under good solvent conditions (13, 14). For example, it has been shown that DNA of a length that is roughly the same as the VWF fibers studied here will exhibit drastic changes of elongation for shear rates as low as 30 s⁻¹ at a viscosity of 1 cP (1 P = 0.1 Pa·sec) (i.e., water or the PBS used here) (12). Our studies, however, indicate that significant changes in conformation occur only at shear rates γ̇_crit ≥ 5,000 s⁻¹. This value is more than two orders of magnitude higher than that reported for DNA. To explain this large discrepancy, it is necessary to account for the presence of attractive interactions between repeating units (presumably hydrophobic or H bonds) that would hold each VWF fiber tightly together, even under strong shear conditions. Therefore, we propose that a single VWF multimer forms a compact or collapsed structure similar to a folded protein (Fig. 2a Left). The difference to a regular protein is that here, all of the repeating units are attracted to each other most likely without any sequence-specific binding preference, assuring the reversible character of the transition, as experimentally confirmed in Fig. 2b.

Hydrodynamic Computer Simulations.

To gain more insight into the unfolding mechanism, we perform hydrodynamic simulations of a single polymer in shear flow under different solvent conditions. Our simulation method incorporates hydrodynamics and solvent flow effects (15). The effective monomer–monomer attraction is modeled by a Lennard–Jones potential (16). Note that the monomers forming the polymer in our simulation are spherical beads of radius a and correspond to the repeating unit forming the VWF in our experiment. In the simulations, the only parameters are three dimensionless numbers, namely the rescaled shear rate γ̇τ (where τ = 6 πηa³/k_BT is the characteristic diffusion time of a single bead); N, the number of repeating units; and the interaction potential strength, ΔU, between two beads (in units of k_BT). Our results for the normalized extension (i.e., the average extension divided by the contour length) of a 50-mer are presented in Fig. 3d Inset. The left (open circles) and right (open squares) curves correspond to a polymer in the coil and globular states, respectively. The attractive well depth (in units of k_BT) between monomers for the coil and collapsed case are ΔU = 0.416 and ΔU = 2.08, respectively. On the lower horizontal axis in Fig. 3d Inset, we show the rescaled units for the shear rate, γ̇τ, that we use in our simulations. Note that the monomer radius a and solvent viscosity η only enter this rescaled shear rate, and thus our simulations are valid for arbitrary monomer radius a and solvent viscosity η. In the upper horizontal axis in Fig. 3d Inset, we restore physical units by making a specific choice for these parameters, namely a repeating unit or radius of a = 80 nm in a fluid with a viscosity similar to that used in the experiments, i.e., η = 1 cP. We have purposely chosen a relatively large value for the bead (monomer) size so that the critical shear rate for the collapsed polymer is close to the experimental value. As shown by the upper scale in Fig. 3d Inset, the extension of the coiled polymer (circles) grows for γ̇ > 10 s⁻¹ (vertical dotted line) and saturates at a value of approximately one half the contour length, in agreement with previous experimental and theoretical studies (12, 17). In comparison, the collapsed chain (squares) abruptly “unfolds” at shear rates γ̇ > 5,000 s⁻¹ (vertical dashed line), which is more than two orders of magnitude higher compared with that for the coiled polymer. Thus a 5-fold increase in attractive strength leads to a >100-fold increase in the threshold shear rate. Changing the monomer size a leads to drastic changes in the critical shear rate; using scaling arguments based on the presence of protrusion excitations, it can be shown that the critical shear rate for unfolding obeys the scaling law γ̇_crit ≈ ΔU²L^1/3a^−10/3/(ηk_BT) (16), where L is the polymer length and a is the monomer size. An important conclusion from the scaling law is that the critical shear rate depends much more sensitively on the effective monomer size a than it does on the polymer length L. Consequently, to tune the critical shear to a low enough value to observe unfolding at the typical shear rates found in small arteries, it is more efficient to increase the effective monomer size (repeating unit) at constant length L than to decrease the length of the polymer at constant monomer size a. Seemingly, this is the strategy adopted by nature, because it has been recently confirmed by neutron scattering experiments that the repeating unit of VWF in solution is a prolate ellipsoid with dimensions of 70 nm and 10 nm along its major and minor axes, respectively (7). For ΔU ≈ 2 (in units of k_BT), the monomer radius that gives a critical shear rate close to the experimental results is 80 nm, which is of the order of the long axis of the VWF repeating unit. The almost quantitative agreement might be fortuitous, as in the simulations we model repeating units as spheres, whereas the VWF units are ellipsoidal. Along the same lines, we note that the effective potential between VWF monomers is unknown to this date, so the value chosen in the simulations is only a reasonable guess for VWF monomer interactions, considering that it is a rather weakly collapsed multimeric protein. It is possible to reduce the attractive interaction to even smaller values while still retaining the collapse character of the multimer. In particular, one could consider ΔU ≈ 1 (in units of k_BT), which would reduce the dimensionless critical shear rate by a factor of 5 and imply an effective monomer size of a ≈ 50 nm, which would still be compatible with experimental values. Modifications of the interaction strength could in fact be triggered by mutations in the amino acid sequence and might be the cause for VWF-related diseases. Finally, our simple simulation model captures the essential ingredients of shear-induced unfolding of collapsed polymers and predicts that unfolding at physiological shear rates occurs only if the effective hydrodynamic size of the repeating unit is large (on the order of tens of nanometers). The simulation further provides a hint as to why the effective monomeric size of VWF is so large. More detailed experimental information on the structure and interactions of VWF, such as its rigidity and the mechanical properties of the connecting regions, would be very helpful for more accurate modeling and for a better understanding of the phenomenology of globular proteins under hydrodynamic shear.

Force-Induced VWF Adhesion and Network Formation.

After studying the effect of shear flow on the shape of VWF multimers, we investigated the role of the conformation (compact or elongated) on its adhesive properties. We therefore loaded a collagen-coated microfluidic channel with labeled protein (c ≈ 1 μg/ml) and monitored the number of immobilized fluorescently labeled proteins per area and time while slowly increasing the shear rate. As can be seen in Fig. 3, the rate of adhesion (filled diamonds) as a function of shear rate precisely follows the jump in protein length as observed for the free (unattached) protein. Because there is nearly no adsorption detectable below the critical shear rate of γ̇_crit ≈ 5,000 s⁻¹, we conclude that VWF adhesion on a collagen-coated surface is triggered by its conformation. At first glance, this seems contradictory because one would expect that adhered proteins should be ripped away more readily at higher flow rates. However, the number of exposed binding sites (indicated by the little yellow dots in Fig. 2) is strongly increased during the stretching of the VWF multimer. As soon as one of the elongated fibers touches the surface, it simultaneously binds at multiple sites and is therefore more likely to be held and attached to the surface. As more and more VWF fibers adhere to the surface they eventually start to form a protein network (Fig. 4) by self association or polymerization (9, 18, 19), representing a very sticky substrate for blood platelets.

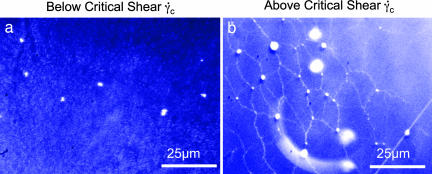
Fig. 4.

Adhesion of VWF. (a) Below the critical shear rate γ̇_crit, only few VWF coils adhere to the collagen coated surface. (b) VWF adhered at high shear rates forms a spider web like network, which represents a very adhesive substrate for blood platelets.

The critical shear rate γ̇_crit is expected to be somewhat lower in the microcirculatory system of the human body. The most obvious candidates responsible for this are the increased viscosity as well as the binding or adsorption of platelets or plasma proteins on the VWF surface. Both conditions are supposed to decrease the critical shear rate of VWF stretching.

In Fig. 5 we show that blood platelets do not only bind to surface-immobilized VWF but also to unbound VWF under flow, showing that soluble VWF is still haemostatically active. The qualitative behavior of the binding process (a rather sharp transition at a certain shear rate) and the order of magnitude of γ̇_crit is similar to the VWF–collagen interaction presented in Fig. 4. However, our first results clearly indicate that the absolute value of γ̇_crit is reduced by at least 25% (<3,500 s⁻¹), probably due to an increased dragging force once platelets start to bind to the protein surface. The formation of aggregates between blood platelets and soluble VWF raised the question of why (to our knowledge) no such aggregates have been found under physiological conditions. There are probably two reasons. From a hydrodynamical point of view, the high shear flow conditions necessary to initiate the blood platelet–VWF associations are rather rare away from the surface, decreasing the probability to find the protein in the haemostatically active (stretched) conformation. From a biochemical perspective, the presence of the VWF degrading enzyme ADAMTS13 may avoid aggregate formation by cleaving VWF (20). Indeed, when we added ADAMTS13 into our microfluidic channel and exposed it to high shear, the formation of an adhesive VWF web was significantly decreased [see supporting information (SI) Fig. 6]. Taking both arguments together, we conclude that the in vivo association of VWF with blood platelets under bulk conditions is a rather unlikely scenario when compared with immobilized VWF–platelet association. However, under rather pathopysiological conditions (e.g., ADAMTS13 deficiency or stenotic conditions) the probability of VWF–platelet association is significantly increased (21).

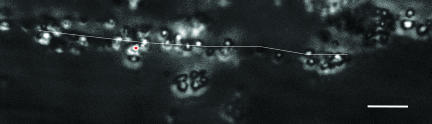
Fig. 5.

Blood platelet –VWF aggregation under high shear flow (γ̇ ≈ 4,000 s⁻¹). Blood platelets (≈1 μm) are immobilized on the free end of a VWF fiber only when γ̇ ≈ 3,500 s⁻¹. The white line indicates the underlying VWF and is given as a guide to the eye (see also SI Fig. 7). (Scale bar, 10 μm.)

Conclusion

To summarize, we have identified VWF fibers as hydrodynamically activated biopolymers, being haemostatically active only under high shear rates. We point out that the observed critical activation threshold (γ̇_crit ≈ 5,000 s⁻¹) falls in the same range as the wall shear rate found in small vessels γ̇_crit > 1,000 s⁻¹ (1). Therefore, the probability for VWF to undergo a discontinuous, conformational transition and thereby become hemostatically active increases dramatically under rather harsh hydrodynamic conditions, for which mechanically induced vessel damage due to high wall shear rates is more likely. This finding unravels the dynamics of VWF as the foundation of a self-adjusting repair mechanism for vascular injury under strong shear conditions and provides clues for understanding vessel and clotting dysfunctions, such as arteriosclerosis, thrombosis, and von Willebrand disease.

Generalizing these results, we envision the possibility for engineering functional polymers that could serve, for example, as local shear stress detectors. A second application would be smart materials that, as additives, would automatically detect and seal small holes in pipes at sights of high mechanical stress.

Materials and Methods

The Flow Chamber Chip.

To study the hydrodynamic response of VWF, we used a planar microfluidic device (described in Fig. 1) (22) that mimics blood flow in small blood vessels (SI Movie 4). Applying a high-frequency signal to a set of electrodes (interdigital transducers) on a piezoelectric substrate (LiNbO₃) excites a surface acoustic wave. When the wave hits the solid–liquid interface, it transmits its acoustic energy into the liquid over a very small distance. The resulting pressure gradient acts like a localized nanopump, a phenomenon called acoustic streaming (23, 24).

To confine the water laterally, a hydrophilic channel on an otherwise hydrophobic substrate (silanized with octadecyltrichlorsilane) is created by optical lithography. In this way, we are able to design a microfluidic flow chamber on the chip surface. To keep the standard protocols for surface biofunctionalization, the chip surface is sputtered with a 20-nm-thick layer of glass (SiO₂). Because of the fast attenuation of the surface acoustic wave once it enters the water channel, this nanopump does not modify the conformation of molecules adsorbed or grafted to the substrate surface. Additional experimental advantages are the exact tunability of the applied shear rate (we checked by measuring the shear rate with tracer particles), and the optical transparency of the piezoelectric substrate.

By mounting the microfluidic chip on a fluorescent microscope, we are able to directly visualize and track the conformation of individual fluorescently labeled VWF multimers freely flowing in the channel (SI Movie 1).

Labeling of VWF.

A tetrafluorophenyl ester was used to attach the fluorophore Alexa Fluor 488 (Invitrogen, Karlsruhe, Germany) to the primary amines of the protein. Dye and protein were incubated and dialyzed according to the Invitrogen protocol. VWF was purchased from Calbiochem (La Jolla, CA).

Fluorescence Microscopy and Image Acquiring.

Fluorescence microscopy is performed by using an inverted microscope equipped with a mercury lamp (Zeiss, Göttingen, Germany) and a CCD camera (Hamatsu, Photonics Deutschland, Hersching, Germany). Usually, images are taken at a rate of 25 frames per second. To avoid artifacts when determining the protein length while acquiring the image, small amounts of fluorescently labeled beads of a different absorption wavelength than VWF are added. From the measured speed of the beads and their spread in the microscope image (caused by the finite exposure time), the actual protein length without any artifacts due to the finite exposure time is deduced.

The rate of adhesion is measured by simply counting the increase of light intensity on a fixed area of the chip surface as a function of time (intensity/m²·s) and define 1.0 as the maximum increase in fluorescence intensity per area and time.

Buffers.

All experiments are performed in PBS (including 1 mM Mg and 1 mM Ca).

Abbreviation

VWF

von Willebrand factor.