Hippocampal place cell assemblies are speed-controlled oscillators

Abstract

The phase of spikes of hippocampal pyramidal cells relative to the local field θ oscillation shifts forward (“phase precession”) over a full θ cycle as the animal crosses the cell's receptive field (“place field”). The linear relationship between the phase of the spikes and the travel distance within the place field is independent of the animal's running speed. This invariance of the phase–distance relationship is likely to be important for coordinated activity of hippocampal cells and space coding, yet the mechanism responsible for it is not known. Here we show that at faster running speeds place cells are active for fewer θ cycles but oscillate at a higher frequency and emit more spikes per cycle. As a result, the phase shift of spikes from cycle to cycle (i.e., temporal precession slope) is faster, yet spatial-phase precession stays unchanged. Interneurons can also show transient-phase precession and contribute to the formation of coherently precessing assemblies. We hypothesize that the speed-correlated acceleration of place cell assembly oscillation is responsible for the phase–distance invariance of hippocampal place cells.

While animals navigate in an environment, the hippocampal local field potential (LFP) is characterized by a highly regular θ oscillation (8–10 Hz). Principal cells in the hippocampus show place-specific firing by two criteria. First, the firing is tuned to a particular location (“place field”), showing a bell-shaped tuning curve centered around its preferred location (1). Second, the timing of spikes within subsequent θ cycles systematically shifts forward (“phase precession”), ≈1 full cycle in total, as the rat runs through the place field of the neuron (2, 3) (see also Fig. 1 A and B). Both the firing rate and discharge phase within a θ cycle are correlated with the rat's position. However, how the rate change and θ-phase precession of spikes are related is poorly understood. The available experiments support both a rate-phase interdependence (4–6) and independence (7).

Fig. 1.

Speed affects oscillation frequency of place cells. (A) Trajectories of the rat through a place field on two trials with different speeds [Top: green, slow trial (mean speed 31 cm/sec); blue, fast trial (mean speed 55 cm/sec)]. (Middle and Bottom) Spikes of one place cell and the corresponding LFP of the same two trials. The black arrows indicate the time it takes for the rat to cross the place field. (B) Smoothed firing rates (tuning curves) and position vs. spike phase of θ (spatial-phase precession) of the neuron (phases are plotted twice for better visibility). Trials were sorted by speed and divided into fast (upper 20%, 11 trials) and slow (lower 20%, 11 trials) trials. (C) Autocorrelograms of spike phases during slow (Upper) and fast (Lower) trials. (D) Autocorrelograms of spike times and above spike-triggered average of the LFP using all spikes in the 20% fastest and 20% slowest trials, respectively. Note the larger phase advance of place cells during fast runs.

Several explanations for the place–phase relationship were put forward (4–6, 8–18). To confront these models, we examined the relationship among running speed, oscillation frequency of place cells and LFP θ, and timing of spikes within the θ cycle. We show that principal cells oscillate at a frequency faster than the simultaneously recorded LFP θ oscillation, and that this oscillation frequency depends on the rat's running speed. Together with the place- and speed-dependent oscillation frequencies of interneurons, the findings support the hypothesis that place coding results from coordinated network activity. We propose that the locomotion speed-dependent oscillation of place cell assemblies may underlie the mechanisms responsible for distance encoding in the hippocampus.

Results

We recorded the firing patterns of pyramidal cells, interneurons, and the LFP from the CA1 pyramidal layer of rats as they ran on a U-shaped or circular track for water reward. Fig. 1A shows the relationship among LFP θ oscillation, place cell firing, and the rat's position on the track in two selected trials, during which the average speed of the rat in the place field was slow (31 cm/sec) and fast (55 cm/sec), respectively. During the slow trial, it took the rat 12 θ cycles to run through the place field of the neuron. In contrast, during the fast trial, it took only seven cycles. The average number of spikes per θ cycle was higher during the faster run, but the total numbers of spikes emitted in the place field are comparable in the two trials (11 spikes during the slow trials and 12 spikes during the fast trial). This shortening of the interspike intervals during faster runs leads to a higher average firing rate within the place field [see ref. 7 and supporting information (SI) Fig. 7]. Nevertheless, the relationship between the rat's position on the track and the θ phase at which the place cell emitted spikes (“spatial-phase precession”) was very similar, as indicated by the distance–phase relationship of the 20% slowest (11 trials, average speed 24 cm/sec) and 20% fastest trials (11 trials, average speed 54 cm/sec) (Fig. 1B). The autocorrelogram of the spike phases relative to θ shows a strong oscillatory modulation (Fig. 1C). Furthermore, the phase advance of the spikes relative to θ was steeper in fast than in slow trials. Similarly, the autocorrelogram of the spike times oscillated faster in fast trials compared with slow trials and accelerated relative to the spike-triggered average of the LFP (Fig. 1D).

Oscillation Frequency of Place Cells Correlates with Running Speed.

Running speed affected the oscillation frequency of place cells and the relationship between spikes and θ phase (Fig. 1 C and D). As illustrated in Fig. 1 C and D, speed exerted a larger effect on the oscillation frequency of place cells relative to the spike-triggered LFP so that at a faster speed the cycle-by-cycle phase advancement of spikes (temporal phase precession) was steeper.

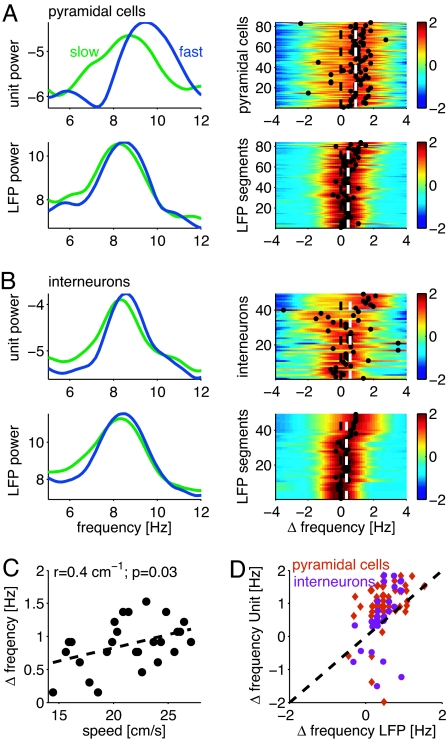
For cell-group comparison, we computed the power spectra of the spike trains of all place cells during place field crossing, interneurons during complete trials, and the corresponding LFP segments separately for fast (upper 50%) and slow (lower 50%) speed runs (Fig. 2). The oscillation frequency of place cells increased with speed in 79 of 85 (94%) place fields, and, as evidenced, the peak in the power spectra of place cells is shifted to higher frequencies for faster runs (Fig. 2A). The speed-dependent frequency increase was larger for place cells than for the LFP corresponding to the segments while the rat crossed the place fields (Fig. 2A: place cells, 0.9 ± 0.7 Hz; LFP, 0.4 ± 0.3 Hz; P = 4e-7, rank-sum test; see also Fig. 2 C and D). Furthermore, the frequency shift was larger for greater speed differences between the fast and slow trials. Although interneurons also oscillated faster at faster running speeds, the speed-dependent increase in oscillation frequency for the whole group was not significantly larger than the speed-dependent frequency increase of the corresponding LFP segments, when the spectra were computed over the entire length of the running track (Fig. 2B: interneurons, 0.6 ± 1.2 Hz; LFP, 0.3 ± 0.3 Hz; P = 0.24, rank-sum test; see also Fig. 2D and SI Fig. 8).

Fig. 2.

Speed modulates oscillation frequency of place cells. (A) (Left) The power spectra of fast (upper 50%) and slow (lower 50%) runs of a single place cell and the LFP segments during the place field crossing. The frequency shift between these spectra was determined by computing the maximum of their cross-correlograms. (Right) Most place cells show a positive frequency shift between fast and slow runs. The cross-correlograms for all place cells are normalized by their SD, and their amplitude is color-coded. The black dots mark the maxima of the cross-correlograms, and the dashed line marks zero frequency lag. The place fields are sorted by the speed difference between the fast and slow trials (ranging from Δf = 5 cm/sec to Δf = 25 cm/sec). Note the larger frequency shift for a larger speed difference (n = 84 place fields from 48 CA1 pyramidal cells). (B) Same as in A, but for interneurons. Speed difference between the fast and slow trials ranges from Δf = 4 cm/sec to Δf = 19 cm/sec (n = 20 CA1 interneurons; the two running directions were treated separately). (C) Frequency difference between neuronal and LFP oscillations as a function of speed (dots, mean of five trials). Note the positive correlation between speed and the frequency shift. (D) Frequency shifts of units as a function of the associated shifts in LFP θ. Values above the dashed line indicate a larger frequency increase due to speed for units than for the corresponding LFP. Note that most of the pyramidal cells lie above the diagonal.

Time Compression of Place Cell Sequences Is Speed-Dependent.

Previous works have shown that information about the past, present, and future positions of the animal and the distances among the respective place fields is “compressed” into time lags between spikes within a θ cycle (3, 19). The time compression is defined as a ratio of the time it takes the animal to travel between two place fields and the time lag between the spikes of the two corresponding place cells within one θ cycle (19). Because speed affected the phase vs. time slope of individual neurons, we examined whether speed also affects the temporal compression. Fig. 3A illustrates a pair of neurons with overlapping place fields. As expected, the time difference between the peak firing of the respective neurons varied as a function of running speed because during slower runs it took proportionally more time for the rat to traverse the same distance (Fig. 3 B and C). In contrast, the time offsets of the neuron pair at the time scale of the θ period was speed-independent for the population (Fig. 3D). Similarly, the phase difference of the neurons within the θ cycle remained unaffected by the speed differences (see SI Fig. 9). Because the temporal distance between place fields within the θ cycle does not depend on speed, but the travel time between place fields does, the temporal compression of place cell sequences is interpretable only if information about speed is also available.

Fig. 3.

Sequence compression of place cells varies as a function of speed. (A) Tuning curves of two place cells (P1, P2) with overlapping fields and a distance d between field centers. (B) Cross-correlograms between the two neurons for slow (Left, lower 50%) and fast (Right, upper 50%) trials, low-pass filtered at 1.5 Hz (time scale of travel time between place fields) and 40 Hz (time scale of θ). The peak of the cross-correlogram filtered at 1.5 Hz indicates the travel time between the centers of two place fields. (C) The cross-correlograms filtered at 1.5 Hz from B for fast and slow trials. (Left) It takes Δτ longer to cross between the place fields in slow runs than in fast runs. (Right) This travel time difference Δτ is linearly correlated with the distance d between the place fields, as shown for all cell pairs. (D) (Left) The cross-correlograms filtered at 40 Hz from B for fast and slow trials. (Right) The time difference Δτ_θ between the fast and slow trials within one θ cycle does not depend on the distance d, as shown for all cell pairs. For all group plots, n = 96 place fields of 55 CA1 pyramidal cells were used, corresponding to 801 pairs.

Interneurons Shape Cell Assemblies.

Interneurons form heterogeneous groups (20), and identification of group members by physiological criteria alone is not always possible (21). Consequently, we could not rationally cluster all individual interneurons into subgroups. When viewed as a single group, the oscillation frequency of most interneurons also increased with speed (Fig. 2 B and D). However, in agreement with previous observations, several interneurons showed definable place fields, although these were typically multiple and less pronounced than those of the pyramidal cells (22, 23, 25, 59). Because spike-transmission probability between place cells and interneurons can be quite reliable (23, 26, 27), it is expected that some spikes emitted by interneurons are driven by their presynaptic place cells (59). In support of this hypothesis, we found that 8 of the 25 interneurons showed phase precession in at least one location of the track (Fig. 4).

Fig. 4.

Interneurons segregate place cell assemblies. (A) Firing rates of two pyramidal cells (red, P1; magenta, P2) and an interneuron (black, IN) as a function of distance on the running track. (B) Phase precession of interneuron spikes. The interneuron's color-coded smoothed density of firing is plotted as a function of θ phase and the rat's position on the track. Phase distributions are shown twice for better visibility. Stars and dots indicate the running mean phase of P1 and P2, respectively. Note the similar phase slope of P1 and the interneuron. (C) Temporal cross-correlation between P1 and interneuron IN and P2 and the same interneuron IN. Note the opposite phase relationship of P1 and P2. The dashed lines indicate the 95% confidence interval (C.I.) for shuffled spike trains such that the phase is conserved. Distribution that exceeds the C.I. is significantly more correlated or anticorrelated than could be expected simply by common phase locking. (D) Autocorrelogram, θ-spike cross-correlogram, and ripple-spike cross-correlogram of the interneuron. (E) Autocorrelogram of the interneuron's spike phases during 10% slowest (five trials, average speed 19 cm/sec) and 10% fastest (five trials, average speed 40 cm/sec) runs across the field marked by black arrows in B. (F) Superimposed autocorrelograms of spike times of the same trials as in E and the spike-triggered average (using all spikes from the slow and fast trials, respectively) of the related θ oscillation from the CA1 pyramidal layer during slow and fast runs across the field marked by black arrows in B. Note the steeper phase advancement of the interneuron spikes during faster speed.

Even interneuron–pyramidal cell pairs that were not directly monosynaptically connected (Fig. 4) showed comparable phase precession and correlated firing (cell P1 and interneuron in Fig. 4 A–D), suggesting that both cells belonged to the same cell assembly and their spiking was timed by some common input. In contrast, interneuron–pyramidal cell pairs with anticorrelated discharge within the θ cycle had shifted place fields (cell P2 and interneuron in Fig. 4 A–D) and likely belonged to different, competing assemblies. The consequence of this interaction is that an interneuron driven by a place cell can exert a precisely timed inhibition on other pyramidal cells and effectively segregate the current assembly from other competing assemblies.

Interneurons that displayed phase precession showed an increased oscillation frequency beyond that of LFP, with increased running speed within their place fields similar to what was found for pyramidal cells (compare Fig. 1 C and D with Fig. 4 E and F). The overall speed-dependent frequency change of interneurons within their place fields was comparable to that of pyramidal cells (compare Fig. 2A with Fig. 5).

Fig. 5.

Oscillation frequency of phase-precessing interneurons is speed-dependent. The power spectra are calculated only for spikes and LFP during segments when the rat crosses the interneuron's place field (compare with Fig. 2B). Interneurons increase their oscillation frequency significantly more with faster running speed than the LFP [interneurons, mean (Δf) = 0.8 ± 0.7; LFP, mean(Δf) = 1.5 ± 0.9; P < 0.01]. Fields were sorted according to the speed difference between fast and slow trials (speed differences ranged from 5 to 25 cm/sec). Spectra were computed for 12 place fields of eight interneurons.

Some interneurons showed no indication of phase precession, but instead displayed a relatively fixed-phase relationship with the θ cycle (Fig. 6). The illustrated cell's preferred θ phase of discharge (circular mean phase 297°), its increased firing preceding sharp-wave ripples, and its location above the pyramidal cell layer suggest that it may correspond to an oriens lacunosum-moleculare or long-range interneuron (21). Thus, some interneuron classes may keep a fixed θ-phase relationship, whereas other types can be effectively driven by place cell assemblies.

Fig. 6.

Nonphase-precessing interneuron. (A) Firing rates of two pyramidal cells (red, P1; magenta, P2) and an interneuron (black, IN) as a function of distance on the running track. (B) The spikes of the interneuron are locked to a small phase range (compare Fig. 4). The circular mean phases of the two simultaneously recorded pyramidal cells are marked with red dots and magenta stars, respectively. (C) Temporal cross-correlograms between P1 and interneuron IN and P2 and the same interneuron IN. Note that both pyramidal cells are anticorrelated to the activity on the interneuron. The dashed lines give the 95% C.I. for phase locking; cross-correlograms exceeding this C.I. have a significant correlation beyond phase locking. (D) Autocorrelogram, θ-spike cross-correlogram, and ripple–spike cross-correlogram of the interneuron.

Discussion

The main finding of these experiments is a correlation between speed and oscillation frequency of hippocampal place cells and interneurons. We hypothesize that the “gain” of the oscillation frequency of pyramidal cell–interneuron assemblies with respect to speed can account for the invariant travel distance vs. spike–phase relationship. This hypothesis offers a novel perspective on the cell assembly coordination by hippocampal θ oscillation. We hypothesize that the combination of speed and spatial inputs gives rise to a transient oscillation of sequentially activated cell assemblies. Phase precession is a consequence of this more fundamental mechanism.

Speed-Dependent Oscillation of Place Cells Can Keep the Spike Phase Versus Position Relation Invariant.

Previous experiments have shown that the phase precession slope of place cells correlated with the size of its place field (7, 19, 28) so that the total phase precession is always about one full θ cycle, and that both the phase precession slope and field size increase along the septotemporal axis of the hippocampus (29). It has been suggested that phase precession can be produced by faster oscillating pyramidal cells than the LFP, and it has been shown that the phase–space relationship is speed-independent (2), but no mechanisms were provided. Here we directly show that the temporal-phase precession slope, and therefore the oscillation frequency of place cells, is positively correlated with the locomotion speed of the rat, such that the phase–distance relationship remains invariant.

One possible explanation for the speed effect on the oscillation frequency of place cells is that the frequency is controlled by the activation of voltage-dependent intrinsic mechanisms that support oscillations in single pyramidal cells (5, 8, 9, 13, 30–34). However, this individuated oscillation cannot account for several experimental observations (7, 24, 35). As an alternative, we hypothesize that simultaneously activated neurons interact and form oscillating assemblies whose oscillation frequency is controlled by afferents that correlate with the locomotion speed of the animal.

The phase of spikes within the θ cycle correlates with a number of variables, including the position of the animal, the time from the beginning of the run, the time since entering the place field, and the instantaneous firing rate of the neuron (2–4, 6, 7, 36). Because the strongest correlation occurs between position and spike phase (7), it has been suggested that the spike phase is determined by sensory inputs, and that the spike-phase precession phenomenon can be regarded as a mechanism for coding the spatial relations between environmental signals (2, 3, 7, 16, 36, 37). However, it is not clear what mechanism is responsible for aligning the environmental signals to the phase of the internally generated θ rhythm. Furthermore, the slope of the phase precession remains the same in the dark (38), eliminating the crucial role of visual cues in the spike phase.

An alternative explanation for the strong phase–position correlation is that environmental, idiothetic, or internal cues trigger a transient oscillation in a unique cell assembly. We assume that assembly oscillation of place cells is a transient phenomenon, lasting for ≈1 sec in the dorsal hippocampus (7, 19, 39). The oscillation frequency of an active place cell assembly is under the control of speed inputs as shown here. If the running speed is constant, the cycle-by-cycle phase shift (i.e., the temporal-phase precession determined by the frequency of the oscillating assembly) and the phase–distance relationship provide the same accuracy in predicting distance (8, 13). However, because the speed variability, the temporal-phase precession, and the phase–distance relationship are out of register, it is necessary to tune the oscillation frequency of the activated cell assembly as shown here. The result of this adjustment is that the spike-phase assignment remains invariant relative to travel distance.

However, it remains unanswered what tunes the oscillation frequency precisely, such that phase precession spans ≈1 full θ cycle and starts at the same phase. One possibility is that the phase-precessing assemblies should not be viewed as independent units, but as part of the rhythm-generating mechanism. The transiently oscillating cell assemblies may be coupled through variable delays so that the successive oscillators are trailing relative to each other (40). By way of this hypothetical mechanism, place cells may play a critical role in θ-rhythm generation, although they individually oscillate faster than the θ field.

Distance Representation by Time Compression Is Speed-Dependent.

In the CA1 region of the hippocampus, the ordered spatial distances between sequential locations are represented by multiple assemblies and “compressed” into the θ cycle because of the location-specific phase segregation of cells (3, 19, 36, 41). It has been suggested that the distances between place fields, represented by the respective assemblies, are encoded by the synaptic strengths between CA3-CA3 and CA3-CA1 connections (42). A prediction of this hypothesis is that the temporal intervals of assembly sequences within θ cycles should reflect distance representations, independent of other variables, such as the speed of motion. Our observations confirm this prediction. The temporal relationship of cell pairs within the θ cycle, representing distances, remained constant within the natural variability of running speed. Because the θ scale–time relationship between cell pairs is fixed, whereas the elapsed time required to run from one place field to the other depends on the speed of locomotion, the magnitude of temporal compression should vary as shown here. Thus, the magnitude of temporal compression is informative only if corrected by the speed.

Without speed information, the discharge rate of place cells alone is ambiguous for defining the animal's current location because the firing rate of hippocampal place cells is correlated with speed (25, 43, 44). Conversely, the discharge rate of pyramidal cells may not independently “code” for speed either (but see refs. 7 and 37) because the rate is a combined effect of speed and the rat's position. Instead, we hypothesize that the assemblies that receive similar information (representing the same location) will oscillate at a similar speed-adjusted frequency and synchronize with a constant phase–time relationship.

Interneurons Contribute to the Formation of Cell Assemblies.

Further support for the assembly representation of external information in the hippocampus is the phase precession of interneurons. Although interneurons are usually not considered to carry specific information, several previous studies have noted that interneuron spikes are not distributed homogeneously over the visited places (22, 25), and interneuron firing rates can vary specifically with task demands (45).

A potential mechanism responsible for the place-specific firing and phase precession of some interneurons (see also ref. 59) is the firing-frequency tunability of the pyramidal cell–interneuron synapse (23, 46–48) and their low-discharge threshold (26, 27). Furthermore, soma targeting interneurons are endowed with resonant properties that allow them to respond maximally when presynaptic neurons fire in the γ-frequency range (23, 34), whereas dendrite-targeting interneurons respond best at θ frequency (49, 50). Therefore, the recruited interneurons have the ability to segregate small assemblies of principal cells by temporarily silencing competing assemblies.

We hypothesize that, within the place field, perisomatic interneurons are entrained to the fast-firing place cells, and the spikes of the formed assembly members oscillate coherently. As shown here, the magnitude of the cycle-by-cycle temporal shift of spikes is controlled by speed. Conversely, during episodes where the interneuron does not phase precess, it might receive input from many place cells equally. Because the highest firing probability of place cells is at the trough of θ, the interneuron receives the strongest input at the trough of θ during each cycle. We hypothesize that interneurons phase precess only when a particular place cell assembly dominates their drive.

The absence of phase precession in some interneurons may be explained in two different ways. First, all interneurons show phase procession when driven exclusively or predominantly by a given oscillating cell assembly. Under this hypothesis, our failure to observe phase precession in every interneuron might be explained by not testing the neuron exhaustively in multiple environments. Second, dendrite-targeting interneuron types are not effectively recruited by place cells. Our finding that some interneurons showed a very narrow phase preference of spiking is in favor of this possibility. It will be important in future research to determine the anatomical identity of such θ phase-fixed interneurons.

The speed-controlled assembly oscillator hypothesis, as opposed to the individuated cell oscillator (4–6, 8, 9, 13, 32), can explain why on individual trials with dramatically different firing rates the spatial-phase precession slope of single place cells can remain unaltered (7). Rate variability can occur because assembly oscillation is a cooperative product where timing of spikes remains robust despite the variation of individual firing rates (51–53). In addition, the oscillating cell assembly hypothesis can also account for the observation that spikes of single place cells can switch assembly membership even within a single θ cycle (24).

Methods

Experimental Procedures.

Six adult male Long-Evans rats (250–300 g) were implanted with either movable tetrodes in the hippocampus (35) or silicon probes (54) following National Institutes of Health guidelines. They were trained to shuttle back and forth between two water cups on a U-shaped maze (35) or on an elevated circular maze (55). Two small light-emitting diodes (10-cm separation) mounted above the head stage were used to track the rats' positions (sampled at 40 Hz).

Data Acquisition and Analysis.

Wide-band (1 Hz–5 kHz) signals were acquired at 20 kHz on a 64-channel DataMax system (RC Electronics, Santa Barbara, CA). For offline spike sorting, the wide-band signals were digitally high-pass filtered (0.8–5 kHz). Units were then identified and isolated by a semiautomatic cluster-cutting algorithm (56, 57).

Cell Identification and Place Fields.

Cells were classified into putative interneurons and pyramidal cells by their firing rate, autocorrelogram, and spike-wave shape (26). Pyramidal neurons without clearly defined place fields (4) were not included. The place field was defined as the continuous area in one direction of running within which the firing rate was >0 or when the neuron would fire over large parts of the maze, >10% of the maximal firing rate (7). The place fields of interneurons that showed clear phase precession were selected manually. A total of 96 place fields of 55 CA1 pyramidal cells were analyzed. Further, 25 interneurons were included in this study. Different directions of running were treated separately, resulting in 49 interneuron firing fields. For the analysis of interneurons in Fig. 5, episodes of phase precession were selected manually when phase precession was clearly visible. The firing within those place fields was then analyzed identically to that of pyramidal cells.

Running Speed.

The instantaneous running speed was calculated offline from the rat's position on the maze. The speed was low-pass filtered to eliminate large speed changes due to the rat's head movement. Because running speed varied in different parts of the testing apparatus and the size of the place fields showed large variability, even for neurons recorded with the same electrode (19), the measurement of the rat's speed was restricted to the place field.

Speed-Dependent Trial Sorting.

Trials were sorted by direction and average speed. Trials in which the rat did not complete the full path or stopped for exploration were discarded. The maze was linearized semimanually by orthogonally projecting all position points onto the averaged trajectory of the rat. To investigate the differences between fast and slow runs, the fastest 50% and slowest 50% were used unless mentioned otherwise.

Spectral Analysis and Frequency Shift.

The spectra were computed by using multitaper estimators (58). The spectra were averaged across the 50% slowest and 50% fastest trials, respectively. To compute the speed-dependent frequency shift between units and LFP, we computed the cross-correlograms between the spectra and determined the frequency lag of the maximal correlation.

Distance Between Place Fields.

The temporal relationship between overlapping place cells on the time scale of place field crossing and within a θ cycle was computed for fast and slow trials separately as described in ref. 19. The phase relationship between cells was determined by computing the cross-correlogram of the unwrapped θ phase of each spike.

Abbreviations

C.I.

confidence interval

LFP

local field potential.