Structural analysis of viral nucleocapsids by subtraction of partial projections

Abstract

The nucleocapsid of flavivirus particles does not have a recognizable capsid structure when using icosahedral averaging for cryo-electron microscopy structure determinations. The apparent absence of a definitive capsid structure could be due to a lack of synchronization of the symmetry elements of the external glycoprotein layer with those of the core or because the nucleocapsid does not have the same structure within each particle. A technique has been developed to determine the structure of the capsid, and possibly also of the genome, for icosahedral viruses, such as flaviviruses, using cryo-electron microscopy. The method is applicable not only to the analyses of viral cores, but also to the missing structure of multicomponent complexes due to symmetry mismatches.

The density contributed by external glycoprotein and membrane layers, derived from previously determined three-dimensional icosahedrally averaged reconstructions, was subtracted from the raw images of the virus particles. The resultant difference images were then used for a three-dimensional reconstruction. After appropriate test data sets were constructed and tested, the procedure was applied to examine the nucleocapsids of flaviviruses, which showed that there is no distinct protein density surrounding the genome. Furthermore, there was no evidence of any icosahedral symmetry within the nucleocapsid core.

1. Introduction

There is now a large body of information about the structure of icosahedral viruses based on both crystallography and electron microscopy (EM). However, the genome of these viruses consists of one or a few nucleic acid molecules that lack the symmetry of the capsid. The process of crystallization is dependent on the external icosahedral symmetry of the particles. Hence, the virus is unable to maintain a similar orientation of the genome within the crystal, assuming that the genome has a unique structure. Similarly, when combining EM images of icosahedral virus particles, their relative orientations are dominated by the external capsid. Thus, both methods, as practiced at this time, produce three-dimensional density of the virus in which the genome is averaged out to some low uniform density. Whether or not there is a unique structure of the nucleic acid within the viral capsid remains unknown. However, in some special cases such as cowpea mosaic virus (CpMV) (Chen et al., 1989), nodaviruses (Tihova et al., 2004) and especially satellite tobacco mosaic virus (STMV) (Larson et al., 1993), a proportion of the genome becomes associated with the internal surface of the icosahedral capsid and, hence, the genome adopts a significant amount of icosahedral symmetry. Indeed, for STMV, about 44% of the genome can be recognized in the crystal structure.

Attempts at orienting viruses by use of gravitational or electrostatic forces during crystallization have failed. However, the growing power of cryoEM reconstruction may make it possible to determine whether the structure of some viral genomes have a unique fold. This should be possible by subtracting the known capsid structure from the observed projections of the cryoEM particle images and then performing an asymmetric reconstruction using the difference images. This “re-projection-subtraction” method was used in the study of the inner scaffolding protein of phage φ29 (Morais et al., 2003) and the external, symmetry mismatched, components of Kelp fly virus (Briggs et al., 2005). A somewhat similar procedure has also been applied to the study of viral DNA in herpes simplex virus, although, in this case, no further three-dimensional density analysis was pursued of the difference. (Baker et al., 1990; Booy et al., 1991). In the above examples, the critically important scale factors between the raw images and the corresponding calculated images were determined either with a least-squares method (Morais et al., 2003) or by matching the mean and the variance of the observed and calculated densities (Baker et al., 1990; Booy et al., 1991). The procedure has now been used to study the structure of flavivirus cores.

Flaviviridae is a large family of enveloped RNA viruses. Their RNA genome is a single positive strand, approximately 11 kB long, that contains one long open reading frame (Lindenbach and Rice, 2001). The three structural proteins, the capsid (C), precursor membrane (prM), and envelope (E) proteins, are assembled into immature particles when the nucleocapsid core buds to the lumen of the endoplasmic reticulum (ER) containing the E and prM proteins (Lindenbach and Rice, 2001). Maturation is initiated when furin cleaves prM, resulting in a rearrangement of the E proteins (Zhang et al., 2003b), and activates the virus for subsequent entry and fusion.

The C protein of flaviviruses, like many other nucleocapsid proteins, is highly basic. In many naked RNA plant viruses, as well as the enveloped alphaviruses, the C protein has an N-terminal, basic region that neutralizes the packaged genome. Thus, the small, about 100, amino acids of the flavivirus C protein might act in a similar manner, suggesting it would be closely associated with the RNA genome. Nevertheless, crystallographic and NMR studies show that the flavivirus C protein has a unique structure (Dokland et al., 2004; Ma et al., 2004).

CryoEM studies have shown that, unlike alphaviruses, neither mature (Kuhn et al., 2002; Zhang et al., 2003a) nor immature (Zhang et al., 2003b) flavivirus particles appear to have a capsid structure surrounding the genomic RNA, notwithstanding the ability of the C protein to fold into a unique structure. Possibly (1) the nucleocapsid structure is icosahedral, but its symmetry axes do not align with the dominant external glycoprotein shell; or (2) the nucleocapsid has an asymmetric structure that is the same in every particle; or (3) the nucleocapsid has a different structure in each virion.

In this paper, we have investigated the three-dimensional structure of flavivirus cores using the re-projection-subtraction procedure. A new technique was developed to scale the raw images to the calculated images of the external region. We have shown that the absence of a recognizable C protein in immature or mature dengue virus (DENV) cryoEM reconstructions is not the result of assuming icosahedral symmetry of the nucleocapsid core. However, there were insufficient cryoEM data to determine whether the nucleocapsid has the same unique, but asymmetric, structure in each particle.

2. Results

2.1. Development of the reconstruction technique

Single particle cryoEM reconstruction of spherical viruses usually assumes icosahedral symmetry. The orientation of each particle is defined relative to a standard icosahedral axial system. This process is biased by the dominant structural features of the virus, such as the ectodomain of flaviviruses. Therefore, some structural components may be averaged-out during the reconstruction if they do not have icosahedral symmetry or do not match the icosahedral symmetry of the dominant structure. If the less dominant features are located inside the dominant external icosahedral layers, the central area of the observed two-dimensional (2D) images is a co-projection of both external and internal components. In order to obtain structural information for the less dominant features, it is necessary to mask the more dominant icosahedral components in the 2D images. A four-step procedure was developed to isolate the projected density of the core from that of the external dominant glycoprotein layer,

1. A reconstruction of the whole particle was performed assuming icosahedral symmetry (Baker and Cheng, 1996; Baker et al., 1999). This provided the three-dimensional (3D) density distribution of the dominant external layer. Therefore, the projected density of this external layer could be calculated using the known orientation of the external layer for each individual 2D cryoEM image.

2. The calculated 2D projections of the external layer were subtracted from the processed 2D images of the whole virus particles (see Materials and Methods). These difference images were generated using the same scale factor, k, for all the images on any one micrograph. The best scale factor should produce merely noise in the external region of the reconstruction derived from the difference images using the known orientations. Hence, the scale factor appropriate for each micrograph was determined by selecting that value of k for which a 3D reconstruction using the difference images taken from that micrograph gave the lowest correlation with the original structure in the external region.

3. The difference images were subjected to multivariate statistical analysis in order to assign them to different classes (Frank, 1996; van Heel et al., 2000). The class averages were then calculated to improve the signal-to-noise ratio over the individual cryoEM images.

4. Class averages of these difference images could then be combined to produce a 3D reconstruction. The new reconstruction was then used to reassign the difference images in a projection-matching procedure. This process was repeated until there was no further improvement of the reconstruction, indicated by the convergence of the orientational and positional parameters.

2.2. Relationship between the number of images, resolution, and symmetry

If there are a total of T observed particles and if n particles are sorted on average into each class, there would be T/n classes. The orientation of the particles can be defined by two polar angles, which would need to be explored in the range of 0-2π for the first angle and 0-π/2 for the second angle in order to cover all orientations of an asymmetric object. These orientations can be represented by a radius vector mapped onto the surface of a hemisphere of radius r. Assuming that the angular interval between classes is Δ radians, then the number of required classes would be the area of the hemisphere (2πr²) divided by the area $(\sqrt{3}∕2){\left(r\Delta \right)}^2$ of the elementary rhombus representing a change, Δ, in both angles. Thus, the total number of classes would be $\left(4\sqrt{3}\pi \right)∕\left(3{\Delta }^2\right)$.

Hence, $T∕n=\left(4\sqrt{3}\pi \right)∕\left(3{\Delta }^2\right)$or

$$\Delta =\frac{2}{\sqrt[4]{3}}\ast {\left(\frac{n\pi }{T}\right)}^{1∕2}$$ (2.2.1)

If the particle had icosahedral symmetry, it would only be necessary to explore (1/60)^th of the surface of the hemisphere, equivalent to using only T/60 particles to achieve the same angular increment, Δ, between classes. Hence, for an icosahedral object

$$\Delta =\frac{2}{\sqrt[4]{3}}\ast {\left(\frac{60n\pi }{T}\right)}^{1∕2}$$ (2.2.2)

(Note that Δ and the particle radius both contribute to the final resolution of the reconstruction.)

An empirical procedure was used to establish the effective resolution of a specific object when classes were separated by an angle Δ. The specific asymmetric object chosen for this purpose was yeast ribosome, which has a maximum diameter of about 300 Å, roughly the same as the diameter of flavivirus nucleocapsid core density. Two projections of the ribosome structure, separated by Δ, were computed. The Fourier coefficients of the resultant densities were compared as a function of resolution. Consistent with usual practice in the analysis of EM reconstructions, the resolution attainable by using classes separated by the given angle was then taken to be the point where the correlation between the Fourier amplitudes of neighboring classes fell below 0.5 (Table 1). These results were more or less independent of the chosen projection and can be assumed to be similar for any particle of about 300 Å diameter. Although these results were computed without considering the impact of noise on individual images, the noise effect will diminish proportionally to $\sqrt{n}$ as the number of images, n, in each class is increased. As the particles, in general, are not equally distributed in all orientations, it may require somewhat more particles than would be suggested by Table 1 to produce a reconstruction at a resolution corresponding to the angular separation of the classes.

Table 1.

The angular separation^a, Δ, in degrees versus resolution^b

Δ (°)	Resolution (Å)	Calculated number of classes [see (2.2.1)]
4	12.3	1489
5	15.7	953
6	18.2	662
7	23.0	486
8	26.9	372
9	30.7	294
10	35.8	238
12	42.3	165
14	51.4	122

^aThe table was computed for particles with about 300 Å diameter. The attainable resolution should be multiplied by (300/D), where D is the diameter of the particle under consideration.

^bA series of projections were calculated from the atomic structure of the yeast ribosome (PDB accession numbers 1S1H and 1S1I) using the angular separation Δ in the range of 4-14°. The FSC between two neighboring projections were calculated, and the resolution was established using the FSC cut-off of 0.5.

Table 1 shows, for instance, that to attain a resolution of 25 Å, the angular difference between different classes, Δ, should be no greater than 7.5° for asymmetric objects with a similar size to ribosomes, assuming no noise. From (2.2.1), it is seen that the number of classes (T/n) would have to be about 420. If the signal-to-noise ratio on the observed image is 1:e_r at the desired resolution, then in order to achieve a signal greater than the noise, it is necessary to have $n>{\mathrm{e}}_{\mathrm{r}}^2$. For instance, about 36 images would be required if the signal-to-noise ratio is about 1:6 at 25 Å resolution. Hence, assuming about 36 images per class (n), there would need to be at least 15,000 particles to achieve about 25 Å resolution when considering the reconstruction of particles that have an approximate diameter of 300 Å. Similarly, from (2.2.2), only about 300 particles would be required to determine the structure of an icosahedral object to the same resolution.

Only about 4600 and 1700 observed cryoEM images were available for immature and mature DENV, respectively. Assuming n is required to be about 36, Δ would be about 14° from (2.2.1) when performing a reconstruction of an asymmetric object. This would correspond to ∼50 Å resolution (Table 1) for the more abundant immature particles, insufficient to determine whether the nucleocapsid has a unique asymmetric structure. However, if the nucleocapsid core had icosahedral symmetry, then Table 1 and Equation 2.2.2 show that it would be possible to achieve a resolution of better than 10 Å, roughly consistent with experience (Zhang et al., 2003a).

2.3. The test data sets

A data set of 2D images was simulated by combining the external dominant glycoprotein layer of DENV with an internal nucleocapsid core represented by the known CpMV structure (Lin et al., 1999; Zhang et al., 2003b) (PDB accession number 1NY7). The CpMV structure was chosen because its external diameter is about 300 Å, very similar to the diameter of the nucleocapsid core of DENV. The symmetry of the internal CpMV core was randomly oriented with respect to the symmetry axes of the external shell. Noise was added in a two-step procedure as described in Materials and Methods (Fig. 1). The signal-to-noise ratio was set at 1 to 20 within the 200 to 16 Å resolution range, much worse than the corresponding value of 1 to 3 in the immature DENV cryoEM images calculated by a procedure described by J. Frank et al. (Frank et al., 1981). This corresponds to the signal-to-noise ratio being 1:20 in the test data set and 1:6 in the observed immature DENV data set at 25 Å resolution.

Fig. 1.

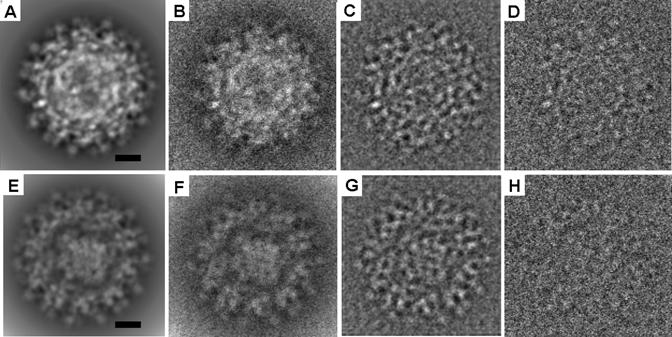
Simulated images of the test data sets. (A) A representative theoretical projection of the CpMV test data set. (B) The same as (A) but with added noise to obtain the signal-to-noise ratio of 1:1. (C) The same as (B) after applying the CTF. (D) The same as (C) except more noise was added to the image to make the signal-to-noise ratio of 1:20. (E), (F), (G), and (H) correspond to (A), (B), (C), and (D), but use the ribosome test data set. The scale bar represents 100 Å.

The test procedure was initiated by subtracting the external immature DENV glycoprotein structure from the simulated images (Materials and Methods) given the original determination of the particle orientations. The resultant, approximately 4600 difference images were then divided either into 100 classes, averaging about 46 images per class, or into 200 classes, giving 23 images per class. Both these classification procedures gave similar results. Class averages of the difference images showed a high density ring between radii of about 110 to 145 Å, consistent with the annulus occupied by the CpMV capsid protein. The correlation coefficient between the class averages and the corresponding 2D projections of the CpMV atomic model was about 0.65, using the data within the resolution range of 20-150 Å. The resultant icosahedral reconstruction (Table 2 and Fig. 2) of CpMV particles resembles the original structure, with a correlation of ∼0.7 to 25 Å resolution. This demonstrates that the above proposed approach works well even for a test data set that was much nosier than is usually encountered.

Table 2.

Classifications of various data sets

Data set	Number of particles	Number of classes	Resolutiona (Å)	Annulusb (Å)	Resolution of final 3D model (Å)
Nucleocapsid cores of immature DENV	4602	423	50	110-150	-
		100	45	110-150	-
			54	10-150	-
Nucleocapsid cores of mature DENV	1691	80	70	110-150	-
			61	10-150	-
The CpMV test data set	4602	100	30	110-150	20
	1691	80	32	110-150	-
The ribosome test data set	15,000	423	32	10-150	24
	4602	100	41	10-150	-
Whole immature DENV	4602	100	28	10-280	16

^aThe members within one class were randomly grouped into two sets, followed by the calculation of the FSCs between the average of each set. The resolution was determined using a FSC cut-off of 0.5.

^bThe classification was performed using only the pixels within the stated annulus.

Fig. 2.

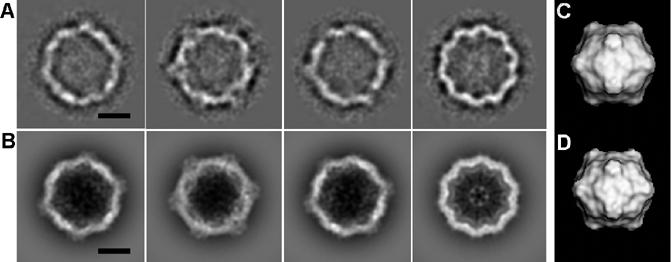
Test using the CpMV data set. (A) Four class averages of difference images that have the highest FSCs. (B) Projections of the atomic structure calculated to 20 Å resolution with orientations corresponding to (A). (C) 3D reconstruction of the CpMV core using the difference images. (D) The structure of CpMV calculated to 25 Å resolution in the same orientation as (C). The scale bar represents 100 Å.

Another test data set was generated to simulate 2D projections of particles with an external icosahedral layer and an internal structure lacking any symmetry. The structure of yeast ribosomes was used for this purpose (PDB accession numbers 1S1H and 1S1I (Spahn et al., 2004)) because its maximum radius is about 150 Å, which fits well into the internal cavity of DENV. The subtraction, classification procedure and noise addition were performed as before except that the number of classes and images was increased to about 423 and 15,000, respectively. The resultant reconstruction at 25 Å resolution clearly showed that the reconstruction resembled the original structure, with a correlation of 0.6 (Table 2 and Fig. 3).

Fig. 3.

Test using the ribosome data set. (A) Four class averages of difference images that have the highest FSCs. (B) Projections of the atomic structure calculated to 20 Å resolution with orientations corresponding to (A). (C) 3D reconstruction of the ribosome core using the difference images. (D) The structure of ribosome calculated to 25 Å resolution in the same orientation as (C). The scale bar represents 100 Å.

2.4. Nucleocapsid core of flaviviruses

The above method was used for the structural analysis of the internal nucleocapsid core of both mature and immature flavivirus particles. The results were similar for both cases. However, the number of images of immature virus particles (about 4600) was much greater than that of mature particles (about 1700), making the classification of cores for immature particles more reliable. Therefore, only the results for the immature particles are discussed here.

Visual inspection of the class averages of difference images, representing the nucleocapsids of immature particles, showed little structural detail, compared to those of the raw images of immature particles or to those of the CpMV test data set (Figs. 2 and 4). The grouping of the difference images of the flavivirus nucleocapsid cores had not converged even after 20 cycles of classification, whereas ten cycles were sufficient to classify the raw images of the original immature particles and the difference images of the test data set. In addition, there was greater variability of density between the members of each class (Table 2). This suggests that the flavivirus nucleocapsid core does not have a unique icosahedral structure. Another explanation of the greater variability of images in each class might be that after removing the external glycoprotein layer, the classification process is dominated by the genome structure (∼3.5 MDa) in the remaining difference density. Thus, even if there were an icosahedral capsid layer (∼2 MDa) in the nucleocapsid core, it would be lost in the class-averaging process. In order to exclude this possibility, the classification was attempted based only on the projected density values in an outer annulus (110-150 Å) for each 2D difference image. However, the resultant classification did not improve (Table 2 and Fig. 4). Hence, there appears to be no distinct icosahedrally symmetric layer surrounding the genome in the nucleocapsid.

Fig. 4.

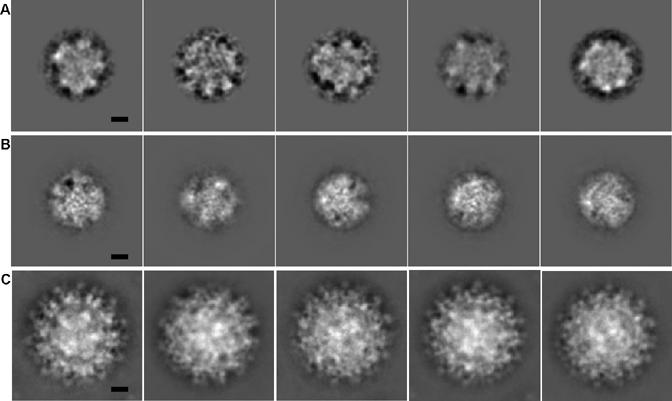
Five selected class averages that have the highest FSCs: (A) nucleocapsid cores of immature DENV, (B) nucleocapsid cores of mature DENV, and (C) immature DENV. The scale bar represents 100 Å.

To confirm the above conclusion, half of the class averages were selected to make an initial reconstruction using the self-common line procedure as described for the test CpMV data set. However, unlike the test data set, the orientation and position of each nucleocapsid core was not stable, even after 30 cycles of refinement. Similar results were also obtained when the same procedures were performed on difference images using only density values within an annulus (as described above) to exclude much of the RNA.

Although the above results showed that the nucleocapsid of DENV does not have icosahedral symmetry, it could have a unique asymmetric structure that is the same in each particle. To investigate this possibility with the available 4600 cryoEM particle images, using the same classification procedure as used in the test ribosome data set, would have led to a resolution of about 48 Å (see Section 2.2). Thus, it was not possible to determine whether the DENV nucleocapsid cores had the same unique structure in each particle with the available data set.

3. Discussion

3.1. Method implications

The most critical part in the re-projection-subtraction technique is to determine the best scale factor between the observed image projection and the calculated projection of the known external structure. An independent least-squares fit between the two projections for each image was found to be unsatisfactory, as shown by a reconstruction of the resultant difference images having a fairly strong remnant of the external glycoprotein structure. Another unsuccessful technique was to standardize the density, ρ, of each image to ρ-<ρ>/σ, where <ρ> is the mean density of the pixels in the image and σ is their standard deviation. Both these methods proved to be unsuccessful, probably because of the large amount of noise in each individual image. The method described here assumes the same scale factor for each image, thus reducing the influence of noise in a single micrograph, and aims at minimizing the icosahedral impact of the difference density. However, this method requires a large number of particle images on each micrograph as these are required to make an initial reconstruction of the difference densities. Although this process is aided by high symmetry of the particles, effectively multiplying the number of difference images by the redundancy of the symmetry, the method is quite general.

The results demonstrate that it will be necessary to collect a very large number of particle images in order to determine whether a viral genome of an icosahedral virus has a unique structure. No such study has yet been completed, leaving open for now the question of whether some icosahedral viruses have a unique genome structure.

3.2. Biological implications

Unlike alphaviruses, it appears that flaviviruses lack an ordered capsid protein shell separating the lipid envelope from the RNA genome. Furthermore, in flaviviruses there is little, if any, specific interaction between the glycoprotein ectodomain and the capsid protein molecules (Zhang et al., 2003a). Furthermore, the transmembrane helices of the E and prM proteins do not penetrate beyond the inner leaflet of the lipid bilayer (Zhang et al., 2003a; Zhang et al., 2003b), showing that there is no explicit interaction of the external icosahedral glycoprotein layer with the nucleocapsid. In contrast, when alphaviruses assemble, the nucleocapsid cores are preformed in the cytoplasm and then bud out of the plasma membrane while interacting with the external glycoproteins. In addition, there are at most 180 copies of the 100 amino acid-long capsid protein molecules per virion in flaviviruses, too small and too few to be able to form a closely-packed protein layer. In comparison, alphaviruses utilize 240 copies of a protein that uses 150 amino acids to form a well-ordered capsid to encompass the 11 kB-long RNA genome.

Apart from one possible exception (Ng et al., 2001), no cores or other capsid intermediates have been observed in the cytoplasm of flavivirus-infected cells, Thus, cores are probably assembled concurrently with the acquisition of the envelope from the ER membrane. Therefore, a preformed nucleocapsid core would not be required for the budding of the flavivirus particles, consistent with the production of recombinant flavivirus subviral particles without the capsid protein (Allison et al., 1995; Fonseca et al., 1994; Konishi et al., 1992; Pincus et al., 1992).

Lack of sufficient data made it impossible to determine whether the nucleocapsid complex of flaviviruses has the same unique structure in each virion, but the cryoEM technique to determine this has been established. Furthermore, this technique can also now be used to examine the genome structure of many other icosahedral viruses.

4. Materials and Methods

The programs used for all of the following procedures were taken from SPIDER, an EM reconstruction package (Frank et al., 1996), unless otherwise indicated.

4.1. Production of test data set

The electron density of CpMV (Lin et al., 1999) was calculated from atomic coordinates (PDB accession number 1NY7) using EMAN (Lin et al., 1999; Ludtke et al., 1999). The density of the flavivirus external protein layer was scaled with that of the capsid layer of CpMV to have the same mean value and standard deviation. The external glycoprotein layer of the immature flaviviruses and the structure of CpMV were then projected to produce separate 2D images. These projections were then randomly combined, resulting in a lack of synchronization of icosahedral symmetry axes between the external and internal structures. The center of the CpMV projections were randomly moved by up to 5 pixels (where pixels were separated by 4.24 Å) from that of the projected external structure. The centers of the combined projections were randomly moved by up to 10 pixels from the center of the box. The resultant 2D images were then added to noise images that had been generated from cryoEM images of ice to make a 1:1 signal-to-noise ratio (Fig. 2). A total of 4600 images were randomly grouped into 26 sets, each representing one micrograph. Images in each set were multiplied by a scale factor and convoluted with a contrast transfer function (CTF), corresponding to the scale factor, defocus values, and temperature factors found for the images that had been used in the reconstruction of immature flavivirus particles. Finally, additional noise images were added, making the final signal-to-noise ratio of 1:20.

Another test data set was generated using the above procedure except the internal structure was represented by the ribosome structure of yeast (Spahn et al., 2004). This data set consisted of a total of 15,000 images separated into sets representing 26 micrographs.

4.2. Generation of difference images

The 2D raw images of virus particles were first CTF corrected, followed by smooth band-pass filtering to remove data outside the 16-300 Å range (Fig. 1). The center of each particle was shifted to the center of the box according to the previously determined translational parameters used for the reconstruction of immature flavivirus particles. In addition, 2D projections of the glycoprotein layer were calculated from the 3D structure of the immature particle, in which the disordered nucleocapsid core had been removed.

The preprocessed 2D images of immature DENV (ρ₁) and the 2D projections of the ectodomain glycoprotein structure calculated as described above (ρ₂) were normalized to the same mean value and standard deviation (Morais et al., 2003). The difference image was defined as (ρ₁-kρ₂) where k is a scale factor to be determined for each micrograph. A series of k values in the range of 0 to 2 were applied to create the difference images. For each k value, the difference images on one micrograph were utilized to make a reconstruction. The best k value was chosen such that the correlation between this reconstruction and the original structure of the glycoprotein layer was minimized to less than 0.001.

4.3. Classification and reconstruction using the difference images

A standard procedure (Furst et al., 2003) was used for each image to determine the center of the internal core. These images were then subject to a multivariable statistical analysis (MSA) and classified using their eigenvector components (Frank, 1996; van Heel et al., 2000). Class averages, showing different views of the particles, were calculated and used as new references for multi-reference alignment (MRA). The cycle of MRA, MSA, and classification was repeated until the classes were stable.

The similarity among members of one class was determined by the Fourier shell correlation (FSC) between the averages of two randomly separated sub-groups within this class (Table 2). The classes with high FSC, accounting for about one-half of the data, were used in the next reconstruction step. The self-common line method (Crowther, 1971; Fuller et al., 1996) was used to determine the orientation of each class average when icosahedral symmetry was expected, namely in the reconstruction of the flavivirus cores and the test data based on a CpMV core structure. Given these orientations, an initial model was reconstructed from the selected class averages. Subsequently, the origin position and orientation were refined for each difference image with the polar Fourier transform technique assuming icosahedral symmetry (Baker and Cheng, 1996). However, the cross-common line method was used to determine the relative orientation of each class average (Frank et al., 1996; van Heel et al., 2000) for the reconstruction of the asymmetric internal structure, represented by the ribosome test data and flavivirus cores. The reconstructions were performed using the filtered back projection method (Frank et al., 1996; van Heel et al., 2000).