Characterizing Acoustic Attenuation of Homogeneous Media Using Focused Impulsive Acoustic Radiation Force

Abstract

A new method to characterize a material’s attenuation using acoustic radiation force is proposed. Comparison of displacement magnitudes generated in a homogeneous material by acoustic radiation force excitations can be used to estimate the material’s attenuation when the excitations are applied over a range of focal depths while maintaining a constant lateral focal configuration. Acoustic attenuations are related to the inverse of the excitation focal depth that yields the greatest focal zone displacement for this protocol. Experimental studies in calibrated tissue-mimicking phantoms are presented to demonstrate the feasibility of this method. Attenuations ranging from 0.3 – 1.5 dB/cm/MHz were characterized over excitation focal depths ranging from 5 – 30 mm, with an accuracy of 0.1 ± 0.15 dB/cm/MHz. As currently implemented, this method is limited to characterizing materials that have homogeneous material properties and acoustic attenuations. This method for characterizing acoustic attenuation can be performed using conventional diagnostic scanners without any additional hardware and could also be performed concurrently with acoustic radiation force-based imaging modalities to generate images of mechanical properties and attenuation that are spatially co-registered with B-mode images.

INTRODUCTION

Acoustic radiation force-based imaging methods are being studied to characterize the mechanical properties of tissue.^1–8 The relative displacement magnitudes generated in a homogeneous material when acoustic radiation force excitations are applied over a range of focal depths are related to the material’s acoustic attenuation. This observation has motivated the development of an algorithm based on the application of multiple acoustic radiation force excitations over a range of focal depths to estimate the acoustic attenuation of a homogeneous material. This paper explores the feasibility of such a method with calibrated, homogeneous, tissue-mimicking phantoms. The background section reviews current methods that are used to quantify acoustic attenuation and describes how acoustic radiation force magnitude and the resulting displacements in elastic media are dependent on the acoustic attenuation of the material. The methods section presents the proposed algorithm for characterizing acoustic attenuation and describes the experimental methods that were used to demonstrate the feasibility of this algorithm. The results section presents the phantom data compared with theoretical predications, and the discussion section examines the strengths and limitations of this method. This method of characterizing acoustic attenuation using acoustic radiation force excitations would potentially allow for images of stiffness and attenuation to be generated concurrently with spatial co-registration of B-mode images.

BACKGROUND

Acoustic Attenuation Measurement Methods

The acoustic attenuation of a material refers to the loss of acoustic energy with propagation distance, and it has traditionally been characterized using through transmission substitution techniques. In an inter-laboratory study by Madsen et al.⁹, 10 independent groups measured the attenuation coefficients of the same phantoms with different backscatter, attenuation, and propagation speed with reasonably good agreement. Most participants in this study used a through transmission substitution technique, where two ultrasound signals, one propagating through water and one through the sample of interest, were compared at a fixed distance from the transmitting transducer to quantify the acoustic attenuation of the sample.⁹ Although this method is considered to be the gold standard for attenuation measurements, physical constraints limit its in vivo applications. As a result, several other methods have been developed, including spectral, statistical, radiation force, and temperature techniques, with many variants.^10–22

For in vivo attenuation estimation, multiple spectral methods can be employed from pulse echo data. Lizzi et al. developed a spectral difference method, in which linear regression analysis is applied to the averaged power spectra from normalized, backscattered radio-frequency (RF) data scan lines to derive the rate of change of spectral slope for a series of Hamming windowed regions of interest at increasing depths. The attenuation is then reported as half of the average spatial rate of change in slope.^9–11 A similar method (mid-band technique) involves specifying several frequency bands within the transducer bandwidth and calculating the attenuation coefficient from the spatial rate of change of the average regression line value at the center of each band.^9,12,13 A Spectral Shift Central Frequency (SSCF) method relates attenuation to the change in the center frequency with depth and the spectral variance using Fourier or autoregressive techniques.^12,13 Flax et al. reported a zero-crossing method, where the zero crossing density is found to be proportional to the square root of the second moment of the power spectrum and can be related to attenuation in a similar manner to the center frequency in SSCF9. Studies indicate a high degree of stochastic variability for the spectral shift zero crossing and spectral shift central frequency methods, which can be improved by using alternative methods like evaluating the change in the zero order moment with depth.^14,15 The spectral substitution method involves finding the pulse echo data magnitude spectra from an acoustic reflector with and without a sample of known thickness present. The attenuation coefficient is the decibel loss due to the round-trip propagation of sound through the sample thickness.^17,18

Statistical methods exist for characterizing attenuation in vivo. For example, an entropy difference method has been applied to determine the attenuation coefficient by taking the envelope of filtered and rectified RF-data multiplied by a depth-dependent gain function based on an initial guess for the attenuation.¹⁹ Histograms of equally segmented adjacent envelope sets are calculated as the estimated attenuation is increased by 0.05 dB/cm/MHz for a reasonable range of attenuations. The entropy values from the histograms are fitted by a second order polynomial with respect to the attenuation coefficient for each region, and the crossing point of the two curves is calculated to determine the final attenuation coefficient.¹⁹ In a variant of this method, diffraction effects are also incorporated and a minimization is performed on the noise to signal ratio of the envelope peaks modified by the gain functions to find the best attenuation estimate.²⁰ This type of method has a reduced calculation time and increased statistical performance over some spectral methods.²⁰

Radiation force balance methods for measuring attenuation also exist. Such setups require a force balance to be suspended above a water tank with a transducer transmitting through a submerged sample toward an oblique reflector or directly toward the balance if positioned on the opposite side of the tank.^21,22 The attenuation coefficient (in dB/cm) is proportional to the logarithmic difference of the forces, with and without the sample present, divided by the sample thickness with correction factors for the attenuation of the water and any acoustic windows in the beam path.²¹ As with the through-transmission method, this technique is limited in its application to in vivo cases and yields lower attenuation values than several other methods in the literature.²¹

As reported by Parker et al., attenuation coefficients with accuracies within 10% of true attenuations have also been estimated using the integral-differential relationships between attenuation and the rate-of-heating measured by thermocouples.¹⁸ The rate-of-heating is governed by

$$\rho C\frac{dT}{dt}=2\alpha I,$$ (1)

where ρ represents density, C represents specific heat, T represents temperature, t represents time, α [Np/cm] represents the absorption coefficient, and I [W/cm²] represents intensity.¹⁸ These methods are analogous to the acoustic radiation force method presented herein; however, the thermal methods require measurement of the total power emitted by the transducer and can be subject to thermocouple-related artifacts such as viscous heating.^18,22

Acoustic Radiation Force

Acoustic radiation force can be used to generate localized displacements in tissue, and the dynamic tissue response can be monitored using ultrasonic correlation-based methods. Acoustic radiation force has been utilized in several imaging modalities, including: (1) Kinetic Acoustic Vitroretinal Examination (KAVE) method where radiation force is used to generate steady-state stresses within soft gels and the vitreous of the eye,¹ (2) Shear Wave Elasticity Imaging (SWEI) where shear waves generated by radiation force are monitored to reconstruct the shear moduli of materials,^2,23 (3) supersonic imaging where acoustic radiation force is used to generate shear waves in tissue,³ (4) Vibro-acoustography where frequency-shifted, confocal acoustic beams generate an oscillating radiation force within tissue and the tissue response is monitored with a hydrophone,^24–26 (5) Harmonic Motion Imaging (HMI) where the beat frequency of two concurrent excitation pulses is used to generate radiation force to excite tissue and characterize its material properties,⁴ and (6) radiation force elastography and Acoustic Radiation Force Impulse (ARFI) imaging where impulsive acoustic radiation force is applied to tissue, and the resulting dynamic tissue response is used to characterize the tissue’s material properties.^5,7,8,27 Acoustic radiation force is also being studied in conjunction with High Intensity Focused Ultrasound (HIFU) therapy to monitor ablation treatments,²⁸ and radiation force is also being used to manipulate ultrasonic contrast agents in vitro and in vivo.^29–31

When high-intensity acoustic pulses are applied to tissue, momentum is transferred from the propagating ultrasound waves to the material that results in the generation of acoustic radiation force and tissue deformation. The magnitude of acoustic radiation force, F [kg/(s²cm²)], can be described as:³²

$$\left|\stackrel{\rightharpoonup }{F}\right|=\frac{2\alpha (f)I(z)}{c},$$ (2)

where F is in the form of a body force, c (1540 m/s) is the sound speed, α(f) (Np/m) is the frequency-dependent absorption coefficient of the tissue, and I(z) (W/cm²) is the in situ temporal average intensity.³² As Eq. (2) indicates, the radiation force magnitude is related to the material’s acoustic attenuation, along with the in situ acoustic intensity, which is also attenuation-dependent. In a linear, isotropic, elastic solid, the acoustic radiation force and the resulting displacements are linearly related;^33,34 therefore, in a homogeneous material with a given sound speed, these displacements are linearly related to the material’s attenuation (α).

In addition to a material’s sound speed and attenuation, the spatial distribution of a radiation force field is determined by the transmit configuration of the transducer. The shape of the transmitted intensity field, and thus the volume of tissue to which radiation force is applied (i.e., the region of excitation, ROE), is dependent on the transducer focal configuration. This focal configuration can be characterized by the dimensionless f-number $(\text{F}/\#=\frac{z}{d})$ of the system, where z is the acoustic focal length, and d is the active aperture width. For linear arrays, d = Nw, where N is the number of active elements in the lateral dimension and w is the element width. The number of active elements, and thus the transmit aperture’s width, can be electronically selected for linear arrays on commercial scanners. The result is a continuous, variable magnitude body force applied throughout the tissue within the ROE.³³

METHODS

Theory

The method presented herein relies on the linear relationship between the displacement magnitude and the magnitude of acoustic radiation force within the focal zone. This method assumes that the material is homogeneous throughout the propagation path (i.e., stiffness, density, and sound speed remain constant within the ROE).³³

If a plane wave propagates through an attenuating medium, the intensity (I) as a function of distance (z) away from the source can be expressed as:

$$I(z)=I_s{e}^{-2\alpha f^{n}z},$$ (3)

where I_s is the intensity of the source. If the attenuation of the material is assumed to be linear with frequency (n = 1 in Eq. (3) and α(f) = αf in Eq. (2)), the acoustic intensity will exponentially decay at a rate of 2αfz. By substituting Eq. (3) into Eq. (2), the acoustic radiation force magnitude generated in this material by a plane wave can be expressed as:

$$|\stackrel{\rightharpoonup }{F}(z)|=\frac{2(\alpha f)I_S{e}^{-2\alpha fz}}{c}.$$ (4)

As indicated by Eq. (4), the radiation force magnitude (and the induced displacement) at a given depth (z) is a function of both the attenuation of the intervening material (e^−2αfz term) and the attenuated intensity (I(z)) at that depth (αf terms).

A substitution method similar to those already used to characterize attenuation could be implemented to measure the attenuation of an unknown sample by measuring the depth-dependent displacement profile in a material with a known attenuation, and comparing that displacement profile with one measured in a material with an unknown attenuation. The difference in the displacement profiles could be used to estimate the unknown material’s acoustic attenuation using Eq. (4). While such a method would not rely on through transmission of the acoustic wave, it would require (1) knowledge of the source intensity (I_S) and (2) a reference material with a known attenuation. These two limitations can be overcome, however, by using relative displacement measurements in response to focused excitations in only the unknown material.

To generate displacement of adequate magnitude that can be ultrasonically tracked in tissue, the ultrasound energy from a linear array needs to be focused.^33,35,36 While the intensity of the plane wave used to derive Eqs. (3) and (4) is only dependent on depth (z), a focused beam is spatially variant in all dimensions (elevation, lateral, and depth). To simplify the analysis of such a beam, we assume a weak elevation focus and a stronger lateral focus shallower than the elevation focal depth. For these conditions, the elevation dimension can be considered unfocussed. For a focused array, the intensity generated by the array (source) is no longer simply described by an exponentially decaying function (Eq. (3)), but the intensity profile experiences a gain around the focus. In the absence of attenuation, neglecting diffraction effects and not applying apodization, the intensity at the focus (I_F) can be related to the intensity emitted by each element (I_es) as I_F = N_e I_es, where N_e represents the number of active elements. In the presence of attenuation and neglecting propagation path length differences from the elements in the active array, the intensity and radiation force magnitude at the focus (z_F) can be expressed as:

$$I_F=N_e{I}_{es}{e}^{-2\alpha {fz}_F},$$ (5)

$$|{\stackrel{\rightharpoonup }{F}}_F(z_F)|=\frac{2(\alpha f)N_e{I}_{es}{e}^{-2\alpha {fz}_F}}{c}.$$ (6)

It should be noted in Eq. (6) that the radiation force magnitude at the focus varies linearly with the attenuation at the focus, but it is also dependent upon (decreased by) the attenuation of the material in the propagation path.

At locations other than the focus, simplified expressions for the intensity and radiation force magnitude (Eqs. (5) and (6)) are not easily achievable analytically, and require solution via numerical methods.³³ Therefore, to get relative measures of displacement to estimate the attenuation of a material without a reference sample, radiation force excitations must be made at several focal depths (z_F). If a constant aperture width is used for the different focal depths, the F/# of the excitation beam would change, and diffraction effects would void the assumptions used to derive Eqs. (5) and (6) (i.e., the beamwidth at the focus would change as a function of depth). This problem can be avoided by electronically scaling the lateral active aperture width to maintain a constant lateral F/# such that N_e can be represented by $\frac{z_F}{(F\hspace{0.17em}/\#)w_e},$ where w_e is the width (pitch) of each element. Substituting this expression for N_e into Eq. (6), the radiation force magnitude at the focal depth (z_F) in an attenuating medium can be represented as:

$$|{\stackrel{\rightharpoonup }{F}}_F(z_F)|=\frac{2(\alpha f)z_F{I}_{es}{e}^{-2\alpha {fz}_F}}{(F\hspace{0.17em}/\#)w_{e}c}.$$ (7)

Inspection of Eq. (7) reveals that for multiple foci where a constant lateral F/# is maintained, $|{\stackrel{\rightharpoonup }{F}}_F(z_F)|$ is dependent on the product of the focal depth with the exponential decay of the source intensity, which scales as a function of focal depth. Therefore, the attenuation a material can be estimated by determining which focal depth generates the greatest radiation force magnitude. Maximizing the radiation force expression (Eq. (7)) as a function of depth $(\frac{d{\stackrel{\rightharpoonup }{F}}_F(z_F)}{d{z}_F}=0),$ the focal depth yielding the maximum radiation force (z_max) can be related to the attenuation of the material by:

$$z_{max}=\frac{1}{2\alpha f}.$$ (8)

Note that the denominator of Eq. (8) is the magnitude of the exponential decay coefficient from Eq. (7). It should be noted again that both the local attenuation and the attenuation in the propagation path of the acoustic wave to focal depth impact the radiation force magnitude at the focal depth (Eq. (7)).

Directly measuring the acoustic radiation force magnitude in a material is not possible; however, by taking advantage of the linear relationship between the radiation force magnitude and the displacement that it induces, focal zone displacements provide an indirect measurement of this magnitude. Therefore, the attenuation of a material can be quantified using Eq. (8) by determining the focal depth (z_max) that yields the greatest displacement in response to an excitation at a known frequency (f). Figure 1 demonstrates that as the acoustic attenuation of a material increases, the excitation focal depth that yields the greatest displacement will be shallower than in a less attenuating medium. Note that the abscissa in Figure 1 represents the product of 2αf (Np/cm).

Figure 1.

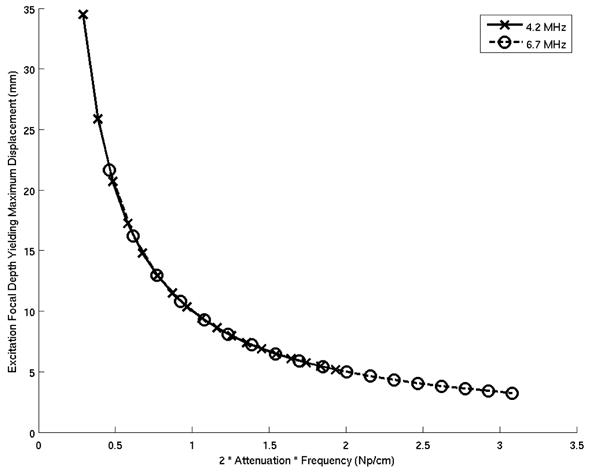
Excitation focal depths generating the greatest radiation force magnitudes (z_max) as a function of acoustic attenuation for transmit frequencies of 4.2 and 6.7 MHz. Note that the abscissa represents the product of 2αf (Np/cm).

Implementation

This method compares relative focal zone displacement magnitudes from focused, constant lateral F/#, impulsive acoustic radiation force excitations over a range of focal depths to characterize the acoustic attenuation of a homogeneous material using Eq. (8).

Excitations were performed at focal depths ranging from 5 – 30 mm in 0.5 mm increments. For a given transducer, pulse duration remained constant and the lateral excitation F/# was also held constant by electronically growing the active aperture with increasing focal depth. All excitations were unapodized. Focal zone displacements were estimated as a function of depth for each excitation using normalized cross-correlation methods.^35,36 The maximum displacement within ±25% of each focal depth was plotted versus excitation focal depth (Fig. 2). The peak of this curve was identified by fitting a second order polynomial to the data to determine the excitation focal depth yielding the greatest displacement. This location (z_max) varies with acoustic attenuation and can be used to estimate the material’s attenuation, as predicted by Eq. (8) and demonstrated in Figure 1.

Figure 2.

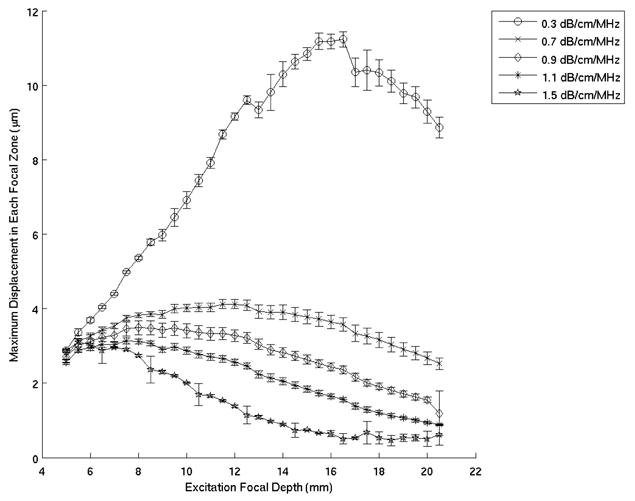
Mean maximum focal zone displacements ± one standard deviation measured over 120 phantom locations, for excitation focal depths ranging from 5 – 20 mm. These experiments were performed in five different phantoms using the VF10-5 linear array operating at 5.7 MHz. This data was processed at 0.34 ms after the radiation force excitation

Experimental Methods

Experiments were performed using five homogeneous, tissue-mimicking CIRS phantoms (Computerized Imaging Reference Systems, Inc., Norfolk, VA) with acoustic attenuations ranging from 0.3 – 1.5 dB/cm/MHz, as calibrated by CIRS using pulse echo measurements. The Young’s moduli of these phantoms were near 4 kPa.³³ Imaging was performed on a Siemens SONOLINE Antares^TM Scanner (Siemens Medical Solutions USA, Inc., Ultrasound Division, Issaquah, WA) with two linear arrays: a VF10-5 (center frequency of 6.7 MHz with an elevation focus near 20 mm) operating at 5.7 MHz, and a VF7-3 (center frequency of 4.2 MHz with an elevation focus near 35 mm) operating at 4.2 MHz. The transducers were coupled directly to each phantom with ultrasonic gel. For each phantom, data were acquired at excitation focal depths ranging from 5 – 20 mm in 0.5 mm increments for the VF10-5 array, and 5 – 30 mm in 0.5 mm increments, for the VF7-3. For both arrays, a constant, unapodized F/2 lateral focal configuration was used for all excitation focal depths. Displacement estimation was performed using normalized cross-correlation on RF data acquired before and after excitation with acoustic radiation force. Before each excitation, a short-duration reference “tracking” line was obtained, followed by a single, long-duration, high intensity excitation pulse. This excitation pulse was followed by a series of “tracking” lines for correlation with the reference line to estimate displacements. Pinton et al. provides additional details about how radiation force induced displacements are estimated from RF data.³⁶ For the VF10-5, a region of interest (ROI) comprised of 30 lateral locations, spaced 0.30 mm apart, was interrogated, with four randomly located ROIs measured in each phantom. The excitation pulse duration was 35 μs (200 cycles), and the tracking pulses were fired at a PRF of 12.5 kHz for 6 ms after the excitation. For the VF7-3, an ROI comprised of 30 lateral beams, spaced 0.35 mm apart, was interrogated, with four randomly located ROIs measured in each phantom. The excitation pulse duration was 47.5 μs (200 cycles), and the tracking pulses were fired at a PRF of 9.7 kHz for 7.7 ms after the excitation. For both linear arrays, the excitation intensities were consistent with those used in Power Doppler imaging, while the tracking pulses were fired at intensities associated with diagnostic B-mode imaging on the Antares scanner.

The RF data from each excitation location were processed offline using normalized cross-correlation (3λ kernel, 99% overlap) to determine displacement data as a function of depth.³⁶ Displacement estimates with correlation coefficients less than 0.9 (which occurred in < 5% of the data sets) were assumed to be corrupted by noise and were not included in the attenuation estimates. To remove jitter artifacts associated with the cross-correlation algorithm, the displacement data from each excitation were smoothed using an axial spatial running average with a 0.16 mm kernel. The data from all 30 lateral locations in each of the four ROIs (for a total of 120 locations) were averaged and processed using the method outlined earlier in this section.

RESULTS

Figure 2 shows the mean maximum focal zone displacements ± one standard deviation over 120 phantom locations, 0.34 ms after excitation for excitation focal depths ranging from 5 – 20 mm. The data was acquired using the VF10-5 linear array. The excitation focal depths yielding maximum displacements, as determined by a least square second order polynomial fit of the data (Fig. 2), are plotted as a function of phantom attenuation in Figure 3 and compared with the theoretical curve predicted by Equation 5. The plot on the right in Figure 3 shows the difference between the experimental data and the theoretical curve. Figures 4 and 5 show the corresponding data acquired with the VF7-3 linear array, 0.46 ms after the radiation force excitation. Note the similarity between Figures 3 and 5.

Figure 3.

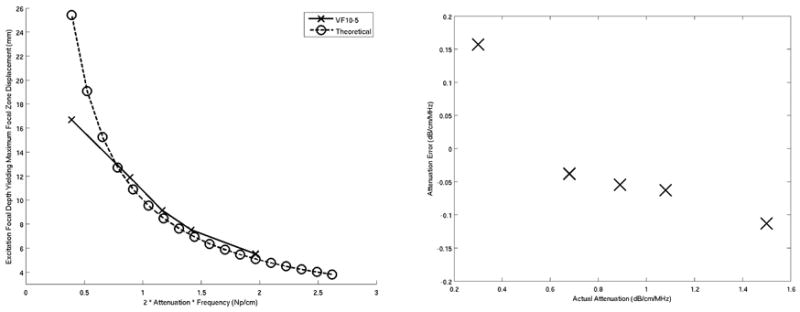
(Left) Comparison of the attenuation estimates based on the excitation focal depths generating maximum focal zone displacements for each phantom using the VF10-5 linear array operating at 5.7 MHz with the theoretical predictions. Note that the units of attenuation are normalized for frequency (Np/cm). (Right) Attenuation estimates errors between predicted and actual values for the VF10-5 experimental data. The mean error over the range of measured attenuations was −0.02 ±0.1 dB/cm/MHz.

Figure 4.

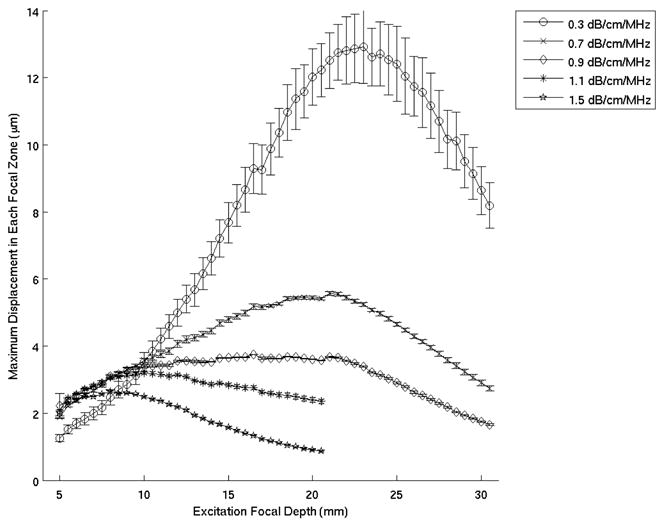
Mean maximum focal zone displacements ± one standard deviation measured over 120 phantom locations for excitation focal depths ranging from 5 – 30 mm. These experiments were performed in five phantoms with the VF7-3 linear array operating at 4.2 MHz. This data was processed at 0.46 ms after the radiation force excitation.

Figure 5.

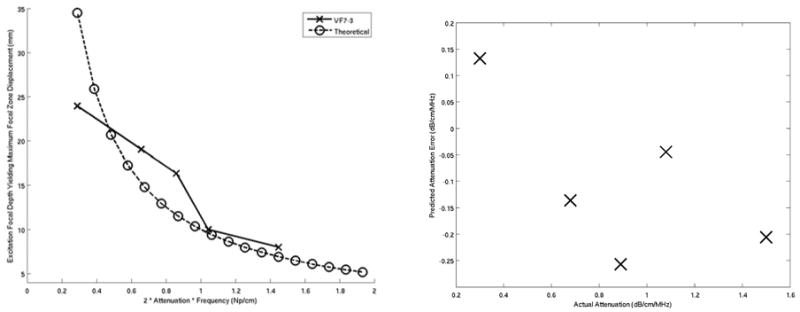
(Left) Comparison of the attenuation estimates based on the excitation focal depths generating maximum focal zone displacements for each phantom using the VF7-3 linear array operating at 4.2 MHz with the theoretical predictions. Note that the units of attenuation are normalized for frequency (Np/cm). (Right) Attenuation estimate errors between predicted and actual values for the VF7-3 experimental data. The mean error over the range of measured attenuations was −0.1 ± 0.15 dB/cm/MHz.

To determine if the precision and accuracy of the attenuation estimates derived from this method are dependent on the time after excitation, the algorithm was applied to a range of times following the radiation force excitation. Figure 6 shows the mean acoustic attenuation estimate error ± one standard deviation (i.e., the deviation from the ideal theoretical curve in Figs. 3 and 5) over all 120 locations for each phantom for the first nine time steps that were tracked for the VF10-5 (left) and VF7-3 (right) linear arrays.

Figure 6.

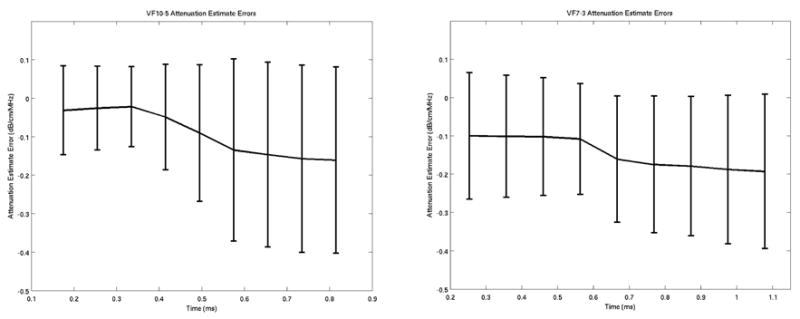
Mean ± one standard deviation acoustic attenuation estimate errors (i.e., difference between theoretical and experimental attenuation estimates) over the 120 excitation locations for the first nine tracked time steps after the radiation force excitation for the VF10-5 (left) and VF7-3 (right) experimental data.

DISCUSSION

The method presented herein uses acoustic radiation force induced displacements to estimate the absorbed and scattered acoustic energy in a material. Acoustic attenuation can be estimated by performing multiple radiation force excitations with varying focal depths (with constant lateral F/#s) and determining which excitation focal depth yields the greatest focal zone displacement (Eq. 8). This measurement reflects the acoustic attenuation that occurs during wave propagation to the focus.

Figures 1, 3, and 5 demonstrate good agreement between theory and experiment, and support the feasibility of the proposed method to quantify the acoustic attenuation in linear, isotropic, elastic solids. The error plots in Figures 3 and 5 show the accuracy of this method over the range of acoustic attenuations measured with VF10-5 and VF7-3 linear arrays, respectively, with both implementations being accurate to within 0.1 dB/cm/MHz of the attenuations measured using the pulse echo method. This is comparable to the accuracy achieved with through transmission and spectral methods.^{9,13,14,19,20}

The derivation of Eq. (8), which relates the acoustic attenuation of the material to the excitation focal depth associated with the greatest focal zone displacement, requires that the material’s stiffness, sound speed, and attenuation are homogeneous throughout the propagation path. Heterogeneities in these material properties were not characterized in the CIRS phantoms and may contribute to errors in the attenuation estimates (Figs. 3 and 5).

In addition to requiring homogeneous material properties along the propagation path, the theory presented in Eq. (8) and Figure 1 is based upon several simplifying assumptions, including: (1) neglecting the elevation dimension, and (2) neglecting differences in path length across the transducer aperture. As mentioned in the Theory section, neglecting the elevation focus is reasonable if the lateral focus is shallower and more tightly focused (i.e., smaller F/#) than the elevation dimension. However, as the lateral excitation foci approach the elevation focus, the focal depths yielding the greatest displacement magnitudes will deviate from those predicted by Eq. (8). This effect becomes more significant in the data for less attenuating media where appreciable energy remains in the acoustic wave as it approaches the elevation focus. This is apparent in Figure 3, where the less attenuating phantom data is tending toward the elevation focus (20 mm) and deviating more from the theoretical curve. In Figure 5, this behavior is not as apparent due to the deeper elevation focus of the VF7-3, which is greater than the range of excitation foci used in the experiment.

While a linear dependence on frequency is typically assumed for soft tissue attenuation,³⁷ this method is not limited to such an assumption. A power-law relationship between attenuation and frequency can be accommodated by modulating the value of n appropriately in Eq. (3) and carrying the appropriate frequency dependence throughout the derivation.

The proposed method also assumes a linear relationship between the measured tissue displacement and the applied radiation force since radiation force magnitude cannot be directly measured in tissue. This assumption has been shown to be accurate for linear, isotropic elastic solids.³³ Therefore, accurate attenuation estimates using this method are dependent upon accurate displacement tracking. Correlation-based ultrasonic displacement estimation methods suffer from jitter³⁸ and underestimation in the presence of scatterer shearing and displacement gradients underneath the point spread function of the tracking beams.^35,39 For homogeneous materials, averaging over multiple locations and performing a spatial running average on the displacement data, as was done herein, decreases the impact of jitter. However, the Cramer Rao Lower Bound (CRLB) estimates the lowest achievable displacement estimation error variance and hence, the smallest trackable displacement (i.e., noise floor) with these methods, as related to the center frequency of the tracking beams, the transducer bandwidth, RF data SNR, the correlation kernel length, and the correlation coefficient between reference and tracking RF data.³⁸ Clearly, the displacements generated by the radiation force excitations must be larger than this noise floor to successfully apply this method to estimate attenuation.

Attenuation estimates can be made over a range of times after the excitation, as demonstrated by Figure 6. However, it is beneficial to use data soon after the excitation for this method to take advantage of greater displacement magnitudes that will yield improved displacement estimates.³⁶ It should be noted that the variances in the attenuation estimates in Figure 6 are over all 120 different locations in each phantom and do not reflect the variance of an attenuation estimate made at a single location in each phantom.

The precision of an individual estimate is dependent on the ability to resolve the location of peak displacement from the curves shown in Figures 2 and 4. Given the inverse relationship that exists between z_max and α, more accurate attenuation estimates are possible in less attenuating materials. Therefore, reducing the effective attenuation of the material by using a lower excitation frequency may improve the accuracy of attenuation estimates.

The proposed method is similar in concept to that proposed by Parker et al.;^18,22 however, in their work, ultrasonic heating was measured to characterize absorbed acoustic energy. In the work herein, radiation force induced displacements are characterized. This radiation force is generated by both the absorption and scattering of acoustic energy, though differentiation between these two phenomenon is not possible. For the intended application of this method (i.e., characterization of the attenuation of soft tissues, which includes both losses due to scattering and absorption), the combination of both phenomena is reasonable.

Since acoustic radiation force-based imaging modalities are currently being studied to characterize the mechanical properties of tissue, the method proposed herein would allow for concurrent characterization of mechanical properties and attenuation in homogeneous media. For example, in ARFI imaging protocols that utilize multiple excitation focal zones to improve lesion contrast,⁴⁰ the displacement data acquired to create images based on material stiffness could also be used to provide attenuation estimates in regions of tissue that can be considered homogeneous.

CONCLUSIONS

The feasibility of using the relative displacement data from acoustic radiation force excitations at multiple focal depths to characterize the acoustic attenuation of a homogeneous material has been demonstrated using calibrated phantoms. These studies indicate that materials with homogeneous elastic and acoustic attenuation properties in the range of those found in biological materials can be characterized with this method using linear arrays operating between 4 and 6 MHz. More attenuating materials require the use of lower excitation frequencies to improve the accuracy of the attenuation estimates, while less attenuating materials benefit from using arrays with deeper elevation foci to avoid biasing the attenuation estimates. This acoustic radiation force-based method provides a convenient way to characterize the acoustic attenuation of a material using a commercial diagnostic scanner that can be performed concurrently with measurements of the mechanical properties of materials that are spatially co-registered with B-mode images.