Microabstract/Abstract
We evaluated the effects of resorption cavities on cancellous bone strength using computational methods. Adding cavities to cancellous bone caused reductions in strength and stiffness that were greater than expected from the associated changes in bone volume and more pronounced when cavities were targeted to regions of high tissue strain.
Introduction
The amount of bone turnover in the skeleton has recently been implicated as a factor influencing bone strength. One mechanism proposed to explain this effect is that resorption cavities reduce the effective thickness of trabeculae and modify local stress distributions leading to reduced mechanical performance of the entire structure. In this study we test the plausibility of this mechanism.
Materials and Methods
High-resolution finite element models were created from microcomputed tomography images of 16 vertebral cancellous bone samples, as well as from images of the samples in which cavities had been added digitally – either at regions of high strain (targeted) or placed at random on the bone surface (non-targeted). The effect of resorption cavities on predicted bone strength and stiffness was evaluated by comparing the relationships between mechanical properties and bone volume fraction among the three groups (the original images, those with non-targeted cavities, and those with targeted cavities).
Results
Addition of resorption cavities modified the relationship between mechanical properties and bone volume fraction in the finite element models such that, for a given bone volume fraction, stiffness and yield strength were reduced as compared to the original images (p < 0.05). The differences in yield strength-volume fraction relationships between the original models and those with targeted cavities were significantly greater than those between the original models and those with non-targeted cavities (p < 0.05). None of the differences in predicted mechanical properties per unit bone volume fraction could be accounted for by three-dimensional measures of microarchitecture (BS/BV, Tb.Th, Tb.N, Tb.Sp, MIL, DA, SMI).
Conclusions
Resorption cavities can influence cancellous bone strength and stiffness independent of their effect on bone volume. The effects of cavities on bone mechanical performance relative to bone volume are greater when cavities are targeted to regions of high strain and cannot be predicted using standard microarchitecture measures.
Keywords: bone mechanics, bone quality, cancellous bone, bone remodeling, osteoporosis treatments
INTRODUCTION
Recent observations that reductions in fracture risk associated with anti-resorptive therapies are greater than would be expected from changes in areal bone mineral density (aBMD, g/cm2) (1,2) have led to increased interest in other determinants of bone strength. Observations that biochemical markers of bone remodeling can predict fracture risk independent of areal bone mineral density (3,4) have led to the suggestion that the amount of bone turnover influences bone mechanical performance (5–7). Although bone turnover can regulate bone volume and the degree of mineralization (8–10), cavities formed during the remodeling process (referred to here as resorption cavities) can influence bone microarchitecture by perforating and disconnecting individual trabeculae (5–7). It has also been suggested that the very presence of a resorption cavity on a trabecula can influence bone strength by modifying local tissue strains and increasing the likelihood that the trabecula will buckle (7,11,12). Since anti-resorptive agents can fill and/or reduce the number of cavities but cannot replace disconnected trabeculae (13), understanding the influence of cavities independent of perforation should provide insight into how these agents might alter bone strength.
Given the difficulty of isolating the microarchitectural effect of resorption cavities experimentally, our current understanding of their effects on bone mechanics is based on computational studies. Finite element analyses of individual trabeculae have demonstrated that the presence of a resorption cavity can greatly increase local tissue strains (14–16), supporting the idea that cavities may act as “stress risers.” In addition, in models of the entire cancellous bone structure, removal of bone tissue experiencing the greatest strains during loading caused large changes in the distribution of strain throughout the structure, suggesting that where a cavity is placed can be very important mechanically (15). Because these studies utilized only elastic finite element analysis techniques they did not address bone strength directly nor could they account for the large deformation and buckling failure mechanisms that have been proposed to explain the potential effects of cavities on cancellous bone strength.
The overall goal of this research was to improve understanding of the link between bone turnover and cancellous bone strength. Using micro-computed tomography-based, non-linear finite element models of vertebral cancellous bone, the objectives of this study were to: 1) determine the biomechanical effects of adding resorption cavities that do not disconnect trabeculae, after accounting for differences in bone volume fraction and 2) determine the degree to which preferential placement of cavities at highly strained regions influences any of the observed effects. Compared to related studies in this area, this study is novel in that it utilizes finite element methods that have been validated for prediction of cancellous bone strength and addresses the effects of resorption cavities independent of trabecular connectivity and bone volume fraction.
MATERIALS AND METHODS
Sample Preparation
Sixteen fresh frozen vertebral bodies (L4 or L5) were harvested from donors aged 54–90 years (7 male aged 54–90 years, mean 72.4 and 9 female aged 54–85 years, mean 73.2) with no history of diseases known to influence bone metabolism. One cylindrical core was taken from each vertebral body in the superior-inferior direction. Each specimen was imaged at 22μm resolution using micro-computed tomography (μ-CT 40, SCANCO Medical AG, Basserdorf, Switzerland). The resulting image was thresholded using a mass-compensated hexahedral method (17) and a cube (5mm in each dimension) was removed from the center of the image for subsequent analysis. Bone volume fraction of the cubes ranged from 5.1% to 18.1% and was not significantly related to donor age or sex.
Addition of Resorption Cavities
Resorption cavities were added to the cancellous bone structure in the following manner (Figure 1): A seed point was selected from surface voxels. Paths across the bone surface emanating from the seed point were labeled to define cavity length and width. Although resorption cavities are typically illustrated as hemispherical, existing evidence suggests that they are much longer than they are wide (18). Cavity surface size was set to 500 μm long and 200 μm wide (22 voxels long by 9 voxels wide), matching the typical cavity surface size reported by Mosekilde (19). Cavity depth was defined by labeling voxels within a specified radius of the surface so that cavity edges were gradual. Cavity depth was set in this manner to 44 μm (two voxels), a value approximating the median erosion depth found in the iliac crest of healthy postmenopausal females (49.1 μm) 20) and typical of erosion depth measured by others (21). The process was repeated by adding additional cavities until a total of 6% of the original bone volume was labeled for removal. The value of 6% was based on estimates of the volume occupied by cavities in the lumbar spine of postmenopausal women (8). Resorption cavities were allowed to overlap each other but the seed point for each new cavity was required to be on a bone surface not yet associated with a cavity. After all cavities were placed, labeled voxels were removed from the model simultaneously. Any remaining bone voxels that were isolated from the cancellous bone structure (floating within the porous volume) were also removed. If the resulting bone volume was less than 93.9% of the original volume or if any trabeculae were disconnected, the resulting image was discarded and the entire process repeated.
Figure 1.
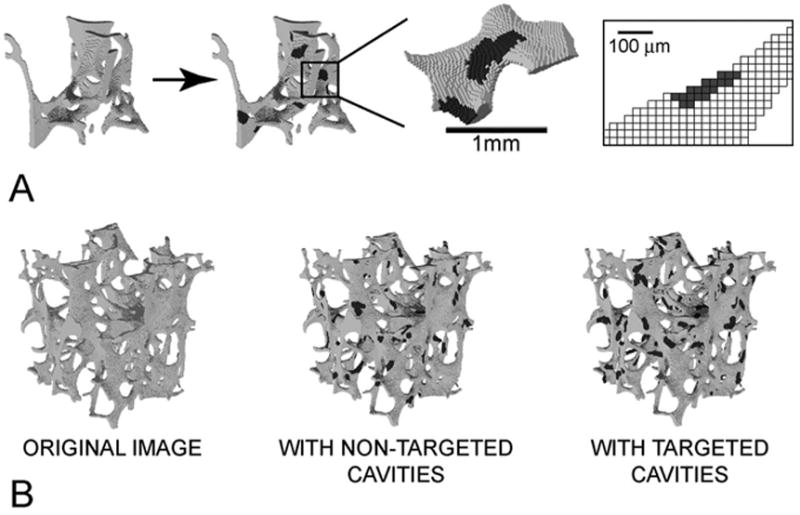
(A) Cavities were added to the image of each specimen using custom software that prevented the cavities from disconnecting any trabeculae. Colored regions represent resorption cavities added to the bone surface. (B) Three finite element models were generated for each sample, one of the original image, one with resorption cavities placed at random (non-targeted), and one with resorption cavities placed on surface tissues experiencing the greatest tissue strain (targeted).
In order to isolate the independent effects of cavity existence and cavity location, a series of parameter studies was performed. Three cases were analyzed for each specimen: 1) the original image of the bone specimen without cavities added; 2) the same specimen with resorption cavities added to the bone surface at random (non-targeted); and 3) the same specimen with resorption cavities placed at regions of greatest magnitude maximum principal strain (targeted). Seed points for targeted simulations were selected in order of greatest absolute principal strain as observed in a linear elastic finite element analyses performed on the original image. To determine if trabecular microarchitecture differed between the three models, three-dimensional measures of trabecular thickness (Tb.Th), trabecular number (Tb.N), trabecular separation (Tb.Sp), bone surface to volume ratio (BS/BV), degree of anisotropy (DA) and structure model index (SMI, a measure that describes the degree to which the structure is plate-like or rod-like) were performed using three-dimensional model-independent algorithms (22,23).
Mechanical Properties and Evaluation of Bone Strength
Each image was converted into a high-resolution finite element model made up of 8-noded brick elements. Linear elastic high-resolution finite element models have long been capable of predicting cancellous bone elastic modulus (24). Recent advancements have also accounted for tissue and geometric nonlinearities (buckling and large deformation), important for the prediction of cancellous bone strength (25–27). The inclusion of such details is necessary for this study, since buckling has been proposed as a potential mechanism behind the unique effect of resorption cavities (7,11,12). The finite element model of bone tissue used in the current study accounts for these details utilizing a finite plasticity model modified to include tension-compression asymmetry via pseudo-kinematic hardening (28). Tissue-level yield was based on von-Mises yielding, resulting in tissue yield strains of 0.81% and 0.33% in compression and tension, respectfully, matching those determined in calibration studies (29). The model was validated in another study using 54 fresh frozen cancellous bone cadaver specimens that had undergone micro-computed tomography imaging as well as mechanical testing (22 tested in compression, 32 in tension) (27). Differences in elastic modulus, yield strain and yield strength between experimental measures and those obtained using this finite element formulation were not significantly different from zero (p > 0.13)(27). Thus, these models provide realistic predictions of elastic modulus and yield strength of cancellous bone specimens. In the current study a specimen-specific tissue elastic modulus was assigned using a combined experimental-computational analysis (24).
Each model (16 original images, 16 with non-targeted cavities, 16 with targeted cavities) was loaded to 1% apparent strain in compression along the primary loading direction (superior-inferior) to generate predictions of the yield strength, yield strain and elastic modulus. The finite element models contained between 0.56 to 2.12 million elements and were solved on the IBM Datastar supercomputer (National Partnership for Advanced Computational Infrastructure, San Diego Supercomputer Center, San Diego, CA, USA). The 48 simulations performed for this study utilized approximately 1800 supercomputer processor hours.
Simulations with resorption cavities had less bone volume and therefore were expected to show reduced strength and stiffness as compared to the original sample. To determine if the reduction in strength and/or stiffness was greater than would be expected from the imposed 6% reduction in bone volume, the relationships (regression lines) between these mechanical properties and bone volume fraction were compared between the three model types. In this way we accounted statistically for effects of cavity presence independent of variation in bone volume fraction. As a secondary evaluation, the average strength:bone volume fraction and elastic modulus:bone volume fraction ratios were compared between the three model types (30). A difference in the yield strength-bone volume fraction or modulus-bone volume fraction characteristics between the original images and those with cavities indicated a change strength or stiffness per unit bone volume. Comparison of the relationships between mechanical properties (strength or elastic modulus) and bone volume fraction were performed using repeated measures ANCOVA (SPSS, version 11.0.3, SPSS Inc., Chicago, IL, USA). Repeated measures techniques were used since the computational analysis produced outcome parameters for all cases on each specimen. Differences in the yield strain, yield strength:bone volume fraction and elastic modulus:bone volume fraction ratios between models were compared using repeated measures ANOVA and confirmed through matched pairs comparisons. Repeated measures ANCOVA was also used to determine if there were differences in trabecular microarchitecture measures between model types after accounting for the effect of bone volume fraction. Additional analyses were performed to determine if accounting for variations in trabecular microarchitecture measures could explain any observed differences between the three model types. Multiple comparisons were performed using the Holm test.
RESULTS
The addition of resorption cavities changed the relationships between all predicted compressive mechanical properties and bone volume fraction (Figure 2). Percent reductions in yield strength and elastic modulus associated with the addition of cavities to each sample ranged from 13–61% even though only a 6% decrease in bone volume was imposed. By contrast, in the original data set, a 6% decrease in bone volume across specimens was associated with only a 6–7% decrease in yield strength and elastic modulus. Percent reductions in yield strength and elastic modulus caused by cavities were greatest in specimens having lower initial bone volume (Figure 3). Percent reductions in yield strength were significantly greater than the reductions in elastic modulus (p < 0.001). The slopes of the linear strength-bone volume fraction and modulus-bone volume fraction relationships differed significantly among model types, (p < 0.05 for all possible comparisons, Table 1). The repeated measures statistical tests were found to be highly sensitive to differences among groups, allowing for the detection of differences that were very subtle (Figure 2, slopes for Original and Non-Targeted groups). The slope of the strength-bone volume fraction relation in models having targeted cavities was 25% lower than that for models without cavities. The ratios of yield strength to bone volume fraction and of elastic modulus to bone volume fraction for models with targeted cavities were 36 and 25% lower than those observed for the original images. Significant differences in these ratios were observed between each of the three model types (p<0.01, Table 1). Minor but significant differences in yield strain were observed among the three model types (p<0.001 for each comparison). Donor age and sex did not significantly contribute to the slopes of the yield strength-bone volume fraction or elastic modulus-bone volume fraction relationships.
Figure 2.
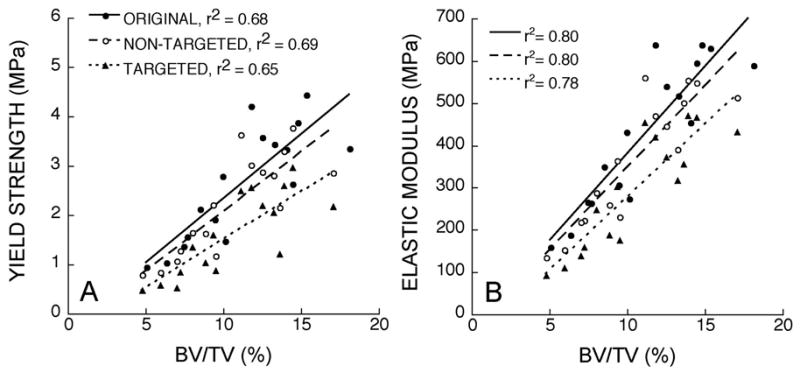
The relationships between sample bone volume fraction and A) yield strength and B) elastic modulus are shown. The three types of models differed from each other in terms of regression slopes (p < 0.05). The sensitivity of repeated measures techniques allowed the detection of small differences in slope between the original and non-targeted models.
Figure 3.
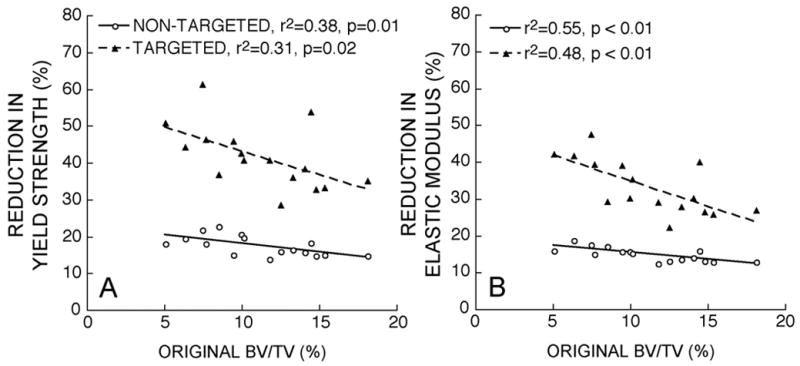
The percent difference in A) yield strength and B) elastic modulus from that measured in the original models was negatively correlated with original bone volume fraction.
Table 1.
Parameter estimates (SE) for the strength – bone volume fraction and elastic modulus –bone volume fraction characteristics are shown for the original models, those with non-targeted cavities and those with targeted cavities. Multiple comparisons were performed with the Holm test.
| σy = a + b (BV/TV) | E = c + d (BV/TV) | σy/(BV/TV) | E/(BV/TV) | εy | |||
|---|---|---|---|---|---|---|---|
| a | b | c | d | ||||
| Original | −0.27 (0.55) | 25.98* (4.71) | −31.14 (65.33) | 4105* (556.39) | 22.98* (1.43) | 3763.03* (172.08) | 0.80%* (0.02) |
| Non- Targeted | −0.34 (0.43) | 24.11* (4.36) | −40.55 (57.85) | 3868* (523.70) | 20.23* (1.34) | 3409.83* (166.23) | 0.79%* (0.02) |
| Targeted | −0.45 (0.42) | 19.45* (3.84) | −68.13 (54.48) | 3444* (493.23) | 14.50* (1.23) | 2694.10* (172.81) | 0.73%* (0.02) |
- p < 0.05 v. both other model types
Small differences in microarchitecture parameters were observed among groups (Table 2). With the exception of degree of anisotropy (DA), all the measured microarchitecture parameters were correlated with bone volume fraction within each group (p < 0.01, magnitude of Pearson’s r ranged from 0.65 to 0.88). Yield strength and elastic modulus were significantly correlated with all of the microarchitecture measures except degree of anisotropy (p<0.05 within each group, Table 3). After accounting for the effects of bone volume fraction, many of the correlations between microarchitecture and mechanical properties were no longer significant (Table 4).
Table 2.
Average (SD) of measured microarchitecture indices are shown. Multiple comparisons were performed using the Holm Test (α = 0.05).
| Measure | Original | Non-Targeted | Targeted |
|---|---|---|---|
| BV/TV (%) | 11.185b,c (3.693) | 10.521 (3.476) | 10.520 (3.476) |
| BS/BV (mm−1) | 20.14b,c (3.557) | 21.42a,c (3.667) | 21.29a,b (3.637) |
| Tb.Th (mm) | 0.103b,c (0.020) | 0.096a,c (0.018) | 0.097a,b (0.018) |
| Tb.N (mm−1) | 1.074 (0.241) | 1.077c (0.247) | 1.070b (0.246) |
| Tb.Sp (mm) | 0.877b,c (0.247) | 0.883a,c (0.252) | 0.889a,b (0.254) |
| MIL | 0.207b,c (0.040) | 0.194a,c (0.036) | 0.195a,b (0.037) |
| DA | 1.423b,c (0.157) | 1.399a (0.145) | 1.395a (0.149) |
| SMI | 1.286c (0.417) | 1.292c (0.399) | 1.351a,b (0.409) |
– significantly different from original,
– significantly different from non-targeted,
–significantly different from targeted (p<0.05).
Table 3.
Pearson correlation coefficients between microarchitecture measures and mechanical properties within each group are shown (O-Original, NT-Non-Targeted, T-Targeted).
| σy | E | εy | |||||||
|---|---|---|---|---|---|---|---|---|---|
| O | NT | T | O | NT | T | O | NT | T | |
| BV/TV | 0.83* | 0.83* | 0.80* | 0.89* | 0.89* | 0.88* | 0.24 | 0.25 | 0.22 |
| BS/BV (mm−1) | −0.57* | −0.55* | −0.55* | −0.72* | −0.70* | −0.67* | 0.11 | 0.15 | 0.09 |
| Tb.Th (mm) | 0.53* | 0.51* | 0.51* | 0.69* | 0.67* | 0.66* | −0.16 | −0.18 | −0.13 |
| Tb.N (mm−1) | 0.85* | 0.86* | 0.82* | 0.80* | 0.81* | 0.80* | 0.56* | 0.57* | 0.48 |
| Tb.Sp (mm) | −0.87* | −0.87* | −0.83* | −0.86* | −0.87* | −0.86* | −0.44 | −0.45 | −0.38 |
| MIL | 0.53* | 0.51* | 0.51* | 0.69* | 0.67* | 0.66* | −0.16 | −0.19 | −0.13 |
| DA | 0.09 | 0.06 | 0.14 | 0.14 | 0.13 | 0.16 | −0.16 | −0.22 | −0.04 |
| SMI | −0.80* | −0.83* | −0.84* | −0.70* | −0.74* | −0.77* | −0.63* | −0.62* | −0.63* |
p < 0.05
Table 4.
Partial correlations accounting for effect of BV/TV within each group are shown (note that yield strain is not included since it was not correlated with bone volume fraction).
| σy | E | |||||
|---|---|---|---|---|---|---|
| Original | Non-Targeted | Targeted | Original | Non-Targeted | Targeted | |
| BS/BV (mm−1) | 0.41 | 0.44 | 0.35 | 0.13 | 0.16 | 0.17 |
| Tb.Th (mm) | −0.50 | −0.52* | −0.43 | −0.20 | −0.22 | −0.23 |
| Tb.N (mm−1) | 0.53* | 0.54* | 0.44 | 0.24 | 0.26 | 0.25 |
| Tb.Sp (mm) | −0.53* | −0.52* | −0.43 | −0.35 | −0.36 | −0.34 |
| MIL | −0.48 | −0.50 | −0.41 | −0.19 | −0.21 | −0.21 |
| DA | −0.01 | −0.05 | 0.10 | 0.11 | 0.09 | 0.16 |
| SMI | −0.62* | −0.62* | −0.70* | −0.35 | −0.37 | −0.52* |
p < 0.05
Microarchitecture measures were not able to explain the observed differences in biomechanics-bone volume fraction characteristics among the groups. None of the measured microarchitecture indices contributed to the slope of the elastic modulus-bone volume fraction relation (p > 0.09). Trabecular thickness and mean intercept length both showed significant contributions to the slope of the yield strength-bone volume fraction relation (p< 0.05) but could not explain the observed differences among model types (p <0.05). The strength:bone volume fraction ratio was significantly correlated with trabecular number, trabecular separation and structure model index within each group (p<0.05, magnitude of Pearson’s r ranged from 0.53 to 0.77). The elastic modulus:bone volume fraction ratio was significantly correlated to trabecular separation and structure model index in the models with cavities (p <0.05, r ranged from −0.67 to −0.51) and marginally correlated in the original images (p < 0.10, r = −0.46 in both cases). Differences in strength:bone volume fraction and elastic modulus:bone volume fraction ratios among groups (original, non-targeted, targeted) were maintained even after accounting for the variation in measured microarchitecture indices. Trabecular number and structure model index both showed significant correlations to yield strain (p < 0.05), but could not account for differences among model types.
DISCUSSION
Using a validated, high-resolution non-linear finite element method we sought to determine if the addition of resorption cavities that do not disconnect trabeculae can influence cancellous bone yield strength and elastic modulus more than would be expected from the associated change in bone volume fraction, and if such effects depended on the location of the cavities. We found that typically-sized resorption cavities can modify the slope of the relationship between bone strength and bone volume fraction by as much as 25%. In addition, we found that the effect of cavities on the slope of the strength-bone volume fraction relationships can be much greater if cavities are targeted to regions of high strain, suggesting that such cavity placement can be important biomechanically. Taken together these findings provide evidence that resorption cavities can indeed influence the mechanical behavior of cancellous bone, particularly if the cavities are placed in regions of high tissue strain.
A number of characteristics of the study lend support to our conclusions. First, our finite element methodology is one of the most realistic available, accounting for material nonlinearities including tension-compression asymmetries in bone tissue strength as well as geometric nonlinearities (large deformations and buckling). The methodology has been shown to give accurate predictions of cancellous bone elastic modulus and yield strength as measured experimentally (27). Second, the size of resorption cavities added to the bone surface was typical of that observed histologically (including the surface length and width). Lastly, the current study utilized statistical methods to detect differences in mechanical properties after taking into account differences in bone volume fraction. As a result, our analysis was able to separate the mechanical effects of the addition of resorption cavities from those associated with reductions in bone volume.
The results of the study should be interpreted with regard to limitations of the mechanical modeling and the simulation of resorption cavities. As finite element modeling involves the conversion of a structure into individual elements, insights gleaned from the models will be limited by their discretized nature. The magnitude of this effect will be related to the element shape and size and can limit the ability of the model to simulate stress riser effects. In the current study the resolution of the finite element mesh (22 μm) was comparable in size to the depth of resorption cavities (44 μm), a fact that may effect local strain concentrations, possibly influencing the absolute differences in bone strength and modulus between models with and without cavities. The use of a non-linear model in the current study is expected to minimize this effect on apparent mechanical properties because, unlike linear models, the tangent modulus of each element is greatly reduced after it yields, limiting the effect of local stress concentrations on neighboring tissue. For these reasons the results of this study do not represent all possible biomechanical effects of stress risers associated with cavities but instead describe only the gross changes in structure associated with the presence of cavities. In addition, the overall resolution of the models, expressed as the ratio of average trabecular thickness to element size, was 3.8–4.0 at the smallest, a resolution sufficient to predict the stiffness of cancellous bone (31,32). Second, because the current study sought to isolate the structural effects of cavities from any other effects, the finite element models used homogeneous (but specimen-specific) tissue properties. Localized variations in tissue properties can influence cancellous bone mechanics (33–35) and may therefore modulate the effects of cavities in vivo. These limitations in mechanical modeling may influence absolute values of strength and stiffness, but since they are consistent in all three groups of this study they are not expected to influence the relative differences between groups, especially the comparisons made between models having targeted and non-targeted cavities.
Although simulation of resorption cavities was performed based on existing evidence, variations in some characteristics between individuals and groups may influence our findings. For example, the volume of bone removed in the form of cavities will have an important effect on net changes in strength and stiffness. The prescribed bone loss in the current study was set to 6% of the original volume, matching estimates of the volume occupied by cavities in the lumbar spine of postmenopausal women (8). As a result, the addition of cavities in this study may represent as much as a doubling of bone turnover – a large change, yet one that is similar to what is observed around the time of menopause (36). In addition, the placement of cavities relative to local microarchitecture may also have an effect on strength and stiffness. Because no disconnections of trabeculae were allowed it is possible that cavity placement might have been biased to thicker trabeculae. While this restriction was necessary to separate the role of cavities from that of disconnections, because disconnections themselves are known to modify bone stiffness relative to volume fraction (37,38), lifting this restriction would most likely increase the observed differences between groups.
In addition, because it was not feasible to identify pre-existing cavities on the original bone surface, it is possible that some cavities in the simulations were added on top of natural cavities, essentially doubling the cavity depth. A supplementary analysis using a cavity depth twice as large (88 μm) as that used in this study (39) found that doubling of cavity depth did indeed modify the magnitude of the changes in strength and stiffness, but did not change the relative differences between groups, supporting our conclusions. In addition, there are aspects of resorption cavities that are not yet well understood, yet may modulate their mechanical effects on cancellous bone. For example, it is not known if the surface size (length and width) and/or the number of cavities can influence cancellous bone mechanics independent of bone volume. Information regarding cavity surface size and number is extremely limited because such measures cannot be performed in two-dimensional sections and precise three-dimensional techniques for making such measures have not yet been developed. Since cavity size was consistent in non-targeted and targeted models it is unlikely that variations in cavity size would affect the statistical significance of the differences between groups.
Lastly, the biomechanical analyses in this study were limited to compressive yield strength and elastic modulus in the primary loading direction. It is possible that the magnitude of observed effects could differ under other loading conditions (shear, fatigue, creep) or in other directions (transverse or multiaxial as opposed to longitudinal) or if other mechanical properties were used as analysis endpoints (toughness, post-yield deflection). It is unclear at this juncture if any of these other loading conditions/mechanical endpoints would be more closely related to vertebral fracture risk than those measured in the current study.
We found that variation in microarchitecture measures could not explain the observed differences in strength-bone volume fraction characteristics was surprising because the differences between model types were entirely microarchitectural. However, most of these microarchitecture measures express averages over the entire specimen (particularly trabecular thickness, number and separation) and may therefore be insensitive variations in surface morphology caused by resorption cavities when measured at this resolution. Additional microarchitecture measures (such as standard deviation of trabecular thickness or separation, direct measures of trabecular thickness or orientation, etc.) that may be more sensitive to variations caused by cavities have been proposed (40,41), but are not yet regularly utilized.
The current study builds upon that presented by van der Linden and colleagues (15). Using linear finite element models they demonstrated that removal of bone tissue experiencing the greatest strain resulted in much larger changes in strain distribution throughout the structure than were observed when bone was lost at random. The current study demonstrates that changes in apparent yield strength can occur when bone is removed in the form of cavities and when no trabeculae are disconnected. Furthermore our study shows that cavities targeted to regions of high strain can have greater effects on cancellous bone strength from those that are placed randomly on the bone surface. Our findings that the percent changes in cancellous bone strength were greater than those in elastic modulus suggests that cavities can have an effect on bone strength different from the effect on modulus, supporting the idea of a “stress riser” effect.
It has been suggested that resorption cavities, even when they do not disconnect trabeculae, may influence cancellous bone strength (12). The current analysis supports this theory – but suggests that the location of the resorption cavity can be a critical factor. This is important in that regions of cancellous bone experiencing the greatest tissue strain are the most likely to sustain tissue damage. Microscopic tissue damage in the form of diffuse damage and microcracks have been found to be spatially and temporally related to the initiation of new bone resorption events in cortical bone (42,43). The current study therefore supports the idea that remodeling targeted to regions of tissue damage may be the most detrimental to bone strength (44). Remodeling associated with tissue damage is commonly referred to as “targeted remodeling,” while “non-targeted remodeling” identifies bone cell activity that is not associated with tissue damage (it is placed randomly or initiated by other factors) (44). It is not yet known what proportion of remodeling in cancellous bone is targeted remodeling. Although no direct measurements have been made, it has been suggested that as much as 30% of remodeling in cortical bone is targeted (45).
Although intended to study the biomechanical effects of resorption cavities, the results of this study can provide insights into the effects of anti-resorptive therapy. By viewing models with cavities as a pre-treatment condition and models without cavities as a post-treatment condition (in which the resorption cavities have been filled) the current study can be viewed as a simulation of anti-resorptive therapy. In this light, the current study suggests that improvements in bone strength caused by the filling of existing resorption cavities may be much greater when remodeling targeted to regions experiencing high strain is affected rather than remodeling that is not specifically targeted to regions of high strain. Concerns regarding the long-term effects of anti-resorptive therapy on the removal of tissue damage have led some to suggest that an ideal anti-resorptive therapy would inhibit non-targeted remodeling without disrupting remodeling targeted to regions of tissue damage (45–47). The current analysis suggests that, with regard to the effects of cavities on strength and stiffness, such an anti-resorptive therapy may not be as effective as a therapy that inhibited both targeted and non-targeted remodeling.
Acknowledgments
The authors thank Sreenu Konda and Harold Haller at the Case Statistical Consulting Center for help with data analysis. This work was supported by NIH/NIAMS AR49570, AR43784, AR049828 and Case Western Reserve University. Computational support was provided in part by the National Science Foundation through the San Diego Supercomputer Center NPACI grant UCB 256. Structure model index measures were performed using 3D Calculator (Erasmus Orthopaedic Research Laboratory and Skyscan, http://www2.eur.nl/fgg/orthopaedics).
Footnotes
Funding Sources: NIH AR49570, AR43784, AR049828, Case Western Reserve University Conflict of Interest: Dr. Keaveny has a financial interest in O.N. Diagnostics and both he and the company may benefit from the results of this research. No other authors have any potential conflict of interest.
References
- 1.Cummings SR, Karpf DB, Harris F, Genant HK, Ensrud K, LaCroix AZ, Black DM. Improvement in spine bone density and reduction in risk of vertebral fractures during treatment with antiresorptive drugs. American Journal of Medicine. 2002;112:281–289. doi: 10.1016/s0002-9343(01)01124-x. [DOI] [PubMed] [Google Scholar]
- 2.Delmas PD, Seeman E. Changes in bone mineral density explain little of the reduction in vertebral or nonvertebral fracture risk with anti-resorptive therapy. Bone. 2004;34:599–604. doi: 10.1016/j.bone.2003.12.022. [DOI] [PubMed] [Google Scholar]
- 3.Garnero P, Hausherr E, Chapuy MC, Marcelli C, Grandjean H, Muller C, Cormier C, Breart G, Meunier PJ, Delmas PD. Markers of bone resorption predict hip fracture in elderly women: the EPIDOS Prospective Study. J Bone Miner Res. 1996;11:1531–8. doi: 10.1002/jbmr.5650111021. [DOI] [PubMed] [Google Scholar]
- 4.Garnero P. Markers of bone turnover for the prediction of fracture risk. Osteoporos Int 11 Suppl. 2000;6:S55–65. doi: 10.1007/s001980070006. [DOI] [PubMed] [Google Scholar]
- 5.Riggs BL, Melton LJ., 3rd Bone turnover matters: the raloxifene treatment paradox of dramatic decreases in vertebral fractures without commensurate increases in bone density. J Bone Miner Res. 2002;17:11–4. doi: 10.1359/jbmr.2002.17.1.11. [DOI] [PubMed] [Google Scholar]
- 6.Heaney RP. Is the paradigm shifting? Bone. 2003;33:457–65. doi: 10.1016/s8756-3282(03)00236-9. [DOI] [PubMed] [Google Scholar]
- 7.Parfitt AM. What is the normal rate of bone remodeling? Bone. 2004;35:1–3. doi: 10.1016/j.bone.2004.03.022. [DOI] [PubMed] [Google Scholar]
- 8.Heaney RP. The bone-remodeling transient: implications for the interpretation of clinical studies of bone mass change. J Bone Miner Res. 1994;9:1515–23. doi: 10.1002/jbmr.5650091003. [DOI] [PubMed] [Google Scholar]
- 9.Boivin GY, Chavassieux PM, Santora AC, Yates J, Meunier PJ. Alendronate increases bone strength by increasing the mean degree of mineralization of bone tissue in osteoporotic women. Bone. 2000;27:687–694. doi: 10.1016/s8756-3282(00)00376-8. [DOI] [PubMed] [Google Scholar]
- 10.Hernandez CJ, Beaupré GS, Marcus R, Carter DR. A theoretical analysis of the contributions of remodeling space, mineralization and bone balance to changes in bone mineral density during alendronate treatment. Bone. 2001;29:511–16. doi: 10.1016/s8756-3282(01)00613-5. [DOI] [PubMed] [Google Scholar]
- 11.Parfitt AM. In: Christiansen C, Riis BJ, editors. Pathophysiology of bone fragility; Proceedings of the 4th International Symposium on Osteoporosis; Handelstrykkeriet Aalborg AP, Aalborg, Denmark, Hong Kong. 1993. pp. 164–6. [Google Scholar]
- 12.Parfitt AM. High bone turnover is intrinsically harmful: two paths to a similar conclusion. The Parfitt view. J Bone Miner Res. 2002;17:1558–9. doi: 10.1359/jbmr.2002.17.8.1558. author reply 1560. [DOI] [PubMed] [Google Scholar]
- 13.Parfitt AM. Age-related structural changes in trabecular and cortical bone: cellular mechanisms and biomechanical consequences. Calcified Tissue International. 1984;36(Suppl 1):S123–128. doi: 10.1007/BF02406145. [DOI] [PubMed] [Google Scholar]
- 14.Smit TH, Burger EH. Is BMU-coupling a strain-regulated phenomenon? A finite element analysis. J Bone Miner Res. 2000;15:301–7. doi: 10.1359/jbmr.2000.15.2.301. [DOI] [PubMed] [Google Scholar]
- 15.van der Linden JC, Homminga J, Verhaar JA, Weinans H. Mechanical consequences of bone loss in cancellous bone. J Bone Miner Res. 2001;16:457–65. doi: 10.1359/jbmr.2001.16.3.457. [DOI] [PubMed] [Google Scholar]
- 16.McNamara LM, van der Linden JC, Weinans H, Prendergast PJ. Stress-concentrating effect of resorption lacunae in trabecular bone. J Biomech. 2005 doi: 10.1016/j.jbiomech.2004.12.027. In Press. [DOI] [PubMed] [Google Scholar]
- 17.Ulrich D, Van Rietbergen B, Weinans H, Ruegsegger P. Finite element analysis of trabecular bone structure: a comparison of image-based meshing techniques. Journal of Biomechanics. 1998;31:1187–1192. doi: 10.1016/s0021-9290(98)00118-3. [DOI] [PubMed] [Google Scholar]
- 18.Parfitt AM. Osteonal and hemi-osteonal remodeling: the spatial and temporal framework for signal traffic in adult human bone. J Cell Biochem. 1994;55:273–86. doi: 10.1002/jcb.240550303. [DOI] [PubMed] [Google Scholar]
- 19.Mosekilde L. Consequences of the remodelling process for vertebral trabecular bone structure: a scanning electron microscopy study (uncoupling of unloaded structures) Bone Miner. 1990;10:13–35. doi: 10.1016/0169-6009(90)90046-i. [DOI] [PubMed] [Google Scholar]
- 20.Eriksen EF, Hodgson SF, Eastell R, Cedel SL, O'Fallon WM, Riggs BL. Cancellous bone remodeling in type I (postmenopausal) osteoporosis: quantitative assessment of rates of formation, resorption, and bone loss at tissue and cellular levels. Journal of Bone and Mineral Research. 1990;5:311–9. doi: 10.1002/jbmr.5650050402. [DOI] [PubMed] [Google Scholar]
- 21.Compston JE, Croucher PI. Histomorphometric assessment of trabecular bone remodelling in osteoporosis. Bone Miner. 1991;14:91–102. doi: 10.1016/0169-6009(91)90086-f. [DOI] [PubMed] [Google Scholar]
- 22.Odgaard A. Quantification of Cancellous Bone Architecture. In: Cowin SC, editor. Bone Mechanics Handbook. 2. CRC press; Boca Raton, FL, USA: 2001. pp. 14.1–19. [Google Scholar]
- 23.Hildebrand T, Ruegsegger P. Quantification of Bone Microarchitecture with the Structure Model Index. Comput Methods Biomech Biomed Engin. 1997;1:15–23. doi: 10.1080/01495739708936692. [DOI] [PubMed] [Google Scholar]
- 24.Van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite element models. Journal of Biomechanics. 1995;28:69–81. doi: 10.1016/0021-9290(95)80008-5. [DOI] [PubMed] [Google Scholar]
- 25.Stolken JS, Kinney JH. On the importance of geometric nonlinearity in finite-element simulations of trabecular bone failure. Bone. 2003;33:494–504. doi: 10.1016/s8756-3282(03)00214-x. [DOI] [PubMed] [Google Scholar]
- 26.Bayraktar HH, Adams MF, Gupta A, Papadopoulos P, Keaveny TM. The role of large deformations in trabecular bone mechanical behavior; ASME Bioengineering Conference; Key Biscayne, FL. 2003. pp. 31–32. [Google Scholar]
- 27.Bevill G, Gupta A, Papadopoulos P, Keaveny TM. Orthop Res Soc; Washington D.C.: 2005. Large deformation effects in the failure behavior of trabecular bone Trans. [Google Scholar]
- 28.Papadopoulos P, Lu J. On the formulation and numerical solution of problems in anisotropic finite plasticity. Computer Methods in Applied Mechanics and Engineering. 2001;190:4889–4910. [Google Scholar]
- 29.Bayraktar HH, Morgan EF, Niebur GL, Morris GE, Wong EK, Keaveny TM. Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. J Biomech. 2004;37:27–35. doi: 10.1016/s0021-9290(03)00257-4. [DOI] [PubMed] [Google Scholar]
- 30.Hernandez CJ, Keaveny TM. A biomechanical perspective on bone quality. 2006. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Guldberg RE, Hollister SJ, Charras GT. The accuracy of digital image-based finite element models. Journal of Biomechanical Engineering. 1998;120:289–295. doi: 10.1115/1.2798314. [DOI] [PubMed] [Google Scholar]
- 32.Niebur GL, Yuen JC, Hsia AC, Keaveny TM. Convergence behavior of high-resolution finite element models of trabecular bone. Journal of Biomechanical Engineering. 1999;121:629–635. doi: 10.1115/1.2800865. [DOI] [PubMed] [Google Scholar]
- 33.van der Linden JC, Birkenhager-Frenkel DH, Verhaar JA, Weinans H. Trabecular bone's mechanical properties are affected by its non-uniform mineral distribution. J Biomech. 2001;34:1573–80. doi: 10.1016/s0021-9290(01)00146-4. [DOI] [PubMed] [Google Scholar]
- 34.Jaasma MJ, Bayraktar HH, Niebur GL, Keaveny TM. Orthop Res Soc. Vol. 26. San Francisco: 2001. The effects of intraspecimen variations in tissue modulus on the apparent mechanical properties of trabecular bone Trans; p. 513. [Google Scholar]
- 35.Bourne BC, van der Meulen MC. Finite element models predict cancellous apparent modulus when tissue modulus is scaled from specimen CT-attenuation. J Biomech. 2004;37:613–21. doi: 10.1016/j.jbiomech.2003.10.002. [DOI] [PubMed] [Google Scholar]
- 36.Recker R, Lappe J, Davies KM, Heaney R. Bone remodeling increases substantially in the years after menopause and remains increased in older osteoporosis patients. J Bone Miner Res. 2004;19:1628–33. doi: 10.1359/JBMR.040710. [DOI] [PubMed] [Google Scholar]
- 37.Silva MJ, Gibson LJ. Modeling the mechanical behavior of vertebral trabecular bone: Effects of age-related changes in microstructure. Bone. 1997;21:191–199. doi: 10.1016/s8756-3282(97)00100-2. [DOI] [PubMed] [Google Scholar]
- 38.Guo XE, Kim CH. Mechanical consequence of trabecular bone loss and its treatment: a three-dimensional model simulation. Bone. 2002;30:404–11. doi: 10.1016/s8756-3282(01)00673-1. [DOI] [PubMed] [Google Scholar]
- 39.Hernandez CJ, Gupta A, Keaveny TM. Remodeling cavities and stress risers: A biomechanical study on cancellous bone strength. 27th Annual Meeting of the American Society for Bone and Mineral Research; Nashville, TN, USA. 2005. p. S162. [Google Scholar]
- 40.Borah B, Dufresne TE, Chmielewski PA, Gross GJ, Prenger MC, Phipps RJ. Risedronate preserves trabecular architecture and increases bone strength in vertebra of ovariectomized minipigs as measured by three-dimensional microcomputed tomography. J Bone Miner Res. 2002;17:1139–47. doi: 10.1359/jbmr.2002.17.7.1139. [DOI] [PubMed] [Google Scholar]
- 41.Kinney JH, Stolken JS, Smith TS, Ryaby JT, Lane NE. An orientation distribution function for trabecular bone. Bone. 2005;36:193–201. doi: 10.1016/j.bone.2004.09.023. [DOI] [PubMed] [Google Scholar]
- 42.Mori S, Burr DB. Increased intracortical remodeling following fatigue damage. Bone. 1993;14:103–9. doi: 10.1016/8756-3282(93)90235-3. [DOI] [PubMed] [Google Scholar]
- 43.Bentolila V, Boyce TM, Fyhrie DP, Drumb R, Skerry TM, Schaffler MB. Intracortical remodeling in adult rat long bones after fatigue loading. Bone. 1998;23:275–81. doi: 10.1016/s8756-3282(98)00104-5. [DOI] [PubMed] [Google Scholar]
- 44.Parfitt AM. Targeted and nontargeted bone remodeling: relationship to basic multicellular unit origination and progression. Bone. 2002;30:5–7. doi: 10.1016/s8756-3282(01)00642-1. [DOI] [PubMed] [Google Scholar]
- 45.Burr DB. Targeted and nontargeted remodeling. Bone. 2002;30:2–4. doi: 10.1016/s8756-3282(01)00619-6. [DOI] [PubMed] [Google Scholar]
- 46.Parfitt AM, Mundy GR, Roodman GD, Hughes DE, Boyce BF. A new model for the regulation of bone resorption, with particular reference to the effects of bisphosphonates. J Bone Miner Res. 1996;11:150–9. doi: 10.1002/jbmr.5650110203. [DOI] [PubMed] [Google Scholar]
- 47.Li J, Mashiba T, Burr DB. Bisphosphonate treatment suppresses not only stochastic remodeling but also the targeted repair of microdamage. Calcif Tissue Int. 2001;69:281–6. doi: 10.1007/s002230010036. [DOI] [PubMed] [Google Scholar]


