Molecular Dynamics Simulations Using Temperature-Enhanced Essential Dynamics Replica Exchange

Abstract

Today's standard molecular dynamics simulations of moderately sized biomolecular systems at full atomic resolution are typically limited to the nanosecond timescale and therefore suffer from limited conformational sampling. Efficient ensemble-preserving algorithms like replica exchange (REX) may alleviate this problem somewhat but are still computationally prohibitive due to the large number of degrees of freedom involved. Aiming at increased sampling efficiency, we present a novel simulation method combining the ideas of essential dynamics and REX. Unlike standard REX, in each replica only a selection of essential collective modes of a subsystem of interest (essential subspace) is coupled to a higher temperature, with the remainder of the system staying at a reference temperature, T₀. This selective excitation along with the replica framework permits efficient approximate ensemble-preserving conformational sampling and allows much larger temperature differences between replicas, thereby considerably enhancing sampling efficiency. Ensemble properties and sampling performance of the method are discussed using dialanine and guanylin test systems, with multi-microsecond molecular dynamics simulations of these test systems serving as references.

INTRODUCTION

In recent years theoretical methods, especially molecular dynamics (MD) simulations, have been increasingly applied to study structure-function relationships in proteins. One of the main questions to be answered when assessing the usefulness of MD simulations of proteins in understanding biological functions is the degree to which the simulations adequately sample the conformational space of the protein. If a given property is poorly sampled over the MD simulation, the results obtained are often of limited significance.

A straightforward way to solve this problem is to increase the simulation time. With the improvements in computer power and algorithms, state of the art simulations have progressed to multiple nanoseconds. This timescale is usually too short for the observation of many important functional processes, such as slow conformational changes and protein folding/unfolding.

Inefficiency in sampling is a result of the ruggedness of the energy landscape. Although the exploration of different conformational states and the mechanism of global conformational transitions are of higher interest than the examination of local fluctuations during a simulation, the system will spend most of its time in locally stable states (kinetic trapping).

Various methods have been proposed to remedy this problem. Among them, generalized ensemble algorithms have been widely used in recent years (for a review, see Mitsutake et al. (1)). The idea is to achieve a random walk in potential energy space which allows the system to easily overcome energy barriers separating local minima, thus enabling a much wider sampling of phase space compared to conventional MD simulations. Besides the multi-canonical algorithm (2,3) and simulated tempering (4,5), the replica exchange (REX) method (6–9) is a well-known approach. In the standard temperature formulation (6) of REX, a number of noninteracting simulations of the same system (replicas) is performed in parallel, each having a different temperature; at given time intervals, neighboring temperature replica pairs are exchanged with a specific transition probability. The resulting random walk in temperature space induces a random walk in energy space, thereby allowing kinetically trapped low-energy replicas to escape from local minima with the help of high-temperature replicas.

At full atomic resolution using explicit solvent, for all but the smallest systems simulated temperature REX simulations have one major drawback: Since the number of replicas needed to span a given temperature range is roughly proportional to the square root of the number of degrees of freedom of the system, many replicas need to be simulated, rendering temperature REX simulations of these systems computationally very demanding.

During the last few years, multiple approaches have been devised to deal with the large number of explicit degrees of freedom (10–13). Often, when simulating biomolecular systems, one is mainly interested in a few large-scale motions of the system. For the latter, collective coordinates (14,15) offer a convenient description. They can be obtained through a principal axis transformation of the covariance matrix of structural fluctuations of the system of interest. Principal components analysis (PCA) or essential dynamics analysis (16) are routinely used for this task. It has been shown that selective excitation of such collective modes can yield a significant increase of sampling efficiency (17–19) at the cost, however, of biasing the obtained ensemble.

Here, we present a new method, combining the ideas of REX and essential dynamics aiming at an enhanced sampling efficiency while at the same time approximately preserving the ensemble. Unlike temperature REX, in each replica only a few selected degrees of freedom are coupled to a higher temperature with the remainder of the system staying at a reference temperature, T₀. The excited degrees of freedom—the essential subspace—are given by the dominant collective modes of a subsystem of interest, obtained, e.g., from a PCA or a normal mode analysis (NMA). This selective excitation of the essential subspace along with the replica framework permits efficient conformational sampling and allows much larger temperature differences between replicas, thereby considerably enhancing sampling efficiency. We show that our new method reproduces ensembles generated by MD very well but at much lower computational costs, making temperature-enhanced essential subspace replica exchange (TEE-REX), a powerful simulation technique for large all-atom simulations using explicit solvent.

METHODS

All simulations were carried out using the MD software package GROMACS 3.3.1 (20), supplemented by the TEE-REX module. The OPLS-all-atom force field (21) was used for proteins and TIP4P was used as a water model (22). All simulations were performed in the NPT ensemble. In all MD simulations the temperature was kept constant at T = 300 K by coupling to an isotropic Berendsen thermostat (23) with a coupling time of τ_t = 1 ps. The pressure was coupled to a Berendsen barostat (23) with τ_p = 0.1 ps and an isotropic compressibility of 4.5 × 10⁻⁵ bar⁻¹ in the x, y, and z directions. All bonds were constrained by using the LINCS algorithm (24). An integration time step of Δt = 2 fs was used. Lennard-Jones and coulombic interactions were calculated explicitly at a distance smaller than 10 Å; above 10 Å, long-range electrostatic interactions were calculated by particle mesh Ewald summation (25) with a grid spacing of 0.12 nm and fourth-order B-spline interpolation.

The MD reference simulation system of dialanine was set up as follows. Pymol (26) was used to build an N-acetylated dialanine to neutralize the electrostatic attraction between the N- and the C-termini. The protein was solvated in a rhombic dodecahedral box with box vectors of 2.35-Å length. The system comprised ∼1200 atoms. One Na⁺ ion was added to neutralize the system. Energy minimization of the solvated system using the steepest descent algorithm was followed by a 100-ps MD simulation at the target temperature using harmonic position restraints on the heavy atoms of the protein with a force constant of k = 1000 kJmol⁻¹ nm⁻² to equilibrate the solvent. After 1 ns of equilibration, a 4.1-μs trajectory was produced by free MD simulation. Structures were saved every 1 ps for further analysis.

Four 210-ns TEE-REX simulations of dialanine starting from different equilibrated MD structures were performed. Each TEE-REX simulation consisted of two replicas, with an essential subspace temperature of 500 K for the second replica. A PCA was performed on the first 1.87 μs of the full MD trajectory, taking all backbone atoms into account. The first two eigenvectors, describing 92% of all backbone fluctuations, defined the essential subspace. The essential subspace was coupled to a Berendsen thermostat with a coupling time of 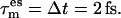Exchanges between replicas were attempted every 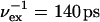and were accepted with 97.7% probability. Structures were saved every 1 ps. After each successful exchange, 40 ps of trajectory were discarded to yield equilibrated structure ensembles.

Free energy landscapes of dialanine were calculated in the subspace spanned by the first two eigenvectors (essential subspace). Assuming equilibrated ensembles, the relative Gibbs free energy

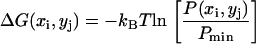(1)

was calculated for discrete grid points (x_i, y_j) using a k-nearest neighbor scheme (27) for the spatial probability function P(x_i, y_j).

The MD reference simulation system of guanylin was set up as follows. From a standard REX simulation a snapshot of the 300-K reference replica served as the MD starting structure. The simulation system is based on the protonated crystal structure (Protein Data Bank (PDB) entry 1GNA), solvated in a rhombic dodecahedral box and neutralized adding Na⁺ ions accordingly. The system comprised ∼6000 atoms. Energy minimization of the solvated system using the steepest descent algorithm was followed by a 100-ps MD simulation at the target temperature using harmonic position restraints on the heavy atoms of the protein with a force constant of k = 1000 kJmol⁻¹ nm⁻² to equilibrate the solvent. After 1 ns of equilibration, a 800-ns trajectory was produced by free MD simulation. Structures were saved every 2 ps for further analysis.

One 130-ns TEE-REX simulation of guanylin starting from an equilibrated MD structure was performed. Three replicas were simulated, having essential subspace temperatures of 450 K and 800 K. A PCA of a 50-ns MD trajectory fragment taking all backbone atoms into account was performed. The first six eigenvectors, describing 87% of all backbone fluctuations, defined the essential subspace. Exchanges were attempted every 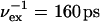and were accepted with 97.8% probability. Structures were saved every 1 ps. After each successful exchange, 40 ps of trajectory were discarded.

Replica exchange

In standard REX MD (6), a generalized ensemble from M + 1 noninteracting trajectories at temperatures {T₀, T₁, …, T_M} (T_m ≤ T_m+1; m = 0, …, M) is constructed. A state of this generalized ensemble is characterized by 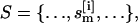where 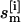represents the coordinates 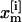and velocities 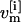of all atoms of the ith replica at temperature T_m. Here, the superscript [i] and the subscript m label the replica and the temperature, respectively. The statistical weight of a state, S, is given by the product of Boltzmann factors exp{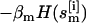} for each replica m, 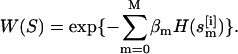Here, 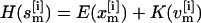denotes the Hamiltonian of replica m, with E(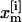) being the potential and K(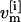) the kinetic energy; 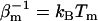denotes the inverse temperature of replica m. The algorithm consists of two consecutive steps: a), independent constant-temperature simulations of each replica, and b), exchange of two replicas 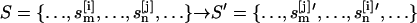according to a Metropolis-like criterion. The exchange acceptance probability follows directly from applying the detailed balance condition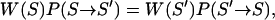

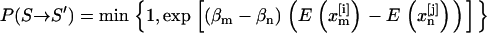(2)

For simulations performed in the NPT-ensemble, Eq. 2 is modified by a pressure correction term (7). Upon exchange, velocities 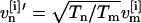and 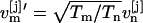are rescaled, thereby eliminating the kinetic energy terms in Eq. 2 (6). Iterating steps a and b, the trajectories of the generalized ensemble perform a random walk in temperature space, which in turn induces a random walk in energy space. This facilitates an efficient and statistically correct conformational sampling of the energy landscape of the system, even in the presence of multiple local minima.

The choice of temperatures is crucial for an optimal performance of the algorithm. Replica temperatures have to be chosen such that a), the lowest temperature is small enough to sufficiently sample low-energy states; b), the highest temperature is large enough to overcome energy barriers of the system of interest; and c), the acceptance probability 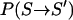is sufficiently high, requiring adequate overlap of potential energy distributions for neighboring replicas. For larger systems simulated with explicit solvent, the latter condition presents the main bottleneck. A simple estimate (13,28) shows that the potential energy difference ΔE ∼ N_dfΔT is dominated by the contribution from the solvent degrees of freedom, 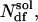constituting the largest fraction of the total number of degrees of freedom, N_df, of the system. Obtaining a reasonable acceptance probability therefore relies on keeping the temperature gaps T_m+1 − T_m small (typically only a few K), which drastically increases computational demands.

Temperature-enhanced essential dynamics replica exchange

The basis for TEE-REX is given by the replica framework, i.e., M + 1 replicas (m = 0, …, M) of the system are simulated simultaneously with periodic exchange attempts. In contrast to standard REX, TEE-REX replicas m = 1, …, M are divided into an essential subspace and its complement. The essential subspace {es}: = {μ_i | i = 1, …, N_es} is defined by a set of eigenvectors, {μ_k}, describing collective modes of a subsystem of interest. A loop region or the protein backbone could be such a subsystem. The collective degrees of freedom, {μ_k}, can be obtained in a variety of ways, e.g., from an NMA of a single structure or a PCA of an ensemble of structures (e.g., NMR or x-ray data or a previous simulation). The latter method is used here. Between exchanges, the essential subspace of replicas m = 1, …, M is coupled to a temperature bath 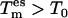with the rest of the simulation system staying at the reference temperature, T₀. For replica m = 0, no partition into {es} and its complement is applied and all degrees of freedom are coupled to the same temperature, 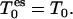The ensemble generated by this reference replica is used for analysis later.

Temperature coupling

The temperature coupling (due to the unique assignment of temperatures with replicas in all TEE-REX simulations reported here, the replica index [i] is dropped henceforth) of the essential subspace {es} is carried out in the following way: Let N_I be the number of atoms of the subsystem of interest by which the eigenvectors 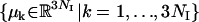are defined. We denote these atoms “index atoms” to distinguish them from the remaining atoms of the system. The total number of atoms in the system is thus given by N = N_I + N_R (R for “remaining”). At each time step, the essential subspace temperature coupling for replica m = 1, …, M is achieved by projecting the velocity vector 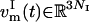of the index group onto the selected modes μ_i, i = 1, …, N_es:

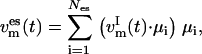(3)

followed by a coupling of 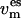(t) to the respective {es} temperature 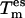using a Berendsen thermostat,

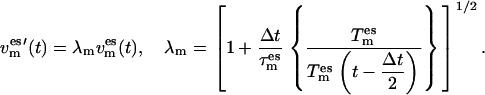(4)

All velocity components not coupled to the essential subspace, i.e., 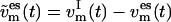and 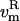(t), are coupled to the reference temperature, T₀, using any standard coupling algorithm (23,29,30). For the Berendsen thermostat used here, the coupling of the nonessential velocity components is given by 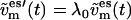and 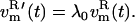Thus, after temperature coupling, the velocity vector v′_m(t) ∈ R^3N of the full system reads

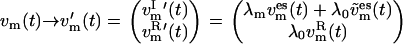The reference replica m = 0 undergoes a standard MD simulation, since v′₀(t) = λ₀v₀(t).

Exchange probability

The coupling of different degrees of freedom to different temperature baths {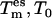} creates an inherent nonequilibrium situation. Except for the reference replica m = 0, the statistical weight of each state in replica m > 0 is therefore no longer known. To account for this new situation, the acceptance probability of Eq. 2 used for standard REX is modified. The additional kinetic energy (Eq. 4) put into the few essential degrees of freedom (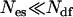) is conceptualized as distributed over the whole system, thus defining an effective temperature. Starting from the kinetic energy of replica m, 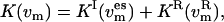and using the equipartition theorem 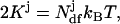we arrive at the effective temperature

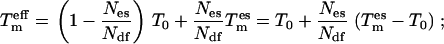(5)

N_df denotes the degrees of freedom of the complete system. Given Eq. 5, the modified acceptance criterion used in TEE-REX thus reads

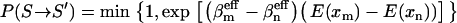(6)

By replacing 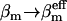in Eq. 2 of the standard REX criterion, one implicitly assumes that the ensemble created by each replica can be described by an equilibrium Boltzmann distribution at the effective temperature introduced in Eq. 5. Since each nonreference replica by construction samples some unknown nonequilibrium distribution, this approximation introduces—upon exchange with the reference replica—some bias in the statistics of the reference ensemble m = 0. However, the number of degrees of freedom of the complete system is much larger than the few excited degrees of freedom comprising the essential subspace {es} (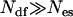). Hence, the approximation made in Eq. 5 can be considered a small deviation from an equilibrium distribution and, therefore, can be expected to be valid for all but the smallest systems simulated with TEE-REX.

The composition of the essential subspace (i.e., what modes have been chosen) is irrelevant with respect to the definition of 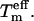However, the excitations obtained using a specific {es} naturally depend on the choice of modes. Each PCA mode represents a single (collective) degree of freedom, contributing via equipartition—like any other degree of freedom—to the kinetic energy. This is independent of whether the respective mode describes a global transition or a more localized motion (e.g., involving a loop). Here, it is important to note that PCA modes describe linearly independent collective modes, thereby neglecting nonlinear couplings. If one specific eigenvector is excited, several other modes are indirectly excited, either outside the {es} (like side chains) or inside the essential subspace.

To validate the approximation made in Eq. 5, extensive tests of the TEE-REX protocol were made using a dialanine peptide. As a converged MD ensemble is available for this system, it allows us to quantitatively assess any systematic deviations possibly introduced by the TEE-REX protocol.

RESULTS AND DISCUSSION

To probe the ensemble generated by TEE-REX, a 4.1-μs explicit-solvent MD simulation of an N-acetylated dialanine peptide was compared to four 210-ns TEE-REX simulations of the same system (see Methods section for computational details). Dialanine was chosen since it constitutes one of the smallest systems with a nontrivial configuration space. Because of its small size, extensive trajectories can be generated within a reasonable amount of time. The main motions of dialanine occur around its (φ,ψ)-pair of dihedrals; hence, the available configuration space of the system is very limited. This increases chances to achieve complete sampling with our simulations. Furthermore, deviations from the equilibrium distribution due to the excitation of the essential subspace {es} are largest for very small systems. For dialanine, the fraction N_es/N_df ∼ 10⁻³ is at least one order of magnitude larger than for systems usually simulated.

Convergence of the MD reference

The thermodynamic behavior of a system is completely known when a thermodynamic potential such as the Gibbs free energy is available. Comparing free energies thus enables us to decide to what degree ensembles created by both methods coincide. However, calculating relative free energies according to Eq. 1 requires a converged ensemble. Therefore, as a first step, we checked whether the MD reference trajectory yielded a converged ensemble, i.e., a complete sampling of the configuration space of the system.

Backbone eigenvectors obtained from a PCA of the full 4.1-μs MD trajectory were compared to eigenvector sets calculated from trajectory fragments of 180-ns to 1.87-μs length. Then, subspaces spanned by the first four eigenvectors of each set were constructed. Therein, 97% of all backbone fluctuations are covered. Overlaps of these different subspaces with the subspace of the full trajectory indicate that structural convergence is reached for trajectory fragments of lengths ≥400 ns (measured subspace overlap of 100%). As a second test for convergence, transitions between the two main dialanine conformations were counted. Fig. 1 B shows representative structures found along the system path overlaid onto a two-dimensional free energy surface (eigenvectors used for projecting are derived from a 1870-ns MD run; see Methods section) derived from a 420-ns MD trajectory piece. The main motion of the system is a rotation around its only dihedral pair around the C_α-C bond between the C_α atom of Ala¹ and the carbon atom of the second peptide unit. Starting from an “open” conformation (with respect to the distance of the N- and C-termini) in the left basin (eigenvector μ₁ ≤ −0.1), a transition to a “closed” conformation in the right basin (eigenvector μ₁ ≥ 0.2) takes place. During the 4.1 μs of MD simulation time, more than 900 transitions between the “open” and the “closed” conformation were observed, giving further evidence for a converged ensemble covering complete configuration space.

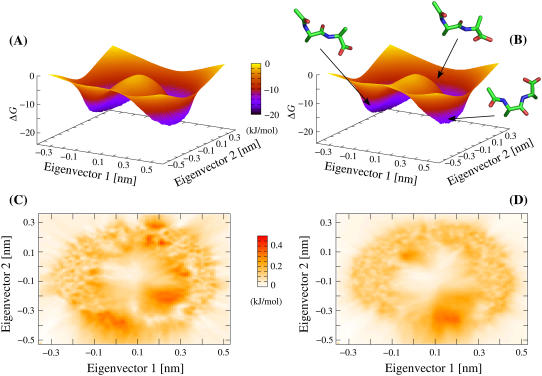
FIGURE 1.

Comparison of dialanine ensembles generated by TEE-REX and MD. Gibbs relative free energy surfaces (in units of kJ/mol) with respect to the first two MD-derived (see Methods section) backbone eigenvectors ({es}) are shown for a TEE-REX ensemble (A) and an ensemble from a 420-ns MD trajectory (B) overlaid by representative structures found along the system pathway. Transitions between the “open” (left basin) and the “closed” (right basin) conformation along the lower pathway are hindered by a free energy barrier (saddle) of ∼15 kJ/mol. The saddle region is sampled more intensely by TEE-REX. All calculations were carried out on an equal number of samples. (C and D): standard deviations (top view, units of kJ/mol) σ_TEE-REX (C) and σ_MD (D), calculated for all four TEE-REX and all nine MD free energy surfaces, respectively. Statistical errors of ≤0.4 kJ/mol ≃ 0.15 k_BT are comparable for both methods.

As a further test for convergence we evaluated relative free energy landscapes for dialanine ensembles generated by MD and TEE-REX (see below).

Ensemble comparison—free energy landscape

Ensembles generated by both methods were compared using relative Gibbs free energy landscapes ΔG(x, y) calculated from trajectory projections onto the two-dimensional essential subspace {es} excited in all dialanine TEE-REX simulations (see Fig. 1). An 1870-ns piece of the full 4.1-μs MD trajectory was used to define the {es} eigenvectors (see Methods section). We used the information that ensembles from trajectory parts of length ≥400 ns are converged to define nine independent nonoverlapping 420-ns MD trajectory fragments out of the full 4.1-μs MD reference. The length of a single two-replica TEE-REX simulation was set to 210 ns. This ensured that ensembles are compared that were generated using the same computational effort. Four 210-ns two-replica TEE-REX simulations with {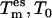} temperatures {300 K, 300 K} and {500 K, 300 K} were started from different MD snapshots taken from the full MD trajectory to check for any dependence of the sampling with respect to the starting structure.

The upper panels of Fig. 1 show typical Gibbs relative free energy surfaces (in units of kJ/mol) for TEE-REX (A) and MD (B) ensembles with respect to the first two backbone eigenvectors comprising the essential subspace {es}. The observed ring structure seen in all ensembles is due to the fact that a nonlinear dihedral rotation is described by two orthogonal linear PCA coordinates. Two distinct conformations are distinguishable, an “open” conformation located in the left minimum of the ΔG surface and a “closed” conformation located in the right minimum. Transitions between the two conformations occur along the free energy “valley” (upper pathway), illustrated by representative structures shown in Fig. 1 B. A free energy barrier of ∼15 kJ/mol (saddle) impedes the conformational transition along the lower pathway. From visual inspection, no apparent difference between the free energy surfaces determined by the two methods is seen, indicating that TEE-REX creates ensembles very similar to that created by MD.

Fig. 1, C and D, displays standard deviations σ_TEE-REX and σ_MD (in units of kJ/mol), calculated from all four TEE-REX and all nine MD ΔG surfaces, respectively. The statistical error of <0.4 kJ/mol of both methods is very low with respect to the absolute ΔG values. This further supports the assumption of converged ensembles in both cases. In the case of MD (D), the largest statistical errors are found in the saddle region, hindering conformational transitions along the lower pathway. These comparatively large errors are due to the poor sampling in this part of the configuration space, since barrier heights of 15 kJ/mol are rarely overcome by MD during 420 ns of simulation time. Although the central region is not sampled by MD (see Fig. 1 D), Fig. 1 C shows that TEE-REX explores this region, indicating the ability of the latter to sample high-energy regions more frequently than MD. In comparing Fig. 1, C and D, it is important to note that σ_TEE-REX was constructed using four samples, whereas nine MD samples were used for σ_MD.

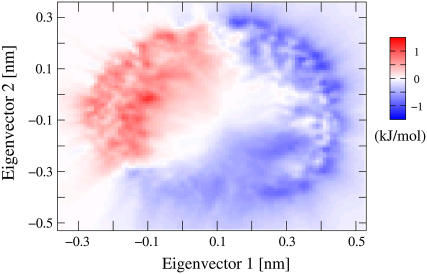
From visual inspection of panels (A) and (B) of Fig. 1, no apparent difference in the ensembles generated by TEE-REX and MD is seen. To investigate the shape of the free energy surfaces generated by both methods in detail, in Fig. 2, the difference 〈ΔG_TEE-REX − ΔG_MD〉 averaged over all combinations 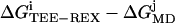(i = 1, …, 4; j = 1, …, 9) is displayed in the top view. Areas colored in blue are sampled more frequently by TEE-REX than by MD since ΔG_TEE-REX < ΔG_MD in these areas. The maximum absolute deviations of 1.5 kJ/mol ≃ 0.6 k_BT from the ideal case ΔG_TEE-REX − ΔG_MD = 0 (see Fig. 2) are commensurate with the maximum statistical errors of 0.15 k_BT (see Fig. 1) found for each method. As can be seen from the distribution of blue regions, high-energy configurations are more frequently sampled by TEE-REX, whereas MD sampling focuses on the stretched low-energy basin containing the “open” conformation. Thus, the excitation of essential subspace modes allows the TEE-REX reference replica to explore high-energy configurations usually not available to a normal MD sampling at the same temperature.

FIGURE 2.

Top view of the difference in free energy 〈ΔG_TEE-REX − ΔG_MD〉, averaged over all combinations 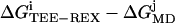(i = 1, …, 4; j = 1, …, 9). Areas colored in blue are more frequently sampled by TEE-REX than by MD. Maximum differences of ±1.5 kJ/mol ≃ ±0.6 k_BT are comparable to the statistical error of 0.15 k_BT for each method. High-energy regions (e.g., saddle region in the lower middle) are better sampled by TEE-REX. Low-energy configurations of the “open” state are preferred by MD.

Sampling efficiency

To judge the sampling efficiency of the TEE-REX algorithm, the 13 amino acid peptide hormone guanylin (PDB code 1GNA) was simulated by both MD and TEE-REX (see Methods section for simulation details).

It is generally accepted that standard REX improves sampling efficiency over classical MD. However, the computational effort associated with explicit solvent simulations is often very high with respect to the gain in sampling. Initial tests with standard temperature REX simulations of guanylin showed only a slight increase in sampling performance over classical MD. On the basis of these results, we omitted REX and directly compared results from MD with TEE-REX.

To provide meaningful statements about sampling efficiency, two independent 60-ns trajectory fragments from the 130-ns TEE-REX reference replica were compared to four independent 180 ns = 3 × 60 ns MD trajectory fragments taken from one 800-ns MD trajectory. Besides employing projections onto eigenvectors drawn from the essential subspace {es}, both methods were compared using (φ, ψ) dihedral space.

Essential subspace

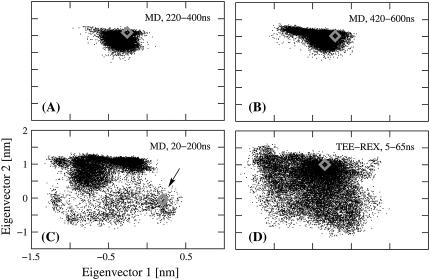
Every MD and TEE-REX reference ensemble was projected onto the first two backbone eigenvectors of the six-dimensional essential subspace {es} used in the TEE-REX simulation. Together, both eigenvectors describe 64% of all backbone fluctuations of the system. In Fig. 3, several of these projections are displayed, together with their respective starting structures (shaded diamonds). Fig. 3 C shows the configuration space sampled by a 180-ns fragment of an MD trajectory ranging from 20 to 200 ns. The intensely sampled region in the upper half of the μ₁μ₂-plane indicates a pronounced local minimum in the free energy surface of the system. For the remaining 600 ns of simulation time, the MD simulation gets trapped in this region of configuration space, as can be seen from the two 180-ns MD pieces depicted in Fig. 3, A and B. A projection of the first 60-ns fragment of the 130-ns TEE-REX reference replica trajectory, ranging from 5 to 65 ns, is shown in Fig. 3 D. Although the starting structure lies within the local minimum amply sampled by MD, the space covered by TEE-REX not only covers that explored by MD but also extends beyond that. This result is independent from the starting structure, as a projection of the second 60-ns TEE-REX reference trajectory fragment confirms (results not shown).

FIGURE 3.

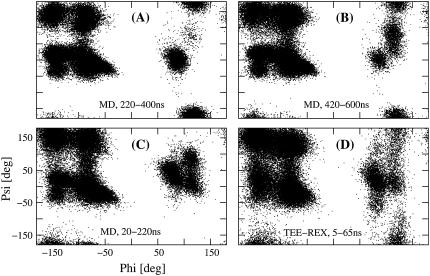
Trajectory projections of guanylin MD and TEE-REX simulations on the first two eigenvectors (for clarity, axes' labels are only shown for panel C). Shaded diamonds represent the starting structure of each simulation window. (A) and (B): projection of MD ensembles at 220–400 ns and 420–600 ns, respectively; (C) MD ensemble from 20 to 220 ns, arrow indicates starting structure; (D) TEE-REX ensemble for the first 60-ns piece, running 5–65 ns. A high dependence of the MD ensembles on the starting structure is observed. Unlike MD, TEE-REX sampling is independent of the starting structure. The low-energy starting configuration does not hinder extensive sampling of the available subspace.

To quantify TEE-REX sampling performance, the time evolution of sampled configuration space volumes, V_i(τ), was measured using projections of all MD and TEE-REX guanylin trajectory fragments along the first two eigenvectors of the six-dimensional essential subspace {es} excited in the TEE-REX simulation. To monitor time evolution, the μ₁μ₂-plane (see Fig. 3) was discretized by a grid of size 0.01 nm. At each time step, the number of occupied grid cells was recorded. Conversion of time into computational effort τ (measured in units of 180-ns MD simulation time) yielded the V_i(τ) curves shown in Fig. 4. TEE-REX sampling performance curves V_TEE-REX(τ) (solid lines) are compared in panel (A) against MD sampling curves V_MD(τ) (dotted lines) for all 180-ns MD trajectory fragments of the 800-ns reference MD simulation.

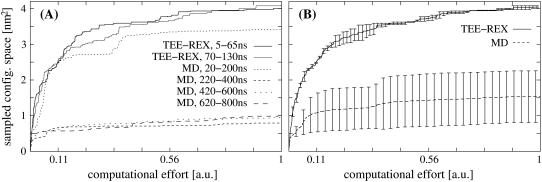
FIGURE 4.

Quantitative comparison of TEE-REX sampling performance with respect to MD for a guanylin test system. Sampled configuration space volumes V_i(τ) (in units of nm²) are measured versus computational effort τ (in units of 180-ns MD simulation time) for trajectory projections onto the first two eigenvectors of the six-dimensional essential subspace excited in the TEE-REX simulation of guanylin. (A) TEE-REX performance curves (dark and light solid lines) versus MD performance curves (dashed lines); (B) Average TEE-REX (solid) and MD (dashed) sampling performance 〈V_i(τ)〉 ± σ_i with error bars denoting standard deviations σ_i. On average, TEE-REX significantly outperforms MD. The large MD error bars show the dependence of the sampling on the starting structure.

Apart from the first 200 ns of simulation time, the sampling performance of MD is quite limited compared to TEE-REX. Here, the dependence of the MD sampling on the starting structure becomes clearly visible. For TEE-REX, sampling performance is independent of the starting structure, displaying the ability of the method to efficiently explore large regions of configuration space within short simulation times. Fig. 4 B summarizes the results of Fig. 4 A, showing average TEE-REX (solid line) and MD (dashed line) performance curves 〈V_i(t)〉 ± σ_i, with error bars representing standard deviations, σ_i. In the 180-ns MD simulation windows of guanylin, on average only 10% (τ = 0.1) of the total computational effort is necessary to sample 80% of the configuration space available to MD. Thus, exploring the remaining 20% of configuration space is computationally very expensive. For TEE-REX, we see a 3.6-fold increase in sampled configuration space using the same computational effort, τ = 0.1. Although the sampling rate of TEE-REX decreases with increasing τ, it outperforms the MD sampling rate by a factor of three.

Dihedral space

To evaluate the sampling performance of TEE-REX in subspaces not related to the essential subspace {es}, ensembles of both methods were compared within full (φ, ψ) dihedral space. Panels A–C of Fig. 5 show Ramachandran plots of several 180-ns fragments of MD trajectory, ranging 220–400 ns, 420–600 ns, and 20–220 ns, respectively. In all three fragments the left half-plane φ ∈ [−180°, 0°] is well sampled by MD, whereas moderate sampling is achieved in the remaining half-plane φ ∈ [0°, 180°]. For the corresponding TEE-REX ensemble (Fig. 5 D), ranging from 5 to 65 ns, a substantial increase in sampling is seen. Whereas covering of the left half-plane is comparable to MD, a notably broader range of ψ values in the right half-plane is sampled by TEE-REX. For a more detailed analysis the volume V(τ = 1) explored in dihedral space was calculated for each of the 11 pairs of dihedrals in all four MD and two TEE-REX ensembles. The average gain in sampling efficiency 〈V_TEE-REX/V_MD〉 for (φ, ψ) space is shown in Table 1 together with results from additional analyses, made on two PCA subspaces linearly independent from the {μ₁, μ₂} ⊂ {es} = {μ₁, …, μ₆} space, namely {μ₇, μ₈} and {μ₁₄, μ₁₅}. For all subspaces independent from {es}, sampling performances are comparable, yielding an ∼2.5-fold gain in TEE-REX sampling efficiency over classical MD. Although these values are lower than the observed 3.6-fold performance gain measured in the {μ₁, μ₂} subspace, they clearly demonstrate the capability of TEE-REX as an efficient sampling method.

FIGURE 5.

Ramachandran plots of different guanylin MD and TEE-REX ensembles (for clarity, axes' labels are only shown for panel C). MD ensembles 20–220 ns (C), 220–400 ns (A), and 420–600 ns (B) are compared with a TEE-REX ensemble, running 5–65 ns (D). Enhanced sampling of TEE-REX with respect to MD is observed.

TABLE 1.

Average TEE-REX sampling efficiency for guanylin, calculated in different two-dimensional subspaces

Subspace	Efficiency gain
(φ, ψ)	2.43
{μ7, μ8}	2.80
{μ14, μ15}	2.62
{μ1, μ2} ⊂ {es}	3.65

The efficiency measured in parts of the excited essential subspace, {μ₁, μ₂} ⊂ {es}, is shown for comparison.

Defining {es} using sparse structure information

The sampling enhancement in TEE-REX is largely due to excitations of the essential subspace {es}. Hence, the question arises of how sampling performance is influenced by the definition of {es}.

To mimic sparse structural information, a 130-ns TEE-REX simulation of guanylin was performed using an essential subspace {es}′ constructed using eigenvectors obtained from a PCA on the backbone atoms of a 1-ns piece of MD trajectory. Compared to the six eigenvectors used originally, the first 10 eigenvectors were necessary in the construction of {es}′ to account for 87% of all observed backbone fluctuations (see Methods section). Projections of 60-ns trajectory pieces from both TEE-REX simulations onto the first two eigenvectors of {es} revealed only minor differences in sampled regions of configuration space. Comparing sampled configuration space volumes measured over computational effort yields an average difference of 7% in sampling efficiency. These results indicate that TEE-REX sampling efficiency is hardly sensitive to the choice of the essential subspace. To further validate these findings the overlap of both ensembles in full (φ, ψ) dihedral space was estimated. To this end, the (φ, ψ) plane was discretized by a grid of size 1° and the grid cells shared by both ensembles were counted, yielding an overlap of more than 84%.

Algorithm sensitivity

During development, extensive tests were made with the TEE-REX algorithm to elucidate its sensitivity with respect to the three main parameters: essential subspace temperature 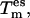size of the essential subspace N_es, and exchange attempt frequency ν_ex.

Excitations of the chosen {es} are controlled by 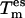and the corresponding coupling constant 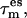defining the coupling strength. Both parameters are not independent of each other since for a weak coupling 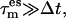dissipation of the excitation energy to colder degrees of freedom leads to a lower {es} temperature and hence reduced efficiency in sampling. Thus, a higher subspace temperature needs to be chosen to achieve the same sampling efficiency as with a tight coupling and a lower {es} temperature. Values for both of these parameters were chosen to find an optimal compromise between sampling efficiency and accuracy. Increasing 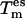to arbitrarily high values may allow sampling of configurations having a low Boltzmann factor at the reference temperature, T₀, leading either to slow convergence of the reference ensemble or to a bias of the latter (in case convergence is not reached).

The exchange frequency, ν_ex, should be chosen low enough to allow equilibration of the reference replica after each exchange. Concerning the essential subspace size, in this study N_es was always chosen such that ∼87% of the total mean-square fluctuation of the respective atoms was included. A large dependence of the sampling efficiency on the chosen {es} dimension is not expected, since sampling along nonexcited modes is also enhanced (see Table 1).

CONCLUSIONS

The applicability of standard REX to all-atom simulations of biomolecular systems using explicit solvent becomes computationally prohibitive for currently studied systems comprising more than a few thousand atoms. Due to the large number of degrees of freedom involved, numerous replicas are needed to span a given temperature range. To overcome this inherent limitation, we developed a new algorithm combining the REX framework with the idea of essential dynamics. In each TEE-REX replica only a selection of essential collective modes of a subsystem of interest is excited, with the rest of the system staying at a reference temperature. The collective modes are taken from a PCA of a subsystem of interest. This selective excitation of functional relevant motions within the replica framework overcomes the computational limitations inherent to REX while at the same time efficiently sampling the configurational space of the system.

Ensembles generated for a dialanine test system agree favorably with converged reference MD ensembles of the same system, making TEE-REX an efficient method for the study of thermodynamic properties of biomolecular systems. The superior sampling performance of TEE-REX with respect to MD was established using guanylin as a test system.

The algorithm can easily be applied to larger systems. Because only a small fraction 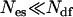of the degrees of freedom of the system are excited in each TEE-REX replica, the exchange probability 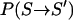is no longer dominated by the solvent contribution to the potential energy. This drastically cuts down computational demands, enabling TEE-REX to address problems currently not readily accessible to MD or other ensemble-preserving methods. The choice of the essential subspace degrees of freedom before any TEE-REX simulation renders the method suitable to address questions related to structural and dynamical properties of biomolecular systems.