Diffusion of Insulin-Like Growth Factor-I and Ribonuclease through Fibrin Gels

Abstract

A fluorescence-based method for simultaneously determining the diffusion coefficients of two proteins is described, and the diffusion coefficient of insulin-like growth factor (IGF-I) and ribonuclease (RNase) in a 0.27% fibrin hydrogel is reported. The method is based on two-color imaging of the relaxation of the protein concentration field with time and comparing the results with a transport model. The gel is confined in a thin (200 μm) capillary and the protein is labeled with a fluorescent dye. The experimentally determined diffusion coefficient of RNase (D = 1.21 × 10⁻⁶ cm²/s) agrees with literature values for dilute gels and bulk aqueous solutions, thus indicating the gel and the dye had a negligible effect on diffusion. The experimental diffusion coefficient of IGF-I (D = 1.59 × 10⁻⁶ cm²/s), in the absence of binding to the fibrin matrix, is consistent with the dimensions of the molecule known from x-ray crystallography and a correlation between D and molecular weight based on 14 other proteins. The experimental method developed here holds promise for determining molecular transport properties of biomolecules under a variety of conditions, for example, when the molecule adsorbs to the gel or is convected through the gel by fluid transport.

INTRODUCTION

Proteins, such as hormones (1), antibodies (2), and proenzymes (3), all must move through the interstitial space of tissues from sources to sinks by diffusion and convection (4). The extracellular matrix (ECM), which is composed of proteins and polysaccharides influences protein transport by providing binding sites and hindering movement (5–7). To effectively study and eventually model the transport of proteins in ECM, each transport component must be studied individually and then in combination. The diffusion coefficient of proteins, especially those relevant to tissue growth, allows for the prediction of concentration profiles and their evolution after trauma (8), during normal tissue growth, or in other tissue engineering applications (9,10). Hormones, such as insulin-like growth factors (IGFs), play an important role in programming tissue growth. Such molecules require dispersal within specific regions of a tissue to initiate the growth process or elicit other biological responses regardless of whether the hormones are derived from local tissue or systemic (blood) sources (11–13). Fibrin, a commonly used surgical glue and tissue engineering scaffold (14,15), has the potential to also function as a matrix for drug delivery (16,17). Understanding the transport of proteins in fibrin is necessary to utilize the full potential of fibrin as a drug delivery device and tissue engineering scaffold (18,19). A method to directly determine transport properties of proteins and other biomolecules in fibrin is needed.

The diffusion coefficient (D) of proteins and other macromolecules can be measured in many ways, including measurement of the diffusion rate across a porous membrane, use of photon correlation spectroscopy, and measurement of the time relaxation of an initially nonuniform concentration profile. The last method requires solution of Fick's second law:

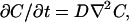(1)

where C(x,t) is concentration and ∇² is the Laplacian operator. The diffusion coefficient (D) is assumed independent of concentration or position. In a gel network, D represents some type of spatial average over the solvent interstices. The solution of the above equation depends on the geometry of the system and the boundary conditions.

In diffusion experiments, the tracer, which is necessary for determining the concentration profile, is often a fluorescent dye attached to the protein. The molecular size of the dye should be significantly less than the protein so as not to influence the diffusion coefficient of the dye-protein conjugate. In experiments utilizing fluorescence recovery after photobleaching (FRAP), the initial “concentration” profile, actually a tracer profile, is formed by transiently increasing the power of a laser focused on a uniform region of the sample to deactivate the fluorescence, and then the time relaxation of fluorescence is measured as the protein having unbleached tags diffuses into the bleached region (20,21). Although this method works well for the determination of simple diffusion, it has limited application to systems where convective transport is important or where the medium in which diffusion occurs is spatially heterogeneous such as when the fiber size distribution is broad or the pore size varies considerably.

In this work we report an in situ method to locally image the concentration of a protein in a fibrin gel confined within a thin rectangular capillary. This method is similar to the visualization techniques employed by others (22,23) to measure the diffusion of proteins in polymer gels. Under our experimental conditions the fibrin gel does not bind the soluble protein (24) or the fluorescent dye that is attached to it (25). At time zero a step function in protein concentration is established at the interface between the free solution and the gel within the capillary. As protein diffuses into the gel, the concentration of the protein is imaged in a fluorescence microscope at several positions and times. From these data and the solution to Eq. 1 for one-dimensional diffusion, the value of D is determined. The veracity of the model is checked by comparing the measured concentration field at different times with the prediction from Eq. 1. The objective of this work is to demonstrate the efficacy of the experimental method for in situ determination of molecular transport properties in gels that mimic ECM. Although the focus here is on simple diffusion, the method can be extended to situations where convection and ECM binding of the protein are important.

EXPERIMENTS

The diffusion experiments were performed in a rectangular microslide (No. 3520,Vitrocom, Mountain Lakes, NJ) made of borosilicate glass with dimensions 0.02 cm path length (z), 0.2 cm width (y), and 5 cm in length (x). Microslides were pretreated simply by cleaning with deionized water and air drying. Fibrinogen and thrombin stocks (Aventis Behring, King of Prussia, PA) were stored at −80°C as aliquots. To make the gel, the stocks were thawed and then stored at 4°C for at least 10 min before mixing them at room temperature in a buffered solution at pH 7.4 (50 mM Tris, 150 mM NaCl, and 2 mM CaCl). The buffer also contained 20 μg/mL Tween-20 nonionic surfactant to reduce nonspecific binding of the soluble protein to the gel (24). Unless noted otherwise, chemicals were purchased from Sigma-Aldrich. The fibrinogen and thrombin concentrations were 2.25 mg/mL and 1.75 units/mL, respectively. The microslide was quickly filled by capillary action until it was 50% full of the gelling solution. After the gel had formed, a thin layer of the Tris buffer solution was added at the gel interface using a 34-gauge syringe needle (World Precision Instruments, Sarasota, FL) to prevent drying or skinning of the gel interface. The volume fraction of the gel (φ) was calculated from a protein partial specific volume of 0.73 ml/gm (26), and the mass difference between the capillary with a wet gel and a dried gel, after the mass of electrolyte was subtracted out. More details of the gel formation process are presented elsewhere (25).

Diffusion of two proteins was studied: ribonuclease (RNase, R5500, molecular weight (MW) 13,800; Sigma Aldrich, St. Louis, MO) and IGF-I (MW 7,600; Chiron, Emeryville, CA). Succinimidyl esters of Cy3 (MW 756) and Cy5 (MW 800) were used as fluorescent protein tags. To label each protein, the protein was added to 1 mL of 0.1 M sodium bicarbonate at pH 8.5. Trifluoroacetic acid (TFA) (0.01% in water) was ice cooled. Less than a milligram of dye was added to 50 μL of the acid, and the concentration of the dye solution was determined with a spectrophotometer. The protein and dye solutions were then mixed to achieve a 3:1 mol ratio of dye/protein. The reaction progressed for 30 min at room temperature, and then a solution of 50 mM Tris at pH 7.4 was added to quench the reaction. The unreacted dye was separated from the protein using a centrifugal concentrator (Ultrafree-15 Biomax 5-K filter unit, Millipore, Billerica MA). Three cycles of dilution to 15 mL and ultrafiltration to 0.15 mL reduced free dye by a factor of 10⁶ to an undetectable level. The labeling ratios were determined by spectrophotometry and found to be 0.8–0.9 for RNase and 0.6–0.7 for IGF-I.

Because of the excellent spectral separation obtainable with Cy3 and Cy5 fluorescent labels, the diffusion of both proteins could be measured simultaneously in a single gel specimen by two-color imaging. For imaging the gels, a fluorescence microscope (Zeiss, Thornwood, NY) was equipped with a cooled charge-coupled device (CCD) camera (CH220, Photometrics, Tucson, AZ), a motorized stage (Ludl Electronics Products, Hawthorne, NY), and filter sets for Cy3 and Cy5 (Cy3 No. 31002a: D540/25x, 565DCLP, D620/60m; Cy5 No. 41008: HQ620/60x, Q660LP, HQ700/75m; Chroma Technology, Rockingham VT). Calibration images using Cy3 and Cy5 dyes showed that cross talk from the Cy3 image into the Cy5 image and vice versa amounted to <1% under the least favorable conditions of the study.

To eliminate pressure differences across the gel that would otherwise cause convection, a fluid shunt was set up to bypass the gel. Fluorescent polystyrene latex particles (Polysciences, Warrington, PA) of diameter 1 μm, which were large enough to be excluded from the gel, were added to the solution at the interface. Bead movement was monitored to determine if convection was present in the solution adjacent to the gel-solution interface. Experiments were conducted when drift of the beads was visually undetectable and only Brownian motion of the beads was observed. Over many hours, accumulation or depletion of the particles from the fluid volume immediately adjacent to the gel interface was never observed. The beads were also used to define the location of the interface and the zero of the x axis. In none of the specimens did we observe diffusion or convective transport of latex particles along the gel-glass interface. This, plus inspection of gel structure, led us to conclude that the gel was completely adhered to the microslide wall.

Each experimental run was initiated by adding one or both labeled proteins in gel buffer at the gel-solution interface using a flexible needle to create a step function of concentration. Initial protein concentration was set at 800 nM for IGF-I and 3000 nM for RNase for diffusion measurements. Introduction of the protein solution was accomplished in <60 s, and convection in the fluid phase was observed to damp out on a much faster timescale (<1 s). Convection was always fully suppressed at the gel-solution interface. The timer was started and the shunt was opened. The field of view (FOV) for each position was 0.62-mm wide in the direction of the diffusion (x axis). Position 1 (x = 0.44 mm) was set as the midpoint of the first FOV and marked in the microscope coordinate system (Fig. 1). Position 2 was centered on x = 0.872 mm, approximately double the distance from the gel interface. A third image was acquired at least 5 mm outside of the gel region in the solution side of the capillary to determine the fluorescence level and hence the protein concentration C₀ (Eq. 3). Within the gel, position 1 images were taken for IGF-I-Cy5 at 20, 30, 40, 50, and 60 min, and position 2 at 120, 140, 160, 180, and 200 min. For RNase-Cy3, image time points were offset by 1 min. Images were analyzed using NIH Image processing and analysis software (27). Intensity profiles were normalized by subtracting the background intensity and dividing by a digital image of a uniform fluorescence standard. The protein concentration was assumed to be proportional to fluorescence intensity; this was verified experimentally over the range of concentrations used by imaging uniform concentration standards (see Table 3; 0–4000 nM RNase-Cy3, 0–1000 nM IGF-I-Cy5) and producing a standard curve. Imaging of the uniform fluorescence standards was carried out for every experimental run to obtain the best correction for illumination nonuniformity and other instrumental factors.

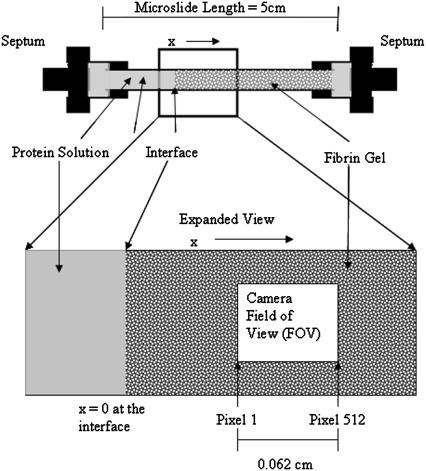
FIGURE 1.

Imaging positions within the gel. The x coordinate is the position within the gel, measured from the interface with the protein solution. Two fields of view were established: position 1 (x at midpoint = 0.044 cm) and position 2 (shown, x at midpoint = 0.087 cm). At both ends, the capillary was tightly inserted into a rubber septum, which connected it to a fluid-filled shunt manifold. This guaranteed zero pressure difference across the gel.

TABLE 3.

Numerical parameters used in computations

Fibrin gel volume fraction (v/v, dry)	0.27%
Microslide dimensions
Length (x)	5 cm
Width (y)	0.2 cm
Path length (z)	0.02 cm
CCD camera FOV (x)	0.062 cm
Solute concentration range
IGF-I–Cy5	200–1000 nM
RNase–Cy3	800–4000 nM
Molecular weight (×103)
IGF-I	7.6
RNase	13.8
Cy5	0.79
Cy3	0.76
Partition of solute	≥0.99
Hydraulic (Darcy) permeability of fibrin gel:	7.49 × 10−10 cm2
Hydraulic fiber radius (af)	21 nm
IGF-I Stokes-Einstein radius (a)	1.54 nm

RESULTS

The diffusion of the proteins is assumed to obey Fick's equation in one dimension (x) along the length of the microslide:

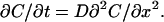(2)

The following boundary conditions were applied in the analysis of this experiment:

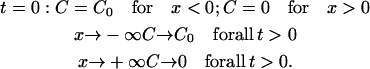(3)

The well-known solution to the above equation and boundary conditions (28),

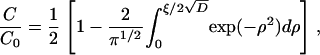(4)

is expressed in terms of the similarity variable, ξ = x/t^1/2. In this model C/C₀ = 0.5 at the interface (x = 0) at all times ≥0.

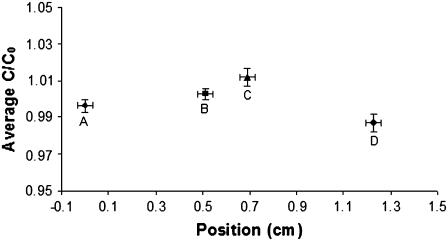
The important assumptions in the above model include i), a stagnant liquid outside the gel; ii), equal partitioning of the protein between the solution and gel, and equal diffusion coefficients in both regions; and iii), uniform tracer protein concentration over the gel cross section (in the y-z plane). When the dye-labeled protein is first injected into the solution to produce a uniform concentration, mixing is essential; however, care must be taken afterward to avoid convection due to pressure differences and nonuniform temperature. Absence of convection of one micron beads introduced at the interface confirmed (i). Partitioning was shown to be an insignificant effect by imaging a uniform solution of RNase-Cy5 under conditions of slow convection from the fluid phase through the gel driven by a small pressure head (10-cm H₂O) (25). Corrected fluorescence values between image fields in the fluid and image fields in the gel phase were shown to be equal to within 0.8% (Fig. 2). The third assumption was validated by considering the time (τ) required for protein molecules to diffuse the width of the gel cross-section gap (δ) = 0.02 cm: τ ≈ δ²/2D ≈ 120 s. Because image sampling occurred at 10 times this period, a uniform concentration across the gel cross section is justified.

FIGURE 2.

Absence of significant partition between fluid and gel phases. Average RNase-Cy5 fluorescence at four positions in the microslide is shown. Positions A and B were located on the fluid side of the gel interface. Positions C and D were located on the gel side of the interface. Points represent the average fluorescence in 25 images taken over 3 h at each location under conditions of slow convection of a uniform RNase solution from the fluid phase through the gel. y axis error bars show standard deviation across each image. x axis error bars show actual width of each FOV.

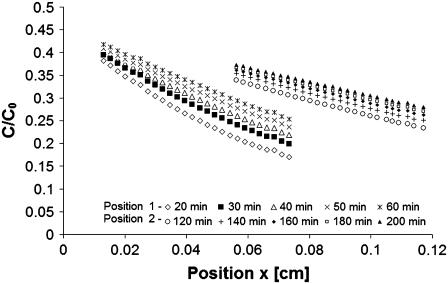
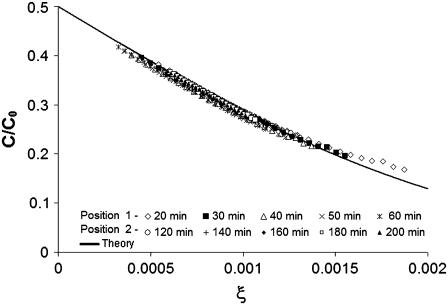
In a typical experimental run, the tracer concentration was observed to increase with time at any fixed position as the protein diffused into the gel. This can be seen in plots of the normalized concentration of IGF-I versus x or versus the similarity variable ξ (Figs. 3 and 4). By combining x and t in the variable ξ, the data from different FOVs and elapsed time periods collapse onto one curve (Fig. 4). Varying only a single parameter (D), the global best fit of Eq. 4 to >5000 data points was found using an equation solver and plotted as the theoretical curve in Fig. 4. For individual data sets, root mean-square error (RMSE) in fitting C/C₀ versus position was typically 0.008 (2.8%). The data shown gave a diffusion coefficient of D = 1.56 × 10⁻⁶ cm²/s for IGF-I (24°C). A two-parameter solver that varied D and C/C₀ produced slightly better fits (RMSE 0.007) and a higher diffusion coefficient (1.79 × 10⁻⁶ cm²/s) but also a partition effect (2C/C_{0, x=0} = 0.96) more severe than observed (0.99).

FIGURE 3.

Concentration of IGF-I labeled with Cy5 dye as a function of position (x) from the solution/gel interface at different times. The fields of view shown are centered at x = 0.044 cm for position 1 and 0.087 cm for position 2 from the interface. For each image, 27 equispaced data points were plotted. The actual data set contains 512 data points from each of 10 images.

FIGURE 4.

Scaling plot of IGF-I-Cy5, all data shown in Fig. 3 for both fields of view and all time delays. Points are replotted versus ξ = x/t^1/2. The global single-parameter best fit of Eq. 4 is the solid line. For each image, 27 equispaced data points were plotted. The actual data set contains 512 data points from each of 10 images.

All experiments were run at 24°C, and the results corrected to 25°C using the relation Dη/T = constant, where η is the viscosity of water and T is the absolute temperature. Table 1 shows the values of D obtained by fitting Eq. 4 to the data from each experiment for the two labeled proteins, combining data from both image fields at five time points each. The average values over 10 experiments for RNase and IGF-I, respectively, were 1.21 ± 0.12 × 10⁻⁶ cm²/s and 1.59 ± 0.16 × 10⁻⁶ cm²/s.

TABLE 1.

Values of diffusion coefficient (10⁻⁶ cm²/s) determined from each two-color experiment by fitting Eq. 4 to the C(x,t) data for each protein. All values corrected to 25°C using the expression Dη/T = constant

Experiment	IGF-I	RNase
1	1.62	1.17
2	1.46	1.28
3	1.60	1.12
4	1.62	1.31
5	1.87	1.25
6	1.59	1.12
7	1.77	1.26
8	1.63	0.96
9	1.46	1.23
10	1.29	1.39
Average	1.59	1.21
Standard deviation	0.16	0.12

Using crystallographic coordinates for IGF-I (Protein Data Bank accession number 1imx (29)) and RasMol software (30), external dimensions of the molecule were estimated by rotating the space-filling structure to orientations showing the maximum and minimum projected widths, then selecting pairs of atoms to obtain outer dimensions. By this procedure, major axes of 51.16, 34.52, and 21.47 Å were determined. The IGF monomer consists of a globular domain with two small diametrically opposed projections which define the long axis. The external dimensions of the globular domain only were taken as 31.28, 34.52, and 21.47 Å. To account for the 1.1 Å water-of-hydration layer described by Aragon and Hahn (31), 2.2 Å was added to each of the principal dimensions. Assuming an ellipsoidal shape for the protein, the hydrodynamic resistance tensor (R) was computed as described by Happel and Brenner (32). The diffusion coefficient was then computed from the trace of the inverse of R,

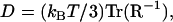(5)

where k_BT is the thermal energy. Upper and lower bounds on the diffusion coefficient were found to be 1.34 × 10⁻⁶ cm²/s and 1.59 × 10⁻⁶ cm²/s, respectively, using the outer dimensions of the hydrated particle or the dimensions of the hydrated globular domain alone. The measured value of D (1.59 ± 0.16 × 10⁻⁶ cm²/s) agrees with the calculation using the smaller estimate of the first axis.

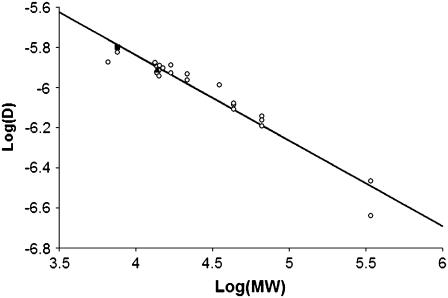
For RNase, the diffusion coefficient is in good agreement with literature values for free solution (33) and in a polyacrylamide gel (20,34). In Fig. 5 we plot the literature values of the diffusion coefficient for several proteins versus MW (also Table 2). Our value for IGF-I falls on a log-linear extrapolation of the literature data. Our measurement is very close to a previous report by Schneiderman et al. (35) for diffusion of IGF in proteoglycan-depleted cartilage.

FIGURE 5.

Diffusion coefficient of proteins (cm²/s) versus MW. The values determined in our experiments are shown as filled symbols (triangle = RNase, square = IGF-I), and values from the literature are shown as open symbols. All values corrected to 25°C. See Table 2 for the individual values of D. The slope of the best-fit straight line is −0.4264.

TABLE 2.

Literature values of diffusion coefficient (× 10⁻⁶ cm²/s) for various proteins of different MWs (× 10³) in water; all values corrected to 25°C using Dη/T = constant

Protein	D	MW
EGF (39)	1.34	6.6
IGF-I (35)	1.50*	7.6
cytochrome c (40)	1.33	13.4
RNase (33)	1.20	13.8
RNase (34)	1.27	13.8
RNase (20)	1.18	13.8
Lysozyme (41)	1.28	14.3
α-Lactalbumin (2)	1.21	14.2
Lactalbumin (40)	1.14	14.2
Trypsin (42)	1.25	15.1
Myoglobin (41)	1.18	16.9
Myoglobin (42)	1.29	16.9
α-Chymotrypsin (41)	1.17	21.6
Chymotrypsinogen (41)	1.09	21.6
Pepsin (43)	1.03	35.0
Ovalbumin (42)	0.78	43.5
Ovalbumin (40)	0.82	43.5
Ovalbumin (41)	0.83	43.5
BSA (40)	0.72	66.5
BSA (41)	0.64	66.5
BSA (44)	0.69	66.5
Fibrinogen (40)	0.34	339.7
Fibrinogen (42)	0.23	339.7

EGF, epidermal growth factor; BSA, bovine serum albumin.

^*Diffusion in proteoglycan-depleted cartilage.

The gel matrix could affect both the diffusion coefficient and the measurement of diffusion through its effect on partition, obstruction (tortuosity), and hydrodynamics (Table 3). Partition would influence measurement of D because we determine C₀ outside of the gel and image the concentration gradient inside the gel. However, in the dilute gels used in this study (φ = 0.27%), partition effects are insignificant (Fig. 2), as was binding of both RNase and IGF-I (24) to the gel.

The Ogston relation (36) for the partition coefficient (K),

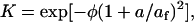(6)

depends on the bare fiber volume fraction (φ), the gel fiber radius (a_f), and the radius (a) of the diffusing particle. From measurements of the hydraulic permeability (k, 7.49 × 10⁻¹⁰ cm²) for the gels used in this work (25), we estimate a_f = 21 nm. From our diffusion coefficient and the Stokes-Einstein equation, a = 1.54 nm. Using these values in Eq. 5, K = 0.997, which is so close to 1.00 that it does not have a significant effect on our determination of D. The diffusion coefficient of a compact molecule in a gel network composed of fibers will be reduced to some degree by two factors: direct obstruction of diffusion paths and hydrodynamic drag between the molecule and the fiber network. In dilute systems D/D₀ is the product of an obstruction factor and a hydrodynamic factor. Following Johnson et al., Tong and Anderson, and Solomentsev and Anderson (20,37,38),

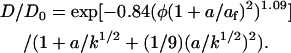(7)

Under our experimental conditions this ratio equals 0.998; therefore, the diffusion coefficient determined in our experimental system should be essentially identical to D₀.

SUMMARY AND CONCLUSIONS

A method for determining the diffusion coefficient of proteins and other biomolecules in gel-like matrices has been demonstrated. Using this method, the diffusion coefficient of IGF-I was found to be 1.59 ± 0.16 × 10⁻⁶ cm²/s at 25°C in a dilute fibrin gel. Although this is the value for diffusion in the gel, the volume fraction (0.27%) of polymer forming the gel was sufficiently low that it had no significant effect on the diffusion rate. This conclusion is supported by Fig. 5, which shows that our value of D for IGF-I is consistent with the correlation of D versus MW for low MW proteins, and the theoretical prediction that D/D₀ = 0.988 (Eq. 7).

There are several important characteristics of this novel experimental system. First, the use of distinguishable fluorescent tags and multi-band imaging allows for codetermination of diffusion coefficients. This is of particular importance in heterogeneous specimens in which it would be difficult to make the measurements sequentially. Second, the shunt installed around the microslide eliminates any pressure gradients across the gel and therefore prevents any small leaks or temperature gradients from influencing the experiment. The automated microscope stage allows for imaging at any position or level within the 200-micron-deep and 3-cm-long visible portion of the microslide which would enable the imaging of cells were they embedded in the fibrin gel (J. Nauman, B. Smith, F. Lanni, J. L. Anderson, and P. G. Campbell, unpublished data). The required data collection time is significantly shorter than when employing the porous membrane method to determine the diffusion coefficient. Because conventional fluorescence optics are used in our method, optimized filter sets can be chosen for best spectral separation. Multi-color imaging allows extension of this method to specimens in which the two proteins have differential binding affinity to the matrix or three-way binding between all components (13,24). Most important is that this technique allows direct in situ determination of molecular transport within tissue-like matrices and can be modified to study the simultaneous diffusion, convection, and binding of proteins.