Abstract
Examining calcium spark morphology and its relationship to the structure of the cardiac myocyte offers a direct means of understanding excitation-contraction coupling mechanisms. Traditional confocal line scanning achieves excellent temporal spark resolution but at the cost of spatial information in the perpendicular dimension. To address this, we developed a methodology to identify and analyze sparks obtained via two-dimensional confocal or charge-coupled device microscopy. The technique consists of nonlinearly subtracting the background fluorescence, thresholding the data on the basis of noise level, and then localizing the spark peaks via a generalized extrema test, while taking care to detect and separate adjacent peaks. In this article, we describe the algorithm, compare its performance to a previously validated spark detection algorithm, and demonstrate it by applying it to both a synthetic replica and an experimental preparation of a two-dimensional isotropic myocyte monolayer exhibiting sparks during a calcium transient. We find that our multidimensional algorithm provides better sensitivity than the conventional method under conditions of temporally heterogeneous background fluorescence, and the inclusion of peak segmentation reduces false negative rates when spark density is high. Our algorithm is robust and can be effectively used with different imaging modalities and allows spark identification and quantification in subcellular, cellular, and tissue preparations.
INTRODUCTION
In cardiac myocytes, excitation-contraction coupling is initiated by the initial influx of Ca2+ into the sarcolemmal space (1); this occurs as highly localized subcellular changes in the intracellular concentration ([Ca2+]i) either spontaneously (2) or elicited by an influx through L-type channels (3), triggering Ca2+-induced Ca2+ release (CICR) from the sarcoplasmic reticulum (SR). Since their discovery, the spatial and temporal summation of these elementary entry events (called Ca2+ “sparks”) have been thought to potentiate the Ca2+ wave (2,4,5).
Ca2+ sparks are customarily measured with fluorescent Ca2+ indicators (6) and laser scanning confocal microscopy involving a laser raster scan along a single line with a temporal resolution of ∼1–2 ms. This procedure generates stacked (x,t) data that are visualized in the form of a two-dimensional (2-D) image. This approach is limited in three ways: 1), the line scan monitors a slice on a single spatial axis, so that the lack of spatial information may cause an underestimation of spark number and morphology as a function of location (see Fig. 2 in Goldhaber et al. (7) for an example of this effect); 2), sparks outside of the scan line may still be detected due to Ca2+ diffusion but attenuated in peak intensity, with the result that the spark amplitude distribution is skewed as a function of distance from the scan line (8,9); and 3), spark morphology is known to be variable even under line scan conditions when Ca2+ release is stimulated to insure high spatial localization (10). Also, Ca2+ diffusion associated with spark formation is known to be anisotropic in 2-D (11). Automatic detection methods have been developed to detect sparks in confocal line scans to overcome sampling bias (9). However, these algorithms were optimized for isolated sparks amid uniform background fluorescence, and are not sufficient for spark detection under conditions of larger scale Ca2+ release (12) or the presence of overlapping sparks (13).
FIGURE 2.
Example of adjacent spark segmentation. (A) Two neighboring sparks, highlighted as three regions in (x,y,t) space: suprathreshold regions (green), relative maxima (blue), actual maxima (black dots). A plane intersecting the actual maxima and bisecting the relative maxima and suprathreshold regions is shown in black outline. (B) The Euclidean distance transformation on the plane shown in panel A with respect to the relative maxima. The actual maxima are shown as black dots. The watershed line is shown in red, dividing the space into two regions, labeled 1 and 2. (C) The same plot as that in panel A, with the watershed surface superimposed in red, dividing the (x,y,t) space into two regions, labeled 1 and 2.
To address these issues, we have developed an alternative means of detecting sparks. Our computational algorithm analyzes image data obtained with either line scan or high-speed fluorescent charge-coupled device (CCD) microscopy, performs spark identification by their spatiotemporal profile, and provides a means of quantitative characterization of sparks and statistical profiles of spark ensembles. Such analyses are expected to be important in light of recent studies suggesting that 2-D imaging of sparks may elucidate the subcellular structure-function relationships that regulate Ca2+ metabolism in muscle cells (7,10,12,14–21).
METHODS
Experimental protocol
Briefly, ventricular myocytes were isolated from 2-day-old neonatal rats using trypsin and collagenase, and cultured on fibronectin-coated coverslips to form confluent tissue monolayers. Two-dimensional fluorescence Ca2+ imaging was performed with a CCD camera recording with 4 × 4 binning to yield an output full-frame format of 128 × 128 pixels (corresponding to 130 × 130 μm2) per frame at 90 fps. The full details of cell isolation and culture and Ca2+ imaging are provided in the Supplementary Material.
Spark detection algorithm
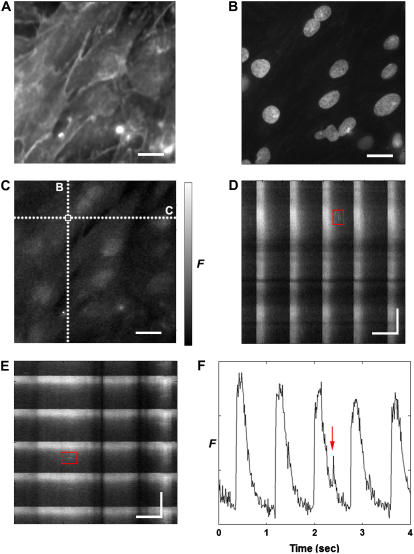
In both line scans and full-frame scans, a spark appears as a sudden increase in the local fluorescence intensity. At maximum intensity, (typical rise time, 10 ms), Ca2+ release halts and the intensity decreases as the Ca2+ diffuses away from the source and Ca2+ reuptake mechanisms are activated (22). The spark also expands radially for a full-width, half-maximum (FWHM) amplitude value of ∼2 μm with a full-duration, half-maximum (FDHM) of 20–40 ms for intact myocytes isolated from adult rat (23). Therefore, spark detection consists of locating a short duration spatiotemporal peak in a scalar field changing with a longer timescale. Fig. 1 shows fluorescence (x,y) images obtained from neonatal rat cardiac myocytes, where the sarcolemma is labeled using di-8-ANEPPS in panel A and the nuclei are shown using DAPI in panel B. Panel C shows [Ca2+]i measured by fluo-4 fluorescence (see the online Supplementary Material, movie M1), whereas panels D and E show cross sections of panel C in (x,t) and (y,t); these cross sections would be equivalent to a confocal line scan taken over a section of tissue. Identifying a localized increase in fluorescence as a calcium spark (as is highlighted in Fig. 1 C) requires analysis of its temporal development to distinguish it from noise or some other artifact (Fig. 1 D–F).
FIGURE 1.
Example of raw fluorescence data obtained by a CCD camera from an engineered two-dimensional cardiac tissue. (A–C) A single (x,y) fluorescence (F) map taken at t = 2.38 s labeled with (A) di-8-ANEPPS, highlighting the cell membranes, (B) DAPI, highlighting the nuclei, and (C) fluo-4, showing [Ca2+]i. (D,E) Development in time of F along the dotted lines labeled D and E shown in panel C. The red boxes outline the same spark in panels D and E. The periodic pattern represents spontaneous, large-scale Ca2+ transients that occupy the entire tissue area simultaneously. (F) Temporal trace at the location shown in panel C with a white box, illustrating the spontaneous Ca2+ transients and the spark highlighted in panels D and E. Spatial scale bar is 20 μm, temporal scale bar is 0.5 s. A movie of the Ca2+ fluorescence shown in panel C is provided as Supplementary Material.
The modules for image input, preprocessing, detection, and visualization were written and implemented in MATLAB (MathWorks, Natick, MA). The methodology is described for image (x,y,t) data but is applicable to data in two dimensions (i.e., line scan (x,t) data). The test data used and the spark detection algorithm described below are available at http://www.deas.harvard.edu/diseasebiophysics/SparkAnalysis/.
Determination of nonspark fluorescence
The data sequences record the spark activity superimposed upon native background fluorescence in addition to fluorescence that is often heterogeneous in space (e.g., intracellular buffering and organelle dye compartmentalization) and time (e.g., photobleaching or a Ca2+ transient). For example, the highlighted spark in Fig. 1 F is not located within quiescent tissue but on the recovery phase of the previous Ca2+ transient, for which the simple subtraction of a constant value representing the baseline fluorescence would be inadequate. The normalized fluorescence ΔF/F0 is calculated as (24):
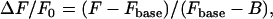 |
(1) |
where Fbase(x,y) is the baseline (i.e., quiescent) fluorescence and B is the background fluorescence of an area adjacent to the cell or tissue. For optimal processing, sparks must be identified both against Fbase and the underlying nonspark Ca2+ activity. This dynamic fluorescence is estimated by using a nonlinear iterative method using the following steps:
The fluorescence time sequence F(t) associated with each spatial point (x,y) is fitted with a cubic spline G(t).
G(t) is then fitted with a weighted cubic spline H(t). In calculating the weighted spline, the points of F(t) that lie below G(t) are weighted significantly more than those that are not. As a result, this procedure shifts H(t) toward the baseline values.
F(t) is then set equal to H(t).
Steps 2–3 are repeated in an iterative fashion until the difference in the residual between iterations falls below 10% of the initial value.
The resultant (x,y,t) image sequence representing the nonspark activity is subtracted from the original fluorescence sequence and then normalized with (Fbase − B). For the experimental data, Fbase(x,y) is the time average of F(x,y,t) during the quiescent period before the next transient.
Threshold determination
Spark detection requires the isolation of sparks from the background noise. The most common method is determining the mean fluorescent noise level in the image, and then defining the threshold as a multiple of standard deviations (σ) above this mean. Cheng et al. (9) use a twofold thresholding operation with 2σ as the first threshold to distinguish spark events from noise, followed by a second threshold (Cri) defined as 3.5σ based on their detection criteria (i.e., maximize the number of true detections while minimizing the number of false detections). However, locations with increased spark frequency (such as changes in SR Ca2+ content or rest period (25)) or sustained Ca2+ release (such as under voltage clamp (9)) will exhibit higher variance in fluorescence than the surroundings. In these instances, a global computation of the fluorescence standard deviation can yield a misleading value. Here, we derive an alternative method of determining the threshold that is less sensitive to these conditions.
First, the ΔF/F0 sequence is spatiotemporally smoothed, followed by calculation of the intensity histogram. For a typical image sequence, the majority of the pixels represent background fluorescent noise and the histogram will have a global maximum at the mean of the noise intensity. The histogram is asymmetric around the maximum, with the bins less than the mean of ΔF/F0 (denoted as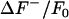 ) representing the negative noise component. In contrast, the bins greater than the mean (
) representing the negative noise component. In contrast, the bins greater than the mean (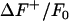 ) represent the positive noise component in addition to the intensity values comprising the sparks, since sparks are represented by an increase in ΔF/F0.
) represent the positive noise component in addition to the intensity values comprising the sparks, since sparks are represented by an increase in ΔF/F0.
For our purposes, we take the primary noise process to be photon (shot) noise, which is described by a Poisson probability distribution. However, the signal intensity achieved by our experimental setup is sufficiently high such that the background noise may be approximated by a Gaussian distribution. Furthermore, the 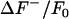 values alone are sufficient to calculate the standard deviation and the mean of the background intensity distribution. As the histogram values typically span several orders of magnitude, using the natural logarithm of the histogram to determine the mean and standard deviation is less prone to fitting error. Taking the natural log of a Gaussian distribution gives the formula for the curve φ encompassing
values alone are sufficient to calculate the standard deviation and the mean of the background intensity distribution. As the histogram values typically span several orders of magnitude, using the natural logarithm of the histogram to determine the mean and standard deviation is less prone to fitting error. Taking the natural log of a Gaussian distribution gives the formula for the curve φ encompassing 
 |
(2) |
where μ and σ are the mean and standard deviation of the ΔF/F0 distribution, respectively, and a is the natural logarithm of the histogram maximum value. Thresholding the data sequence by Cri × σ produces a set of bounded regions (R) in two or three dimensions.
Spark detection
Each thresholded region R is analyzed for the presence of potential sparks, which is a maximum embedded in the scalar n-dimensional data set. First, we define the ΔF/F0 values in R as a multivariate function f(ξ1, ξ2, … ξn); n is equal to 2 and 3 for line scan (x,t) and full frame (x,y,t) data, respectively. The actual maxima are calculated as the intersection of the zero level sets of the spatial partial derivatives of f, i.e., ∂f/∂ξ1 = 0 ∩ ∂f/∂ξ2 = 0 ∩ … ∩ ∂f/∂ξn = 0. The function f is fit with an interpolating spline to precisely calculate the partial derivatives and the level sets are 2-D contour lines (for line scan data) or 3-D isosurfaces (for full-frame data).
Next, the relative maxima of R are calculated to avoid discretization effects (such as grid coarseness surrounding a peak) that may produce false negatives; and to produce a defined border delimiting the boundaries of the spark region for further processing. The relative maxima are obtained analytically using the general second derivative test, as follows:
- For each R, define the Hessian matrix H as the Jacobian of [∂f/∂ξ1, ∂f/∂ξ2, …, ∂f/∂ξn], that is,
(3) Define the k-th leading principal minor Mk as the determinant of the k × k submatrix of the n × n matrix H obtained by deleting the last (n–k) rows and columns from H.
The function f has a relative maxima at the location [ξ1(o), ξ2(o), …, ξn(o)] if H evaluated at that location is negative definite, i.e., (−1)k · Mk > 0 for each k = 1,…, n.
This procedure produces a set of subregions that represent relative maxima in R, the neighborhoods that contain actual maxima (i.e., spark peaks). If a relative maximum region does not have a corresponding actual maximum, the region is labeled for removal.
In some cases, sparks are sufficiently close together (in either space or time) so that multiple actual maxima lie within a single (x,t) or (x,y,t) relative maximum region, or multiple relative maxima lie within a single suprathreshold region (Fig. 2 A). These joined regions are split using marker-controlled watershed segmentation; the maxima are used as starting markers (Fig. 2 B) and the resulting watershed lines are used to divide the region (Fig. 2 C).
The next task is the identification and removal of actual maxima that are peaks in the intensity field but are so low in amplitude that they are probably either spurious noise or out-of-focus sparks above the threshold Cri · σ. For each relative maximum region in f(ξ1, ξ2, … ξn), a function of the form a1ξ1 + a2ξ2 + … + anξn = 0 (a plane in two dimensions, a hyperplane in n dimensions) is fit to each region using a multivariate linear least-squares regression. If the correlation coefficient r2 exceeds 95%, the region is close to being linear (i.e., “flat”) and is probably not a substantive spark, marking it for removal.
Data analysis
Once the spark has been identified, all desired spark parameters can be extracted. The following parameters were determined (calculated from the raw data to avoid low-pass filtering effects in the smoothed data; results are presented as mean ± SE):
Location. This parameter is calculated as the location of the maximum, (xp,yp,tp)
Amplitude. This value is calculated as the value of ΔF/F0 at (xp,yp,tp)
- Full-width half-maximum. For the (x,y,t) data set, a 2-D Gaussian function,
is fitted to the (x,y) data at tp, the time of the peak amplitude, and x and y are fixed to xp and yp, respectively, to find A, μx, μy, σx, and σy. The FWHM for a given direction is σ·[8 ln(2)]1/2, where σ is the variance in the respective direction.
(4)
The full-duration half-maximum of the spark is a temporal parameter that is also commonly measured. The estimation procedure is straightforward: calculating the FWHM for each time point encompassed by the relative maxima yields a series of Gaussian parameters for the spark at each time t. The values of A (the peak amplitude) at (xp,yp) for each t forms a temporal profile of the spark and the FDHM is calculated as the time between the points where the profile has the value of A/2. Likewise, the rise time (the time to peak) of the spark may also be extracted by this means. However, sparks recorded with our CCD imaging system span only two to four frames in duration. Therefore, our frame rate precludes accurate reporting of the FDHM for this study. Using full-frame (x,y) high-speed confocal microscopy would overcome this technical limitation, allowing a full comparison of this procedure against real values.
Numerical protocol
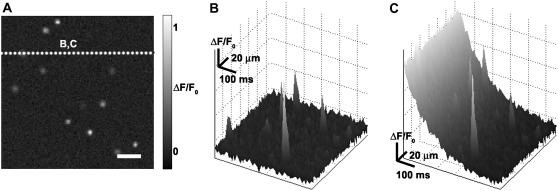
To test the performance of the algorithm under controlled conditions, we generated synthetic (x,y,t) data sets composed of sparks added to embedded noise, as shown in Fig. 3. A stereotypical spark was produced by averaging a set of sparks obtained from quiescent tissue. Each synthetic data set was generated with a random number of stereotyped sparks at random (x,y,t) locations; all sparks were constrained to be within the boundaries of the data field-of-view. The number of sparks per data set varied from 1 to 480, so that for the spatial and temporal sampling parameters used, the maximum spark frequency for a given data set would be 0.05 sparks/μm2/s, which is at the upper limit on spark frequency reported in rat ventricular myocytes (7). Gaussian noise with a mean of 0 and a standard deviation of 1 was added to each spark, with the sparks scaled in amplitude according to a random uniform distribution so that the SNR would match that of the experimentally collected data (Fig. 3 A).
FIGURE 3.
Creation of synthetic sparks. (A) A sample frame from t = 1 s. Scale bar is 20 μm. (B,C) Space-time plot of ΔF/F0 along the line shown in panel A, showing synthetic sparks in the presence of (B) added baseline fluorescence noise and (C) added baseline fluorescence noise in addition to the fluorescence change associated with tissue-wide Ca2+ reuptake.
These data sets were used as input in two forms: a), the original unmodified format with uniform baseline fluorescence, shown in Fig. 3 B; and b), modified with a nonuniform decrease in fluorescence representative of the falling phase of a Ca2+ transient, shown in Fig. 3 C. The stereotypical reduction in fluorescence during Ca2+ reuptake was obtained from raw experimental data during which the entire tissue was activated by a Ca2+ transient. The fluorescence curve represented the fluorescence temporal average from 75% of full recovery to quiescence; this curve was then added to the sparks and noise to form a new synthetic data set.
RESULTS
Performance on synthetic data
Uniform baseline fluorescence
Sixty sets of synthetic data (denoted DS0) were created, for a total of n = 8789 sparks. In addition, five sets of two control cases were produced: 1), DS1, consisting of zero-mean Gaussian noise and no sparks; and 2), DS2, containing 160 stereotypical sparks and no added noise.
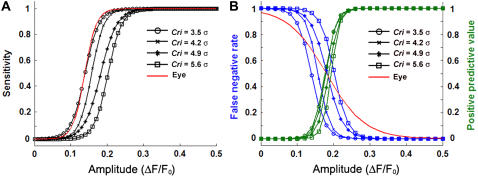
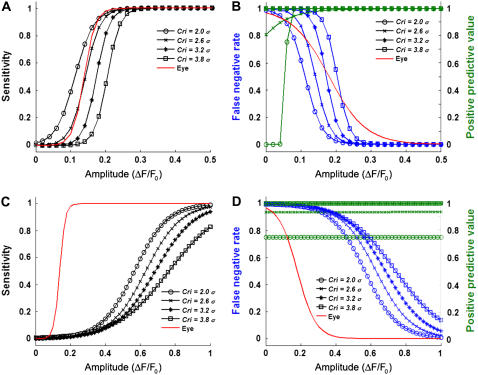
To optimize the spark detection parameters, the algorithm performance was tested on the DS0 data sets for a variety of Cri threshold values. Three statistical metrics were examined: a), sensitivity, defined as the probability of the correct detection of a spark of a given amplitude; b), the false negative rate, defined as the probability that a spark of a given amplitude will be missed by the algorithm; and c), the positive predictive value (PPV), defined as the probability that a detection by the algorithm will be correct as a function of amplitude. In addition, the algorithm was tested against eye detection on a DS0 data set by a well-trained experimentalist; Fig. 4 illustrates the results for the DS0 data. As expected, the sensitivity of the algorithm (Fig. 4 A) and the PPV (Fig. 4 B) increased while the false negative rate (Fig. 4 B) decreased as the spark amplitude increased for all Cri values. Based on the sensitivity metric, the appropriate Cri value for the algorithm would be 3.5σ, in agreement with Cheng et al. (9). However, for ΔF/F0 ∼ 0.10–0.17 (the range where the Cri = 3.5σ curve spans 10–90% sensitivity), the PPV is only 1–44%. Therefore, the algorithm would yield a high proportion (>66%) of low-amplitude false positive detections at the Cri = 3.5σ sensitivity. To avoid an unacceptable number of false positives, we note that the close juxtaposition of the PPV curves in Fig. 4 B indicates that a higher Cri value can be chosen without significantly compromising the proportion of true positives at higher ΔF/F0 amplitudes. Furthermore, a Cri value may be matched to the false negative rate of eye detection (the red line in Fig. 4 B) by examining the 50% detection probability of both curves. Therefore, we used Cri = 4.9σ for subsequent calculations to balance between Type I (false positive detections) and Type II (false negative misses) errors.
FIGURE 4.
(A) Sensitivity of the algorithm as a function of synthetic spark normalized amplitude for various threshold criteria, Cri. (B) False negative rate (blue) and positive predictive values (green) as a function of synthetic spark normalized amplitude for values of Cri. The average results of eye detection by a coauthor were fitted to a sigmoid curve and given as the solid red lines in panels A and B.
The distortion in amplitude introduced by the algorithm was examined for the DS0 and DS2 cases (see supplemental Fig. S1, Supplementary Material). The algorithm shows high accuracy for high amplitude sparks in both instances as expected. As the synthetic spark amplitude decreases, the difference between the detected amplitude between DS0 and DS2 increases. The spatial localization error of the detected sparks was 1.83 ± 0.06 μm for DS0 and 1.8 ± 0.06 μm for DS2.
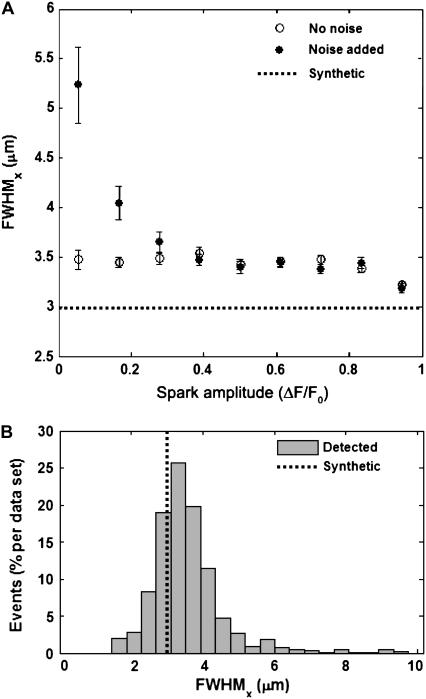
Fig. 5 A shows the FWHM estimation as a function of calculated spark amplitude in the x-direction from the DS0 and DS2 synthetic data (the results in the y-direction are virtually identical; data not shown). As ΔF/F0 increases, both the signal/noise ratio (SNR) and the estimation of FWHM in x and y improved. When the spark amplitude in DS0 approached the level of the added noise (SNR ∼ 1), the FWHM estimation tended toward larger values as expected. Fig. 5 B illustrates FWHM estimation in x as a histogram, showing the expected distribution around the actual value (similar results in the y-direction; data not shown). Therefore, the overall performance on the DS0 synthetic data yielded measurements of FWHM that fit the true values to within 25% even without discriminating against low SNR. The same performance was displayed in DS2 data sets as well (data not shown). The deviation in the estimated FWHM value was consistent irrespective of spark amplitude in the absence of noise. This suggests that appropriate fluorescence subtraction is a substantial factor in accurate spark parameter estimation.
FIGURE 5.
(A) Accuracy of fullwidth, half-maximum (FWHM) estimation in the x-direction using the detection algorithm on DS0 (noise added, •) and DS2 (no noise, ○) synthetic data. All synthetic sparks have the same FWHM but varying amplitudes, given by the horizontal black dotted line. Error bars show SEM. (B) Histograms of the estimated FWHM measurements in the x-direction from the DS0 synthetic data sets, given as the average number of detected events per image. The actual FWHM in x is given by the vertical black dotted line.
Algorithm reliability was also tested using the DS1 data set, which produced few false positives (Cri = 4.9σ: total of 0.4 per data set with a mean estimated ΔF/F0 of 0.18 ± 0.04). The false positives in DS1 were consistently localized to within 55 ms of the end frames regardless of Cri threshold value. Because the nonlinear nature of the fluorescence subtraction (see Methods) produced fluctuations at the temporal limits of the data, ΔF/F0 is slightly underestimated at these points, yielding false positives. Such edge distortion is a well-known problem in image processing and filter construction, and can be minimized by either 1), truncating the temporal boundaries or 2), extending the temporal sequence by padding (or extrapolating) the data. Therefore, the automatic selection of threshold is effective in isolating the spark regions provided that the fluorescence subtraction preprocessing step is performed robustly.
Inclusion of nonuniform fluorescence during Ca2+ reuptake
The same stereotypical spark distribution was used to create additional synthetic data sets, DS3, which embedded a uniformly decreasing fluorescence field representing the falling phase of a tissue-wide Ca2+ transient. The performance in spark amplitude estimation was similar to that of the data sets with uniform baseline fluorescence, permitting the use of the same Cri value as that for the DS0 data. Estimated FWHM values for Cri = 4.9σ were also similarly distributed as compared to DS0 (values of 3.65 ± 0.05 and 3.66 ± 0.05 μm in the x- and y-directions, respectively) with a spatial localization error of 1.83 ± 0.06 μm. The comparable performance between the DS0 and DS3 data sets indicates that the fluorescence subtraction adequately removes the nonlinear change in intensity.
Comparison to conventional spark detection algorithm
The automated spark detection algorithm by Cheng et al. (9) (hereafter referred to as the conventional algorithm) is the most commonly used algorithm in the literature. To quantitatively examine the effectiveness of our algorithm (hereafter called the multidimensional algorithm), we compared them by analyzing a set of DS0 synthetic data. As indicated in Cheng et al. (9), the optimal Cri value for the conventional algorithm was determined to be 3.5. However, to confirm that the performance of the conventional algorithm was not altered by the data, we applied the statistical metrics described above to the synthetic data for a variety of Cri values. The only modifications made to the conventional algorithm were: 1), the spatiotemporal filtering parameters from Cheng et al. (9) were scaled to the spatial extent of (x,y) images used; and 2), all 2-D specific operations were extended to 3-D operations.
The performance of the conventional versus the multidimensional algorithm upon DS0 data (uniform baseline fluorescence) is shown in Fig. 6, A and B. An optimal Cri value of 3.2 achieves a false negative rate similar to that determined by eye while retaining comparable sensitivity (we note that since determination of σ is different between the two methods, Cri values cannot be strictly compared). If the baseline fluorescence is quiescent, the conventional algorithm yields a lower PPV rate (i.e., lower false positives) than the multidimensional algorithm. Both exhibit the same performance in sensitivity (50% detectable at ΔF/F0 ∼ 0.17–0.18) at their respective selected Cri values. However, Fig. 6, C and D, highlight a notable performance difference between the conventional and multidimensional algorithms with respect to the DS3 (Ca2+ reuptake) data. Here, the sensitivity and false negative rate curves for the conventional algorithm are all shifted toward the right, with a 50% sensitivity and false detection rate at ΔF/F0 ∼ 0.68. This result indicates that the nonuniform fluorescence drastically reduces the spark detectibility by the conventional algorithm, whereas the detection statistics of the multidimensional algorithm remain constant in the same conditions.
FIGURE 6.
Statistical parameters obtained for the conventional algorithm for uniform baseline fluorescence (top row) and Ca2+ reuptake (bottom row). (A and C) Sensitivities as a function of synthetic spark normalized amplitude for various threshold criteria, Cri. (B and D) False negative rate (blue) and positive predictive values (green) as a function of synthetic spark normalized amplitude for values of Cri. The average results of eye detection by a coauthor were fitted to a sigmoid curve and given as the solid red lines. Curves shifted to the right indicate diminished detection properties. Note the change in x axis limits between panels A and B and panels C and D.
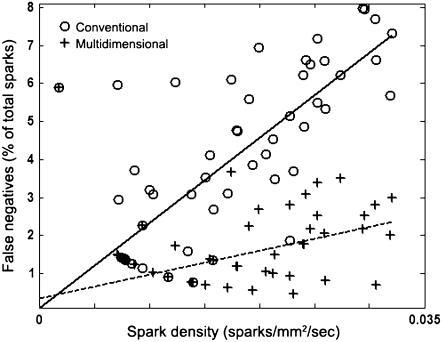
The effect of spark density on the probability of spark detection is also of interest since sparks that are closer together are more difficult to distinguish and may lead to false negatives. Figs. 4 and 6 indicate that the false negative rates for all DS0 data sets are approximately zero for sufficiently high amplitudes at all Cri values. Fig. 7 shows the false negative rate in the DS0 data sets as a function of spark density for sparks whose ΔF/F0 > 0.3 (excluding false negatives due to low amplitude). The graph indicates that as the density of high amplitude sparks increases, the multidimensional algorithm decreases the false negative detection rate by about fourfold.
FIGURE 7.
Number of false negatives as a function of spark density for synthetic data. Circles and fitted solid line indicate those detected using the conventional algorithm; plus signs and fitted dotted line indicate those detected using the multidimensional algorithm. Only those sparks with ΔF/F0 > 0.3 are considered.
Performance on experimental data
Data were obtained from isotropic monolayers of cardiac myocytes in which the myocytes exhibited spontaneous CICR. Each data set was subdivided into intervals containing a single, whole-tissue Ca2+ transient. Each interval was then segmented into episodes spanning the period beginning with the point at which the mean fluorescent signal across the tissue had recovered to 25% of the maximum amplitude and ending with the start of the next transient, before which the tissue is quiescent. To minimize temporal boundary effects (see above), the beginning of the segment was padded with the prior 55 ms of data whereas the end just before the transient was truncated by 55 ms.
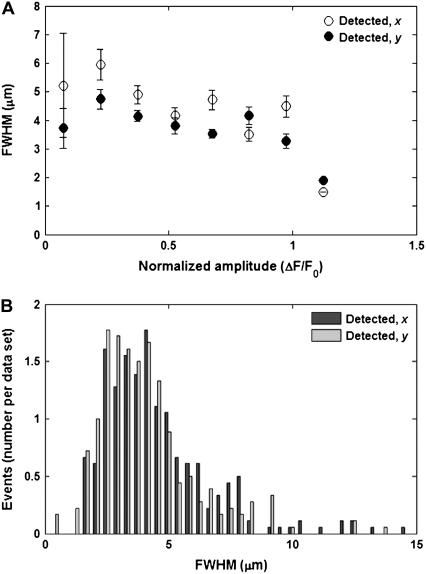
Spark events were detected from an ensemble of Ca2+ transient episodes (n = 16) using the multidimensional algorithm. Any sparks for which an FWHM measure could not be estimated in either the x or y axis were excluded from further ensemble analysis. Large amplitude sparks tended to cluster around a consistent FWHM value, whereas weak sparks displayed a larger spatial spread (Fig. 8 A) in a manner analogous to the synthetic data. The FWHM was estimated as 4.93 ± 0.2 μm in the x-direction, 4.09 ± 0.12 μm in the y-direction, with a greater trend toward lower values than that seen in the synthetic data (Fig. 8 B). Overall, the amplitude and FWHM distributions resembled those of the synthetic data, but with larger FWHM values than those normally reported (23).
FIGURE 8.
(A) Estimated FWHM values in x and y as a function of estimated amplitude using the detection algorithm on data collected from Ca2+ transient events (n = 21). Error bars show mean ± SE. (B) Histograms of the estimated FWHM values in x and y for the experimental data sets.
In contrast, the conventional algorithm on the same transient episodes was able to detect a portion of the sparks in the data. All the detected sparks were localized within the first few milliseconds of the transient episode, for the period during which the fluorescence intensity was still above the detection threshold. However, as Ca2+ reuptake occurred, the number of sparks detected became dependent on the growing difference between the estimated (x,y) baseline fluorescence (constant) and the mean fluorescence (decreasing) + Cri × σ. Hence, the number of sparks detected also decreased as the fluorescence approached the detection threshold and required increasingly higher amplitude to be detected. Once the fluorescence fell below this threshold, no further sparks were found. In addition, the Ca2+ transient associated with the nuclei was delayed with respect to the cytosolic Ca2+ transient and lasted longer (26), as seen in the online supplemental movie in Supplementary Material. This phenomenon created additional intensity peaks in the normalized fluorescence field, biasing the calculation of the fluorescence standard deviation. As a result, the presence of the Ca2+ transient compromised the performance of the conventional algorithm upon experimental data.
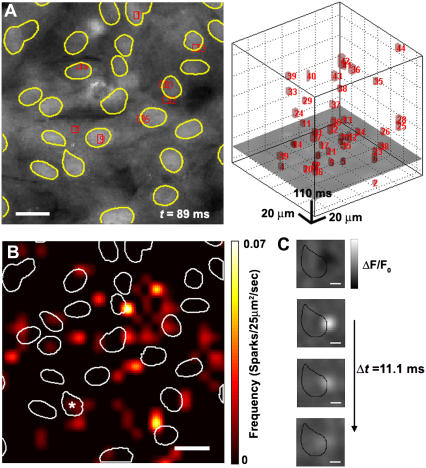
Fig. 9 A shows an example of the experimental results obtained using the multidimensional algorithm with the detected sparks marked with boxes; Fig. 9 B illustrates a spark spatial frequency map, displayed as a smoothed 2-D histogram to avoid discretization effects. The map shows that some Ca2+ sparks appear around, or even within, the nucleus boundaries. In part, this is due to the fact that the frequency histogram is a sum over a binned square area. Even so, observed sparks that overlapped the nuclear area were not uncommon; the temporal development of a representative spark from one nucleus is shown in Fig. 9 C. Closer observation of these sparks revealed that the spark foci begins in the perinuclear area and diffuses outward from that point. Laser scanning confocal microscopy may reveal that such spark activity is above or below the nucleus. Investigating the origin of sparks proximal to the nucleus is a subject for future study.
FIGURE 9.
(A) An example of spark detection algorithm performance of experimental data taken at t = 89 ms; t = 0 is the point at which the tissue fluorescence has fallen to 25% of its maximum intensity. (Left) [Ca2+]i fluorescence of the tissue. Red rectangles indicate the boundaries of a detected spark in (x,y) and borders of nuclei are shown in yellow outline. Scale bar is 20 μm. (Right) (x,y,t) image sequence (x,y, horizontal axes; t, vertical axis; t = 0 at the bottom face) with the red boxes indicating the (x,y,t) boundaries of a detected spark. The image frame shown in the left panel is illustrated as a horizontal cross section in the right panel. (B) Spatial map of spark frequency. Detected spark locations are expressed as a 2-D smoothed histogram with 25 × 25 μm2 bins. Scale bar is 20 μm. Borders of nuclei shown with a white outline. (C) Image of ΔF/F0 smoothed with 3 × 3 spatial average filter depicting the development of a perinuclear spark. Black outline indicates contour of nucleus labeled with an asterisk in panel B. Scale bar is 5 μm.
DISCUSSION
The goals of this study were to develop a means of identifying Ca2+ sparks from 2-D spatiotemporal fluorescence data and measuring their important morphological parameters. For line scanning techniques, various methods have been implemented to automatically detect and isolate sparks for analysis, the conventional algorithm developed by Cheng et al. and its variants being the most widely used (9). The conventional algorithm corrects the line scan image for baseline fluorescence by subtracting a constant value for each spatial location. Such an approach would be appropriate for long periods of quiescence but inadequate during a Ca2+ transient, in which not only the global [Ca2+]i is above baseline levels, but the associated fluorescence varies nonlinearly. An algorithm for identification of Ca2+ release sites in 2-D confocal images has been developed previously using a specialized detection kernel to enhance contrast (14,16) but relies on a priori knowledge of the spark properties to define the kernel characteristics. Furthermore, if sparks occur in close proximity, any detected spark must be distinguished from its neighbors. This is not a concern when single sparks are evoked (27), but may be problematic when the sparks originate from multiple foci or the activation frequency is high (28). Here, we have presented a means of localizing sparks spatiotemporally, with a generalized mathematical formulation that lends itself to either (x,t) or (x,y,t) spark analysis.
Refinement of detection techniques has particular implications in elucidating the link between spark morphology to pathophysiological cardiac states. For example, Lindner et al. examined the differences between Ca2+ sparks in myocytes obtained from normal and terminally failing human hearts (29). Their results indicate that factors such as decreased SERCA expression and activity contribute to significant alterations in time-to-peak and half-time of decay. Changes in spark frequency have also been reported from myocytes isolated from patients exhibiting atrial fibrillation (30), although the results are inconsistent with those of Lindner et al. Other changes in spark characteristics have been noted: hypertrophic myocytes isolated from spontaneously hypertensive rats displayed an increase in the average Ca2+ spark amplitude (31), although yet again, differing results have been reported (32). These discrepancies on the cellular level coupled with the presence of subcellular heterogeneities indicates the need to visualize the Ca2+ spark fully to better assess the impact of cardiomyopathic cellular remodeling.
The full-width half-maximum is a standard measurement in spark analysis, and has been applied to the derivation of other parameters such as spark “mass” (the volume integral of the change in fluorescence) (33), as well as inferring the necessary amount of current required to generate a spark (34). Because it has been observed that Ca2+ diffusion is anisotropic with respect to the sarcomeric Z-lines (11) and that sparks are asymmetric in shape (35), our algorithm computes the Gaussian profile along two perpendicular spatial axes. Such an approach may facilitate calculations of spark mass, which often assumes an isotropic distribution implying a spherical or cylindrical symmetry (13,36) that may not be appropriate for some experimental conditions. The FWHM values seen here were in the range of 2–4 μm, which is larger than those previously reported in ventricular neonatal rat myocytes (1.5–2 μm) (37). One possible reason for this disparity is that the values described in the literature were obtained from single dissociated myocytes, whereas this study uses monolayer tissue cultures; sparks with a spatial extent >2 μm have been observed in multicellular rat papillary muscle preparations (38). Another reason is that a spark may activate Ca2+ release from neighboring ryanodine receptors to form a compound spark (“macrospark”) (2,28,39). Several additional reasons include: 1), additional blurring introduced by the wider depth-of-field associated with the CCD camera; and 2), the use of binning to increase the temporal frame rate but with the side effect that sparks with a smaller spatial extent may go undetected since the effective pixel size is now larger.
Several factors may increase spark frequency, ranging from increasing [Ca2+]i or SR [Ca2+] content (25), decreasing extracellular [Na+] (7), and altering the intracellular pH (40), as well as the presence of sites that exhibit sudden bursts of high spark activity (41). When sparks are occurring in close proximity in either space or time, the conventional algorithm will produce a proportion of false negatives. This results from the presence of multiple sparks within a suprathreshold region, since the peak with the highest amplitude will be selected but the adjacent peaks will be omitted. If this occurs, either the single detected spark is retained or the entire region must be discarded from consideration. In addition, the spark clustering may lead to poor estimation of spatiotemporal parameters. Although our synthetic data possessed a relatively low number of adjacent sparks, the number of sparks recovered by proper separation will vary depending on the experimental conditions. For example, a study by Hollingsworth et al. estimated that up to 15% of detected sparks obtained from frog skeletal muscle failed to be analyzed for this reason (13). Our results indicate that the multidimensional maxima and watershed computation will improve detection in conditions associated with increased spark activity (30) and without the use of a separation threshold, as has been attempted previously (20).
The quality of spark detection was found to be highly dependent upon multiple factors. Temporal nonlinear heterogeneities arise from several sources: 1), monotonic decreases in intensity (such as during photobleaching); and 2), large-scale changes in intensity from nonspark activity. Such temporal changes may also be spatially heterogeneous, such as the difference between cytosolic and perinuclear [Ca2+]i diffusion (26). These problems can be minimized with an estimated fluorescence distribution that accommodates these nonlinear changes in space and time. If performed correctly, sparks may be extracted during the high [Ca2+]i levels associated with a whole-cell Ca2+ transient, as illustrated by the comparison of the conventional and multidimensional algorithms. Our results corroborate a recent study (42) demonstrating the positive predictive value (PPV) as a useful performance metric in light of Type I errors caused by low-amplitude sparks. The conventional algorithm achieved a higher PPV overall compared to the multidimensional algorithm. However, the sensitivity of the conventional algorithm is largely abolished when the underlying large-scale [Ca2+]i activity is temporally nonuniform. The inability of the conventional algorithm to accommodate such changes for 2-D Ca2+ focal release imaging has been noted previously (12). Because the performance of the spark detection procedure is dependent on the quality of input, further refinement of the fluorescence subtraction methodology would be needed to bring the PPV to a comparable level with the conventional algorithm while maintaining the improved sensitivity under the [Ca2+]i conditions modeled here.
In summary, the algorithm presented here provides a basis for extracting Ca2+ sparks from 2-D cell cultures of cardiac ventricular myocytes. The complexity of Ca2+ release in multiple spatial dimensions necessitates the development of more sophisticated spark detection methodologies. The morphological data obtained from such studies are needed to further examine the relationship of spark function at the microscopic and macroscopic structural levels, as well as cardiac myocyte behavior under normal and pathological conditions.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http:/www.biophysj.org.
Acknowledgments
We are grateful to Sean Sheehy for carrying out the cell harvests, and to Dr. Patrick Wolfe and Benjamin Olding for helpful discussions and suggestions during manuscript preparation.
This work has been supported by the Nanoscale and Material Research Science and Engineering Centers of the National Science Foundation under NSF award numbers PHY-0117795 and DMR-0213805.
References
- 1.Fabiato, A. 1983. Calcium-induced release of calcium from the cardiac sarcoplasmic reticulum. Am. J. Physiol. 245:C1–C14. [DOI] [PubMed] [Google Scholar]
- 2.Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart. Science. 262:740–744. [DOI] [PubMed] [Google Scholar]
- 3.Cannell, M. B., H. Cheng, and W. J. Lederer. 1994. Spatial non-uniformities in [Ca2+]i during excitation-contraction coupling in cardiac myocytes. Biophys. J. 67:1942–1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cheng, H., M. R. Lederer, W. J. Lederer, and M. B. Cannell. 1996. Calcium sparks and [Ca2+]i waves in cardiac myocytes. Am. J. Physiol. Cell Physiol. 270:C148–C159. [DOI] [PubMed] [Google Scholar]
- 5.López-López, J. R., P. S. Shacklock, C. W. Balke, and W. G. Wier. 1995. Local calcium transients triggered by single L-type calcium channel currents in cardiac cells. Science. 268:1042–1045. [DOI] [PubMed] [Google Scholar]
- 6.Minta, A., J. P. Kao, and R. Y. Tsien. 1989. Fluorescent indicators for cytosolic calcium based on rhodamine and fluorescein chromophores. J. Biol. Chem. 264:8171–8178. [PubMed] [Google Scholar]
- 7.Goldhaber, J. I., S. T. Lamp, D. O. Walter, A. Garfinkel, G. H. Fukumoto, and J. N. Weiss. 1999. Local regulation of the threshold for calcium sparks in rat ventricular myocytes: role of sodium-calcium exchange. J. Physiol. (Lond.). 520:431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pratusevich, V. R., and C. W. Balke. 1996. Factors shaping the confocal image of the calcium spark in cardiac muscle cells. Biophys. J. 71:2942–2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cheng, H., L.-S. Song, N. Shirokova, A. González, E. G. Lakatta, E. Ríos, and M. D. Stern. 1999. Amplitude distribution of calcium sparks in confocal images: theory and studies with an automatic detection method. Biophys. J. 76:606–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shen, J.-X., S.-Q. Wang, L.-S. Song, T. Han, and H. Cheng. 2004. Polymorphism of Ca2+ sparks evoked from in-focus Ca2+ release units in cardiac myocytes. Biophys. J. 86:182–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Parker, I., W. J. Zang, and W. G. Wier. 1996. Ca2+ sparks involving multiple Ca2+ release sites along Z-lines in rat heart cells. J. Physiol. (Lond.). 497:31–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fukumoto, G. H., S. T. Lamp, C. Motter, J. H. B. Bridge, A. Garfinkel, and J. I. Goldhaber. 2005. Metabolic inhibition alters subcellular calcium release patterns in rat ventricular myocytes: implications for defective excitation-contraction coupling during cardiac ischemia and failure. Circ. Res. 96:551–557. [DOI] [PubMed] [Google Scholar]
- 13.Hollingworth, S., J. Peet, W. K. Chandler, and S. M. Baylor. 2001. Calcium sparks in intact skeletal muscle fibers of the frog. J. Gen. Physiol. 118:653–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cleemann, L., W. Wang, and M. Morad. 1998. Two-dimensional confocal images of organization, density, and gating of focal Ca2+ release sites in rat cardiac myocytes. Proc. Natl. Acad. Sci. USA. 95:10984–10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tanaka, H., K. Nishimaru, T. Sekine, T. Kawanishi, R. Nakamura, K. Yamagaki, and K. Shigenobu. 1997. Two-dimensional millisecond analysis of intracellular Ca2+ sparks in cardiac myocytes by rapid scanning confocal microscopy: increase in amplitude by isoproterenol. Biochem. Biophys. Res. Commun. 233:413–418. [DOI] [PubMed] [Google Scholar]
- 16.Woo, S.-H., L. Cleemann, and M. Morad. 2002. Ca2+ current-gated focal and local Ca2+ release in rat atrial myocytes: evidence from rapid 2-D confocal imaging. J. Physiol. (Lond.). 543:439–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Woo, S.-H., L. Cleemann, and M. Morad. 2005. Diversity of atrial local Ca2+ signalling: evidence from 2-D confocal imaging in Ca2+-buffered rat atrial myocytes. J. Physiol. (Lond.). 567:905–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brum, G., A. González, J. Rengifo, N. Shirokova, and E. Ríos. 2000. Fast imaging in two dimensions resolves extensive sources of Ca2+ sparks in frog skeletal muscle. J. Physiol. (Lond.). 528:419–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ohi, Y., H. Yamamura, N. Nagano, S. Ohya, K. Muraki, M. Watanabe, and Y. Imaizumi. 2001. Local Ca2+ transients and distribution of BK channels and ryanodine receptors in smooth muscle cells of guinea-pig vas deferens and urinary bladder. J. Physiol. (Lond.). 534:313–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Parsons, S. P., and T. B. Bolton. 2003. Localised calcium release events in cells from the muscle of guinea-pig gastric fundus. J. Physiol. (Lond.). 554:687–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pabelick, C. M., Y. S. Prakash, M. S. Kannan, and G. C. Sieck. 1990. Spatial and temporal aspects of calcium sparks in porcine tracheal smooth muscle cells. Am. J. Physiol. Lung Cell. Mol. Physiol. 277:L1018–L1025. [DOI] [PubMed] [Google Scholar]
- 22.Gõmez, A. M., H. Cheng, W. J. Lederer, and D. M. Bers. 1996. Ca2+ diffusion and sarcoplasmic reticulum transport both contribute to [Ca2+]i decline during Ca2+ sparks in rat ventricular myocytes. J. Physiol. (Lond.). 496:575–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ríos, E., and G. Brum. 2002. Ca2+ release flux underlying Ca2+ transients and Ca2+ sparks in skeletal muscle. Front. Biosci. 7:1195–1211. [DOI] [PubMed] [Google Scholar]
- 24.Takahashi, A., P. Camacho, J. D. Lechleiter, and B. Herman. 1999. Measurement of intracellular calcium. Physiol. Rev. 79:1089–1125. [DOI] [PubMed] [Google Scholar]
- 25.Satoh, H., L. A. Blatter, and D. M. Bers. 1997. Effects of [Ca2+]i, SR Ca2+ load, and rest on Ca2+ spark frequency in ventricular myocytes. Am. J. Physiol. Heart Circ. Physiol. 272:H657–H668. [DOI] [PubMed] [Google Scholar]
- 26.Genka, C., H. Ishida, K. Ichimori, Y. Hirota, T. Tanaami, and H. Nakazawa. 1999. Visualization of biphasic Ca2+ diffusion from cytosol to nucleus in contracting adult rat cardiac myocytes with an ultra-fast confocal imaging system. Cell Calcium. 25:199–208. [DOI] [PubMed] [Google Scholar]
- 27.Wang, S.-Q., M. D. Stern, E. Ríos, and H. Cheng. 2004. The quantal nature of Ca2+ sparks and in situ operation of the ryanodine receptor array in cardiac cells. Proc. Natl. Acad. Sci. USA. 101:3979–3984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Blatter, L. A., J. Hüser, and E. Ríos. 1997. Sarcoplasmic reticulum Ca2+ release flux underlying Ca2+ sparks in cardiac muscle. Proc. Natl. Acad. Sci. USA. 94:4176–4181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindner, M., M. C. Brandt, H. Sauer, J. Hescheler, T. Böhle, and D. J. Beuckelmann. 2002. Calcium sparks in human ventricular cardiomyocytes from patients with terminal heart failure. Cell Calcium. 31:175–182. [DOI] [PubMed] [Google Scholar]
- 30.Hove-Madsen, L., A. Llach, A. Bayes-Genis, S. Roura, E. Rodriguez Font, A. Aris, and J. Cinca. 2004. Atrial fibrillation is associated with increased spontaneous calcium release from the sarcoplasmic reticulum in human atrial myocytes. Circulation. 110:1358–1363. [DOI] [PubMed] [Google Scholar]
- 31.Shorofsky, S. R., R. Aggarwal, M. Corretti, J. M. Baffa, J. M. Strum, B. A. Al-Seikhan, Y. M. Kobayashi, L. R. Jones, W. G. Wier, and C. W. Balke. 1999. Cellular mechanisms of altered contractility in the hypertrophied heart: big hearts, big sparks. Circ. Res. 84:424–434. [DOI] [PubMed] [Google Scholar]
- 32.Gõmez, A. M., H. H. Valdivia, H. Cheng, M. R. Lederer, L. F. Santana, M. B. Cannell, S. A. McCune, R. A. Altschuld, and W. J. Lederer. 1997. Defective excitation-contraction coupling in experimental cardiac hypertrophy and heart failure. Science. 276:800–806. [DOI] [PubMed] [Google Scholar]
- 33.Sun, X.-P., N. Callamaras, J. S. Marchant, and I. Parker. 1998. A continuum of InsP3-mediated elementary Ca2+ signalling events in Xenopus oocytes. J. Physiol. (Lond.). 509:67–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Izu, L. T., J. R. Mauban, C. W. Balke, and W. G. Wier. 2001. Large currents generate cardiac Ca2+ sparks. Biophys. J. 80:88–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cheng, H., M. R. Lederer, R. P. Xiao, A. M. Gõmez, Y. Y. Zhou, B. Ziman, H. Spurgeon, E. G. Lakatta, and W. J. Lederer. 1996. Excitation-contraction coupling in heart: new insights from Ca2+ sparks. Cell Calcium. 20:129–140. [DOI] [PubMed] [Google Scholar]
- 36.Zhou, J., G. Brum, A. González, B. S. Launikonis, M. D. Stern, and E. Ríos. 2003. Ca2+ sparks and embers of mammalian muscle. Properties of the sources. J. Gen. Physiol. 122:95–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Seki, S., M. Nagashima, Y. Yamada, M. Tsutsuura, T. Kobayashi, A. Namiki, and N. Tohse. 2003. Fetal and postnatal development of Ca2+ transients and Ca2+ sparks in rat cardiomyocytes. Cardiovasc. Res. 58:535–548. [DOI] [PubMed] [Google Scholar]
- 38.Wier, W. G., H. E. D. J. ter Keurs, E. Marbán, W. D. Gao, and C. W. Balke. 1997. Ca2+ ‘sparks’ and waves in intact ventricular muscle resolved by confocal imaging. Circ. Res. 81:462–469. [DOI] [PubMed] [Google Scholar]
- 39.Woo, S.-H., L. Cleemann, and M. Morad. 2003. Spatiotemporal characteristics of junctional and nonjunctional focal Ca2+ release in rat atrial myocytes. Circ. Res. 92:e1–e11. [DOI] [PubMed] [Google Scholar]
- 40.Balnave, C. D., and R. D. Vaughan-Jones. 2000. Effect of intracellular pH on spontaneous Ca2+ sparks in rat ventricular myocytes. J. Physiol. (Lond.). 528:25–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Parker, I., and W. G. Wier. 1997. Variability in frequency and characteristics of Ca2+ sparks at different release sites in rat ventricular myocytes. J. Physiol. (Lond.). 505:337–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.von Wegner, F., M. Both, and R. H. A. Fink. 2006. Automated detection of elementary calcium release events using the à trous wavelet transform. Biophys. J. 90:2151–2163. [DOI] [PMC free article] [PubMed] [Google Scholar]