Molecular Dynamics Simulations of Lipid Vesicle Fusion in Atomic Detail

Abstract

The fusion of a membrane-bounded vesicle with a target membrane is a key step in intracellular trafficking, exocytosis, and drug delivery. Molecular dynamics simulations have been used to study the fusion of small unilamellar vesicles composed of a dipalmitoyl-phosphatidylcholine (DPPC)/palmitic acid 1:2 mixture in atomic detail. The simulations were performed at 350–370 K and mimicked the temperature- and pH-induced fusion of DPPC/palmitic acid vesicles from experiments by others. To make the calculations computationally feasible, a vesicle simulated at periodic boundary conditions was fused with its periodic image. Starting from a preformed stalk between the outer leaflets of the vesicle and its periodic image, a hemifused state formed within 2 ns. In one out of six simulations, a transient pore formed close to the stalk, resulting in the mixing of DPPC lipids between the outer and the inner leaflet. The hemifused state was (meta)stable on a timescale of up to 11 ns. Forcing a single lipid into the interior of the hemifusion diaphragm induced the formation and expansion of a fusion pore on a nanosecond timescale. This work opens the perspective to study a wide variety of mesoscopic biological processes in atomic detail.

INTRODUCTION

The fusion of a membrane-bounded vesicle with a target membrane is a key step in intracellular trafficking, exocytosis, and drug delivery. In vivo, membrane fusion is highly controlled by proteins and promoted by specific sets of SNARE proteins that form membrane-bridging complexes and pull the fusion partners into close proximity (1,2). In addition, the proteins are believed to induce local curvature (3–5). The curvature stress provides the energy to drive the subsequent fusion process, which is governed by the lipid physics. The molecular details of the fusion process are difficult to assess experimentally. Continuum models based on curvature elasticity theory (6,7), static (8), or dynamic (9) self-consistent mean-field theory and computer simulations using simplified particle-based models (10–16) suggest membrane fusion to be initiated by the formation of stalks between two opposed membranes.

Here we apply the MD simulation technique using an atomistically detailed model to test the predictions made by the simplified models. We chose to mimic protein-free fusion assays used in experimental measurements by Zellmer et al. (17). In these experiments, the aggregation and lipid mixing of dipalmitoyl-phosphatidylcholine (DPPC)/palmitic acid (PA) 1:2 vesicles at pH < 5.5 and temperatures in the range 280–350 K was monitored, suggesting the vesicles to fuse above ≈310 K. To mimic these experiments, we have simulated a small DPPC/PA 1:2 vesicle with a diameter of 13.6 nm. The size of the vesicle is at the lower limit of phospholipid vesicles observed experimentally (18,19). The PA molecules were modeled in a protonated state to mimic low pH. To facilitate fusion on the nanosecond timescale of the simulations, the simulations were started from a preformed stalk between the vesicle and its periodic image and performed at elevated temperatures in the range 350–370 K. The simulation protocol was chosen similar to that used recently to reproduce the fusion-relevant transformation between a lamellar and an inverted hexagonal phase of a DPPC/PA system (20).

METHODS

System preparation

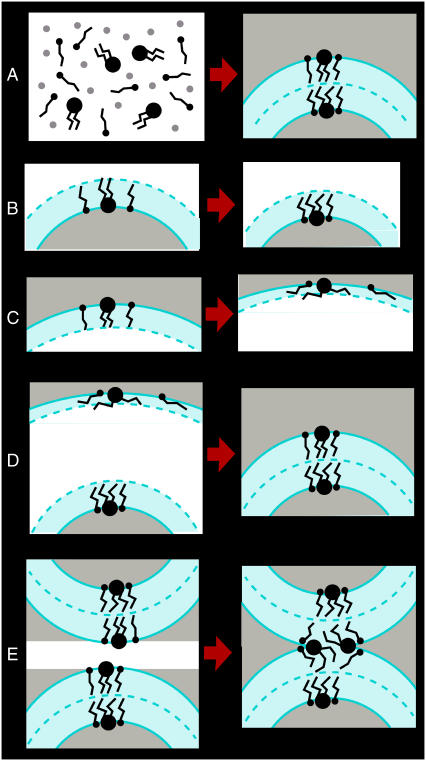
Fig. 1 shows the procedure chosen to model an atomistic DPPC/PA 1:2 vesicle with a diameter of 13.6 nm. In part 1, a coarse-grained (CG) model was used to simulate the spontaneous aggregation of DPPC and PA molecules into a vesicle (Fig. 1 A). In part 2, the CG vesicle was used as a template to model an atomistic vesicle (Fig. 1, B–D). Finally, a stalk between the vesicle and its periodic image was modeled (Fig. 1 E).

FIGURE 1.

Procedure chosen to model the initial configuration of the vesicle fusion simulations. (A–D) Modeling of an atomistic DPPC/PA 1:2 vesicle. (E) Modeling of stalk between the vesicle and its periodic image. Each step included molecular dynamics simulations using a coarse-grained (A) or an atomistic model (B–E). Lipid and fatty molecules are depicted in black, water molecules are shown in gray. Lipid (cyan) and water phase (cyan) are indicated. For details see text.

Self-assembly of a DPPC/PA 1:2 vesicle using a coarse-grained model

The self-assembly of a DPPC/PA 1:2 vesicle was simulated using a CG model by Marrink et al. (21). A DPPC is described by 12 and a PA molecule is modeled by five interaction sites. A water bead represents four real water molecules. The pairwise interactions between CG beads are described using Lennard-Jones interactions, ranging from weak (hydrophobic interactions) to strong (polar interactions) with three levels in between. The COOH headgroup of a PA molecule was described by a polar bead (type P in (21)), and the tail was described by four nonpolar beads (type C in (21)). The parameters of DPPC and water molecules are described elsewhere (21). A screened Coulomb interaction is used for the interaction between the zwitterionic headgroups. Both Lennard-Jones and Coulomb interactions are short-ranged, using a shift-based cutoff of 1.2 nm. Bonded interactions are modeled by a weak harmonic potential. Angle potentials provide the adequate stiffness of the lipid molecules.

To model the initial configuration of the simulation, 509 DPPC and 1018 PA molecules were solvated distributed randomly in a cubic box of 14.7 nm edge length (Fig. 1 A, left). To avoid interference with the boundaries (for which periodic boundary conditions were used), an additional layer of 1.3 nm of pure water was added. The total amount of CG water beads was 28,384. The system was simulated for 360 ns (effective timescale) using a time-step of 200 fs (effective timescale, 50 fs actual timestep). Constant temperature (350 K) and isotropic pressure conditions were chosen to mimic experimental conditions in vesicle fusion studies by Zellmer et al. (17). During the simulation, a vesicle formed spontaneously (Fig. 1 A, right). The number of DPPC molecules was 140 in the inner leaflet and 368 in the outer leaflet, the number of PA molecules was 365 in the inner leaflet and 653 in the outer leaflet. The number of water beads was 1735 inside and 2649 outside the vesicle.

Modeling of an atomistic DPPC/PA 1:2 vesicle using the CG vesicle as a template

The CG vesicle obtained from spontaneous aggregation was used as a template to model an atomistic vesicle as follows. The coordinates of the CG vesicle were scaled by a factor of 1.6, and atomistic lipid or fatty acid molecules with conformations obtained from a simulation of a planar DPPC/PA 1:2 bilayer (20) were fitted on their coarse-grained counterparts. The scaling was required to avoid overlap between the atomistic lipid or fatty acid molecules due to curvature effects. To optimize the packing, the inner and outer leaflet were first modeled separately each as a monolayer in a water-vapor interface in a cubic box of edge length 21 nm. The headgroups of the inner leaflet were solvated by adding 6896 water molecules in the region enclosed by the leaflet (Fig. 1 B, left, system A). The amount of water contained in system A corresponded to the amount of water enclosed by the self-assembled CG vesicle. The headgroups of the outer leaflet were solvated by filling the region outside the vesicle with 181,089 water molecules (Fig. 1 C, left, system B). The systems thus comprised a water droplet surrounded by a vapor phase (system A) or a vapor bubble in water (system B) with a lipid-fatty acid monolayer in each water/vapor interface. The systems were energy-minimized and simulated for 350 ps (system A) or 120 ps (system B) at 350 K, using fixed box dimensions, to improve the packing. The final configurations are indicated in Fig. 1, B and C (right). Two-hundred-and-thirty-five water, 55 fatty acid, and 11 lipid molecules residing in the vapor or water region of systems A and B due to nonequilibrium conditions from the initial loose packing were removed. The remainder of the two systems were put together, nested in the same simulation box (Fig. 1 D left, system C). Note that the change in the number of lipid and fatty acid molecules was only 4% and thus comparable to the uncertainty of the experimental values of the area per lipid (22) used to parameterize lipid force fields. The removal of the molecules is thus not expected to affect the quality of the vesicle model. A shell of vacuum separating the two lipid-fatty acid monolayers in system C was closed by simulating the system for 360 ps at 350 K and an isotropic pressure of 1 bar (Fig. 1 D, right). During the initial 140 ps, the two leaflets came into contact due to rescaling of the box down to an edge length of 18.9 nm such that a vesicle was formed. Subsequently, the water molecules outside the vesicle were removed and the size of the box was reduced to an edge length of 16.0 nm. The region outside the vesicle was refilled with 93,242 water molecules, except for a slab of 3 nm thickness between the vesicle and its periodic image in z direction (Fig. 1 E, left, vacuum gap) left free to create a stalk between the vesicle and its periodic image. The number of DPPC molecules was 140 in the inner and 358 in the outer leaflet, the number of PA molecules 362 in the inner and 601 in the outer leaflet, and the number of water molecules 6676 inside and 69,310 outside the vesicle. This system was simulated for 200 ps at 350 K with fixed box dimensions in x and y direction and a constant pressure of 1 bar in z direction. During the simulation, the vacuum gap closed due to deformation of the box, and a stalk between the vesicle and its periodic image formed (Fig. 1 E, right). The final dimensions of the box were 16 × 16 × 13.2 nm³.

Simulations

Two molecular dynamics simulations at 350 K and four simulations at 370 K were carried out starting from the same initial configuration comprising a preformed stalk in z direction, but different sets of initial velocities. Each simulation covered a timescale of at least 5 ns. One of the simulations at 370 K was extended to 13 ns. The final configuration of this simulation included a hemifusion diaphragm (HD) parallel to the xy plane and was used as initial configuration for a simulation at 370 K in which an external force was used to create a local defect in the HD. In this simulation, the z coordinate of the phosphate atom of a lipid molecule in the middle of the HD was subjected to a harmonic potential whose minimum was located in the center of the HD and whose force constant was 500 kJ mol⁻¹ nm⁻¹. A similar approach has been used in a recent simulation study to create a local defect in a small bilayer patch (23).

DPPC molecules were described using the force field of Berger et al. (24) in which aliphatic hydrogen atoms are described using united atoms. PA molecules were modeled in the protonated state and described using a force field derived from the lipid force field. The carboxyl group was parameterized using parameters for the carboxyl group of the protonated form of glutamic acid from the GROMOS-87 force field (25). Water molecules were described using the three-site simple-point-charge model (26). The covalent bond lengths in the lipid and water molecules were constrained using the LINCS and SETTLE methods, respectively (27,28). In addition, the total mass of the molecule was redistributed to increase the mass of the hydrogen atoms. Together this allowed the use of a time-step of 4 fs (29). Simulations were performed using periodic boundary conditions. The dimension of the box in z direction was kept fixed to keep the vesicle close to its periodic image. The x and y directions were coupled to a pressure of 1 bar using a Berendsen barostat (30). The temperature was kept constant by separately coupling DPPC, PA, and water to an external heat bath (30). Electrostatic interactions were described using a long-range cutoff of 1.4 nm with a reaction field correction (31). Each simulation was performed using the GROMACS code (32) using eight Intel Itanium 2 1.3 GHz processors in parallel under MPI. The rate of the simulations was 3 ps per CPU hour. Figures were prepared using RasMol (33) and Xfig (34).

RESULTS

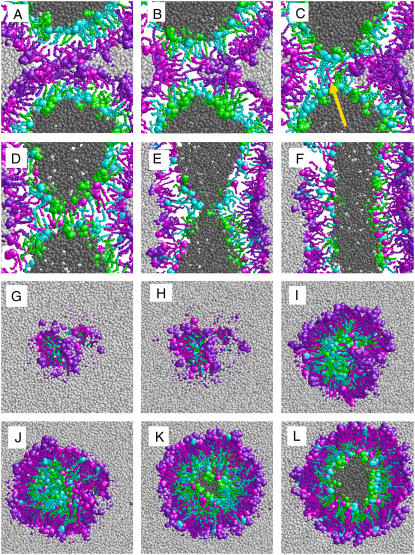
Fig. 2 shows configurations in a transformation from the preformed stalk (Fig. 2, A and G) to a fused state at 370 K. The stalk expanded quickly (Fig. 2 B, H, and I). The two proximate monolayers merged (Fig. 2 C). Their small size and protonated state enabled PA headgroups to traverse the hydrophobic core of the lipid bilayer and to exchange between the inner and outer leaflet of the vesicle. In Fig. 2 C, a fatty acid molecule, initially residing in the outer leaflet (magenta) that flipped to the inner leaflet, is marked with an arrow. A contact between the distal monolayers formed (Fig. 2 C), characterizing a hemifusion diaphragm (HD). Partially hydrated lipid headgroups were transiently trapped in the contact zone between the vesicles (Fig. 2 C). Instead of expanding radially, the HD adopted a bananalike shape (Fig. 2 I). Lipid headgroups trapped in the center of the contact (Fig. 2 I) were gradually driven to the rim of the contact (Fig. 2 J). The HD was stable for 11 ns (Fig. 2 D). A similar pathway (pathway I) for the transformation from the preformed stalk to a hemifusion intermediate was observed in two further independent simulations at 370 K and two simulations at 350 K using different initial velocities. In all these simulations, the hemifused state formed within 2 ns and was stable for the remaining 3 ns. A local defect created by forcing the headgroup of a lipid molecule in the middle of the HD into the hydrophobic core of the diaphragm induced the formation of a cracklike fusion pore within 4 ns (Fig. 2, E and K). The pore quickly expanded and fusion was completed after further 3 ns (Fig. 2, F and L).

FIGURE 2.

Fusion of DPPC/PA 1:2 vesicles in a molecular dynamics simulation. The initial configuration included a preformed stalk between the proximal monolayers (A and G). (A–F) Cuts through the vesicle along the fusion axis, showing molecules whose center of mass lies within a slab of 1.2 nm thickness, after 0.6 ns (B), 2 ns (C), 13 ns (D), 17 ns (E), and 19 ns (F). (G–L) Cuts through the stalk parallel to the contact area between the vesicles after 0.1 ns (H), 2 ns (I), 5 ns (J), 17 ns (K), and 19 ns (L). Water molecules and headgroup atoms are depicted as spheres, tails are shown as bonds. The coloring distinguishes between water molecules initially inside (dark gray) or outside (light gray) the vesicle, DPPC molecules in the inner (green) or outer leaflet (purple), and PA molecules in the inner (cyan) or outer leaflet (magenta).

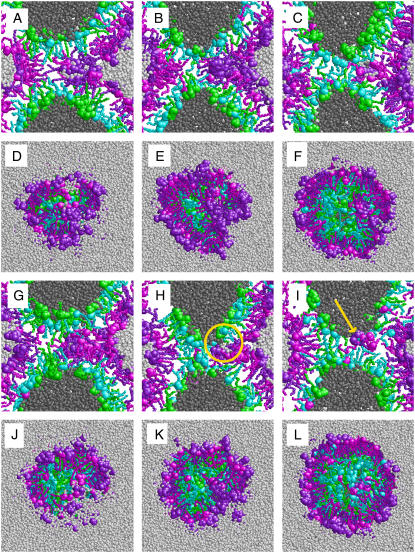
Fig. 3 shows a comparison of two different hemifusion pathways observed in our simulations. Pathway I taken by five out of six simulations as discussed above is shown in Fig. 3, A–F. Pathway II was taken by one out of six simulations (Fig. 3, G–L) and included the formation of a pore (H, circle) adjacent to the HD, connecting the region inside and outside the vesicle. The pore facilitated solvent leakage and exchange of DPPC molecules between the inner and the outer leaflet (Fig. 3 I, arrow) and closed again. The HD (Fig. 3, I and L) was similar to those observed in pathway I (Fig. 3, C and F), apart from the fact that lipid flip-flops had occurred and solvent had exchanged between the inner and the outer volume.

FIGURE 3.

Alternative pathways for lipid vesicle hemifusion. Snapshots of DPPC/PA 1:2 vesicles in two molecular dynamics simulations using the same initial configuration comprising a preformed stalk, but a different set of initial velocities. (A–F) Fusion pathway similar to that shown in Fig. 2 (pathway I). (G–L) Fusion pathway including the formation of a pore adjacent to the stalk (pathway II, H, circle). The pore allowed a DPPC molecule to flip from the outer to the inner leaflet (I, arrow) and closed again. The figures show slabs of 1.2 nm thickness along the fusion axis (A–C and G–I) or cuts through the stalk parallel to the contact area between the vesicles (D–F) and (J–L) after 0.6 ns (left), 1.2 ns (middle), and 3 ns (right). The representation chosen is similar to that used in Fig. 2.

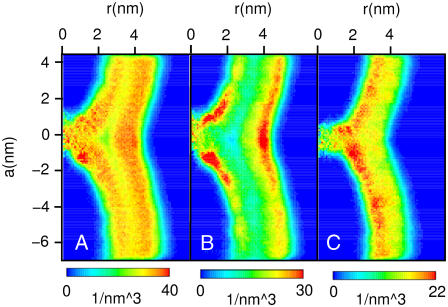
Fig. 4 shows the distribution of hydrocarbon tails in the hemifused state. An asymmetry in the distribution of DPPC (Fig. 4 B) and PA (Fig. 4 C) between the leaflets is observed, arising from the distribution of molecules in the vesicle obtained from spontaneous aggregation using a coarse-grained model as a template to model the atomistic vesicle. The density of DPPC tails is higher in the outer than in the inner leaflet, whereas the densities of PA tails behave contrarily. A similar asymmetry in vesicles composed of lipid mixtures has been observed in a previous simulation study and arises from an interplay between molecular shape and the difference in curvature between the leaflets (35). Besides the well-known density dip in the midplane (neutral surface) of a lipid bilayer, a more pronounced density dip is observed at the intersection of the neutral surfaces of the HD and the outer vesicle membrane (Fig. 4 A), which is most pronounced for the density of DPPC tails (Fig. 4 B). Early continuum models predicted fusion intermediates to exhibit unfavorable voids (36), whereas modified continuum models (37) or simulations using particle-based simplified models (11,13) suggested voids to be prevented by suitable lipid packing. Our analysis gives an intermediate picture of a hemifused state, showing that voids are prevented but specific regions of low lipid density do occur. For the DPPC/PA mixture studied here, the tendency of DPPC tails to leave regions of low lipid density is partially compensated by the PA tails, which show a more uniform distribution (Fig. 4 C).

FIGURE 4.

Distribution of hydrocarbon tails in the hemifused state. Distribution of hydrocarbon tails of DPPC and PA molecules (A), DPPC molecules (B), or PA molecules (C) averaged over the period between 10 ns and 13 ns of the simulation shown in Fig. 2. The vertical coordinate represents the position along the fusion direction, the horizontal coordinate represents the distance from the fusion axis, and the number of carbon atoms per volume element is color-coded choosing a bin width of 0.04 nm.

DISCUSSION

As part of the system preparation, a water layer of 3 nm thickness between a DPPC/PA vesicle and its periodic image was removed, and a short simulation at constant pressure normal to the vacuum slab was performed. The vacuum slab induced 1), reorientation of lipid molecules leading to exposure of lipid tails to the vacuum region driven by the hydrophobic effect; and 2), transient low pressure between the vesicles, leading to an attraction between the vesicles and rescaling of the box. Lipid reorientation and close contact between the vesicles induced the formation of a stalk. Stalk formation is also facilitated by the presence of the negatively curved lipid PA in the proximate monolayers. The presence of PA in bilayer stacks can induce stalk formation and transformation into an inverted phase at elevated temperatures (20,38). Note that, normal to the fusion direction, the vesicle and its periodic image remained separated by a water layer of 3 nm thickness (not visible in Figs. 2 and 3 focusing on the fusion site), preventing contact and suppressing correlations between the vesicles in these directions.

The preformed stalk quickly transformed into a hemifused state stable on the timescales of the simulations. Previous simulation studies using simplified models suggest a hemifused state to be in a local free energy minimum and the transformation from a hemifused to a fully fused state to involve a free energy barrier (11,16). Negatively curved lipids such as PA can stabilize the hemifused state as shown in a previous simulation study using a coarse-grained model (11). A stabilization of the hemifused state for fusion-impaired systems has also been observed experimentally (39,40). DPPC/PA vesicles such as studied here, in fact, were only shown to aggregate and exchange lipids (17). Available experimental data are thus not sufficient to discriminate between a hemifused or a fully fused state for the DPPC/PA vesicles studied here.

The creation of a local defect in the HD using an external force facilitated the formation and expansion of a fusion pore on a nanosecond timescale. Constraining a lipid in the center of a bilayer can induce the formation of a small water pore, which is stable in a stress-free bilayer (23). In our simulations here, in contrast, the fusion pore induced by forcing a PC lipid into the interior of the HD was not stable, but quickly expanded, leading to full fusion. From the quick pore-induced rupture of the HD, the following conclusions might be drawn: 1), the HD formed in the simulations is only metastable, and the state of lowest energy is the fully fused state; 2), the stability of the HD in the simulations arises from kinetic trapping; and 3), the formation of a local defect is the rate-limiting step in the decay of the HD. If the simulations had run for a sufficiently long time, thermal fluctuations would have induced the spontaneous formation of a fusion pore. However, pore nucleation is a rare event. To observe fusion pore formation on the nanosecond timescale of our simulations, nonequilibrium conditions were required. Simulation studies using simplified models suggest fusion pore nucleation to involve timescales between tens of nanoseconds (11) and tens of microseconds (13). On the minute timescale of the fusion experiments (17), fusion pores are likely to form spontaneously. The pore-induced rupture of the HD in our simulations therefore suggests the final state in the experiments by Zellmer et al. (17) to be a fully fused state. Simulations might thus be used to predict whether vesicles with a specific lipid composition, known to aggregate and exchange lipids, show full fusion or only hemifusion. On the other hand, the metastability of the HD in our simulations is in line with the current belief that sufficiently fast destabilization of the HD in biological membrane fusion requires the action of fusion proteins (41).

The instability of the HD might arise from a high mechanical tension. The usual tension leading to pore formation within seconds in the membranes of unilamellar vesicles of a diameter of ∼40 nm is σ ≈ 10 mN/m (42). A recent HD model predicts a lateral tension of σ ≈ 12 mN/m in the narrow region along the HD rim (43). Specific destabilization at the HD rim in our simulations is suggested from the observation of a cracklike fusion pore different from the usual circular pores in homogeneously stressed membranes (44). High local lateral tension at the HD rim was proposed to be generated by elastic stresses of tilt and bending (43). Our results suggest that, in addition, high lateral tension in the HD might arise from an unfavorable low-density region at the HD rim.

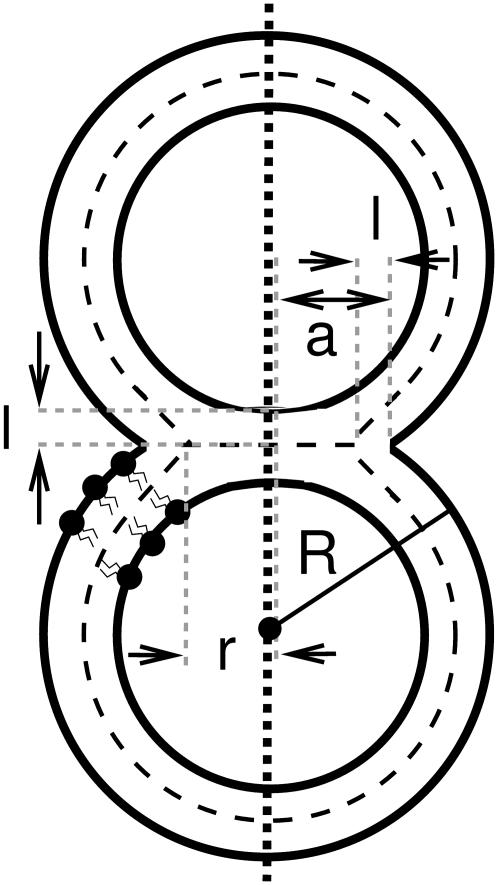
The radius of the HD in our simulations, defined as the radial distance of the intersection of the neutral surfaces of the HD and the outer vesicle membrane (Fig. 4 A), was ∼2.4 nm. This value may be rationalized from simple geometrical considerations using a model sketched in Fig. 5. Here, each of two equal-sized vesicles in a hemifused state is assumed to be a spherical cap obtained from the initial spherical vesicle with radius R by removing a spherical cap with a height equal to the thickness of a lipid monolayer, l ∼ 2.5 nm. Lipid flip-flops, vesicle leakage, redistribution of the lipid molecules in the outer leaflet from the contact zone into the remaining part of the leaflet, and possible deformation of the vesicle are neglected. The radius of the base circle of the spherical cap be denoted as a. For the general case of vesicles with unequal size, or the fusion of a vesicle with a planar membrane (R = ∞), the size of the HD is determined by the radius R_min of the smallest vesicle. Using the Pythagorean theorem yields

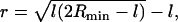(1)

for the radius r of the HD.

FIGURE 5.

Geometric parameters of two vesicles in a hemifused state. The three-dimensional structure is obtained by rotating the illustrated cross section around the fusion axis (i.e., the vertical dotted line). Bold solid lines are drawn along the polar headgroups of the lipid molecules and dashed lines along the neutral surface of the bilayer. The vesicle radius R, the monolayer thickness l, the base radius a of the spherical caps formed by the individual vesicles, and the radius r of the hemifusion diaphragm are indicated.

Neglected by the model, lipid redistribution of the lipid molecules in the outer leaflet from the contact zone into the remaining part of the leaflet is expected to lead to a slight deformation of the vesicle into a prolate shape indeed visible in Fig. 4 A. This deformation reduces the size of the HD, the dimension of the HD estimated by Eq. 1 thus being an upper bound. For the small vesicle of radius of 13.6 nm/2 ≈ 6.8 nm studied here, Eq. 1 predicts a HD radius of r = 2.8 nm. This is fairly close to the dimension of the HD in our simulations. With increasing vesicle size, the effect of lipid redistribution is expected to decrease and the value of r from Eq. 1 to become more realistic. For synaptic vesicles with a typical radius of ∼25 nm (45), an HD radius of ∼8 nm is predicted. For vesicles whose radius R_min is large compared to the thickness of their lipid monolayers, l, the ratio of HD and vesicle radius scales as

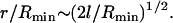(2)

Kuzmin et al. have proposed an analytical model suggesting a fusion pore to form directly from the stalk, avoiding the stage of hemifusion (46). Simulations by Kasson et al. using a coarse-grained model (16) suggest stalk-pore transformations to proceed via two different pathways including or avoiding a hemifused intermediate. Other numerical studies using simplified models (10,11,13) and our study using an atomistic model suggest a hemifused intermediate to be obligatory. This, however, will depend on the compositional details and state point (temperature, stress conditions) of the vesicle. In line with studies using simplified models (10–13,15), our results support a model of HD formation as a result of circular stalk elongation rather than its radial expansion. Our simulations suggest two alternative fusion pathways, including or avoiding the formation of a transient pore leading to vesicle leakage adjacent to the HD. Such transient pores in fusion intermediates were observed previously in studies using simplified models (10–12,15) and result from a reduced line tension in the vicinity of the hemifusion diaphragm. Pore formation is a stochastic process (12), therefore pores adjacent to the HD may or may not form during a stalk-hemifusion transformation.

CONCLUSION

To summarize, we have demonstrated the possibility to reproduce the experimental vesicle fusion behavior using atomistically detailed models. At the same time, our results give confidence to the use of CG models, which seem to capture the essential features, including the fact that a transient pore can form adjacent to the hemifusion diaphragm, leading to leakage and exchange of phospholipids between the inner and outer leaflets. In addition, our study reveals features specific for the given lipid mixture. In their protonated state at low pH, fatty acid molecules can easily traverse the hydrophobic core of a lipid bilayer and thus be exchanged between the leaflets even in the absence of a pore. This may facilitate adaptation of the lipid distribution to the curvature changes in the leaflets during membrane fusion. The hemifused state was metastable on the nanosecond timescale of simulations at equilibrium due to kinetic trapping, but quickly transformed into a fully fused state once a local defect was induced in the hemifusion diaphragm. This work opens the possibility to investigate in detail how vesicle fusion is influenced by lipid composition and (fusion) peptides.