Pore Formation in a Lipid Bilayer under a Tension Ramp: Modeling the Distribution of Rupture Tensions

Abstract

The rupture of fluid membrane vesicles with a steady ramp of micropipette suction has been shown to produce a distribution of breakage tensions, with a mean that rises rapidly with tension rate. Starting from a lattice model that incorporates the essential features of the lipid bilayers held together with hydrophobic forces, and developing it to handle varying tension rates, we reproduce the main features of the experimental results. In essence, we show that the rupture kinetics are driven by the nucleation and growth of pores, with two limiting kinetics—growth-limited and nucleation-limited. The model has been extended to address the role of peptides in solution that can adsorb and insert themselves into the bilayer. At concentrations below those required to spontaneously rupture the membrane, the effect of the peptides is to lower the rupture tensions systematically for all tension rates.

INTRODUCTION

Lipid molecules are essential components of living organisms. In fact, they are the most important structural components of cell membranes, which separate the contents of a cell from its environment. Lipid molecules are polymorphic in the sense that they can form many surfactant phases because of their molecular architecture. However, in cell membranes, they self-organize into a lipid bilayer, which contains several types of intrinsic molecules such as proteins and sterols. One important advantage of the lipid bilayer in a cell membrane is that it is almost impermeable to ions. Cell membranes are thus able to control and maintain the ion concentration gradients essential to intercellular communication. Most lipid molecules found in cell membranes are composed of a hydrophilic headgroup and two hydrophobic fatty acid tails and the membrane bilayers comprise two lipid monolayers with their tails facing each other to minimize exposure to the solvent (1). The stability of the lipid bilayer is vital to the life of the cell because if the membrane is breached, cell function may be disrupted enough to kill the cell. Despite this requirement, cell membrane rupture is a frequent phenomenon in living systems. For example, red blood cells release hemoglobin through thermal swelling (2). Cell rupture can also be induced by the capacitor effect (3,4), by extrusion through a pore (5,6), by exposure to an intense light source (7), and by osmotic swelling (8).

It is generally accepted that lipid bilayers rupture at a relative expansion of the order of 2–4%, which corresponds to an applied tension of 1–25 mN/m. As lipid bilayers are essentially two-dimensional fluids, rupture is expected to occur via pore formation in the following manner (9): As the tension is increased, metastable pores (pores with very short lifetimes) form and disperse in the bilayer. For each value of the applied tension, there corresponds an ideal pore radius, which minimizes the energy of the system below a critical pore radius. Above this radius, pores grow irreversibly, thereby rupturing the cell.

The rupture of lipid bilayers and biological membranes can also be caused by adsorption of certain proteins and peptides onto the membrane surface. This is the case for antimicrobial peptides, such as melittin, which act as a defense mechanism in the immune system of animals (10–15). These peptides attack intruders such as bacteria and kill them by rupturing their cell membranes. It has been suggested that rupture-inducing amphiphilic peptides could serve as replacements for antibiotics because they are very efficient at repelling bacterial attacks and the bacteria are unlikely to evolve a mechanism to resist them (16,17). Replacement of antibiotics by peptides would be of great importance to medicine since the overuse of antibiotics weakens their defensive capabilities (multidrug resistance) and it is more difficult and more expensive to develop new antibiotics.

This phenomenon of bilayer rupture is clearly related to the observation that lipid bilayers can lose their solvent content in the presence of amphiphilic peptides. Furthermore, the amount of solvent content lost and the rate of loss depend on the concentration of peptides. It has also been shown that the loss of cellular material is an all-or-none process. If the peptide concentration is too small, there is no loss of material. However, when a threshold concentration is reached, the peptides induce pore formation in the bilayer of the vesicle, which progressively loses its content at a rate that depends on the size of the pores. Even when a lipid bilayer is in presence of peptides in insufficient concentration to cause its rupture, it becomes fragile and ruptures at a tension lower than usual ((18) and E. Evans, University of British Columbia, personal communication, 2005).

The mechanism by which antimicrobial peptides interact with biological membranes and lipid bilayers can to some extent be related to their structure. For example, α-helical antimicrobial peptides are amphipathic (i.e., one side of the peptide is hydrophilic and the other hydrophobic). There are other types of antimicrobial peptides such as gramicidin, which forms β-sheets (19), but we only consider antimicrobial peptides with an amphiphilic α-helical structure. These peptides are able to insert into the rim of a pore, exposing their hydrophilic side to the solvent in the pore and their hydrophobic side to the lipid tails. They thus protect the hydrophobic lipid tails from the solvent in the pore and at the same time stabilize the pore by lowering its edge energy. We will refer to these structures as peptide-pores. Peptide-pores do not result exclusively from the applied tension on the membrane but of a combination of the applied tension and the peptide concentration.

The complete mechanism of action of the peptides has not yet been resolved, though there is consensus on some points. One should first note that antimicrobial peptides can be divided into two categories—weakly charged peptides (net charge of approximately one electronic charge) and highly charged peptides (net charge greater than four electronic charges). The first group contains peptides such as alamethicin and pardaxin, whereas the second group includes melittin and magainin.

Weakly charged peptides cause bilayer leakage at very low concentrations (of the order of 1:1000) (10,20–23). The majority of these peptides, however, only align in the trans-membrane direction when the concentration exceeds 1:100 (19,24). They are postulated to form pores in which the peptides are tightly aligned next to one another. These pores have been named barrel-staves (15,25).

Highly charged peptides, on the other hand, are postulated to act via a “carpet” mechanism in which the peptides first adsorb on the membrane-solvent interface, thereby causing a thinning of the bilayer (19). When the concentration reaches a threshold value (∼1:100) the peptides insert in the membrane to form peptide-pores (10,25). Highly charged peptides form toroidal pores, in which the lipid polar heads intercalate between the peptides to complete the protection of hydrophobic tails. It is important to note that the peptides in toroidal pores are not closely stacked, because they repel each other due to their charge.

Pore formation in lipid bilayers has been examined experimentally by many groups (see for instance (26–31)). In this article, we are particularly interested in the results of micropipette aspiration experiments by Evans et al. (31). The micropipette aspiration technique was originally developed by Evans et al. to study the mechanical properties of membranes, such as the effect of chain length and degree of insaturation on membrane elasticity (29), and the permeability and mechanical resistance of membranes (30). Modification of this technique allowed Evans et al. to study the effect of applying a tension at different loading rates (31). Evans et al. then showed that the tension at which a vesicle ruptures depends on the loading rate. The faster the loading rate, the higher the tension at which the vesicle ruptures. They also showed that the increase in loading rate is accompanied by an increase in the width of the distribution of rupture tensions. Evans et al. have also recently applied their micropipette aspiration technique to the study of the effect of melittin in the bilayer below the critical concentration at which the bilayer ruptures (E. Evans, University of British Columbia, personal communication, 2005, and (31)).

To analyze their experiments with varying loading rates, Evans et al. (31) considered the classical cavitation theory for opening a hole in a two-dimensional film. Using kinetic master (Markov) equations, they examined two regimes; at slow loading rate, rupture-limited by the opening of a critical pore, having to overcome a precursor barrier; and at fast loading rates, rupture-limited by the time required for the creation of the initial defect. To bring further light into these same experiments, we use and extend a microscopic nucleation model due to Fournier and Joós (32), which is described in Model, below. This is a nanoscale lattice model, which takes into account local interactions along the pore edge at the molecular length scale. Each site represents a lipid molecule, a peptide, or a vacancy (hole) state. A pore is then represented by one or more adjacent vacancies (or hole sites). The details of the simulation methods are given for bilayers both in the absence and presence of peptides in Calculational Methods. It should be noted that the model parameters are uniquely determined by experimental quantities such as the physical characteristics of the lipids and their mechanical properties, namely the modulus of compressibility (for expansion) K and the tension at rupture τ_max at low loading rate. In the last two sections, Results for the simulation are given, and Discussion concludes the article.

It is important to note that a variety of simulations have been performed for pore formation in lipid bilayers (32–44). However, to our knowledge, numerical simulation of the application of a tension ramp to a lipid bilayer has never been done.

MODEL

In this section, we describe the main features of our model, which is an extension of the model of Fournier and Joós (32), and has been developed to study the kinetics of rupture of a lipid bilayer and bilayers made of amphiphilic diblock copolymers (45). We discuss first the original lattice model and then modify it to describe the adsorption and insertion of peptides.

Model for pore formation in the absence of peptides

The physical picture underlying the model

The basic physical picture of our model is one where the membrane ruptures by the nucleation of a fast growing pore (46). Nucleating a pore in a stretched membrane creates a gain in energy through relaxation, but an energy cost through the exposure of the bilayer to water along the edge of the pore. This situation can be summarized for a finite size membrane by the following energetic expressions. The cost in energy associated with the stretching of a membrane of total relaxed area, a_m, and molecular area, a₀ is given in the elastic regime, by

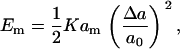(1)

where K is the area compression modulus of the lipid bilayer (47), Δa = a – a₀ is the change in the molecular area of the lipids, and a is the molecular area after expansion. The value of the area compression modulus is found experimentally using a micropipette technique (29,30). Furthermore, the surface tension, τ, is related to Δa by (32)

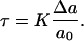(2)

When a pore is created, assuming uniform relaxation of the lipids, the change in molecular area becomes

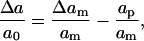(3)

where Δa_m is the total expansion of the membrane and a_p is the area of the pore. Equation 1 gives the energy change in the membrane surface.

The cost associated with the exposure of the hydrophobic lipid tails around the edge of the pore can be calculated using a line energy, λ. For small circular pores, the energy cost is (32)

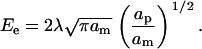(4)

The sum of the energies given in Eqs. 1 and 4 (with Eq. 3) gives the classical nucleation energy for the formation of a pore in a stretched membrane. This expression can be minimized with respect to a_p to yield expressions for the energy barrier and the pore area at rupture. Tolkepina et al. (40) have analyzed this model in terms of its finite size effects. Reasonable values are obtained for an edge energy λ comparable with values deduced from experimental articles reporting a value of λ of ∼0.5 to 3.0 × 10⁻¹¹ mN (10–14,27).

In our model, we relate K to the water exposure of the hydrophobic tails, and the line energy in the following way (32): In equilibrium, the polar heads would have the strongest effect in protecting the tails from water penetration. When the bilayer is stretched an area Δa per lipid, the hydrophobic lipid tails rearrange to minimize water exposure, but they are limited by their lack of flexibility. Therefore, a larger area would be exposed. A rigidity factor, γ ≥ 1, is introduced to take this effect into account and is defined such that γΔa represents the actual area per molecule exposed to solvent (see Fig. 1 in (32)). The increased energy per molecule is assumed to be of the form σγΔa, where σ is an effective hydrophobicity. The value γ = 1 corresponds to a fully flexible membrane. Increasing γ reduces the ability of the bilayer to stretch, since water exposure increases more rapidly with extension. This is what happens with phosphatidylcholine (PC) lipids as the number of unsaturated bonds is increased along the tails (30). In the case of DHA, the number of unsaturated bonds is so large that the membrane is unstable (48).

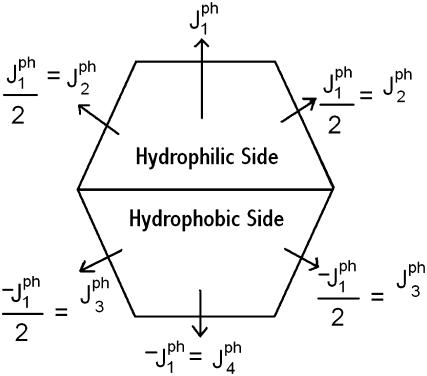
FIGURE 1.

Schematic representation of the interaction of a peptide and neighboring hole sites. The separation of the hydrophilic and the hydrophobic sides of the peptide is indicated by a horizontal line. All interactions are defined using one constant

The lipid tails also repel one another via a steric repulsion, D/a, (1,49), where D is a positive constant. The energy per molecular site in the bilayer can then be written as

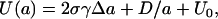(5)

where U₀ is a reference energy, which does not depend on the molecular area.

Minimization of U(a) with respect to a gives the following value for D: 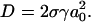Comparing the curvature of U(a) with that of the potential given by Eq. 1 yields

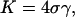(6)

which relates the area compression modulus K to the apparent hydrophobicity σ, and the rigidity factor γ.

The factors σ and γ also enter into our expression of the line energy. With the assumption of a hydrophobic pore edge, the line energy, λ, which is the excess free energy per unit length required to create the pore edge, depends on the height of the unexposed hydrophobic lipid tails h_ne

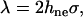(7)

where the factor of two arises because we have a bilayer. For a stretched membrane, h_ne = h_t – h_e, where h_t and h_e are, respectively, the total and exposed lengths of the hydrophobic lipid tails. From the definition above, γ can be viewed as the ratio of the surface of the sides of a cone of length h_e, the exposed length of the lipid tails, and base Δa, the area expansion per lipid (see Fig. 1 in (32)). Hence,

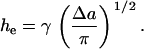(8)

The model assumes, as stated above, that the initially nucleated pore has hydrophobic edges in a membrane under tension (43). Nucleation is the crucial step in the rupture process. It is generally accepted, and has been seen in simulations (43,44), that the polar heads will eventually rearrange in such a way that the larger pores will have beveled hydrophilic edges, with the polar heads positioned along the surface. Our main interest, however, is the initial nucleation and growth of the pores up to the critical size, as we are interested in finding the point at which the bilayers rupture. In terms of the functional dependence of K, and λ, an important feature in our model is that stretching reduces λ.

We emphasize that K is determined from experiment, so only one of the two parameters σ and γ is adjustable, and it will be fixed using the rupture tension at low loading rate, as described in the next section.

Translation into a lattice model

Having presented the physical foundation to the model, we now show how it is implemented in terms of a two-state, two-dimensional lattice model similar to the Ising model for binary mixtures (32). Although a real vesicle is a three-dimensional object, in view of the size of the vesicles and the small curvature of the bilayers, a two-dimensional model contains the essential topology of the nucleation of pores in a stretched membrane. In addition, fluctuations in the third dimension do not change this topology, and can in effect be included in the thermal fluctuations allowed by the Boltzmann factor. This model is defined on a hexagonal lattice with N sites. Each site can be in one of two states: lipid molecule or vacancy (hole). The total number of sites is fixed, i.e., we work in a constant area ensemble. The number of lipid molecules is fixed, but the number of vacancies can vary. To achieve this on a lattice with a fixed number of sites, the occupancy of lipid sites and the distance between the lipids are allowed to change when vacant sites are created. These become functions of the number of vacancies, as stated below (see (32) for details).

As mentioned above, the energy of a lipid bilayer contains two terms: the surface energy and the line (or edge) energy. To calculate the surface energy, we could use a distance-dependent interaction potential between lipid sites. It is, however, easier to use the expression for the surface energy in Eq. 1, which has one input parameter, the area compression modulus, extracted from experiment (see (29)). Therefore, all that is required is an expression for the relative change in molecular area for the lipids defined in Eq. 3, which can be written as

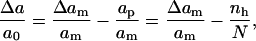(9)

where n_h is the number of hole sites. Equation 9 shows that the creation of hole sites relaxes the bilayer and that the surface energy vanishes when the number of vacancies completely relaxes the imposed bilayer expansion, Δa_m/a_m.

The edge energy is the energy increase associated with the exposure of lipid tails to solvent. In the model, the edge energy is given by the interaction energy between a lipid site and a vacant site. The line energy thus depends on the location of the hole site in the lattice. As the lattice is hexagonal, the interaction energy between neighboring lipid and hole sites is the energy of exposing one-sixth of the hydrophobic surface of a lipid to the solvent, multiplied by two to account for the two lipid monolayers of a lipid bilayer. This interaction is an interaction between nearest neighbors, which is given by (32)

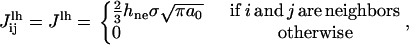(10)

where h_ne = h_t – h_e is the hydrophobic height of the section of lipid tails not exposed to the solvent (before pore formation), as defined in the previous section. The hydrophobic height exposed to water as the bilayer is stretched, h_e, is the origin of the surface energy, and is given by Eq. 8. In that equation, σ is given by Eq. 6, in terms of K and γ. Hence, only γ is adjustable.

In our simulations, we follow Fournier and Joós in setting the rigidity γ to obtain rupture at the observed critical tension τ_max at low loading rate. Note that the critical expansion at rupture, which is near 4% for lecithin (PC) bilayers, is related to τ_max through Eq. 2. In practice, simulations are performed for a range of γ to determine the value appropriate for a given lipid (32) (see Calculational Details for Simulations in the Absence of Peptides).

The edge energy is given by the number of interactions between lipid and hole sites multiplied by the interaction energy between a lipid and a vacancy. In the simulation, the occupancy of a site is a binary value (either hole or lipid, 0 or 1) and the edge energy to leading order is

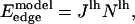(11)

where N^lh is the number of lipid-hole interactions along the edge of the pore. However, the following correction is required. As hole sites are created, the number of lipids per site increases, as N lipids now occupy N – n_h sites. This reduces the average interlipid distance to

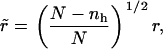(12)

where r is the initial interparticle distance. The edge energy, E_edge, can be considered as the line energy per unit length 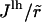multiplied by the circumference of the pore, N^lhr, (32) enabling us to rewrite the edge energy as

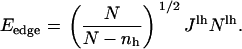(13)

Combining Eqs. 1 and 13 and using Eq. 9 gives the total energy of the membrane:

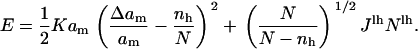(14)

Table 1 gives the values of the parameters used in the simulation. We emphasize that only one parameter is not directly input from the literature. This is γ, the tail rigidity, chosen as mentioned above to have the observed expansion at rupture in the slow loading limit. Physically, this fit gives us the link between hydrophobicity (e.g., the edge energy) and the area expansion modulus K, a relationship that is hard to quantify.

TABLE 1.

Parameter values for two different lipids used in the simulations

Lipid	K (mN/m)	ht nm	a0 nm2	τmax mN/m	γ	σ mN/m	λ 1011J/m
C18:0/1	235	3.07	0.6	6.8	9.2	6.39	3.9
diC22:1	263	3.37	0.6	11	8.2	8.02	5.4

The first four parameters are obtained from the literature; K from Rawicz et al. (29), and h_t from Rawicz et al. (29) (with the assumption that the height of the headgroup is ∼0.5 nm as reported in Wortis and Evans (1)), a₀ from Nagle and Tristram-Nagle (55), and τ_max from Evans et al. (31). The value γ is fitted to the observed τ_max, σ is deduced from Eq. 6, and λ is the unstretched value for the line tension obtained from Eq. 7.

Model for pore formation in the presence of peptides

The properties of antimicrobial peptides were summarized in the Introduction. Of the many types of such peptides, we are interested in those peptides that have an amphiphilic α-helical structure and insert with their main axis perpendicular to the plane of the bilayer. It has been predicted that such peptides insert into the rim of pores and can form thereby either barrel-stave or toroidal pores at certain concentrations depending on their charge. Many models for membrane permeation by amphiphilic peptides have been proposed and studies have shown that at certain concentrations the mode of action of melittin is described by the toroidal model. The principal difference between the barrel-stave model and the toroidal model is that in the barrel-stave model, the lipid molecules neighboring the peptides are completely shielded from the solvent, whereas, in the toroidal model, the shielding is not complete and the lipids tilt and insert their hydrophilic headgroups between the peptides. The precise mechanisms are still under investigation. However, some suggested configurations can be found in the literature (15,25).

Another model, known as the carpet model, has also been presented in the Introduction. In this case, it is proposed that, when heavily charged peptides insert in the bilayer, they do not form pores immediately. Instead, they first form a carpet of peptides on the surface of the bilayer. Then, when a certain threshold concentration is reached, they aggregate and begin to form peptide-pores. It should be mentioned at this point that the barrel-stave and toroidal model also involve the assumption that peptides adsorb onto the bilayer-solvent interface. It is our contention that all three scenarios for peptide insertion can be described by the theoretical model presented in this subsection.

In this context, we consider a vesicle immersed in the solvent with peptides (for example, melittin) in solution. To insert into the membrane, the peptide first goes through multiple steps of rearrangement thereby displacing lipids in the process. We describe this entire process by a chemical potential, which acts as an effective energy barrier for insertion. The relationship between the chemical potential μ and the concentration C of peptides in solution is given by

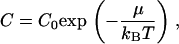(15)

where C₀ is a reference concentration, which we take equal to 1 for simplicity. The value C₀ therefore sets the scale for μ. The simulations will therefore be performed in the grand canonical ensemble at fixed temperature since the number of peptides is not conserved and the mass of the bilayer changes. The concentration of peptides in solution is taken to be constant, and the number of lipids and the area per molecule are conserved as in Model for Pore Formation in the Absence of Peptides.

Upon insertion, the peptides take up space in the membrane with a tendency to compress the lipid molecules in their vicinity, thus reducing the stress on the membrane. The change in lipid molecular area upon expansion now becomes

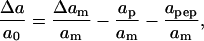(16)

where a_pep is the total area occupied by peptides. Assuming that a peptide occupies one site on the lattice, we can rewrite the surface energy as

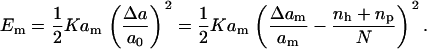(17)

where n_p is the number of peptides in the bilayer.

Similar to the case of vacancies, the interaction energy of an inserted peptide depends on its location within the bilayer and its orientation with respect to neighboring lipid molecules and vacancies. Due to the amphipathic nature of the peptide, its hydrophilic side attracts vacancies (solvent molecules), thereby repelling lipid molecules, whereas its hydrophobic side repels vacancies, thereby attracting lipid molecules. In our model, the peptide occupies a single site on a hexagonal lattice and is at the center of an hexagon with six edges as shown in Fig. 1, which also shows that each peptide is given an intrinsic orientation with respect to the lattice. The hexagon would be the Wigner-Seitz cell of the triangular lattice if we were dealing with a solid. The interactions with the vacancies are fixed by the orientation and are repulsive on the three hydrophobic edges and attractive on the three hydrophilic edges. These interactions are specified in Fig. 1. This figure shows that corresponding attractive and repulsive interactions have the same magnitude but opposite sign, so that the energy of the peptides in solution is zero. There is no additional explicit interaction with the lipid molecules, as this is included in the chemical potential. We also assume for simplicity that the peptides do not interact with each other.

Fig. 1 shows that there are four different interaction energies given by 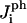: i = 1 – 4. The line energy for a bilayer containing peptides can then be written

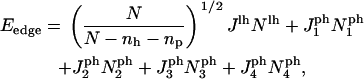(18)

where the 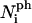are the numbers of interactions of peptides with water corresponding to the four energies 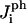(note that two pairs of the six sides have the same interaction energies with water). The first term in Eq. 18 is the line energy for vacancies for pure bilayers given in Model for Pore Formation in the Absence of Peptides. It has been modified to include the effect of peptides.

Collecting the terms from Eqs. 17 and 18 gives a total energy

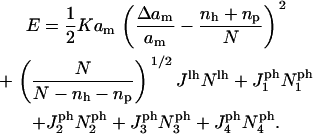(19)

Simulation and programming details for the models presented in this section and the tension ramp procedure are given in the next section for both the absence and presence of peptides.

CALCULATIONAL METHODS

Calculational details for simulations in the absence of peptides

All the simulations whose results are presented in this article were performed using the Metropolis Monte Carlo (MMC) method. Our algorithm is described as follows: A site on the lattice is selected at random, and an attempt is made to change its state (lipid to vacancy or vacancy to lipid). The new state is then accepted or rejected, according to the rule

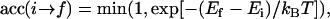(20)

where k_B is the Boltzmann constant and E_i and E_f are the energies of the bilayer before and after the trial move, respectively. Here the bilayer energy is given by the sum of the surface energy of Eq. 1 and the edge energy of Eq. 13. The tension is calculated using Eq. 2.

The number of lipid molecules in the bilayer is conserved via multiple occupancy of the sites in a lipid state. Periodic boundary conditions are also applied to all simulations. A hexagonal lattice with 200 × 200 sites (corresponding to 80,000 lipids in a bilayer), which is approximately the size of a small vesicle, was used in all calculations. It should also be noted that the algorithm of Eq. 20 preserves detailed balance.

In their simulations, Fournier and Joós (32) expanded the system very slowly (quasi-statically) to keep the system in equilibrium. To this purpose, they fixed the value of the excess area per molecule, Δa_m, and equilibrated the system over 1000 runs per site. They then increased Δa_m incrementally and repeated the process until the condition for rupture was reached. This calculation was repeated for a range of values of γ, to establish a “phase diagram” of the bilayer as a function of γ and the area expansion. This was used to determine the most likely value of γ that would be in agreement with experiment. The value γ, the tail rigidity, is the only parameter not directly input from experiment. The same procedure was followed in this work to determine γ, as mentioned in Translation into a Lattice Model.

The focus of this article is the formation of pores under the application of a tension ramp. This can be achieved by modifying the MMC procedure to generate kinetic behavior as follows. First, a value for an increment in Δa_m/a_m is chosen, namely 0.01%. The simulation is then performed for a number, N_kin, of trials per site at a fixed value of Δa_m/a_m after which the value of Δa_m/a_m is increased by the chosen increment without the necessity of having attained equilibrium. Then the procedure is repeated until rupture is achieved. The value of the tension at this point is known as the rupture tension. The loading rate is defined as

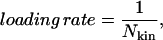(21)

and a decrease in N_kin is equivalent to an increase in loading rate.

In general, there is no way of finding a direct link between the number of MMC steps (trials) per site, N_kin, and real time. However, if the sites are chosen randomly at each trial and the temperature is fixed, the number of MMC steps per site is proportional to real time with a fixed constant of proportionality. This procedure was implemented in our simulations. Fitting our results to experiment and using known values for the compression modulus can yield an estimate for the time equivalent of a MMC step per site: for instance for C18:0/1, it is 2.35 ms.

Calculational details for simulations in the presence of peptides

When peptides are present, the MMC method is modified as follows. First, a site in the lattice is randomly selected. Next, a random attempt is made to change the state (peptide, lipid molecule, or vacancy) at that site. For example, if a pore site is selected we would choose a lipid molecule with 50% probability and a peptide with 50% probability for the trial move. If a peptide is chosen, an orientation must also be selected for the trial move. For this, we use a biased scheme similar to a Rosenbluth sampling scheme as described in Frenkel and Smit (50). Every time we try to insert a peptide, we only calculate the energy associated with the orientation of the peptide for each of the six possible orientations. This corresponds to calculating the sum of the line energy associated with each orientation. We define the Rosenbluth factor as

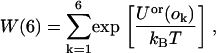(22)

where U^or(o_k) refers to the line energy associated with the k^th orientation of the peptide. One orientation, k, is then selected with probability:

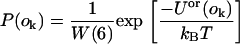(23)

Next, we define

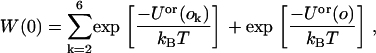(24)

where the sum over k is a sum over the orientations that were not selected and U^or(o) is the line energy of the peptide immersed in the solvent, which is zero because we set the magnitude of the attractive and repulsive potentials to be equal. Hence, Eq. 24 reduces to

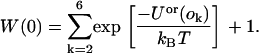(25)

The acceptance probability then becomes

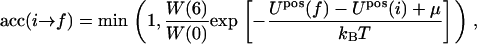(26)

where U^pos(i) is the initial energy of the bilayer, as given by Eq. 19 and U^pos(f), the energy of the bilayer with the additional peptide inserted, but without the orientational contribution already dealt with in the W(6)/W(0) factor. This procedure is used in the simulations to insert a peptide into the bilayer at a site occupied by a lipid or a vacancy.

If a peptide site is selected, first a random attempt is made in deciding whether the peptide should be replaced by a vacancy or a lipid molecule. The next step is similar to Eq. 20, but in this case, the chemical potential must be added to the initial energy:

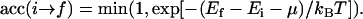(27)

Allowing the peptides to return to the solution from the membrane appears at first sight to be in contradiction with results of Benachir and Lafleur (51), who showed that melittin once inserted in one vesicle will not move to another vesicle. This is due to the irreversibility of the process as the insertion of the peptides is favored entropically. However, our model does not represent precise molecular states of a bilayer, but instead, average states. The state of the lattice during the equilibration phase is of no importance and only the final result matters for it indicates an average possible configuration. This is why to have relevant results, we must carry out simulations over many trials to fully explore the set of possible configurations. Also, the acceptance rule for changing a lipid site into a hole site or the reverse remains the same in the case when the peptides are absent (see Eq. 20).

The model in the presence of peptides is again simulated on a lattice of 40,000 sites (80,000 lipids). The procedure used to increase the expansion, Δa_m, is the same as before, except that the number of runs per site is doubled to produce the same results as in the absence of peptides. This is because there are now three possible choices of state per site rather than two. At the start of the simulation, just before the lattice is equilibrated, lipid molecules are removed and replaced by peptides in conformity with the peptide concentration to avoid incorrect relaxation at high loading rates. The lattice is next equilibrated in the presence of peptides for 10,000 runs per site before the bilayer is expanded. This is because, in the experimental situation, the vesicles are already in presence of peptides before a tension is applied and it is therefore reasonable to allow the peptides both to insert into the bilayer and return to solution from the bilayer before imposing a rate of expansion in the simulations. We did not include peptide and vacancy diffusion in the simulations, as detailed balance would not have been obeyed given the need for multiple occupancy of lipid sites. This absence of diffusion is, however, compensated by the simulation technique as it allows us to generate all possible configurations.

RESULTS

Results for pore formation in the absence of peptides

The parameters of the lattice model are the area compression modulus, K, of the bilayer, the length of the hydrophobic tails, h_t, and the rupture tension at very slow loading rate, τ_max. The value of τ_max is found by extrapolating the experimental results of Evans et al. (31), and is used to obtain the rigidity factor, γ. The values of the parameters used in the simulations are presented in Table 1 for the two types of lipid molecule studied by our model. The two lipid types are cis unsaturated 1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (C18:0/1) and 1,2-dierucoyl-sn-glycero-3-phosphocholine (diC22:1). They were chosen because of the availability of experimental data for the compression modulus, chain length, and rupture tension.

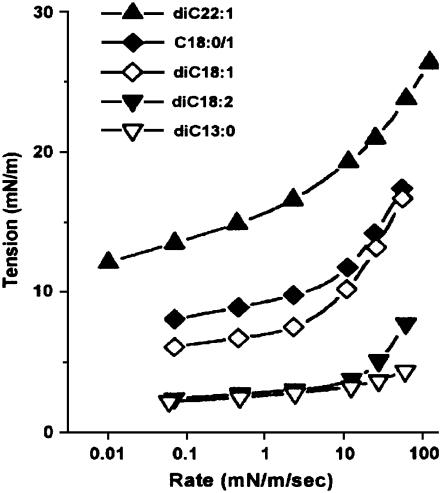
Fig. 2 shows the experimental results of Evans et al. (31) for the rupture tension as a function of loading rate for several lipids. This figure also shows that the rupture tension decreases with increasing chain length and increasing number of unsaturated bonds. Furthermore, for all lipids examined, the critical tension at slow loading rates increases slowly with increasing loading rate. In contrast, the critical tension at fast loading rates becomes a steep function of the loading rate. Evans et al. characterize these two regimes as follows. For slow loading rates, rupture is limited by pore growth, and for fast loading rate, it is limited by the nucleation of pores. Evans et al. labeled these regimes as cavitation-limited and defect-limited, respectively.

FIGURE 2.

Experimental data for the rupture tension as a function of the loading rate for different lipids (from Evans et al. (31); with permission).

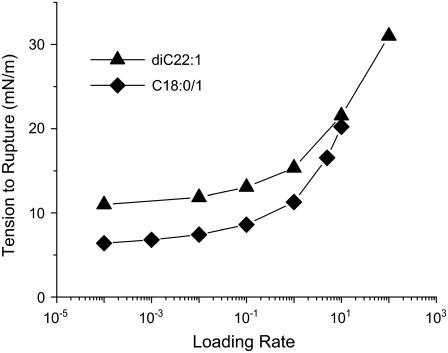
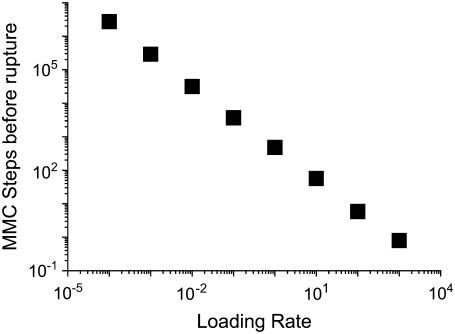
Our simulation results for the rupture tension versus loading rate are shown in Fig. 3. Visual comparison of this figure with Fig. 2 shows that our model reproduces the main features observed experimentally for both lipids. Hence, our model describes, without any additional hypothesis, both regimes for lipid bilayer rupture postulated by Evans et al. (31). Fig. 4 shows the average number of MMC steps observed before rupture occurs.

FIGURE 3.

Simulation results for the rupture tension as a function of the loading rate (see Eq. 21 for definition) for two different lipids. These should be compared with the experimental results in Fig. 2.

FIGURE 4.

Number of MMC steps before rupture as a function of the inverse of the number of MMC steps between increments of tension (the loading rate) for the C18:0/1 membrane. It is clear that rupture takes less time when the loading rate is fast even though the membrane ruptures at a higher tension.

The simulation results can be explained as follows, in accord with the physical picture presented by Evans et al. (31). At slow loading rates, the tension increases slowly. Thus, nucleation of a single hole has an increased likelihood, benefiting from the advantage of time (see Fig. 4). Since the energy barrier for the creation of additional hole sites decreases slowly, the growth of a pore to critical size is the limiting factor for rupture. But shortly after the energy barrier becomes comparable to the thermal energy, a hole site would quickly grow into a critical size pore, and the distribution of rupture tensions is consequently fairly narrow. At fast loading rates, the situation is the opposite, as the energy barrier for the creation of a pore decreases quickly. There is, however, a distribution of nucleation times for a hole site as it is a thermally activated process. The tension in the bilayer therefore may increase beyond the quasi-static failure tension, before a critical pore forms in the bilayer. This leads to large fluctuations in critical tension, and the faster the loading rate, the broader the distribution of rupture tensions. Furthermore, we observe an increase in the rupture tension with increasing length of the hydrophobic tails. This is related to the fact that longer hydrophobic chains have a larger hydrophobic surface and hence a larger energetic cost is required for the creation of a hole in the bilayer. The rupture tension also decreases with increasing rigidity.

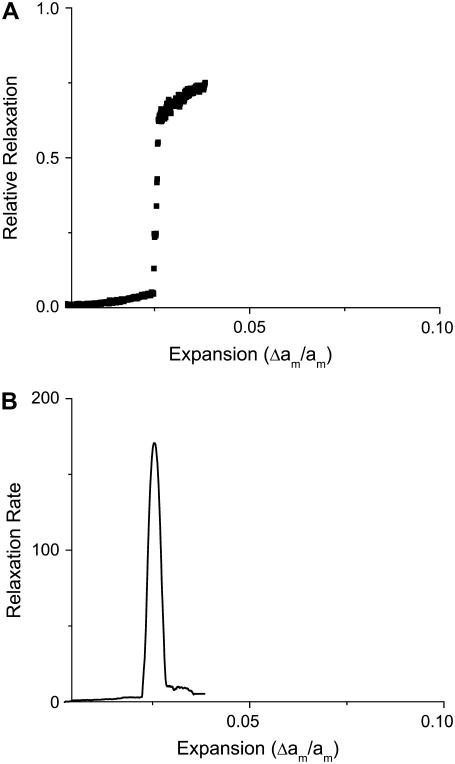
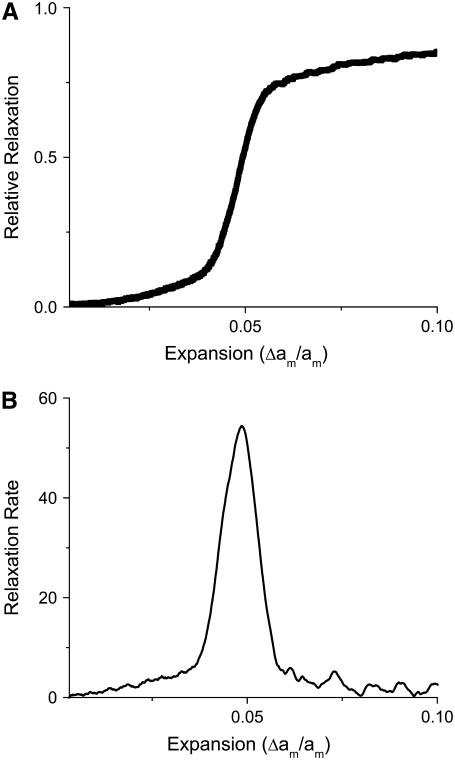
For slow loading rates, rupture has characteristics similar to a first-order transition in the sense that the relative relaxation of the bilayer (defined as the pore area divided by the area expansion) exhibits a discontinuity at the rupture point as a function of expansion (see Fig. 5). This curve, which can be called the “relative relaxation curve,” becomes less steep as the loading rate is increased (see Fig. 6). The MMC simulation gives the average relative relaxation over many samples. The precise point of rupture can no longer be ascertained, as the membrane now has an intrinsic distribution of rupture tensions, with each membrane yielding at a different expansion.

FIGURE 5.

Relative relaxation (upper curve) and relaxation rate (lower curve) as a function of the expansion for a loading rate of 10,000 MMC steps between expansion increments. The membrane relaxes at a specific expansion in a process resembling a first-order transition. The lower curve corresponds to the derivative of the lower curve with respect to expansion.

FIGURE 6.

Relative relaxation (upper curve) and relaxation rate (lower curve) as a function of expansion for a loading rate of one MMC step between increments of the expansion. The system does not relax at a specific expansion as for a slower loading rate and rupture no longer resembles a first-order transition. The lower curve again corresponds to the derivative of the upper curve.

If we take the derivative of the relative relaxation curve, we obtain the relaxation rate as a function of expansion. The maximum of this curve corresponds to the most likely point of rupture. At slow loading rates, the relaxation rate is sharply peaked, implying that the membrane ruptures precisely at the expansion corresponding to the maximum (see Fig. 5). When the loading rate is faster, we obtain a bell-shaped curve that can be interpreted as the probability that the membrane ruptures at a given expansion (or tension) (see Fig. 6).

Evans et al. analyzed their experiment by solving “kinetic (Markov) equations for defect formation and annihilation, or evolution to an unstable hole under a ramp of tension” (31). They consider three different states: the defect-free state, the defect state, and the ruptured state. To fit the data, Evans et al. (31) postulate an additional free energy barrier, E_P, for the formation of a metastable defect with energy E* in the membrane, which changes significantly the energy landscape of the problem. Such an additional defect state is not required in our molecular length scale model, and has not been seen in recent molecular dynamic simulations (43,44). The model of Evans et al. (31) gives an interesting perspective on the rupture, with its two-step process. Our MMC model, with its continuous growth scenarios of the pores, indicates that this additional barrier, E_P, must have its origin in the free energy; in other words, revealing the importance of entropy in the rupture of the bilayer. One implication of a “continuous” pore growth is that as pore sites are created, activation energies evolve with the relaxation of the membrane.

Results for pore formation in the presence of peptides

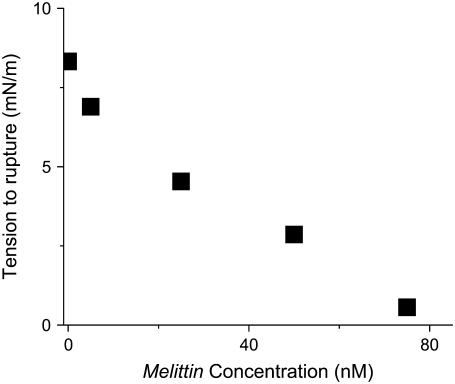
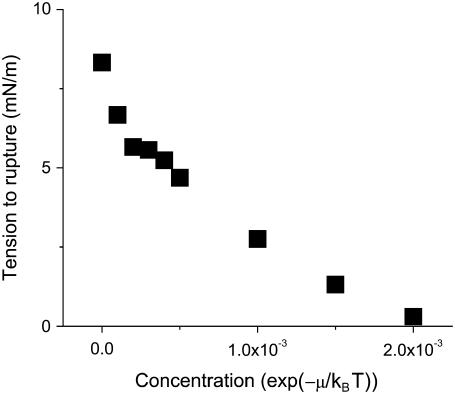
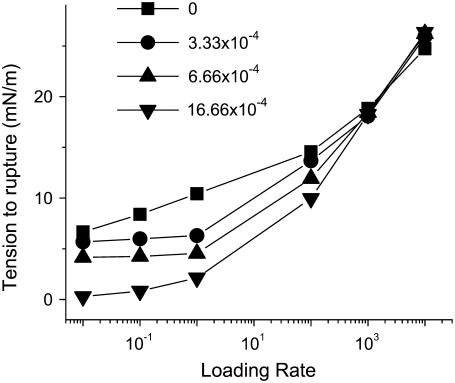
In this subsection, we introduce amphiphilic peptides into our simulations for the kinetics of rupture of a lipid bilayer under a tension ramp, and will compare our findings with those of Evans et al. ((18) and E. Evans, University of British Columbia, personal communication, 2005). The model used in conjunction with these simulations is described in this section and the computational details in Calculational Details for Simulations in the Presence of Peptides. The parameter value for the peptide-vacancy interaction is taken to be 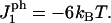The difference in hydrophobicity between the two sides of the peptide is then 24 k_BT. This value gives the correct threshold for the formation of pores (15), which is found to occur at a concentration of ∼0.002. In this case, the rupture tension again increases with increasing loading rate in the same manner as in the absence of peptides, except that the critical tensions are lower because the membrane is weakened by the peptides. This is because amphiphilic peptides are able to stabilize pores in the membrane by lowering their edge energy. We also find that the rupture tension decreases with increasing peptide concentration at fixed loading rates. Note that the concentration, C, defined in Eq. 15 can be calibrated using Figs. 7 and 8. In particular, 80 nM corresponds approximately to 2 × 10⁻³.

FIGURE 7.

Rupture tension as a function of concentration of melittin for a loading rate of 0.1 mN/m/s as obtained from the data by E. Evans (2005, personal communication). These results show an abrupt initial decrease in rupture tension followed by a monotonic decrease with increasing melittin concentration.

FIGURE 8.

Rupture tension as a function of peptide concentration for a loading rate of 20 MMC steps between expansion increments. The interaction parameter used was 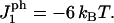Note that at a concentration near 0.002, rupture occurs at a near-zero tension; compare with Fig. 7.

Fig. 9 gives the rupture tension as a function of loading rate for several peptide concentrations. It is worth noting that with increasing tension, the effect of peptides on the membrane decreases until it becomes zero at a loading rate of 10³ (or 0.001 iterations per site between tension increments). The four curves for different peptide concentrations all converge as a function of loading rate. The insertion of the peptides is thermally activated and strain-induced insertion is less likely to occur at fast loading rates due to the small time elapsed between the beginning of the loading and rupture (see Fig. 4). Hence, the amphiphilic peptides have a limited effect on membrane rupture at those loading rates. Fig. 4 shows that rupture occurs after less than one full MMC step at the highest values of loading rate. Experimentally this convergence at high loading rate is observed for the three higher concentrations of melittin (25, 50, and 75 nM), but not for the smaller concentration (5 nM). This difference in behavior between theory and experiment can be explained as follows. Peptides, when they absorb onto a lipid bilayer, affect its structural properties. They cause the bilayer to thin locally, like depositing an object on a mattress (52), and consequently to be weakened by the ensuing chain disordering (53,54). This is not reflected in our model, where the peptide goes from the solution into the bilayer without the intermediate step of adsorption on the bilayer. The area compressibility modulus K used is that of the pure lipid bilayer, and does not include the weakening with the absorption on the bilayer. Nevertheless, this mattress effect appears to saturate, since the critical tensions for concentrations of 25 nM and higher converge at large loading rates.

FIGURE 9.

Rupture tension as a function of loading rate (see Eq. 21 for definition) for several peptide concentrations. Each curve represents a fixed peptide concentration. For high concentrations, the membrane ruptures at a very low tension. At fast loading rates, the peptides have only a limited effect upon the membrane because they do not have time to insert and weaken the membrane before it ruptures.

DISCUSSION

We have modified the Monte Carlo lattice gas model for rupture of a lipid bilayer established by Fournier and Joós (32) to include the change in rupture tension when different loading rates are applied. The basic assumption of the model is that rupture is driven by the nucleation and growth of pores. Rupture is identified as the point where the rate of growth of the pores is maximum.

The area compression modulus K and the height of the hydrophobic chains h_t, are used as input parameters in the model. The rigidity parameter γ, as defined in The Physical Picture Underlying the Model, which relates K to the line energy λ, is deduced from the rupture tension τ_max at very slow loading rate. The main features of the results of Evans et al. (31) are reproduced by our model. This adds further confirmation to the argument made by Evans et al. (31) that rupture is driven by the nucleation and growth of the pores. The model has also been successfully applied to include the effect of peptides on the rupture kinetics. The peptide concentration is controlled by a chemical potential μ for insertion of the peptides in the membrane and a peptide-pore hydrophilic interaction parameter 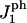characterizes the behavior of the peptide within the membrane; 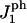regulates the interactions of the hydrophilic side of the peptide with water (the other side is hydrophobic). The modified model explains the essential behavior of the rupture tension with peptides, observed by Evans et al. ((18) and E. Evans, University of British Columbia, personal communication, 2005): an overall decrease with peptide concentration and an increase with loading rate. What also appears to dominate is a rupture process driven by the formation of pores. Our model does not include the weakening of the bilayer itself with the adsorption of the peptides (the modulus of compressibility K used is that of the pure lipid bilayer). We predict a convergence of the rupture tension to a single curve at high loading rates. Interestingly, this convergence is observed for concentrations of 25 nM and higher ((18) and E. Evans, University of British Columbia, personal communication, 2005).

The next step would be to include the specific features of weakly and highly charged peptides such as their mutual interactions, and their effect on the bilayer integrity. It is also possible to study with this lattice model other problems in membrane biophysics involving large-scale kinetics, which would be difficult to tackle using atomistic models even with our rapidly increasing computer power. Thermally driven processes abound in living systems, which usually operate at higher-than-room temperature, and Monte Carlo methods are ideally suited to the study of such types of phenomena.