Abstract
A systematic new approach to derive multiscale coarse-grained (MS-CG) models has been recently developed. The approach employs information from atomistically detailed simulations to derive CG forces and associated effective potentials. In this work, the MS-CG methodology is extended to study two peptides representing distinct structural motifs, α-helical polyalanine and the β-hairpin V5PGV5. These studies represent the first known application of this approach to peptide systems. Good agreement between the MS-CG and atomistic models is achieved for several structural properties including radial distribution functions, root mean-square deviation, and radius of gyration. The new MS-CG models are able to preserve the native states of these peptides within ∼1 Å backbone root mean-square deviation during CG simulations. The MS-CG approach, as with most coarse-grained models, has the potential to increase the length and timescales accessible to molecular simulations. However, it is also able to maintain a clear connection to the underlying atomistic-scale interactions.
INTRODUCTION
In recent years, there has been rapidly growing interest in the coarse-grained (CG) modeling of polymers (1), lipids (2,3), and proteins (4–7). In biological systems, many phenomena such as protein folding and peptide aggregation occur on long timescales and may involve large lengthscales. These characteristics hinder efforts to probe such processes with current atomistic molecular dynamics (MD) methods. Lower resolution CG models provide a practical way to surmount the limitations of current molecular simulation studies. Simplified yet accurate CG models are therefore required to extend the scope of simulations to larger length and longer timescales to unravel complex biological processes.
 models are some of the earliest reduced models for proteins (8). Primarily employed for folding studies, such models employ native state residue contacts to parameterize an energy landscape that is smoothly funneled toward the native state configuration. Other approaches to producing CG models include the generation of knowledge-based statistical potentials by using frequency distributions of pair-distances to extract effective potentials between residues. For example, Pliego-Pastrana et al. used 196 crystal structures to derive the average radial distribution function (RDF) for the centroid of alanine (5). They then used this RDF to determine an effective potential for alanine through the Ornstein-Zernike equation with an appropriate closure approximation. Giessen and Straub also investigated the coil-to-helix transition for polyalanine with a CG residue-residue interaction model derived from a statistical analysis of the protein data bank (9). One possible limitation of such knowledge-based effective potentials is that it is unclear whether the distribution of radial distances for residues in crystal structures accurately represents the corresponding distribution in solvent.
models are some of the earliest reduced models for proteins (8). Primarily employed for folding studies, such models employ native state residue contacts to parameterize an energy landscape that is smoothly funneled toward the native state configuration. Other approaches to producing CG models include the generation of knowledge-based statistical potentials by using frequency distributions of pair-distances to extract effective potentials between residues. For example, Pliego-Pastrana et al. used 196 crystal structures to derive the average radial distribution function (RDF) for the centroid of alanine (5). They then used this RDF to determine an effective potential for alanine through the Ornstein-Zernike equation with an appropriate closure approximation. Giessen and Straub also investigated the coil-to-helix transition for polyalanine with a CG residue-residue interaction model derived from a statistical analysis of the protein data bank (9). One possible limitation of such knowledge-based effective potentials is that it is unclear whether the distribution of radial distances for residues in crystal structures accurately represents the corresponding distribution in solvent.
Effective potentials have also been derived from atomistic molecular simulations. Usually an empirical functional form for the effective interactions is assumed and simulation results are used to parameterize this functional form. One example of this approach is the UNRES model of Scheraga and co-workers (10,11). These researchers developed a CG model by fitting free energy functions from all-atom simulations of oligopeptides. In another example, Smith and Hall used discontinuous molecular dynamics to study α-helix formation with an intermediate-resolution polyalanine model (12). Iterative Boltzmann inversion (13) or reverse Monte Carlo (14) methods are also often used to extract such effective potentials. In these schemes, the effective potentials are iteratively refined so that the radial distribution functions obtained by these potentials coincide with those obtained by atomistic simulations.
Force-matching (FM) is another method that can be used to extract effective potentials from molecular systems by minimizing the difference between atomistic and predicted effective forces. The method was originally developed to extract interatomic potentials from ab initio MD data (15). Izvekov et al. have recently described a new FM approach to systematically derive such potentials (16,17). Subsequently, we recognized that the method could be generalized to employ the atomistic forces derived from an MD simulation to systematically generate a pairwise additive, CG representation of a given molecular system (18,19). The essence of the approach is to use the trajectory and force data from atomistic MD simulations to derive a corresponding CG force field via a statistical least-square fitting procedure. This approach has been effectively used to reproduce structural properties for lipid bilayers (18,20), liquid water and methanol (19), ionic liquids (21), and nanoparticles (22). In this work, we extend this methodology to extract a CG force field for peptides, which in many ways represents a more significant challenge. The nature of the CG interactions obtained necessarily depends on the conditions under which the original atomistic simulations were performed. These conditions encompass the specific thermodynamic state investigated and the region of configuration space explored during the simulations. Because the effective potentials represent averaged interactions, the nature of this averaging is expected to change as different regions of configuration space are explored. However, the primary goal of this work is to determine how well the MS-CG approach can reproduce the effective interactions represented in a given set of MD simulations. The manner in which these interactions differ with simulation conditions will be explored in future studies. Furthermore, we are principally concerned with accurate reproduction of equilibrium structural properties rather than dynamical quantities in our first application of this approach. Coarse graining procedures can in general modify the properties of the free energy landscape underlying the CG models compared to that present in the original atomistic systems. For example, one would expect that the averaging of atomistic interactions that is inherent to coarse-graining methods will smooth the underlying free energy landscape, facilitating exploration of the corresponding phase space. Indeed, this is thought to be one advantageous feature of CG models. Although the details of CG and atomistic landscapes may deviate, our primary focus of this work is to ensure that the essential features of the free energy landscape are maintained by the CG model. In this regard our main goal is to ensure that the locations of free energy minima within the CG landscape correspond to those present in a CG representation of the original atomistic system. As a consequence, average (i.e., equilibrium) properties of both systems will be comparable despite the fact that some detailed properties of the individual free energy landscapes differ. For these studies, the region of configuration space investigated is the folded conformation of two simple peptides with common structural motifs: an α-helical polyalanine pentadecamer (Ala-15) and the β-hairpin peptide V5PGV5. This work demonstrates for the first time the feasibility of ultimately applying this methodology to protein systems.
METHODS
Atomistic simulations
Atomistic MD simulations for the solvated peptide systems were first performed. The initial helical conformation for α-helical Ala-15 was generated by using the CHARMM c30b2 package (23) and setting backbone dihedral values of φ = −53.2°, ψ = −47.5°. For the β-hairpin peptide V5PGV5, the structure from Ferrara et al. was adopted (24). For each system, five peptides were solvated in a cube of TIP3P (25) water with edge length of 40 Å. Water molecules whose oxygen atom was closer than 2.8 Å to peptide atoms were deleted, leaving 1919 and 2130 water molecules for the Ala-15 and V5PGV5 systems, respectively. Each system was subjected to 1000 cycles of steepest descent minimization followed by another 1000 minimization steps using the conjugate gradient method. Peptide atoms were kept fixed during minimization. Each system was then heated to 310 K and preequilibrated for 3000 steps of MD using CHARMM. The peptides were kept constrained at their initial configuration during this stage. Then, each preequilibrated configuration was used to initiate MD simulations using the CHARMM force field and the DL_POLY molecular simulation package (26). The temperature was kept at 310 K using a Nose-Hoover thermostat with a relaxation time of 0.5 ps. Bonds containing hydrogen were held rigid using the SHAKE (27) method with a geometric tolerance of 10−6. The cutoff distance for short-range nonbonded interactions was set at 10 Å. Electrostatic interactions were calculated using the particle mesh Ewald summation and a time step of 2 fs was employed. Each system was equilibrated for 2 ns followed by a production stage in which a 4-ns trajectory with 2000 configurations was generated for further analysis.
Coarse graining
Each amino acid side chain was treated as one CG group, which each comprises a virtual “bead”. Two levels of resolution for the peptide backbone (–NH–CH–CO–) were investigated, with either one or three beads per peptide unit (i.e., for a total of two or four beads per amino acid residue). For the latter models the backbone groups –NH–, –CH–, and –CO– were each treated as CG sites called NBB, CBB, and OBB respectively. For proline, the backbone N atom was represented as a separate group (NBP). For glycine, the whole residue backbone was considered a group (CBG). Each water molecule was represented by a one-site bead CGW, allowing solvent effects to be explicitly manifest in the present MS-CG models. This contrasts with other CG approaches that often account for solvent in an implicit manner (11). The positions of CG sites were usually placed either at the center of geometry or at the center of mass of the corresponding atoms. When the positions of all CG groups are placed at the center of mass of the corresponding atomistic groups, this scheme is referred to as COM. Likewise, placing all CG groups at the geometrical centers of atomistic groups leads to COG. Various combinations of COM and COG coarse graining were employed. Full descriptions of the various CG schemes are provided as Supplementary Material. Comparisons of the atomistic and two-bead-per-residue COM models for Ala-15 are shown in Fig. 1.
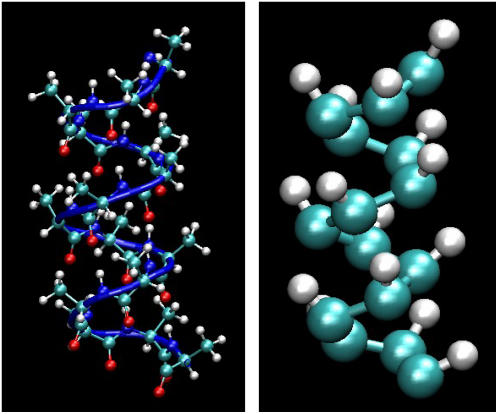
FIGURE 1.
Atomistic (left) and two-bead-per-residue COM-CG (right) models of Ala-15. Note the dramatic reduction in system size that is associated with the conversion from atomistic to MS-CG representations. This greatly reduces the time and memory requirements necessary for MS-CG versus atomistic simulations.
Coarse-grained force fields
The coarse-grained force field is composed of nonbonded and bonded interactions derived from FM and statistical analysis of the atomistic simulation trajectories, respectively. This was done for reasons of simplicity. During the course of our investigations we found that the fluctuations of the virtual CG bonded interactions are well represented by simple analytic expressions. Thus, it was relatively easy to fit these probability distributions with the appropriate potentials as described in the section “Bonded interactions” without employing the FM approach. The FM procedure described below was applied only to the nonbonded interactions between CG sites.
Force matching
The core of the FM method lies in minimizing the difference between atomistic forces projected unto CG sites and predicted CG forces, which is equivalent to minimizing the residual χ2 given by:
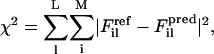 |
(1) |
where 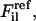
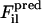 are, respectively, a reference force computed from the atomistic simulations and a CG force predicted to act on the ith atom in the lth atomic configuration. The summation runs over all M atoms found in the L atomic configurations used in the fit. The force for each CG site is the algebraic sum of the corresponding atomic forces in each direction. The method divides the radial distance between pairs of CG sites into bins and fits the force inside each bin using a cubic spline so that the computed CG force field is no longer restricted to a simple analytic form. The use of splines to represent the CG forces dramatically simplifies the least-squares fitting procedure by making these forces linear functions of the system coordinates. Consequently, the conditions embodied by Eq. 1 can be enforced simply by framing the problem as a matrix equation. Details of the implementation have been previously described (18,19). For this study,
are, respectively, a reference force computed from the atomistic simulations and a CG force predicted to act on the ith atom in the lth atomic configuration. The summation runs over all M atoms found in the L atomic configurations used in the fit. The force for each CG site is the algebraic sum of the corresponding atomic forces in each direction. The method divides the radial distance between pairs of CG sites into bins and fits the force inside each bin using a cubic spline so that the computed CG force field is no longer restricted to a simple analytic form. The use of splines to represent the CG forces dramatically simplifies the least-squares fitting procedure by making these forces linear functions of the system coordinates. Consequently, the conditions embodied by Eq. 1 can be enforced simply by framing the problem as a matrix equation. Details of the implementation have been previously described (18,19). For this study, 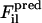 were fit so that effective interactions for a given CG type were identical regardless of position along the peptide chain. The grid spacing for the force-distance relationship was set to 0.5 Å and the cutoff for computation of CG forces was set to at least 12 Å. Equation 1 was solved repeatedly for 40 configuration sets, with each set consisting of 50 configurations. The resulting solutions were averaged over all sets to obtain the effective CG forces. This data was then placed into a numerical DL_POLY format table file with tabulated forces and potential energies for later CG simulations.
were fit so that effective interactions for a given CG type were identical regardless of position along the peptide chain. The grid spacing for the force-distance relationship was set to 0.5 Å and the cutoff for computation of CG forces was set to at least 12 Å. Equation 1 was solved repeatedly for 40 configuration sets, with each set consisting of 50 configurations. The resulting solutions were averaged over all sets to obtain the effective CG forces. This data was then placed into a numerical DL_POLY format table file with tabulated forces and potential energies for later CG simulations.
Bonded interactions
It was assumed that CG bonded interactions are composed of stretching, angle bending, and dihedral torsion terms. Both stretching and bending are assumed to be harmonic whereas dihedral interactions are represented by a cosine series:
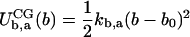 |
(2) |
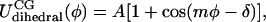 |
(3) |
where b and a represent specific bond or angle terms, k is the force constant, b0 is the equilibrium value, A is the torsion force constant, m is the multiplicity, and δ is the phase angle. In accordance with Boltzmann statistics the normalized probability distribution Px of CG bond length, angle, or dihedral x satisfies:
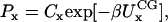 |
(4) |
where 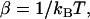 kB is Boltzmann's constant, T is the temperature, and C is a fitted constant. The CG bonded parameters were determined by a conventional least-square fit of the probability distributions obtained from atomistic simulations employing Eqs. 2–4. For two-bead models of Ala-15, only bonded parameters for stretching and bending were fit.
kB is Boltzmann's constant, T is the temperature, and C is a fitted constant. The CG bonded parameters were determined by a conventional least-square fit of the probability distributions obtained from atomistic simulations employing Eqs. 2–4. For two-bead models of Ala-15, only bonded parameters for stretching and bending were fit.
Assessment of efficiency
An often touted benefit of CG models is that they can enhance the efficiency of molecular simulations. Enhanced efficiency can be separated into two main components. One comes from reduced computational expense due to the decreased number of degrees of freedom that must be considered for CG simulations. Another stems from the enhanced exploration of configuration space induced by the smoother effective interactions present in CG simulations. The first factor can be subdivided into a reduced complexity factor C and an increased time step factor I. C can be simply represented by C = Natm/NCG, where Natm and NCG represent the number of atomistic and coarse-grained degrees of freedom, respectively. Increased values of C represent savings in memory and computational manipulations that will be needed to generate a given step of simulation data in the CG system. For the systems discussed here C is determined primarily by solvent degrees of freedom. As each water molecule (three atoms) is represented by a single bead in these MS-CG models, C exhibits a value of ∼3. Values of C observed for Ala-15 MS-CG models are 3.028 for two-bead models and 2.986 for four-bead models, whereas V5PGV5 models exhibit a value of 3.018 (only four-bead models are discussed for this peptide). The reduction in complexity denoted by C itself implies a possible enhancement in the time step possible for CG dynamics I that depends on the masses of the coarse-grained particles. I stems from the increased integration time step that can be applied while solving the CG equations of motion because certain degrees of freedom are not explicitly considered. This can be represented by I = tCG/tatm where the numerator and denominator are the integration time steps possible in CG and atomistic simulations, respectively. The necessary integration time step is determined by the lightest particles in each system and can be assessed by comparing the ratios of the lightest masses present in MS-CG and atomistic simulations. A detailed description of how I may be computed is presented as Supplementary Material. For the systems employed in this work, I was found to be on the order of fourfold, suggesting that it should be possible to employ an integration time step in the MS-CG simulations approximately four times as large as that used for the atomistic simulations. However, to facilitate comparisons this factor was not incorporated into this MS-CG simulation protocol.
The contribution due to enhanced sampling of configuration space is harder to assess. In this work we focus on the peptide degrees of freedom to evaluate this capability for two reasons. Firstly, obtaining a meaningful representation of peptide properties is usually the main motivation for carrying out solvated peptide simulations. Secondly, spatial and temporal correlations tend to decay much more quickly in the solvent than in the protein. The extent to which configuration space is explored will be limited by the longest-lived correlations and thus will be determined primarily by the peptide. As a result, the efficiency of conformational sampling for the peptide system was used as a proxy for the overall rate of sampling in each simulation. The approach employed in this study is to separate the total sampling enhancement STot into two components SFlu and SExp that can be evaluated separately: STot = SFluSExp. The first factor SFlu incorporates effects that arise due to more rapid fluctuations in the MS-CG systems. This leads to increases in the rates of processes observed in MS-CG simulations compared to the corresponding atomistic systems. This factor indicates how many fewer simulation steps are needed to observe a given phenomenon in MS-CG simulations. When the rates observed in atomistic and CG simulations are denoted by katm and kCG, SFlu can be represented by SFlu = kCG/katm. If one takes the simple approximation that the observed rates are linearly dependent on the inverse of some correlation time τ that characterizes the decay of fluctuations in the systems, k = ατ−1, then SFlu is proportional to τatm/τCG. This is intuitively the behavior one expects: processes that occur more quickly in the CG simulations lead to larger values of SFlu. In this study it is assumed that the prefactor α for atomistic and MS-CG simulations is approximately the same. This allows the ratio of correlation times measured in MS-CG and atomistic simulations to be directly employed to evaluate SFlu. This approach is reasonable because the fundamental processes that govern correlations (i.e., peptide conformational fluctuations) are identical in each system. Root mean-square deviation (RMSD) fluctuations with respect to a given initial conformation were used to compute these correlation times. RMSD fluctuations were employed because this measure can be explicitly related to conformational fluctuations. Systems that exhibit rapid fluctuations in RMSD should tend to exhibit more rapid conformational fluctuations and accelerated decorrelation processes. The time course of RMSD values occurring in MS-CG simulations and in CG representations of the corresponding atomistic simulations (e.g., see Figs. 5 and 9) were used to compute autocorrelation functions. These autocorrelation functions were then fit to multiexponential expressions to derive correlation times characterizing the decay of RMSD correlations as described in the Supplementary Material. Ratios of these correlation times were employed to compute the values of SFlu shown in Table 1.
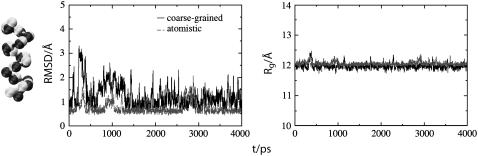
FIGURE 5.
Far left shows the backbone of two-bead COM-CG Ala-15 (dark gray) superimposed upon the corresponding MS-CG backbone derived from an atomistic configuration (light gray). This color relationship is maintained throughout the figure, with data for this MS-CG model denoted by dark lines and the corresponding atomistic data denoted by light lines. The center plot compares RMSD during the respective simulations. Although the average RMSD for both curves is similar, note the larger RMSD fluctuations for the MS-CG model. The plot on the far right displays the corresponding comparison for radius of gyration and demonstrates that the overall shape of the peptide is maintained throughout the MS-CG simulations.
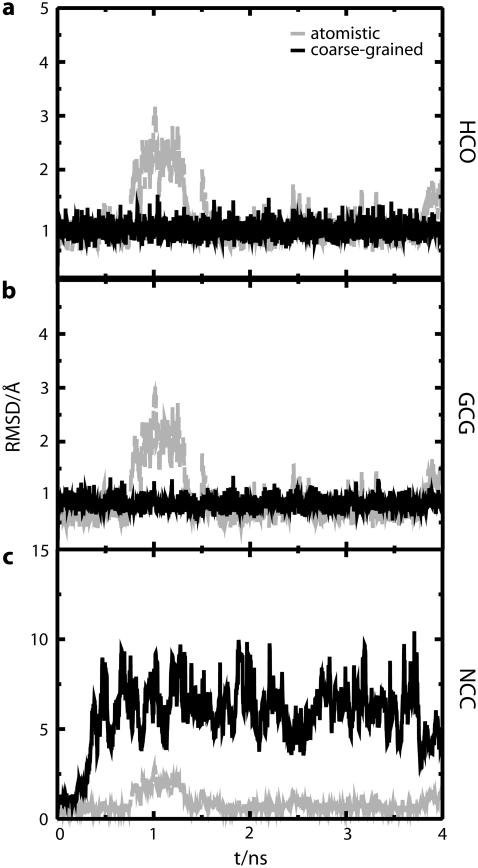
FIGURE 9.
Comparison of RMSD between atomistic (light gray) and MS-CG (dark gray) simulations for four-bead models of V5PGV5 from the (a) HCO-CG, (b) GCG-CG, and (c) NCC-CG schemes. Note the change of scale in panel c. Although the other two models fluctuate close to the atomistic structure, NCC-CG rapidly causes unfolding of the peptide as described in the text.
TABLE 1.
Enhanced sampling factors computed for different MS-CG peptide models
| SFlu | SExp | STot | |
|---|---|---|---|
| Ala-15 | |||
| COM | 1.16 | 4.08 | 4.73 |
| CMG | 7.77 | 3.47 | 27.0 |
| COG | 2.87 | 3.61 | 10.4 |
| ACG | 15.93 | 4.08 | 64.9 |
| HCO | 67.85 | 0.053 | 3.60 |
| NCC | 22.23 | 0.29 | 6.42 |
| GCG | 301.1 | 0.085 | 25.6 |
| V5PGV5 | |||
| HCO | 448.3 | 0.087 | 39.0 |
| NCC | 2.13 | 14.6 | 31.1 |
| GCG | 4.25 | 0.056 | 0.238 |
The second factor SExp incorporates efficiency enhancements that arise when additional regions of conformational space are visited in the MS-CG simulations compared to atomistic simulations. Any metric chosen to evaluate SExp should reflect the breadth of the conformational distributions present in the two systems. RMSD was also employed for this purpose because it directly measures the Euclidean distance between two conformations. Thus, the breadth of a distribution of RMSD values is commensurate with the size of a given conformational space. One simple and effective indicator that provides this information is the variance obtained for the RMSD distributions described above. Thus, the variance of RMSD values Δ2 in MS-CG and atomistic simulations was employed to evaluate SExp: 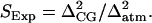 Computed values of SExp are presented in Table 1 whereas the observed values of Δ2 are provided as Supplementary Material. The overall efficiency (OE) gains expected from the MS-CG simulations can then be evaluated via OE = CISTot, where STot = SFluSExp.
Computed values of SExp are presented in Table 1 whereas the observed values of Δ2 are provided as Supplementary Material. The overall efficiency (OE) gains expected from the MS-CG simulations can then be evaluated via OE = CISTot, where STot = SFluSExp.
RESULTS AND DISCUSSION
Nonbonded interactions
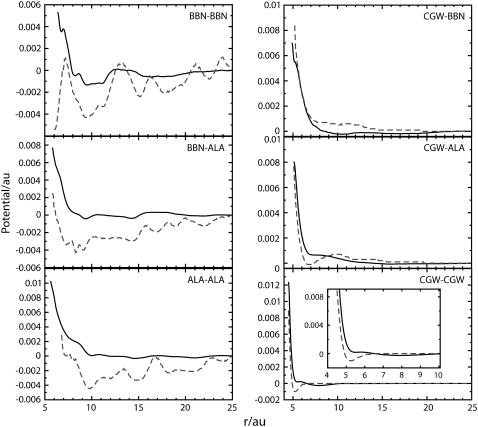
Nonbonded forces and potentials obtained from the MS-CG procedure are displayed in Figs. 2 and 3. Although they do incorporate information about the forces that occur in a given system, the MS-CG forces are not simply the averaged forces at a certain radial distance for a given CG pair. It is well known that potential of mean force (PMF) for any coordinate can be obtained by evaluating the average forces that arise at a given value of this coordinate. This average is equal to the gradient of the PMF; integrating the average forces obtained in this way provides the free energy of the system with respect to the coordinate of interest. We must stress that the effective MS-CG forces represent more than just the gradient of the conventional PMF and that the MS-CG potentials do not correspond to a PMF in the sense described above. The MS-CG interactions do represent many-dimensional free energy functionals since they involve averaging over certain degrees of freedom (i.e., those that have been coarse grained away). However, a conventional PMF only provides information about the direct (two-body) correlations that occur in a system. In contrast, MS-CG interactions incorporate information about both two- and three-body correlations that are present in the underlying MD simulations. This issue is discussed at length in a forthcoming publication from our group (28). To demonstrate the difference, the gradient of the radial PMF for the CG sites from atomistic MD data is compared to the corresponding MS-CG force for various sites from the two-bead COM model of Ala-15 in Fig. 2. The bead representing each residue backbone is referred to as BBN whereas each side-chain bead is called ALA. Radial PMFs W(r) were obtained via 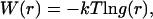 where g(r) is the radial distribution function computed from the atomistic simulations. The PMF curves were then numerically differentiated to provide gradient information.
where g(r) is the radial distribution function computed from the atomistic simulations. The PMF curves were then numerically differentiated to provide gradient information.
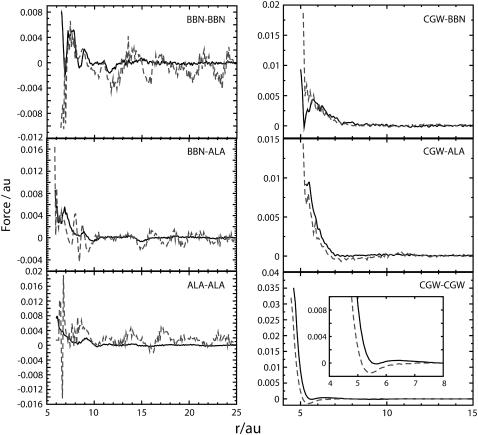
FIGURE 2.
MS-CG force profiles (solid lines) and PMF derivatives (dashed) for the interaction of CG site pairs in the two-bead COM-CG model of Ala-15. Peptide-peptide interactions are displayed in the left plot whereas interactions involving water (CGW) are displayed in the right plot. Note that the MS-CG forces are significantly different from the PMF derivatives. Also note that the inset of the bottom right plot provides a detailed illustration of the differences between the curves at small separations. In general the profiles do not resemble simple analytic functions. This observation demonstrates that the effective MS-CG forces in molecular systems are not easily predicted a priori. The ability to represent essentially any type of effective interaction is one of the distinct strengths of our FM approach. All data are reported in atomic units (au).
FIGURE 3.
Effective potentials between MS-CG sites in the two-bead COM-CG model of Ala-15 are compared to radial PMFs derived from atomistic radial distribution functions. Peptide-peptide interactions are displayed in the left plot whereas interactions involving water (CGW) are displayed in the right plot. Note that the PMFs are significantly different from the MS-CG potentials, and in particular are more attractive in nature. The inset of the bottom right plot provides a detailed illustration of the differences between the two curves at small separations. MS-CG effective interactions are dominated by repulsion between CG groups, particularly at short distances. However, favorable interactions do exist at intermediate distances. Note that the depth of energy minima in the MS-CG potentials progressively increase with the strength of the underlying atomistic interactions: BBN-BBN > CGW-CGW > BBN-CGW > ALA-CGW (see text). This reflects electrostatic and hydrogen bonding interactions subsumed into the effective potentials. Data reported in atomic units.
It can be seen that the MS-CG forces and the PMF gradients are qualitatively different for the peptide CG groups. This is particularly evident at large separations, where the PMF gradients display substantial fluctuations whereas the MS-CG forces have largely decayed to zero. The MS-CG forces and PMF gradients are more similar for solvent interactions, although a distinct offset between the two curves is apparent. This difference becomes more pronounced as the van der Waals radius is approached. This observation suggests that the unique many-body nature of the MS-CG forces is primarily manifest via nearest neighbor effects.
In contrast to the usual assumption underlying most CG force fields that employ preselected analytical forms for all interactions, the characteristics of the nonbonded CG force profiles obtained in this work could not likely have been predicted a priori from the underlying atomistic data. The force profiles derived using other two-bead CG schemes are similar to those displayed in Fig. 2. The nonbonded force profiles of CG site pairs for four-bead models of Ala-15 and V5PGV5 are provided as Supplementary Material. It was found that all CG forces converge to zero at long range. At short and intermediate ranges, there are both repulsive and attractive forces. As constrained by the conformation of the peptides in the atomistic simulations, distinct relative orientations between CG sites exist at different distances. This anisotropic effect is implicitly included in the nonbonded interactions determined in the MS-CG methodology. The nonbonded interactions for CG pairs effectively incorporate both van der Waals and electrostatic interactions present in the atomistic system (including hydrogen bonding). However, at the two-bead level the net charge of each peptide and solvent CG group is zero. Consequently, van der Waals and dipole interactions play a primary role in determining the net forces. The relatively high density present in condensed phase systems causes the overall effect of these interactions to be dominated by collisions between particles. Consequently, the MS-CG forces chiefly reflect the repulsive part of the van der Waals curve. Nonbonded interactions between CG beads thus look very much like interactions within a Lennard-Jones fluid at this level of coarse graining. This effect is evident in the primarily repulsive nature of the force profiles displayed in Fig. 2.
MS-CG potentials are compared to the corresponding radial PMFs in Fig. 3. The MS-CG potentials were obtained by numerically integrating the MS-CG forces. Curves have been shifted to match zero at long distances. It is clear that the PMFs exhibit significant qualitative differences from the MS-CG potentials and in particular are much more attractive. The highly structured nature of the peptide is apparent from the many fluctuations observed in the peptide PMFs that persist to quite long lengthscales. These structural correlations decay more quickly for the solvent interactions. In general the MS-CG potentials decay to zero much more rapidly than the PMFs and, in a similar manner to the MS-CG forces, are dominated by repulsive interactions at short range. Thus, MS-CG interactions at this lengthscale are governed by excluded volume effects. At intermediate distances only the BBN-BBN interaction exhibits a significantly attractive nature (i.e., negative potential). This is likely due to the hydrogen bonding interaction between backbone atoms. Further evidence of the contribution of atomistic interactions to CG properties is the deeper energy minimum that exists at short range for polar pair CGW-CGW compared to that of the less polar pair BBN-CGW or the nonpolar/polar pair ALA-CGW. Even though the constituent atoms of both the BBN and CGW groups are polar and able to form hydrogen bonds, the BBN-CGW interaction is less favorable than BBN-BBN or CGW-CGW because the peptide units are oriented to preferentially interact with each other along the helical axis and not with solvent (since the helix exhibits a folded configuration). Note that the radial PMF for the CGW-ALA interaction exhibits a distinct minimum whereas the corresponding MS-CG interaction does not. One might consider it surprising that this minimum in the PMF exists because the interaction between polar CGW and hydrophobic ALA is expected to be negligible. This observation can be rationalized by considering that the PMF reflects preferential ordering of the polar solvent at the surface of the hydrophobic ALA site due to favorable solvent entropy. As the intersite potential for a given CGW-ALA pair, the MS-CG interaction does not include contributions due to interactions between sets of CGW-ALA pairs and thus does not incorporate this effect. These components of the PMF are recovered by performing MS-CG MD simulations to include the contributions from each of the CGW and ALA sites in the system. Carrying out this procedure does generate the correct distribution functions: this can be assessed by comparing the CGW-ALA RDFs obtained from atomistic and MS-CG simulations (see Fig. 7 below). While MS-CG interactions involving solvent molecules decay quickly to their bulk values, interactions between the peptide CG beads decay very slowly and extend over a much longer range. Thus, these potentials may be very sensitive to the detailed physical properties of the underlying atomistic system. It is worth noting the damped oscillations in the BBN-BBN potential that may reflect the periodic nature of the helical backbone. These oscillations are also present to a lesser extent in the other protein-protein interactions. As noted above for the forces, the precise nature of the CG potentials could not necessarily have been predicted a priori without using the present multiscale FM procedure.
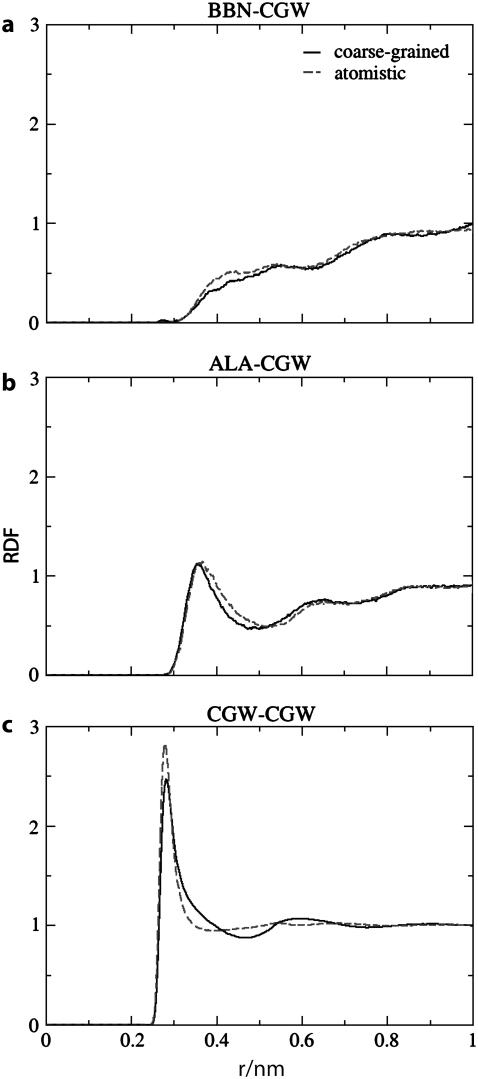
FIGURE 7.
Radial distribution functions associated with solvent interactions for solvated Ala-15 computed from atomistic (dashed lines) and two-bead CMG-CG (solid lines) simulations. As noted for Fig. 6 there is good agreement between the two sets of data. The minor differences observed for the CGW-CGW pair are not expected to adversely impact protein properties.
Bonded interactions
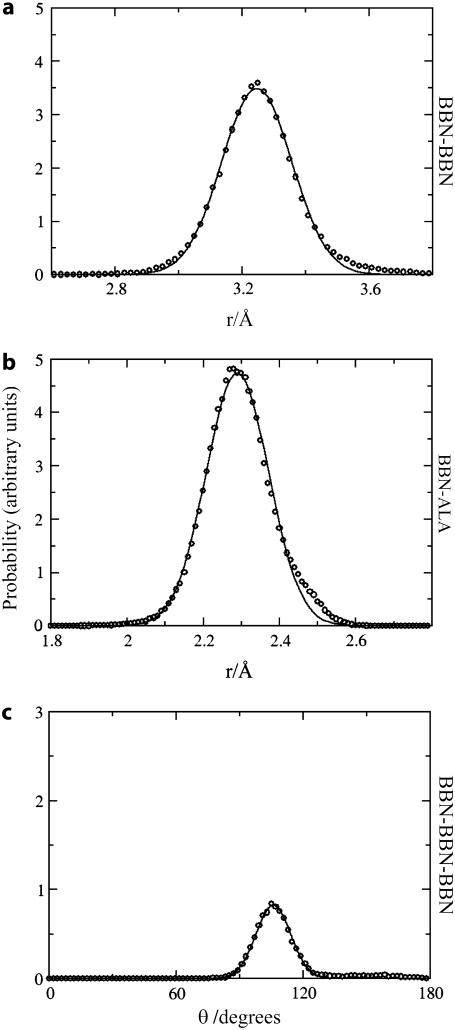
Parameters for the CG bonded interactions are provided as Supplementary Material. A comparison of distribution functions for stretching and bending between the two-bead COM model of Ala-15 and atomistic simulations are displayed in Fig. 4. The agreement between atomistic and CG probability distributions is observed to be quite good, which indicates that the harmonic assumption for CG bonded interactions performs well. Similar agreement is observed for V5PGV5 (data not shown). It should be noted that the angles BBN-BBN-ALA and ALA-BBN-BBN in the two-bead CG model for Ala-15 need to be differentiated. The CG site ALA in ALA-BBN-BBN is closer to the N-terminus than that in BBN-BBN-ALA for the same two consecutive BBN sites and this asymmetry must be reflected in the underlying CG force field.
FIGURE 4.
Comparison between atomistic (circles) and fitted analytic (solid lines) distribution functions for stretching and bending in the two-bead COM-CG model of Ala-15. The distributions were fit according to Eqs. 2–4 in the text. Note the agreement between the two sets of curves, validating the choice of harmonic potentials to represent these interactions.
Structural properties
MS-CG simulations were performed using the computed force profiles and parameters for comparison with atomistic MD simulations. For the Ala-15 and V5PGV5 systems, a single peptide was solvated in a cubic box (box length 40 Å) with 2136 and 2130 MS-CG water molecules, respectively. For the sake of comparison, most of the MS-CG simulation conditions are the same as those in the atomistic MD simulations, except that a slightly larger nonbonded cutoff of 12.0 Å was used. RDFs, RMSD, radius of gyration (Rg), and intersite dihedral angles were calculated for each peptide.
Two-bead model: Ala-15
Displayed in Fig. 5 is the average structure for the COM model of Ala-15 superimposed on the CG representation of a structure from the atomistic trajectory. The helical structure of the peptide is seen to be well preserved by the model. A comparison of the evolution of RMSD in MS-CG and atomistic simulations is also shown in Fig. 5. Note that the time axes in this and ensuing figures do not have the same meaning for the atomistic and MS-CG systems because of the sampling enhancement inherent to the MS-CG models. On average, the time axes for the MS-CG simulations should be scaled by the appropriate factors presented in Table 1 (see the discussion of sampling efficiency below). As such, there is not a one-to-one correspondence between atomistic and MS-CG timescales. However, as was stated previously, the emphasis of this study is more to reproduce equilibrium structural properties than to describe time-dependent phenomena. Consequently, we focus on average quantities in the discussions that follow. The reference structure used for the RMSD calculation is a CG representation of an atomistic structure that was equilibrated for 2 ns in the all-atom MD simulations. The average backbone RMSD computed during the last 2 ns of the MS-CG simulation is 1.08 Å; the corresponding RMSD value for an atomistic trajectory is ∼0.73 Å. These values vary slightly for different CG definitions (Supplementary Material), with models based on a center of mass description displaying the best agreement in general. However, three out of the four two-bead MS-CG models generated an average RMSD of <1.7 Å. The fourth (ACG) generated a slightly larger value of 2.14 Å (see Supplementary Material). This shows that native state interactions can be well represented by MS-CG effective potentials. It is worth noting that although the average RMSD is similar for atomistic and MS-CG simulations, there are more excursions into high RMSD regions with the MS-CG force field (Fig. 5). The larger RMSD fluctuations indicate that the MS-CG model explores a larger distribution of conformations than the atomistic system in addition to maintaining the correct equilibrium structure; this feature will be discussed in greater detail in the section on “Sampling efficiency” below. This occurs because the averaging procedure smooths the effective potentials compared to the corresponding atomistic interactions. The reduced roughness of the free energy landscape facilitates enhanced sampling of the underlying phase space. This feature is one of the distinct advantages of performing dynamics with a CG potential. Other measures of overall similarity between the MS-CG and atomistic trajectories indicate that structural properties are well preserved by the MS-CG method. The evolution of Rg in the COM and atomistic simulations is also shown in Fig. 5. The Rg value computed during the last 2 ns of the MS-CG trajectory is 11.96 Å; the corresponding value for the CG representation of an atomistic configuration is 12.05 Å. As noted above for the RMSD, the average Rg for MS-CG models varies slightly according to CG scheme. However, all Rg values lie between 11.5 and 12 Å; the corresponding properties computed from an atomistic trajectory differ by <2.05% (Supplementary Material). The agreement of multiple independent ensemble averaged properties for both the atomistic and MS-CG simulations suggests that the free energy landscapes of both systems share important general features. In particular, the high level of agreement observed suggests that the locations of the free energy minima that determine the properties of the atomistic system are largely maintained in the effective MS-CG phase space.
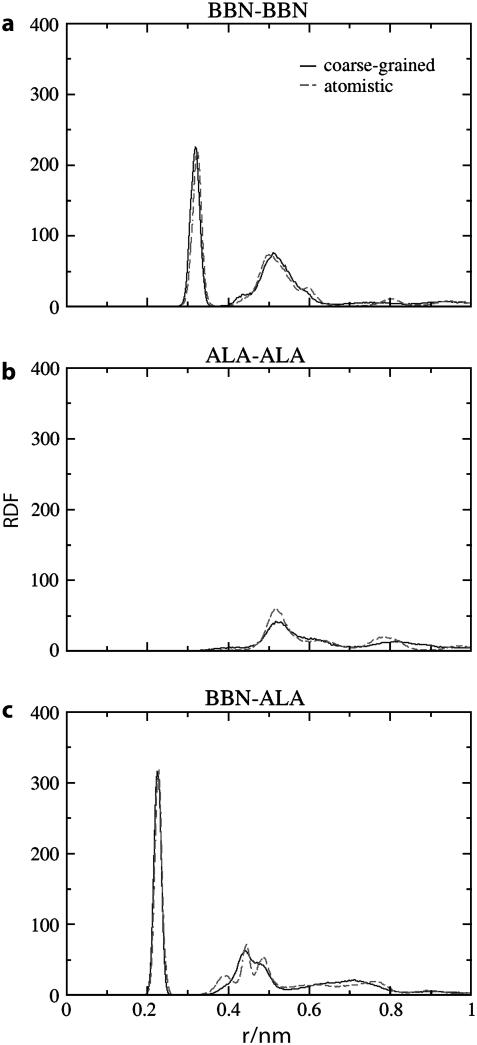
The comparison of peptide and solvent RDFs from atomistic and two-bead CG models is shown in Figs. 6 and 7 for the CMG scheme. In this scheme the peptide CG sites are located at their center of mass whereas the water molecule sites are located at their center of geometry. RDFs obtained for the COM scheme are similar to those obtained for CMG. Very good agreement is observed between atomistic and MS-CG simulations for the peak heights and positions, indicating that the MS-CG models correctly represent the equilibrium structural distributions present in the underlying atomistic simulation. For the peptide interactions the largest discrepancy between atomistic and CG data occurs for BBN-ALA. The second peak in Fig. 6 c (∼0.45 nm) is significantly less ordered for the MS-CG simulations. It is likely that the fine structural details present in the atomistic simulation have been “averaged” away by the MS-CG procedure. This is a natural consequence of using a reduced representation: lower resolution models necessarily entail some loss of information. The most apparent dissimilarity between the solvent associated RDFs occurs for the solvent-solvent (CGW-CGW) distribution function; the first peak is a bit too small whereas there are undulations at intermediate distances not observed in the atomistic simulations. The first observation reflects decreased structure in the nearest neighbor water interactions whereas the second indicates enhanced ordering of water groups at intermediate distances. However, the CGW-CGW distribution function is still quite similar to that observed during the atomistic simulations overall. Peptide-CGW RDFs are very well represented throughout the whole range of the plots. Because many protein properties are governed by the details of peptide-solvent interactions, this observation bodes well for efforts to employ MS-CG potentials to understand the molecular properties of peptides and proteins. On the whole, the differences between the atomistic and MS-CG data appear rather small. As stated in previous sections, it is well known that the RDF is related to the radial two-body PMF and thus to the average force between two sites at a given radial distance. However, because the MS-CG forces are not simply the averaged forces (see Fig. 2), the fact that the MS-CG interactions are able to effectively reproduce each of the CG particle pair RDFs is quite significant.
FIGURE 6.
Radial distribution functions between protein MS-CG sites in Ala-15 calculated from atomistic (dashed lines) and two-bead CMG-CG (solid lines) simulations. Although there is some loss of detail due to the reduced resolution of the MS-CG model, there is quite good agreement between the curves overall. This indicates that protein structural properties are well preserved by the MS-CG model.
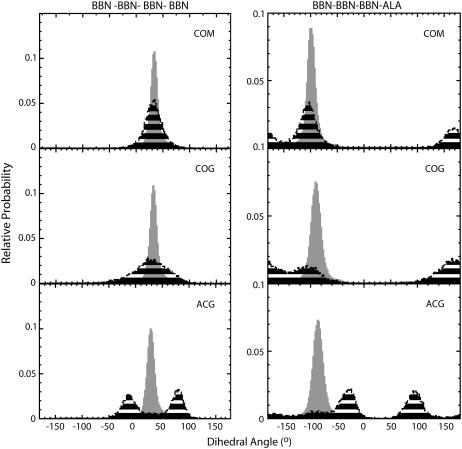
Before ending our discussion of the two-bead models it is enlightening to examine the distribution of dihedral angles observed for both MS-CG and atomistic simulations. For a conventional protein system, the φ/ψ dihedral angles of the peptide backbone provide an efficient way to characterize the conformational space explored by the peptide. With a CG model the procedure is not quite so straightforward. Much of the information needed to reconstruct a φ/ψ map is simply no longer available as it has been coarse-grained away. However, it is possible to reconstruct a measure comparable to the φ/ψ map for low resolution protein models if certain assumptions are made. Tozzini et al. have demonstrated that an analog of the φ/ψ map for two-bead peptide models can be reconstructed by considering α-carbon positions (29). For the MS-CG models used in this work, CG sites are not necessarily located at the α-carbon positions, making direct application of the approach of Tozzini et al. difficult. However, our primary goal is to assess the similarity of probability distributions in the atomistic and MS-CG simulations. For these purposes it is sufficient to consider the internal coordinates defined by the dihedral angles between CG sites to compare the conformational space explored by each system. This represents a particularly stringent test for the two-bead MS-CG models because, unlike the bond and angle interactions, no terms in the MS-CG force field were explicitly parameterized to reproduce these quantities.
In Fig. 8 it can be seen that the atomistic and MS-CG dihedral probability distributions overlap significantly. Peak heights are typically located at the correct positions, although the distributions tend to be more diffuse for the MS-CG simulations. This is consistent with the existence of a smoother free energy landscape containing more modest free energy barriers in the MS-CG models. As for the other coordinates discussed above, similar peak positions for the two sets of distributions indicates that minima in the free energy landscape are located at approximately the same locations. In contrast, differences in the width of each indicate that the detailed features surrounding these minima are altered in the MS-CG systems relative to the atomistic systems. For the ALA (side-chain) beads, minima that differ from the atomistic minimum also exist for the CG models. This indicates that ALA spends an appreciable portion of the trajectory in conformations not visited by the atomistic system. These fluctuations do not greatly impact the overall helical conformation of the peptide, which is determined primarily by dihedrals containing only BBN sites. This is apparent from the distribution of dihedrals involving only backbone beads, which overlaps considerably with the atomistic distributions. This is also illustrated in Fig. 5, where the peptide backbone corresponding to atomistic and MS-CG models is observed to superimpose quite well. The best overlap with the atomistic data is provided by the COM and CMG models. The COG model displays overlap that is not quite as good but is still quite similar to COM and CMG. Slight deviations of COG dihedrals from the atomistic distributions indicate that the peptide helix is not wound as tightly in COG. This agrees with an assessment based on visual inspection and is consistent with the higher RMSD of 1.69 observed for COG (Supplementary Material). The very good agreement observed is remarkable considering that, as stated earlier, these interactions are not explicitly parameterized in the MS-CG models. This demonstrates that the MS-CG approach can capably account for the structural correlations present in the peptide.
FIGURE 8.
Distributions of dihedral angles containing only BBN sites (left) or three BBN sites and an ALA site (right). Coarse-grained atomistic data is shown in gray whereas the MS-CG data is shown in black stripes. Note that, except for ACG, the MS-CG distributions overlap significantly with the atomistic distributions. This indicates that the conformational space of the CG models encompasses that of the atomistic system. One can observe that ALA sites spend an appreciable portion of the trajectory in regions of conformation space not explored in the atomistic trajectories, demonstrating the amplified fluctuations of ALA in these models. These fluctuations do not greatly impact the helical conformation of the peptide, which is determined primarily by dihedrals containing only BBN sites. Note that the ACG model differs from the atomistic distribution with respect to both dihedral coordinates.
The only situation where the MS-CG and atomistic distributions markedly differ is for the ACG model. For each of the dihedrals in this model the distribution peaks at a distinctly different value from that observed in the atomistic trajectory (Fig. 8). The atomistic CG dihedrals are consistent with a staggered conformation for CG backbone, similar to the gauche conformation defined in a Newman projection. It appears that there is a shift in the register of the dihedrals along the helix backbone for ACG that maintains a staggered conformation but alters the overall twist of the peptide chain. It is also consistent with the fairly large average RMSD of 2.14 with respect to an atomistic structure that we observe for ACG (Supplementary Material). This is the highest RMSD we observe for any of the two-bead models. In the ACG model BBN sites are located at the α-carbon positions. This location may be problematic for the current MS-CG approach because it directly incorporates information about the atomistic forces acting on CG sites. The point of action of forces acting on backbone atoms is the center of mass of these atoms, which is not located at the α-carbon position.
It is interesting to note that dihedrals involving terminal peptide groups in the MS-CG systems diverge most from the corresponding atomistic distributions. Enhanced flexibility is observed for the termini of the atomistic simulations; however, this effect is magnified in the MS-CG models. The most affected CG groups are ALA sites close to the peptide termini. The distributions of dihedral angles for these sites are very diffuse and display little resemblance to the atomistic data (Supplementary Material). ALA sites have greater conformational freedom than BBN sites because they are constrained by fewer bonded interactions in the MS-CG force field. When this situation is combined with the additional flexibility afforded to the peptide terminus, terminal ALA sites exhibit significantly enhanced fluctuations relative to the atomistic system. However, we note that the dihedrals of even the terminal BBN sites do not deviate dramatically from the atomistic results (Supplementary Material). Because it is the BBN dihedrals that primarily determine the conformation of the peptide chain, the MS-CG models do quite well at reproducing the internal coordinates of the peptide overall. Finally, it is also worth noting that the MS-CG simulations required approximately fives times less sampling than the atomistic simulation to generate similar dihedral distributions, demonstrating the enhanced sampling capabilities of the models.
Structural properties obtained using a four-bead Ala-15 model are presented as Supplementary Material. MS-CG models incorporating four beads per amino acid residue generally exhibit even smaller differences in RMSD, Rg, and RDFs when compared to atomistic simulations than two-bead MS-CG models. This is to be expected given that more CG sites allow for a greater level of detail to be incorporated into the effective potentials. These results indicate that two-bead models are sufficient to reproduce the structural properties of Ala-15. However, two-bead models were unable to adequately reproduce structural properties of V5PGV5. One reason for this observation may be that the high degree of asymmetry present in β-hairpins causes residues with the same amino acid identity to be subject to disparate effective interactions depending on their position along the peptide chain. This prevents identical FM forces from being employed for a given residue type (the procedure employed in this study; see “Force matching” section). As a result, it was necessary to incorporate more detail into the model to properly delineate interparticle interactions by employing the more complex four-bead representation for V5PGV5. In contrast, the more symmetric α-helical interactions of Ala-15 are well represented with identical interactions for the sole residue type, facilitating the use of two-bead models with this particular MS-CG implementation. It is anticipated that allowing interactions to vary based on position along the peptide chain rather than on amino acid identity will enable two-bead models to also be employed to effectively represent β-hairpin interactions. This issue will be investigated more thoroughly in a later publication. In any case, the results observed for the V5PGV5 four-bead model are instructive in what they reveal about the physical interactions present in the peptide system.
Four-bead model: V5PGV5
The RMSD observed for atomistic and MS-CG simulations of V5PGV5 is shown in Fig. 9 for three different CG schemes. The average backbone RMSD of MS-CG simulations when compared to corresponding CG representations of an atomistic configuration are 0.88, 0.86, and 5.90 Å for HCO, GCG, and NCC schemes, respectively (the three CG schemes will be described in more detail below). The corresponding averages computed from an atomistic trajectory are 0.94, 1.12, and 0.72 Å. Note that, apart from NCC, the RMSD fluctuation of these four-bead models during MS-CG simulations is relatively small. Similar observations are made if the four-bead Ala-15 models are compared to the two-bead models described above (Supplementary Material). This is in contrast to the excursions into high RMSD regions observed for the two-bead Ala-15 model that we associate with the exploration of a wider distribution of configurations. It is likely that these large RMSD fluctuations do not occur because the effective interactions in the four-bead models have not been as smoothly averaged as in the case of the two-bead models. Consequently, these interactions are still fairly rugged, leading to a more frustrated energy landscape. The average Rg computed during the last 2 ns of MS-CG simulations and for the corresponding CG representations of an atomistic trajectory are 7.37 and 7.55 Å for the HCO scheme; 7.20 and 7.49 Å for the GCG scheme; and 9.37 and 7.40 Å for the NCC scheme, respectively. The RMSD and Rg values indicate that the β-hairpin structure of the peptide is well preserved by the HCO and GCG models but not by NCC. Indeed, this was confirmed by visual inspection of the trajectories.
The NCC scheme fails to preserve V5PG5 structure because of the placement of the CG beads. The reason for this phenomenon can be understood if the details of the CG schemes are considered. The positions of beads CBB or CBG were placed at the α-carbon of the –CH– group for all three models. For the HCO scheme, NBB was placed at the hydrogen atom of each –NH– group whereas OBB was placed at the oxygen atom of each –CO– group. For the GCG scheme NBB and OBB were located at the center of geometry of their respective atoms. For the NCC scheme, NBB was located at the nitrogen atom of each –NH– group whereas OBB was located at the carbon atom of each –CO– group.
Recall that MS-CG forces are algebraic summations over the respective atoms. A large component of the force on backbone groups is due to hydrogen bonding interactions. The points of action for these hydrogen bonding forces are closer to the H and O positions on the backbone than to the N and C positions where the sites for NBB and OBB were located for the NCC model. Assigning hydrogen bonding forces to these sites no doubt leads to a systematic error in the MS-CG forces; such an error will not be reduced by the least-squares fit described by Eq. 1. This can be readily appreciated if one notes that solving this equation can be framed as a minimization problem where the target function is the derivative of Eq. 1. The least-squares solution occurs when this derivative is zero. Because addition of a constant to each member of the solution set does not affect the gradient, solutions can be identified where the predicted forces are offset from the optimal forces by a constant value. Any such systematic deviation will prevent an accurate representation of the hydrogen bonding forces from being achieved during MS-CG simulations. The other two MS-CG schemes place the –NH– and –CO– beads closer to the points at which the effects of hydrogen bonding forces are mediated, leading to more faithful representations of these forces. This observation indicates the importance of partitioning the MS-CG system in a manner that is consistent with the underlying physical interactions. This requirement was noted in previous applications of the MS-CG method to simple liquids carried out by our group (19). For larger MS-CG groups, averaging of the forces over an increased number of atoms presumably reduces the potential for such systematic errors. In these cases, errors in the MS-CG forces may be more likely random rather than systematic: such errors will be minimized by the FM procedure (Eq. 1).
Sampling efficiency
Sampling enhancement (S) factors for the MS-CG models examined in this study are presented in Table 1. Generally, the total sampling enhancement (STot) values are positive, demonstrating that the MS-CG models tend to explore conformational space more efficiently than the corresponding atomistic simulations. This effect ranges from a modest threefold for the HCO model of Ala-15 to ∼65-fold for the ACG model of the same peptide. Unfortunately, it is apparent from the dihedral angle distributions that the ACG model is not completely able to reproduce the structure of Ala-15. Thus, it is more appropriate to discuss the characteristics of a model such as CMG, which properly recapitulates the peptide structure and demonstrates an STot value of 27. This result suggests that the CMG model has the potential to explore conformational space with as few as 1/27 the number of simulation steps required for a full atomistic simulation. One way to interpret this number is that a given time unit in the MS-CG model actually represents a time period that is 27 times as long as the corresponding time unit in atomistic simulations. This would represent a significant saving of computational expense, extending the sampling capabilities of atomistic simulations by at least an order of magnitude. With current simulation studies limited to the 100-ns regime, such capabilities could allow one to probe events that occur on the order of microseconds. This would make processes such as protein folding more readily accessible, as the most rapidly folding proteins fold on microsecond timescales. This rough estimate illustrates the tremendous potential of MS-CG models.
The wide variation observed for STot reveals that the method of coarse graining employed can have a significant impact on the sampling efficiency. STot depends on rapid decay of conformational correlations as well as the exploration of conformations not readily observed in atomistic simulations. Models with the most rapidly decaying correlations often explore very little conformational space, leading to partial cancellation of SFlu and SExp factors so that STot is more modest. This is particularly apparent for the four-bead models. Although SFlu is often quite large for these models, SExp is usually <1, indicating that the four-bead models explore a smaller distribution of conformations than the atomistic simulations. The only exception is the NCC model of V5PGV5. Unfortunately, the large SExp displayed by this model is associated with an inability to maintain the folded conformation of the hairpin as highlighted previously. Even though SFlu tends not to be as large for the two-bead models, both S terms are positive and act synergistically to amplify sampling efficiency. It appears that the four-bead models tend to overstabilize the native state, inhibiting exploration of conformation space. Despite this, these models in general do generate greater STot values than the two-bead models because they exhibit large values of SFlu.
Although four-bead models did display a slight edge in sampling efficiently overall, the results displayed in Table 1 suggest it is possible to obtain similar efficiencies using two-bead models. Thus, there does not seem to be a fundamental reason to choose one CG scheme over the other as far as overall sampling efficiency is concerned. In fact, it is likely that particular CG schemes will be of more or less utility based on the intended purpose of the model. For example, two-bead models seem to explore a more diverse collection of conformations than the four-bead models, so one might prefer to use such models if the sampling of new configurations is the primary concern. This might be the case if one desired to generate a diverse collection of protein configurations such as is often required for protein structure prediction studies. The rapid decay of RMSD correlations in the four-bead models indicates that they have the capacity to explore a well-defined region of conformational space very quickly. These models may be useful if one only requires a simplified and accurate representation of a limited set of conformations. For example, in enzyme studies it is often the case that only a few of the conformations accessible to the protein are catalytically competent. Thus, such a model could be employed to limit the sampling that occurs during the MS-CG simulations to catalytically active conformations.
However, it must be noted that there may be other reasons to prefer one type of CG scheme. For example, the physical properties that underlie the system under study may constrain the types of coarse graining possible. As a case in point, recall that it was not possible to reproduce the equilibrium structure of V5PGV5 using the two-bead models employed for this study because of the highly asymmetric nature of the peptide. However, as we noted previously, two-bead models may no longer exhibit this deficiency if MS-CG approaches are employed that can adequately incorporate such asymmetry. For example, one could take the local environment of each residue into account when deriving effective interactions rather than employing a single set of interactions for a given residue type. An additional consideration is that the four-bead models require only ∼3% more computational effort than the two-bead models. Consequently, for the systems studied here it may be advantageous to use the slightly more detailed four-bead CG scheme with the additional flexibility to represent a wider range of interactions given the modest additional effort.
One reason the two-bead and four-bead models require such similar computational effort despite their differing levels of resolution is that most simulation time is spent evaluating solvent interactions. Solvent makes up the bulk of each simulation and is represented by a one-site model that is essentially the same for each of the different MS-CG approaches. In principle, it should be possible to elicit the maximum theoretically achievable sampling enhancement if one is able to remove explicit solvent altogether and describe solvent effects implicitly. In this case the C, I, and Sexp factors may give two-bead models an edge in efficiency. One possible route to achieving this goal might be to average over and remove solvent degrees of freedom when the effective interactions are being computed. Another approach could be to generate a distinct, novel implicit solvent model for use in MS-CG simulations. Such models are already in use for atomistic simulations and could be of considerable utility for MS-CG models as well.
GENERAL REMARKS
Care must be taken in partitioning atoms into CG groups to ensure that the physical interactions are well represented by the resulting MS-CG effective forces. Although coarser two-bead representations were successful in reproducing the structure of Ala-15, it was necessary to use higher resolution four-bead models to also reproduce equilibrium structural properties of V5PGV5. However, employing MS-CG groups composed of more atoms as done for the two-bead models reduces the size of the resulting simulations, allows a larger integration time step to be used, and is expected to decrease any systematic error in the associated FM potentials as more degrees of freedom are averaged. Moreover, the results suggest that coarser levels of granularity make the effective interactions between sites smoother so that more extensive exploration of the underlying configuration space is possible. These considerations indicate that further examination of low resolution two-bead peptide models is warranted. It is expected that a CG scheme that defines particle types based on local environmental factors rather than on residue identity alone will allow such models to be more widely applicable.
Overall, our results show that it is possible to obtain good agreement between the MS-CG models and atomistic simulations with respect to internal coordinates, RMSD, Rg, and RDFs for realistic peptides. This indicates that our MS-CG strategy incorporating the FM methodology is successfully able to represent equilibrium properties that occur during atomistic trajectories. One advantage of these MS-CG models is that they have a rigorous origin in the underlying atomistic simulations. Thus, one can more readily make connections between characteristics of the MS-CG models and properties of the actual atomistic systems, providing a well-defined link between multiple lengthscales. This allows for straightforward extensions of the MS-CG method to include other possible interactions. Furthermore, the multibody nature of the MS-CG effective interactions effectively incorporates structural correlations present in the atomistic simulations.
CG models such as these offer potential savings of computational time and memory by using fewer particles to represent biomolecular systems. In addition, the smoother, averaged “effective” interactions computed during the MS-CG procedure can lead to enhanced sampling. Both of these features will serve to extend the length- and timescales accessible to molecular simulations. As we continue to develop this method, we will address technical issues such as the treatment of bonded interactions. In principle, it should be possible to compute bonding interactions using FM as well so that the entire MS-CG potential is obtained in the same framework with no need for statistical fitting (18,20).
Although the present study focuses on the description of equilibrium structural features and thus on maintaining the general locations of minima on the peptide free energy landscape, it will also be important to determine whether the character of dynamical properties is maintained in the MS-CG systems. Dynamical quantities are expected to be more greatly impacted by details of the free energy landscape. For example, the rate of diffusion between adjacent minima will be increased if the intervening free energy landscape is smoothed. This issue will affect the capacity to accurately compute dynamical quantities using MS-CG representations and is being actively addressed by our group. Recently, we have described a method that allows the dynamics occurring in MS-CG models of liquids to conform more closely to the exact dynamics observed in the corresponding all-atom systems (30). In the future we will apply these and related methodologies to investigate the dynamical properties of peptides.
CONCLUSIONS
This work represents the first application of the MS-CG method to peptides. The force-matching approach allows a MS-CG force field to be directly extracted from atomistic simulations, so that the resulting effective CG interactions have rigorous connections to the underlying atomistic simulations. These interactions incorporate some of the many-body effects inherent to the underlying MD simulations in a systematic manner, implicitly accounting for degrees of freedom that have been removed as a result of the coarse-graining process. The new MS-CG models are able to preserve the native states of Ala-15 and V5PGV5 within ∼1 Å backbone RMSD and also exhibit good agreement with other structural properties. The models demonstrate that equilibrium peptide properties can be reproduced quite well with the MS-CG approach. This suggests that these models can preserve the location of global minima in the peptide free energy landscape, even though intervening regions in the landscape may be slightly altered.
The MS-CG peptide models are computationally efficient and demonstrate the possibility of simulating real peptides or proteins. Thorough and systematic evaluation of sampling efficiency reveals that each of the MS-CG models investigated in this study exhibits the capacity for enhanced sampling compared to atomistic systems. These analyses demonstrate the potential of MS-CG models to extend the capabilities of molecular simulations. These models can extend time- and lengthscales accessible to simulation in two ways. Firstly, they reduce the number of particles that must be used to represent a molecular system. Secondly, the smoother effective potentials computed can facilitate exploration of the underlying phase space. In this regard, each model displays unique sampling efficiency characteristics that may be of particular utility for specific applications. Furthermore, the MS-CG interactions are useful in their own right as probes of the effective interparticle interactions that occur in biomolecular systems, providing insight into the physical properties that govern the behavior of these systems. In future studies we hope to use the MS-CG methodology to study problems such as peptide folding and aggregation as well as extend the methodology to encompass larger protein systems. We will also seek to examine whether dynamical properties can be accurately represented using MS-CG simulations.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
J.Z. thanks Dr. Yanting Wang for stimulating discussions.
This research is supported by grants from the National Science Foundation (grant Nos. CHE-02187839 and CHE-0628257). The computational resources for this project were provided by the National Center for Supercomputing Applications (No. MCA94P017).
References
- 1.Muller-Plathe, F. 2002. Coarse-graining in polymer simulation: from the atomistic to the mesoscopic scale and back. ChemPhysChem. 3:755–769. [DOI] [PubMed] [Google Scholar]
- 2.Shelley, J. C., M. Y. Shelley, R. C. Reeder, S. Bandyopadhyay, P. B. Moore, and M. L. Klein. 2001. Simulations of phospholipids using a coarse grain model. J. Phys. Chem. B. 105:9785–9792. [Google Scholar]
- 3.Marrink, S. J., and A. E. Mark. 2003. Molecular dynamics simulation of the formation, structure, and dynamics of small phospholipid vesicles. J. Am. Chem. Soc. 125:15233–15242. [DOI] [PubMed] [Google Scholar]
- 4.Cieplak, M., T. X. Hoang, and M. O. Robbins. 2002. Folding and stretching in a Go-like model of titin. Proteins. 49:114–124. [DOI] [PubMed] [Google Scholar]
- 5.Pliego-Pastrana, P., and M. D. Carbajal-Tinoco. 2003. Effective pair potentials between protein amino acids. Phys. Rev. E. 68:011903. [DOI] [PubMed] [Google Scholar]
- 6.Buchete, N. V., J. E. Straub, and D. Thirumalai. 2004. Orientational potentials extracted from protein structures improve native fold recognition. Protein Sci. 13:862–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tozzini, V. 2005. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 15:144–150. [DOI] [PubMed] [Google Scholar]
- 8.Go, N., and H. Abe. 1981. Noninteracting local-structure model of folding and unfolding transition in globular proteins. I. Formulation. Biopolymers. 20:991–1011. [DOI] [PubMed] [Google Scholar]
- 9.van Giessen, A. E., and J. E. Straub. 2005. Monte Carlo simulations of polyalanine using a reduced model and statistics-based interaction potentials. J. Chem. Phys. 122:024904. [DOI] [PubMed] [Google Scholar]
- 10.Liwo, A., C. Czaplewski, J. Pillardy, and H. A. Scheraga. 2001. Cumulant-based expressions for the multibody terms for the correlation between local and electrostatic interactions in the united-residue force field. J. Chem. Phys. 115:2323–2347. [Google Scholar]
- 11.Khalili, M., A. Liwo, and H. A. Scheraga. 2006. Kinetic studies of folding of the B-domain of staphylococcal protein A with molecular dynamics and a united-residue (UNRES) model of polypeptide chains. J. Mol. Biol. 355:536–547. [DOI] [PubMed] [Google Scholar]
- 12.Smith, A. V., and C. K. Hall. 2001. Assembly of a tetrameric alpha-helical bundle: computer simulations on an intermediate-resolution protein model. Proteins. 44:376–391. [DOI] [PubMed] [Google Scholar]
- 13.Ashbaugh, H. S., H. A. Patel, S. K. Kumar, and S. Garde. 2005. Mesoscale model of polymer melt structure: self-consistent mapping of molecular correlations to coarse-grained potentials. J. Chem. Phys. 122:104908. [DOI] [PubMed] [Google Scholar]
- 14.Reith, D., M. Putz, and F. Muller-Plathe. 2003. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 24:1624–1636. [DOI] [PubMed] [Google Scholar]
- 15.Ercolessi, F., and J. Adams. 1994. Interatomic potentials from first-principles calculations: the force-matching method. Europhys. Lett. 26:583–588. [Google Scholar]
- 16.Izvekov, S., M. Parrinello, C. J. Burnham, and G. A. Voth. 2004. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: a new method for force-matching. J. Chem. Phys. 120:10896–10913. [DOI] [PubMed] [Google Scholar]
- 17.Izvekov, S., and G. A. Voth. 2005. Effective force field for liquid hydrogen fluoride from ab initio molecular dynamics simulation using the force-matching method. J. Phys. Chem. B. 109:6573–6586. [DOI] [PubMed] [Google Scholar]
- 18.Izvekov, S., and G. A. Voth. 2005. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B. 109:2469–2473. [DOI] [PubMed] [Google Scholar]
- 19.Izvekov, S., and G. A. Voth. 2005. Multiscale coarse graining of liquid-state systems. J. Chem. Phys. 123:134105. [DOI] [PubMed] [Google Scholar]
- 20.Izvekov, S., and G. A. Voth. 2006. Multiscale coarse-graining of mixed phospholipid/cholesterol bilayers. J. Chem. Theory Comput. 2:637–648. [DOI] [PubMed] [Google Scholar]
- 21.Wang, Y. T., S. Izvekov, T. Y. Yan, and G. A. Voth. 2006. Multiscale coarse-graining of ionic liquids. J. Phys. Chem. B. 110:3564–3575. [DOI] [PubMed] [Google Scholar]
- 22.Izvekov, S., and A. Violi. 2006. A coarse-grained molecular dynamics study of carbon nanoparticle aggregation. J. Chem. Theory Comput. 2:504–512. [DOI] [PubMed] [Google Scholar]
- 23.MacKerell, A. D. Jr., B. Brooks, C. L. Brooks III, L. Nilsson, B. Roux, Y. Won, and M. Karplus. 1998. CHARMM: the energy function and its parameterization with an overview of the program. In The Encyclopedia of Computational Chemistry. P. v. R. Schleyer, editor. John Wiley and Sons, Chichester, UK. 271–277.
- 24.Ferrara, P., J. Apostolakis, and A. Caflisch. 2000. Thermodynamics and kinetics of folding of two model peptides investigated by molecular dynamics simulations. J. Phys. Chem. B. 104:5000–5010. [Google Scholar]
- 25.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 26.Smith, W., T. R. Forester, I. T. Todorov, and M. Leslie. 2006. DL_POLY. CCLRC Daresbury Laboratory, Daresbury, Warrington, UK.
- 27.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of Cartesian equations of motion of a system with constraints: molecular-dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 28.Noid, W. G., J.-W. Chu, G. S. Ayton, and G. A. Voth. 2007. Multiscale coarse-graining and structural correlations: connections to liquid state theory. J. Phys. Chem. B. In press. [DOI] [PMC free article] [PubMed]
- 29.Tozzini, V., W. Rocchia, and J. A. McCammon. 2006. Mapping all-atom models onto one-bead coarse-grained models: general properties and applications to a minimal polypeptide model. J. Chem. Theory Comput. 2:667–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Izvekov, S., and G. A. Voth. 2006. Modeling real dynamics in the coarse-grained representation of condensed phase systems. J. Chem. Phys. 125:151101. [DOI] [PubMed] [Google Scholar]