Unraveling Individual Molecules by Mechanical Forces: Theory Meets Experiment

Unlike computer-generated cartoons of molecules in motion, experiments probing single-molecule dynamics only hint at actual molecular motions. Uncovering maximum information about the underlying dynamics of individual molecules from the time-dependent observables provided by such experiments remains an illusive goal.

In an article published in this issue, Dudko et al. (1) have tackled this problem for the particular class of single-molecule experiments that probe “molecular rupture” transitions induced by mechanical forces. One example is provided by atomic force microscopy single-molecule pulling, where a stretching force F applied between the N- and the C-termini of a protein domain causes it to unfold. This unfolding process can be viewed as activated barrier crossing from the native minimum on the molecule's free energy surface to a manifold of extended, unfolded states. In a reduced view of this problem, the free energy surface U(x), considered as a function of the protein extension x, becomes tilted by the force, U(x) → U(x) − Fx, favoring large extensions and lowering the barrier that separates the compact and the extended states. As a result, the force accelerates the barrier crossing rate k(F).

With the appropriate choice of the generalized reaction coordinate x that couples to the force, the same picture can be applied to other mechanically driven molecular transitions. Dudko et al. (1) focus on a system where the mechanical force is generated by an electric field driving a DNA hairpin across a transmembrane protein pore and causing it to unzip. Experimental studies of this system involve repeated application of a time-dependent force F(t) and measuring the statistics of the unzipping events. The question is then: given these data, what is the best estimate for the molecule's free energy surface U(x)?

Historically, mechanically driven conformational transitions have often been interpreted in terms of the phenomenological model due to Bell, which qualitatively accounts for the force effect by assuming exponential force dependence of the barrier crossing rate, 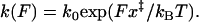The phenomenological formula can be recovered from the picture of activated barrier crossing only by assuming a pathologically shaped U(x) such that the relative location of the transition state x^‡ is not affected by the force. Although this deficiency of the phenomenological model has been pointed out by theorists (2), it was not evident from experimental data until recent studies (1,3). A typical experiment probes a relatively narrow range of the force, in which the dependence of lnk(F) on F is not much different from linear. Consequently, the phenomenological formula often appears to provide a satisfactory fit in the experimental force range even though the physical interpretation of the adjustable parameters k₀ and x^‡ as, respectively, the rupture rate in the absence of the force and the “true” transition state position is questionable (2).

The study by Dudko et al. (1) showed that significant deviations from the phenomenological model can be revealed by a careful analysis of the statistics of the rupture events. At the same time more realistic models for U(x) describe the experimental data much better. In particular, the force dependence of lnk(F) inferred from the data shows a curvature (cf. their Fig. 5), which supports the notion that the force moves the transition state toward the minimum on the free energy surface.

Why are these findings important? Firstly, the use of a microscopic model has allowed the authors to estimate the free energy barrier of activation for DNA unzipping, which could not be directly obtained from the phenomenological fit. Secondly, both mechanical stretching of certain “load-bearing” proteins and mechanically driven translocation of biomolecules are implicated in a number of biological processes. However, the forces that act on biomolecules under physiologically relevant conditions are often quite different from those probed by single-molecule mechanical experiments (4), necessitating extrapolation of measured k(F) outside experimental range. Fig. 5 in Dudko et al. (1) shows that the phenomenological formula overestimates k(F) by about an order of magnitude at low forces, emphasizing the importance of having a good model for such extrapolation.

The authors, however, caution that the “best” model is not unique. Without additional physical insight a single-barrier model cannot be differentiated from more complex, multistate models. Simulations (5) and experiments (6) suggest that complex free energy landscapes involving multiple barriers may be common in protein translocation. Depending on the value of the force applied, such complexities may be “hidden” from measurements yet they may come into play when the force is changed (5,7).

Although the no free lunch principle still applies to the analysis of single-molecule data, interpretation of single-molecule force probe spectroscopy in terms of a physically appealing microscopic model (1) offers a viable middle ground between crude, purely phenomenological models and the desirable but computationally prohibitive first principles all-atom simulations.