Modeling the optimum duration of antibiotic prophylaxis in an anthrax outbreak

Abstract

A critical consideration in effective and measured public health responses to an outbreak of inhalational anthrax is the optimum duration of antibiotic prophylaxis. We develop a competing-risks model to address the duration of antibiotic prophylaxis and the incubation period that accounts for the risks of spore germination and spore clearance. The model predicts the incubation period distribution, which is confirmed by empirical data. The optimum duration of antibiotic prophylaxis depends critically on the dose of inhaled spores. At high doses, we show that exposed persons would need to remain on antibiotic prophylaxis for at least 4 months, and considerable morbidity would likely occur before antibiotic prophylaxis could even be initiated. At very low doses, 60 days of antibiotic prophylaxis is adequate. Exposure doses can be estimated from the cumulative attack rate up to the point antibiotic prophylaxis begins. The model explains that whereas ≤60 days of antibiotics were enough to protect persons in the 2001 U.S. outbreak, because doses were very low, at moderate or high doses considerably longer durations would be necessary to adequately protect exposed populations.

Inhalational anthrax is of significant concern to global health because of its potential use as a biological weapon (1, 2). Although anthrax vaccines administered before exposure can provide long-term protection, current vaccine supplies are limited, and their use as a postexposure prophylaxis has not been licensed by the U.S. Food and Drug Administration, nor has their safety in children and pregnant women been fully evaluated (3). Antibiotics are an effective postexposure prophylaxis if persons are on antibiotics at the time of spore germination. The public health guidelines for exposed persons in the 2001 U.S. outbreak included a 60-day regimen of antibiotic prophylaxis (4). These recommendations were based on limited data (1), which included incubation periods as long as ≥40 days from the 1979 Sverdlovsk anthrax outbreak (5, 6) and some primate studies (7–9). The optimum duration of antibiotic prophylaxis after inhalational exposure to anthrax spores is uncertain and is a critical public health question.

Competing-Risks Model

We use a competing-risks model to describe the pathogenesis of inhalational anthrax and the impact of antibiotic prophylaxis on the attack rate and the incubation period. Inhalational anthrax occurs when inhaled spores are ingested by pulmonary macrophages and transported to mediastinal lymph nodes, where they may germinate to vegetative cells capable of multiplying, releasing toxins, and causing disease (2, 10, 11). An inhaled spore that is deposited in the lung may be cleared by one of several mechanisms, including either being expelled through the bronchus or destroyed by macrophages (10, 11). It is assumed that disease will occur if at least one spore germinates before it is cleared by any of these mechanisms, provided antibiotics are not circulating at the time of germination. The competing risks in the model are the risk a spore is cleared that occurs at rate θ and the risk a spore germinates that occurs at rate λ. Based on the competing-risks model, the probability that a spore germinates before it is cleared, in the absence of antibiotic prophylaxis, is . The number of spores that germinate, x, from an initial dose of D spores in the lungs has approximately a Poisson distribution with mean Dλ/(λ + θ). Then, the probability that at least one spore germinates, the attack rate, is p = 1 – exp(–Dλ/(λ + θ)). This exponential functional form for the attack rate is consistent with empirical data from animal studies in the experimental dose ranges studied (9–14).

Experimental studies with rhesus macaque monkeys that tracked the declining percentages of initially retained spores that remained in the lung over time (7) suggested that the clearance rate is on the order of θ = 0.07 (7% per day) based on an exponential decay model. Studies in primates showed that the LD₅₀ is variable ranging, from 4,000 to nearly 100,000 inhaled spores (9, 15). We estimated λ from these studies by solving for λ in the expression for the attack rate, λ = –θ ln(1 – p)/(LD₅₀ + ln(1 – p)). These calculations show that λ is small compared with θ. However, some experimental studies suggested that only ≈15% of all inhaled spores are delivered to the lungs (7, 16). Because the expression for the attack rate involves the dose D of initial spores in the lung, we adjusted the reported LD₅₀ values from the primate studies by multiplying by 15%. The resulting estimates of λ ranged between 3.2 × 10^–6 and 8.1 × 10^–5 per day. Even after accounting for these adjustments and the range of uncertainty for λ, all available experimental data suggest that λ is small compared with θ (i.e., λ ≪ θ).

The TD(P) is the dose that causes toxicity or disease in P percent of the population; that is, disease occurs with probability p = P/100. From the formula for the attack rate, the dose TD(P) = –ln(1 – p)(λ + θ)/λ. Here we consider how long a person who is exposed to the TD(P) would need to remain on antibiotic prophylaxis to reduce the probability of disease to r. Our calculations assume that disease will result if at least one spore has the opportunity to germinate. The probability that a spore germinates after cessation of antibiotics in an individual who terminates antibiotic prophylaxis at τ days after exposure is . Thus, the probability that at least one of D spores germinates, from the Poisson distribution, is

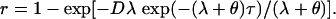After solving for τ, and noting that λ ≪ θ, we obtain the following result. We find that persons exposed to the TD(P) should remain on antibiotic prophylaxis until τ days after exposure to reduce their probability of contracting disease to r, where

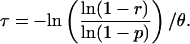[1]

The denominator of Eq. 1 is technically λ+ θ but, because λ ≪ θ, we have approximated λ + θ by θ. Eq. 1 is expressed in terms of p and θ and does not explicitly involve the parameter λ.

The competing-risks model can be used to derive the cumulative attack probability function, which is the probability that at least one spore germinates on or before the tth day after exposure in the absence of antibiotics. The probability that a spore germinates within t days is , which is equal to ϕ(t) = λ[1 – exp(–(λ + θ)t)]/(λ + θ). Then, by using the Poisson distribution, the probability at least one of D spores germinates within t days is 1 – exp[–Dϕ(t)]. Using the approximation that λ + θ is nearly equal to θ, we find that the cumulative attack probability function at the dose TD(P) is approximately

[2]

The incubation period is defined as the time from exposure to onset of symptoms among cases of disease. Once a spore germinates it is believed that it replicates rapidly, producing toxins that eventually produce symptoms (11), and here we will ignore the short duration of time from germination to the onset of symptomatic disease. The incubation-period distribution is the probability that the incubation period of an anthrax case is <t and is obtained by normalizing F(t, p) so that it approaches 1.0 rather than p as t gets large; that is, the incubation-period distribution is calculated by dividing F(t, p) by p. Some external validation of the model and its underlying assumptions could be obtained if the incubation-period distribution predicted by the model is in agreement with empirical observations from the Sverdlovsk outbreak.

Model Implications

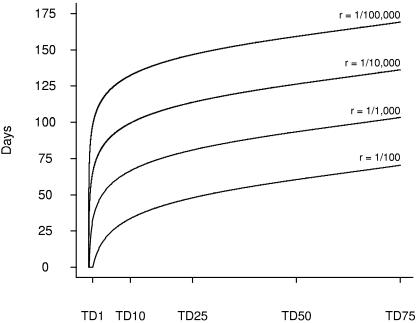
Fig. 1, which is based on Eq. 1, shows the duration of antibiotic prophylaxis τ to reduce risk of disease to 1/100, 1/1,000, 1/10,000, and 1/100,000 according to dose of inhaled spores. For example, to reduce risk of disease to less than 1/1,000, a person exposed to the TD(0.5), TD(1), TD(10), and TD(50) should remain on antibiotic prophylaxis for at least 23, 33, 67, and 93 days, respectively, beyond exposure. To reduce the risk of disease to <1/10,000, persons exposed to the TD(0.5), TD(1), TD(10), and TD(50) should remain on antibiotic prophylaxis for at least 56, 66, 99, and 126 days, respectively. Fig. 1 demonstrates that ≥4 months of antibiotic prophylaxis are necessary to reduce risk to <1/10,000 for doses as high as the TD(50). However, considerably shorter durations of antibiotic prophylaxis are indicated at lower doses.

Fig. 1.

Optimum duration of antibiotic prophylaxis. Durations of antibiotics after inhalational exposure to Bacillusanthracis spores to reduce probability of subsequent disease to 1/100, 1/1,000, 1/10,000, and 1/100,000 by TD(P) of exposure to anthrax spores.

The cumulative attack probability function based on Eq. 2 is shown in Fig. 2 at the doses TD(10), TD(25), TD(50), and TD(75). The cumulative attack probability function rises rapidly with increasing dose. At TD(50) and TD(75), respectively, 24% and 41% of exposed persons would develop disease by day 7. Thus, at the highest doses, significant morbidity could result before antibiotic prophylaxis could even be initiated, unless the public health response was extremely rapid.

Fig. 2.

Anthrax cumulative attack probability. Cumulative probability of disease by time since exposure and by TD(P) of exposure to anthrax spores.

Table 1 gives the quartiles of the incubation-period distribution assuming θ = 0.07/day predicted by the competing-risks model, which was obtained by dividing Eq. 2 by p. The 25th, 50th, and 75th quartiles of the incubation-period distribution at the TD(50) are 3.1, 7.7, and 16.2 days, respectively. It is useful to explore the behavior of the incubation-period distribution at low doses. Taking the limit of F(t, p)/p as p goes to 0 by application of L'Hospital's rule shows that the incubation-period distribution approaches the clearance distribution 1 – exp(–θt). Thus, at very low doses and with the clearance rate θ = 0.07/day, the median and mean incubation periods are approximately ln 2/θ = 9.9 days and (θ)^–1 = 14.2 days, respectively. These results are consistent with the median and mean incubation periods from the Sverdlovsk outbreak, which were reported to be 11.0 and 14.2 days, respectively (5, 6), and in which the overall attack rate was believed to be <2% (5). The concordance between empirical results from the Sverdlovsk outbreak and the competing-risk model at low doses supports the value of the clearance rate estimated from primate studies.

Table 1. Quartiles (25th, 50th, and 75th) of the distribution of incubation periods among anthrax cases by dose level of inhaled spores predicted by the competing-risks model.

	Incubation,* days
Toxic dose level	25th quartile	50th quartile (median)	75th quartile
Limiting†	4.1	9.9	19.8
TD(10)	3.9	9.5	19.2
TD(25)	3.6	8.9	18.3
TD(50)	3.1	7.7	16.2

^*In general, the q × 100 percentile of the incubation-period distribution at dose level TD(P) is -In[1 - (In(1 - qp)/In(1 - p))]/θ; q is set equal to 0.25, 0.50, and 0.75 at the quartiles.

^†Limit of the incubation period at low doses (p → 0) with clearance rate θ = 0.07/day.

Our result that the incubation-period distribution approaches the clearance distribution at low doses also holds for competing-risks hazards that are not constant over time. In particular, if the hazard rate of spore germination is proportional to the hazard rate of spore clearance, the incubation-period distribution approaches the clearance distribution as p goes to 0. This finding means that the distribution of incubation periods even at the very lowest doses cannot get longer than the distribution of clearance times of a single spore.

The optimum duration of antibiotic prophylaxis depends on dose of inhaled spores as shown by Eq. 1. Accordingly, a critical challenge to the formulation of public health guidelines in an anthrax outbreak is to estimate the dose of inhaled spores among exposed persons. Although environmental sampling methods are useful in identifying areas of contamination with Bacillus anthracis spores, such methods are unlikely to provide reliable quantitative assessment of the numbers of inhaled spores. Here we use an alternative approach to estimate doses based on the observed attack rates in an outbreak before the initiation of antibiotic prophylaxis. Epidemiological investigation can identify clusters of persons exposed to similar doses of inhaled spores. The basic idea is to set the proportion of anthrax cases in a cluster that occurred up to t days after exposure but before the initiation of antibiotic prophylaxis, equal to F(t, p), and then to solve for p. Confidence intervals (C.I.) for p are found by transforming the endpoints of exact binomial confidence intervals for the proportion that are cases by inverting Eq. 2.

We performed these calculations in three main clusters of the 2001 inhalational anthrax outbreak in the United States (17–19). These calculations were based on 4 cases of 2,747 exposed persons through the 4th day after exposure in the Brentwood postal facility in Washington, DC, 2 cases of 1,404 through the 6th day in the Hamilton postal facility in New Jersey, and 2 cases of 1,084 through the 9th day in the Florida media publishing company.

We found that the estimated TD levels were 0.6 (95% C.I. 0.17–1.52) in the Brentwood postal facility in Washington, DC, 0.41 (95% C.I. 0.05–1.50) in the Hamilton postal facility in New Jersey, and 0.40 (95% C.I. 0.05–1.42) in the Florida media publishing company. The estimated TD levels among the three clusters were consistent with each other ranging between TD(0.4) and TD(0.6). Based on Eq. 2, at the TD(0.6), ≈26 and 59 days of antibiotic prophylaxis would be adequate to reduce the probability of disease to <1/1,000 and 1/10,000, respectively.

The adherence rates to the 60-day regimen of antibiotics in the 2001 U.S. outbreak were only 64%, 61%, and 31% in the Washington, DC, New Jersey, and Florida clusters, respectively (19). No anthrax cases occurred among any persons who started antibiotic prophylaxis, which at first may seem surprising considering the low adherence rates to the antibiotic regimen. We calculated the probabilities that there would not have been any anthrax cases among these persons who started antibiotic prophylaxis taking into account the antibiotic adherence rates and the estimated doses of anthrax spores as follows. The numbers of cases of disease in a cluster of N persons exposed to the TD(P) who begin and cease antibiotic prophylaxis, respectively, at t₀ and t₁ days after exposure, has a Poisson distribution with mean NR(t₁, p), where R(t₁, p) = 1 – [(1 – p)^exp(–θt1)] is the expression for r evaluated at dose TD(P). We assume that the cluster is composed of a fraction f who adhere to a 60-day antibiotic regimen and a fraction 1 – f who complete only half the regimen (30 days). Then the probability that no cases surface in the cluster is ρ = exp(–NR̄), where R̄ = f R (60 + t₀, p) + (1 – f) R(30 + t₀, p). That analysis assumes all persons were exposed to the TD(P). The probabilities that there would not have been any anthrax cases surfacing among persons who initiated antibiotics prophylaxis in the Washington, DC, New Jersey, and Florida clusters were 0.51, 0.80, and 0.81, respectively. The probability there would not have been any anthrax cases among any persons on antibiotics in the three communities was 0.51 × 0.80 × 0.81 = 0.33. Accordingly, even though the adherence rates to the antibiotic regimen were modest, the fact that no anthrax cases surfaced among persons who initiated but may have prematurely discontinued antibiotic prophylaxis should not be surprising because the doses of inhaled spores were low.

Discussion

The analyses we have presented depend on several critical assumptions. One key assumption is the value of the clearance rate θ. The optimum duration of antibiotics, τ, is inversely proportional to the clearance rate. The cumulative attack probability function decreases with increasing θ. We used data from experimental studies in monkeys to estimate θ. The incubation-period distribution that was predicted by the competing-risks model from this value of θ was consistent with the epidemiological data from the human outbreak in Sverdlovsk, which lends support to the value of θ estimated from the primate studies. However, further studies are needed to refine the estimates of the clearance rate. Other factors may also affect the clearance rate. Some studies have suggested that the clearance rate decreases with decreasing spore size (16) or may depend on other factors that characterize the immune competence of the host, including age. Quantification of the effect of these factors, in addition to dose that was considered here, will further refine estimates of the optimum duration of postexposure antibiotic prophylaxis in an anthrax outbreak.

A second key assumption is that antibiotics prevent germination as long as they are administered, but otherwise, they alter neither the clearance rate θ nor the germination rate λ after the cessation of antibiotics. The competing-risks model could be extended to allow the values of λ and θ to change after cessation of antibiotics. However, hardly any experimental evidence exists to indicate whether the parameters change and, if so, by how much. One study suggested that certain specific antibiotics may alter the dynamics of spore germination and clearance after the cessation of antibiotics in the direction of reducing the risks of spore germination (20). If that were the case, our estimates of the optimum duration of antibiotic therapy, τ, would be conservatively overestimated.

A third assumption is that our probabilistic calculations were based on an underlying Poisson model for the number of spores in a host that germinate. Implicit in this assumption is that the spores within a host act independently of each other.

The optimum duration of antibiotic prophylaxis depends critically on the exposure dose, TD(P), which we have shown can be estimated from the cumulative attack rate up to the time when antibiotic prophylaxis begins. Specifically, Eq. 2 or Fig. 2 can be used to estimate the toxic dose level. Then Eq. 1 or Fig. 1 together with the toxic dose level can be used to estimate the duration of antibiotic therapy required to reduce risk to acceptable levels. Our analysis assumed all persons in a cluster were exposed to the same TD(P) level. If, however, variation in dose occurs among persons in a cluster, the mean dose among persons in the cluster would be conservatively overestimated slightly. This slight overestimation follows because F(t, p) is a convex function of p and Jensen's inequality implies that the true mean value is less than the approximation.

Rapid detection of anthrax outbreaks is critically important to reduce disease, and new methods of detection may help in that regard (21, 22). The importance of rapid emergency response once an anthrax outbreak has been detected, including medical surge capacity and the implications of some response strategies, have been demonstrated (23). Our results indicate that at doses as high as the TD(50), >4 months of antibiotic prophylaxis may be necessary to reduce risk adequately to <1/10,000, and it is likely considerable morbidity would occur before antibiotic prophylaxis could even be initiated. The use of anthrax vaccine as a postexposure prophylaxis that can confer long-term immunity could shorten the duration of antibiotic prophylaxis, but limited data on its postexposure efficacy exist (3, 24). At doses lower than the TD(1), antibiotic prophylaxis of 60-day duration should be adequate. Because of the need to respond immediately to an anthrax outbreak, having strategies in place to determine rapidly effective and measured public health responses to future acts of bioterrorism is critical to public health preparedness.