Coexistence of periodic modulation of quasiparticle states and superconductivity in Bi₂Sr₂CaCu₂O_8+δ

Abstract

In this article we show, using scanning tunneling spectroscopy, the existence of static striped density of electronic states in nearly optimally doped Bi₂Sr₂CaCu₂O_8+δ in zero field. This modulation is aligned with the Cu—O bonds, with a periodicity of four lattice constants, and exhibits features characteristic of a two-dimensional system of line objects. We further show that the density of states modulation manifests itself as a shift of states from above to below the superconducting gap. The fact that a single energy scale (i.e., the gap) appears for both superconductivity and stripes suggests that these two effects have the same origin.

One of the most important outstanding problems in condensed-matter physics is determination of the ground state of a strongly correlated electron system, in particular, high-temperature superconductors (HTSCs). For these materials, theoretical (1–7) and experimental (8–14) evidence has been mounting in support of the possibility that their ground state exhibits spin and charge density waves, which are primarily one-dimensional (i.e., stripes) and either compete with or promote superconductivity. Coexistence of charge or spin density waves and superconductivity has been reported previously in the lower Tc materials (9–11, 14) and in the presence of large magnetic fields (12, 13). The absence of data showing stripes in the higher Tc materials in zero field has lent support to the idea that stripes are competing with high-temperature superconductivity. However, here we show, using scanning tunneling spectroscopy, the existence of static striped density of electronic states in nearly optimally doped Bi₂Sr₂CaCu₂O_8+δ in zero field. This modulation is aligned with the Cu—O bonds, with a periodicity of four lattice constants, and exhibits features characteristic of a two-dimensional system of line objects. We further show that the density-of-states (DOS) modulation manifests itself as a shift of states from above to below the superconducting gap. The fact that a single energy scale (i.e., the gap) appears for both superconductivity and stripes suggests that these two effects have the same origin. Scanning tunneling spectroscopy allows one to measure, on an atomic scale, the electronic DOS. This measurement of the local DOS (LDOS) makes it a powerful tool for investigating correlated electron systems. In this study we used Bi₂Sr₂CaCu₂O_8+δ because it cleaves easily, yielding large, stable, atomically flat surfaces and has a high Tc (90 K). The single crystals of Bi₂Sr₂CaCu₂O_8+δ used in this study, grown by a floating-zone method, were annealed to be slightly overdoped, yielding a superconducting transition temperature of 86 K. The samples were cleaved (between the BiO planes) at room temperature in a vacuum of >10^–9 torr (1 torr = 133 Pa) and then transferred in <1 min to the low-temperature scanning tunneling microscope, where cryopumping yields an orders of magnitude better vacuum. Data were taken at 8 K with an iridium tip at a sample bias of –200 mV and a setpoint current of –100 pA. These setpoints also establish the relatively arbitrary normalization condition for the differential conductance (dI/dV), proportional to the LDOS. Fig. 1a shows the topography of a typical area: the surface exhibits clear atomic resolution. In particular, the superstructure in the BiO plane (15) with average periodicity ≈27 Å (as well as the location of the individual Bi atoms) is evident in all scans and provides a reference direction for our study. As reported earlier (16–18), all samples also exhibit strong inhomogeneity in the local spectroscopy. This manifests itself here as large variation in the superconducting gap size as measured by the location of the peak in the LDOS (Fig. 1b). The largest gaps (Δ > 60 mV) account for ≈10% of the area. The variation in the spectra is shown in the line scan of Fig. 1c, exhibiting evolution from small superconducting gap (Δ < 40 mV) with large coherence peaks to regions of large gap with much-reduced coherence peaks reminiscent of the pseudogap (19, 20).

Fig. 1.

(a) Topography (160 × 160 Å) of the cleaved BiO surface (spatial units are in angstroms throughout). The height is a contour of constant current, or integrated DOS up to the setpoint voltage. The nearly vertical streaks are the superstructural modulation. Also visible are the Bi atoms as well as irregular variations that are probably due to changes in the LDOS (17), not actual height variation. (b) The superconducting gap magnitude over the same area as measured by the voltage of the maximum in differential conductance (dI/dV). (c) Differential conductance as a function of voltage along the diagonal of a and b (from lower left to upper right). Each spectrum is colored according to its measured gap magnitude by using the same color scale as shown in b.

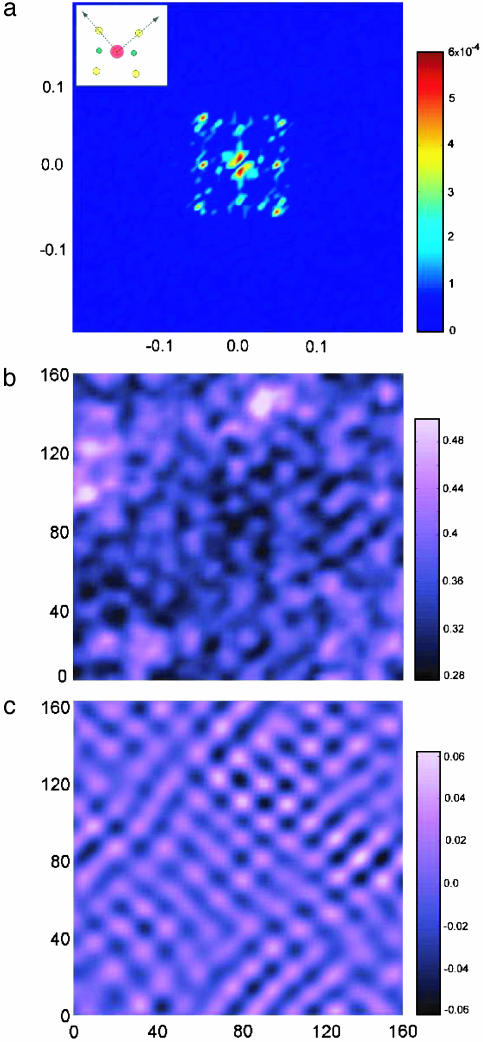
To facilitate our search for charge modulations in the superconducting state, we collected LDOS spectra at each point in the image and subsequently generated LDOS maps at various energies and their corresponding power spectra (intensity of the Fourier transform); one such pair is shown in Fig. 2 a and b for sample bias of 15 mV. Fig. 2 a and b show raw data, i.e., Fourier-transform and real-space map of (dI/dV)_(V=15mV). Fig. 2b is represented in a continuous scheme that averages neighboring pixels and is used to remove noise on a subatomic scale. There is a large amount of weight at small wavevectors, coming from the random contributions of the large inhomogeneities. In addition, there are two bright peaks appearing along the k_x direction which originate from the superstructure. Finally, Fig. 2a clearly shows four peaks oriented 45° to the superstructure and at points corresponding to, within experimental uncertainty, periodicities of (±4a₀, 0) and (0, ±4a₀), oriented along the Cu—O bonds. The real-space data (Fig. 2b) show a two-dimensional pattern in the LDOS that is oriented along the diagonals; however, as is evident from Fig. 2a, contributions from features at other wavelengths obscure this modulation. We can use Fig. 2a to Fourier-filter out from Fig. 2b contributions to the LDOS that are far away from the (2π/4a₀)(±1, 0) and (2π/4a₀)(0, ±1) points. Fig. 2c shows the data after such Fourier filtering with a standard Gaussian filter function by using σ = (2π/15a₀). The filter is performed by multiplying the Fourier transform of the raw data by a sum of Gaussian weighting functions with width centered about the four diagonal points in a and then applying the inverse Fourier transform. Varying the width of this filter has no qualitative effect on the resulting image. The modulation partially visible in Fig. 2b is now clear, appearing as a somewhat-disordered checkerboard pattern. From the separation of the defects in this map we estimate the coherence length to be 25a₀. Similar results were obtained in all samples studied and at temperatures as high as 18 K. Recent experiments on several HTSC systems have found similar charge or spin modulations in the presence of high magnetic fields applied perpendicular to the CuO₂ layers. From general theoretical arguments it is expected that, for coupled spin and charge density waves, spin modulation will have twice the period of charge modulation (1–7). In inelastic neutron-scattering experiments on La_2–xSr_xCuO₄ near optimum doping (x = 0.163), Lake et al. (9, 10) found strong scattering peaks at the four k-space points: (2π/a₀)[(1/2, 1/2) ± δ(0, 1/2)] and (2π/a₀)[(1/2, 1/2) ± δ(1/2, 0)], where δ ≈ 0.25 and a₀ is the lattice constant. This implies a spin density of periodicity 8a₀, which the authors find extends to >50a₀, much beyond the vortex core. Also, Mitrovic et al. (11) reported enhanced spin density wave fluctuations outside the vortex core in a high-field NMR-imaging experiment. In a recent experiment, Hoffman et al. (12) reported scanning tunneling spectroscopy on Bi₂Sr₂CaCu₂O_8+δ single crystals revealing a “checkerboard” of quasiparticle states with four unit-cell periodicity surrounding vortex cores. In k-space this corresponds to Bragg peaks in the LDOS at (2π/a₀)(±1/4, 0), and (2π/a₀)(0, ±1/4). This structure was found around the energy (≈7 meV) of a feature previously observed in the spectra of vortices in the same field range (20, 21). The checkerboard structure extends over ≈20a₀, again indicating ordering outside the vortex cores (22, 23).

Fig. 2.

Periodic spatial variation in the quasiparticle DOS. (a) Power spectrum of the Fourier transform of (dI/dV)_{(15 mV)} fora64 × 64-pixel region. The units are inverse angstroms. (Inset) Schematic of the features in the power spectrum; the arrows show the Cu-O-Cu directions. The central red dot corresponds to the signal at small wavevectors that comes from the randomly distributed inhomogeneities shown in Fig. 1 b and c. The horizontal points, which are green in Inset, correspond to the superstructure. The four diagonal points, yellow in Inset, show a DOS modulation at k = (2π/4a₀)(0, ±1) and (2π/4a₀)(±1, 0). (b) Map of (dI/dV)_{(15 mV)} smoothed by averaging neighboring pixels to remove atomic-scale variations. (c) The data in b filtered to accentuate the periodic modulation (see text.)

We have also found that the modulation in the LDOS exhibits strong energy dependence (Fig. 3). Here we show the value of the Fourier transform at the two independent peaks from Fig. 2a as a function of the bias voltage. The arbitrary phase (dependent on the point about which the Fourier transform is computed) has been set to maximize the real part, plotted in red, which changes sign at approximately ±40 mV. The variation in the imaginary part of the signal is considerably smaller, consistent with zero within the uncertainty. This is important because it shows that the location in real space of the DOS modulation is the same at all measured energies, although at approximately ±40 mV the positions of the maxima and the minima switch.

Fig. 3.

Energy dependence of the periodic LDOS modulation. Plot of the Fourier transform at k = (2π/4a₀)(0, ±1) and k = (2π/4a₀)(± 1,0), the location of the peaks in Fig. 2a, as a function of sample bias. The red and blue traces correspond to the real and imaginary parts, respectively. For each peak, the overall phase used for all energies is chosen to maximize the real part of the signal. The error bars are determined by modeling the variations in dI/dV(x, y) at each energy by uncorrelated noise of the same amplitude.

Furthermore, the energy dependence of the Fourier transform shows that relative spectral weight is shifted to subgap energies (with a peak at ±20–25 mV) from intermediate energies (with weight between 50 and 150 mV). The comparison of the result discussed above with the energy of the superconducting gap (≈40 mV) provides strong circumstantial evidence that the striped quasiparticle density and superconductivity are intimately connected. Because the integrated DOS from zero to infinity is the total charge, the shift of weight from intermediate to low energies coupled with the small magnitude of the Fourier components (5% of the LDOS) indicates that the total charge associated with this DOS modulation is very small, as is expected for itinerant systems with strong Coulomb interactions (24–27). On the other hand, it is important to note that energy-independent spatial variations in the DOS would not appear in this analysis because the normalization is set by maintaining constant current (which is proportional to the integrated DOS from zero to the setpoint voltage). We are sensitive to features in the shape of the LDOS, not the overall magnitude. Energy-independent changes, however, would appear in the so-called topographic signal (Fig. 1a), which actually maps a contour of constant integrated DOS. However, the power spectrum of the topograph reveals no such peaks above the noise.

To examine whether the LDOS modulation is anisotropic, we performed Fourier analysis on many smaller subregions of a slightly larger area. In Fig. 4 c and d we show maps of the spatial variation of the amplitude of the two perpendicular pairs of Bragg peaks. In addition to the small-scale variations that come from noise and finite size E ects, it is clear that each varies on the scale of ≈100 Å. In addition, these large-scale features exhibit significant anticorrelations between the two maps: there are several regions in space where one map shows a local maximum and the other shows a local minimum. This indicates that locally there is a broken symmetry and that the underlying order is not two-dimensional but one-dimensional. The two-dimensional nature of the patterns observed seems to come from the interpenetration of these perpendicularly oriented stripes. Following the work of Zaanen and Gunnarson (1) and Schulz (27), who first suggested spatial segregation in HTSC, Kivelson and Emery (2, 3) pointed out that disordered or fluctuating metallic stripe phases are a natural occurrence in doped Mott–Hubbard insulators. In this scenario, charge-ordered phases will then be formed. This charge ordering in turn drives the modulation of the antiferromagnetic order, hence resulting in an accompanying spin density wave structure. Near optimal doping, it is argued, a mixed state exists with both charge and spin density waves. Although in general stripes are expected to be dynamic in this regime, disorder will pin them easily (2, 3, 5, 28). Vortex-induced pinning of stripes was used by Hoffman et al. (12) to explain the observed density modulation near vortex cores. Random point defects, present in all HTSC samples, could play a similar role, thus explaining the origin of the stripe patterns we observe. In addition to this static striped DOS structure that spans the entire surface, gap structure inhomogeneities are observed in all our samples. The piling of LDOS in midgap, around a particular energy, and their origin from states just above the gap suggest that the density modulation and superconductivity are inseparable. The inhomogeneities in the superconducting gap structure therefore should also be reflected in the striped DOS. Indeed, the striping does show local variation as is shown in Fig. 4, together with topological defects in the striped structure visible in Fig. 2c (28). Because, in our samples, the disorder seems to be uncorrelated, it cannot establish a preferred direction; something else must be breaking rotational symmetry. We further note that because the observed stripes are static, yet superconductivity is strong, these stripes cannot be inherently insulating. Finally, it is remarkable that in this single set of experiments we see locally the d-wave superconducting gap, the pseudogap, and metallic stripes, suggesting that all reflect aspects of the same physics.

Fig. 4.

Spatial variation in the amplitude of the periodic modulation. (a) Constant current topograph (120 × 120 Å). (b) Power spectrum of (dI/dV)_{(15 mV)} over the entire (260 × 260-Å) area showing the peaks used in c and d. Peaks are smaller than those of Fig. 2a because the k-space pixels are smaller and the image size substantially exceeds the coherence length. (c) Magnitude of the Fourier transform of (dI/dV)_{(15 mV)} at one of the (2π/4a₀) points for a number of 32 × 32-pixel regions. The color at each point is the magnitude of this Fourier component for the 32 × 32-pixel dI/dV map centered at this point. The small (≈20-Å) scale variations are due to finite size effects in the Fourier transform. (d) The same map as for c for the other peak.