Abstract
We introduce a coarse-grained model for atomic glass formers. Its elements are physically motivated local microscopic dynamical rules parameterized by observables. Results of the model are established and used to interpret the measured behaviors of supercooled fluids approaching glass transitions. The model predicts the presence of a crossover from hierarchical super-Arrhenius dynamics at short length scales to diffusive Arrhenius dynamics at large length scales. This prediction distinguishes our model from other theories of glass formers and can be tested by experiment.
In this article, we introduce a microscopic model of glass-forming supercooled liquids. It is a coarse-grained model with local dynamical rules, the elements of which can be measured. The rules contain only the physical features of detailed balance, dynamic facilitation, and persistence of particle-flow direction. Our analysis of the model indicates that these features are all that is required to explain the time-dependent and thermal behaviors of supercooled glass-forming liquids. For such systems, relaxation times grow rapidly with decreasing temperature T, usually more rapidly than exponentially in T–1. This non-Arrhenius (or super-Arrhenius) temperature dependence often coincides with a relatively large change in heat capacity at the glass transition. On the other hand, liquids with relaxation times that grow in an Arrhenius fashion with decreasing temperature often display small changes in heat capacity at the glass transition. Apparent correlations such as these between thermodynamic properties and relaxation times have led to a commonly held opinion that a finite-temperature thermodynamic transition somehow underlies a glass transition (for a review of this and other views, see refs. 1 and 2). In contrast, our model explains the empirically observed correlations of relaxation and calorimetric properties at the glass transition without recourse to unusual or precipitous thermodynamics.
Our model is described in terms of a grid or lattice in space-time. Underlying this discrete picture are certain ideas about continuous atomic motions in a supercooled liquid. The first idea is that particle mobility is sparse. Most atomic motions are small-amplitude vibrations and not diffusion steps. Most molecules are effectively jammed. The second idea is that particle mobility in a glass former is the result of facilitation (3–5). Specifically, a region of jammed atoms can become unjammed and thus exhibit mobility only when it is adjacent to a region that is already unjammed. This idea implies that mobile or unjammed particles form chains in space-time. Chains of mobile particles have been revealed by atomistic computer simulations of supercooled liquids (6, 7). The third idea is that mobility carries a direction, and it is possible for this direction to persist in a glass former for significant periods of time. This convective-like quality of particle motion is also revealed by the atomistic computer simulations of supercooled liquids (6, 7).
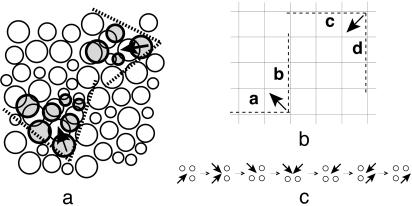
To help illustrate how these ideas motivate a lattice model, Fig. 1a depicts a mostly jammed fluid of spheres (drawn in two dimensions for artistic convenience). It shows, schematically, how mobility is found in unjammed regions, and that directed motion in one of those regions might make similarly directed motion possible in adjacent regions. The arrows are drawn pointing parallel to the mean direction of facilitation and antiparallel to the mean direction of particle motion. Given that particles singly occupy finite volumes, the possible influence of facilitation falls in a cone, as indicated by the dashed lines in Fig. 1a.
Fig. 1.
(a) Facilitation of motion in a nearly arrested fluid. The arrows indicate direction of facilitation, antiparallel to direction of flow. Motion is facilitated in cones indicated by the dotted lines. The white circles depict positions of atoms at one point in time; each gray circle near a white circle of the same size indicates the position of that near atom at a later point in time. (b) Coarse-grained lattice description. The excitation at the bottom facilitates cells a and b, and the excitation at the top facilitates cells c and d. (c) Possible series of steps leading to a diffusive step in d = 2.
The point of each cone in Fig. 1a depicts a position that is made accessible to an atom by prior motion in the vicinity of that point. As large voids dissipate quickly in a dense material, the most likely motions are collective and complicated shuffling of several particles. This shuffling could have a number of causes. One possibility is the presence of local density that is slightly less than a constraining value. Whatever its precise nature, the collective motion will have a definite direction for a period. In highly networked systems, directional persistence will quickly dissipate, decreasing its effect on subsequent motion.
To capture these physical features, we use the coarse-grained description depicted in Fig. 1b. Space is divided into square or cubic regions with side lengths comparable to but not smaller than the bulk correlation length of the fluid. As such, equilibrium fluctuations in one cell are uncorrelated with those in another at the same point in time. Further, time is divided into discrete intervals or time steps of length δt long enough to discriminate whether mobility (i.e., significant particle displacement) has occurred in a particular cell during that interval. An empty cell in Fig. 1b indicates a region that exhibits no mobility during that time step. A cell containing an arrow indicates a region that does exhibit mobility during that time step, and the direction of the arrow is antiparallel to the direction of motion and therefore indicates the direction of facilitation.
This coarse-grained catalog or description of dynamical behavior can be constructed from the trajectories of any system. In this sense, there is no approximation involved in its use. Were the system an ordinary liquid, a typical equilibrium configuration of the coarse-grained model would have essentially all regions occupied. For a sufficiently supercooled liquid, however, the concentration of arrows will be low. In that case, the thermodynamics of the material should be consistent with that of noninteracting arrows on a lattice. As a simplification, we shall consider only discrete orientations of the arrows, restricting them to lie along any one of the principal diagonals of its cell. Placing arrows along cell diagonals rather than edges allows for a cone of influence with positive angle. In particular, an arrow at a specific cell and time step can facilitate the creation or destruction of an arrow in a nearest-neighbor cell at the next time step, where the vector drawn from the specific cell toward that nearest neighbor has a positive inner product with the arrow. For example, in Fig. 1b, the arrow at the lower left can facilitate the birth of an arrow at the next time step in either cell labeled a or b. In this case, the cone of influence spans a quadrant in the square lattice or an octant in the cubic lattice. Different cones of influence can be defined with different choices of spatial grids.
The Model
As the preceding discussion indicates, our model describes the dynamics of
the vector field
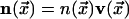 ,
where
,
where 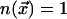 , depending on whether atoms
in cell
, depending on whether atoms
in cell  are mobile or immobile,
respectively, and
are mobile or immobile,
respectively, and 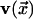 is the
unit vector pointing in the direction of the arrow in cell x
is the
unit vector pointing in the direction of the arrow in cell x
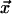 . For a square (d = 2)
lattice,
. For a square (d = 2)
lattice, 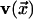 will be one of the
four vectors
will be one of the
four vectors 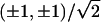 . The
equilibrium concentration of mobile cells is denoted by
. The
equilibrium concentration of mobile cells is denoted by
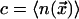 (taking the lattice
spacing to be unit length). The angle brackets indicate equilibrium ensemble
average. The system is isotropic, so that
(taking the lattice
spacing to be unit length). The angle brackets indicate equilibrium ensemble
average. The system is isotropic, so that
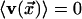 , and only
trivial equal-time correlations exist so that
, and only
trivial equal-time correlations exist so that
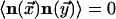 for
for
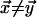 .
Accordingly, the equilibrium distribution for the vector field is
.
Accordingly, the equilibrium distribution for the vector field is
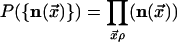 ,
where
,
where
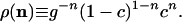 |
[1] |
Here, g is the number of equally likely equilibrium orientations of
an arrow [i.e., a vector 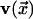 ].
For the square (cubic) lattice, g = 4 (g = 8).
].
For the square (cubic) lattice, g = 4 (g = 8).
The passage from one time interval, t, to the next, t +
δt, is governed in our model by the following single-site Monte
Carlo dynamics. Consider the transition at site
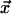 of the vector field
of the vector field
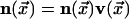 from an unexcited state,
from an unexcited state, 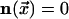 to an excited state
to an excited state 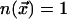 ,
,
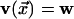 and the
corresponding backward transition. The dynamic facilitation described above is
implemented by defining the corresponding rates as
and the
corresponding backward transition. The dynamic facilitation described above is
implemented by defining the corresponding rates as
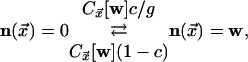 |
[2] |
where the kinetic constraint is implemented by the indicated state-dependent
rates, with 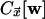 given by
given by
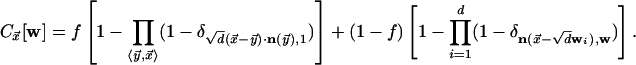 |
[3] |
Here, wi indicates the ith Cartesian
component of w, and nearest neighbors are denoted by
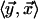 .
Because
.
Because 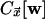 does not
depend on the state of the cell making the transition but only on the state of
its neighbors, it disappears from the ratio between forward and backward
rates, and the dynamics defined by Eq. 2 satisfies detailed balance
with respect to the distribution (Eq. 1). The parameter f
∈ [0, 1] in Eq. 3 determines the probability
p(f) that a newly created arrow will lie parallel to its
facilitating arrow, p(f) = [1 + f(g
– 1)]–1. One of the extremes, f =
1, corresponds to the case where an excitation pointing in any direction can
be created or destroyed as long as its site is facilitated by a neighbor. In
the other extreme, f = 0, only excitations pointing in the same
direction as the facilitating neighbor can be created or destroyed.
does not
depend on the state of the cell making the transition but only on the state of
its neighbors, it disappears from the ratio between forward and backward
rates, and the dynamics defined by Eq. 2 satisfies detailed balance
with respect to the distribution (Eq. 1). The parameter f
∈ [0, 1] in Eq. 3 determines the probability
p(f) that a newly created arrow will lie parallel to its
facilitating arrow, p(f) = [1 + f(g
– 1)]–1. One of the extremes, f =
1, corresponds to the case where an excitation pointing in any direction can
be created or destroyed as long as its site is facilitated by a neighbor. In
the other extreme, f = 0, only excitations pointing in the same
direction as the facilitating neighbor can be created or destroyed.
The above dynamics satisfies time-reversal symmetry and detailed balance. It is designed to be physically realistic for c small, the realm of dynamical arrest in a glass former. When c is not small, the dynamics of a realistic system might proceed through other mechanisms in addition to facilitation. In general, even for c small, space and time coarse graining of an atomistic model will lead to transition rules with non-Markovian elements. We assume these elements are unimportant.
The parameters c and f have clear physical meaning. Observations of trajectories can determine the probability, c, that a microscopic region exhibits mobility over a specified microscopic time period. They can further determine f from the directional persistence probability over a similar time period. For systems where directionality in particle motion can persist over a microscopic time δt (e.g., a nearly jammed fluid of hard spheres), f will be very small. For systems where directionality in particle motion will dissipate over that time (e.g., a highly networked fluid), f will be close to 1. One may use atomistic computer simulations of supercooled fluids to make the observations that determine c and f. Alternatively, one may perform microscopy on colloidal glass formers. In these cases, observed time scales relative to those of an ordinary liquid are modest in length. For glass-forming supercooled liquids exhibiting long relative time scales, experiments using single-molecule spectroscopic probes could be used.
The parameters c and f have energetic and entropic contributions. Because excitations in different sites are statically uncorrelated, their average concentration c must have the usual Boltzmann temperature dependence. Therefore, to the extent that c is small and mainly energetic, –ln(c/g) is proportional to reciprocal temperature, 1/T. Similarly, because f is a local probability independent of the state of the system, it is natural to write f = acb, where a pertains mainly to its entropic contribution and b pertains mainly to its energetic contribution.
Properties of the Model
It is useful to begin by considering the two extreme limits of the model: the f = 1 and f = 0 cases.
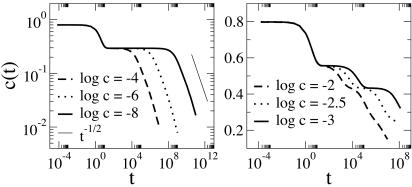
f = 1. Here, motion of an arrow can proceed diffusively as illustrated with the seven-step sequence configurations shown in Fig. 1c. This sequence, involving single activation on three occasions, produces a single diffusive step in either d = 2 or 3. As such, the relaxation time for a length scale l, τf=1(l), will obey τf=1(l) ∼ δtD–1lz1, where the dynamical exponent, z1, will be a constant, and the diffusion constant, D, will be proportional to c for d = 2 and 3. (The quantity D is the diffusion constant for excitations, which is distinct from the diffusion constant for particle motion.) Because the distance between arrows at equilibrium is c–1/d, the system approaches equilibrium with time scale τf=1 ∼ δt c–Δ1, where for d = 2 and 3, Δ1 = 1 + z1/d. From numerical simulations of the model on a square (d = 2) and cubic (d = 3) lattices, we find that Δ1 ≈ 2. Simulation results for the relaxation of the model from a disordered state on a square lattice are shown in Fig. 2 Left. As expected from the diffusive nature of its motion, the behavior of this model is similar to that of the one-spin-facilitated Fredrickson–Andersen (5) model (for a general review of facilitated dynamics see ref. 9). The Arrhenius dependence of τf=1 on c is often called “strong” (1, 2).
f = 0. Here, the motion is hierarchical (10, 11), similar to that of the East model (9, 12, 13) or its generalization to higher dimension,¶ and it is ergodic for d ≥ 2. An arrow can relax only through pathways involving like-pointing arrows. For d = 2 the system is composed of a mixture of arrows of four different directions, with each direction uncoupled from the others. The dynamical behavior of each of the four independent components is similar to that of a North-or-East model, which in turn behaves like the East model. In this case, therefore, τf=0(l) ∼ δtlz0, where now the dynamical exponent is not constant but rather a function of c, namely z0 ∼ ln(g/c)/ln 2, where c/g is the concentration of like-directed arrows. Hence, close to equilibrium, the overall time scale for relaxation is τf=0 ∼ δtc–Δ0, where Δ0 = z0/d. This scaling is consistent with the simulation results for d = 2 graphed in Fig. 2 Right. The super-Arrhenius dependence on c is often called “fragile” (1, 2).
- 0 < f < 1. Here we adopt an interpolation formula by adding rates in series
The corresponding equilibrium relaxation time is therefore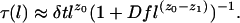
[4]
These equations exhibit a crossover behavior. In particular, for a given c and f, there is a crossover length, l*, such that for l > l*, relaxation is diffusive and thus Arrhenius, and for l < l*, relaxation is hierarchical and super-Arrhenius. Thus, at large-enough length scales, the relaxation of all systems, no matter how fragile, will obey diffusive behavior. The existence of the crossover length, l*, could be demonstrated experimentally from the single-molecule spectroscopy of rotating nanoparticle probes of various lengths. The existence of a crossover length also implies that there is a crossover c* (or T* if one associates c with T as suggested earlier) such that for c < c* (or T < T*), the equilibrium relaxation time of the model is Arrhenius, and for c > c* (or T > T*), it is super-Arrhenius. Implicit in these remarks is an appreciation for the presence of dynamic heterogeneity (11, 14, 15), in this case including flow direction, but because of limitations of space, we cannot discuss it further here.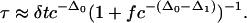
[5]
Fig. 2.
Relaxation of the concentration c(t) after a quench from an initial random state to final equilibrium concentration c in the d = 2 version of the model. (Left) f = 1. (Right) f = 0. Simulations were performed by using continuous-time Monte Carlo (8) on system sizes L = 105 and averaged over 50 samples. Error bars are comparable to line thickness.
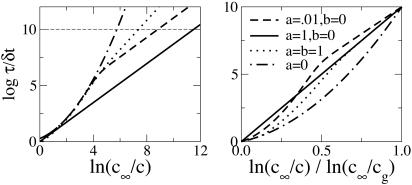
Crossover behavior was already demonstrated for what can be considered a mean field version of our model (16). The presence of a crossover has also been argued for on experimental grounds (17). Fig. 3 illustrates the consequent temperature dependence for the possible crossover behaviors predicted from our model. The graphs in Fig. 3 Left are drawn as Arrhenius plots, and those in Fig. 3 Right show the same quantities but scaled in the fashion proposed by Angell (1, 2). Notice the possibility that relaxation times may fall above the Arrhenius line in the Angell plot. This specific behavior has not been anticipated. It arises in systems where f is both small and mainly entropic (i.e., independent of c).
Fig. 3.
(Left) Arrhenius-like plot of relaxation time against equilibrium concentration for various values of f = acb. The cases a = 1, b = 0, and a = 0 correspond to purely Arrhenius and super-Arrhenius behavior, respectively. The case a = b = 1 leads to an energetic crossover, whereas a = 0.01, b = 0 leads to a mainly entropic one. (Right) Same as before now presented as an Angell-like plot with the glass transition chosen at τ ≈ 1010δt. c∞ = 8/9 is the random concentration value for the cubic lattice.
Comparison with Experiment
The fundamental control parameter is c, and although this quantity could be measured directly, most existing experimental data shows observations of the effects of changing c by changing temperature at the fixed pressure of 1 atm (1 atm = 101.3 kPa). To compare with that data, we therefore use
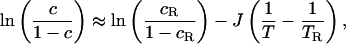 |
[6] |
where cR is the concentration of mobile regions at a
reference temperature TR, and J is the enthalpy
difference between a mobile and immobile region. Eq. 6 is again based
on the idea that, because excitations at different spatial points (at equal
times) are statically uncorrelated, their average concentration c
must have Boltzmann temperature dependence. Because mobile regions should be
liquid-like and immobile regions should be solid-like, we expect that
J/T should be of the order of a few entropy units times the
typical number of molecules in a cell (≈10). With lnc linear in
1/T, ln τf=0 is a
quadratic polynomial in T–1 [the
T–2 form was considered by Bässler
(18)], whereas ln
τf=1 is a linear one. A useful
reference point, which allows for a direct comparison with previous analysis
(e.g., see ref. 19), is
TR = T½, the temperature at
which the logarithm of the relaxation time is one half that at the glass
transition. In this case τR ≡ τ(cR) is of
the order of microseconds (μs). A common measure of fragility is
F½ ≡
2Tg/T½ – 1,
where Tg is the glass transition temperature
(19). A second common measure
is the steepness index, m ≡ d log
τ(Tg)/d(Tg/T)
(20), i.e., the slope at
Tg in the Angell plot. If the relaxation from
T½ to Tg follows the
super-Arrhenius form of τf=0,
then F½ and the elementary time scale
δt determine m:
mf=0 = 32(1 –
F½)–1(1 + Y)(1
+ 2Y)–1, where
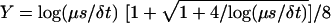 .
In the case of Arrhenius behavior or an energetic crossover that takes place
at T > Tg, the steepness index is
given by mf=1 = 16(1 –
F½)–1, independent of
δt.
.
In the case of Arrhenius behavior or an energetic crossover that takes place
at T > Tg, the steepness index is
given by mf=1 = 16(1 –
F½)–1, independent of
δt.
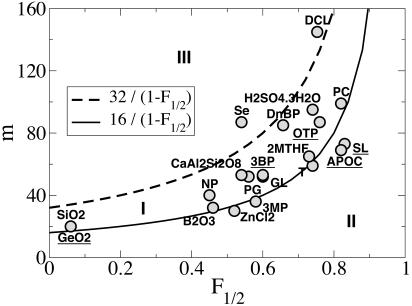
Fig. 4 shows that the ranges of fragility measures (19, 20) are well understood with our model. The dashed line corresponds to the value of mf=0 in the case where δt ≈ μs, mf=0 = 32(1 – F½)–1. The full line is mf=1. The region between this two lines, region I in Fig. 4, corresponds to super-Arrhenius behavior τf=0 with δt ≤ μs. Most glass-forming liquids fall in this region. Liquids on the full line are either those with purely Arrhenius behavior or those that undergo an energetic crossover. Region II below the full line corresponds to liquids that experience the entropic crossover noted above. Salol (SL) and α-phenyl-o-cresol (APOC) fall in this region. Region III above the dashed line corresponds to values of m that are too large to account with the present approach (except with δt ≫ μs, which seems unphysical). Because selenium forms polymer chains, a feature not accounted for in our model, it is perhaps not surprising that it falls in this region (21).
Fig. 4.
Steepness index m against kinetic fragility F½ for various supercooled liquids.
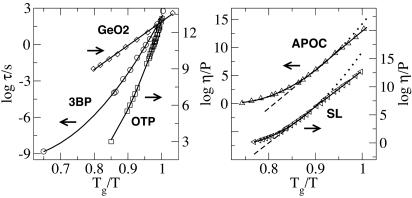
In Fig. 5 we show Angell plots in the regime near Tg for five representative liquids from Fig. 4 (data from refs. 22–24). It shows fits to the dielectric relaxation time scale of 3-bromopentane (3BP) and viscosity of ortho-terphenyl (OTP), by using τf=0, and an Arrhenius fit to the viscosity data of GeO2, by using τf=1. It also illustrates the crossover in the viscosity data of APOC and SL. The fits to the kinetic data determine the parameters of the model. From the coefficients of the terms quadratic in Tg/T in log τf=0 and from the linear one in log τf=1, we obtain the values of J/Tg = 16.7, 26.7, 29.3, 31.8, and 22.6 for 3BP, OTP, APOC, SL, and GeO2, respectively. These values of J/Tg obtained from fitting kinetic data agree with the expectations of our model.
Fig. 5.
Angell plots of dielectric relaxation and viscosity. (Left) Solid lines for 3BP and OTP refer to τf=0, and the solid line for GeO2 refers to τf=1.(Right) The full line corresponds to Eq. 5; dotted and dashed lines indicate τf=0 and τf=1 behavior before and after the crossover. Symbols indicate experimental data.
Further, from the linear and constant terms in log τf=0, we determine log(δt/μs) = –3.3, –4.4, –4.7, and –4.8 and log(cg/g) = –3.2, –3.4, –3.6, and –3.9 for 3BP, OTP, APOC, and SL, respectively, so that in these cases δt is of the order of fractions of nanoseconds. These are physically reasonable times to discern whether a microscopic region exhibits mobility. We also obtain a relation between the concentration at T½ to that at the glass transition, log{cg(1 – c½)/[c½(1 – cg)]} = –1.5, –1.4, –1.5, –1.8, and –4.6 for 3BP, OTP, APOC, SL, and GeO2, respectively. This list of ratios, in principle, could be checked experimentally. Fits to kinetic data do not determine the value of the parameter g. If we assume g ≈ 8 as in the lattice model, then we obtain for the previous liquids log cg = –2.3, –2.5, –2.7, –3.0, and –3.6, where in the case of GeO2 we have taken c½ ≈ O (1). Notice that the mobility concentration at Tg of the two purely super-Arrhenius liquids, 3BP and OTP, is at least 1 order of magnitude larger than that of the purely Arrhenius one, GeO2. Moreover, the two liquids that display a crossover have intermediate values of cg.
The order of magnitude difference between fragile and strong liquids (OTP and 3BP versus GeO2 in our example) in concentration of mobility excitations at Tg is a crucial theoretical prediction of our approach. In the context of the model, this difference has a clear origin. Relaxation time grows with decreasing c much faster in the fragile case (f = 0) than in the strong case (f = 1). Thus, an arbitrarily specified long relaxation time (e.g., some minutes) coinciding to a glass transition is reached at a value of c in the fragile case that is much larger than that in the strong case.
The phenomenological consequences of this difference in concentrations are important. For example, 1/c1/d(T) sets the dynamic correlation length, which in turn gives an upper bound for the size of dynamical heterogeneities (11). Assuming that each cell contains ≈5–10 molecules, so that δx ≈ 1–1.5 nm, we estimate that the size of dynamic heterogeneities for 3BP, OTP, and GeO2 are bounded from above by 5–8, 6–9, and 15–24 nm, respectively. As we have stressed (11), dynamic heterogeneity is self-similar over a range of lengths. Therefore, at a specific thermodynamic state point, no single length scale can be attributed to dynamic heterogeneity. Nevertheless, experimentalists have reported results for a few fragile liquids as if there is but a single specific length (14, 15, 25). The reported experimental lengths are consistent with our predicted bounds, although a definite comparison between theory and experiment must await more complete experimental information on the full range of heterogeneity lengths. Because 1/cg is larger in the strong case than the fragile case, our model predicts that the size of dynamical heterogeneous regions in strong liquids should be appreciably larger than those in fragile liquids. This predicted trend is opposite of that made by other theoretical approaches such as frustrated limited domains (26) or random first-order transitions (27).
From the concentrations cg and the corresponding values of J/Tg we are able to predict the jumps in specific heats at Tg. According to our model, this heat capacity (per mole) relative to that of the solid is
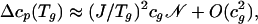 |
[7] |
where N is the number of molecules that contribute to enthalpy fluctuations per mobile cell. With the values obtained from the fits to the kinetic data for OTP, 3BP, and GeO2, for example, we obtain, Δcp(Tg)/N ≈ 2.3, 1.3, and 0.13, respectively. These values are in the ratio 17:10:1, which compares well to the experimental values Δcp(Tg)/kB ≈ 13.6, 9.2, and 0.84 (28–30), the ratio of which is 16:11:1.
Further comparisons between this theory and experiments illustrating subtle counterexamples to the usual correlation between super-Arrhenius behavior and Δcp (31) are left to future papers. Along with comparisons to equilibrium properties, illustrated herein, our model can be applied to out-of-equilibrium behaviors without further assumptions.
Acknowledgments
We are grateful to C. A. Angell for discussions and H. C. Andersen, D. Reichman, F. Ritort, and F. H. Stillinger for discussions and constructive comments on an earlier version of this article. This work was supported at Oxford by the Glasstone Fund and Engineering and Physical Sciences Research Council Grant GR/R83712/01 and at Berkeley in its early stages by the National Science Foundation, and in its later stages by U.S. Department of Energy Grant DE-FG03-87ER13793.
Abbreviations: SL, salol; APOC, α-phenyl-o-cresol; 3BP, 3-bromopentane; OTP, ortho-terphenyl.
Footnotes
References
- 1.Angell, C. A. (1995) Science 267, 1924–1935. [DOI] [PubMed] [Google Scholar]
- 2.Debenedetti, P. G. & Stillinger, F. H. (2001) Nature 410, 259–267. [DOI] [PubMed] [Google Scholar]
- 3.Glarum, S. H. (1960) J. Chem. Phys. 33, 639–653. [Google Scholar]
- 4.Phillips, M. C., Barlow A. J. & Lamb, J. (1972) Proc. R. Soc. London Ser. A 329, 193–218. [Google Scholar]
- 5.Fredrickson, G. H. & Andersen, H. C. (1984) Phys. Rev. Lett. 53, 1244–1247. [Google Scholar]
- 6.Perera, D. N. & Harrowell, P. (1998) J. Non-Cryst. Solids 235, 314–319. [Google Scholar]
- 7.Donati, C., Douglas, J. F., Kob, W., Plimpton, S. J., Poole, P. H. & Glotzer, S. C. (1998) Phys. Rev. Lett. 80, 2338–2341. [Google Scholar]
- 8.Newman, M. E. J. & Barkema, G. T. (1999) Monte Carlo Methods in Statistical Physics (Oxford Univ. Press, Oxford).
- 9.Ritort, F. & Sollich, P. (2003) Adv. Phys. 52, 219–342. [Google Scholar]
- 10.Palmer, R. G., Stein, D. L., Abrahams, E. & Anderson, P. W. (1984) Phys. Rev. Lett. 53, 958–961. [Google Scholar]
- 11.Garrahan, J. P. & Chandler, D. (2002) Phys. Rev. Lett. 89, 035704–035707. [DOI] [PubMed] [Google Scholar]
- 12.Jäckle, J. & Eisinger, S. (1991) Z. Phys. B: Condens. Matter 84, 115–124. [Google Scholar]
- 13.Sollich, P. & Evans, M. R. (1999) Phys. Rev. Lett. 83, 3238–3241. [Google Scholar]
- 14.Sillescu, H. (1999) J. Non-Cryst. Solids 243, 81–108. [Google Scholar]
- 15.Ediger, M. D. (2000) Annu. Rev. Phys. Chem. 51, 99–128. [DOI] [PubMed] [Google Scholar]
- 16.Buhot, A. & Garrahan, J. P. (2001) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 64, 021505–021508. [Google Scholar]
- 17.Ito, K., Moynihan, C. T. & Angell, C. A. (1999) Nature 398, 492–495. [Google Scholar]
- 18.Bässler, H. (1987) Phys. Rev. Lett. 58, 767–770. [DOI] [PubMed] [Google Scholar]
- 19.Martinez, L. M. & Angell, C. A. (2001) Nature 410, 663–667. [DOI] [PubMed] [Google Scholar]
- 20.Bohmer, R., Ngai, K. L., Angell, C. A. & Plazek, D. J. (1993) J. Chem. Phys. 99, 4201–4209. [Google Scholar]
- 21.Bohmer, R. & Angell, C. A. (1993) Phys. Rev. B Condens. Matter 48, 5857–5864. [DOI] [PubMed] [Google Scholar]
- 22.Berberian, J. G. & Cole, R. H. (1986) J. Chem. Phys. 84, 6921–6927. [Google Scholar]
- 23.Napolitano, A. & Macedo, P. B. (1968) J. Res. Natl. Bur. Stand. Sect. A 72, 425–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Laughlin, W. T. & Uhlmann, D. R. (1972) J. Phys. Chem. 76, 2317–2325. [Google Scholar]
- 25.Reinsberg, S. A., Heuer, A., Doliwa, B., Zimmermann H. & Spiess, H. W. (2002) J. Non-Cryst. Solids 307, 208–214. [Google Scholar]
- 26.Viot, P., Tarjus, G. & Kivelson, D. (2000) J. Chem. Phys. 112, 10368–10378. [Google Scholar]
- 27.Xia, X. & Wolynes, P. G. (2000) Proc. Natl. Acad. Sci. USA 97, 2990–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chang, S. S. & Bestul, A. B. (1972) J. Chem. Phys. 56, 503–516. [Google Scholar]
- 29.Takahara, S., Yamamuro, O., Matsuo, T. (1995) J. Phys. Chem. 99, 9589–9592. [Google Scholar]
- 30.Brüning, R. & Crowell, T. (1999) J. Non-Cryst. Solids 248, 183–193. [Google Scholar]
- 31.Huang, D. & McKenna, G. B. (2001) J. Chem. Phys. 114, 5621–5630. [Google Scholar]