Nonparametric regression to the mean

Abstract

Available data may reflect a true but unknown random variable of interest plus an additive error, which is a nuisance. The problem in predicting the unknown random variable arises in many applied situations where measurements are contaminated with errors; it is known as the regression-to-the-mean problem. There exists a well known solution when both the distributions of the true underlying random variable and the contaminating errors are normal. This solution is given by the classical regression-to-the-mean formula, which has a data-shrinkage interpretation. We discuss the extension of this solution to cases where one or both of these distributions are unknown and demonstrate that the fully nonparametric case can be solved for the case of small contaminating errors. The resulting nonparametric regression-to-the-mean paradigm can be implemented by a straightforward data-sharpening algorithm that is based on local sample means. Asymptotic justifications and practical illustrations are provided.

The regression-to-the-mean phenomenon was named by Galton (1), who noticed that the height of sons tends to be closer to the population mean than the height of the father. The phenomenon is observed in uncontrolled clinical trials, where subjects with a pathological measurement tend to yield closer-to-normal subsequent measurements (2, 3) and motivates controlled clinical trials for the evaluation of therapeutic interventions (4, 5). Classical regression to the mean has been studied mainly in the context of multivariate normal distributions (6).

In the typical regression-to-the-mean situation, one has observations that are contaminated by random errors. The well known basic result for the situation of a multivariate normal distribution corresponds to shrinkage to the mean and provides the best prediction for a new observation based on past observations and also a method for denoising contaminated observations.

Extensions of the normality-based regression-to-the-mean strategies have been studied by various authors. Although the contaminating errors are still assumed to be normal, Das and Mulder (7) derived a regression-to-the-mean formula allowing for an arbitrary distribution of the underlying observations. This result was combined with an Edgeworth approximation of this unknown distribution in ref. 8, and it forms the starting point of our investigation as well, see Eq. 2 below. Regression to the mean for more complex treatment effects has been studied in refs. 9 and 10.

We propose a procedure for the case where both the distribution of the true underlying uncontaminated observations (which are to be predicted) as well as the distribution of the contaminating errors are unknown. As we demonstrate, if repeated observations are available, it is possible to obtain consistent predictors under minimal assumptions on the distributions if either the error variance declines or the number of repeated measurements increases asymptotically. We establish asymptotic normality and propose an intuitively appealing and simple implementation based on local sample moments that is illustrated with a data set consisting of a bivariate sample of repeated blood-sugar measurements for pregnant women.

The Regression-to-the-Mean Problem

The general problem can be stated as follows: Given unknown independently and identically distributed (i.i.d.) random variables X_i, we observe a sample of data contaminated with errors δ_i,

Here, X_i and δ_i are independent, and the contaminating errors δ_i are i.i.d. with zero means. The goal is to predict the uncontaminated values X_i from the observed contaminated data X̃_i. The best linear unbiased predictor for X_i is given by the Bayes estimator . Assuming the existence of probability density functions (PDFs) f_X̃ for X̃, f_X for X, and f_δ for δ, we find by elementary calculations

and

where we denote the joint PDF of (X̃, X) by f_X̃,X. This leads to the following general form for the regression-to-the-mean function:

[1]

We show that the difficulty that is caused by the fact that both f_δ and f_X are unknown can be addressed with a nonparametric method. The proposed method produces consistent predictors of the uncontaminated X, whenever the errors δ can be assumed to be shrinking asymptotically, as in situations where an increasing number of repeated measurements become available. In classical regression to the mean, a critical assumption is that the contaminating PDF f_δ is Gaussian; even then its variance is typically unknown and must be estimated, requiring the availability of repeated measurements for at least some subjects.

The key argument for the Gaussian case can be found in ref. 7 (see also refs. 11 and 12). We reproduce the argument here for the one-dimensional case. Assume 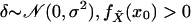for a given x₀ and denote the standard Gaussian density function by ϕ. Then, substituting (1/σ)ϕ(·/σ) for f_δ in Eq. 1, and using the fact that x = –ϕ⁽¹⁾(x)/ϕ(x),

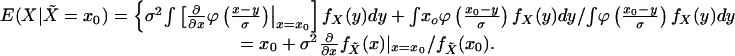[2]

Under the additional assumption , we have . Substituting

for f_X̃ in Eq. 2 then produces the classical regression-to-the-mean formula

[3]

Both Eqs. 1 and 2 reveal that regression to the mean corresponds to shrinkage toward the mean; in Eq. 2, this becomes shrinkage to the mode, rather, as 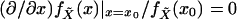at a mode of the density f_X̃.

Extending Eq. 2 to the p-dimensional case, one finds analogously

[4]

Here V = cov(δ) is the p × p covariance matrix of the contaminating errors δ, which are assumed p-variate normal, , and is the gradient of the p-dimensional PDF f_X̃.

The Nonparametric Case

The general regression-to-the-mean formula (Eq. 1) is not applicable in practice when neither f_δ nor f_X are contained in a parametric class; indeed it is easily seen that these components are then unidentifiable. The derivation of Eqs. 2–4 is tied to the feature that the Gaussian PDF is the unique solution of the differential equation g⁽¹⁾(x)/g(x) = –x.

The following basic assumptions are made.

Assumption A1. The p-dimensional (p ≥ 1) measurements that are observed for n subjects are generated as follows:

where the uncontaminated unobservable data X_i are i.i.d. with PDF f_X, and the measurement errors δ_i are i.i.d. with PDF

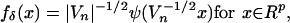[5]

where ψ is an unknown PDF and V_n is a sequence of covariance matrices V = V_n = (v_kl)_{1≤k, l≤p} of full rank, with ∥V_n∥ → 0, where and |V| denotes the determinant of V. Moreover, X_i and δ_i are independent for all i. For the case p = 1, we set V_n = (σ_n) = σ. The X̃_i are i.i.d. with PDF f_X̃.

Assumption A2. At a given point x₀ in the interior of the support of f_X such that f_X(x₀) > 0, the PDFs ψ and f_X are twice continuously differentiable, and ψ satisfies the moment conditions (p = 1)

and for p > 1, ψ satisfies

and all third-order moments are bounded.

We note that in the case of repeated measurements per subject,

[6]

assuming all δ_ij and (X_i, δ_ij) are independent, one may work with averages

[7]

where , and analogously for X̃_i, X_i. Then, for p = 1, Eq. 5 is replaced by

[8]

for fixed m (and analogously for p > 1). If the number of repeated measurements is large, we may consider the case m = m(n) → ∞ as n → ∞, where

[9]

for σ_m(n) = σ/m(n)^1/2, with ψ replaced by ψ_n, satisfying the moment properties as in Assumption A2; this case is covered as long as ψ_n and its first-order derivatives are uniformly bounded for all n.

For simplicity, we develop the following argument for the case p = 1; the extension to p > 1 is straightforward. The central observation under Assumptions A1 and A2 is the following argument: From Eq. 1,

[10]

and for the denominator

Let μ_j = ∫ψ(x)x^jdx for j ≥ 1. Combining a Taylor expansion with the moment conditions (Assumption A2) and observing that, because ψ is a PDF, ∫ψ⁽¹⁾(z)dz = 0, ∫ψ⁽¹⁾(z)zdz = –∫ψ(z)dz = –1, ∫ψ⁽¹⁾(z)z²dz = –2∫ψ(z)zdz = 0, and ∫ψ⁽¹⁾(z)z³dz = –3μ₂, we find

[11]

We note that in the Gaussian case, where ψ = ϕ, the term on the left-hand side of Eq. 11 vanishes, because then ψ⁽¹⁾(z) = –zψ(z). In case the contaminating errors have a symmetric PDF or, more generally, whenever μ₃ = 0, and the PDFs are three times continuously differentiable, the Taylor expansion can be carried one step further to yield

[12]

Likewise, the difference in Eqs. 11 and 12 can be made of even smaller order by requiring additional moments to be equal to those of a Gaussian distribution. Finally,

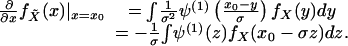[13]

Combining Eqs. 10, 11, and 13,

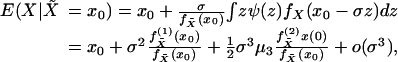[14]

and if μ₃ = 0, the leading remainder term is . Finally, for the multivariate case the same arguments lead to the following extension of Eq. 14:

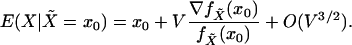[15]

Local Sample Means for Nonparametric Regression to the Mean

The concept of local moments and local sample moments is related to the data-sharpening ideas proposed in ref. 13 and was formulated in ref. 14. The special case of a local sample mean is used implicitly in “mean update” mode-finding algorithms (15, 16) and provides an attractive device for implementing nonparametric regression to the mean.

The starting point is a random variable Z with twice continuously differentiable density f_Z. Given an arbitrary point 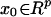, x₀ = (x₀₁,..., x_0p)′, and choosing a sequence of window widths γ = γ_n > 0, define a sequence of local neighborhoods

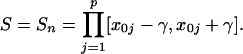The local mean at x₀ is defined as μ_z = (μ_z1,..., μ_zp)′, with

[16]

where in e_j = (0,..., 1,..., 0)′ the 1 occurs in the jth position. According to ref. 14,

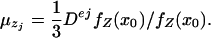[17]

The empirical counterpart to these local means are the local sample means. Given an i.i.d. sample (Z₁,..., Z_n) of random variables with PDF f_Z, where Z_i = (Z_i1,..., Z_ip)′, the local sample mean is μ_Z = (μ_Z1,..., μ_Zp)′, where

[18]

and γ = γ_n > 0 is a sequence with γ → 0as n → ∞. This is the sample mean found from the data falling into the local neighborhood S(x₀), standardized by γ^–2. By equations 3.4 and 3.8 in ref. 14,

[19]

motivating the connection to nonparametric regression to the mean as in Eq. 15.

Usually the covariance matrix V of the contaminating errors δ is unknown and can be estimated via the sample covariance matrix

[20]

given a contaminated sample with repeated measurements, (X̃_ik1,..., X̃_ikp)′, 1 ≤ i ≤ n, 1 ≤ k ≤ m_i, and , where m_i ≥ 2, 1 ≤ r ≤ p.

We note that consistency V̂ = V(1 + o_p(1)) holds asa long as , n → ∞. Then the estimate

[21]

satisfies

[22]

as long as γ → 0, σ → 0 and nγ^2+p → ∞.

The following additional regularity conditions are needed for asymptotic results.

Assumption A3. As n → ∞, γ → 0, nγ^2+p → ∞, and for a λ ≥ 0, nγ^2+p+4 → λ².

Assumption A4. It holds that V = 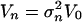for a fixed covariance matrix V₀ with trace(V₀) = p and a sequence as n → ∞. Here, V₀ is the covariance matrix associated with the error PDF ψ defined in Assumption A2.

Assumption A5. As n → ∞, (nγ^2+p)^1/2σ → 0, σ/γ → 0.

We then obtain, using local sample means of Eq. 18 and estimates V̂ of Eq. 20, the following main result on asymptotic normality and consistency of the shrinkage estimates in Eq. 21.

Theorem 1. Under Assumptions A1–A5, as n → ∞,

[23]

in distribution, where B = (β₁,..., β_p)′,

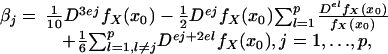[24]

and

[25]

In the one-dimensional case (p = 1), this simplifies to

Simulation Results

To illustrate the advantage of nonparametric regression to the mean in Eq. 21, we compare it with the Gaussian analog. If X ∼ N(μ_X, ∑), δ ∼ N(0, V), X̃ = X + δ, with X, δ independent, the extension of Eq. 3 to the multivariate case is

[26]

A total of 300 observations were generated from the (½, ½)-mixture of two bivariate normal distributions with means (–1, –1) and (1, 1) and common covariance matrix ⅛I, where I stands for the identity matrix. Samples then were contaminated by adding Gaussian noise with zero mean and covariance matrix V = ¼I.

Parametric and nonparametric regression-to-the-mean estimates, assuming that V is known while μ_X is estimated through the sample mean of the observed X̃_i, are presented in Fig. 1 for a typical simulation run. Circles represent the generated uncontaminated data, and arrows point from contaminated data to predicted data, which correspond to the tips of the arrows. The graphical results clearly indicate that the nonparametric procedure tracks the original uncontaminated data well, whereas the parametric procedure shrinks the data toward the origin, which is the wrong strategy for these nonnormal data.

Fig. 1.

Sample of size 300 from a mixture of bivariate normal distributions (Top Left), contaminated sample (Top Right), nonparametic regression to the mean using Eq. 21 (Middle Left), arrows pointing from contaminated to predicted observations (Middle Right), and Gaussian estimates using Eq. 26 (Bottom Left) with corresponding arrows (Bottom Right). Only data falling into the window [–2, 2] × [–2, 2] are shown.

As a measure of accuracy in recovering the original uncontaminated data, we computed the average sum of squared differences between original uncontaminated data and regression-to-the-mean estimates for the Gaussian method of Eq. 26 and the nonparametric method of Eq. 21 over 500 Monte Carlo samples under the specifications described above. The resulting average squared error measures for the Gaussian and nonparametric procedures were 414.44 and 60.19, respectively, indicating an almost 7-fold improvement for nonparametric relative to Gaussian regression to the mean in this example.

Application to Repeated Blood-Sugar Measurements

Blood-sugar measurements are a common tool in diabetes testing. In a glucose-tolerance test, the glucose level in blood is measured after a period of fasting (fasting-glucose measurement) and again 1 h after giving the subject a defined dose of glucose (postprandial glucose measurement). Pregnant women are prone to develop subclinical or manifest diabetes, and establishing the distribution of blood-glucose levels after a period of fasting and after a dose of glucose is therefore of interest.

O'Sullivan and Mahan (17) collected data on 52 pregnant women whose blood-glucose levels (fasting and postprandial) were measured during three subsequent pregnancies, thus establishing a series of repeated bivariate measurements with three repetitions (m = 3, p = 2) (see also ref. 18, p. 211). In a preprocessing step, the data were standardized by subtracting the mean and dividing by the SD for each of the two variables fasting glucose (mean 72.9 mg/100 ml, SD 6.05) and postprandial glucose (mean 107.8 mg/100 ml, SD 18.65) separately. Subsequently, 52 bivariate sample means X̃_i. were obtained by averaging over the three repeated measurements for each subject. These data are shown as open circles in Fig. 2.

Fig. 2.

Bivariate nonparametric regression to the mean (Eq. 21) for glucose measurements for 52 women, with repeated measurements over three pregnancies. Circles are observed sample means obtained from the three repetitions of the standardized values of (fasting glucose, postprandial glucose). Arrows point from observed to predicted values.

Applying Eqs. 19–21 with window width γ = 1.4 and sample covariance matrix , and , we obtain the predictions Ê(X_i|X̃_i.). The arrows in Fig. 2 show the displacement from observed to predicted values, the latter corresponding to the tips of the arrows.

Moving from the original observations to the predictions has a data-sharpening effect. This can be seen quite clearly from Parzen–Rosenblatt nonparametric kernel density estimates of the bivariate density, comparing the density of the original observations (Upper) with that of the predicted observations (Lower) in Fig. 3.

Fig. 3.

Bivariate kernel density estimates of the joint density of (fasting glucose, postprandial glucose) data with bandwidth (1, 1). (Upper) Density estimate based on original observations. (Lower) Density estimate based on predicted values after applying nonparametric regression to the mean (Eq. 21).

Concluding Remarks

We have generalized the regression-to-the-mean paradigm to a nonparametric situation, where both the nature of the target distribution of given observations as well as that of the contaminating errors are unknown. It is shown that in this fairly general situation regression to the mean corresponds to shrinkage towards the mode of the distribution. We propose a straightforward estimation scheme for the shrinkage factor based on local sample means. Thus a connection emerges between nonparametric regression to the mean with data-shrinkage ideas and the mean update algorithm that has been used previously for mode finding and cluster analysis.

Open questions concern choice of smoothing parameters. A plug-in approach could be based on estimating the unknown quantities in the asymptotic distribution provided in Eqs. 23–25, and bootstrap methods based on residuals are another option. Procedures for more elaborate designs where nonparametric regression to the mean would be incorporated into more-complex models involving comparison of means, analysis of variance, or regression components are also of interest, as is the estimation of the contaminating errors and their distribution from the “residuals” Ê(X|X̃) – X̃.

Appendix: Proof of Theorem 1

We first establish the following result on multivariate asymptotic normality of local sample means, computed from random samples (X₁,..., X_n) with PDF f_X.

Theorem A.1. For vectors of local sample means of Eq. 18 and μ = (μ₁,..., μ_p)′, μ_j = D^ejf_X(x₀)/3f_X(x₀) of Eq. 17, it holds under Assumptions A1–A3 that

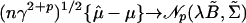[A.1]

in distribution, where B̃ = B/3(see Eq. 24) and (see Eq. 25).

Proof: Extending an argument of ref. 14 (p. 105), consider random variables

By third-order Taylor expansion of and EU_jU_k = O(γ⁴|S|)for j ≠ k. Defining random variables

and using fixed constants α₁,..., α_p, we find that

and

Applying the Cramér–Wold device and Slutsky's theorem completes the proof.

Proof of Theorem 1: Observing Eqs. 15, 19, and 21, Assumptions A4 and A5, and the consistency of V̂,

is seen to have the same limiting distribution as . Therefore, Theorem 1 is a direct consequence of Theorem A.1 once we establish the following two results:

[A.2]

and

[A.3]

The moment conditions for ψ (see Assumption A2) in the multivariate case are, with constants β_α and ζ_α,

and this leads to (see chapter 6 in ref. 19 and ref. 20)

By using these moment conditions in second-order Taylor expansions,

[A.4]

[A.5]

whence Eq. A.2 follows by Assumption A5.

We next discuss the denominators of and . Abbreviating ρ_n = (nγ ^p+2)^1/2, we find, based on the kernel density estimator with uniform kernel and window S, denoting the indicator function by I(·),

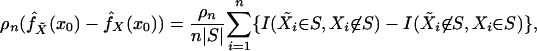and because by Eq. A.4, EI(X̃_i ∈ S) – EI(X_i ∈ S) = O(|S|σ²), we arrive at

[A.6]

Note that due to Assumption A5,

which implies

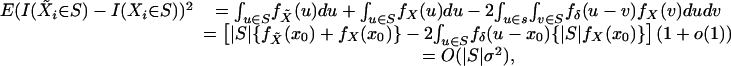again using Eq. A.4. We conclude that var 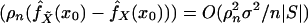, whence, with Eq. A.6,

[A.7]

Regarding the numerator, the terms to consider are

[A.8]

and the terms that include x_0j are handled in the same way as the denominator by using Eq. A.7. Because X̃_ij = X_ij + δ_ij, it therefore remains to consider

The same argument as for the denominator and additional Cauchy–Schwarz bounds lead to EI → 0, EI² → 0, and therefore . For II, note that

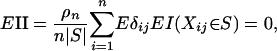because X_ij and δ_ij are independent. Furthermore, E(δ_ijI(X_ij ∈ S))² = O(σ²|S|) leads to var(II) = O(γ²σ²) = o(1), according to Assumption A5. Therefore, , and Eq. A.3 follows, concluding the proof.