The Flory isolated-pair hypothesis is not valid for polypeptide chains: Implications for protein folding

Abstract

Using an all-atom representation, we exhaustively enumerate all sterically allowed conformations for short polyalanyl chains. Only intrachain interactions are considered, including one adjustable parameter, a favorable backbone energy (e.g., a peptide hydrogen bond). The counting is used to reevaluate Flory's isolated-pair hypothesis, the simplifying assumption that each φ,ψ pair is sterically independent. This hypothesis is a conceptual linchpin in helix–coil theories and protein folding. Contrary to the hypothesis, we find that systematic local steric effects can extend beyond nearest-chain neighbors and can restrict the size of accessible conformational space significantly. As a result, the entropy price that must be paid to adopt any specific conformation is far less than previously thought.

 We will have to decide whether the assembly, when left to itself in the way already specified, tends to settle down mainly into one or other of a small preferred group of stationary states, whose properties are or control the equilibrium properties of the assembly; or whether it shows no such discrimination, but wanders apparently or effectively at random over the whole range of stationary states made accessible by the general conditions of the problem (1).

The central thermodynamic question in protein folding is: How can a polypeptide chain overcome conformational entropy and fold to its native state (2)? Typically, the unfolded state is depicted as a rugged energy landscape with an exorbitant number of local minima. Under suitable conditions, the protein negotiates this landscape spontaneously and finds its way to the global minimum—the native state.

This view of the unfolded state corresponds to the latter case referred to by Fowler and Guggenheim (1), in which the assembly wanders apparently at random over the whole range of conceivable stationary states. The view was placed on a rigorous foundation by the work of Flory (3), who showed that each φ,ψ pair in the peptide backbone is sterically insensitive to the values of its neighbors. Flory's simplifying conclusion is known as the isolated-pair hypothesis.

The isolated-pair hypothesis has influenced the development of helix–coil (4–6) and protein-folding theories (7). It follows from the hypothesis that local structural transitions are ruled out as a possible origin of cooperativity in protein folding (8); the entropic price is simply too high for short polypeptide backbones to preferentially populate a small set of highly similar conformations.

In contrast to these ideas, both experiments (9) and calculations (10) suggest the prevalence of biases in polypeptide chains, which motivated us to reevaluate the isolated-pair hypothesis. We find that the former case referred to by Fowler and Guggenheim—in which a small preferred group of states account for the equilibrium properties of the assembly—better describes the situation for polypeptide chains in both folded and unfolded forms. The validity of the isolated-pair hypothesis has also been questioned by Qian and Schellman (although for reasons other than sterics) (6).

We tested the isolated-pair hypothesis by simple enumeration. If the hypothesis holds, the distribution of allowed conformations for any φ,ψ pair in short polyalanine chains will be identical to those expected for an isolated alanine dipeptide. Otherwise, the number of allowed conformations will be abridged.

Exhaustive Enumeration of Allowed Conformations: A Device for Counting.

Our objective is to enumerate all possible conformations for blocked all-atom polyalanine chains: Ac-Ala_n-N′-methylamide. Chain conformation is specified by the backbone dihedral angles φ and ψ. To count, we use a device in which φ,ψ space for an individual φ,ψ pair is tiled into discrete bins called mesostates (Fig. 1). The 14 nonempty mesostates are: {A,G,M,R,L,F,E,K,Q,J,P,O,I,o} (Fig. 1). Not all regions within a mesostate are allowed.

Figure 1.

The labeled coarse-grain bins (mesostates) for a φ,ψ pair are superimposed on a Ramachandran map (gray) of the alanine dipeptide. The 14 populated mesostates are: {A,G,M,R,L,F,E,K,Q,J,P,O,I,o}, and only the L mesostate is fully allowed. The fractional occupancy of each mesostate is listed in Table 1. The Ramachandran map was computed by generating 150,000 independent conformations within each mesostate by using backbone-dependent values for the N–C_α–C′ bond angle (Table 1).

For each mesostate, Γ independent conformations were generated, of which Γ_A are free of steric clashes. Γ and Γ_A define an acceptance ratio, Λ = Γ_A/Γ, where 0 ≤ Λ ≤ 1. Values of Λ for each of the 14 mesostates are shown (Table 1, Fig. 1); only mesostate L, which includes φ,ψ values for canonical parallel and antiparallel β-strands, has unit weight.

Table 1.

Parameters for alanine dipeptide mesostates

Mesostate	Unnormalized mesostate weights Λi	Standard deviations Δi of unnormalized mesostate weights from their mean values Λi	Mesostate dependent τ angles used in all calculations	Observed φ, Ψ-dependent τ values (18)
A	0.38	0.0016	107.6°	110°
G	0.74	0.0010	108.0°	110°
M	0.45	0.0012	110.5°	110°
R	0.74	0.0011	110.5°	110°
L	1.00	0	110.5°	109°
F	0.52	0.0014	108.5°	108°
E	0.50	0.0015	108.3°	108°
K	0.99	0.0003	110.5°	110°
Q	0.25	0.0016	110.5°	110°
J	0.75	0.0010	113.8°	113°
P	0.34	0.0013	113.8°	113°
O	0.61	0.0014	111.5°	112°
I	0.74	0.0014	111.8°	112°
o	0.36	0.0013	111.5°	113°

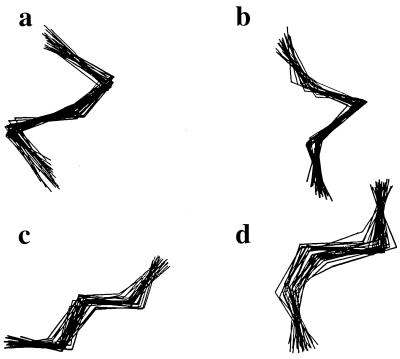
Polypeptide chain conformations are described by a string of mesostates. Every mesostate string represents a collection of highly similar sterically allowed conformers, like the solution set of an NMR structure (Fig. 2). By using the mesostate description, exhaustive counting of allowed conformations becomes tractable.

Figure 2.

“Blurograms” of four mesostate strings in chains of length n = 5: (a) OOOOO, (b) PPPPP, (c) LLLLL, and (d) IoJOP. Within a given mesostate string, sterically allowed conformers are structurally similar, like an NMR solution set. For each string illustrated here, 30 sterically allowed conformers were selected at random and superimposed.

A polyalanine chain of length n can be represented in 14ⁿ mesostate strings, spanning the complete set of conformational possibilities. The computed mesostate weights (Table 1) were used in biased Monte Carlo sampling (11) to estimate the number of allowed conformations in mesostate strings for chains of length two to seven. For a polyalanine chain of length n, enumeration of Γ conformations within a mesostate string should lead to at most Γ_P sterically allowed conformers, where Γ_P = Γ ∏_i Λ_i, and each Λ_i is obtained from Table 1. If the isolated-pair hypothesis is valid, then Γ_A = Γ_P, and enumeration is not required. Otherwise, Γ_A < Γ_P, and it is sufficient to generate Γ_P conformers, so long as individual mesostate φ,ψ values are sampled from allowed regions in an alanine dipeptide (Fig. 1).

Favorable intrachain interactions, such as backbone hydrogen bonds (12–14), stabilize chain conformations. The number of hydrogen bonds, ν, in every allowed conformation of a mesostate string is counted; each is assigned a value of ɛ ≤ 0 (in kcal/mol). The unnormalized Boltzmann weight can be written as: ∑_v=0^v_maxg_vⁱ exp(−βvɛ), where g_vⁱ is the number of conformations in mesostate string i with v hydrogen bonds; β = 1/(RT) is the temperature parameter and R the universal gas constant.

Methods

Hard-Sphere Radii and Contact Distances.

Values for hard-sphere contact distances in this work (Table 2) are similar to literature values (15, 16). A steric clash exists between two atoms when their contact distance is less than the hard-sphere contact distance. Distances between all pairs of atoms separated by four or more bonds were screened for violations, with allowance made for closer contact between hydrogen-bonded atoms.

Table 2.

Hard-sphere contact distances^*

	N	C(sp3)	C(sp2)	O	HN	H
N	2.57 Å	2.85 Å	2.71 Å	2.57 Å	2.32 Å	2.32 Å
				(2.33 Å)
C(sp3)		3.14 Å	2.99 Å	2.85 Å	2.52 Å	2.52 Å
C(sp2)			2.85 Å	2.71 Å	2.38 Å	2.38 Å
O				2.57 Å	2.32 Å	2.32 Å
					(1.71 Å)
HN					1.90 Å	1.90 Å
H						1.90 Å

^*All contact distances were obtained from Hopfinger (16) and softened by a factor of 0.95. Values in parentheses were used when the atoms in question are in a hydrogen bond. 

Mesostate-Dependent N–C_α–C′ Bond Angles.

All bond lengths, bond angles, and peptide torsion angles (ω) were held fixed at recommended values (Table 3). The recommended value for the N–C_α–C′ bond angle (τ) is 110.5° (17). However, the τ angle often deviates from this value, allowing proteins to populate φ,ψ regions that would be otherwise disallowed, as shown by Karplus (18). Moreover, it has also been shown that this deviation is coupled to the backbone conformation (18, 19). Therefore, we use φ,ψ-dependent τ values (Table 1), which were chosen to simultaneously optimize sterically allowed regions and continuity between adjacent mesostates (Fig. 1). Our optimized values (Table 1, column 4) are in good agreement with those observed in protein structures (Table 1, column 5).

Table 3.

Bond-length and bond-angle values for polyalanine chains^*

Atom name	Atom description	Bond type	Bond length, Å	Angle type	Bond angle
C(sp3)	sp3 carbon atom	C(sp3)–C′	1.525	H–C(sp3)–C′	109.6°
C′	Peptide group carbonyl carbon	H–C(sp3)	1.08	C(sp3)–C′–N	116.2°
O	Peptide group carbonyl oxygen	C′–O	1.231	O–C′–C(sp3)	120.5°
N	Peptide group amide nitrogen	N–C′	1.329	O–C′–N	123.3°
Cα	Backbone α carbon	N–H	1.008	C′–N–H	119.15°
H	Hydrogen atom	N–Cα	1.458	C′–N–Cα	121.7°
		Cα–C(sp3)	1.521	N–Cα–C(sp3)	110.4°
		C–C′	1.525	H–C(sp3)–Cα	109.6°
		N–C(sp3)	1.458	C(sp3)–Cα–C′	110.5°
				Cα–C′–O	120.5°
				Cα–C′–N	116.2°
				C′–N–C(sp3)	121.7°
				N–C(sp3)–H	110.0°
				H–N–C(sp3)	119.15°
				H–C(sp3)–H	109.6°

^*Adapted from ref. 17. The torsion angle of the peptide unit is fixed at ω = 179.5°. See Table 1 for N–C_α–C bond angles (τ). 

Identifying Hydrogen Bonds.

The only possible hydrogen bonds in polyalanine are between donors and acceptors separated by at least one residue in sequence. Geometric criteria for hydrogen bond identification are identical to those used for protein structures (20). Each donor or acceptor atom is allowed to participate in only one hydrogen bond, and the maximum number of backbone hydrogen bonds in a chain of length n is n − 1.

Validating the Isolated-Pair Hypothesis.

Γ conformations were generated within each mesostate string, and the number allowed, Γ_A, was counted. If the isolated-pair hypothesis holds, then Γ_A ≈ Γ_expected = Γ ∏_i Λ_i, where the Λ_i are from Table 1. Conversely, if Γ_A < Γ_expected, then the isolated-pair hypothesis fails.

Consider the ratio ρ = Γ_A/Γ_expected. If ρ ≠ 1, then the isolated-pair hypothesis fails, unless the value of this ratio is confounded by sampling error. The latter possibility was tested by determining whether ρ falls within a suitable error interval, bounded above and below by the variances of mesostate weights, Δ_i (from Table 1). Two numbers were calculated: Γ_U = Γ ∏_i=1ⁿ (Λ_i + Δ_i) and Γ_L = Γ ∏_i=1ⁿ (Λ_i − Δ_i). Γ_U > Γ_expected > Γ_L and ρ_U < ρ_expected < ρ_L, where ρ_U = Γ_A/Γ_U and ρ_L = Γ_A/Γ_L. If ρ_L > 1, the isolated-pair hypothesis is valid.

Results

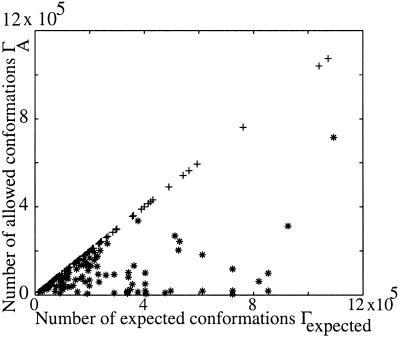
The isolated-pair hypothesis is valid for any combination of the nine mesostates surrounding the extended (i.e., β-strand) region of φ,ψ space—{A,G,M,R,L,F,E,K,Q}—as illustrated in Fig. 3. However, even in chains as short as five residues, the isolated-pair hypothesis fails for any combination of the remaining five mesostates, situated near contracted regions of φ,ψ space—{J,P,O,I,o}—as illustrated in Fig. 3. Mixed strings, comprised of mesostates taken from both sets, with at least two consecutive residues from the contracted region, also violate the hypothesis.

Figure 3.

Testing the isolated pair hypothesis. The 14 populated mesostates were subdivided into two sets: (a) {A,G,M,R,L,F,E,K,Q} and (b) {J,P,O,I,o}. The isolated-pair hypothesis holds only for higher-order conformations derived from set a. In the experiment illustrated, 200 mesostate strings of length n = 5 were generated, half using random combinations of letters chosen from set a, the other half using random combinations of letters from set b. For each string, 1.75 × 10⁶ independent conformations were generated. The number of conformers expected, Γ_expected, is plotted against the number allowed, Γ_A, for the 100 strings in sets a [+] and b [*]. The correlation coefficient between expected and allowed conformations is 0.99 in set a and 0.3 in set b.

Length Scale of Local Effects.

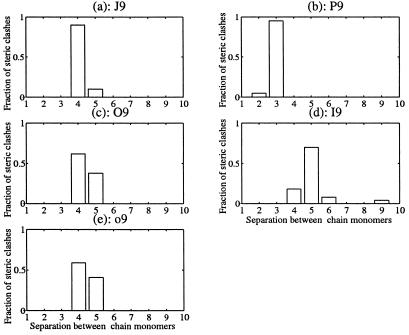
This result raises questions about the conventional polymer definition of a local interaction for polypeptides. In polymer theory, contacts are classified as either local or nonlocal. Local contacts are limited to nearest-chain neighbors; all others are, by definition, nonlocal (7). The classification is a natural one if each φ,ψ pair is independent (3). However, it is inappropriate here because the isolated-pair hypothesis is not general, as shown above. Only nearest-neighbor contacts are possible in an alanine dipeptide. If systematic steric clashes extend between monomers situated at i ± 2, i ± 3, i ± 4, i ± 5, … , i ± x along the linear chain, then local interactions extend beyond nearest-neighbor boundaries. This is exactly the case for the mesostate strings that invalidate the isolated-pair hypothesis. Fig. 4 shows the fraction of non-nearest-neighbor steric clashes as a function of monomer separation in a 9-mer, for conformations in polyJ, polyP, polyO, polyI, and polyo mesostate strings. Almost all non-nearest-neighbor clashes are between monomers at [i, i + 3], [i, i + 4], [i, i + 5], and [i, i + 6]. As a general rule, when two or more mesostates are from the set {J,P,O,I,o}, there are fewer allowed conformations than predicted by the product of independent isolated pairs (i.e., by the product of weights in Table 1).

Figure 4.

Non-nearest-neighbor steric clashes involving the five contracted mesostates in strings of length n = 9: (a) J9, (b) P9, (c) O9, (d) I9, and (e) o9. For each mesostate string, 2 × 10⁷ independent conformers were generated. The fraction of non-nearest-neighbor steric clashes (a proper superset of the steric map for an alanine dipeptide) is plotted as a function of separation between chain monomers. For example, approximately two-thirds of the steric clashes in α helices (O₉) are between residues at sequence separations of i and i + 4, an intuitively reasonable result in an α helix, which has 3.6 residues per helical repeat. Similarly, most of the steric clashes in 3₁₀ helices (P₉) are between residues at separations of i and i + 3.

Steric Clashes in Helical Conformers.

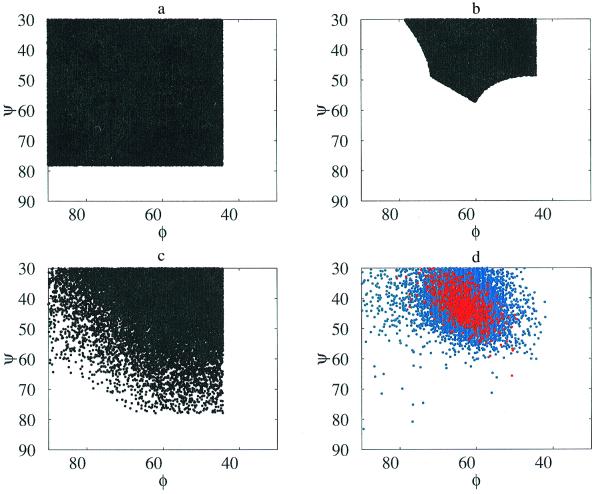
Helical conformations were explored to illustrate the effect of systematic non-nearest-neighbor steric clashes. In detail, conformations accessible to the polyO (i.e., helical) mesostate string were enumerated in N-Ac-Ala₉-N′-methylamide. In four separate experiments, values for the central residue of this peptide were varied uniformly over mesostate O (Fig. 1), while the remaining eight residues were held fixed within each quadrant of this mesostate: (i) (−78°, −67°); (ii) (−78°, −42°); (iii) (−53°, −67°), or (iv) (−63°, −45°). The values assigned in experiment iv are those of an ideal helix (21). If the central residue is independent of its chain neighbors, the distribution of allowed values for this φ,ψ pair resembles the alanine dipeptide map, Fig. 5a. In fact, no sterically allowed conformers were found in three of the four experiments, i–iii. In experiment (iv), steric constraints imposed by chain neighbors in an ideal helix limit the central residue to a small subset of the alanine dipeptide map φ,ψ values (Fig. 5b). A generalized version of these experiments (i–iv) was also performed, in which all φ,ψ values were varied independently for a 9-mer in a completely unrestricted polyO mesostate. Some of the previously proscribed φ,ψ values in the central residue—disallowed in a hydrogen-bonded helix with good geometry—are recovered by compensatory conformational changes in one or more of the other residues. Nevertheless, conformational restrictions still remain, as seen in Fig. 5c. For comparison, Fig. 5d shows the distribution of O mesostate φ,ψ values in 10,879 nonglycine, nonproline residues obtained from high-resolution protein structures. The observed distribution in Fig. 5d is qualitatively similar to that of a central residue in a well-formed helix (Fig. 5b), and unlike that of the allowed region for mesostate O in a Ramachandran map (Fig. 5a). Finally, we repeated Flory's original experiment (3), in which all residues in the 9-mer except the central one are fixed in trans [i.e., (φ_k,ψ_k) ≡ (−180°, 180°), ∀ k ≠ 5], and all allowed values for (φ₅,ψ₅) are sampled. Confirming Flory's result, the distribution is identical to the Ramachandran map of Fig. 1. Clearly, the isolated-pair hypothesis holds in the limited region of φ,ψ-space explored by Flory's experiment, but it is invalid for polypeptide chains in general.

Figure 5.

Distribution of allowed helical φ,ψ values in environments of interest: (a) the O mesostate in an alanine dipeptide; (b) the O mesostate in the central residue of Ac-Ala₉-N′-methylamide, with other residues held fixed at (−63°, 45°); and (c) the central residue of Ac-Ala₉ -N′-methylamide, with all residues allowed to vary uniformly within the O mesostate. In the 9-mer, the allowed region is winnowed substantially by higher-order local steric effects not present in an alanine dipeptide (b). Such effects persist, even when the 9-mer is allowed to relax (c). For comparison, the distribution of O mesostate φ,ψ values for all non-glycine, non-proline residues from 236 proteins of known structure (39) is shown in d. The 10,879 residues are from the December 1998 release of PDB_Select (40). A subset of these database residues was excised from the middle of 9-mers of polyO mesostate strings (shown in red); they cluster tightly around canonical α-helical φ,ψ values. The overall distribution in d is a subset of a relaxed polyalanine peptide constrained to the O mesostate (c), whereas the points in red are a subset of allowed values in a canonical α helix (b).

All-or-None Behavior.

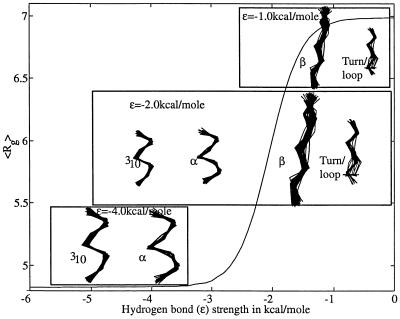
Mesostate string Boltzmann weights were used to address questions about conformational entropy and counterbalancing enthalpy. Specifically, we calculated the mean radius of gyration, <R_g>, as a function of intrachain hydrogen bond strength, ɛ. The radius of gyration is a useful measure that distinguishes between contracted and extended chains. Changing ɛ mimics changes in solvent conditions. As ɛ becomes increasingly negative, intrachain interactions are strengthened, akin to a move toward poor solvent (22, 23). Results are summarized in Fig. 6. Notably, even short polyalanine chains exhibit two-state behavior (Fig. 6); intermediate states are only marginally populated. The two predominant states are a set of extended conformations, favored when chain entropy dominates (weak hydrogen bonding), and a set of contracted conformations, favored when internal energy dominates (strong hydrogen bonding). This behavior resembles the cooperative all-or-none transitions seen in protein folding (24).

Figure 6.

Mean radii of gyration, <R_g>, as a function of hydrogen bond strength, ɛ, for polyalanyl a chain of length n = 7. The mean radii of gyration used here track with other thermodynamic averages of experimental interest. All behave in a discernable “two-state manner,” with contracted conformers favored at stronger hydrogen bond strengths and extended conformers favored at weaker hydrogen bond strengths. Mean radii are calculated from Boltzmann-weighted contributions over all mesostate strings for given values of n and ɛ, i.e., 〈R_g〉 (ɛ) = ∑_i=1¹⁴ⁿ R_gⁱρ_i(ɛ). Here R_gⁱ is the average radius of gyration for allowed conformers in mesostate string i, and ρ_i(ɛ) is the Boltzmann weight of mesostate string i with hydrogen bond strength = ɛ and T = 300 K. The structures that make significant contributions to the Boltzmann-weighted population at key positions along the two-state curve are shown. When hydrogen bonds are strong (ɛ = −4.0 kcal/mol), 3₁₀ helices dominate, although some α helix is also present. At the midpoint (ɛ = −2.00 kcal/mol), other conformations are also seen, including type II turns (turn/loop) and extended conformers (β). When hydrogen bonds are weak (ɛ = −1.0 kcal/mol), extended conformers predominate.

To annotate the all-or-none transition, structures were sampled at three representative points (ɛ = −4.0 kcal/mol, ɛ = −2.0 kcal/mol and ɛ = −1.0 kcal/mol) along the curve of <R_g> vs. ɛ for n = 7 (Fig. 6). The set of structures shown in Fig. 6 account for more than 90% of the Boltzmann-weighted population at the chosen values of ɛ. At ɛ = −4.0 kcal/mol, the chain is mostly 3₁₀ helix, with some α-helix. At the midpoint, ɛ = −2.0 kcal/mol, extended structures begin to contribute significantly, together with type II and type III turns.

Effective Size of Conformational Space.

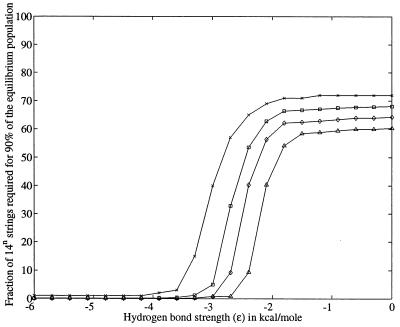
As shown in Fig. 6, the landscape is dominated by two distinct sets of highly similar conformers. To further explore this phenomenon, the fraction of mesostate strings (total = 14ⁿ) required to account for at least 90% of the equilibrium population was calculated as a function of hydrogen bond strength (Fig. 7). For strong hydrogen bonds (small ɛ), the population is determined primarily by a very small number of helical mesostate strings, and the range of ɛ values for which these states dominate increases with chain length. When helical states are not favored (as ɛ→0), the number of states required to account for 90% of the equilibrium population increases sharply and then plateaus. The plateau value decreases as chain length increases. Notably, the effective size of conformational space is winnowed as chain length increases, even when the dominant contribution to equilibrium is entropic (as ɛ→0). This behavior is not anticipated by the isolated-pair hypothesis.

Figure 7.

Fraction of the 14ⁿ mesostate strings needed to account for at least 90% of the Boltzmann-weighted equilibrium population, plotted as a function of hydrogen bond strength, ɛ, for chains of length n = 3 (x), 4 (square), 5 (diamond), and 6 (triangle). Each data point was calculated as follows: for a chain of length n and energy ɛ, the normalized Boltzmann weight of a given mesostate string is w_i(ɛ), with 0 < w_i(ɛ) ≤ 1. The sum of w_i(ɛ) over all 14” such strings is unity. We compute a fraction f(ɛ), 0 < f(ɛ) ≤ 1, such that the sum over 14ⁿ f(ɛ) mesostate strings is ≥ 0.9. In detail, strings are sorted in descending order by population and then summed until a threshold of 0.9 is attained. This fraction, represented as a percentage, is plotted as a function of ɛ. The figure shows that polyalanyl chains visit only two distinct regions in conformational space: a smaller island of contracted conformers and a larger island of extended conformers as shown in Fig. 6. The former can be stabilized by favorable backbone interactions, whereas the latter cannot. Entropy favors the larger island. However, the energy of hydrogen bonds is weighted exponentially, and their contributions to equilibrium quickly outpace entropy. Thus, the smaller island is populated preferentially as either chain length or hydrogen bond strength increases.

In summary, the thermodynamic properties of short polyalanine chains exhibit all-or-none behavior, like a two-state protein-folding transition (Fig. 6). Increased chain length leads to a significant reduction in the number of structured alternatives available to the chain, with a corresponding reduction in the effective size of conformational space (see Fig. 7 at ɛ = 0). In particular, several φ,ψ combinations from allowed regions of the Ramachandran map for a dipeptide become disallowed in longer chains. As a consequence, the entropic price required to constrain the backbone to helical values (within polyO) decreases with chain length, thereby reducing the hydrogen bond strength needed to populate helical conformers. This trend is evident in the family of curves in Fig. 7, where the transition midpoint shifts to the right as n = 3, 4, 5, 6. As chains approach the length of protein-sized helices, ≈12 residues (25), we estimate that the transition midpoint will be around −1.0 kcal/mol, approximating the experimental value of the peptide hydrogen bond in water (26).

Discussion

Using a dipeptide model, Ramachandran and coworkers (15, 19) described an effective upper limit on the conformational possibilities of a φ,ψ pair. Their model has been validated repeatedly in subsequent experimental work. Backbone dihedral angles in proteins of known structure lie well inside the allowed regions of a φ,ψ map, to the extent that the Ramachandran plot is now used routinely to assess the quality of x-ray structures (27).

Despite this success (28), hard-sphere models are seldom used in theoretical work on protein structure. The issue is one of scale. If each φ,ψ pair is independent (3), constraints that sterics impose on the dipeptide are insufficient to limit the conformations accessible to a peptide backbone, even a short one.

In contrast, our analysis of short polyalanyl chains shows that backbone conformations are limited by additional, systematic steric clashes, a superset of those seen in a dipeptide map. This conclusion is supported by results from accurate enumeration of accessible conformations. To count, we use a device in which φ,ψ space is tiled into discrete bins, called mesostates. Conformations of longer chains are described by a string of mesostates. Only two types of interactions are used: one repulsive, the other attractive. Each is constructed to map a continuous variable into a discrete range; a given distance between two atoms is either allowed or disallowed, and a potential hydrogen bond between a donor and acceptor is either made or broken. This approach enables conformations for short polyalanyl chains to be enumerated exhaustively.

There are many shortcomings in the weighting scheme used here. Repulsive interactions are well represented, but attractive interactions are lumped into a single crude approximation. The main issue pertaining to repulsive effects is the choice of hard-sphere radii. Our radii are among the most permissive, close to the lower limits set by Ijima et al. (29). Also, the N–C_α–C′ bond angles are strained slightly to accommodate experimentally confirmed conformations at the edge of allowed regions (18, 30).

Regarding attractive interactions, we ignore explicit peptide-solvent contributions, which are known to be important (31–34), our hydrogen-bonding criteria are incomplete (14, 35), and the mesostate description would be questionable if used in conjunction with a distance-dependent potential, because conformers within a given mesostate string can have similar intrachain contacts but dissimilar intramolecular energies.

Despite these shortcomings, the phenomenological model used here allows us to address the central thermodynamic question in protein folding: How can a polypeptide chain overcome conformational entropy and fold to its native state (2)? Conformational entropy is estimated by exhaustive enumeration of sterically allowed conformations. Further, the attractive interaction energy (ɛ), albeit crude, is sufficient to construct a phase diagram, akin to a folding transition.

A coherent picture emerges from these considerations. Polypeptide backbones form helices when intrachain interactions are sufficiently strong, as is the case in water (26) or water/trifluroethanol mixtures (36). Short chains fluctuate about canonical 3₁₀ and α helices, but fluctuations are reduced in longer chains, which are helical over a wider range of ɛ values. Outside the helical regime, the backbone populates extended conformations preferentially. Thermodynamic averages for these chains exhibit the characteristic two-state behavior seen in natural proteins (37, 38). The two states are ensembles of either energetically favored contracted hydrogen-bonded helical structures or entropically favored extended strand-like structures (Fig. 6). Intermediate constructs are only marginally populated.

Since its inception, the isolated-pair hypothesis has played a pivotal role in helix–coil theories and protein folding. In helix–coil theory, the entropic cost of helix formation increases as the volume of the accessible coil region increases. It is this entropic cost that sets the expected length of stable helix under given solvent conditions. In water, stable short helices would be strongly disfavored. Similarly in protein folding, as the number of conceivable states accessible to the unfolded protein escalates, so does the entropic cost of populating one region uniquely. In general, the notion that allowed conformers grow exponentially with chain length has fostered the popular view that accessible conformational space is vast, and the corresponding energy landscape is rugged.

An ongoing challenge to theorists is to explain the mechanism by which this entropic cost is paid. What energetic factors account for the surprisingly short length of an average protein-sized helix, ≈12 residues (25)? If conformational space is vast, as believed, how can a protein find its native pinhole in biological real time while avoiding metastable traps en route (1)? Yet protein-sized helices can be stable in water (9), and proteins do fold.

The foregoing analysis demonstrates these problems are more conceptual than actual. In helix–coil theory, the volume of the coil region is much smaller than predicted by the isolated pair hypothesis, lowering the entropic barrier for helix formation. In protein folding, most conceivable states are inaccessible, winnowing the effective size of conformational space and biasing the unfolded molecule toward organized structure (10). We anticipate that both theory and experiment are poised to provide further insight into the unfolded state of proteins.